Impedance Decoupling in DC Distributed Systems to Maintain Stability and Dynamic Performance

Abstract

DC distributed systems are highly reliable and efficient means of delivering DC power or adopting renewable energy resources. However, DC distributed systems are prone to instability and dynamic performance degradation due to the negative incremental input impedance of DC-DC converts. In this paper, we propose a generic method to eliminate the impact of the negative input impedance on DC systems by shaping the source output impedance such that its bode-plot is restricted in the area that is contained below the product of the source’s duty ratio and its characteristic impedance. The performance deterioration originates whenever the output impedance of the source exceeds, in magnitude, the input impedance of the load converter due to deficiency in stability margins. Hence, confining the impedance in the proposed region helps decouple the interaction between the converters and preserve their own dynamic performances. The proposed method was proven by analytical analysis, time-based simulation, and practical experiments. All of their outcomes were in agreement, proving the effectiveness of the proposed method in preserving the dynamic performance of distributed systems.

1. Introduction

DC distributed power systems are a remarkable application of power electronics and include a wide range of applications, such as in DC microgrids, motor drive systems, hybrid vehicles, aircrafts, ships, submarines, and satellites [1,2]. Most such applications are size-limited, so they require highly reliable power sources with high efficiency and power density based on DC distributed systems, to fulfill their power requirement [3]. A typical distributed DC system consists of a DC-DC load converter connected in series with a DC-DC source converter or an input filter, as illustrated in Figure 1 [4], which is also referred to as a cascaded DC system [5]. Each converter in cascaded systems represents a module that can be designed individually and then integrated with the rest of the components of the system [6]. Thus, cascaded systems are modular, scalable, and capable of meeting various load requirements, which adds to their attractiveness.

Despite these appealing characteristics of cascaded DC systems, they are susceptible to dynamic performance degradation and instability problems. These problems arise because the load converter tightly regulates its output current or voltage, regardless of the voltage or current variations at the DC bus [7,8,9]. As a consequence, the load converter supplies its load with constant power, so the load converter acts as a power sink attached to the source [10,11]. The small-signal ac analysis of DC-DC converters shows that they have negative input impedance within the bandwidth of their controllers. Therefore, the source converter or the input filter sees the load converter as a negative impedance [12], whereas they are designed to supply non-negative resistive loads [13].

The performance of cascaded systems was first investigated by R.D. Middlebrook in the 1970s. He studied a cascaded system that consisted of a load converter with an input filter. His study concluded that adding the input filter reduces the relative stability margins of the load converter. If the output impedance magnitude ($|Z_o\left(s\right)|$) of the filter exceeded the input impedance of the load ($|Z_{in}\left(s\right)|$), the system would become unstable [14]. On the other hand, $Z_o\left(s\right)$ represents the closed-loop output impedance, if the source was a DC-DC converter. The ratio of the impedances is referred to as the minor loop gain ($T_m\left(s\right)=Z_o\left(s\right)/Z_{in}\left(s\right)$), and plays an important role in stability analysis of the overall system.

Several approaches and criteria have been proposed in the literature to ensure stability and proper dynamic performance of cascaded systems. R.D. Middlebrook proposed a criterion that confines the polar plot of $T_m\left(s\right)$ within a circle with a radius of $1/GM$ in order to ensure stability without degradation in the dynamic performance, where $GM$ is the gain margin of $T_m\left(s\right)$ [14]. The criterion is artificially stringent [8]; it requires high capacitance at the DC bus to be fulfilled. Therefore, other criteria such as gain margin phase margin (GMPM) [15], the opposing argument [16], Energy Source Analysis Consortium (ESAC) [17], three-steps [18], and passivity-based [19] were introduced to relax the conservativeness of the Middlebrook criterion, or to expand its approach to cover a load system that consists of multiple load modules. All criteria are sufficient to ensure stability and/or dynamic performance [20]. Applying the Nyquist criterion to $T_m\left(s\right)$ is the only necessary and sufficient condition to ensure both stability and dynamic performance, because all criteria presume that every converter in the system is standalone stable except the three-steps criterion, which defines its minor loop gain differently. Since every converter is standalone stable, the polar plot of $T_m\left(s\right)$ must not encircle ($-1,j0$)—in the complex plane— in order to ensure stability [21].

The Middlebrook, opposing argument, GMPM, and ESAC are design-oriented criteria [8]. They assume that the output impedance of the source converter is known; hence, the load system must be designed accordingly [22]. This assumption limits the modularity feature of cascaded systems because the dynamic performance would not be guaranteed for any other load converters. Thus, passive damping methods were introduced to damp cascaded systems using bulky passive components connected to the DC bus [7]. Nevertheless, they incur extra power loss, and increase both the system size and weight. As a result, the efficiency, reliability, and power-density of the cascaded systems are compromised.

In order to tackle the drawbacks of passive damping methods, active damping methods have become a popular substitute. The system stability and/or dynamic performance are preserved by modifying the control loop of the source or the load converters. These methods do not typically incur extra power losses; however, some of them reduce the power-density of cascaded systems, such as the solution proposed in [23]. Several noticeable limitations or disadvantages are observed in the proposed solutions in the literature, which can be classified into ensuring stability with poor dynamics (i.e., long settling time) [24], limiting the controller application to a single converter topology (e.g., buck converters) [25,26], and inability to handle multiple converter load systems [27,28,29,30].

In this paper, we propose an active damping method that preserves both the stability and dynamic performance of cascaded systems. The approach is compatible with any minimum-phase DC-DC converter configuration and with any linear feedback control scheme. It is based on shaping the output impedance of the source converter such that its bode-plot is consistently less than the region below the product of the source characteristic impedance and its duty ratio. In addition, a quantifiable approach is proposed to shrink the impedance in that area in order to preserve the dynamic performance without artificial conservativeness.

This paper discusses the dynamic performance of cascaded systems in Section 2. Then, the proposed controller is demonstrated in Section 3. Section 4 illustrates the proposed reshaping method of the source output impedance. Next, a prototype cascaded system is analytically discussed in Section 5, and the analytical results are validated by simulations and experiments in Section 6. Finally, Section 7 sums up the main conclusions and outcomes.

2. Analysis of Cascaded System Dynamics

2.1. Dynamic Performance

The impact of the negative input impedance on cascaded systems can be studied using the canonical model [12] of a single-load-single-source, as shown in Figure 1. For such a system, the input-to-output voltage relationship can be described as

$${\displaystyle \frac{{\tilde{v}}_o}{{\tilde{v}}_{in}}}={\displaystyle \frac{G_{vg,s}{G}_{vg,L}}{(1+T_S)(1+T_L)(1+T_m)}}$$

(1)

where ${\tilde{v}}_{in}$ is the input voltage of the source converter, ${\tilde{v}}_o$ is the output voltage of the load converter, and $G_{vg,s}$ and $G_{vg,L}$ are the input-to-output voltage transfer functions of the source and the load converters, respectively. $T_S$ and $T_L$ denote the voltage loop gains of the source and load converters, respectively. Interconnecting the converters adds more poles to the system due to the added term ($1+T_m$) in Equation (1), which alters the overall dynamic response of the system [31]. According to Equation (1), if $|T_m|\ll 1$, each converter of the cascaded system will operate as it was individually designed. Hence, the Middlebrook criterion mathematically describes the change in the load converter control-to-output transfer function ($G_{vd,L}$) as:

$$G_{vd,L}^S=G_{vd,L}{\displaystyle \frac{1+\stackrel{\stackrel{T_m}{︷}}{{\displaystyle \frac{Z_o}{Z_{in}}}}}{1+{\displaystyle \frac{Z_o}{Z_{in,o}}}}}$$

(2)

where $G_{vd,L}^S$ is the source-affected control-to-output transfer function of the load, and $Z_{in,o}$ is the load input open-loop impedance. In order to minimize the loading impact and eliminate the source-load dynamic coupling,

$$\left\{\begin{array}{c}|Z_o|\ll |Z_{in}|\hfill \\ |Z_o|\ll |Z_{in,o}|\hfill \end{array}\right.$$

(3)

should hold for the entire range of frequency according to the Middlebrook criterion. Consequently, the extra poles in (1) will be eliminated and $G_{vd,L}^S\approx G_{vd,L}$. Thus, each converter will operate as initially designed [32]. The terms $|Z_o/Z_{in}|$ and $|Z_o/Z_{in,o}|$ are approximately equal to each other within the load controller bandwidth ($f_{L\_\mathrm{BW}}$) [33,34]. Diminishing $|T_m|$ would preserve the dynamic performance of the load converter.

2.2. Impedance Interaction and Instability

$T_m$ is crucial to ensuring both stability and dynamic performance. In order to ensure the stability of the system, ($1+T_m$) in (1) must have no zeros in the right-half-plane (RHP). These undesirable zeros would occur [20] if and only if:

$$\left\{\begin{array}{c}\left|{\displaystyle \frac{Z_o}{Z_{in}}}\right|\ge 1\hfill \\ \phi \left(Z_o\right)-\phi \left(Z_{in}\right)\ge {180}^{\circ }\hfill \end{array}\right.$$

(4)

where $\phi \left(Z_o\right)$ and $\phi \left(Z_{in}\right)$ are the phase angles of source output and load input impedances, respectively. Figure 2 shows typical plots of $Z_o$ and $Z_{in}$ for $f_{L\_\mathrm{BW}}=1.60$ kHz. Any impedance overlap that occurs within the controller bandwidth would satisfy (4) because $\phi \left(Z_{in}\right)=-{180}^{\circ }$ and $\left|Z_o/Z_{in}\right|>1$, which implies that the overall cascaded system will have unstable poles.

2.3. The Source Performance

The Middlebrook criterion was initially developed to study the impact of the input filter on the performance of DC-DC converters. Replacing the filter with a source DC-DC converter has an impact on the load converter, as described in (2). On the other hand, the loop gain of the source converter is modified by the load converter, due to the loading impact given by [32].

$$T_S^L={\displaystyle \frac{T_S}{1+T_m(1+T_S)}}$$

(5)

where $T_S^L$ is the loaded loop gain of the source converter. Similarly, diminishing $|T_m|$ would preserve the dynamic performance of the source because $T_S^L\approx T_S$. In (5), $T_S^L$ will have RHP poles if and only if $T_m$ satisfies (4).

3. The Proposed Controller

In order to preserve the dynamic performance of voltage mode controlled converters in cascaded systems, the control loop should not change the relationship between the reference voltage (${\tilde{v}}_{ref}$) and the output voltage of the converter (${\tilde{v}}_o$), so their relationship has to be preserved as

$${\displaystyle \frac{{\tilde{v}}_o}{{\tilde{v}}_{ref}}}={\displaystyle \frac{G_c{G}_{PWM}{G}_{vd,s}}{1+G_c{G}_{PWM}{G}_{vd,s}}}={\displaystyle \frac{T_S}{1+T_S}}$$

(6)

where $G_c$ is the controller transfer function, and $G_{PWM}$ is the pulse-width modulator. In addition, the controller must be capable of actively shaping the output impedance in order to eliminate the impedance interaction between the source and the load converters. Thus, we used the controller topology that is introduced in [35,36], which modified a conventional control scheme, as in Figure 3a, to the controller that is shown in Figure 3b. Then, we modified it to comply with our proposal.

The output voltage of a standalone converter implementing this controller (displayed in Figure 3b) is expressed as:

$${\tilde{v}}_o={\tilde{v}}_{ref}\frac{T_S}{1+T_S}-{\tilde{i}}_o{\displaystyle \frac{Z_o}{1+H{G}_{PWM}{G}_{vd,s}}}+{\tilde{v}}_{in}\frac{G_{vg,s}}{(1+H{G}_{PWM}{G}_{vd,s})(1+T_S)}$$

(7)

where H is the transfer function that is used to shape $Z_o$, and $Z_o$ is derived using the open-loop output impedance ($Z_{ol}$) as $Z_o=Z_{ol}/(1+T_s)$. The variations in the input voltage (${\tilde{v}}_{in}$) can be ignored, because the source voltage is assumed to be ideal. It is noteworthy that we aim to preserve (7), because once the source converter is loaded, the dynamics of the system will be changed by substituting (5) into (7), resulting in the following:

$${\tilde{v}}_o={\tilde{v}}_{ref}\frac{T_S^L}{1+T_S^L}-{\tilde{i}}_o{\displaystyle \frac{Z_o}{1+H{G}_{PWM}{G}_{vd,s}}}$$

(8)

The dynamics of the system in (6) would have been modified if $|Z_o|\ll |Z_{in}|$ is violated according to (8). In order to eliminate the interaction, we propose to shape the output impedance according to:

$$Z_{o,new}={\displaystyle \frac{Z_o}{1+\lambda }}$$

(9)

where $Z_{o,new}$ is the reshaped output impedance of the source, and $\lambda$ is a constant (its selection method is illustrated in the next section). Reducing $|Z_o|$ as proposed in (9) is challenging because ($1+H{G}_{PWM}{G}_{vd}$) in (8) is a transfer function whose magnitude should be converted into a constant that equals $1+\lambda$. Choosing $H=\lambda G_{PWM}^{-1}{G}_{vd,s}^{-1}$ is not a practical choice because the reciprocation results in a transfer function that has more zeros than poles; $G_{vd,s}$ is a strictly proper transfer function for any DC-DC converter. A transfer function of more zeros than poles is non-realistic. In control theory, such transfer functions describe non-causal systems because their current output depends on their future outcomes. To overcome this impediment, we propose to realize $G_{vd,s}^{-1}$ within a certain frequency band using low-pass filters. The transfer function of a low-pass filter ($G_F$) is described [37] as:

$$G_F={\displaystyle \frac{1}{{\left(1+\frac{s}{w_c}\right)}^{\alpha }}}$$

(10)

where $w_c$ is the cut-off frequency of the filter and $\alpha$ is a constant that dictates the order of the low-pass filter to be used. The order of the filter is chosen to ensure $\lambda G_F{G}_{PWM}^{-1}{G}_{vd,s}^{-1}$ as a strictly proper transfer function. For instance, a buck converter has two storage elements (a capacitor and an inductor), so its $G_{vd,s}$ will be of second order; $\alpha$ must be at least equal to 2. Other converters, like the minimum-phase fourth-order buck DC-DC converter [38] have four storage elements; therefore, $\alpha$ must be at least 4. Setting:

$$H=\lambda G_F{G}_{PWM}^{-1}{G}_{vd,s}^{-1}$$

(11)

and then substituting (11) in (8) changes the dominator of the impedance ($1+H{G}_{PWM}{G}_{vd,s}$) to:

$$1+\lambda G_F{\cancel{G}}_{PWM}^{-1}{\cancel{G}}_{PWM}{\cancel{G}}_{vd,s}^{-1}{\cancel{G}}_{vd,s}$$

(12)

which can be interpreted as:

$$1+\lambda \omega \le {\omega }_c$$

(13)

Thus, the output voltage of the proposed controller can be re-expressed as:

$${\tilde{v}}_o\approx {\tilde{v}}_{ref}\frac{T_S^L}{1+T_S^L}-{\tilde{i}}_o{\displaystyle \frac{Z_o}{1+\lambda }}\omega \le {\omega }_c$$

(14)

Figure 4a shows the reshaped output impedance ($Z_{o,new}$), using a low-pass filter with ${\omega }_c={10}^5$ rad/s, subjected to different values of $\lambda$. With these proposed modifications to the controller, the magnitude of the source output impedance can be precisely controlled within the filter bandwidth; however, beyond ${\omega }_c$, the magnitude of $Z_{o,new}$ consistently converges to coincide with the magnitude of $Z_o$.

Thus, in order to effectively reshape $Z_o$ such that the source and the load converters are decoupled, ${\omega }_c$ should be greater than ${\omega }_i$, as shown in Figure 4b. Otherwise the shaping will fail to improve the dynamic performance. Ultimately, the implemented controller with the proposed modifications is shown in Figure 5.

4. Impedance Reshaping for Decoupling the Source-Load Interaction

The impedance overlap in cascaded systems tends to occur in the vicinity of the peak impedance of the source converter [10]. The dynamic response of the system is compromised due to the impedance interaction around that region. The peak impedance occurs either at the cut-off frequency of the source controller ($f_{s\_\mathrm{BW}}$) due to low phase margins, or at the source resonant frequency ($f_o=1/\sqrt{LC}$) if the the bandwidth of the controller was less than the resonance frequency of the converter. In the latter case, the peaking is more severe because DC-DC converters are designed to be highly efficient, which lightly damps the converter. The peaking of the output impedance can be expressed [39] as:

$$|Z_{o,max}|={\displaystyle \frac{|Z_{ol}\left(f_{s\_\mathrm{BW}}\right)|}{\sqrt{(2-2cos\left({\varphi }_m\right))}}}{f}_{s\_\mathrm{BW}}>f_o$$

(15)

$$|Z_{o,max}|={\displaystyle \frac{|Z_{ol}\left(f_o\right)|}{1-{10}^{(-\mathsf{\Psi }/20)}}}{f}_{s\_\mathrm{BW}}<f_o$$

(16)

where ${\varphi }_m$ and $\mathsf{\Psi }$ are the phase and the gain margins of the source controller, respectively. A low gain or phase margin causes severe peaking, as depicted in Figure 6. For instance, a phase margin of ${30}^{\circ }$ adds $5.8$ dB to the output impedance, while a gain margin of 5 dB adds $7.20$ dB.

Reducing the magnitude of $Z_o$ below $Z_{in}$ to ensure stability is mathematically quantifiable because $Z_{in}$, within the load controller bandwidth, can be described as [40]:

$$Z_{in}=-{\displaystyle \frac{V_{bu{s}^2}}{P_o}}\forall f<f_{L\_\mathrm{BW}}$$

(17)

where $V_{bus}$ is the DC bus voltage, and $P_o$ is the power consumed by the load. Hence, the system will be stable as long as $|Z_o|<|Z_{in}|$. However, the system dynamic performance would still be compromised if $|Z_o\left|\cancel{\ll }\right|Z_{in}|$, so we are proposing a method to quantify (≪). The earlier mentioned criteria are used to design the load input impedance. Yet, we propose to shape the output impedance of the source converter to be confined in the region that is below the characteristic impedance of the source converter ($Z_x=D\sqrt{L/C}$), as demonstrated in Figure 7. Shrinking the impedance in the proposed region ensures the dynamic performance of the system, regardless of the attached load. The peaking is more pronounced as the relative stability margins decrease; as a result, the peak impedance will exceed the stability limit. The dynamic performance can be ensured if $|Z_{o,max}|<|Z_x|$, so $|Z_o|$ can be reduced to the proposed region of Figure 7 by dividing $Z_o$ by:

$$\rho ={\displaystyle \frac{|Z_{o,max}|}{|Z_x|}}$$

(18)

where $\rho$ is the reduction factor in the magnitude of $Z_o$, and $Z_{o,max}$ is the peak impedance of $Z_o$. Hence, equating the dominators of ($Z_o/\rho$)—which falls in the proposed region—with (9) yields:

$$\lambda =\rho -1$$

(19)

Mathematical Validation of Performance Preservation

The shaped output impedance of the source can be expressed as:

$$Z_{o,new}={\displaystyle \frac{Z_o}{\rho }}={\displaystyle \frac{Z_{o}D}{|Z_{o,max}|}}\sqrt{\frac{L}{C}}$$

(20)

As a result, the new minor loop gain ($T_m^{new}$) is given by:

$$T_m^{new}={\displaystyle \frac{Z_{o,new}}{Z_{in}}}={\displaystyle \frac{Z_{o}D}{Z_{in}\left|Z_{o,max}\right|}}\sqrt{\frac{L}{C}}={\displaystyle \frac{T_{m}D}{|Z_{o,max}|}}\sqrt{\frac{L}{C}}$$

(21)

so substituting (21) in (5) modifies $T_S^L$ to $T_S^{LR}$ as follows:

$$T_S^{LR}={\displaystyle \frac{T_S}{1+{\displaystyle \frac{T_m(1+T_S)D}{|Z_{o,max}|}}\sqrt{\frac{L}{C}}}}$$

(22)

where $T_S^{LR}$ is the reshaped loop gain by implementing the proposed shaping in (18).

In order to prove $T_S^{LR}\approx T_S$, the denominator of (22) is evaluated where $|Z_{o,max}|$ occurs, where:

$$|T_m|=|Z_{o,max}/Z_{in}|$$

(23)

$$\delta =|1+T_S|=\left\{\begin{array}{cc}\sqrt{(2-2cos\left({\varphi }_m\right))}\hfill & f_{s\_\mathrm{BW}}>f_o\hfill \\ 1-{10}^{(-\mathsf{\Psi }/20)}\hfill & f_{s\_\mathrm{BW}}<f_o\hfill \end{array}\right.$$

(24)

In addition, the characteristic equation can be rewritten using (18) as:

$$\sqrt{{\displaystyle \frac{L}{C}}}={\displaystyle \frac{|Z_{o,max}|}{\rho D}}$$

(25)

Plugging $|Z_{in}|$, (23), (24) and (25) into (22) yields:

$$T_S^{LR}={\displaystyle \frac{T_S}{1+{\displaystyle \frac{\delta }{\rho V_{bu{s}^2}}}{Z}_{o,max}{P}_o}}$$

(26)

By inspecting the second term of the denominator, the term $\delta /\left(\rho V_{bus}^2\right)\ll 1$, and hence, $1+\delta Z_{o,max}{P}_o/\left(\rho V_{bus}^2\right))\approx 1$. As a result, $T_S^{LR}\approx T_S$, which validates the proposed shaping method.

5. Theoretical Analysis

The effectiveness of the proposed solution to retain the dynamic performance of cascaded systems has been examined using a prototype that consists of two buck converters connected in series, as shown in Figure 8. The source converter tightly regulates the bus voltage at 7 V, while the load converter was designed to supply a resistive load of 16 W, with an output voltage of 4 V. $G_{PWM}$ was chosen to be 1 V${}^{-1}$. Each converter was devised to be standalone stable, as the polar plots of their voltage loop gains, $T_S$ and $T_L$, imply in Figure 9. However, cascading the converters was not possible, because the overall system would suffer from instability as impedance overlap occurred, as shown in Figure 10a.

Impedance Reshaping and Performance Improvement

In order to preserve both the stability and the dynamic performance of cascaded systems, we propose to shape $Z_o$ according to (20). The characteristic impedance of the source converter is $748.02\mathrm{m}\mathsf{\Omega }$, and the peak impedance of the source is $11.5$ dB$\mathsf{\Omega }$, which corresponds to $3.76\mathsf{\Omega }$. Thus, the resultant divisor factor $\rho$, using (18), is $14.5$, which yields $\lambda =13.5$. Using Figure 10a, ${\omega }_i$ was found to be $2.2\times {10}^3$ rad/s, so $w_c$ was set to ${10}^5$ rad/s. As buck converters have two storage elements, $\alpha$ was chosen to be 2 in order to guarantee that H is invertible. Plugging ${\omega }_c$ and $\alpha$ in (10) gives:

$$G_F={\displaystyle \frac{1}{{\left(1+{\displaystyle \frac{s}{{10}^5}}\right)}^2}}$$

(27)

so H, using (11), will be:

$$H={\displaystyle \frac{6.597\times {10}^6{s}^2+7.612\times {10}^{9}s+2.427\times {10}^{13}}{s^3+2.143\times {10}^5{s}^2+1.287\times {10}^{10}s+1.435\times {10}^{14}}}$$

(28)

As a result, the shaped output impedance of the source converter ($Z_{o,new}$) is substantially reduced compared to $Z_o$, which emphasizes the ability of the proposed method to decouple the impedances, as shown in Figure 10b.

In order to show the improvement in the dynamic performance, Figure 11 compares the unity feedback closed loop response of $T_S$ to its counterpart $T_S^{LR}$. The response of $T_S^{LR}$ closely tracks its reference response, which highlights the effectiveness of the proposed shaping to stabilize and improve the dynamic performance of cascaded systems.

6. Simulation and Experiment Case Studies

6.1. Time-Domain Simulations

The system illustrated in Figure 8 was simulated using PLECS Standalone Package (Plexim, Zurich, Switzerland) in order to evaluate the effectiveness of the proposed controller. Two test cases were carried out. The first test was conducted while the system was at the verge of instability; the load converter was supplying 8 W. Once the system reached steady state, the other 8 W load was added at $t=0.15$ s. The second test was conducted by starting the system while the load converter was supplying the 16 W in order to compare its response to the theoretical response of $T_S$.

The system equipped with the conventional controller (as in Figure 3a) was tested in order to demonstrate the impact of the negative input impedance on the system dynamics. For the first test, the system was stable at the start-up with compromised dynamic response because the settling time was $50\mathrm{m}\mathrm{s}$ compared to $20\mathrm{m}\mathrm{s}$ in Figure 11. Connecting the other 8 W destabilized the bus voltage permanently, as shown in Figure 12a. Then, the second test was run; Figure 12b shows that the system was also unstable. These tests agree with the analytical analysis, which expected the instability of the system using the conventional controller.

The system was then equipped with the proposed controller as in Figure 5 or Figure 8. The first test was conducted, and the system reached the steady state in $20\mathrm{m}\mathrm{s}$. In addition, increasing the output power by 8 W had negligible impact on the system as Figure 13a depicts. Conducting the second test, as shown in Figure 13b, shows that the system response was similar to the of $T_S$ in Figure 11, which proves the effectiveness of the proposed reshaping to stabilize and improve the dynamic performance of cascaded systems.

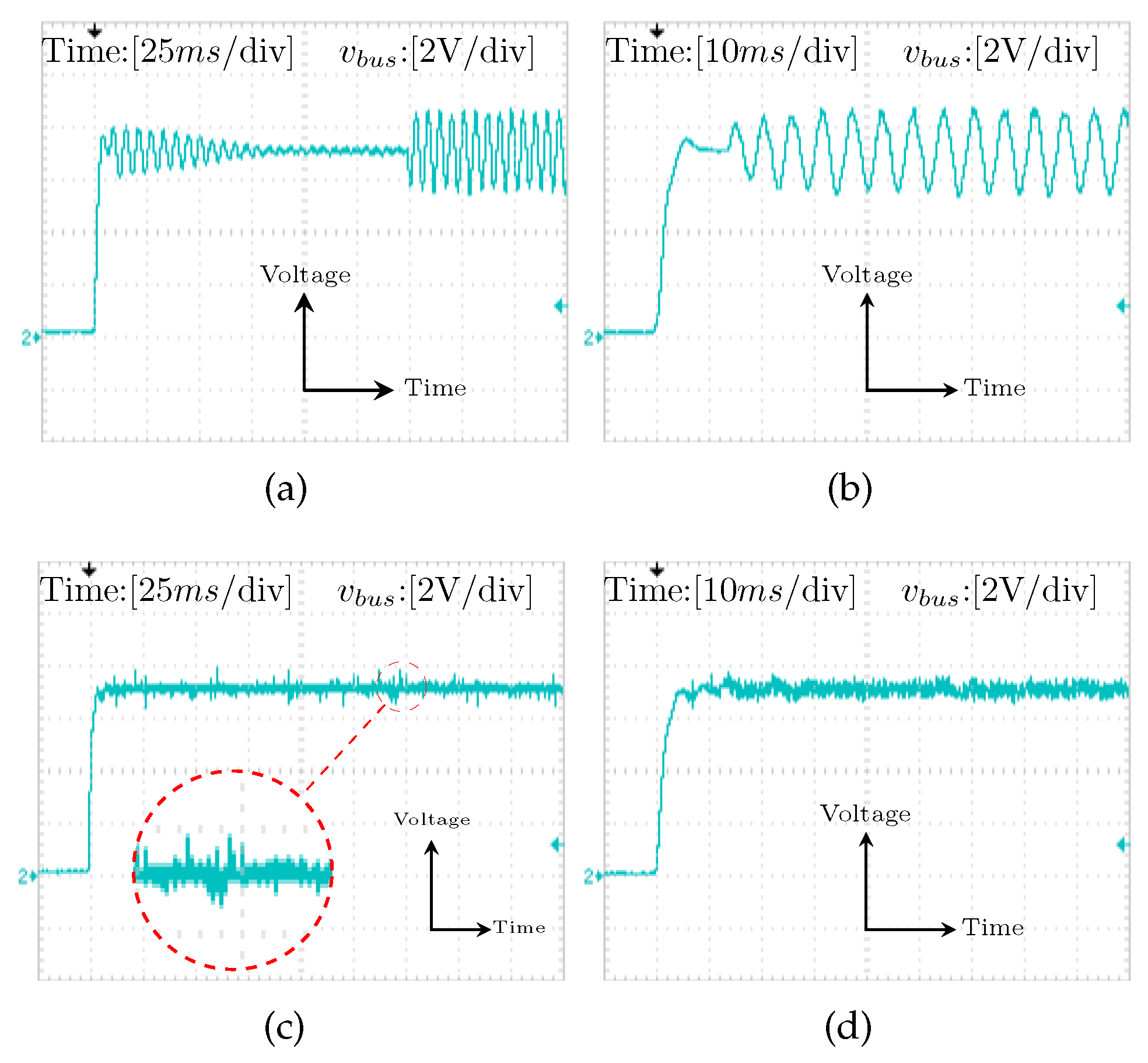
6.2. Experimental Cases

The prototype cascaded system was physically built as shown in Figure 14. The digital controller platform NIcRio 9024 (National Instruments, Austin, TX, USA) was used to control the output voltages of the converters, with a sampling rate of 30 Ksample/s. Similar to the simulation, the system with the conventional controller was tested using the two test procedures, where $v_{bus}$ denotes the DC bus voltage. Increasing the load sequentially—as in the first test—destabilized the bus voltage as soon as the load power reached 16 W, as shown in Figure 15a. A similar result was yielded by starting up the system supplying the entire load, as shown in Figure 15b. Hence, the determined impact of the negative input impedance is obvious.

The proposed controller was implemented to demonstrate its effectiveness in preserving the dynamic performance of the cascaded system. The first test was run, and Figure 15c shows the improvement in the response at the start up, while increasing the load had no impact on the stability of the system. Moreover, the second test was conducted, and the response of the system at the start-up while supplying the entire load was identical to the simulated and theoretical responses of $T_S$ as Figure 15d depicts. Hence, the experimental results have proven the efficacy of the proposed shaping in preserving the dynamic response of cascaded systems.

7. Conclusions

In this paper, we proposed an active damping method to stabilize and retain the dynamic performance of cascaded systems by reshaping the impedance of the source converter. The magnitude of the shaped impedance was absolutely restricted to be in the region limited by the source characteristic impedance in order to prevent dynamic performance degradation. The proposed method is compatible with any linearized feedback control scheme and any DC-DC converter topology. The mathematical approach was developed in order to evaluate every parameter required to shrink the impedance of the source in the proposed region.

A prototype DC cascaded system was built and analyzed, where the performance of the system with and without the proposed method were compared. Analytical analyses, time-domain simulations, and practical experiments have proven the ability of the proposed method to decouple the interaction of the source and the load converters, and hence preserve their dynamic performances. In contrast, the conventional control method suffered from permanent oscillations at the DC bus.