Adaptive Model Predictive Control-Based Energy Management for Semi-Active Hybrid Energy Storage Systems on Electric Vehicles

Abstract

This paper deals with the energy management strategy (EMS) for an on-board semi-active hybrid energy storage system (HESS) composed of a Li-ion battery (LiB) and ultracapacitor (UC). Considering both the nonlinearity of the semi-active structure and driving condition uncertainty, while ensuring HESS operation within constraints, an adaptive model predictive control (AMPC) method is adopted to design the EMS. Within AMPC, LiB Ah-throughput is minimized online to extend its life. The proposed AMPC determines the optimal control action by solving a quadratic programming (QP) problem at each control interval, in which the QP solver receives control-oriented model matrices and current states for calculation. The control-oriented model is constructed by linearizing HESS online to approximate the original nonlinear model. Besides, a time-varying Kalman filter (TVKF) is introduced as the estimator to improve the state estimation accuracy. At the same time, sampling time, prediction horizon and scaling factors of AMPC are determined through simulation. Compared with standard MPC, TVKF reduces the estimation error by 1~3 orders of magnitude, and AMPC reduces LiB Ah-throughput by 4.3% under Urban Dynamometer Driving Schedule (UDDS) driving cycle condition, indicating superior model adaptivity. Furthermore, LiB Ah-throughput of AMPC under various classical driving cycles differs from that of dynamic programming by an average of 6.5% and reduces by an average of 10.6% compared to rule-based strategy of LiB Ah-throughput, showing excellent adaptation to driving condition uncertainty.

1. Introduction

As concerns about energy crisis and environmental issues mount, electric vehicles (EVs) have been considered as the most promising substitutes for internal combustion engine vehicles. EVs’ performance is strongly effected by their energy storage sources (ESS) [1,2]. ESSs for EVs must simultaneously possess high specific energy, high specific power and long cycle life, which is impossible for a single ESS. Consequently, hybrid energy storage system (HESS) have becomes favorable options. Among all ESSs, Li-ion batteries (LiB) are the most extensively used for their high specific energy, however, low specific power and short cycle lives limit their application [3]. Compared with LiB, ultracapacitors (UCs) have longer cycle life and higher specific power [4]. Therefore utilizing HESSs that include LiB and UC and possess both the high specific energy of LiB and high specific power of UC is an advisable choice. In this way, the LiB burden would be reduced remarkably by the assistance of UC, and LiB lifetime would be effectively extended.

HESS performance in extending LiB life is mainly influenced by three factors: HESS structure selection, parameter matching and the energy management strategy (EMS). Among all structures, passive, semi-active and active structures have been widely researched [5,6,7,8,9,10]. In passive structures, the LiB and UC are directly combined in parallel, and the power distribution between them only depends on their internal resistances. This structure is the most cost effective, yet the controllability is poor. In active structures, both the LiB and UC are connected to a direct current (DC) bus by two full-size bi-directional DC/DC converters, and they can be controlled independently, although the need for two converters increases the HESS cost significantly. In semi-active structures, either the LiB or UC are connected to the DC bus with a bi-directional DC/DC converter as the controlled component, and this structure provides a tradeoff between cost, controllability and complexity. As the control process gives rise to a slight delay, peak HESS power demand will result in a pulsed current to the passive component and cause damage. For this reason, LiB is chosen as the controlled component in this paper, and UC is left to deal with the pulsed current passively.

After determining the structure, the priority for the HESS is to develop an appropriate energy management strategy (EMS) to decide how the HESS power demand is allocated to LiB and UC. Lots of EMSs have been put forward, and they can mainly be classified into two categories: rule-based controllers (RBCs) and optimization-based strategies. With off-line optimization [11,12,13], an optimal power distribution can be obtained, but it’s not viable for real-time application since the whole future driving conditions must be known a priori. Instead, RBC is suitable for real-time application, because the future conditions are not needed.

In [14], RBC is proposed for the active HESS structure. After optimizing both UC parameters and RBC parameters under a certain cycle, the proposed RBC is capable of reducing the battery peak current by 49%. In [15], a fuzzy-logic energy management based on Markov random prediction is designed for a semi-active HESS structure. Simulation results show that the average battery current rate is effectively reduced. In [16], an optimal power distribution for minimizing HESS energy consumption is solved by gradient method. Based on the optimal distribution, a neural network (NN) controller is developed, and the performance is near-optimal. The aforementioned EMSs are easily implemented online, and the performance are satisfactory under certain cycle. Nevertheless, due to the stiffness of parameters, their performance would degrade when applied to other cycles. In [17,18,19], wavelet transform (generally a 3-level Haar wavelet) is adopted to split HESS power demand into high as well as low frequency parts. Different parts are allocated to different sources based on their characteristics. This method is easy to implement online, yet both power demand prediction and the ultracapacitor state of charge (USOC) adjustment remain challenges.

The RBCs mentioned above do not guarantee optimal performance. Besides, the robustness is poor when the driving cycle is uncertain. To conquer the weaknesses, online optimization-based strategies are increasingly getting attention. Optimization-based EMSs artificially design a cost function with constraints, and solve its minimum online by using different kinds of algorithms: model predictive control (MPC), dynamic programming (DP), convex optimization (CVX) or some evolutionary algorithms [20,21]. Among them, model predictive control (MPC) is a kind of model-based control design method which has been introduced in the EMSs for HESS recently. In [22,23], a detailed control-oriented state space model of an active HESS is constructed for MPC, and the battery current magnitude/fluctuation were minimized successfully. In [24], an explicit MPC (EMPC) was designed by solving piecewise linear functions of states and control laws offline to replace online QP calculation, reducing the computational burden dramatically. MPC and EMPC are suitable for designing EMSs of linear HESS. Conversely, it’s difficult for MPC and EMC to design proper EMSs for highly nonlinear semi-active HESS. To handle the nonlinearity of multi-sources, some researchers have adopted DP instead of quadratic programming (QP) in MPC [25,26]. Unfortunately, a large states number or a small states discretization step size would cause a heavy computational burden for real-time implementation. As DP has computational problems when handling nonlinear multi-states optimization problems, CVX could be a reasonable substitute. In [27,28], HESS parameters and EMS are optimized simultaneously to extend battery life, as well as reduce total energy consumption. In [29,30], EMS for HESS is designed based on CVX to minimize battery current magnitude/ fluctuation. CVX is an effective tool in dealing with optimization problems with multi-states, whereas, it is only applicable to convex cost functions with convex constraints, and its application in non-convex models is limited.

From the literature described above, optimization-based EMSs are preferred over RBC-based EMSs for their optimality and adaptability to driving condition uncertainty, but due to the strong nonlinearity of semi-active HESS, the mentioned optimization methods are not applicable. In this paper, an AMPC-based EMS for semi-active HESS is proposed to handle the model nonlinearity. The proposed AMPC minimizes LiB Ah-throughput in the prediction horizon and ensures HESS operation within constraints. Three aspects of research are conducted on the proposed AMPC. Firstly, a module for generating control-oriented model is designed, including linearization, direct feedthrough elimination, discretization and state augmentation. Secondly, a time-varying Kalman filter (TVKF) is introduced as state estimator to improve the state estimation accuracy. In this way, both control-oriented model and estimated states improve the control action accuracy calculated by the QP solver. Finally, sampling time, prediction horizon and scaling factors of AMPC are determined through simulation. The proposed EMS is created and verified on the Matlab/Simulink (The MathWorks, Natick, MA, USA) platform. Compared with standard MPC (SMPC), TVKF reduces estimation errors by 1~3 order of magnitude, AMPC reduces LiB Ah-throughput by 4.3% under UDDS conditions, indicating superior model adaptivity. Furthermore, simulation results under various driving cycles differ from those of DP by an average of 6.5% and reduce an average of 10.6% compared to RBC, indicating that AMPC is able to minimize the LiB Ah-throughput online effectively when the HESS is nonlinear and the driving conditions are uncertain.

The rest of the paper is organized as follows: in Section 2, the detailed HESS model is introduced. In Section 3, the control-oriented model updating process is performed, and TVKF is specified. In Section 4, AMPC parameters are discussed, and AMPC is compared with SMPC, RBC and DP to verify the model adaptivity and adaptability to driving condition uncertainty. Moreover, the influence of the weights is researched and a suggested range is given. Section 5 presents the conclusions.

2. The Hybrid Energy Storage System Modeling

The structure of the semi-active HESS is shown in Figure 1, in which UC is connected to the DC bus directly. LiB is connected to the DC bus through a full-size bi-directional DC/DC converter. The LiB power output is determined by EMS, and the UC delivers rest power demand passively.

2.1. LiB Model

The LiB cell used in this paper is a Panasonic NCR 18650B (Panasonic Co., Ltd, Osaka, Japan), and the main parameters are listed in

Table 1. LiB Parameters.

Nominal Capacity	3.35 Ah	Maximum Discharge Current	6.6 A
Nominal Voltage	3.6 V	Maximum Charge Current	2 A
Voltage Range	2.5 V~4.2 V	Specific Energy	243 Wh/kg

.

The Partnership for a New Generation of Vehicles (PNGV) battery model is selected as the LiB equivalent circuit model [31], as shown in Figure 2.

In the PNGV model, E and V_bb approximate the voltage source of the LiB, in which E is a constant evaluated as the open circuit voltage (OCV) value when the LiB is fully discharged. V_bb represents a linear relationship between the variation of source voltage and variation of remaining source energy, just like a capacitor approximately, and C_bb is corresponding capacity. C_bp and R_bp reflect the electrode polarization phenomenon; R_bb is the equivalent dc resistance. V_bl is the cell terminal voltage, P_b is pack power, n_b is cell number in pack.

LiB state of charge (BSOC) is defined as:

$$BSOC=BSO{C}_{init}-\frac{1}{Q_b}{\displaystyle \int i_b(t)dt}$$

(1)

where, BSOC_init is the value of BSOC when the simulation starts, which is set as 0.7. Q_b is the LiB cell nominal capacity.

The OCV under different BSOC is obtained by experiment. When BSOC is between 0.2 and 0.9, the OCV increases nearly linearly with BSOC. Limiting BSOC within the range of [0.2, 0.9], and we linearized the relationship of BSOC and OCV to obtain E and C_bb:

$$OCV=a+b\times BSOC=E+V_{bb}$$

(2)

Thereafter, BSOC = V_bb/b, E = a [32]. V_bb and V_bp are two states expressed by:

$$\{\begin{array}{c}{\dot{V}}_{bb}=-\frac{1}{C_{bb}}{i}_{bb},C_{bb}=\frac{Q_b}{b}\\ {\dot{V}}_{bp}=-\frac{1}{C_{bp}{R}_{bp}}{V}_{bp}+\frac{1}{C_{bp}}{i}_b\end{array}$$

(3)

Terminal voltage V_bl is expressed by:

$$V_{bl}=E+V_{bb}-V_{bp}-i_b{R}_{bb}$$

(4)

Based on Kirchhoff Voltage Laws, i_b is obtained:

$$i_b=\frac{(E+V_{bb}-V_{bp})-\sqrt{{(E+V_{bb}-V_{bp})}^2-4P_b{R}_{bb}/n_b}}{2R_{bb}}$$

(5)

where, P_b is the only manipulated variable of the HESS.

A hybrid pulse power characterization test is conducted, and the lumped parameters C_bp, R_bb and R_bp are fitted under different BSOC (0.1 as interval). As BSOC is limited to [0.2, 0.9], R_bb, R_bp and C_bp are evaluated by taking an average within the range. The bi-directional DC/DC converter is simplified as an efficiency module with constant efficiency of 95%.

2.2. UC Model

As UC is directly connected to the electric machine (EM) controller, the working voltage must be limited to the range of the controller protection voltage which is 220 V~400 V in this paper. The cell voltage upper bound is set as 2.7 V, and based on the bound, the cell number is calculated as 150. According to the protection voltage lower bound as well as calculated cell number, the cell voltage lower bound is obtained as 1.5 V. The cell capacity selection is a sizing problem coupled with EMS optimization. Based on various literatures [33,34,35], pack capacity is chosen as 100 Wh. Based on the pack capacity, the cell capacity is calculated as 0.67 Wh. A Maxwell BCAP0650 is selected whose cell capacity is 0.66 Wh, the main parameters of which are listed in

Table 2. UC Parameters.

Rated Capacitance	650 F	Absolute Maximum Current	680 A
ESRDC	0.8 mΩ	Specific Power	14 kW/kg
Voltage Range	0 V~2.8 V	Specific Energy	4.1 Wh/kg

.

The equivalent circuit of the UC is shown in Figure 3 [4]. This model consists of two parts: the part for main energy storage (C₀ and C₁) and the part reflecting electrode kinetics (R_ub, R_up and C_up). In the main energy storage part, C₀ and C₁ are connected in parallel. C₀ is characterized by constant capacitance, and C₁ is characterized by capacitance varying linearly with the voltage V_ub. They characterize the nonlinearity of the source jointly. In the electrode kinetics part, R_ub represents the Ohmic resistance, while R_up and C_up represent polarization resistance and polarization capacitance separately.

V_ub and V_up are two states calculated by:

$$\{\begin{array}{c}{\dot{V}}_{ub}=-\frac{1}{C_0+k{V}_{ub}}{i}_u\\ {\dot{V}}_{up}=\frac{i_u{R}_{ub}-V_{up}}{C_{up}(R_{ub}+R_{up})}\end{array}$$

(6)

USOC is obtained by:

$$USOC=\frac{V_{ub}}{V_{ub,max}}\times 100\%$$

(7)

where, V_ub,max is 2.8 V according to the manual.

Terminal voltage V_ul is expressed as:

$$V_{ul}=V_{ub}-V_{up}-C_{up}{R}_{up}{\dot{V}}_{up}$$

(8)

Based on Kirchhoff Voltage Laws, i_u is represented as:

$$i_u=\frac{V_{ub}-\frac{R_{ub}}{R_{ub}+R_{up}}{V}_{up}-\sqrt{{(V_{ub}-\frac{R_{ub}}{R_{ub}+R_{up}}{V}_{up})}^2-4\frac{R_{ub}{R}_{up}(P_d-P_b)}{(R_{ub}+R_{up})n_u}}}{2\frac{R_{ub}{R}_{up}}{R_{ub}+R_{up}}}$$

(9)

where, P_u is replaced by P_d − P_b, indicating that P_b and P_d decide the working conditions of UC jointly. V_ub, i_u and V_ul reveal strong nonlinearity, and standard state space model is insufficient to characterize the model precisely.

3. AMPC-Based Energy Management Implementation

When the C-rate is within 2C, BSOC is within the range of [0.2, 0.9], Ah-throughput is capable of representing numerically the ageing condition of batteries [36]. The purpose of the EMS is: (1) to minimize LiB current (or plus current variation), thereby reduce LiB Ah-throughput and extend battery life; (2) to ensure HESS is operating within the constraints. This is a finite horizon optimization problem with constraints, and MPC is excellent for managing optimization problems like this. In SMPC, the control-oriented model is designed off-line, and remains unchanged during simulation. If the plant is linear or weak nonlinear, the model prediction accuracy is acceptable. However, as the proposed semi-active HESS is highly nonlinear, the constant prediction model isn’t accurate, AMPC is used to address the degradation by adapting the prediction model for changing the working conditions. Intrinsically, AMPC has the same structure as SMPC but allows the model parameters and optimization cost function to evolve with time. At each interval, a state space model is obtained by linearizing the HESS model around current working conditions. The original HESS model is:

$$\{\begin{array}{c}\left[\begin{array}{c}{\dot{V}}_{bb}\\ {\dot{V}}_{bp}\\ {\dot{V}}_{ub}\\ {\dot{V}}_{up}\end{array}\right]=\left[\begin{array}{c}-\frac{i_b}{C_{bb}}\\ -\frac{1}{C_{bp}{R}_{bp}}{V}_{bp}+\frac{i_b}{C_{bp}}\\ -\frac{1}{C_0+k{V}_{ub}}{i}_u\\ \frac{R_{ub}{i}_u-V_{up}}{C_{up}(R_{ub}+R_{up})}\end{array}\right]=\left[\begin{array}{c}{f}_1(V_{bb},V_{bp},V_{ub},V_{up},P_b,P_d)\\ f_2(V_{bb},V_{bp},V_{ub},V_{up},P_b,P_d)\\ f_3(V_{bb},V_{bp},V_{ub},V_{up},P_b,P_d)\\ f_4(V_{bb},V_{bp},V_{ub},V_{up},P_b,P_d)\end{array}\right]\\ \begin{array}{l}{i}_b=\frac{E_b+V_{bb}-V_{bp}-\sqrt{{(E_b+V_{bb}-V_{bp})}^2-4R_{bb}{P}_b/n_b}}{2R_{bb}}=g_1(V_{bb},V_{bp},V_{ub},V_{up},P_b,P_d)\\ i_u=\frac{V_{ub}-\frac{R_{ub}}{R_{ub}+R_{up}}{V}_{up}-\sqrt{{(V_{ub}-\frac{R_{ub}}{R_{ub}+R_{up}}{V}_{up})}^2-4\frac{R_{ub}{R}_{up}(P_d-P_b)}{(R_{ub}+R_{up})n_u}}}{2\frac{R_{ub}{R}_{up}}{R_{ub}+R_{up}}}=g_2(V_{bb},V_{bp},V_{ub},V_{up},P_b,P_d)\end{array}\end{array}$$

(10)

To ensure i_b and i_u have real solutions, the following two expressions are added to outputs:

$$\{\begin{array}{c}{y}_b={(E_b+V_{bb}-V_{bp})}^2-4R_{bb}{P}_b/n_b\\ y_u={(V_{ub}-\frac{R_{ub}}{R_{ub}+R_{up}}{V}_{up})}^2-\frac{4R_{ub}{R}_{up}(P_d-P_b)}{R_{ub}+R_{up}{n}_u}\end{array}$$

(11)

As AMPC is able to set limits for inputs and outputs only, states V_bb and V_ub who have engineering constraints are also added to outputs. Besides, as state estimator is required, the model observability must be guaranteed. To this end, V_bl and V_ul are added to outputs as measured variables. By this means, two current sensors and two voltage sensors are needed. The final model is with inputs U = [P_b, P_d], internal states X = [V_bb, V_bp, V_ub, V_up] and outputs Y = [V_bb, i_b, V_bl, y_b, V_ub, i_u, V_ul, y_u].

3.1. Control-Oriented Model Implementation

3.1.1. Linearization

At each control interval, the plant is linearized around current operation point (X_t, U_t) by first approximation of Taylor expansion. The linearized plant is described as:

$$\{\begin{array}{c}\dot{X}=AX+BU+f(X_0,U_0)-A{X}_0-B{U}_0\\ Y=CX+DU+g(X_0,U_0)-C{X}_0-D{U}_0\end{array}$$

(12)

where, the constant matrices f(X₀,U₀) − AX₀ − BU₀ and g(X₀,U₀) − CX₀ − DU₀ are set as measured disturbances with constant inputs of 1, and the new inputs are augmented as U = [P_b, P_d, M_d]. The state space model is augmented as:

$$\{\begin{array}{c}\dot{X}=AX+\left[\begin{array}{cc}B& f(X_0,U_0)-A{X}_0-B{U}_0\end{array}\right]U\\ Y=CX+\left[\begin{array}{cc}D& g(X_0,U_0)-C{X}_0-D{U}_0\end{array}\right]U\end{array}\Rightarrow \{\begin{array}{c}\dot{X}=AX+BU\\ Y=CX+DU\end{array}$$

(13)

Matrix A, B, C and D are calculated as:

$$A=\frac{\partial f}{\partial X},B=\frac{\partial f}{\partial U},C=\frac{\partial g}{\partial X},D=\frac{\partial g}{\partial U}$$

(14)

3.1.2. Eliminating Direct Feedthrough

Non-empty matrix D which causes direct feedthrough from inputs to outputs is unacceptable by AMPC. To eliminate the feedthrough, the linearized plant in Equation (13) is augmented by adding first-order filters with time constant T_a to inputs, as shown in Equation (15). T_a is chosen as one-tenth or smaller of the AMPC sampling time [37,38]. With this method, the original inputs are turned into new states and new inputs are identical to old ones except a slight delay:

$$T_a\dot{U}=-U+U_a$$

(15)

The linearized model is augmented by:

$$\{\begin{array}{c}{\dot{X}}_a=\left[\begin{array}{cc}A& B\\ 0_{3\times 4}& -\frac{1}{T_a}\times I_{3\times 3}\end{array}\right]X_a+\left[\begin{array}{c}{0}_{4\times 3}\\ \frac{1}{T_a}\times I_{3\times 3}\end{array}\right]U_a\\ Y=\left[\begin{array}{cc}C& D\end{array}\right]X_a\end{array},\Rightarrow \{\begin{array}{c}{\dot{X}}_a=A_a{X}_a+B_a{U}_a\\ Y=C_a{X}_a\end{array}$$

(16)

Augmented states now are X_a = [V_bb, V_bp, V_ub, V_up, P_b, P_d, M_d], and new inputs are U_a = [P_ba, P_da, M_da]. The delay in the inputs intrinsically causes a slight model mismatch, which AMPC is good at dealing with.

3.1.3. Model Discretization

The Zero-Order Hold method is used to discretize the state space model with sample time Ts, the discrete state space is represented as:

$$\{\begin{array}{c}{X}_a(k+1)=G(Ts)X_a(k)+H(Ts)U_a(k)\\ Y(k)=C_a{X}_a(k)\end{array}$$

(17)

where:

$$G(Ts)=e^{A_{a}Ts},H(Ts)={\displaystyle {\int }_0^{Ts}{e}^{A_{a}t}dt\cdot B_a}$$

(18)

The matrix exponential of G (Ts) is calculated using Padé approximant and integral of H (Ts) is implemented using Simpson’s Rule.

3.1.4. LiB Current Fluctuation Suppression

To avoid LiB damage caused by enormous current fluctuation, the current variation is also considered as a control target [27]. Here we define a state:

$$\Delta i_b(k+1)=i_b(k+1)-i_b(k)$$

(19)

Based on the discrete state space, and output increments are represented as:

$$\Delta Y(k+1)=C_a(X_a(k+1)-X_a(k))=C_a(G-I)X_a(k)+C_{a}H{U}_a(k)$$

(20)

∆i_b is expressed by the second row of ∆Y, in which coefficients vector of X_a is expressed by G_dib, coefficients vector of U_a is expressed by H_dib. ∆i_b is expressed as:

$$\Delta i_b(k+1)=G_{dib}{X}_a(k)+H_{dib}{U}_a(k)$$

(21)

The discrete state space model is augmented again:

$$\{\begin{array}{c}\left(\begin{array}{c}{X}_a(k+1)\\ \Delta i_b(k+1)\end{array}\right)=\left[\begin{array}{cc}G& 0_{7\times 1}\\ G_{dib}& 0\end{array}\right]\left(\begin{array}{c}{X}_a(k)\\ \Delta i_b(k)\end{array}\right)+\left[\begin{array}{c}H\\ H_{dib}\end{array}\right]U_a(k)\\ \left(\begin{array}{c}Y(k)\\ \Delta i_b(k)\end{array}\right)=\left[\begin{array}{cc}{C}_a& 0_{8\times 1}\\ 0_{1\times 7}& 1\end{array}\right]\left(\begin{array}{c}{X}_a(k)\\ \Delta i_b(k)\end{array}\right)\end{array}\Rightarrow \{\begin{array}{c}{X}_A(k+1)=G_A{X}_A(k)+H_A{U}_a(k)\\ Y_A(k)=C_A{X}_A(k)\end{array}$$

(22)

The final state space model for AMPC is obtained with internal states X_A = [V_bb, V_bp, V_ub, V_up, P_b, P_d, M_d, ∆i_b], inputs U_a = [P_ba, P_da, M_da] and outputs Y_A = [V_bb, i_b, V_bl, y_b, V_ub, i_u, V_ul, y_u, ∆i_b], as well as control-oriented model matrices G_A, H_A and C_A.

3.2. Optimization Problem

The AMPC is designed based on the model shown in Equation (22), in which P_ba is the only manipulated variable, P_da and M_da are measured disturbances, i_b, i_u, V_bl and V_ul are measured outputs, V_bb, V_ub, y_b, y_u and ∆i_b are unmeasured outputs.

The AMPC solves a QP problem at each control interval and determines the control action of next interval. The QP problem here includes outputs reference tracking and constraints violation, the cost function to be minimized is as follows [39,40]:

$$\begin{array}{l}J={{\displaystyle \sum _{j=1}^{n_y}{\displaystyle \sum _{i=1}^p\left\{\frac{w_j}{s_{y,j}}[r_j(k+i|k)-y_j(k+i|k)]\right\}}}}^2+{\rho }_{\epsilon }{\epsilon }_k^2\\ \mathrm{subject} \mathrm{to}\\ \frac{P_{b,min}}{s_u}-{\epsilon }_{k}EC{R}_{u,min}\le \frac{P_b(k+i-1|k)}{s_u}\le \frac{P_{b,max}}{s_u}+{\epsilon }_{k}EC{R}_{u,max}\\ \frac{y_{j,min}}{s_{y,j}}-{\epsilon }_{k}EC{R}_{j,min}\le \frac{y_j(k+i|k)}{s_{y,j}}\le \frac{y_{j.max}}{s_{y,j}}+{\epsilon }_{k}EC{R}_{j,max}i=1:p,j=1:n_y\end{array}$$

(23)

where, n_y is the number of outputs, p is prediction horizon, w_j is the weight of jth output, ${\rho }_{\epsilon }$ is the constraints violation penalty weight, and ε is the slack variable at interval k. J involves a trade-off between the output reference tracking and constraint violation by weighting, and corresponding QP decision is [U_a (k|k) U_a(k + 1|k) … U_a (k + p − 1|k) ε]. The first part of J represents the output reference tracking with weight matrix w_j, while the second part shows the constraint violation with weight ${\rho }_{\epsilon }$. When ${\rho }_{\epsilon }$ increases, ε tends to be smaller or zero, meaning J is more inclined to suppress constraint violation. If ε is zero, U_a and Y_a are strictly limited within constraints; if ε is positive, at least one soft constraint is reached. While, when ${\rho }_{\epsilon }$ is smaller, ε tends to be greater, soft constraints are more likely to be activated, and the controller performance can be substandard. S_y,j and s_u are scaling factors (SFs) whose roles are to scale inputs and outputs to the same magnitude. ECRs are nonnegative parameters used to soften inputs and outputs constraints, the larger the ECRs are, the greater constraints violation are allowed to obtain optimal solution.

Suppose H_Au is coefficient matrix of P_ba, and H_Av is coefficient matrix of [P_da, M_da], the model in Equation (22) is rewritten as:

$$\{\begin{array}{c}{X}_A(k+1)=G_A{X}_A(k)+H_{Au}{P}_{ba}(k)+H_{Av}\left[\begin{array}{c}{P}_{da}(k)\\ M_{da}(k)\end{array}\right]\\ Y_A(k)=C_A{X}_A(k)\end{array}$$

(24)

Assign U_au = P_ba and U_av = [P_da, M_da], based on Equation (23), the predicted output is:

$$\begin{array}{l}{Y}_A(k+1|k)=C_A{G}_A{X}_A(k)+C_A{H}_{Au}(U_{au}(k))+C_A{H}_{Av}{U}_{av}(k)\\ Y_A(k+2|k)=C_A{G}_A^2{X}_A(k)+C_A{G}_A{H}_{Au}{U}_{au}(k)+C_A{H}_{Au}{U}_{au}(k+1)+\\ C_A{G}_A{H}_{Av}{U}_{av}(k)+C_A{H}_{Av}{U}_{av}(k+1)\\ ⋮\\ Y_A(k+i|k)=C_A{G}_A^i{X}_A(k)+{\displaystyle \sum _{h=0}^i{C}_A{G}_A^{i-h-1}(H_{Au}{U}_{au}(k+h)}+H_{Av}{U}_{av}(k+h))\end{array}$$

(25)

Define $\Delta U_{au}\left(k\right)=U_{au}\left(k\right)-U_{au}\left(k-1\right)$, we can derive that $\Delta U_{au}\left(k+i\right)=U_{au}\left(k-1\right)+{\sum }_{j=0}^i\Delta U_{au}\left(k+j\right)$. Then substitute ΔU_au into Equation (25), the predicted output is expressed as:

$$\begin{array}{l}{Y}_A(k+i|k)=C_A{G}_A^i{X}_A(k)+{\displaystyle \sum _{h=0}^i{C}_A{G}_A^{i-h-1}(H_{Au}}(U_{au}(k-1)+{\displaystyle \sum _{j=0}^h\Delta U_{au}(k+j)})+H_{Av}{U}_{av}(k+h))\\ i=1:p\end{array}$$

(26)

where, H_Au is coefficient matrix of P_ba from H_A, H_Av is coefficient matrix of [P_da, M_da] from H_A. As shown in Equation (26), G_A, H_A (H_Au and H_Av) and C_A are used by QP solver for calculation.

ECRs for inputs and outputs are decided based on whether their upper or lower bounds are allowed to be violated or how great their bounds are allowed to be violated. Constraints for P_b are not set for they are limited intrinsically by the limitation of V_bb and i_b, and their ECRs are set as 1 by default. V_bb is limited to the range of 0.18 V~0.81 V based on BSOC constraints, both constraints leave some margin and can be violated, ECR_1,min and ECR_1,max are set as 1. Constraints for i_b are −3.2 A~6.4 A according to the manual, the lower bound is strictly limited by the manufacturer, while the upper bound can be set as high as 10 A in our experiment, ECR_2,min is 0 and ECR_2,max is 1. Constraints for V_bl and V_ul are not set for they are intrinsically limited by other states, corresponding ECRs are set as 1. Outputs y_b and y_u must be non-negative, and the constraints are not allowed to be violated. Considering linearization error, the lower bounds for y_b and y_u are set as 0.5, ECR_3,min and ECR_6,min are 0. V_ub is limited to meet the voltage range of DC bus, cell voltage range is thus between 1.5 V~2.7 V. As the energy stored in the UC increases exponentially with V_ub, the upper bound would be violated slightly by absorbing much energy, which is acceptable, ECR_4,max is 1. While the lower bound would be violated severely by even delivering little energy, which is unacceptable, ECR_4,min is 0. Constraints for i_u are −1200 A~1200 A and can be violated, for huge current do not harm the UC cell obviously, ECR_5,min and ECR_5,max are 10. Constraints for ∆i_b are not set for the constraints of i_b intrinsically avoid severe variation of ∆i_b, meanwhile weights for i_b and ∆i_b prevent them from wide variation.

3.3. Controller State Estimation

QP solver receives states for calculation, as shown in Equation (26). As HESS states can’t be measured directly, a state estimator is needed. Currents and terminal voltages of LiB and UC are related to all four states to be estimated, and they are all measured variables. By gathering voltage and current signals, the HESS observability is guaranteed.

TVKF is applied to construct the estimator. Different from the standard Kalman filter, TVKF calculates the gain matrix with varying model matrices G_A, H_A and C_A. The model in Equation (22) is augmented with noise vector w(k) and v(k) [26]:

$$\{\begin{array}{c}{X}_A(k+1)=G_A{X}_A(k)+H_A{U}_a(k)+H_{A}w(k)\\ Y_A(k)=C_A{X}_A(k)+v(k)\end{array}$$

(27)

where, w(k) is process noise with covariance matrix Q, its gaining matrix is the same as inputs, and v(k) is measurement noise with covariance matrix R. Q is n-by-n diagonal matrix, n is equal to the number of states. R is m-by-m diagonal matrix, m is equal to the number of measured outputs. Suppose w(k) and v(k) are driven by white noise with unity gain, Q =$H_A{H}_A^T$, and R is diagonal matrix with diagonal elements [SF₂, SF₃, SF₆, SF₇] considering influence of scaling.

The estimation process at control interval k is as follows:

(1)

Prediction updating:

$${\widehat{X}}_A(k|k-1)=G_A{X}_A(k-1|k-1)+H_A{U}_a(k)$$

(28)

$$P(k|k-1)=G_{A}P(k-1|k-1)G_A^T+Q$$

(29)

(2)

Measurement correction:

$$K_g(k)=\frac{P(k|k-1)C_A^T}{C_{A}P(k|k-1)C_A^T+R}$$

(30)

$${\widehat{X}}_A(k|k)={\widehat{X}}_A(k|k-1)+K_g(k)(Y_A(k)-C_A{\widehat{X}}_A(k|k-1))$$

(31)

$$P(k|k)=(I-K_g(k))P(k|k-1)$$

(32)

where ${\widehat{X}}_A(k-1|k-1)$ is the corrected states prediction of previous interval, ${\widehat{X}}_A(k|k-1)$ is the uncorrected states prediction of current interval, $P(k-1|k-1)$ is the corrected states estimation error covariance matrix of previous interval, $P\left(k|k-1\right)$ is the uncorrected error covariance matrix of current interval, K_g(k) is gain matrix for measurement correction, ${\widehat{X}}_A(k|k)$ is the corrected states prediction of current interval, P(k|k) is the corrected error covariance matrix of current interval. It’s obvious that time-varying G_A, H_A and C_A influence the value of K_g significantly.

3.4. Measured Disturbance

The control-oriented model of AMPC has two measured disturbances: P_da and M_da. M_da is a constant set as 1, while P_da is HESS power demand determined by vehicle power balance equation shown below:

$$P_{da}=v(mgf+\frac{C_{D}A}{21.15}{v}^2+\delta ma)$$

(33)

where, v is vehicle velocity from driving cycle, m is vehicle mass, f is rolling resistance coefficient, C_D is drag coefficient, A is windward area, δ is correction coefficient of rotating mass, a is vehicle acceleration.

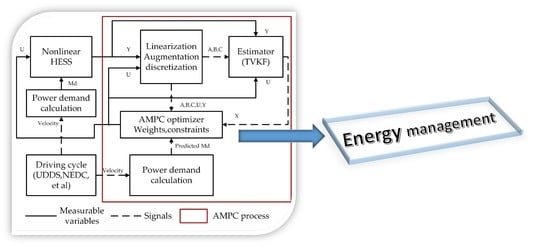
As AMPC solves the QP problem with the assumption that measured disturbances in the prediction horizon are known, the velocity needs to be predicted. Yet, model prediction inevitably causes errors, and the predicted power demand wouldn’t improve AMPC efficiency, and sometimes it may even deteriorate the efficiency if the velocity prediction is not that accurate. As a result, current power demand is applied to AMPC, and remains unchanged in prediction horizon. The whole process of the AMPC is shown in Figure 4, in the red box is the AMPC.

4. Results and Discussion

4.1. Sampling Time, Prediction Horizon and Scaling Factor

As sampling time (Ts) decreases, rejection of unmeasured disturbance as well as model error improves. Once prediction duration (p_d) and Ts are determined, prediction horizon (p_h) is calculated by p_h = p_d/Ts. p_h decides how many steps the model prediction is conducted, as p_h increases, the prediction accuracy gradually decreases. p_h also decides the size of the matrices in the QP problem, as p_h increases, the matrices become large and the computation burden is heavy. The AMPC with different Ts and p_h is conducted under UDDS, and the results are shown in

Table 3. Influence of sample time and prediction duration.

Ah-Throughput/As		pd/s
		2	5	10
Ts/s	0.1	387	387	398
	0.2	391	391	400
	0.5	430	429	452
	1	654	577	712

. Finally, Ts is set as 0.1 s, p_d is chosen as 2 s, p_h is 20.

Scaling factors (SFs) are set to adjust inputs and outputs to the same magnitude, and improper SFs may cause inaccurate states estimation as well as poor QP solutions. As the magnitudes of HESS inputs and outputs vary a lot, it is important to choose proper SFs. SFs are usually determined empirically as their respective spans, whereas the simulation results may not be optimal. Based on spans of inputs and outputs, SFs of inputs [P_b, P_d, Md] are initially selected as [10,000, 10,000, 1], and SFs for outputs [V_bb, i_b, V_bl, y_b, V_ub, i_u, V_ul, y_u, ∆i_b] are initially selected as [0.0005, 1, 1, 1, 0.01, 10, 1, 1, 1]. Among them, SF of P_b and i_u are found to be sensitive to the simulation results.

Table 4. Influence of SFs.

Ah-Throughput/As		SFPb
		100	1000	10,000
SFiu	5	389.5	398	551
	10	386	390	492
	20	385.5	387	440
	30	385	386	418

shows the results under different SFs:

Finally, SFs for P_b and i_u are reselected as 1000 and 30.

4.2. Model Adaptivity Verification

To validate the AMPC adaptivity to a nonlinear model, SMPC is introduced for comparison. SMPC is designed off-line with the same process of AMPC around HESS initial working points, and keeps constant through the simulation. A steady state Kalman filter (SSKF) is used as the estimator of SMPC.

SSKF estimation of SMPC is shown in Figure 5, TVKF estimation of AMPC is shown in Figure 6. We can see from Figure 5 that u_ub estimation gradually deviates from the real value, and the error is accumulative. This is because the gain matrix solved by SSKF is constant through the simulation, an the state estimation error is not applied to update the gain matrix. For the same reason, excessive deviation happens in the remaining four estimations. In Figure 6, TVKF exhibits a pretty precise estimation. TVKF of AMPC solves gain matrix with updated G_A, H_A and C_A at each control interval, it is obvious that varying G_A, H_A and C_A could approximate the real HESS model better, TVKF thus significantly outperforms SSKF in estimation accuracy.

Average estimation errors of SSKF and TVKF are listed in

Table 5. Average states estimation errors of SSKF and TVKF.

	Vbb	Vbp	Vub	Vup	∆ib
SSKF	3.08 × 10−4	3.88 × 10−4	0.22	2.72 × 10−3	0.18
TVKF	2.35 × 10−7	2.55 × 10−6	5.76 × 10−4	4.13 × 10−4	0.05

. Estimation errors of TVKF are lower than those of SSKF in order of 1~3 magnitude, quantitatively proving TVKF is more accurate and model adaptive.

G_A, H_A and C_A elements of AMPC under UDDS are shown in Figure 7, in which elements with marked change are shown in bold. It’s obvious that elements variation in three matrices are non-negligible, further indicating that a single model is unable to approximate the real HESS, and SSKF is unable to make accurate estimation.

Figure 8 shows the SMPC and AMPC comparison for i_b, Figure 8b,c is zooms of Figure 8a. In Figure 8b, the LiB current of SMPC is charging and discharging dramatically, which is not observed in AMPC. In Figure 8c, the LiB current of SMPC is fluctuating remarkably around 0 when HESS is charging. Furthermore, the LiB current of SMPC distinctly goes beyond that of AMPC. All the situations mentioned above lead to an increase of LiB Ah-throughput, as shown in Figure 8d. The phenomena indicate that time-varying prediction model matrices as well as accurate state estimation by TVKF significantly improve accuracy of control action calculated by QP solver of AMPC. Besides, as SMPC isn’t able to estimate states precisely, the constraints on V_ub and y_u may be violated, resulting in SMPC failure, which will cause damage to HESS.

By comparison, the superior model adaptivity of AMPC is validated.

4.3. Driving Condition Uncertainty Adaptation Verification

To verify the adaptation to uncertain driving conditions, AMPC is simulated under various classic driving cycles, DP and RBC are constructed for comparison.

4.3.1. DP and RBC Description

As DP solution time increases exponentially with the number of states, to reduce computation burden, USOC is selected as the only state. Within DP, LiB and UC are simplified as resistor capacitor (RC) circuits, USOC discretization step size is 0.001, and the cycle discretization step size is 1 s. To numerically understand the efficiency of different EMSs on extending LiB life, DP cost function includes LiB current absolute only. The cost function is:

$$J={\displaystyle \sum _{i=1}^N|i_b(i)|}$$

(34)

where, i_b is calculated by:

$$i_b(i)=\frac{E_b-\sqrt{E_b^2-4R_{bb}{P}_b/n_b}}{2R_{bb}}$$

(35)

where, P_b is calculated by P_d − P_u, in which P_u is obtained from USOC variation.

The DP process is shown in Figure 9. Forward iteration calculation is conducted. LiB Ah-throughput from the initial USOC point to different end USOC points are calculated, and the minimal solution as well as corresponding USOC path are recorded. Due to USOC discretization and model simplification, there is slight deviation between the DP result and real optimum value of the semi-active structure. Yet, considering that more accurate computation companies with much heavier computation burden and this result is accurate enough, it is adopted as comparison.

The RBC process is shown in Figure 10a, in which P_d and USOC are inputs, P_b is the output. P_b,avg represents the average power delivered by LiB, P_b,char represents the complementary power supplied from LiB to UC to maintain adequate energy for coming peak power demand. Both of them are tuned and keep constant for all driving cycles. Hysteresis control is shown in Figure 10b, which is designed for preventing USOC from frequent fluctuation round the bounds. The USOC range for hysteresis control is determined based on the UC capacity. As the capacity increases exponentially with USOC, the upper range could be set smaller compared with the lower range. Besides, considering the DC bus voltage constraint, the upper range is chosen as [0.9, 0.92], the lower range is chosen as [0.54, 0.59].

4.3.2. EMSs Results Comparison

Figure 11 shows the AMPC result under UDDS. From Figure 11a, when the HESS power demand is negative (charging), the UC absorbs almost all the braking energy, which is exactly what the AMPC expect. When the demand is positive (discharging), V_ub frequently reaches the lower bound. This situation is dealt with by AMPC very softly, for V_ub lower bound isn’t allowed to be violated. In addition, the AMPC operational mechanism of dealing with hard constraints is shown in Figure 11b,c, which are a zoom from 450 s to 470 s of Figure 11a,d, respectively. We can see from Figure 11b that at about 453 s, when V_ub is around 1.65 V and P_d is 20 kW, P_b starts to increase, while P_u gradually decreases to cope with the upcoming lower bound of V_ub. After about 10 s, V_ub reaches the lower bound softly without going beyond it. By this means, AMPC avoids any hard constraints violation. This mechanism is essential to Ah-throughput minimization, as each violation of V_ub will cause an extra charging process from LiB to UC, which significantly increases LiB Ah-throughput. Besides, pulse power in P_u is observed when transient power demand comes across, as mentioned in introduction. This phenomenon happens several times in Figure 11b, and would inevitably cause damage to LiB if it’s passive, which is exactly what the HESS tries to avoid. Hence, designing LiB as the controlled component is reasonable and necessary.

The results of AMPC, DP and RBC are shown in Figure 12, in which 12b and 12c are zooms of 12a. Figure 12b shows i_b of three EMSs under a continuous peak power demand which lasts for about 20 s. With the peak demand, optimal i_b of DP changes gradually and magnitude is satisfactory, for peak power demand is known in advance. While, i_b of AMPC is almost 0 at first to avoid the increase of LiB Ah-throughput, and gradually increases when USOC is about to fall to the lower bound to avoid violation. Though the i_b of AMPC is relatively larger, the duration is shortened significantly by QP solver compared with DP and RBC, and the LiB Ah-throughput is reduced through the simulation greatly, indicating excellent flexibility and adaptation of AMPC. LiB current i_b of RBC keeps nearly constant at first for P_b keeps at P_b,avg to maintain USOC. At about 200 s, a sudden change in i_b appears when USOC reaches the lower bound, as shown in Figure 12e. This indicates that RBC is rigid in handling operation mode transitions caused by constraints, and adjustment of USOC by constant P_b,avg is poor. In Figure 12a, i_b of DP and AMPC remain nonnegative, while with RBC, LiB charges several times. One of the phenomena is shown in Figure 12c. Referring to Figure 12e, and we can find that the situation appears due to USOC reaches upper bound, again indicating that constant P_b,avg can’t adjust USOC flexibly to leave a margin for the braking energy. Consequently, frequent charge obviously increases LiB Ah-throughput, as shown in Figure 12d. As AMPC minimizes i_b, energy in UC is always utilized firstly, and USOC always leaves a margin for braking energy, charging to LiB hardly appear. When the power demand is 0, LiB outputs a very small current to UC with DP, which adjusts USOC to deal with peak power demand. Though RBC designs P_b,avg to simulate this action, P_b,avg of RBC can’t be real-time optimized based on future demand as well as control target. In Figure 12e, USOC of AMPC fluctuates mainly at the bottom of the range, whereas USOC of RBC fluctuates mainly at the top of the range, again revealing that with AMPC, HESS can take better advantage of UC as a buffer, and absorb more braking energy to reduce LiB Ah-throughput. As a result, when encountering changing driving conditions, AMPC makes the best use of UC as a buffer, while ensuring UC voltage remains within its range, revealing considerable flexibility and adaptivity. Conversely, RBC is rigid in managing bound problems, meanwhile P_b,avg can’t be adjusted for real-time, RBC adaptability is poorer and the result is not optimal compared with AMPC.

AMPC is tested under four other typical driving cycles to further verify its adaptation to driving condition uncertainty. Both the structures and parameters of three EMSs remain constant during the test, and the results are shown in

Table 6. LiB Ah-throughput of different EMSs.

Ah-Throughput/As	AMPC	DP	Difference	RBC	Reduce
UDDS	387	371	4.3%	461	16.1%
FTP75	635	594	6.9%	718	11.6%
India_urban	462	438	5.5%	601	23.1%
NEDC	605	561	7.8%	635	4.7%
HWFET	850	786	8.1%	861	1.3%
Hybrid	1870	1762	6.1%	2000	6.5%
average	/	/	6.5%	/	10.6%

. Among the cycles, UDDS, Federal Test Procedure 75(FTP75), and India urban are urban cycles with frequent acceleration and deceleration, while New European Drive Cycle (NEDC) and Highway Fuel Economy Test (HWFET) have more continuous acceleration/deceleration or high-speed cruise. Under urban cycles, the AMPC results differ from DP results by about 5%, and reduce by about 17% compared to RBC results. The results reveal that receding optimization process of AMPC effectively resists disturbance uncertainty caused by varying driving condition, while different cycles have different characteristics and constant RBC parameters can’t adapt to cycle change. Under highway cycles, the superiority of AMPC over RBC is not evident, for when the vehicle is accelerating continuously or cruising at high speed, HESS will first exhaust the energy stored in UC. After that, as there is no braking energy for a long time, the UC can’t fully utilized as a buffer. Yet, the AMPC results are still a little better than those of RBC for its optimality and adaptivity. DP results are relatively superior to those of AMPC and RBC, indicating that it’s difficult to obtain the optimal results in highway roads by online EMSs.

A hybrid cycle composed of UDDS, NEDC and HWFET is created, and three EMSs are simulated, in which RBC parameters are adjusted to obtain best performance. The results of three EMSs are listed at the bottom of Table 6. AMPC result is satisfactory compared with DP result without any adjustment. While, even parameters are adjusted to optimal, the adaptivity of RBC is worse than AMPC when facing complex driving conditions. Finally, LiB Ah-throughput of AMPC differ from that of DP by only an average of 6.5%, and educes by an average of 10.6% compared to that of RBC, further revealing the superior optimality as well as adaptivity to driving condition uncertainty of AMPC.

4.4. Weights

When i_b and ∆i_b are to minimize simultaneously, w₂ and w₇ should be adjusted. Fix w₂ at 1, and set w₇ as 1, 5, 10 and 20, simulation results are shown in Figure 13. From Figure 13a we can see that, weight adjustment significantly influences the AMPC control performance. When w₇ increases, i_b changes more and more slowly, LiB Ah-throughput increases for this reason and accumulative ∆i_b absolute reduces, as shown in Figure 13b,d, while, when w₇ is 20, the trend has been broken. As shown in Figure 13a,c, i_b fluctuates severely at 100 s~500 s, ∆i_b absolute inevitably increases. As a result, both Ah-throughput and accumulative ∆i_b absolute significantly increase during this period, as shown in Figure 13b,d. The accumulative ∆i_b absolute when w₇ is 20 is nearly the same with that when w₇ is 5, which is conflicting with the original target of increasing the weight. The situation arises for two reasons: (1) to suppress i_b change; (2) to provide energy to UC so that UC could face huge power demand fluctuation. To satisfy two conditions simultaneously, i_b absolute has to retain high magnitude and changes drastically between positive and negative. As a result, when w₇ is too big, it’s difficult to obtain optimal solution within all constraints.

Define k_w = w₇/w₂, simulation results under different w₂ and k_w are listed in

Table 7. LiB Ah-throughput under different k_w and w_2.

Ah-Throughput/As		w2
		1	10	20
kw	0.1	387	387	387
	1	388	388	388
	5	407	407	407
	10	570	570	570
	15	761	761	761
	20	989	989	989

and

Table 8. LiB accumulated ∆i_b under different k_w and w_2.

Accumulated ∆ib/A		w2
		1	10	20
kw	0.1	236	236	236
	1	217	217	217
	5	136	136	136
	10	82	82	82
	15	82	82	82
	20	122	122	122

. No matter how much w₂ is, when k_w remains unchanged, LiB Ah-throughput and accumulated ∆i_b are always the same, indicating that k_w is the only decision variable no matter how w₂ and w₇ change.

Furthermore, when k_w increases from 0.1 to 20, LiB Ah-throughput increases gradually as well, while accumulated ∆i_b first decreases then increases, and the minimum value appears when k_w is 10 or 15. As LiB Ah-throughput when k_w is 10 is significantly smaller than that when k_w is 15, we can conclude that k_w should not exceed 10 when both goals are optimized. Based on analysis above, when setting w₂ as 1, and if the ∆i_b is to taken into account, w₇ should be set between 5 and 10 (e.g., k_w range is between 5 and 10). The proposed AMPC is capable of optimizing multiple objects simultaneously by appropriate weighting, and it’s suitable for designing EMS of HESS which usually includes various targets.

5. Conclusions

In this paper, an AMPC-based EMS for the semi-active HESS is proposed, which minimizes LiB Ah-throughput to extend its life as well as ensures HESS operation within the specified ranges. In contrast to standard MPC, the AMPC solves the control action by calculating a QP problem in which prediction model matrices are updated online and model states are estimated by TVKF. In this way, the control action accuracy is significantly improved and LiB Ah-throughput is effectively minimized. The proposed EMS is implemented and verified on the Matlab/Simulink platform, and the simulation results show that compared with SMPC, TVKF reduces the estimation error by 1~3 orders of magnitude, and AMPC reduces LiB Ah-throughput by 4.3% under UDDS. Furthermore, all HESS states are operating within specified ranges, indicating superior model adaptivity. The LiB Ah-throughput of AMPC under six classical driving cycles differs from that of DP by only an average of 6.5%, and is reduced by an average of 10.6% compared to that of RBC, revealing excellent optimality and adaptation to driving condition uncertainty. This method is ideal for managing nonlinear optimization problems with unpredictable disturbances as well as engineering constraints, and can be extended to EMSs for other nonlinear multi-source systems of new energy vehicles.