Evolution of Coal Permeability during Gas Injection—From Initial to Ultimate Equilibrium
Abstract
:1. Introduction
2. Conceptual Model and Governing Equations
2.1. Conceptual Model
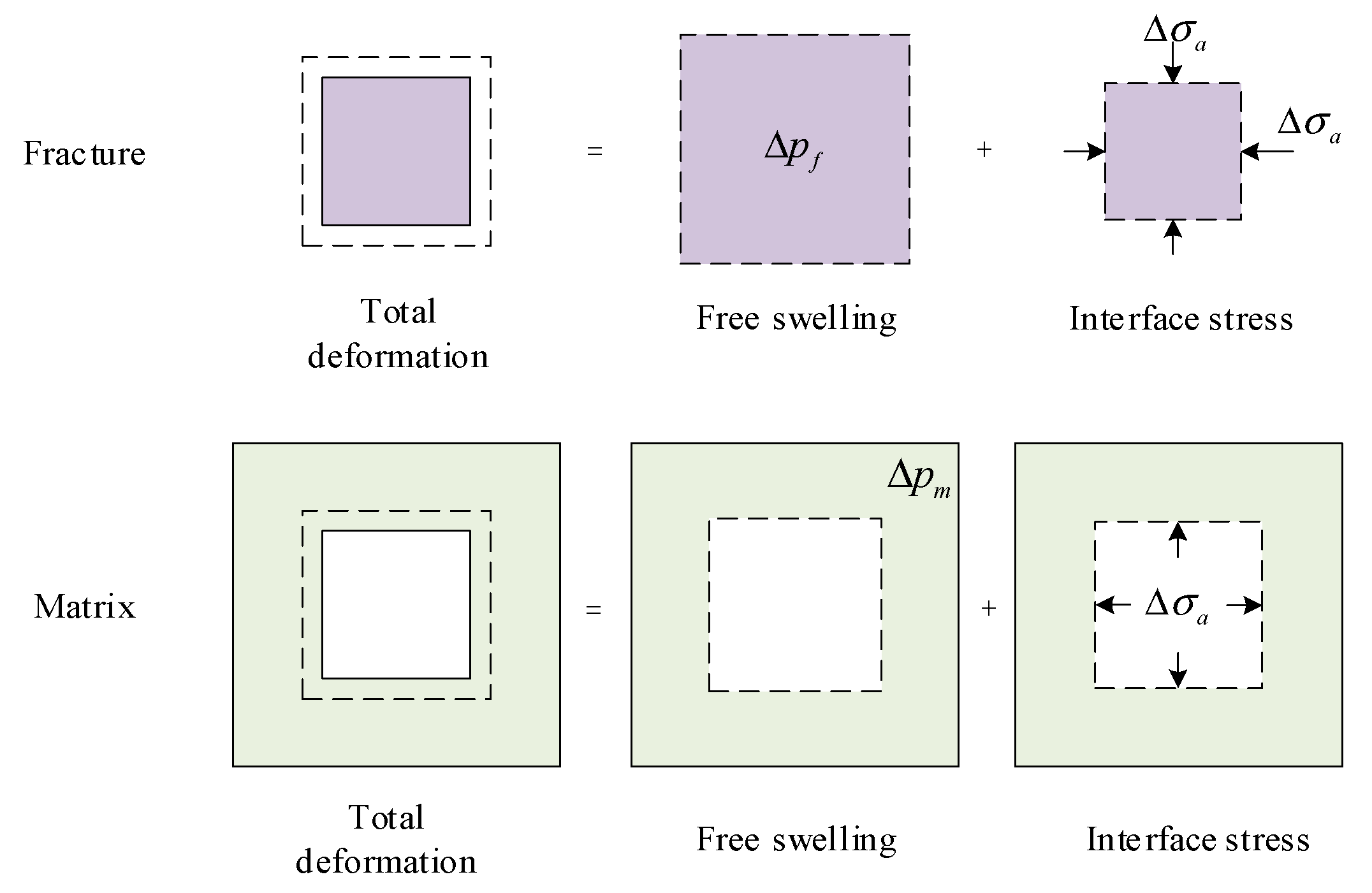
- The fracture may be represented as a void [27,37]. Then the porous matrix is the only object to study, leading to a stress difference between the internal and external boundaries. The external stress boundaries are controlled by the confining stress, while the internal stress boundaries are controlled by the fracture gas pressure.
- The fracture may be represented as a softer material [19,29], with the equilibrium pressure applied on the cross section and no sorption-induced strain. Then, both the matrix and the fracture must be studied and only the external stress boundaries are relevant, and these are controlled by the constant confining stress. If the fracture pressure increases significantly faster than that in the pores in the surrounding matrix, a compressive stress due to fracture swelling will inevitably arise at the interface. This is similar to the internal swelling stress proposed by Liu et al. [24].
2.2. Governing Equation for Mechanical Response
2.3. Dynamic Permeability Model
2.4. Governing Equation for Gas Flow within the Matrix
2.5. Governing Equation for Gas Flow within Fractures
2.6. Coupled Governing Equations
3. Implementation and Simulation
3.1. Finite Element Implementation
3.2. Simulations
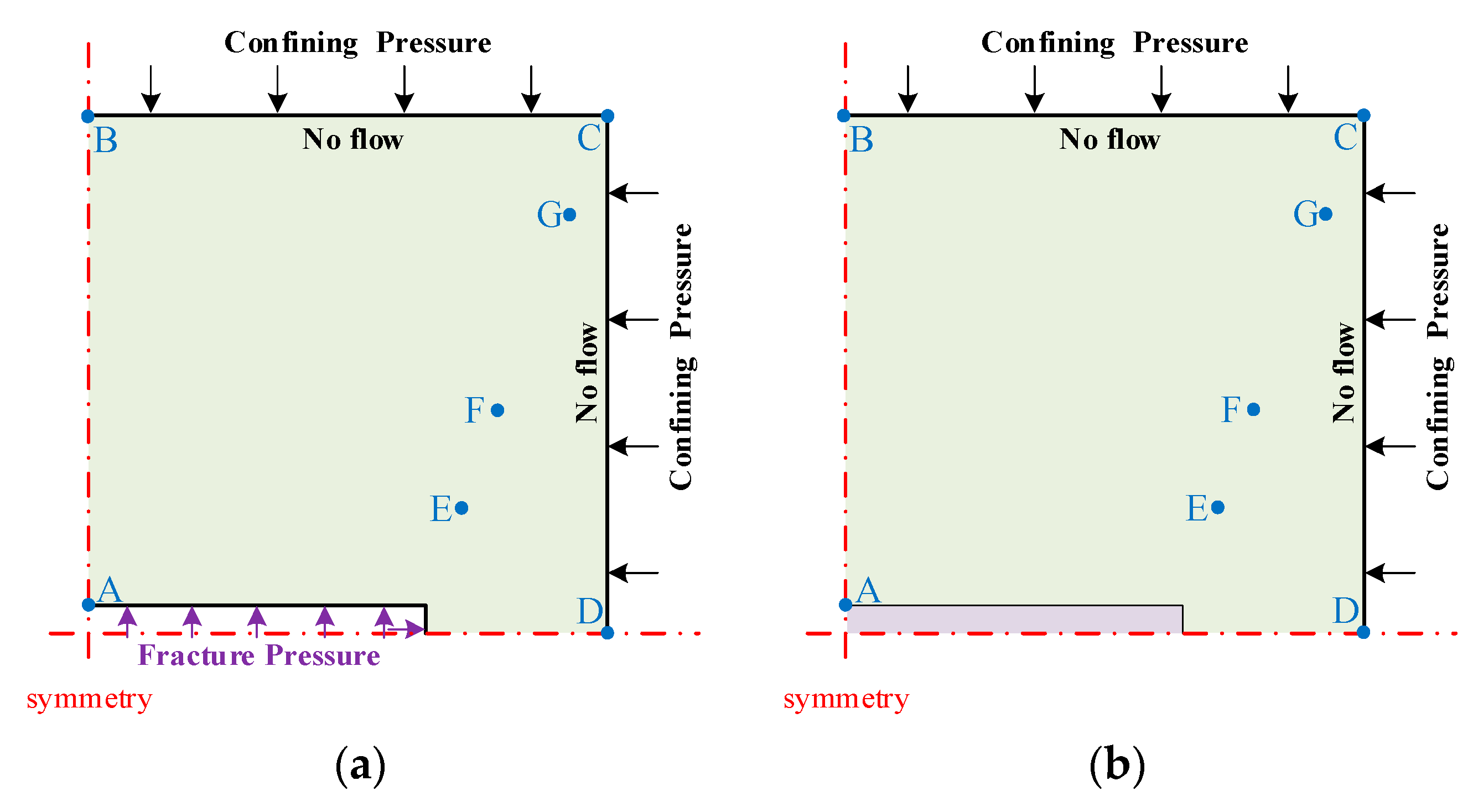
- The fracture is regarded as void. For the deformation model, the confining stress is applied to all the external boundaries and the fracture pressure (injection pressure) is applied to the internal boundaries. For gas flow, the injection pressure in Equation (30) is applied to the internal boundaries and no flow conditions are applied to all the external boundaries.
- The fracture is regarded as a soft inclusion without sorption. For the deformation model, the confining stress is applied to all the external boundaries. For the gas flow model, no flow conditions are applied to all the external boundaries.
4. Results and Discussion
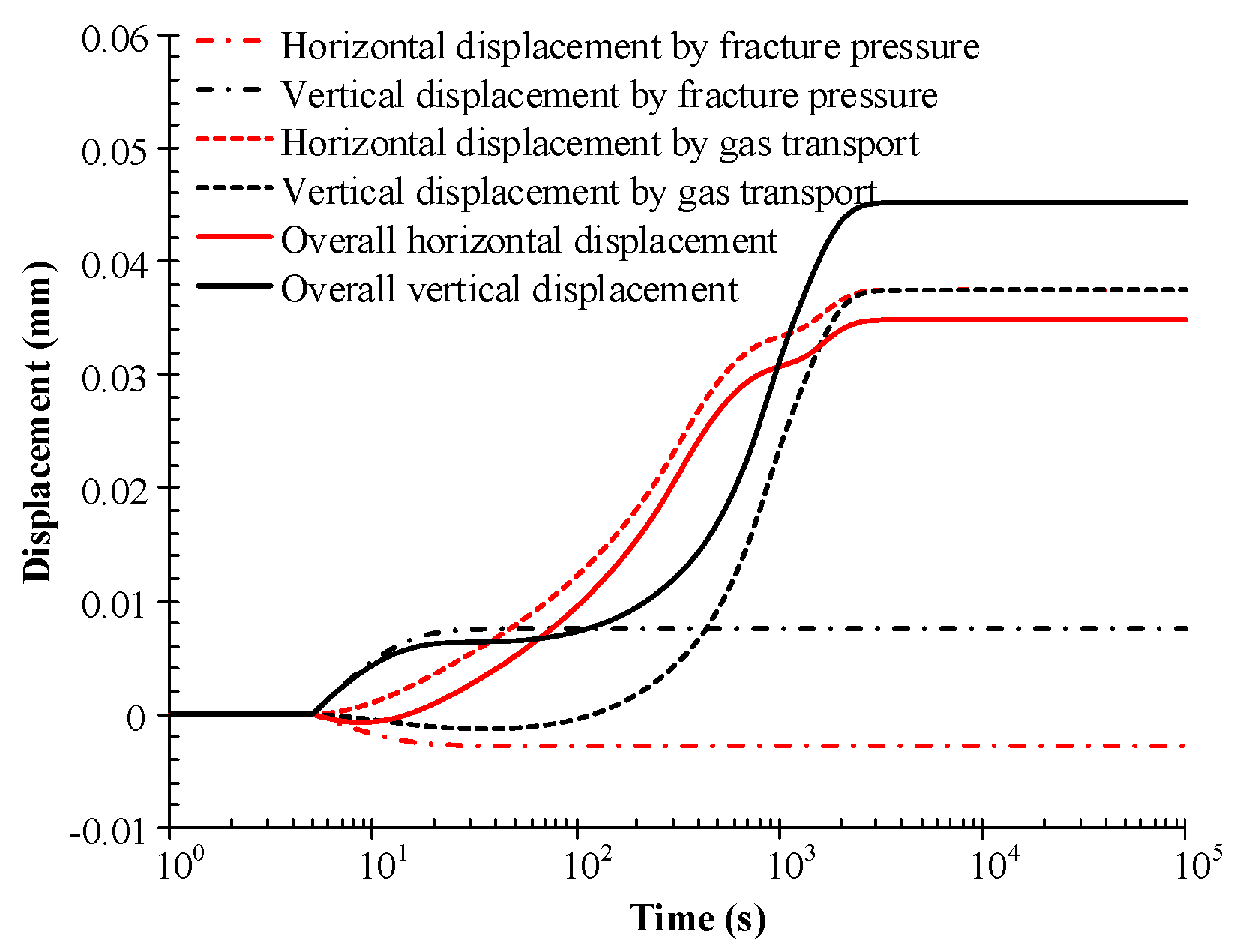
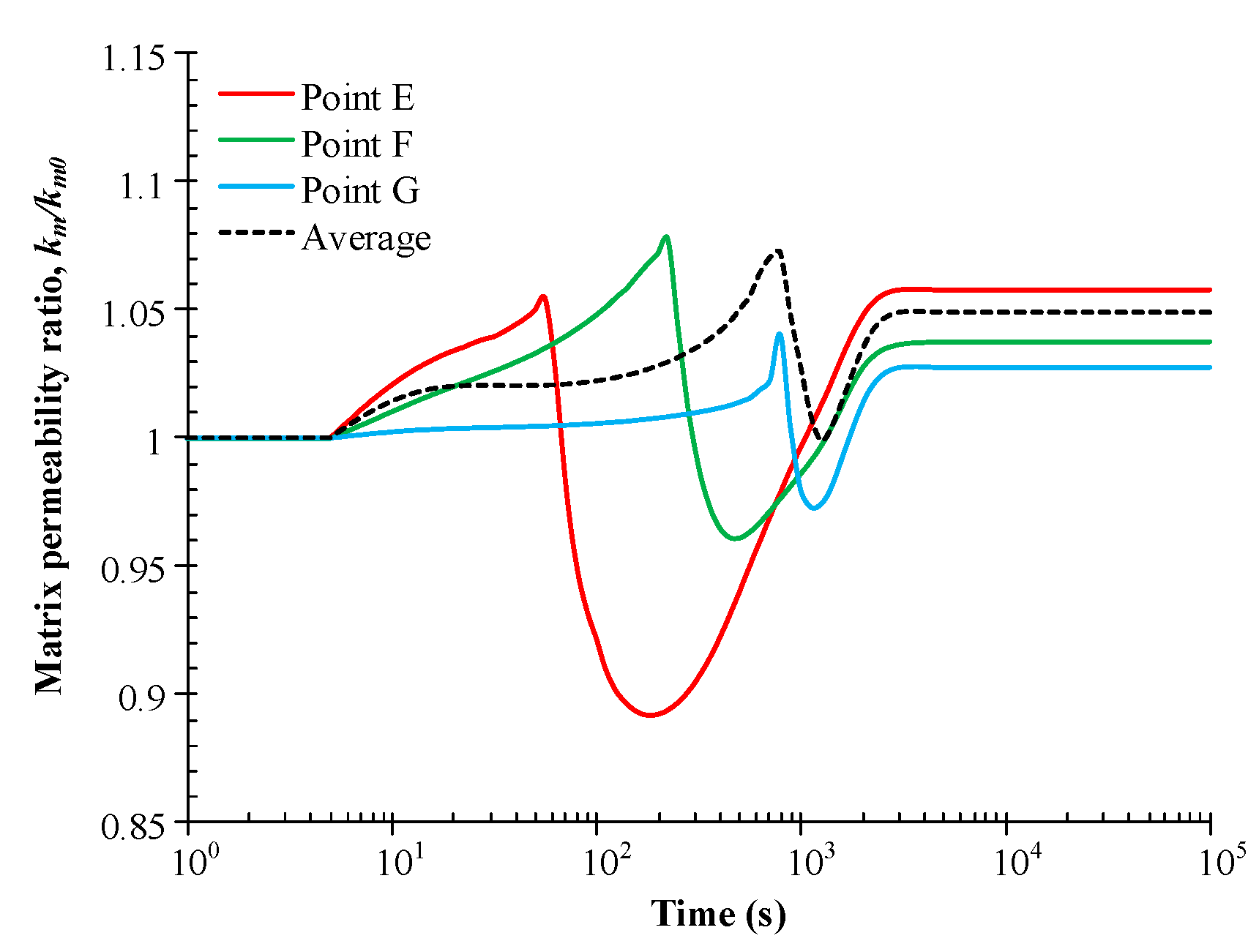
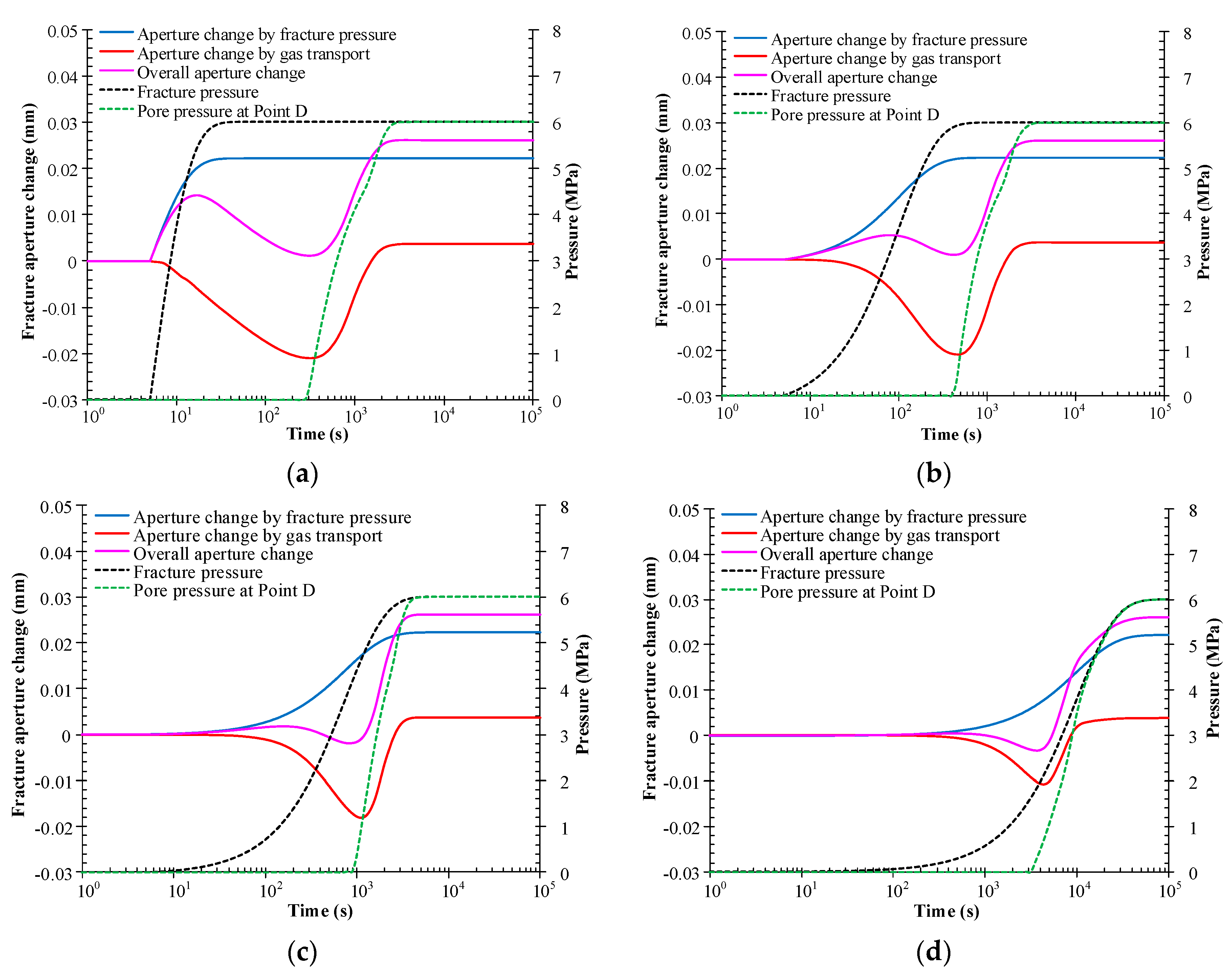
4.1. Analysis of Evolving Mechanisms
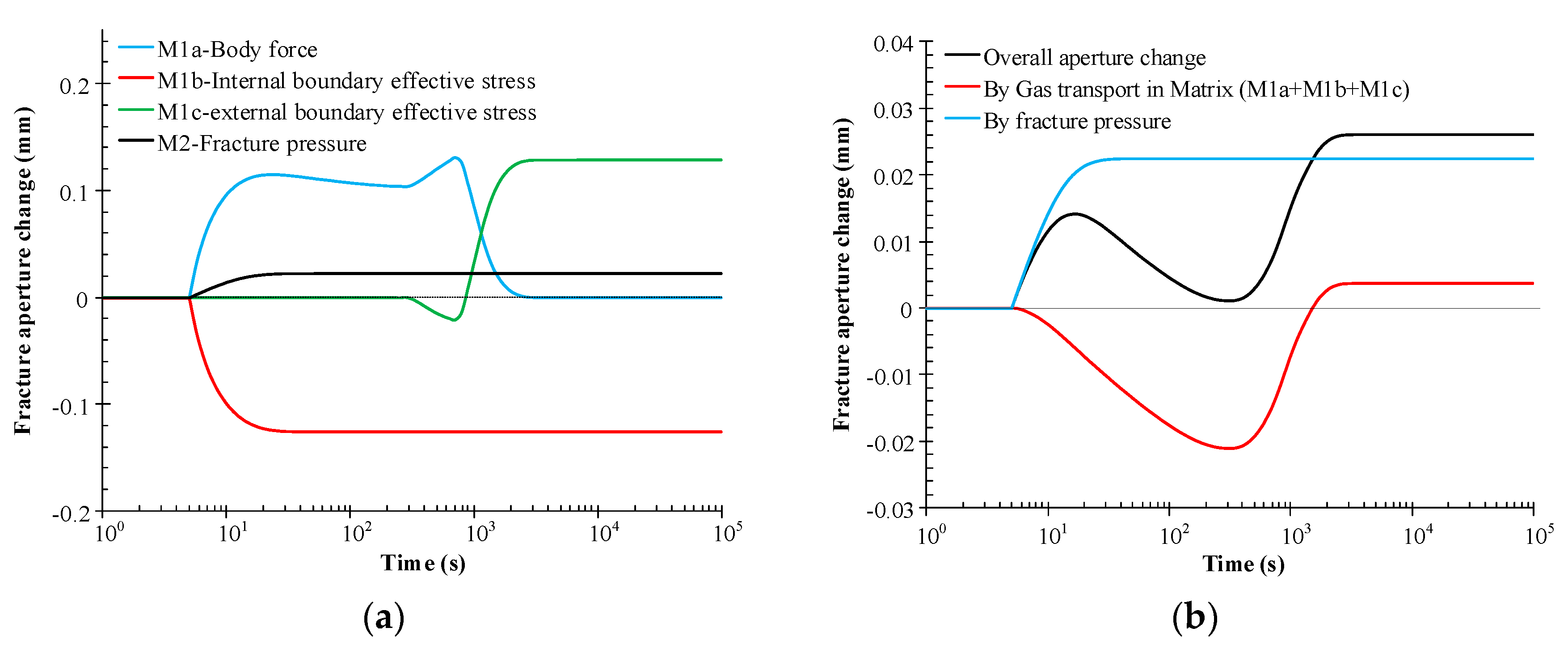
- (1)
- Gas injection with increasing pressure inflates the fracture due to an increase in the external stress applied to the internal boundaries but narrows the fracture aperture due to the increase of the pore pressure on the internal boundaries. These two effects are enhanced from 5 s to 40 s due to the continuous increase in fracture pressure and remain unchanged after the fracture pressure reaches the maximum. It should be noted that the effect of the body force is determined by the gas pressure gradient in the matrix, thus it can be influenced by the increasing rate of the fracture pressure rather than the fracture pressure itself.
- (2)
- From 40 s to 300 s, the fracture pressure remains constant, causing no change to the opening or narrowing effects induced by effective stress on the internal boundaries, and the pore pressure on the external boundaries remains at the initial value. This induces no change in effective stress on the external boundaries and has a null effect on fracture aperture change. However, the opening effect induced by the body force is slightly weakened as the gas propagates into the matrix.
- (3)
- From 300 s to 700 s, the pore pressure on the external vertical boundaries increases gradually and the pressure gradient on the boundary further drives gas transport inside. During this period, the horizontal body force decreases while the vertical body force continues to increase, leading to the enhanced opening of the fracture. The pore pressure increase on the external vertical boundaries results in a horizontal stress, leading to the narrowing of the fracture.
- (4)
- From 700 s to 4000 s, the pore pressure on the external horizontal boundaries increases gradually, and the gas is transported from the center to the corner as driven by the pressure gradient. During this period, both horizontal and vertical body forces decrease, and the fracture recovers from the opening state. The pore pressure increase on the external horizontal boundaries generates vertical stress. This leads to the fracture opening after counteracting the narrowing effect of horizontal stress on the external vertical boundaries.
- (5)
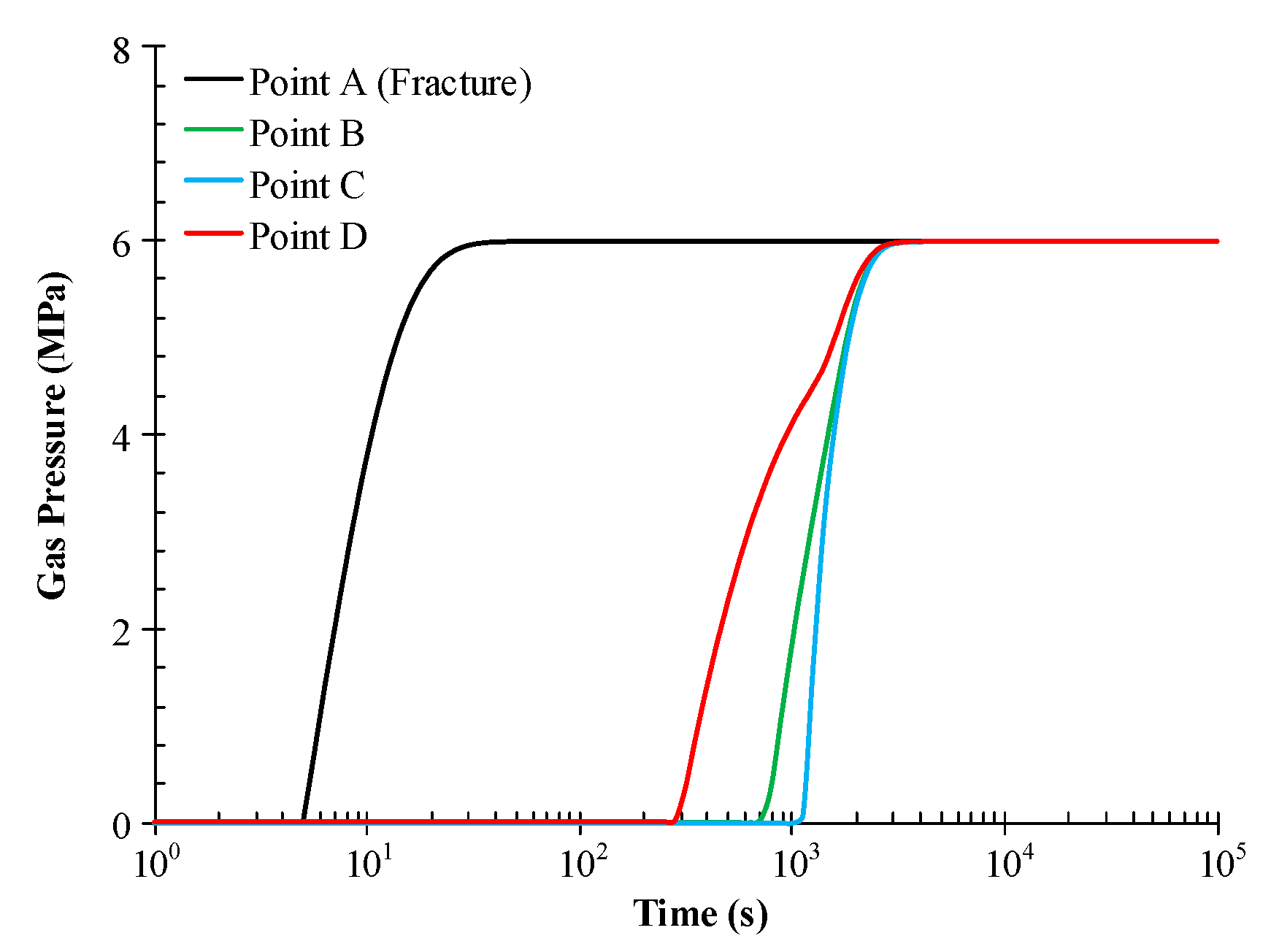
- From 4000 s, the pore pressure in the whole matrix is equalized with the fracture pressure, and an ultimate equilibrium state is achieved.
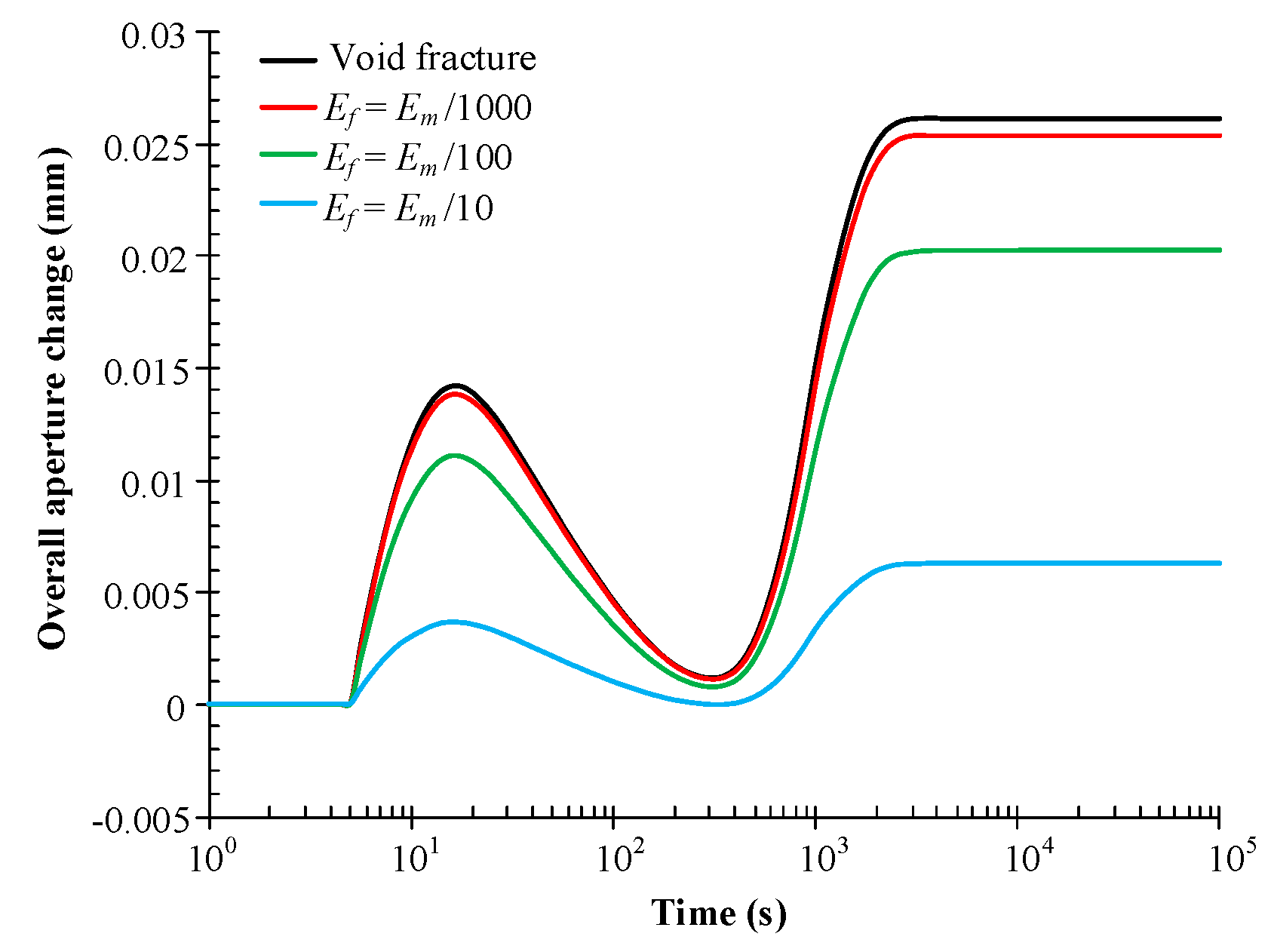
4.2. Impacts of Fracture Properties
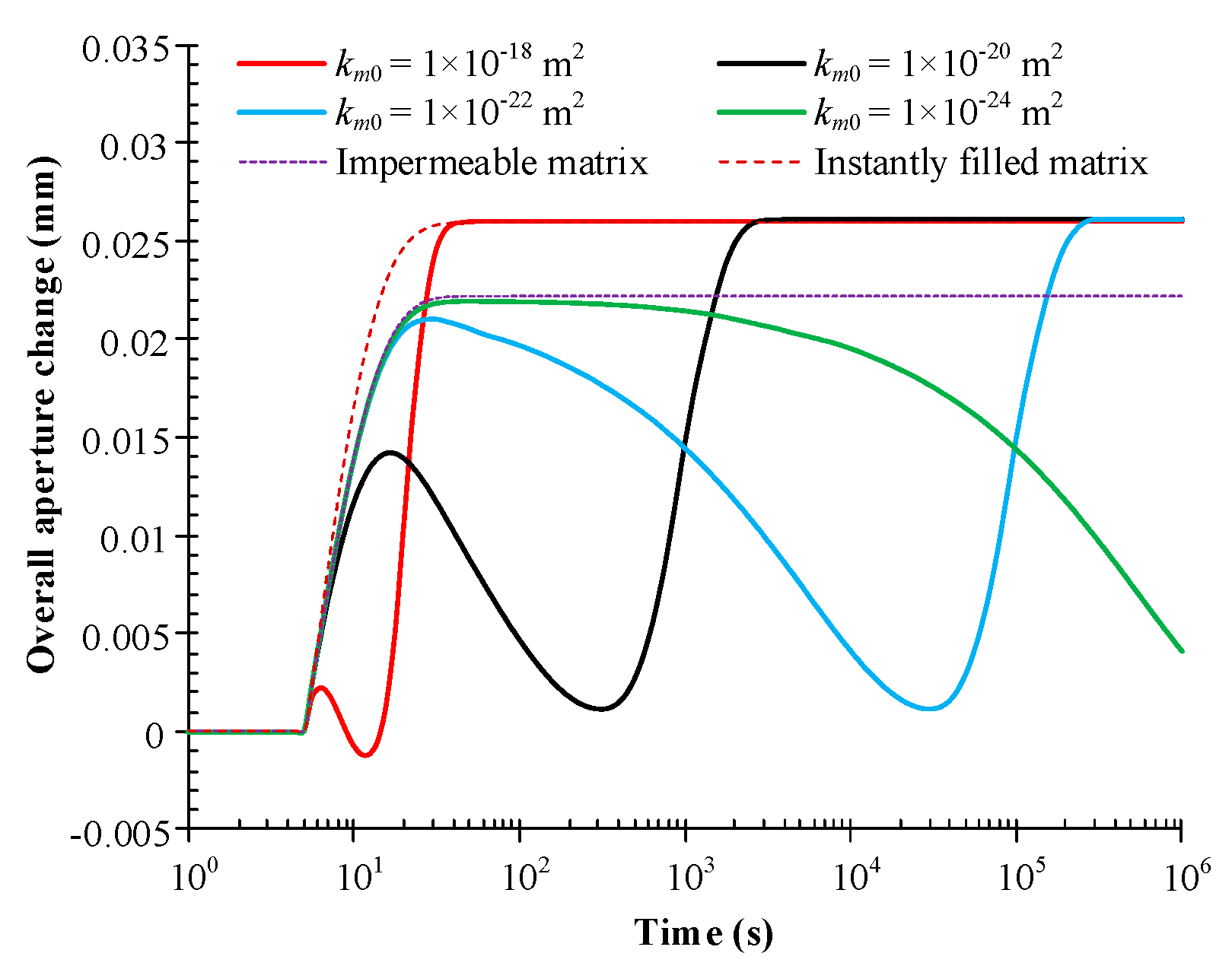
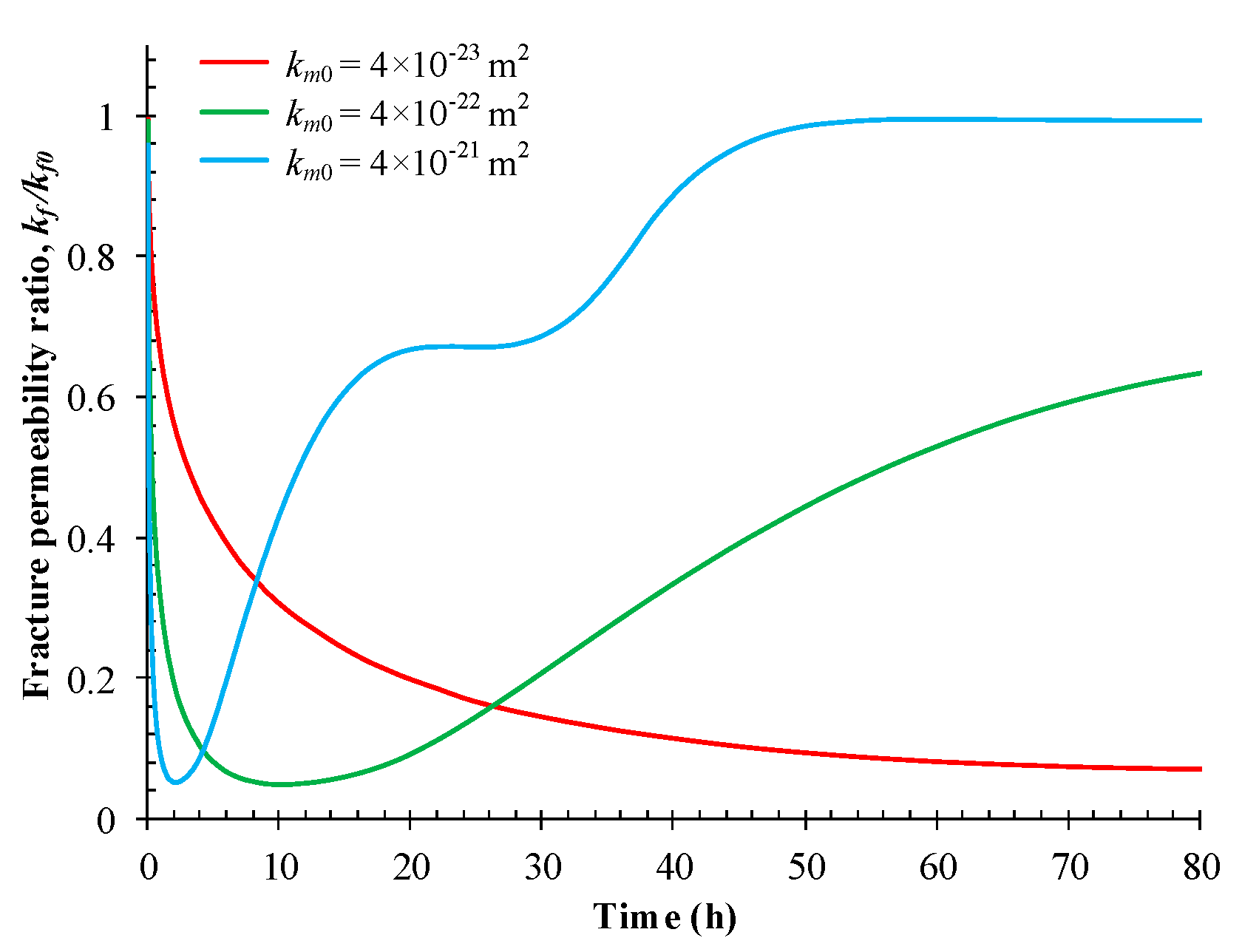
4.3. Impacts of Initial Matrix Permeability
4.4. Impacts of Injection Processes
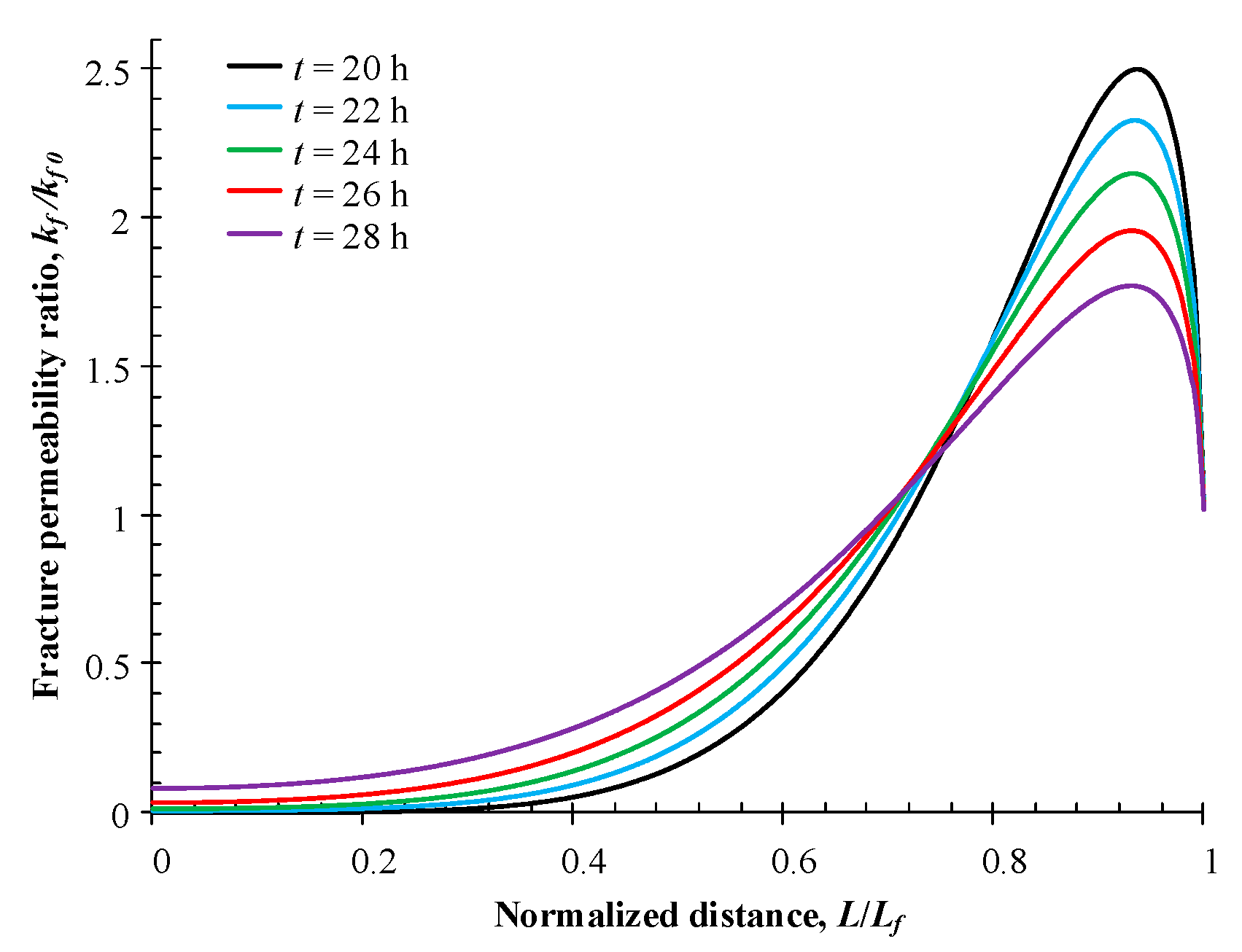
4.4.1. Impacts of Injection Characteristic Time
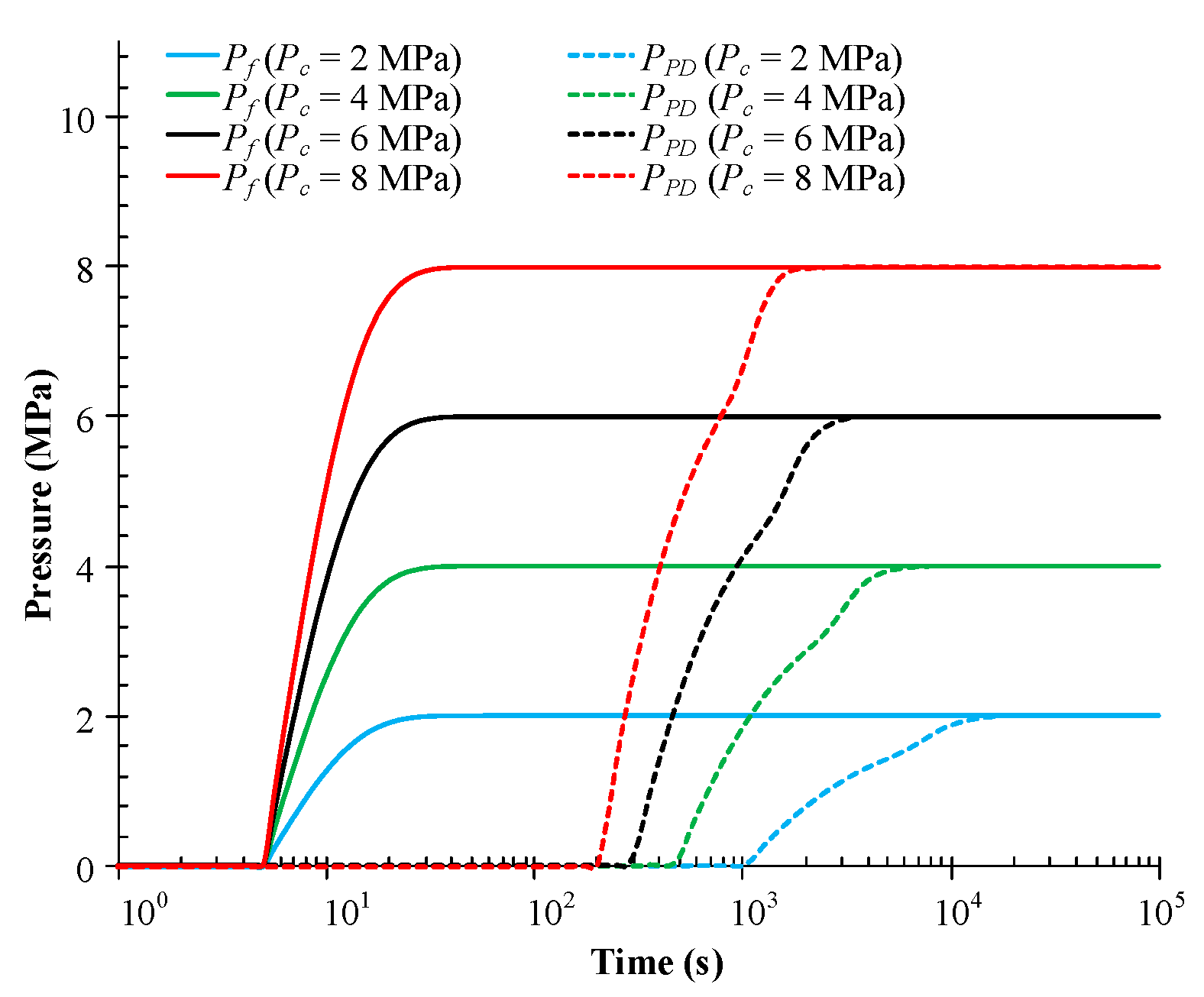
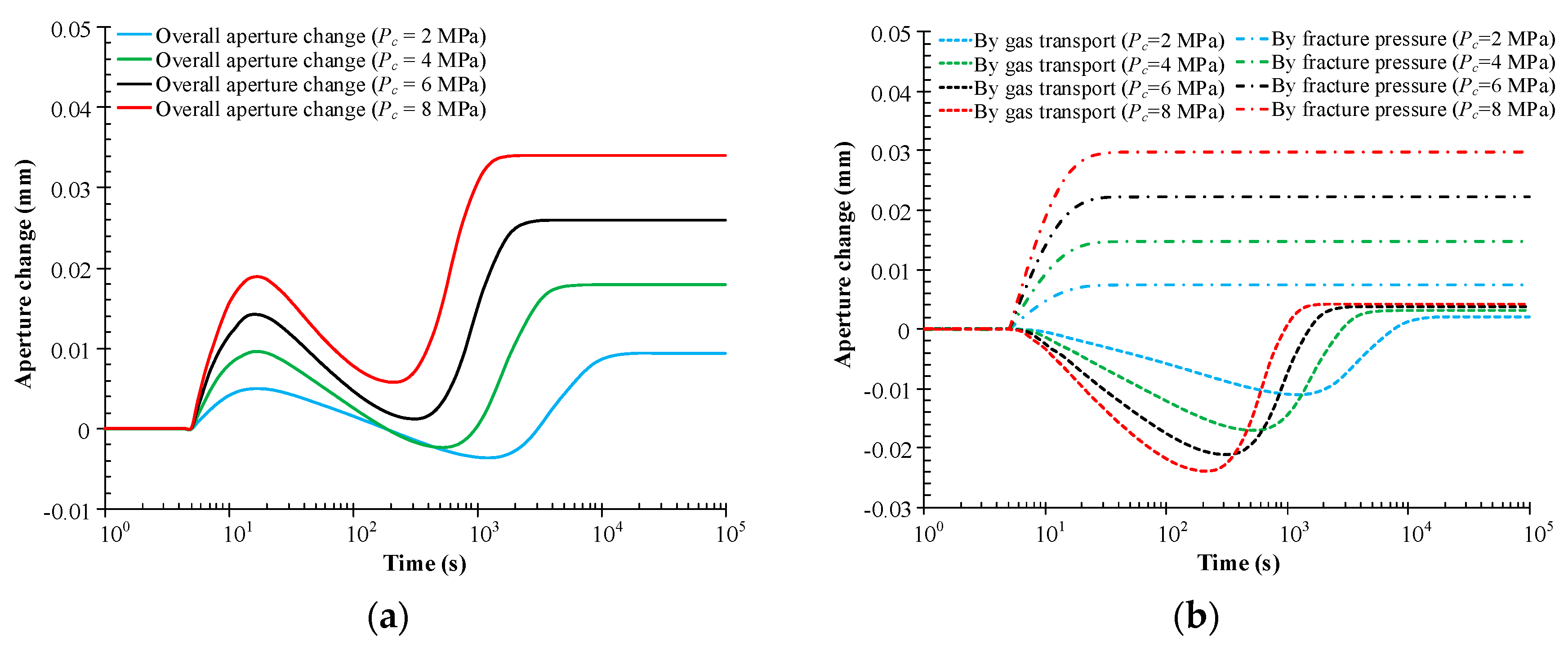
4.4.2. Impact of Injection Pressure Increment
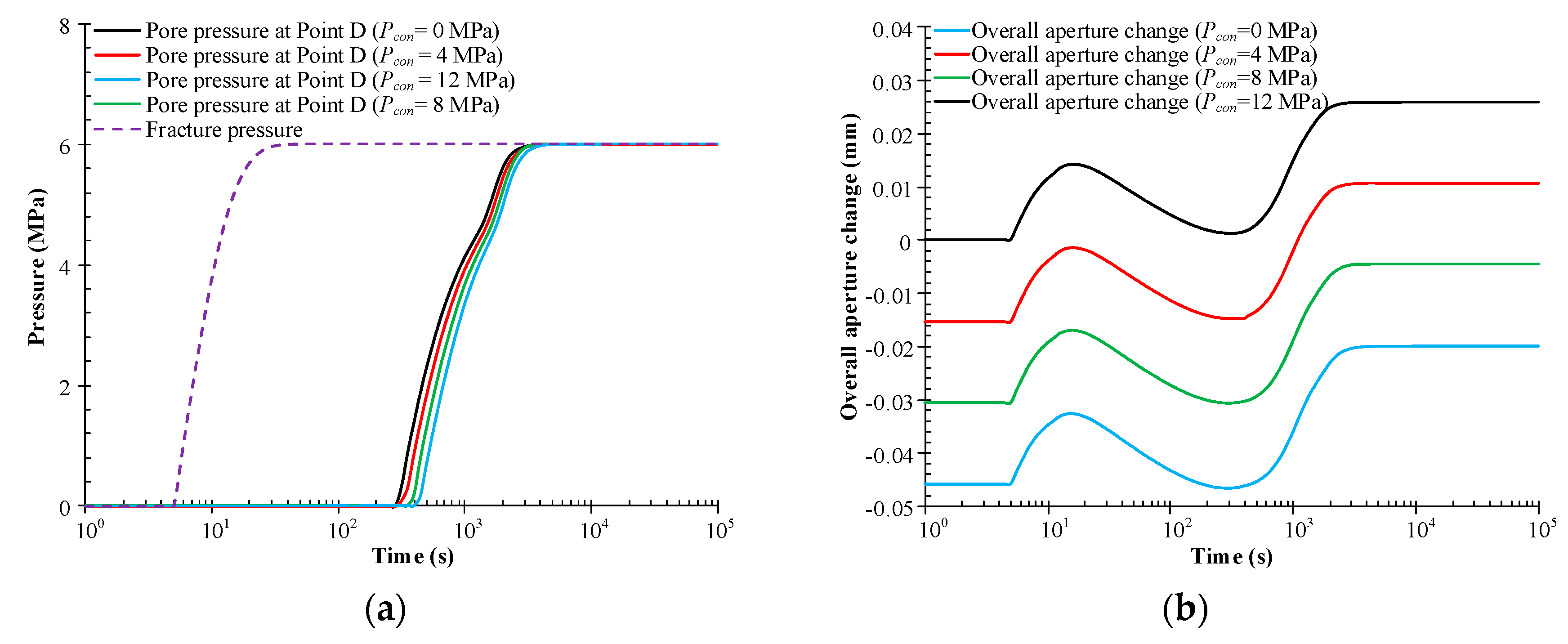
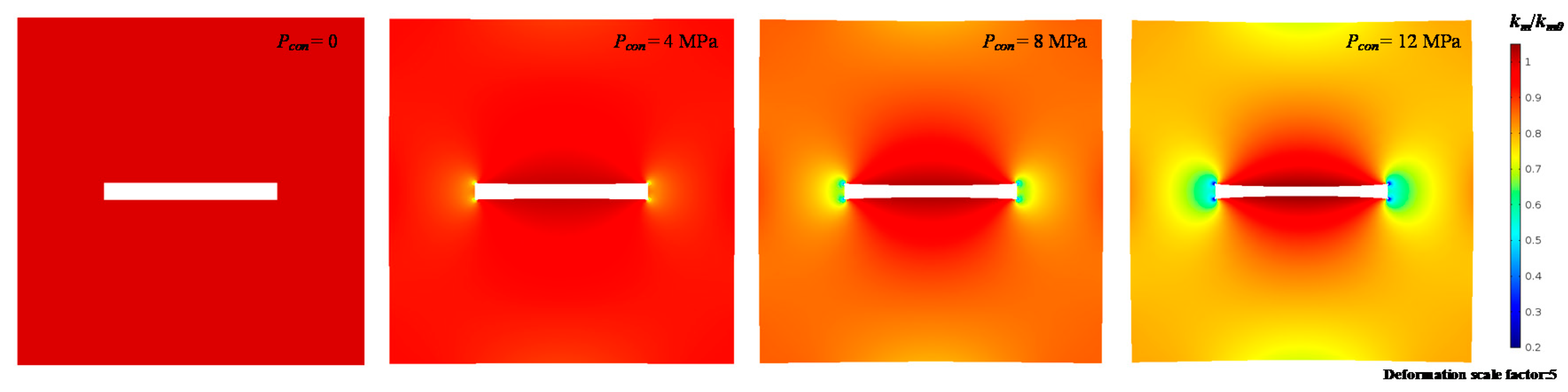
4.5. Impacts of Confining Pressure
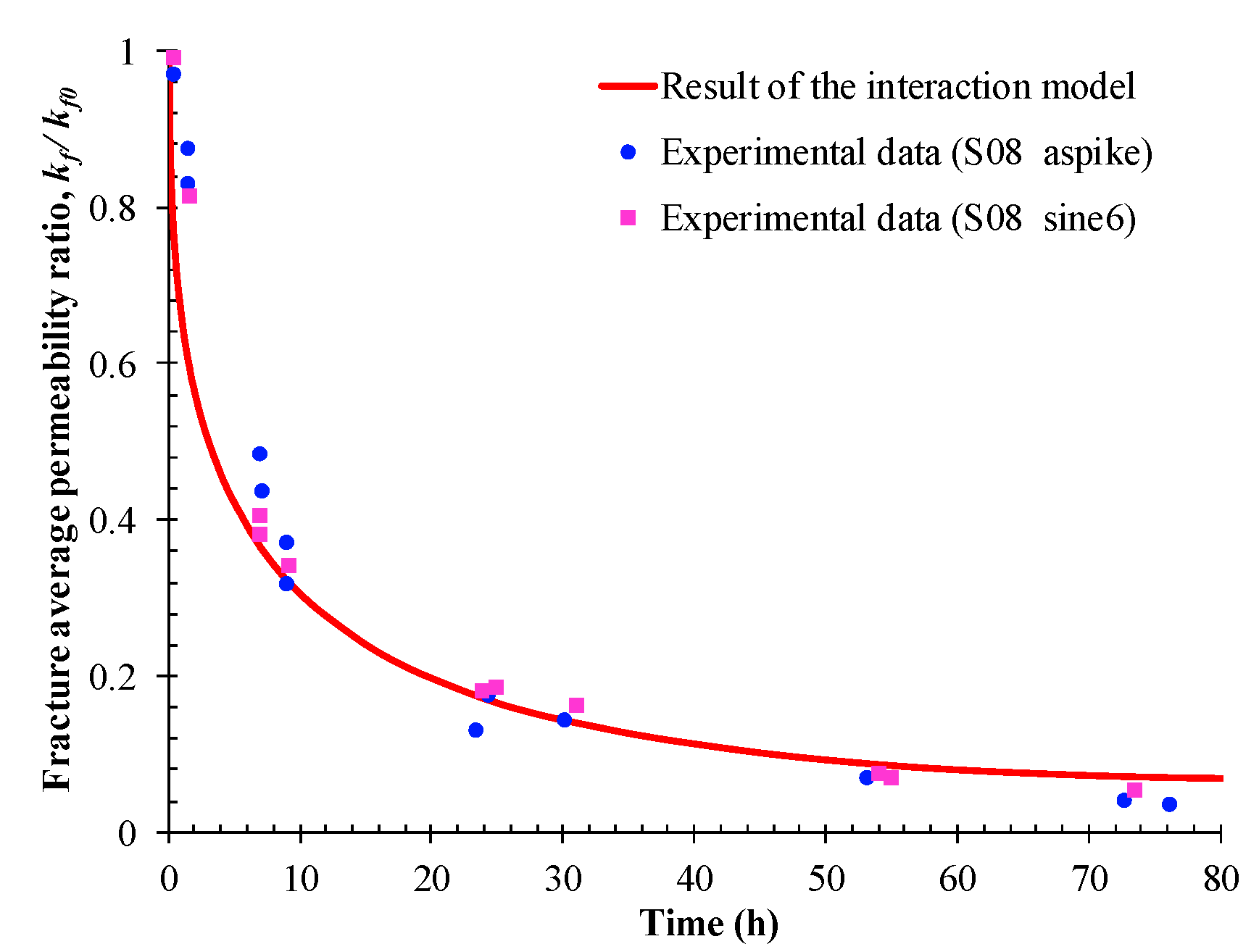
5. Verification with Experimental Data
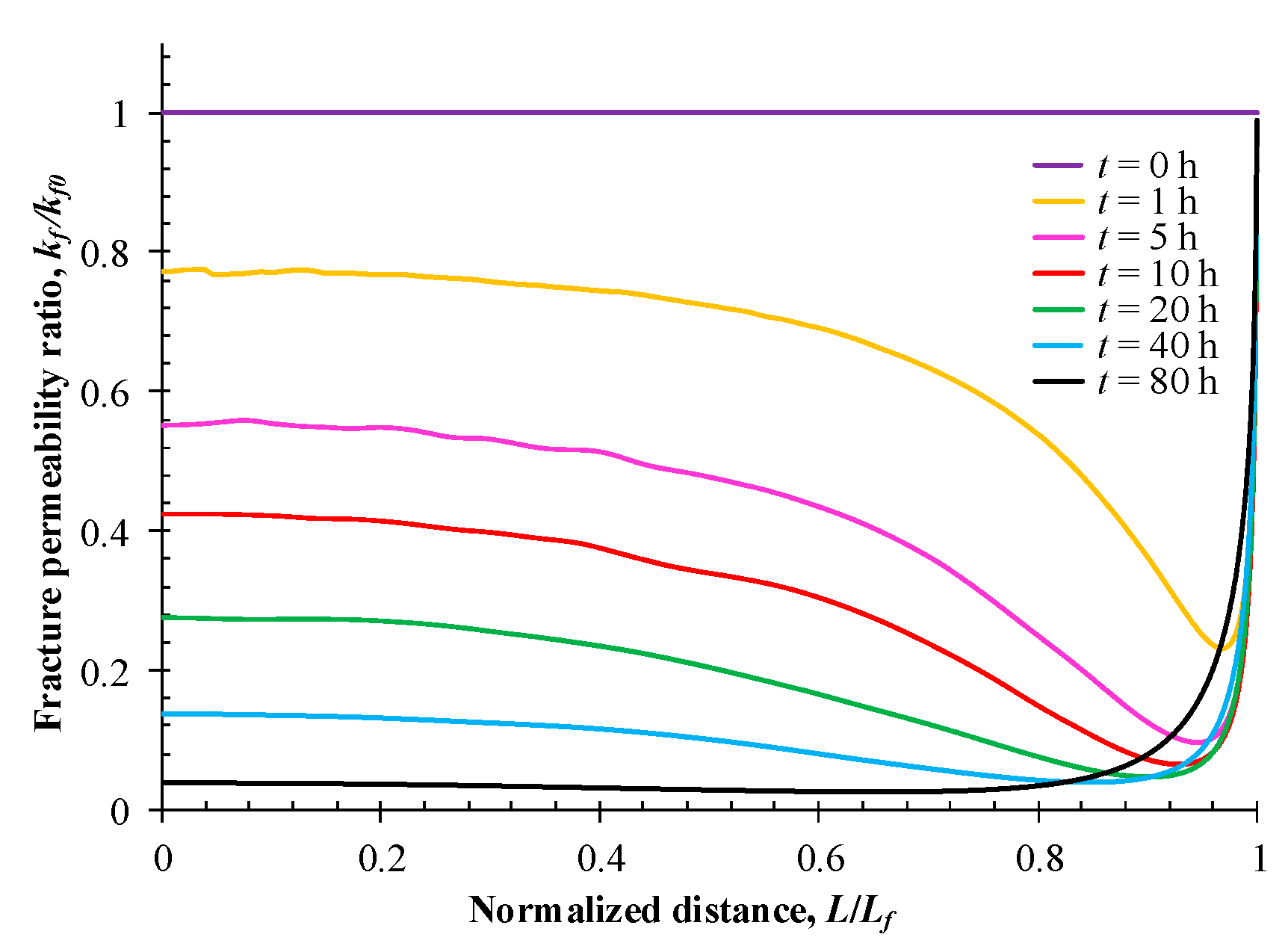
5.1. Evolution of Fracture Permeability
5.2. Sensitivity of Initial Matrix Permeability
6. Conclusions
- The evolution of coal permeability under unconstrained conditions is primarily controlled by the fracture pressure and gas transport in the matrix. The evolution of the non-equilibrium permeability, from the initial equilibrium permeability (when the matrix pressure is equalized with the fracture pressure prior to injection) to the final equilibrium permeability (when the matrix pressure is equalized with the matrix pressure after the gas injection) exhibits three distinct stages. In the case of gas injection, these three stages are (1) an increase in permeability due to the increased injection pressure; (2) a reduction due to the localization of matrix pressure in the vicinity of the fracture wall; and (3) recovery due to the equilibration of matrix pressure throughout the matrix block.
- The duration of the transient period, from the initial equilibrium state to the ultimate equilibrium state, is determined both by matrix transport properties and by loading processes on external boundaries and within the internal boundaries (interfaces between matrixes and fractures). For coal, this transient period may be extremely long, due to its low matrix permeability. This suggests that the permeabilities measured in many laboratory experiments may not indeed be equilibrium permeabilities, as represented in publications, and that experiments of extended duration should be developed to measure the non-equilibrium permeability in the transient state.
Author Contributions
Funding
Conflicts of Interest
References
- Connell, L.D.; Lu, M.; Pan, Z. An analytical coal permeability model for tri-axial strain and stress conditions. Int. J. Coal Geol. 2010, 84, 103–114. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Elsworth, D.; Qu, H.; Chen, D. Interactions of multiple processes during CBM extraction: A critical review. Int. J. Coal Geol. 2011, 87, 175–189. [Google Scholar] [CrossRef]
- Durucan, S.; Edwards, J. The effects of stress and fracturing on permeability of coal. Min. Sci. Technol. 1986, 3, 205–216. [Google Scholar] [CrossRef]
- Somerton, W.H.; Söylemezoḡlu, I.; Dudley, R. Effect of stress on permeability of coal. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Pergamon, Turkey, 1975; pp. 129–145. [Google Scholar]
- Clarkson, C.; Bustin, R. The effect of pore structure and gas pressure upon the transport properties of coal: A laboratory and modeling study. 1. Isotherms and pore volume distributions. Fuel 1999, 78, 1333–1344. [Google Scholar] [CrossRef]
- Gray, I. Reservoir engineering in coal seams: Part 1-The physical process of gas storage and movement in coal seams. SPE Res. Eng. 1987, 2, 28–34. [Google Scholar] [CrossRef]
- Harpalani, S.; Schraufnagel, R.A. Shrinkage of coal matrix with release of gas and its impact on permeability of coal. Fuel 1990, 69, 551–556. [Google Scholar] [CrossRef]
- Robertson, E.P.; Christiansen, R.L. Modeling permeability in coal using sorption-induced strain data. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, Texas, TX, USA, 9–12 October 2005. [Google Scholar] [CrossRef]
- Seidle, J.R.; Huitt, L. Experimental measurement of coal matrix shrinkage due to gas desorption and implications for cleat permeability increases. In Proceedings of the International Meeting on Petroleum Engineering, Beijing, China, 14–17 November 1995. [Google Scholar] [CrossRef]
- Tan, Y.; Ning, J.; Li, H. In situ explorations on zonal disintegration of roof strata in deep coalmines. Int. J. Rock Mech. Min. Sci. 2012, 49, 113–124. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D.; Camilleri, M. Laboratory characterisation of coal reservoir permeability for primary and enhanced coalbed methane recovery. Int. J. Coal Geol. 2010, 82, 252–261. [Google Scholar] [CrossRef]
- Pini, R.; Ottiger, S.; Burlini, L.; Storti, G.; Mazzotti, M. Role of adsorption and swelling on the dynamics of gas injection in coal. J. Geophys. Res.-Solid Earth 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Han, F.; Busch, A.; van Wageningen, N.; Yang, J.; Liu, Z.; Krooss, B.M. Experimental study of gas and water transport processes in the inter-cleat (matrix) system of coal: Anthracite from Qinshui Basin, China. Int. J. Coal Geol. 2010, 81, 128–138. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D.; Camilleri, M.; Connelly, L. Effects of matrix moisture on gas diffusion and flow in coal. Fuel 2010, 89, 3207–3217. [Google Scholar] [CrossRef]
- Siriwardane, H.; Haljasmaa, I.; McLendon, R.; Irdi, G.; Soong, Y.; Bromhal, G. Influence of carbon dioxide on coal permeability determined by pressure transient methods. Int. J. Coal Geol. 2009, 77, 109–118. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Elsworth, D.; Connell, L.D.; Pan, Z. Impact of CO2 injection and differential deformation on CO2 injectivity under in-situ stress conditions. Int. J. Coal Geol. 2010, 81, 97–108. [Google Scholar] [CrossRef]
- Connell, L. Coupled flow and geomechanical processes during gas production from coal seams. Int. J. Coal Geol. 2009, 79, 18–28. [Google Scholar] [CrossRef]
- Cui, X.; Bustin, R.M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams. AAPG Bull. 2005, 89, 1181–1202. [Google Scholar] [CrossRef]
- Izadi, G.; Wang, S.; Elsworth, D.; Liu, J.; Wu, Y.; Pone, D. Permeability evolution of fluid-infiltrated coal containing discrete fractures. Int. J. Coal Geol. 2011, 85, 202–211. [Google Scholar] [CrossRef]
- Palmer, I.; Mansoori, J. How permeability depends on stress and pore pressure in coalbeds: A new model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. Drawdown Induced Changes in Permeability of Coalbeds: A New Interpretation of the Reservoir Response to Primary Recovery. Transp. Porous Media 2004, 56, 1–16. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Elsworth, D. How sorption-induced matrix deformation affects gas flow in coal seams: A new FE model. Int. J. Rock Mech. Min. Sci. 2008, 45, 1226–1236. [Google Scholar] [CrossRef]
- Robertson, E.P.; Christiansen, R.L. A permeability model for coal and other fractured, sorptive-elastic media. In Proceedings of the SPE Eastern Regional Meeting, Canton, OH, USA, 11–13 October 2006. [Google Scholar] [CrossRef]
- Liu, H.H.; Rutqvist, J.; Oldenburg, C.M. A new coal-permeability model: Internal swelling stress and fracture-matrix interaction. Transp. Porous Media 2010, 82, 157–171. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, Z.; Liu, J.; Connell, L.D.; Elsworth, D. Effect of the effective stress coefficient and sorption-induced strain on the evolution of coal permeability: Experimental observations. Int. J. Greenh. Gas Control 2011, 5, 1284–1293. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Pan, Z.; Connell, L.D.; Elsworth, D. Influence of the effective stress coefficient and sorption-induced strain on the evolution of coal permeability: Model development and analysis. Int. J. Greenh. Gas Control 2012, 8, 101–110. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.; Chen, Z.; Wang, S.; Elsworth, D.; Jiang, Y. Impact of transition from local swelling to macro swelling on the evolution of coal permeability. Int. J. Coal Geol. 2011, 88, 31–40. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; Wei, M.; Pan, Z.; Connell, L.D. Why coal permeability changes under free swellings: New insights. Int. J. Coal Geol. 2014, 133, 35–46. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; Zhu, W.; Pan, Z.; Connell, L. Benchmark assessment of coal permeability models on the accuracy of permeability prediction. Fuel 2014, 132, 194–203. [Google Scholar] [CrossRef]
- Robertson, E.P. Measurement and Modeling of Sorption-Induced Strain and Permeability Changes in Coal. Ph.D. Thesis, Colorado School of Mines, Arthur Lakes Library, Golden, CO, USA, 2005. [Google Scholar] [Green Version]
- Bai, M.; Elsworth, D.; Roegiers, J.C. Multiporosity/multipermeability approach to the simulation of naturally fractured reservoirs. Water Resour. Res. 1993, 29, 1621–1634. [Google Scholar] [CrossRef]
- Berryman, J.G.; Wang, H.F. The elastic coefficients of double-porosity models for fluid transport in jointed rock. J. Geophys. Res.-Solid Earth 1995, 100, 24611–24627. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Liu, J.; Feng, J.; Wei, M.; Wang, C.; Jiang, Y. Effects of gas diffusion from fractures to coal matrix on the evolution of coal strains: Experimental observations. Int. J. Coal Geol. 2016, 162, 74–84. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Elsworth, D.; Miao, X.; Mao, X. Development of anisotropic permeability during coalbed methane production. J. Nat. Gas Sci. Eng. 2010, 2, 197–210. [Google Scholar] [CrossRef]
- Cai, M.; Horii, H. A constitutive model of highly jointed rock masses. Mech. Mater. 1992, 13, 217–246. [Google Scholar] [CrossRef]
- Warren, J.; Root, P.J. The behavior of naturally fractured reservoirs. Soc. Petrol. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Elsworth, D.; Pan, Z.; Wang, S. Roles of coal heterogeneity on evolution of coal permeability under unconstrained boundary conditions. J. Nat. Gas Sci. Eng. 2013, 15, 38–52. [Google Scholar] [CrossRef]
- Chilingar, G.V. Relationship between porosity, permeability, and grain-size distribution of sands and sandstones. In Developments in Sedimentology; Straaten, L.M.J.U.V., Ed.; Elsevier Science Publishers: Amsterdam, The Netherlands, 1964; Volume 1, pp. 71–75. [Google Scholar]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Saghafi, A.; Faiz, M.; Roberts, D. CO2 storage and gas diffusivity properties of coals from Sydney Basin, Australia. Int. J. Coal Geol. 2007, 70, 240–254. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Noorishad, J.; Tsang, C.-F. Coupled thermohydroelasticity phenomena in variably saturated fractured porous rocks--formulation and numerical solution. In Developments in Geotechnical Engineering; Stephansson, O., Ed.; Elsevier Science Publishers: Amsterdam, The Netherlands, 1996; Volume 79, pp. 93–134. [Google Scholar]
- Qu, H.; Liu, J.; Pan, Z.; Connell, L. Impact of matrix swelling area propagation on the evolution of coal permeability under coupled multiple processes. J. Nat. Gas Sci. Eng. 2014, 18, 451–466. [Google Scholar] [CrossRef]
- Renshaw, C.E. On the relationship between mechanical and hydraulic apertures in rough-walled fractures. J. Geophys. Res.-Solid Earth 1995, 100, 24629–24636. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Bodvarsson, G.S. Hydraulic conductivity of rock fractures. Transp. Porous Media 1996, 23, 1–30. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Young’s modulus, MPa | 6 × 10−3 |
| Poisson’s ratio | 0.4 |
| Matrix porosity | 0.2 |
| Matrix permeability, m2 | 4 × 10−6 |
| Biot’s coefficient | 1.0 |
| Water density, kg/m3 | 1000 |
| Dynamic viscosity, Pa·s | 1 × 10−3 |
| Thermal conductivity, kJ/(m·s·K) | 0.836 |
| Specific heat, kJ/(m3·K) | 167.0 |
| Linear thermal expansion coefficient, 1/K | 3 × 10−7 |
| Parameter | Matrix-fracture Model CH4 | Verification Model CO2 |
|---|---|---|
| Matrix porosity, φm0 | 0.05 | 0.027 |
| Matrix permeability, km0 (m2) | 10−20 | 4 × 10−23 |
| Matrix density, ρc (kg/m3) | 1500 | 1500 |
| Matrix Young’s modulus, Em (GPa) | 3.95 | 5.42 |
| Fracture Young’s modulus, Ef (GPa) | - | Em/2000 |
| Poisson ratio, v | 0.1 | 0.34 |
| Biot’s coefficient, α | 0.66 | 0.66 |
| Langmuir strain constant, εL | 0.03 | 0.0119 |
| Langmuir volume constant, VL (m3/kg) | 0.01316 | 0.0477 |
| Langmuir pressure constant, PL (MPa) | 3.96 | 2.76 |
| Gas density at standard condition, ρga (kg/m3) | 0.717 | 1.96 |
| Gas viscosity, μ (Pa·s) | 1.2278 × 10−5 | 1.84 × 10−5 |
| Temperature, T (K) | 298.15 | 298.15 |
| Confining pressure, Pcon (MPa) | 0 | 0 |
| Initial reservoir pressure, Pini (MPa) | 0 | 0 |
| Injection pressure increment, Pc (MPa) | 6 | - |
| Injection starting time, tp (s) | 5 | - |
| Injection speed characteristic time, td (s) | 750 | - |
| Parameter Investigated | Value |
|---|---|
| Fracture properties, Ef | Void, Em/1000, Em/100, Em/10 |
| Initial matrix permeability, km0 (m2) | 10−18, 10−20, 10−22, 10−24 |
| Injection speed characteristic time, td (s) | 5, 100, 750, 10,000 |
| Injection pressure increment, Pc (MPa) | 2, 4, 6, 8 |
| Confining pressure, Pcon (MPa) | 0, 4, 8, 12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Sheng, J.; Liu, J.; Hu, Y. Evolution of Coal Permeability during Gas Injection—From Initial to Ultimate Equilibrium. Energies 2018, 11, 2800. https://doi.org/10.3390/en11102800
Liu X, Sheng J, Liu J, Hu Y. Evolution of Coal Permeability during Gas Injection—From Initial to Ultimate Equilibrium. Energies. 2018; 11(10):2800. https://doi.org/10.3390/en11102800
Chicago/Turabian StyleLiu, Xingxing, Jinchang Sheng, Jishan Liu, and Yunjin Hu. 2018. "Evolution of Coal Permeability during Gas Injection—From Initial to Ultimate Equilibrium" Energies 11, no. 10: 2800. https://doi.org/10.3390/en11102800
APA StyleLiu, X., Sheng, J., Liu, J., & Hu, Y. (2018). Evolution of Coal Permeability during Gas Injection—From Initial to Ultimate Equilibrium. Energies, 11(10), 2800. https://doi.org/10.3390/en11102800





