Validation of a Coupled Electrical and Hydrodynamic Simulation Model for a Vertical Axis Marine Current Energy Converter
Abstract
:1. Introduction
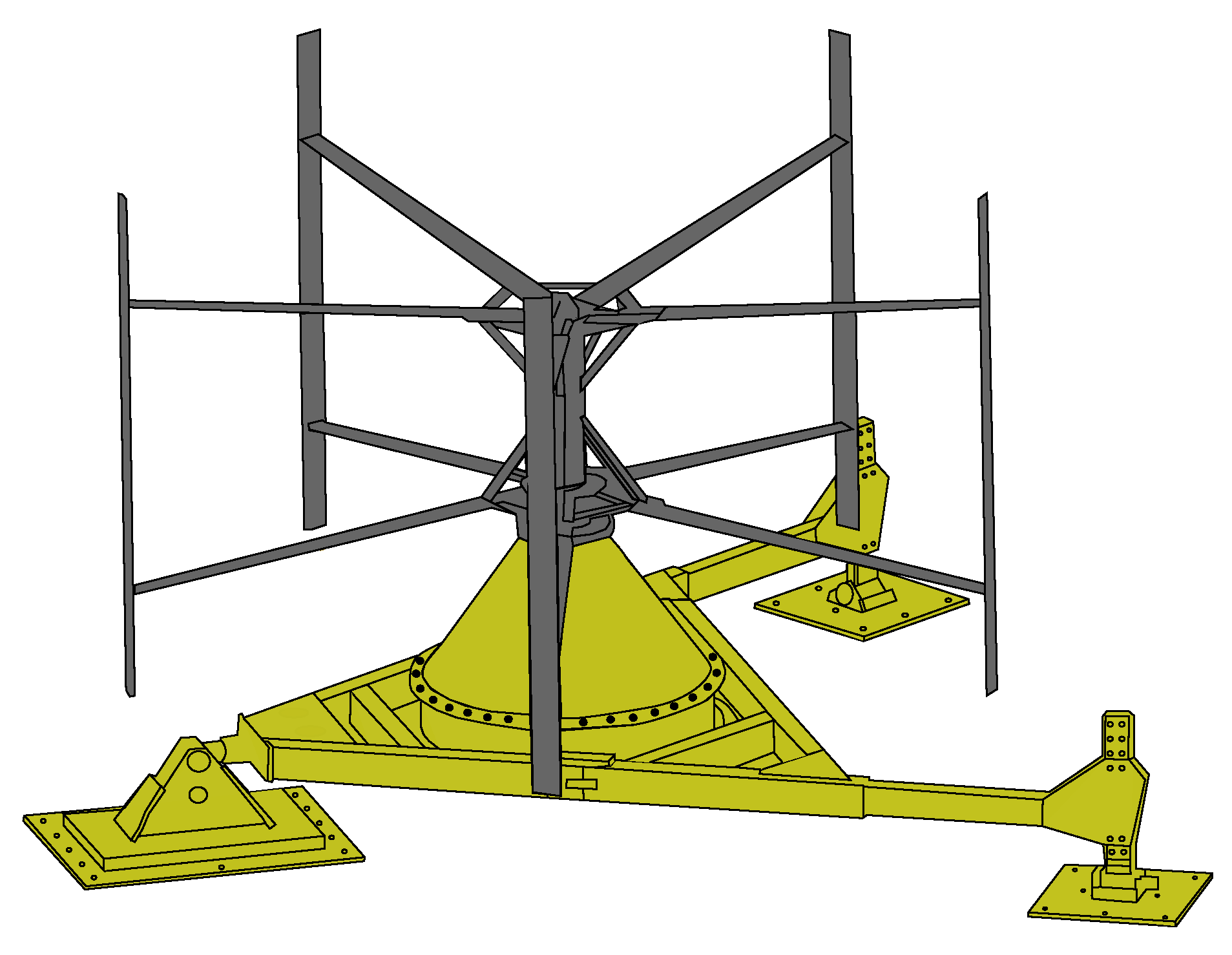
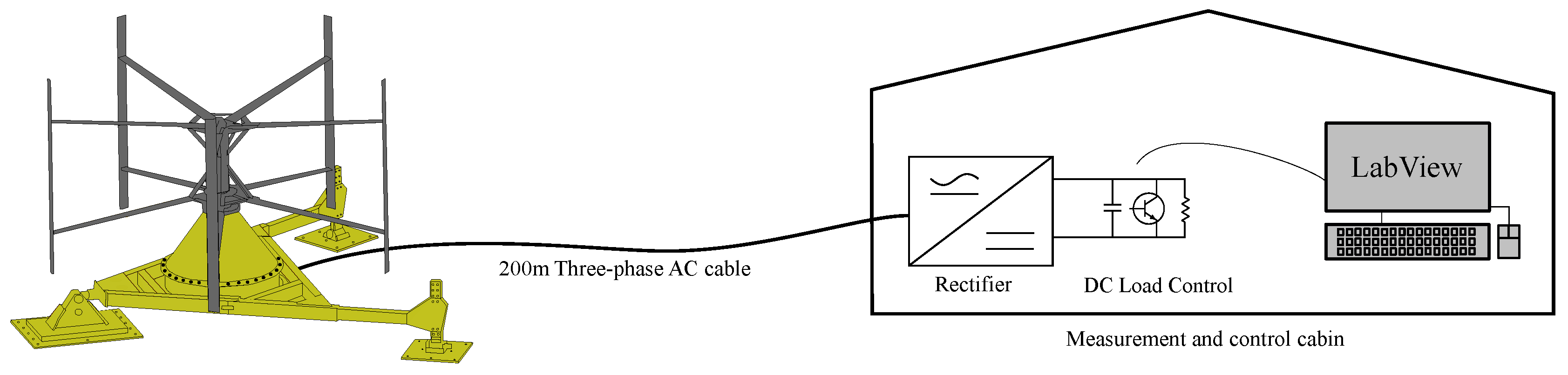
2. The Söderfors Experimental Station
2.1. The Turbine, the Generator and Load Control
2.2. Electrical Layout and Control System
2.3. Water Speed Measurements
3. Coupling of the Electrical and the Hydrodynamic Vortex Model
3.1. Electrical Model in Simulink
3.2. Hydrodynamic Vortex Model for Vertixal Axis Turbines
4. Calibrating the Simulation Model
4.1. Calibration of Generator and Electrical System Losses
4.2. Calibration of Drag Losses
5. Validating the Simulation Model
5.1. Simulations of the Power Capture of the Turbine
5.2. Step Response of Change in Target DC Bus Voltage
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Day, A.; Babarit, A.; Fontaine, A.; He, Y.P.; Kraskowski, M.; Murai, M.; Penesis, I.; Salvatore, F.; Shin, H.K. Hydrodynamic modelling of marine renewable energy devices: A state of the art review. Ocean Eng. 2015, 108, 46–69. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.J.; Bhuyan, G.; Iqbal, M.T.; Quaicoe, J.E. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Uihlein, A.; Magagna, D. Wave and tidal current energy—A review of the current state of research beyond technology. Renew. Sustain. Energy Rev. 2016, 58, 1070–1081. [Google Scholar] [CrossRef]
- Zhou, Z.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.; Tang, T. An up-to-date review of large marine tidal current turbine technologies. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 480–484. [Google Scholar]
- Bahaj, A.S. Marine current energy conversion: The dawn of a new era in electricity production. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef] [PubMed]
- Domenech, J.; Eveleigh, T.; Tanju, B. Marine hydrokinetic (MHK) systems: Using systems thinking in resource characterization and estimating costs for the practical harvest of electricity from tidal currents. Renew. Sustain. Energy Rev. 2018, 81, 723–730. [Google Scholar] [CrossRef]
- Paraschivoiu, I.; Allet, A. Aerodynamic analysis of the darrieus wind turbines including dynamic-stall effects. J. Propuls. Power 1988, 4, 472–477. [Google Scholar] [CrossRef]
- Strickland, J.H.; Webster, B.T.; Nguyen, T. A vortex model of the darrieus turbine: An analytical and experimental study. J. Fluids Eng. 1979, 101, 500–505. [Google Scholar] [CrossRef]
- Murray, J.; Barone, M. The development of CACTUS, a wind and marine turbine performance simulation code. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Sorensen, J.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Lundin, S.; Forslund, J.; Carpman, N.; Grabbe, M.; Yuen, K.; Apelfröjd, S.; Goude, A.; Leijon, M. The söderfors project: Experimental hydrokinetic power station deployment and first results. In Proceedings of the 10th European Wave and Tidal Energy Conference (EWTEC13), Aalborg, Denmark, 2–5 December 2013. [Google Scholar]
- Yuen, K.; Lundin, S.; Grabbe, M.; Lalander, E.; Goude, A.; Leijon, M. The Söderfors Project: Construction of an Experimental Hydrokinetic Power Station. In Proceedings of the 9th European Wave and Tidal Energy Conference, EWTEC11, Southampton, UK, 5–9 September 2011; pp. 1–5. [Google Scholar]
- Forslund, J.; Lundin, S.; Thomas, K.; Leijon, M. Experimental results of a DC bus voltage level control for a load controlled Marine Current Energy Converter. Energies 2015, 8, 4572–4586. [Google Scholar] [CrossRef]
- Grabbe, M.; Yuen, K.; Goude, A.; Lalander, E.; Leijon, M. Design of an experimental setup for hydro-kinetic energy conversion. Int. J. Hydropower Dams 2009, 15, 112–116. [Google Scholar]
- Lundin, S.; Forslund, J.; Goude, A.; Grabbe, M.; Yuen, K.; Leijon, M. Experimental demonstration of performance of a vertical axis marine current turbine in a river. J. Renew. Sustain. Energy 2016, 8, 064501. [Google Scholar] [CrossRef] [Green Version]
- Grabbe, M.; Yuen, K.; Apelfröjd, S.; Leijon, M. Efficiency of a directly driven generator for hydrokinetic energy conversion. Adv. Mech. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Lundin, S.; Goude, A.; Leijon, M. One-dimensional modelling of marine current turbine runaway behaviour. Energies 2016, 9, 309. [Google Scholar] [CrossRef]
- Yuen, K.; Apelfröjd, S.; Leijon, M. Implementation of control system for hydro-kinetic energy converter. J. Control Sci. Eng. 2013, 2013, 10. [Google Scholar] [CrossRef]
- Cottet, G.H.; Koumoutsakos, P.D. Vortex Methods: Theory and Practice; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Goude, A. Fluid Mechanics of Vertical Axis Turbines: Simulations and Model Development. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2012. [Google Scholar]
- Dyachuk, E. Aerodynamics of Vertical Axis Wind Turbines. Development of Simulation Tools and Experiments. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2015. [Google Scholar]
- Dyachuk, E.; Goude, A. Numerical validation of a vortex model against experimental data on a straight-bladed vertical axis wind turbine. Energies 2015, 8, 11800–11820. [Google Scholar] [CrossRef]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; Sandia National Laboratories: Albuquerque, New Mexico, 1981.
- Dyachuk, E.; Goude, A.; Bernhoff, H. Dynamic stall modeling for the conditions of vertical axis wind turbines. AIAA J. 2014, 52, 72–81. [Google Scholar] [CrossRef]
- Goude, A.; Bülow, F. Robust VAWT control system evaluation by coupled aerodynamic and electrical simulations. Renew. Energy 2013, 59, 193–201. [Google Scholar] [CrossRef]
- Goude, A.; Lundin, S. Forces on a marine current turbine during runaway. Int. J. Mar. Energy 2017, 19, 345–356. [Google Scholar] [CrossRef]










| Turbine and generator rating | 7.5 kW |
| Estimated iron, seal and frictional losses | 350 Nm |
| The Vertical Axis Current Turbine | |
| 0.26 at = 3.1 | |
| Rated water speed | 1.35 m/s |
| Rated rotational speed | 15 RPM |
| Number of blades | 5 |
| Blade pitch | Fixed at 0 |
| Blade profile | NACA0021 |
| Rotor Radius | 3 m |
| Rotor Height | 3.5 m |
| Chord length | 0.18 m |
| The Permanent Magnet Synchronous Generator | |
| Minimum efficiency | 80 % |
| Nominal electrical frequency | 14 Hz |
| Poles | 112 |
| Rated Line-to-line rms voltage | 138 V |
| Rated stator rms current | 31 A |
| Stator phase resistance | 0.335 |
| Armature inductance | 3.5 mH |
| The PMSG Generator block | |
| Flux linkage | 1.28 Vs |
| Estimated moment of inertia | 3000 kgm |
| DC load parameters | |
| Rectifier on-resistance | 1 m |
| Rectifier forward voltage drop | 0 V |
| IGBT on-resistance | 0.1 m |
| IGBT forward voltage drop | 1 V |
| Snubber resistance | 47 k |
| Snubber capacitance | 470 nF |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forslund, J.; Goude, A.; Thomas, K. Validation of a Coupled Electrical and Hydrodynamic Simulation Model for a Vertical Axis Marine Current Energy Converter. Energies 2018, 11, 3067. https://doi.org/10.3390/en11113067
Forslund J, Goude A, Thomas K. Validation of a Coupled Electrical and Hydrodynamic Simulation Model for a Vertical Axis Marine Current Energy Converter. Energies. 2018; 11(11):3067. https://doi.org/10.3390/en11113067
Chicago/Turabian StyleForslund, Johan, Anders Goude, and Karin Thomas. 2018. "Validation of a Coupled Electrical and Hydrodynamic Simulation Model for a Vertical Axis Marine Current Energy Converter" Energies 11, no. 11: 3067. https://doi.org/10.3390/en11113067
APA StyleForslund, J., Goude, A., & Thomas, K. (2018). Validation of a Coupled Electrical and Hydrodynamic Simulation Model for a Vertical Axis Marine Current Energy Converter. Energies, 11(11), 3067. https://doi.org/10.3390/en11113067





