Approaches to Methods of Risk Analysis and Assessment Regarding the Gas Supply to a City

Abstract

Analysis and assessment of the reliability and safety of a gas-supply system is a key issue, given its status as critical infrastructure. A gas-supply system is characterised by continuous operation and a consequent need to achieve a high level of operating reliability and safety. Such a system has its unique aspects, with particular elements having their different functions while also simultaneously interacting in the context of the integral whole. In such circumstances, risk analysis can prove useful in planning activity to prevent damage, and also in the devising of rescue scenarios. Thus, the purpose of the analysis presented here has been to supply the information that is necessary in decision-making relating to risk reduction. One of the most comprehensive assessment methods is based on the expected value of gas shortage. Basic formulae with which to determine a generalised indicator of system reliability are also presented, with risk viewed as synonymous with the unreliability of gas supply. This paper then proposes a method by which an indicator of the expected efficiency of operation may also be determined as the quotient of chance and absolute risk. The thinking in this article has been developed on the basis of data from a real gas-supply system, while the computational methods deployed allowed applications to draw conclusions regarding possible modification of the expected gas shortages method.

1. Introduction

The development of safety science is linked inseparably with the development of technology. Fields of interest have included disasters at nuclear power plants and chemical plants, large oil spills from transit pipelines, incidental pollution degrading the quality of surface and groundwater, air contamination, or gas outbursts caused by failures of internal installations or external networks [1,2,3]. The focus has been on the concept of safety, as also related to ecological safety conceived of in broad terms. In this wider context, a biotechnological model for the operation of technical systems of the “human-technology-environment” kind has become an obligatory feature [4,5].

Where risk analysis and assessment are concerned, mention needs to be made of such notions as:

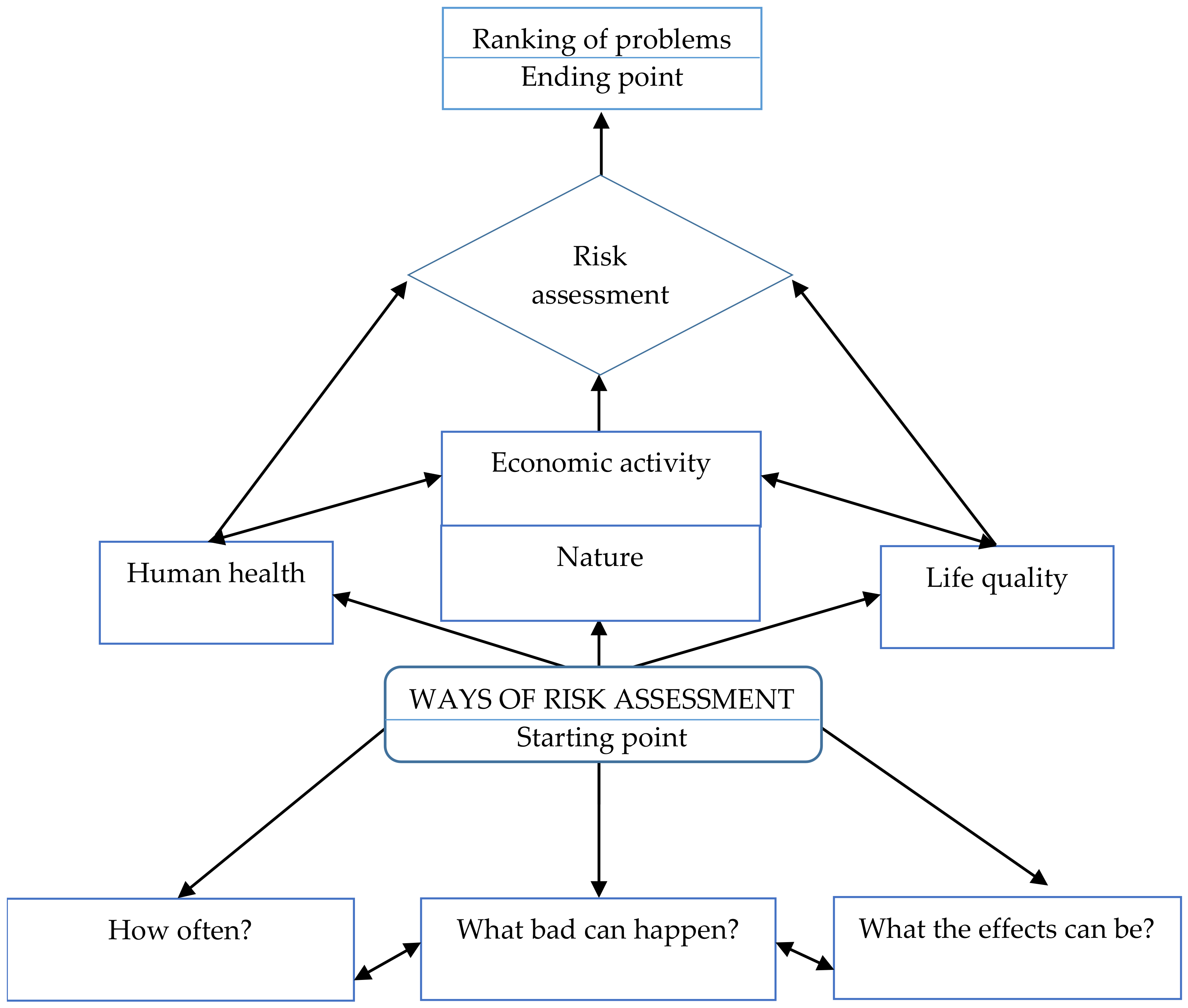
• Safety—i.e., the probability that losses (e.g., to health and human life) will not arise as a result of, and in connection with, undesirable events.
• Risk—i.e., the probability of negative consequences [6], as often understood in terms of the possibility of occurrence of accidents, failures, or disasters that bring different kinds of losses (health, financial, or even cultural).
• Ecological risk—i.e., the likelihood of negative consequences arising in the ecosystem, with a key phase here entailing estimation of the time needed for the ecosystem to achieve a rebalancing following eliminating of the given harmful factor [6].
• The threat to human health—as determined by reference to the likelihood that health or life will be affected [4].

The life-quality risk is defined differently, with the negative impact of various factors measured by reference to costs of an economic nature, be these medical, associated with poor production quality (such as for example with only lower income possible in the food industry when water is of low quality, or with costs generated where interruptions in gas supply impact upon industrial plants with a gas boiler [7,8,9,10]).

The term threat is (though perhaps it should not be) used interchangeably with risk. This reflects the way in which the concept of threat is associated primarily with danger, while risk relates to estimations of probability that are associated with uncertainty [11,12,13,14,15,16,17,18].

Risk analysis should entail [4]:

• Negative events being identified (i.e., with both causes of occurrence and consequences determined);
• Probability of occurrence of events being determined;
• The damage caused when undesirable events occur being assessed.

In turn, risk then becomes a function of [6]:

• Variables characterising the probability of losses, and
• Variables characterising the magnitude or impact of losses.

Given the principle that the higher the probability of a negative result, the higher the level of risk, risk analysis ought to draw on historical knowledge of the operation of a given system, as well as analytical methods and experience.

Where a system supplying gas is concerned, the leading measure describing loss of safety is an assessment of risk bringing together both the probability or likelihood of an undesirable event occurring, as well as the (magnitude or impact of) the related consequences [4,6,19]. In many cases, human factor analysis and human reliability analysis form part of the risk-analysis process, given the importance of the system dispatcher [20]. Safety is deemed to apply where a system is in a state characterised by the lack of any unacceptable risk [6].

The management of risk can be defined as a socio-economic decision-making process in which the term “management” is used appropriately, given that risk cannot be eliminated entirely, although various actions can be taken to minimise it to an acceptable level from the point of view of safety and costs incurred. The concept and essence of the risk is as presented pictorially in Figure 1.

The concept of risk is inseparable from any exploitation of a natural gas supply subsystem (GSS). The construction of gas pipelines and the associated facilities is associated with far-reaching interference in the environment, and poses many threats to it [21,22,23]. Environmental law classifies transmission pipelines as developments that are capable of bringing about a deterioration in the state of the environment [24,25,26,27,28,29]. Natural gas escaping to the atmosphere as systems fail, repairs are carried out, or leaks arise creates a risk of explosion and fire. This denotes more exacting requirements on the part of recipients when it comes to the reliability of operation and safety of gas systems [30,31]. Losses due to interruptions in gas supply or supply characterised by reduced technological parameters will give rise to protests [32,33]. The random nature of failure in infrastructure systems is critical in making research in this area a complex matter, and one based primarily on the analysis of operational data and other sources oriented at environmental impact [34,35].

In extreme cases, the loss of both individual and industrial customers may ensue, especially as the offer of alternative energy sources is becoming cheaper and more accessible to the user. The methane emission that accompanies most failures in GSS creates a threat to the environment, and is often the cause of fatal accidents that result from fire and gas explosions. Victims may be both casual people and employees of gas companies. This paper presents methods by which to analyse for the risk of failure in gas-supply systems.

The specific goals to be attained in the context of this work focus on developing a method by which to determine an indicator of expected efficiency of operation. Analysis of a typical gas network is presented in this work as background to the main aim, while a further objective was to determine unreliability arising out of the so-called power shortage of considerable safety relevance to users of subsystems supplying natural gas. Thus, an expected value for natural gas shortage was arrived at on the basis of the analysis of the network functioning performed previously.

The results of this work are likely to prove helpful in supporting the management of urban gas networks, and application examples of the methods presented have been developed.

2. Losses Arising from Failures in the Natural Gas Supply Subsystem

Losses may entail both lack of income for the gas company on account of gas going undelivered, and possible compensation to recipients deprived of gas, or potential victims of explosions [36].

The estimation of losses, which are often random in nature, is not simple in practice. The easiest way is to start with the formula:

Profit = Income − Expenses

(1)

Losses increase expenses and are associated with costs, with the result that profit is reduced. This justifies an interest, on the part of gas companies, in an assessment of risk that is as accurate as possible. In general, the principle that small losses occur at relatively high levels of probability is proven in practice.

As risk-level calculations can be performed for several thresholds that are adapted to expected gas shortages or possible costs, it is necessary to determine the risks of unreliability of functioning r(UF) and safety unreliability r(US). The principle here is that:

r ≤ r_acceptable

(2)

where r is the risk calculated for the system under consideration, while r_acceptable denotes an acceptable level of risk.

If Inequality (2) is not met, measures should be taken to reduce the risk.

Methodology deriving from security science draws a distinction between instruments of qualitative risk analysis (QRA) and formal-quantitative risk analysis (FRA).

(1) Instruments of qualitative risk analysis relate to the types and effects of failures and exposures, the consequences of failures and errors, and security structures. An example might be the risk assessment expert method, which is so-called because it is performed by a group of experts from various fields of science who are appointed for this purpose. The method is a subjective one based on historical knowledge, professional practice, experience, and intuition. In many cases, it proves very useful and valuable, especially in combination with other risk assessment methods.

(2) Instruments of formal-quantitative risk analysis include fault tree analysis, Markov model analysis, and semi-Markov model analysis.

The event tree method analyses the scenario (sequence of events) whereby a negative effect is generated. It allows for the determination of all possible consequences once undesirable events have occurred, as well as the probability of a given effect arising in line with the aforesaid scenario.

The fault tree method in turn creates a tree of undesirable events, beginning with a certain negative effect thereof. The probability of the effect occurring is determined on the basis of the probability of occurrence of the primary events.

The direct risk assessment method bases itself on historical data, with no analysis of the causes of losses being carried out.

Risk can be defined as the probability that a specified value for financial losses will be exceeded:

r = P{C ≥ C_boundary}

(3)

and:

$$\mathrm{r} = \frac{\mathrm{E}\left(\mathrm{C}\right)}{\mathrm{profit}}$$

(4)

where r is the risk of losses, and E(C) is the value of an expected loss, in calculations based around the formula:

$$\mathrm{E}\left(\mathrm{C}\right) = {\displaystyle \sum _{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}\cdot {\mathrm{C}}_{\mathrm{i}}}$$

(5)

where P_i is the probability of an undesirable event causing losses, and C_i is the absolute value of losses expressed as financial costs, resulting from the occurrence of a single undesirable event and the expected financial profit.

If there is no appropriate database from which appropriate probabilities can be determined, the risk can be derived from the formula:

$$\mathrm{r} = \frac{{\mathrm{C}}_{\mathrm{avg}}}{\mathrm{profit}}$$

(6)

where C_avg is the average annual size of losses and profit that is expected in the given year. This measure is an indicator of financial losses.

The measure of risk can be shown to relate to the measures of unreliability and threat [33]:

(measure of risk) = (measure of unreliability) · (measure of hazard)

(7)

Finally, simulation methods associate mathematical and statistical methods [37,38], often by using digital machines (as with the Monte Carlo method).

3. Methods

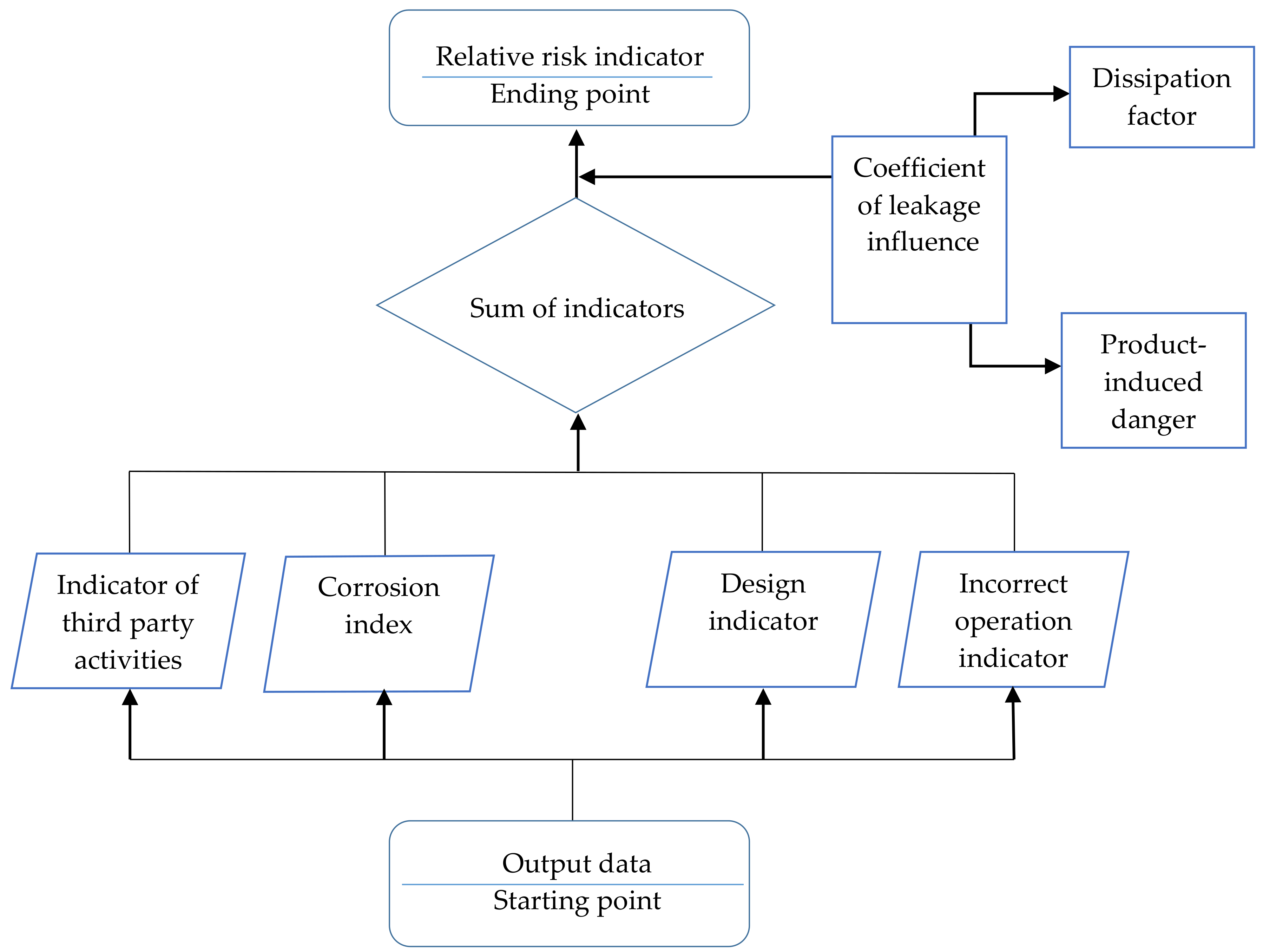
Preliminary Analysis of Risk

The risk inherent in the operation of a gas network can be assessed using the so-called risk assessment point model depicted schematically in Figure 2.

This method distinguishes such risk indicators as:

• Design indicators (e.g., the safety factor for a pipe as the ratio of wall thickness to required thickness, or as designed pressure set against existing pressure, or as tightness of the installation);
• Indicators of improper operation (relating to safety systems, supervision, network operation and maintenance);
• A corrosion index (relating to pipe insulation, external influences, and anti-corrosion measures);
• A third-party activity index (minimum coverage of the gas pipeline, population density, the regularity with which work on the network is carried out).

The determining of individual indicators is preceded by the dividing-up of the gas pipeline into uniform sections, in line with ground conditions, the condition of the protective coating, the age of pipelines and population density. The task is to collect all of the possible information about the network [36]. On this basis, point weights are assigned to individual indicators, with the sum of these weights determining the level of risk that the gas network faces. This method is used in the United States.

As failures in a GSS are of a random nature, assessment of risk should here apply not only qualitative methods, but also a method founded in reliability theory [39]. The fault tree (incapacity) method of assessing the risk of a natural gas shortage to a given industrial plant was proposed in this case.

As the problem of the reliability of functioning as well as the safety of a GSS is being considered, it is necessary to emphasise the importance of gas-supply continuity for consumers (both individual and industrial) [38,39,40,41]. Gas stations of both first and second orders play a special role in this respect. While station failures are rare, gas interruptions that do arise may prove to have serious consequences for a gas company. This is primarily true when this relates to major consumers (production plants, supermarkets, and so on), which can be expected to demand high compensation for undelivered gas and the breaks in production that arise out of that [42,43].

A risk assessment model for an exemplary reduction and measurement station of an industrial plant was proposed. Interruptions in gas supply to the plant interrupt production. The station is equipped with two reduction and measuring sequences operating in line with a parallel, uniform reliability structure, “1 of 2”. The basic elements of the sequence (as presented in Figure 3) are a filter, a gas heater, a reducer, a quick-closing valve, and a meter.

It is necessary to estimate the probability of an event interrupting the supply of gas. The event tree is as depicted in Figure 4. The availability indicators for individual elements can be determined by reference to operating data or those present in the literature [44,45,46].

Unreliability of a station, assuming its independence of operation, was determined from relationships as follows:

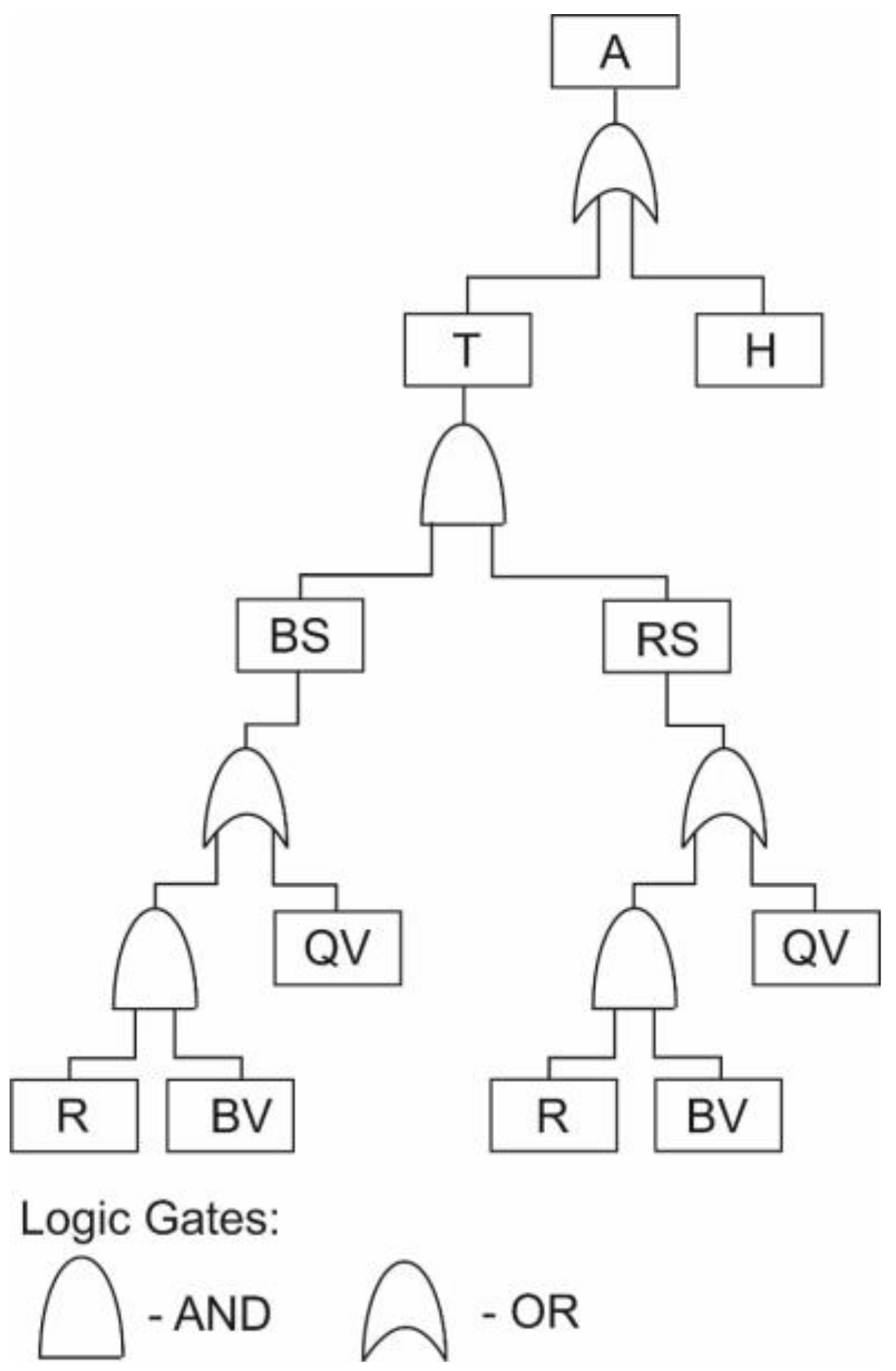
• The technology fails or there is human failure, gate OR:
  U = U(T) + U(H)

  (8)

  where U(T) is the unreliability of the technology and U(H) is human unreliability.
• Failure of the basic and reserve sequences, gate AND:
  U(T) = U(BS) · U(RS)

  (9)

  where U(BS) is the failure of the basic sequence, and U(RS) is the unreliability of the reserve sequence.
• Failure of a reducer and blow-off valve or a quick-closing valve:
  U(BS) = U(RS) = U(R) · U(BV) + U(QV)

  (10)

  where U(R) is a failure of the reducer (no reduction), U(BV) is a failure of the blow-off valve (no blow out of excess gas or too little capacity), and U(QV) is a failure of the quick-closing valve (unfounded closure).

Finally, we obtain:

U= (U(R) · U(BV) + U(QV))² + U(H)

(11)

where U is the station unreliability indicator, U_i = 1 − K_i, U_i is the unreliability indicator for individual elements, and K_i is the availability index for individual elements.

4. Analysis of the Risk that a Supply of Natural Gas will be Lacking

The factor determining the unreliability of the GSS may be the so-called power shortage. This unreliability is determined by the generalised unreliability indicator U, i.e., the ratio of the expected value for the deficit to the expected value of needs [40,41]:

$$\mathrm{U} = \frac{\mathrm{E}(\Delta \mathrm{Q})}{{\mathrm{Q}}_{\mathrm{n}}}$$

(12)

where E(ΔQ) is the expected value associated with the shortage of natural gas (Equation (13)), Q_n is the expected value for the required demand for natural gas, and ΔQ is the shortage in respect to the supply of natural gas.

$$\mathrm{E}(\Delta \mathrm{Q}) = {\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{i}=\mathrm{n}}{\Delta \mathrm{Q}}_{\mathrm{i}}\cdot {\mathrm{P}}_{\mathrm{i}}}$$

(13)

where P_i is the probability associated with system components in a given state, and n is the maximum number of possible reliability states. If m is the number of all power sources, then n = 2^m.

A power shortage occurs with a certain probability P_i [40], which can be calculated in line with the formula:

$$P_i = {\displaystyle \prod _{j\in S}^{}{K}_j}\cdot {\displaystyle \prod _{j\in N}^{}(1-K_j)}$$

(14)

where Kj is the availability indicator for an element, j∈S is a set of those elements that are efficient in the i-th state, (+), and j∈N is a set of those elements that are inefficient in the i-th state, (−).

The value of the power shortage ΔQ can be calculated as the difference between the required (maximum) capacity of the power sources and the capacity of the sources in the i-th state, in line with the relationship [41]:

$${\Delta \mathrm{Q} = \mathrm{Q}}_{\mathrm{n}} - {\displaystyle \sum _{{\mathrm{k}}_{\mathrm{i}}=0}^{{\mathrm{k}}_{\mathrm{idop}}}{\mathrm{Q}}_{\mathrm{ik}}}$$

(15)

where Q_ik is the capacity of individual power sources in the i-th state with k failures, Q_n is the expected value for the required natural gas demand, and k_i is the number of damaged power sources in the i-th state.

The reliability of the system is expressed by the generalised reliability index K equal [40,41]:

K = 1 − U

(16)

If the capacity of all of the sources is greater than the required capacity, then there is a so-called power reserve (i.e., the shortage is zero).

The value of the system reliability index K that is calculated in this way determines the probability of the required capacity of GSS power sources being provided.

5. Application Example

Two high-pressure transmission lines, ϕ700 and ϕ400, (nominal pressure 6.4 MPa) run through the area of the analysed city and supply that city with natural gas (Figure 5).

The medium-pressure ring gas network is supplied from the high-pressure transmission bus through two first-stage reduction-measuring stations (reducing the high pressure of 6.4 MPa to an average of 0.4 MPa) (

Table 1. Capacity of the first-stage reduction and measuring stations.

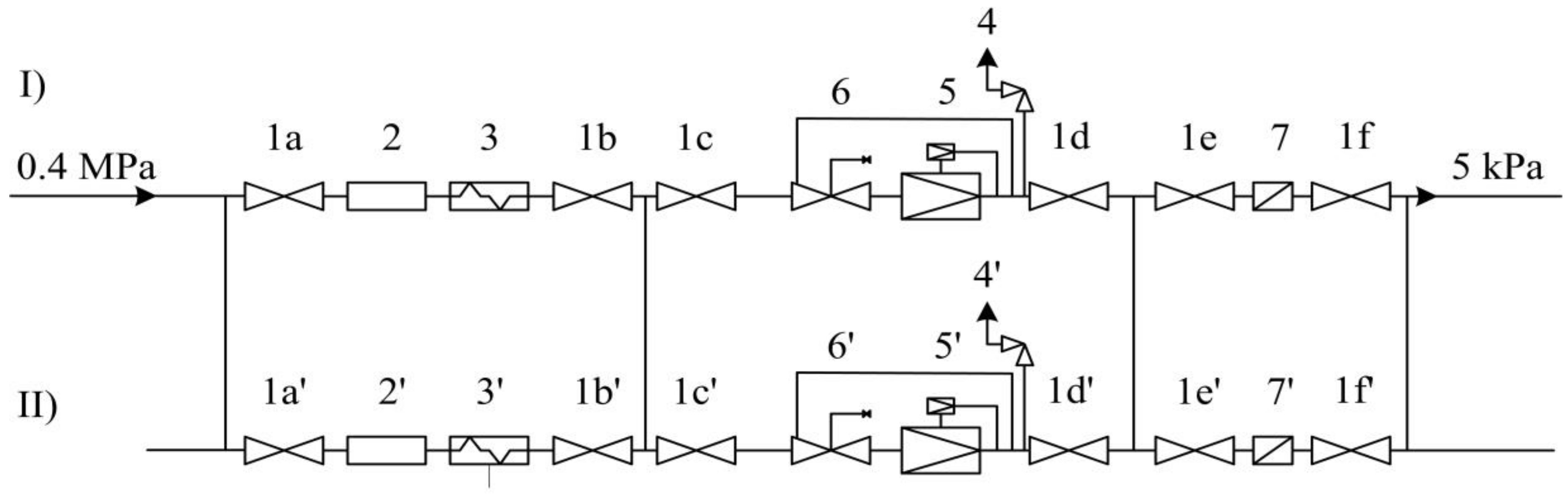
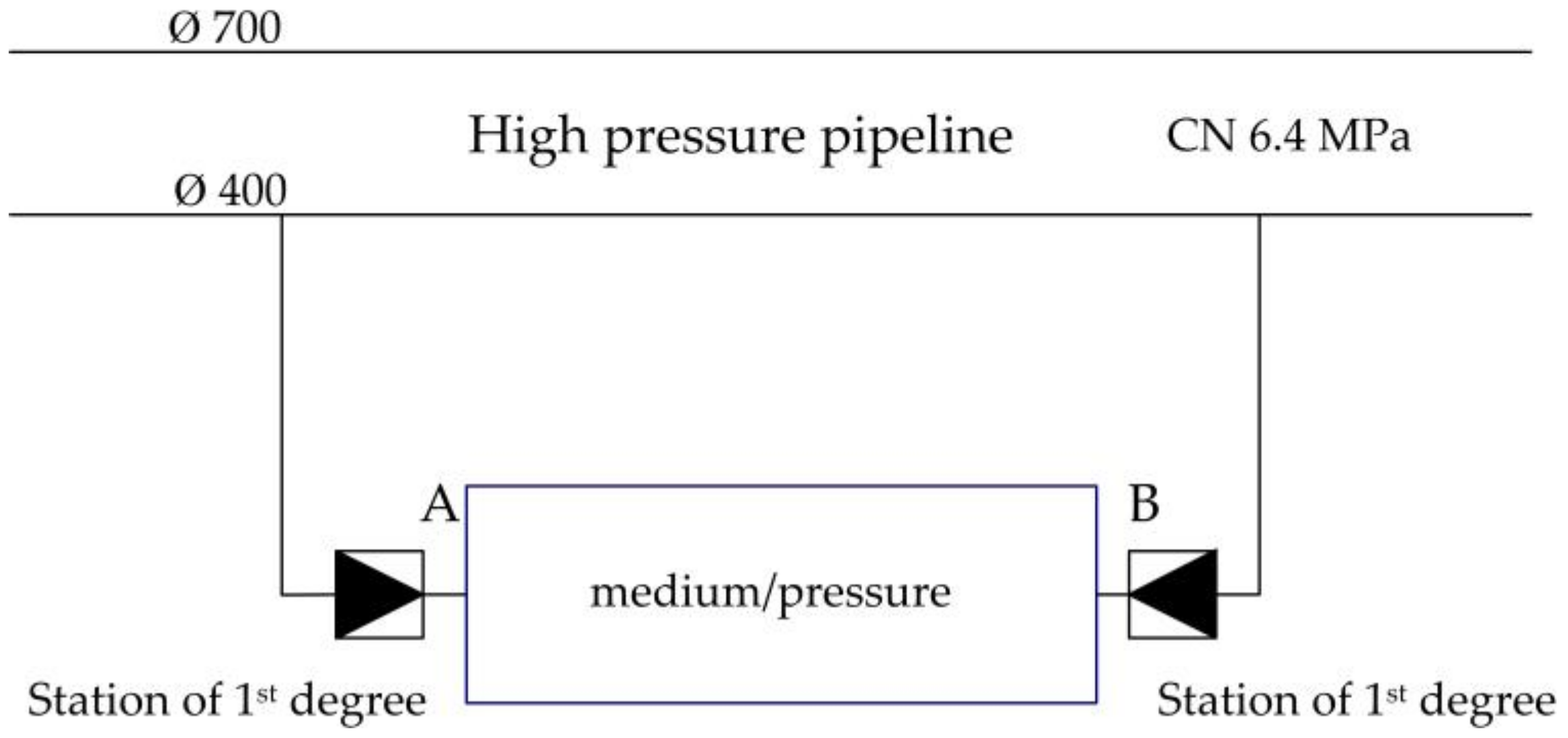
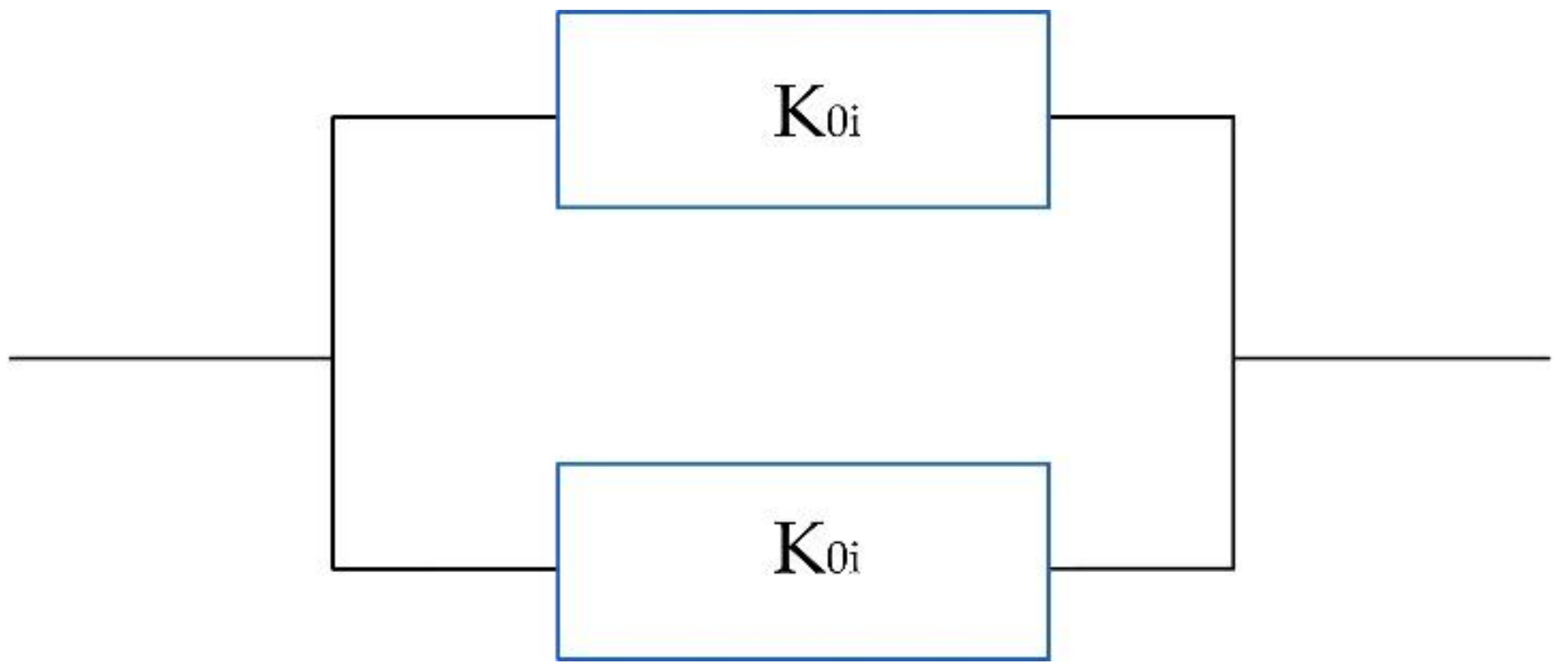
Station Type 1st Degree	Capacity Q, m3/h	Inlet Pressure/Outlet Pressure, MPa
I	25,000	6.4/0.4
II	15,000	6.4/0.4
III	3000	5.5/0.4

). To the main ring of medium pressure, a local natural gas mine was connected through a third first-stage reduction and measurement station. The medium-pressure network supplies all the second-stage reduction stations (21 pcs for the city, reducing the average pressure of 0.4 MPa to the low 0.025 MPa) and some of the buildings in the city directly.

An attempt was made to determine reliability, which is in line with the expected value of the gas shortage. For example, the GSS was considered for a typical scheme consisting of two first-stage reduction stations supplying the medium-pressure ring network and “n” of the second-stage stations supplying the low-pressure network, as presented in Figure 6 [36].

The system is supplied from two first-stage reduction stations A and B, with capacities equal to QA and QB. Each station has two reduction sequences (one reserve), each with the same capacity (QA or QB), operating according to the parallel reliability structure “1 of 2”. One reduction sequence was treated as one element (in terms of reliability with the reliability index K_0i, both sequences are technically uniform) (Figure 7) [36,40].

The availability indicator for such a system (one station) is equal to:

K = 1 − (1 − K₀)²

(17)

where K_0A(B) is the reliability index of one reduction sequence, which has been adopted as K_0A = 0.9925 and K_0B = 0.9508 [36].

The reliability of each station (A, B) was calculated in line with Formula (17) (Equations (18) and (19)):

K_A = 1 − (1 − 0.9925)² = 0.9999

(18)

K_B = 1 − (1 − 0.9508)² = 0.9975

(19)

The expected value for the shortage results from shortages in various states and the probabilities of occurrence of these P_i states, which is in line with Formulae (13) and (14). The probabilities of the occurrence of the i-th state were calculated in line with Formula (13).

The results are as summarised in

Table 2. The probabilities Pi in respect of particular reliability states.

i	Station of 1st Degree A	Station of 1st Degree B	Pi	Reliability State
1	1	1	K1 · K2	work
2	0	1	(1 − K1) · K2	work
3	1	0	K1 · (1 − K2)	work
4	0	0	(1 − K1) · (1 − K2)	failure

and

Table 3. Calculation results in individual reliability states on the basis of Tchórzewska-Cieślak [36].

i	Station of 1st Degree A	Station of 1st Degree B	ki	Pi	∑Qik	ΔQi	ΔQi ·Pi
1	1	1	0	0.9974	1.6 Qn	0	0
2	0	1	1	0.00009975	0.9 Qn	0.1 Qn	0.000009975 Qn
3	1	0	1	0.002499	0.7 Qn	0.3 Qn	0.0007499 Qn
4	0	0	2	0.00000025	0	1.0 Qn	0.00000025 Qn
∑				1	-	-	0.00076 Qn

[36].

Power shortages in different states were determined in line with the assumption that the required demand for the city is Q_n, and the capacity of individual stations, respectively are QA = 0.7 Q_n and QB = 0.9 Q_n, where “+” means efficiency status, and “−” indicates a state of inefficiency. A state of inefficiency is understood as one in which a station does not fulfil its function in any way. The failure rate U and the reliability index K for GSS were calculated at 0.00076 and 0.99923, respectively. Similar results were obtained with the method using the supply reliability of an urban gas network at the service time and the designed capacity supply of the urban gas network [47]. The gas supply reliability of the urban gas network at 10 years was calculated as 0.9623. The literature lacks a reliable analysis in the context of gas supplies to the city. The presented method can be applied in both local and global contexts, analysing a larger number of sources; it can also be used to diversify gas supplies.

6. Conclusions

Risk assessment in the operation of a GSS should be one of the priority activities of a gas company, which should pay more attention to the risk assessment of existing systems, as well as those newly designed or in the course of being implemented. This seems a necessity in the face of increasing pressure from green groups and a tightening of standards as regards permissible environmental pollution. The variety of proposed risk assessment methods allows for the free choice of an optimal solution, but it would seem that the use of two or more methods at the same time might afford an opportunity for the objective assessment of the risk associated with a subsystem, which would also allow a correct decision regarding methods of minimisation to be made. The fault tree method that was suggested in the paper seems suitable for risk assessment in a GSS, especially with reference to subsystem elements such as reduction and measurement stations of the first or second stages. Technological solutions for reduction and measuring stations (protection methods, two reduction sequences, and even a doubling of reducers) allow a reliability diagram to be prepared and appropriate reliability structures to be analysed. This in turn enables analysis of the impact that the failure of individual elements of a reduction and measurement station will exert on the reliability of a station as a whole. This makes possible the precise compilation of the fault tree, and the calculation of the probability that an undesirable event (breaks in the delivery of natural gas to recipients) will occur.

The presented GSS power reliability evaluation method can be useful in regard to the design, as well as the modernisation (extension) of the system, especially in the development phase of technical–economic–reliability analysis (TERA) vis-à-vis a given solution. The study draws attention to the possibilities that reliability theory has to offer. Its application facilitates the making of correct decisions regarding the selection of best solutions, not only in technical terms, but also with respect to reliability. The method should also prove useful as technical systems are operated, allowing the failure rates of systems (objects) to be assessed, with theoretical models of conduct developed to increase the safety of users.