Improving Line Current Distortion in Single-Phase Vienna Rectifiers Using Model-Based Predictive Control
Abstract
:1. Introduction
2. Vienna Rectifier Control
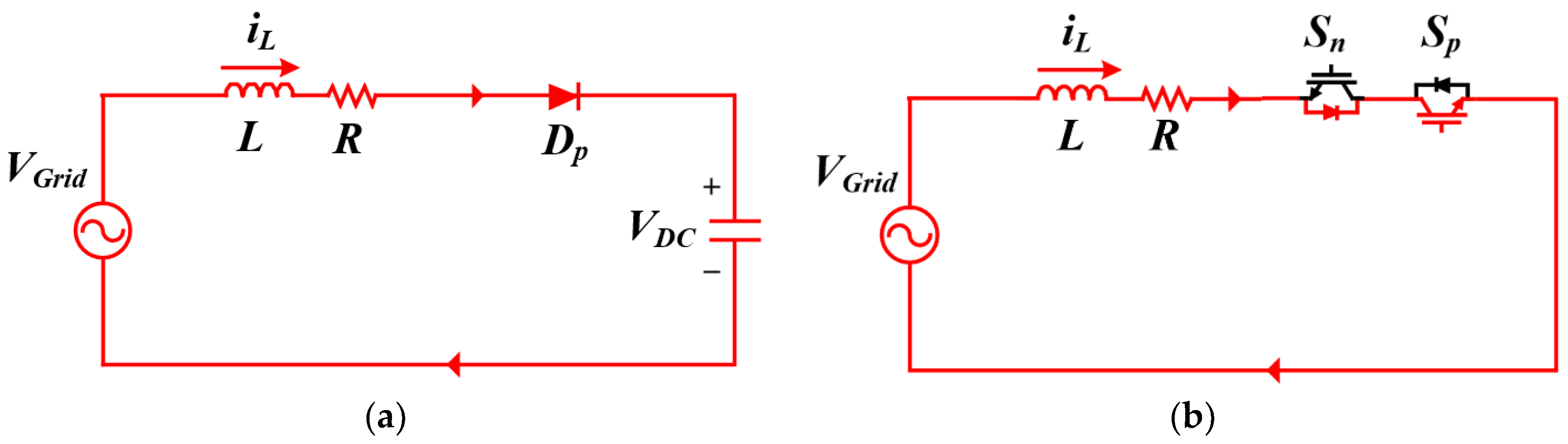
2.1. Operation of the Vienna Rectifier
2.2. Conventional PI Control of a Vienna Rectifier
2.3. Model-Based Predictive Control of a Single-Phase Vienna Rectifier
2.3.1. Estimating the Gradient of the Inductor Current
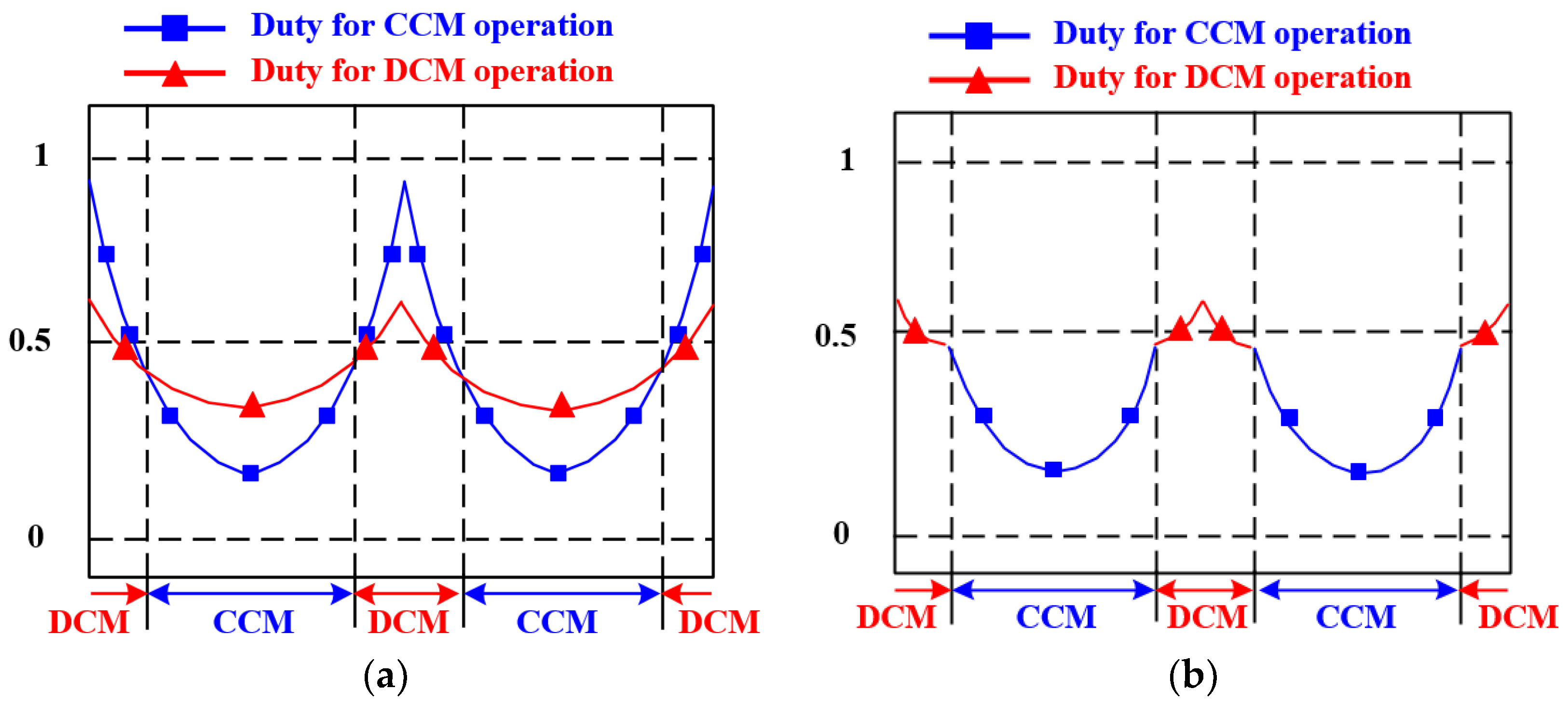
2.3.2. Deriving the Optimal Duty Cycle for CCM Operation
2.3.3. Deriving the Optimal Duty Cycle for DCM Operation
2.3.4. Mode Detection for the Vienna Rectifier
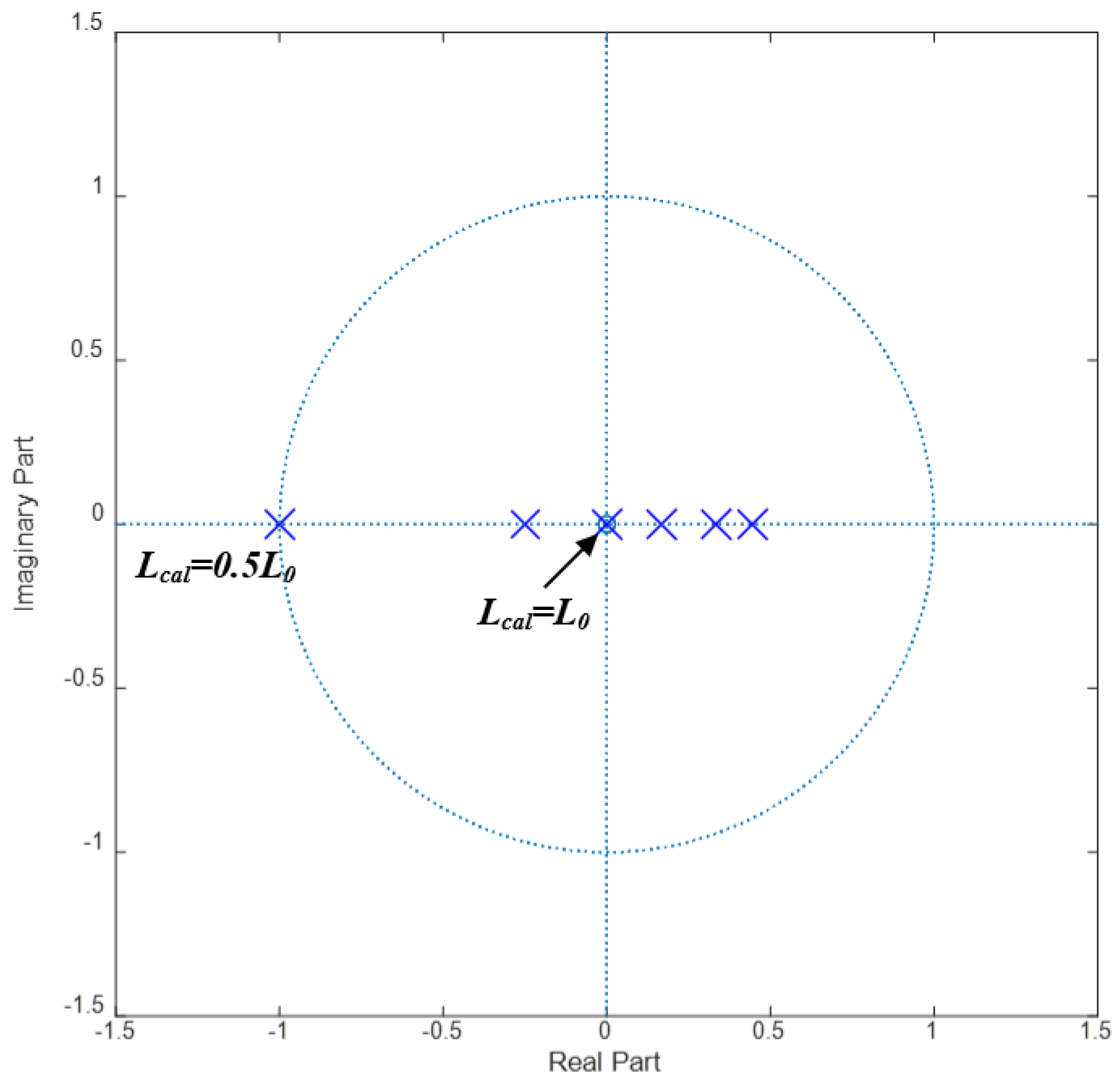
2.3.5. System Stability of Proposed Predictive Control Method
2.3.6. Consideration of Inductance Variation
3. Simulations
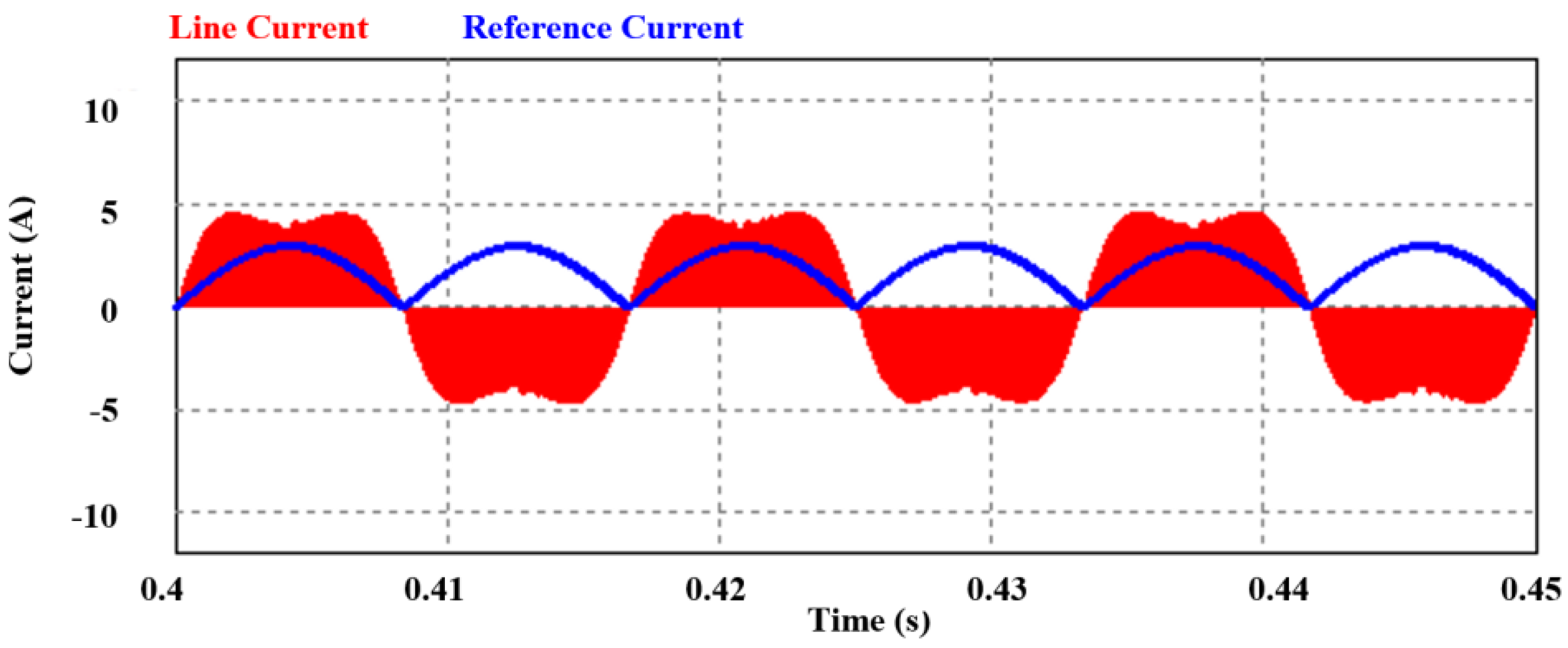
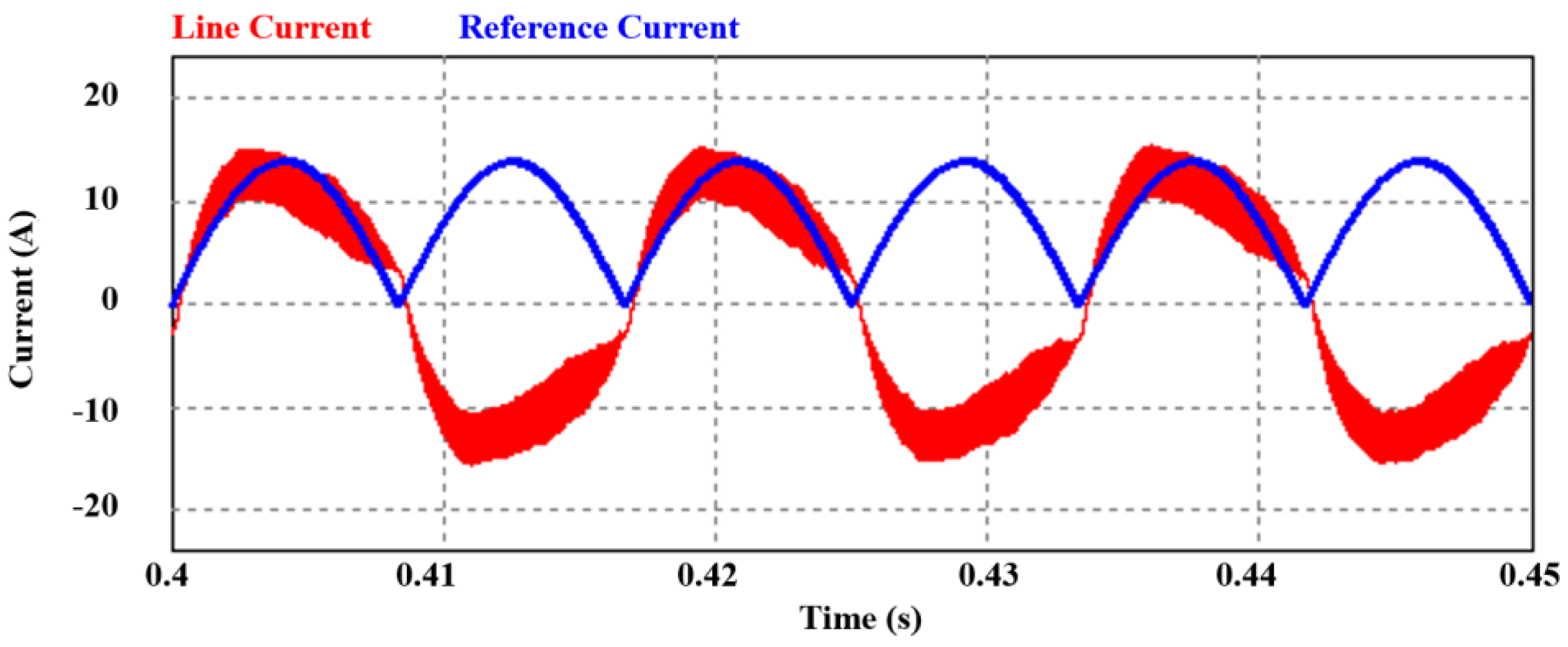
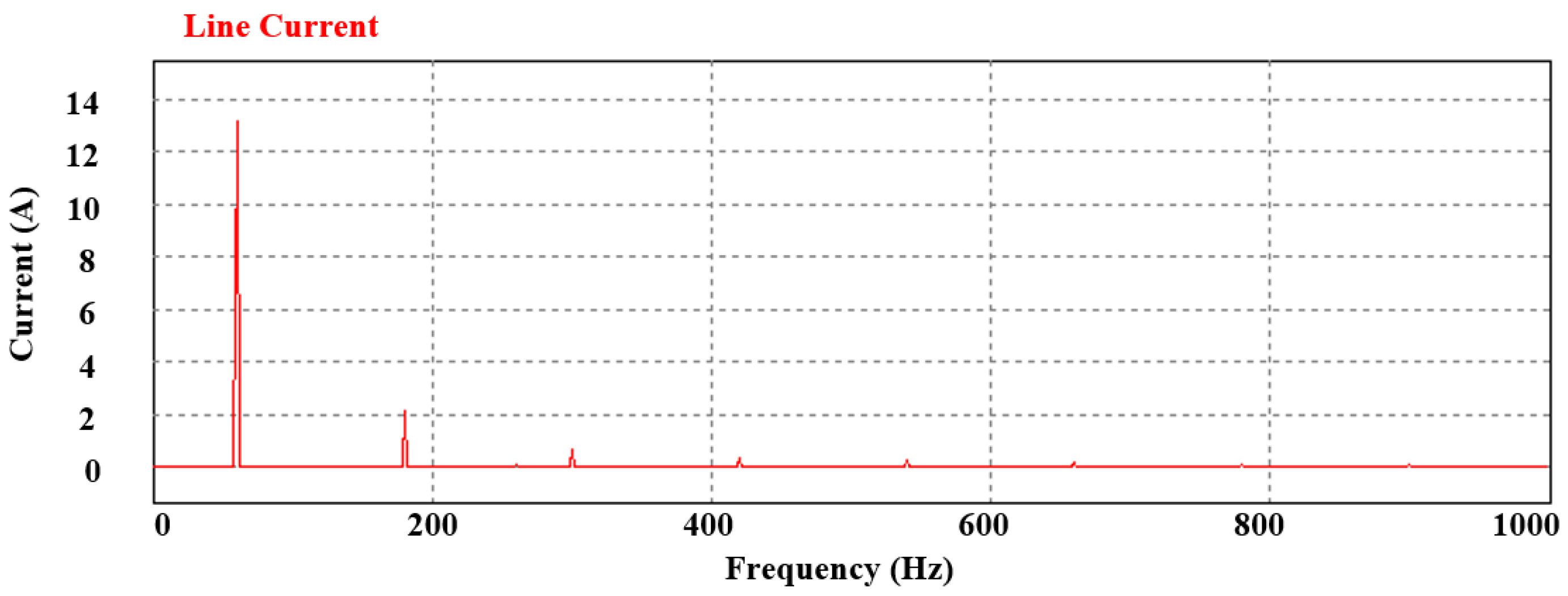
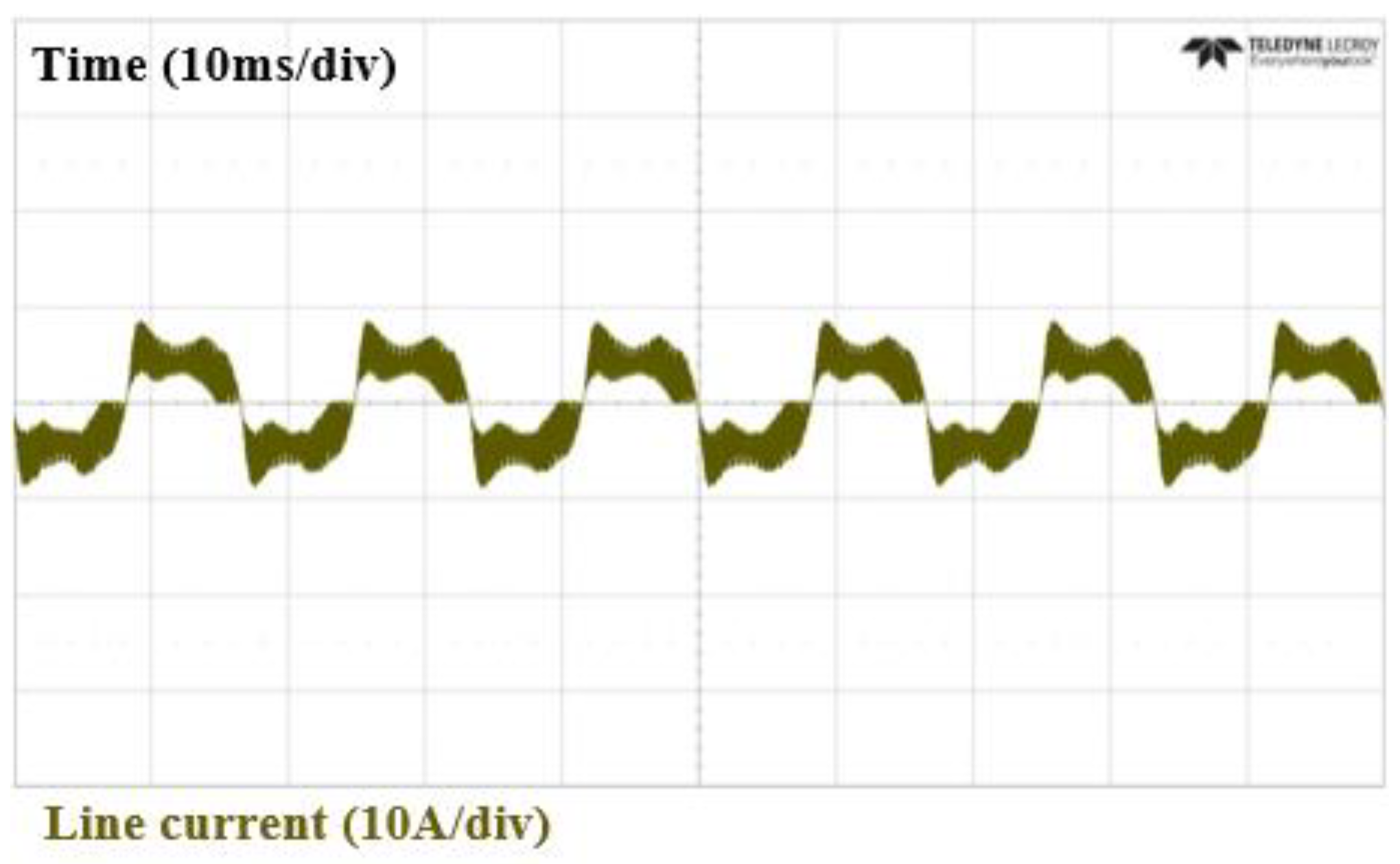
4. Experimental Section
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| Variables/Acronyms/Indexes/Constants | Full Nomenclatures |
|---|---|
| EV | Electric Vehicle |
| MPC | Model-based Predictive Control |
| PWM | Pulse-Width Modulation |
| OBC | On Board Charger |
| THD | Total Harmonic Distortion |
| PF | Power Factor |
| FS-MPC | Finite StateModel-base Predictive Control |
| DSP | Digital Signal Processor |
| ADC | Analog to Digital Conversion |
| PI | Proportional-Integral |
| DCM | Discontinuous Current Mode |
| CCM | Continuous Current Mode |
| L | Filter inductor |
| R | Filter Resistor |
| VGrid | Grid Voltage |
| Dp | Top Diode of Vienna rectifier |
| Dn | Bottom Diode of Vienna rectifier |
| Sp | Top Switch |
| Sn | Bottom Switch |
| Ctop | Top Capacitor |
| Cbot | Bottom Capacitor |
| Rout | Output Resistor |
| VDC | DC Voltage |
| i* | Voltage Controller Output |
| iL | Sensed Inductor Current |
| iL* | Inductor Current Reference |
| ωcc | Bandwidth of PI controller |
| Kp,current | Proportional Gain of PI controller |
| KI,current | Integral Gain of PI controller |
| ζ | Damping-Ratio |
| ipeak | Peak Value of Inductor Current |
| iavg | Average Value of Inductor Current |
| izero | Zero Value of Inductor Current |
| SL,on | Slope during Switch on time |
| Vtop | Top DC link Voltage |
| Vbot | Bottom DC link Voltage |
| SL,bot,off | Slope during Bottom Switch off |
| SL,top,off | Slope during Bottom Switch on |
| iL,k + 1,top | Next State inductor Current |
| iL,k | Current State Inductor Current |
| ierr,top | Error of Inductor Current in CCM |
| Ton,top,CCM | Top Switch on Time in CCM |
| Dutytop,CCM | Top Switch Duty in CCM |
| Ton,bot,CCM | Bottom Switch on Time in CCM |
| Dutybot,CCM | Bottom Switch Duty in CCM |
| Tzero | Zero drop Time of Inductor Current |
| iL,avg,k + 1 | Average Current of Next Current |
| ierr,DCM | Error in DCM |
| Ton,top,DCM | Top Switch on Time in DCM |
| Dutytop,DCM | Top Switch Duty in DCM |
| Ton,bot,DCM | Bottom Switch on Time in DCM |
| Dutybot,DCM | Bottom Switch Duty in DCM |
| L0 | Actual Inductance Value |
| Lcal | Nominal Inductance Value |
References
- Bak, Y.S.; Lee, E.S.; Lee, K.-B. Indirect Matrix Converter for Hybrid Vehicle Application with Three-Phase and Single Outputs. Energies 2015, 8, 3849–3866. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, I.-O.; Moon, G.-W. Integrated Dual Full-Bridge Converter With Current-Doubler Rectifier for EV Charger. IEEE Trans. Power Electron. 2016, 31, 942–951. [Google Scholar] [CrossRef]
- Lee, J.-H.; Lee, J.-S.; Lee, K.-B. A Fault Diagnosis Method in Cascaded H-bridge Multilevel Inverter Using Output Current Analysis. J. Electr. Eng. Technol. 2017, 12, 2278–2288. [Google Scholar]
- Park, J.Y.; Sin, J.O.; Bak, Y.S.; Lee, K.-B. Common-mode Voltage Reduction for Inverters Connected in Parallel Using and MPC Method with Subdivided Voltage Vectors. Journal of Electrical Engineering & Technology 2018, 13, 1212–1222. [Google Scholar]
- Jeong, M.-G.; Kim, S.-M.; Lee, K.-B. Discontinuous PWM Scheme for Switching Losses Reduction in Modular Multilevel Converters. J. Power Electron. 2017, 17, 1490–1499. [Google Scholar]
- Park, J.-H.; Yang, S.H.; Lee, K.-B. Synchronous Carrier-based Pulse Width Modulation Switching Method for a Vienna Rectifier. J. Power Electron. 2018, 18, 604–614. [Google Scholar]
- Jeong, M.-G.; Kim, S.-M.; Lee, K.-B. An Interleaving Scheme for DC-Link Current Ripple Reduction in Parallel-Connected Generator Systems. J. Power Electron. 2017, 17, 1004–1013. [Google Scholar]
- Yang, S.H.; Park, J.-H.; Lee, K.-B. Current Quality Improvement for a Vienna Rectifier with High-Switching Frequency. Trans. Korean Inst. Power Electron. 2017, 22, 181–184. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Y.; Jia, Y. Three-Port Bridgeless PFC Based Quasi Single-Stage Single-Phase AC-DC Converters for Wide Voltage Range Applications. IEEE Trans. Ind. Electron. 2018, 65, 5518–5528. [Google Scholar] [CrossRef]
- Adhikari, J.; Prasanna, I.V.; Panda, S.K. Reduction of Input Current Harmonic Distortions and Balancing of Output Voltages of the Vienna Rectifier under Supply Voltage Disturbances. IEEE Trans. Power Electron. 2017, 32, 5802–5812. [Google Scholar] [CrossRef]
- Kim, D.-H.; Kim, M.-J.; Lee, B.-K. An Integrated Battery Charger with High Power Density and Efficiency for Electric Vehicles. IEEE Trans. Power Electron. 2017, 32, 4553–4565. [Google Scholar] [CrossRef]
- Kwon, M.; Choi, S. An Electrolytic Capacitorless Bidirectional EV Charger for V2G and V2H Applications. IEEE Trans. Power Electron. 2017, 32, 6792–6799. [Google Scholar] [CrossRef]
- Thangavelu, T.; Shanmugam, P.; Raj, K. Modelling and control of VIENNA rectifier a single phase approach. IET Power Electron. 2015, 8, 2471–2482. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, K.-B. Performance Analysis of Carrier-Based Discontinuous PWM Method for Vienna Rectifiers with Neutral-Point Voltage Balance. IEEE Trans. Power Electron. 2016, 31, 4075–4084. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, K.-B. Predictive Control of Vienna Rectifiers for PMSG Systems. IEEE Trans. Ind. Electron. 2017, 64, 2580–2591. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, K.-B. A Novel Crrier Based PWM for Vienna Rectifier with a Variable Power Factor. IEEE Trans. Ind. Electron. 2016, 63, 3–12. [Google Scholar] [CrossRef]
- Mallik, A.; Lu, J.; Khaligh, A. A Comparative Study between PI and Type-II Compensators for H-Bridge PFC Converter. IEEE Trans. Ind. Appl. 2018, 54, 1128–1135. [Google Scholar] [CrossRef]
- Pastor, M.-A.; Idiarte, V.-E.; Pastor, C.-A.; Salamero, M.-L. Interleaved Digital Power Factor Correction Based on the Sliding-Mode Approach. IEEE Trans. Power Electron. 2016, 31, 4641–6453. [Google Scholar] [CrossRef]
- Kanaan, H.Y.; Al-Haddad, K.; Hayek, A.; Mougharbel, I. Design, study, modelling and control of a new single-phase high power factor rectifier based on the single-ended primary inductance converter and the Sheppard-Taylor topology. IET Power Electron. 2007, 2, 163–177. [Google Scholar] [CrossRef]
- Malik, A.; Khaligh, A. An Integrated Control Strategy for a Fast Start-Up and Wide Range Input Frequency Operation of a Three-Phase Boost-Type PFC Converter for More Electric Aircraft. IEEE Trans. Veh. Technol. 2017, 66, 10841–10852. [Google Scholar] [CrossRef]
- Louganski, K.P.; Lai, J.S. Current phase lead compensation in single-phase PFC boost converters with a reduced switching frequency to line frequency ratio. IEEE Trans. Power Electron. 2007, 22, 113–119. [Google Scholar] [CrossRef]
- Kim, D.J.; Park, J.-H.; Lee, K.-B. Scheme for Improving Line Current Distortion of PFC Using a Predictive Control Algorithm. J. Power Electron. 2015, 15, 1168–1177. [Google Scholar] [CrossRef]
- Ren, H.-P.; Guo, X. Robust Adaptive Control of a CACZVS Three-Phase PFC Converter for Power Supply of Silicon Growth Furnace. IEEE Trans. Ind. Electron. 2016, 63, 903–912. [Google Scholar] [CrossRef]
- Youn, H.S.; Park, J.S.; Park, K.B.; Baek, J.I.; Moon, G.W. A digital predictive peak current control for power factor correction with low-input current distortion. IEEE Trans. Power Electron. 2016, 31, 900–912. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, S.-J.; Lee, K.-B. Torque-Ripple Reduction and Fast Torque Response Strategy for Predictive Torque Control of Induction Motors. Int. J. Electron. 2018, 105, 303–323. [Google Scholar] [CrossRef]
- Chen, Y.L.; Chen, Y.M. Line current distortion compensation for DCM/CRM boost PFC converters. IEEE Trans. Power Electron. 2016, 31, 2026–2038. [Google Scholar] [CrossRef]
- Ji, Q.; Ruan, X.; Xie, L.; Ye, Z. Conducted EMI spectra of average current controlled boost PFC converters operating in both CCM and DCM. IEEE Trans. Ind. Electron. 2015, 62, 2184–2194. [Google Scholar] [CrossRef]
- Buso, S.; Caldognetto, T.; Brandao, D.I. Dead-Beat Current Controller for Voltage-Source Converters with Improved Large-Signal Response. IEEE Trans. Ind. Electron. 2016, 52, 1588–1596. [Google Scholar] [CrossRef]
- Xia, C.; Wang, Y.; Shi, T. Implementation of Finite-State Model Predictive Commutation Torque Ripple Minimization of Permanent-Magnet Brushless DC Motor. IEEE Trans. Ind. Electron. 2013, 60, 896–905. [Google Scholar] [CrossRef]
- Baek, J.-B.; Choi, W.-I.; Cho, B.-H. Digital adaptive frequency modulation for bidirectional DC-DC converter. IEEE Trans. Ind. Electron. 2013, 60, 5167–5176. [Google Scholar] [CrossRef]
- Stumper, J.-F.; Hagenmeyer, V.; Kuehl, S.; Kennel, R. Deadbeat control for electrical drives: A robust and performant design based on differential flatness. IEEE Trans. Power Electron. 2015, 30, 4585–4596. [Google Scholar] [CrossRef]
- Saxena, A.R.; Veerachary, M. Robust Digital Deadbeat Control for DC-DC Power Converter with Online Parameter Estimation. In Proceedings of the Joint International Conference on Power Electronics (PEDES), New Delhi, India, 20–23 December 2010; pp. 1–5. [Google Scholar]









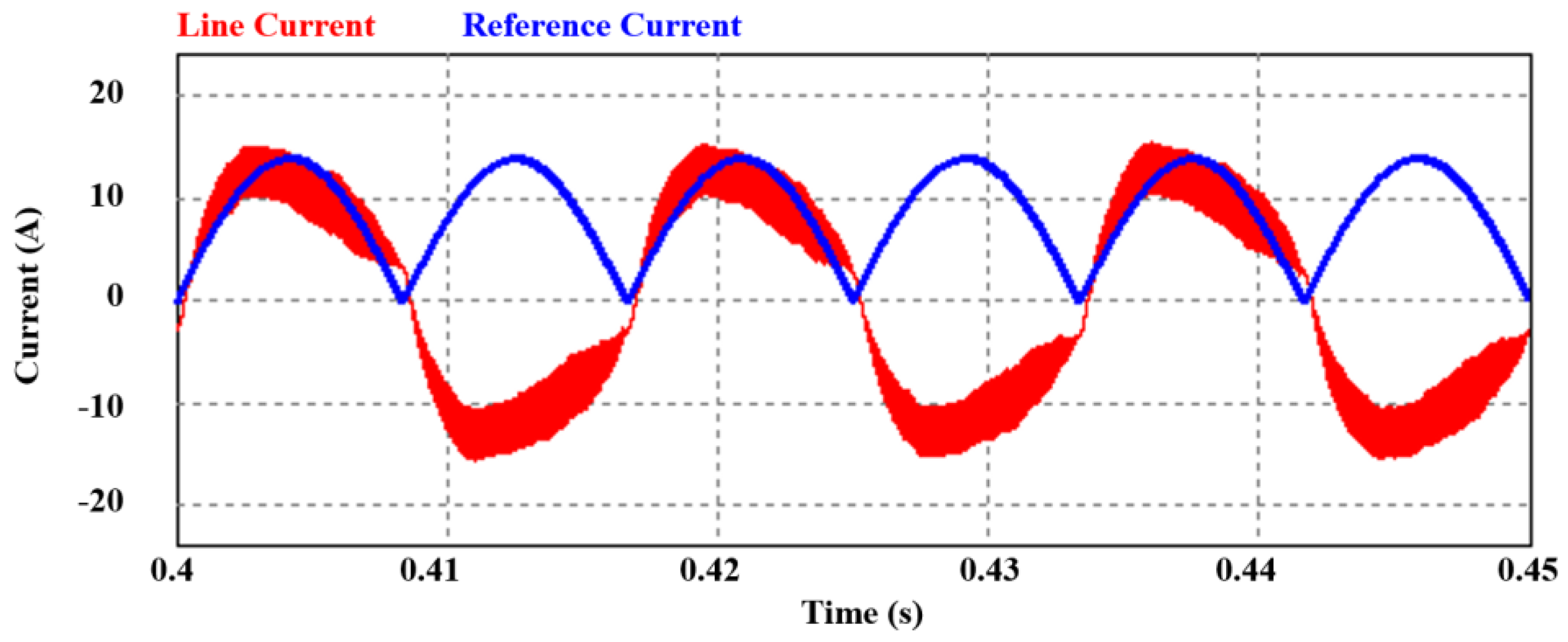
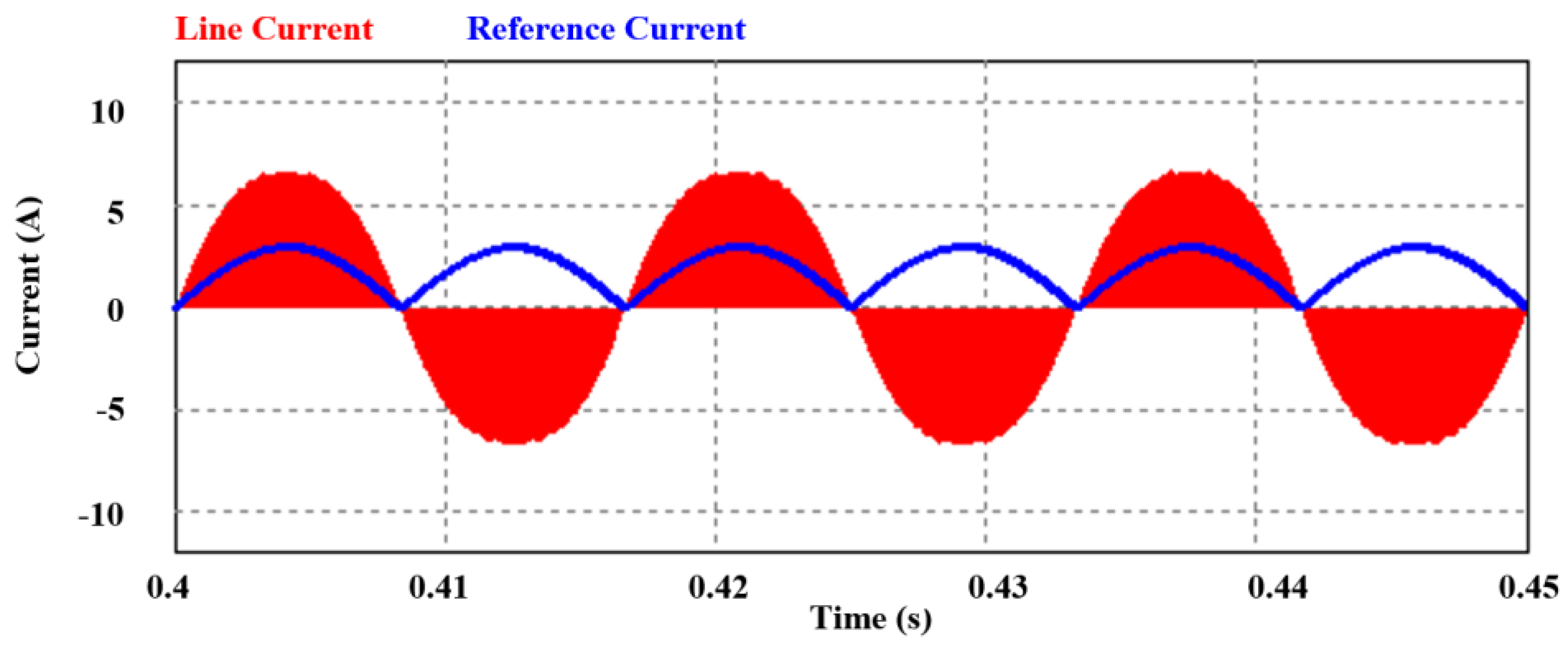
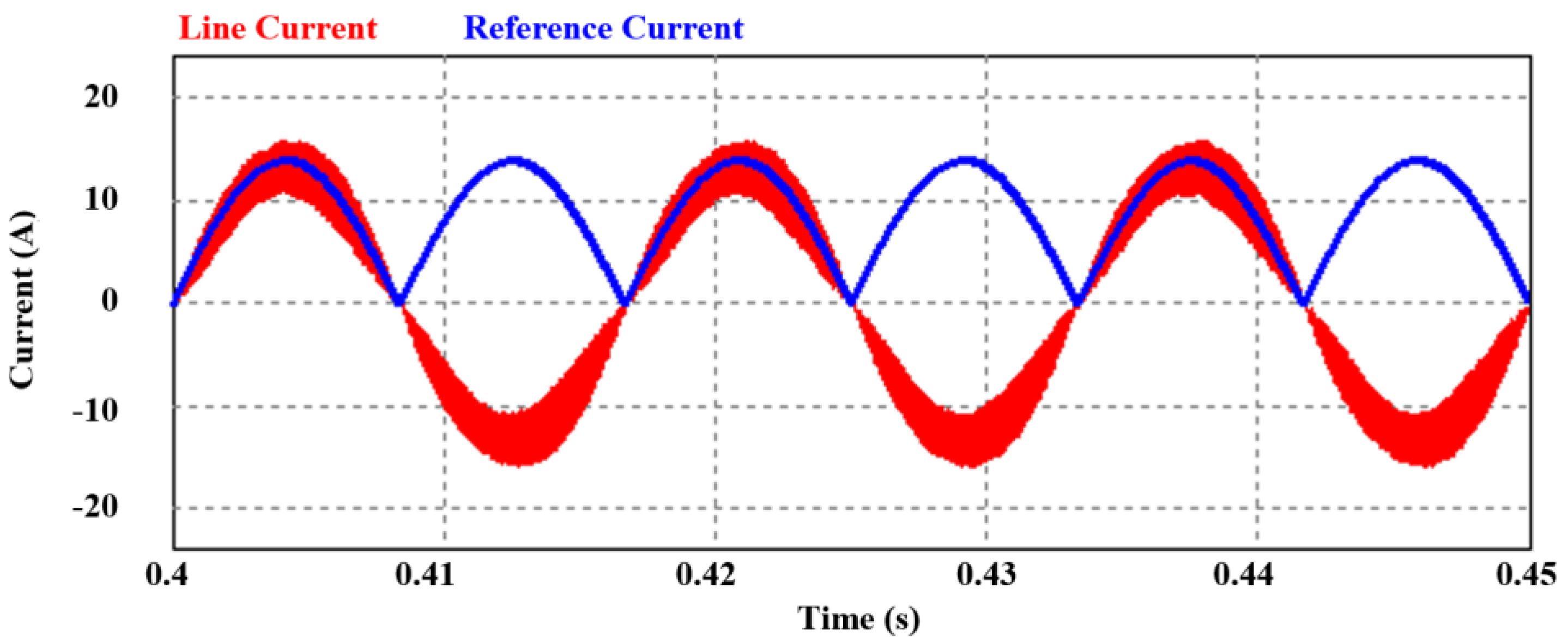
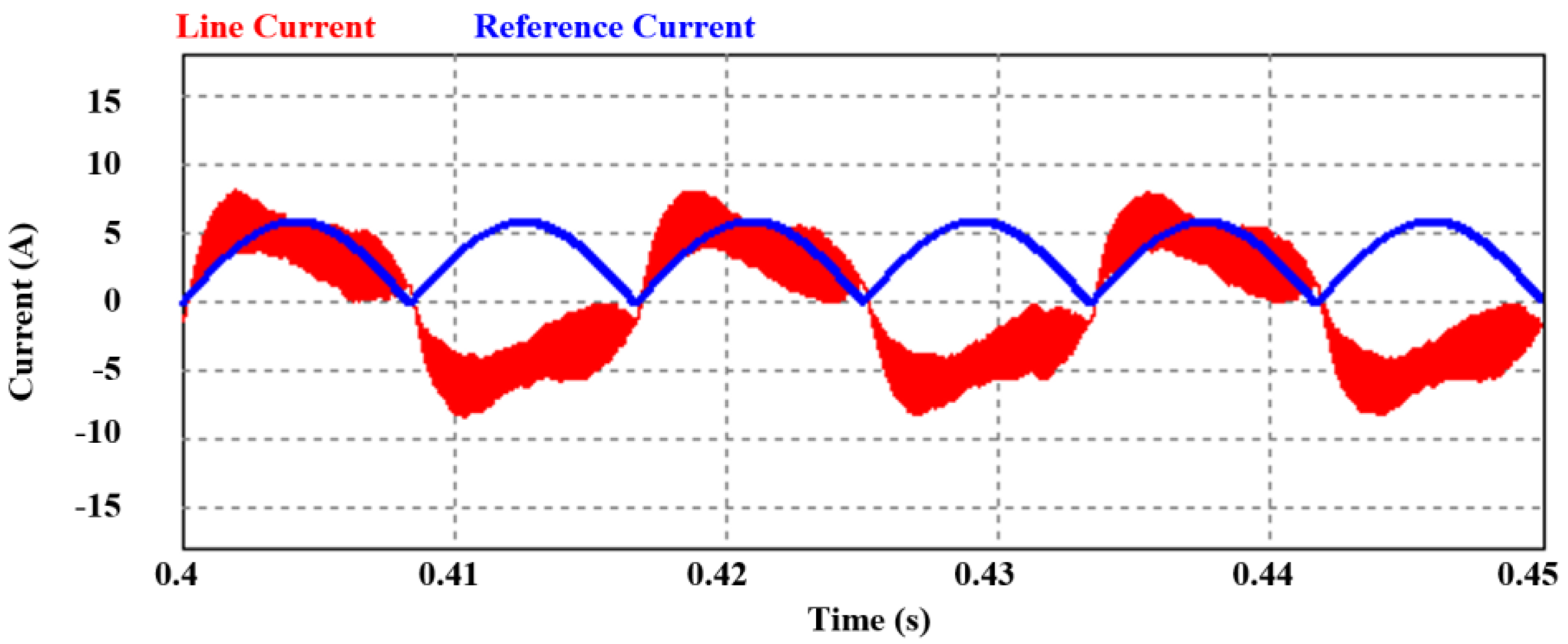





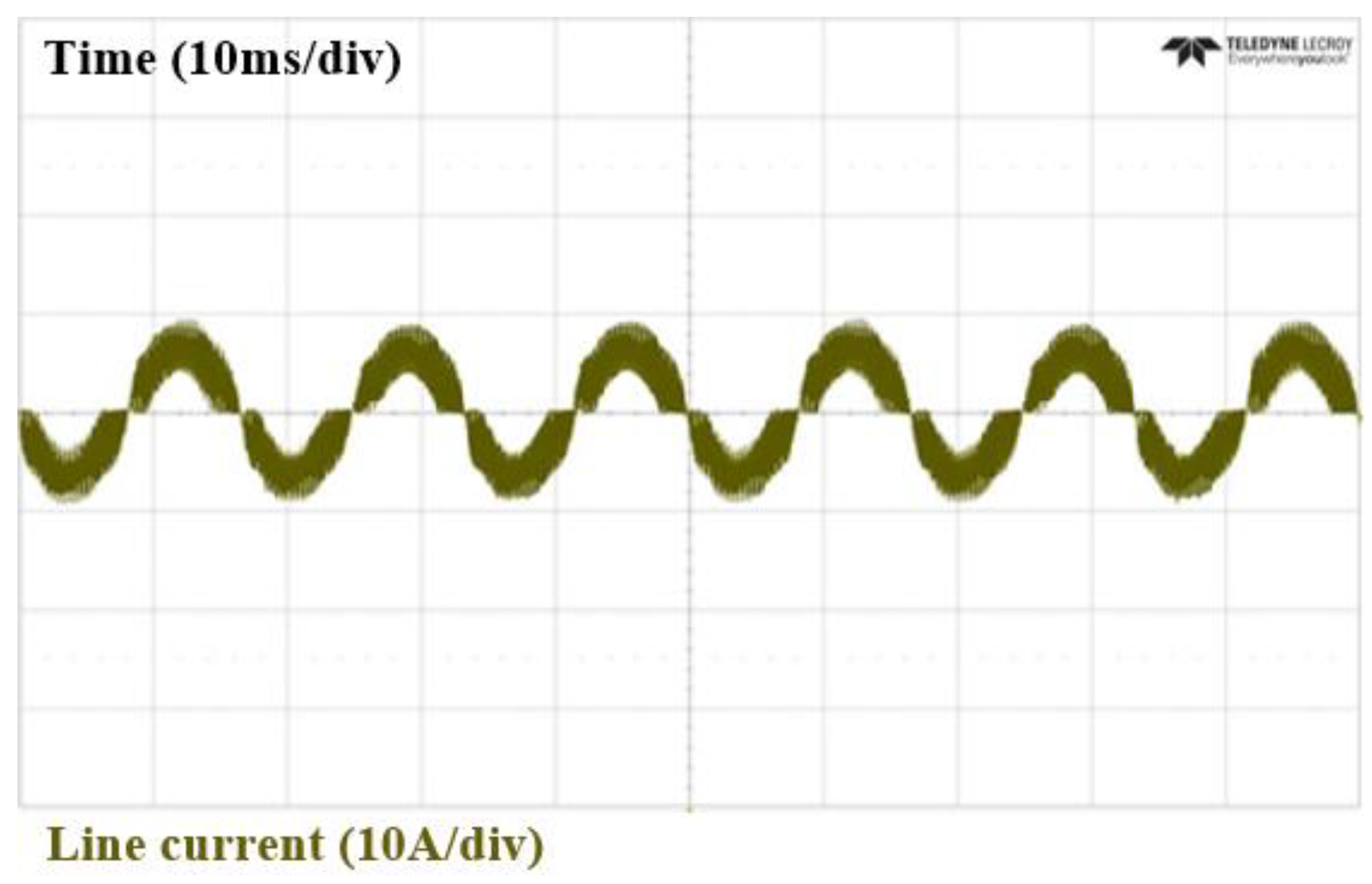
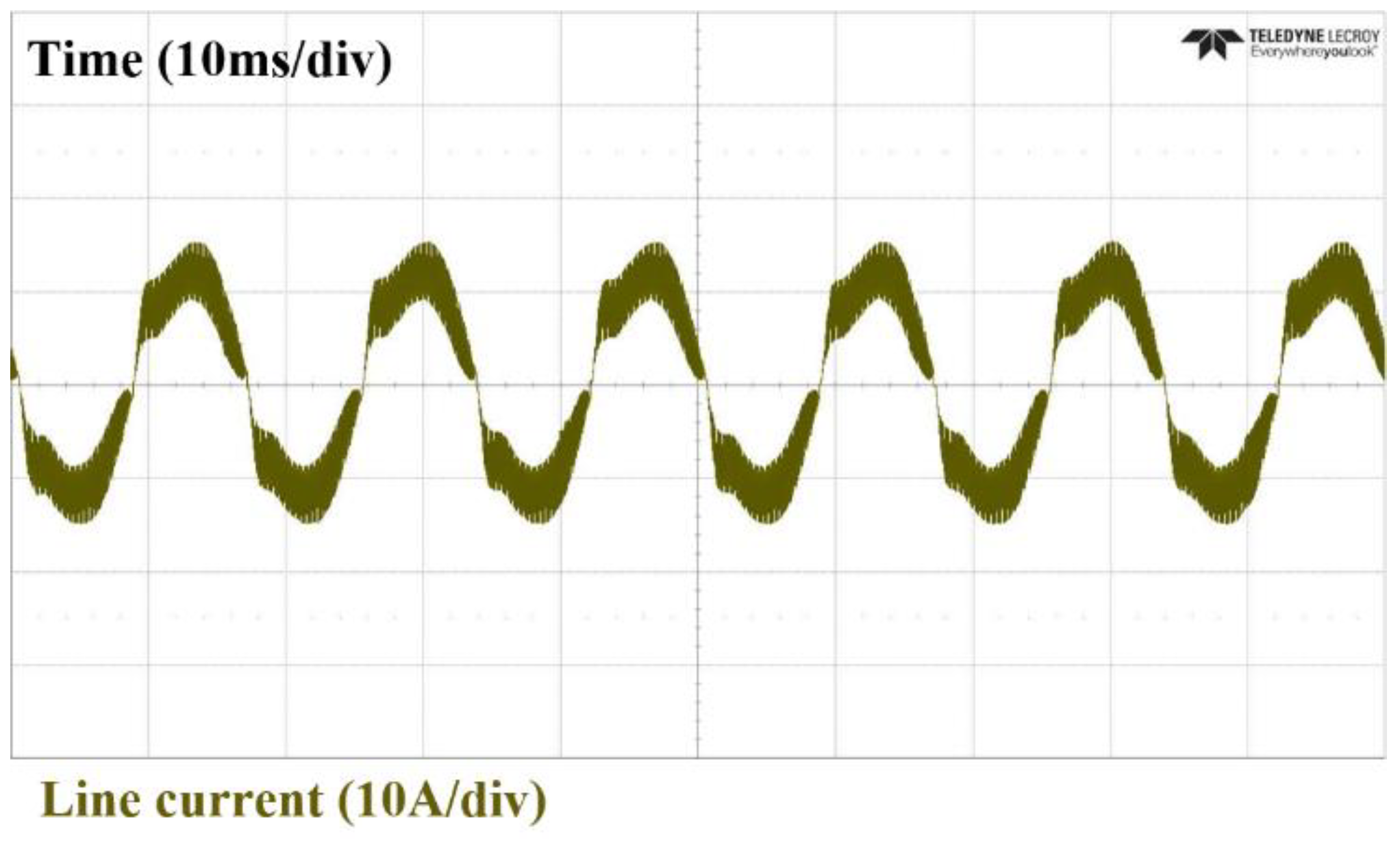
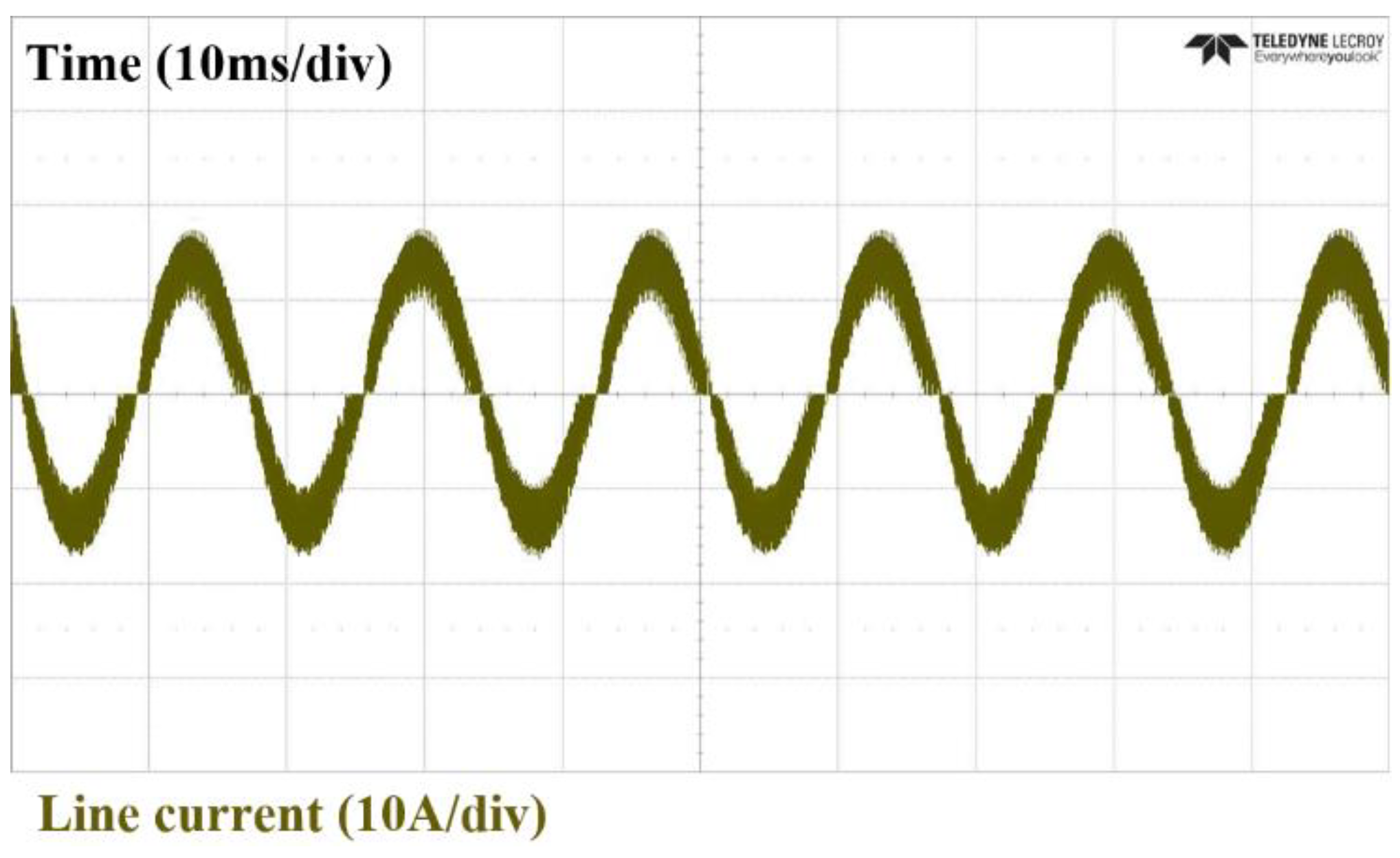



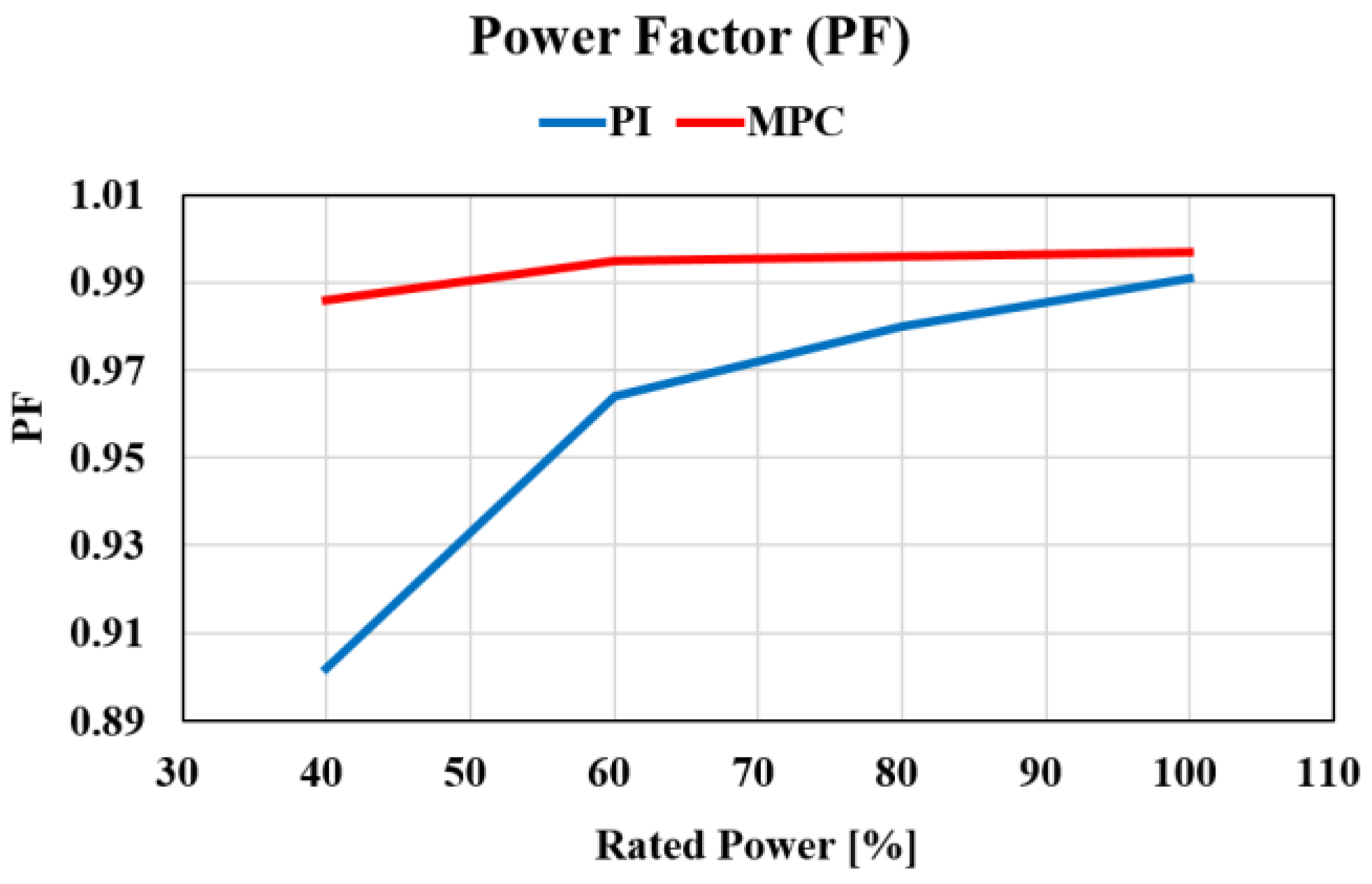
| Parameter | Value |
|---|---|
| Rated power | 1 kW |
| Grid side voltage | 110 Vrms |
| DC-link voltage | 350–400 V |
| Inductor | 1 mH |
| Top/Bottom Capacitor | 450 µF |
| Grid frequency | 60 Hz |
| Switching frequency | 10 kHz |
| Sampling time | 100 µs |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, Y.-D.; Park, J.-H.; Lee, K.-B. Improving Line Current Distortion in Single-Phase Vienna Rectifiers Using Model-Based Predictive Control. Energies 2018, 11, 1237. https://doi.org/10.3390/en11051237
Kwon Y-D, Park J-H, Lee K-B. Improving Line Current Distortion in Single-Phase Vienna Rectifiers Using Model-Based Predictive Control. Energies. 2018; 11(5):1237. https://doi.org/10.3390/en11051237
Chicago/Turabian StyleKwon, Yong-Dae, Jin-Hyuk Park, and Kyo-Beum Lee. 2018. "Improving Line Current Distortion in Single-Phase Vienna Rectifiers Using Model-Based Predictive Control" Energies 11, no. 5: 1237. https://doi.org/10.3390/en11051237
APA StyleKwon, Y.-D., Park, J.-H., & Lee, K.-B. (2018). Improving Line Current Distortion in Single-Phase Vienna Rectifiers Using Model-Based Predictive Control. Energies, 11(5), 1237. https://doi.org/10.3390/en11051237






