A Novel Computational Approach for Harmonic Mitigation in PV Systems with Single-Phase Five-Level CHBMI
Abstract
:1. Introduction
2. Single-Phase Five-Level CHBMI
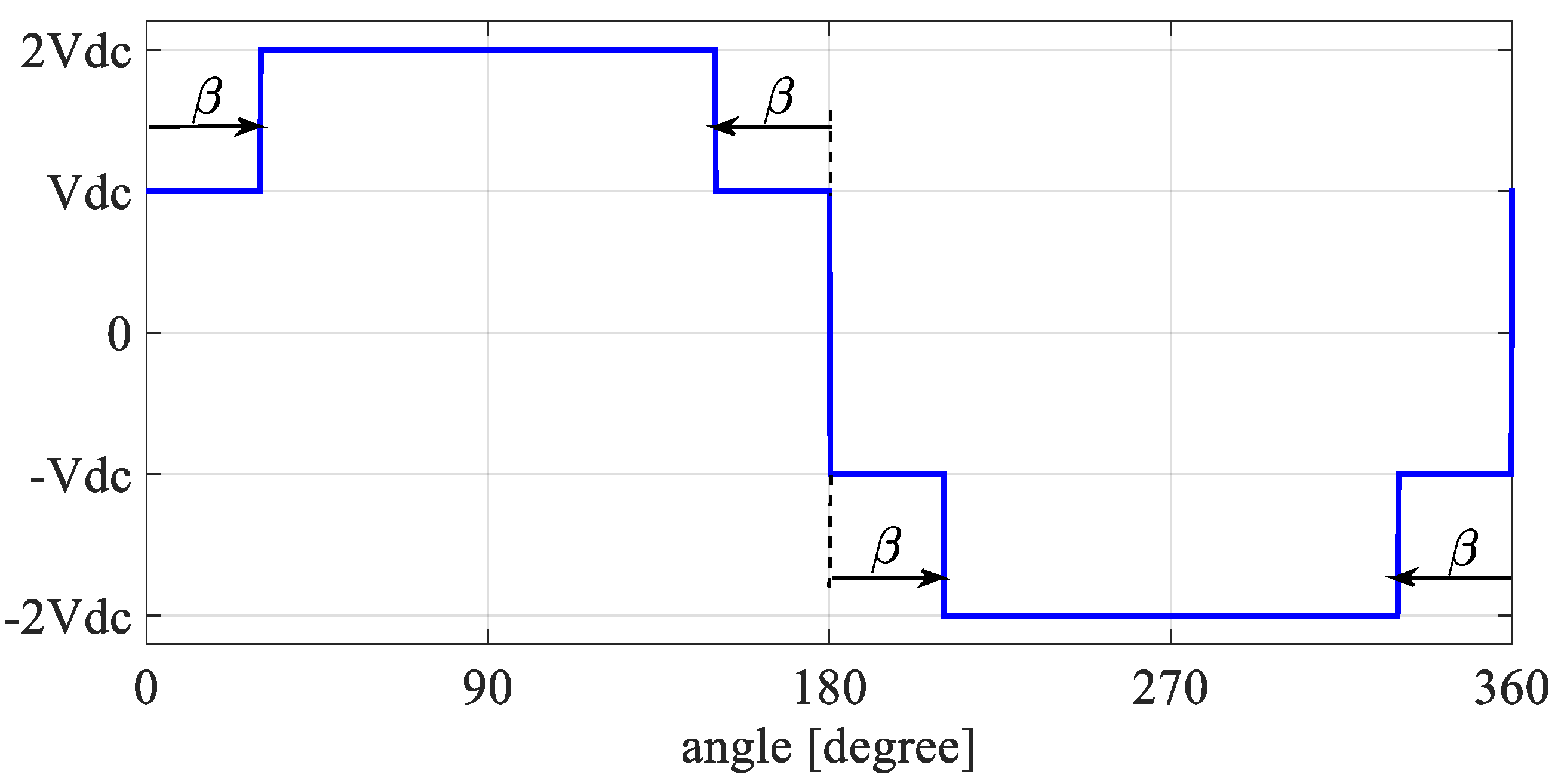
3. Voltage Waveform Analysis
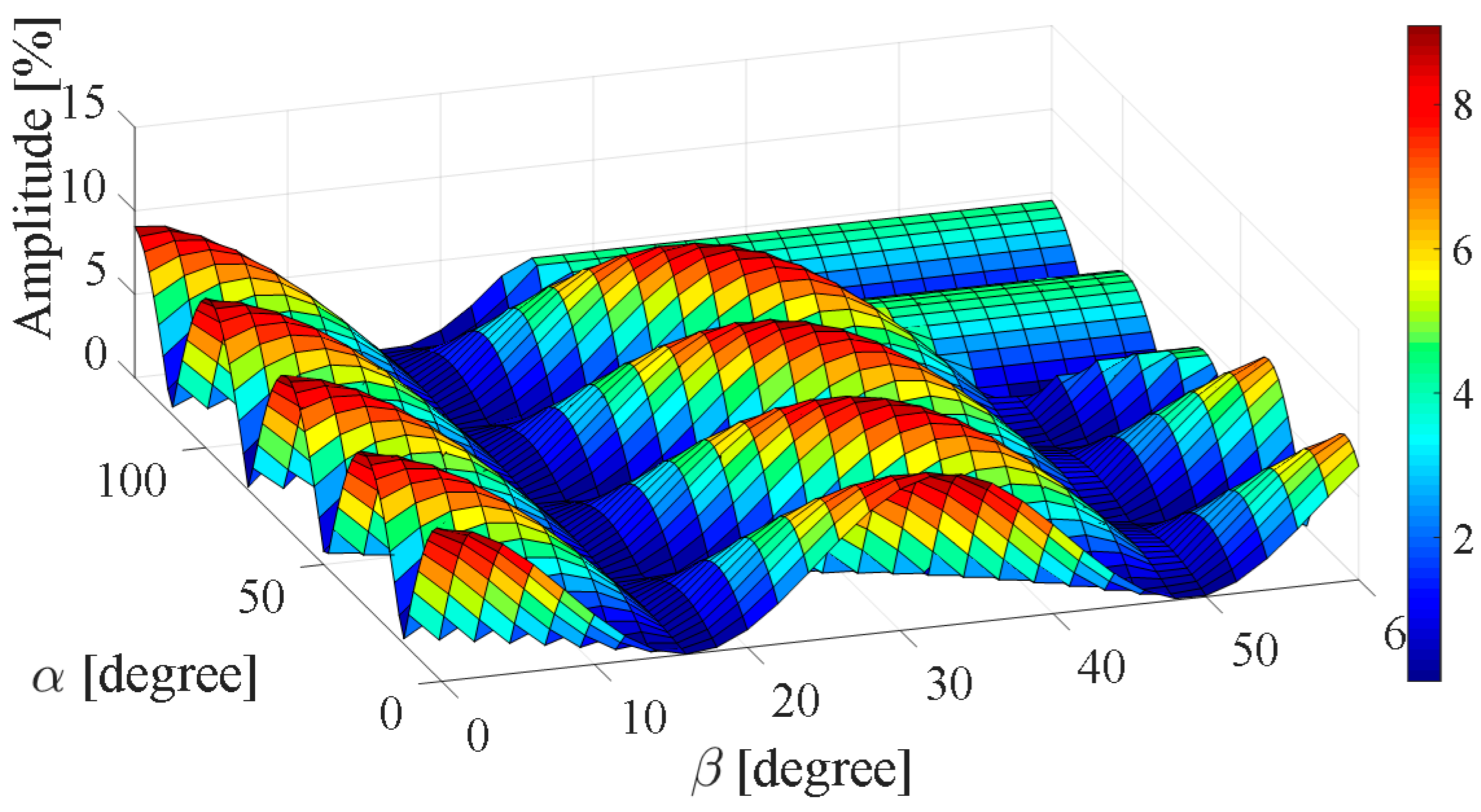
4. Mitigation Method of Reference Harmonics
5. Polynomial Equations for Real-Time Operation
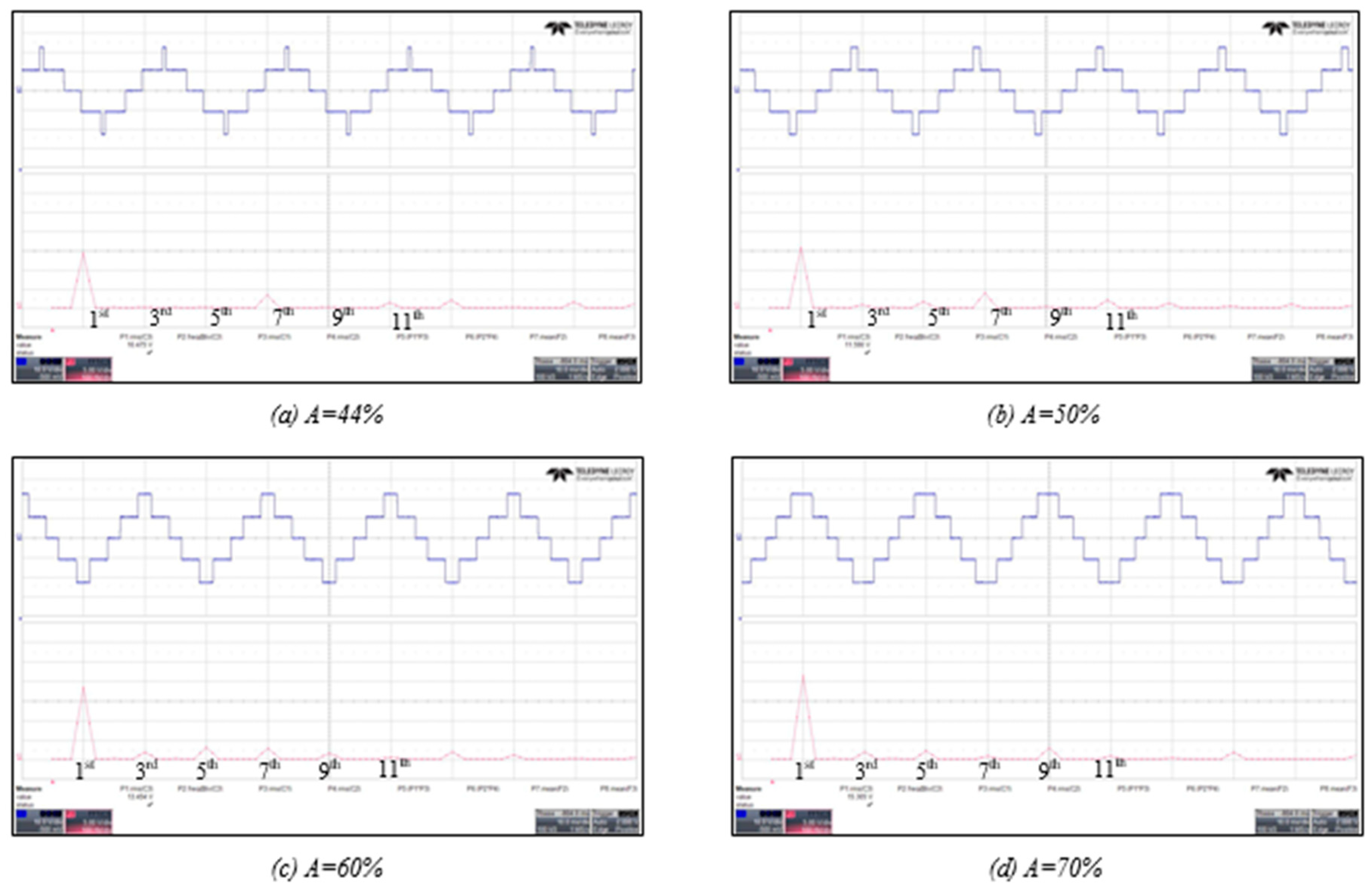
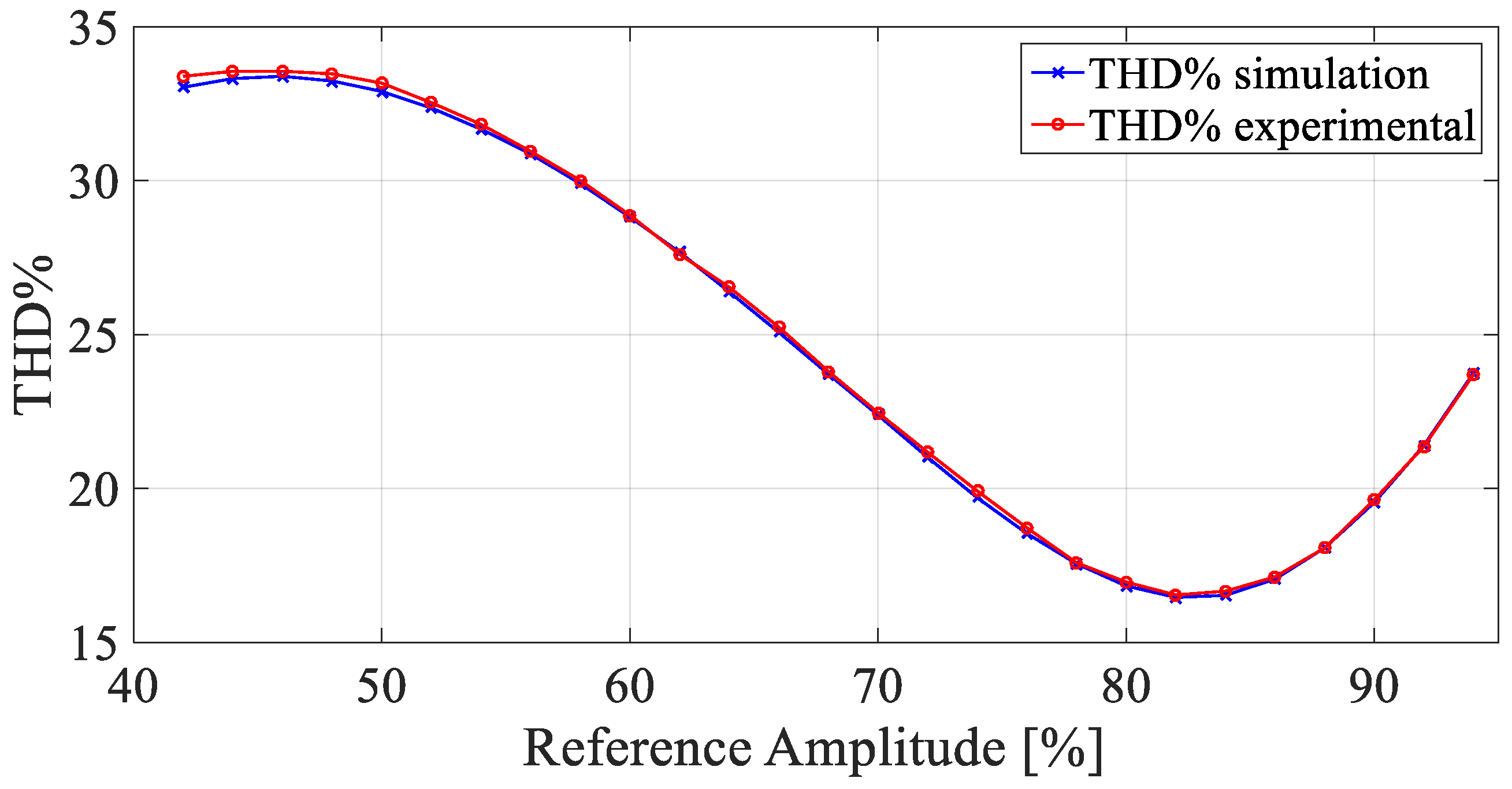
6. Experimental Validation and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings. Available online: http://www.buildup.eu/en/practices/publications/directive-201031eu-energy-performance-buildings-recast-19-may-2010 (accessed on 15 January 2018).
- Miceli, R.; Viola, F. Designing a sustainable university recharge area for electric vehicles: Technical and economic analysis. Energies 2017, 10, 1604. [Google Scholar] [CrossRef]
- Prabaharan, N.; Palanisamy, K. A comprehensive review on reduced switch multilevel inverter topologies, modulation techniques and applications. Renew. Sustain. Energy Rev. 2017, 76, 1248–1282. [Google Scholar] [CrossRef]
- Baker, R.H.; Bannister, L.H. Electric Power Converter. U.S. Patent 3867643, 16 February 1975. [Google Scholar]
- Yuan, X.; Barbi, I. Fundamentals of a new diode clamping multilevel inverter. IEEE Trans. Power Electron. 2000, 15, 711–718. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A survey on neutral-point-clamped inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Huang, J.; Corzine, K.A. Extended operation of flying capacitor multilevel inverters. IEEE Trans. Power Electron. 2006, 21, 140–147. [Google Scholar] [CrossRef]
- Kou, X.; Corzine, K.A.; Wielebski, M.W. Overdistention operation of cascaded multilevel inverters. IEEE Trans. Ind. Appl. 2006, 42, 817–824. [Google Scholar]
- Kala, P.; Arora, S. A comprehensive study of classical and hybrid multilevel inverter topologies for renewable energy applications. Renew. Sustain. Energy Rev. 2017, 76, 905–931. [Google Scholar] [CrossRef]
- Venkataramanaiah, J.; Suresh, Y.; Panda, A.K. A review on symmetric, asymmetric, hybrid and single DC sources based multilevel inverter topologies. Renew. Sustain. Energy Rev. 2017, 76, 788–812. [Google Scholar] [CrossRef]
- Jana, J.; Saha, H.; Bhattacharya, K.D. A review of inverter topologies for single-phase grid-connected photovoltaic systems. Renew. Sustain. Energy Rev. 2017, 72, 1256–1270. [Google Scholar] [CrossRef]
- Monica, P.; Kowsalya, M. Control strategies of parallel operated inverters in renewable energy application: A review. Renew. Sustain. Energy Rev. 2016, 65, 885–901. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Modeling, control and analysis of cascaded inverter based grid-connected photovoltaic system. Int. J. Electr. Power Energy Syst. 2016, 78, 165–173. [Google Scholar] [CrossRef]
- Ravi, A.; Manoharan, P.S.; Anand, J.V. Modeling and simulation of three phase multilevel inverter for grid connected photovoltaic systems. Sol. Energy 2011, 85, 2811–2818. [Google Scholar] [CrossRef]
- Rajkumar, M.V.; Manoharan, P.S. FPGA based multilevel cascaded inverters with SVPWM algorithm for photovoltaic system. Sol. Energy 2013, 87, 229–245. [Google Scholar] [CrossRef]
- Prabaharan, N.; Palanisamy, K. Analysis and integration of multilevel inverter configuration with boost converters in a photovoltaic system. Energy Convers. Manag. 2016, 128, 327–342. [Google Scholar] [CrossRef]
- Iero, D.; Carbone, R.; Carotenuto, R.; Felini, C.; Merenda, M.; Pangallo, G.; Della Corte, F.G. SPICE modelling of a complete photovoltaic system including modules, Energy storage elements and a multilevel inverter. Sol. Energy 2014, 107, 338–350. [Google Scholar] [CrossRef]
- Javad, O.; Shayan, E.; Ali, M. Compensation of voltage sag caused by partial shading in grid-connected PV system through the three-level SVM inverter. Sustain. Energy Technol. Assess. 2016, 18, 107–118. [Google Scholar]
- Prabaharan, N.; Palanisamy, K. A Single Phase Grid Connected Hybrid Multilevel Inverter for Interfacing Photo-voltaic System. Energy Procedia 2016, 103, 250–255. [Google Scholar] [CrossRef]
- Husev, O.; Roncero-Clemente, C.; Romero-Cadaval, E.; Vinnikov, D.; Jalakas, T. Three-level three-phase quasi-Z-source neutral-point-clamped inverter with novel modulation technique for photovoltaic application. Electr. Power Syst. Res. 2016, 130, 10–21. [Google Scholar] [CrossRef]
- Lauria, D.; Coppola, M. Design and control of an advanced PV inverter. Sol. Energy 2014, 110, 533–542. [Google Scholar] [CrossRef]
- Hannan, M.A.; Azidin, F.A.; Mohamed, A. Hybrid electric vehicles and their challenges: A review. Renew. Sustain. Energy Rev. 2014, 29, 135–150. [Google Scholar] [CrossRef]
- Zhai, L.; Lee, G.; Gao, X.; Zhang, X.; Gu, Z.; Zou, M. Impact of Electromagnetic Interforance from Power Inverter Drive System on Batteries in Electric Vehicle. Energy Procedia 2016, 88, 881–888. [Google Scholar] [CrossRef]
- Mese, E.; Ayaz, M.; Tezcan, M.M. Design considerations of a multitasked electric machine for automotive applications. Electr. Power Syst. Res. 2016, 131, 147–158. [Google Scholar] [CrossRef]
- Tolbert, L.M.; Peng, F.Z.; Cunnyngham, T.; Chiasson, J.N. Charge balance control schemes for cascade multilevel converter in hybrid electric vehicles. IEEE Trans. Ind. Electron. 2002, 49, 1058–1064. [Google Scholar] [CrossRef] [Green Version]
- Khoucha, F.; Lagoun, S.M.; Marouani, K.; Kheloui, A.; Benbouzid, M.E.H. Hybrid cascaded H-bridge multilevel-inverter induction-motor-drive direct torque control for automotive applications. IEEE Trans. Ind. Electron. 2010, 57, 892–899. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Du, M.; Zhou, T.; Guo, H.; Zhang, C. Comprehensive comparison between silicon carbide MOSFETs and silicon IGBTs based traction systems for electric vehicles. Appl. Energy 2016, 194, 626–634. [Google Scholar] [CrossRef]
- Kabalyk, Y. Determination of energy loss in power voltage inverters for power supply of locomotive traction motors. Procedia Eng. 2016, 165, 1437–1443. [Google Scholar] [CrossRef]
- Carpita, M.; Marchesoni, M.; Pellerin, M.; Moser, D. Multilevel converter for traction applications: Small-scale prototype tests results. IEEE Trans. Ind. Electron. 2008, 55, 2203–2212. [Google Scholar] [CrossRef]
- Kumar, Y.P.; Ravikumar, B. A simple modular multilevel inverter topology for the power quality improvement in renewable energy based green building microgrids. Electr. Power Syst. Res. 2016, 140, 147–161. [Google Scholar] [CrossRef]
- Kamel, R.M. New inverter control for balancing standalone micro-grid phase voltages: A review on MG power quality improvement. Renew. Sustain. Energy Rev. 2016, 63, 520–532. [Google Scholar] [CrossRef]
- Mohamed, E.E.; Sayed, M.A. Matrix converters and three-phase inverters fed linear induction motor drives-Performance compare. Ain Shams Eng. J. 2016. Available online: https://doi.org/10.1016/j.asej.2016.02.002 (accessed on 21 March 2016).
- Trabelsi, M.; Boussak, M.; Benbouzid, M. Multiple criteria for high performance real-time diagnostic of single and multiple open-switch faults in ac-motor drives: Application to IGBT-based voltage source inverter. Electr. Power Syst. Res. 2017, 144, 136–149. [Google Scholar] [CrossRef]
- Prakash, G.; Subramani, C.; Bharatiraja, C.; Shabin, M. A low cost single phase grid connected reduced switch PV inverter based on Time Frame Switching Scheme. Inter. J. Electr. Power Energy Syst. 2016, 2016 77, 100–111. [Google Scholar] [CrossRef]
- Gupta, V.K.; Mahanty, R. Optimized switching scheme of cascaded H-bridge multilevel inverter using PSO. Inter. J. Electr. Power Energy Syst. 2015, 64, 699–707. [Google Scholar] [CrossRef]
- Mesquita, S.J.; Antunes, F.L.M.; Daher, S. A new bidirectional hybrid multilevel inverter with 49-level output voltage using a single dc voltage source and reduced number of on components. Electr. Power Syst. Res. 2017, 143, 703–714. [Google Scholar] [CrossRef]
- Báez-Fernández, H.; Ramírez-Beltrán, N.D.; Méndez-Piñero, M.I. Selection and configuration of inverters and modules for a photovoltaic system to minimize costs. Renew. Sustain. Energy Rev. 2016, 58, 16–22. [Google Scholar] [CrossRef]
- Schettino, G.; Benanti, S.; Buccella, C.; Caruso, M.; Castiglia, V.; Cecati, C.; Di Tommaso, A.O.; Miceli, R.; Romano, P.; Viola, F. Simulation and experimental validation of multicarrier PWM techniques for three-phase five-level cascaded H-bridge with FPGA controller. Inte. J. Renew. Energy Res. 2017, 7, 1383–1394. [Google Scholar]
- Schettino, G.; Buccella, C.; Caruso, M.; Cecati, C.; Castiglia, V.; Miceli, R.; Viola, F. Overview and experimental analysis of MC SPWM techniques for single-phase five level cascaded H-bridge FPGA controller-based. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 4529–4534. [Google Scholar]
- Benanti, S.; Buccella, C.; Caruso, M.; Castiglia, V.; Cecati, C.; Di Tommaso, A.O.; Miceli, R.; Romano, P.; Schettino, G.; Viola, F. Experimental analysis with FPGA controller-based of MC PWM techniques for three-phase five level cascaded H-bridge for PV applications. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 1173–1178. [Google Scholar]
- Rahim, N.A.; Ping, H.W.; Selvaraj, J. Elimination of harmonics in photovoltaic seven-level inverter with Newton-Raphson optimization. Procedia Environ. Sci. 2013, 2013 17, 519–528. [Google Scholar]
- Kavali, J.; Mittal, A. Analysis of various control schemes for minimal Total Harmonic Distortion in cascaded H-bridge multilevel inverter. J. Electr. Syst. Inf. Technol. 2016, 3, 428–441. [Google Scholar] [CrossRef]
- Al-Othman, A.K.; Abdelhamid, T.H. Elimination of harmonics in multilevel inverters with non-equal dc sources using PSO. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference (EPE-PEMC 2008), Poznan, Poland, 1–3 September 2008; pp. 756–764. [Google Scholar]
- Ganesan, K.; Barathi, K.; Chandrasekar, P.; Balaji, D. Selective harmonic elimination of cascaded multilevel inverter using BAT algorithm. Procedia Technol. 2015, 21, 651–657. [Google Scholar] [CrossRef]
- Marzoughi, A.; Imaneini, H.; Moeini, A. An optimal selective harmonic mitigation technique for high power converters. Inter. J. Electr. Power Energ. Syst. 2013, 49, 34–39. [Google Scholar] [CrossRef]
- Voltage Characteristics of Electricity Supplied by Public Electricity Networks. Available online: http://fs.gongkong.com/files/technicalData/201110/2011100922385600001.pdf (accessed on 15 January 2018).
- Personen, M.A. Harmonics characteristic parameters methods of study estimates of existing values in the network. Electra 1981, 77, 35–54. [Google Scholar]
- Electromagnetic Compatibility (EMC)–Part 3-7: Limits–Assessment of Emission Limits for the Connection of Fluctuating Installations to MV, HV and EHV Power Systems. Available online: https://ieeexplore.ieee.org/document/6232421/ (accessed on 15 January 2018).
- Letha, S.S.; Thakur, T.; Kumar, J. Harmonic elimination of a photo-voltaic based cascaded H-bridge multilevel inverter using PSO (particle swarm optimization) for induction motor drive. Energy 2016, 107, 335–346. [Google Scholar] [CrossRef]
- Rao, G.N.; Raju, P.S.; Sekhar, K.C. Harmonic elimination of cascaded H-bridge multilevel inverter based active power filter controlled by intelligent techniques. Inte. J. Electr. Power Energ. Syst. 2014, 61, 56–63. [Google Scholar]
- Panda, A.K.; Patnaik, S.S. Analysis of cascaded multilevel inverters for active harmonic filtering in distribution networks. Inte. J. Electr. Power Energ. Syst. 2015, 66, 216–226. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M. Power Electronics: Converters, Applications, and Design, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Dordevic, O.; Jones, M.; Levi, E. Analytical formulas for phase voltage RMS squared and THD in PWM multiphase systems. IEEE Trans. Power Electron. 2015, 30, 1645–1656. [Google Scholar] [CrossRef]






















| S1 | S2 | S3 | S4 | Vout (t) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | Vdc |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | −Vdc |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | Vdc |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 2Vdc |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | Vdc |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | −Vdc |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | −2Vdc |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | −Vdc |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | Vdc |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | −Vdc |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miceli, R.; Schettino, G.; Viola, F. A Novel Computational Approach for Harmonic Mitigation in PV Systems with Single-Phase Five-Level CHBMI. Energies 2018, 11, 2100. https://doi.org/10.3390/en11082100
Miceli R, Schettino G, Viola F. A Novel Computational Approach for Harmonic Mitigation in PV Systems with Single-Phase Five-Level CHBMI. Energies. 2018; 11(8):2100. https://doi.org/10.3390/en11082100
Chicago/Turabian StyleMiceli, Rosario, Giuseppe Schettino, and Fabio Viola. 2018. "A Novel Computational Approach for Harmonic Mitigation in PV Systems with Single-Phase Five-Level CHBMI" Energies 11, no. 8: 2100. https://doi.org/10.3390/en11082100
APA StyleMiceli, R., Schettino, G., & Viola, F. (2018). A Novel Computational Approach for Harmonic Mitigation in PV Systems with Single-Phase Five-Level CHBMI. Energies, 11(8), 2100. https://doi.org/10.3390/en11082100







