Electromechanical Transient Modeling of Line Commutated Converter-Modular Multilevel Converter-Based Hybrid Multi-Terminal High Voltage Direct Current Transmission Systems
Abstract
1. Introduction
- (1)
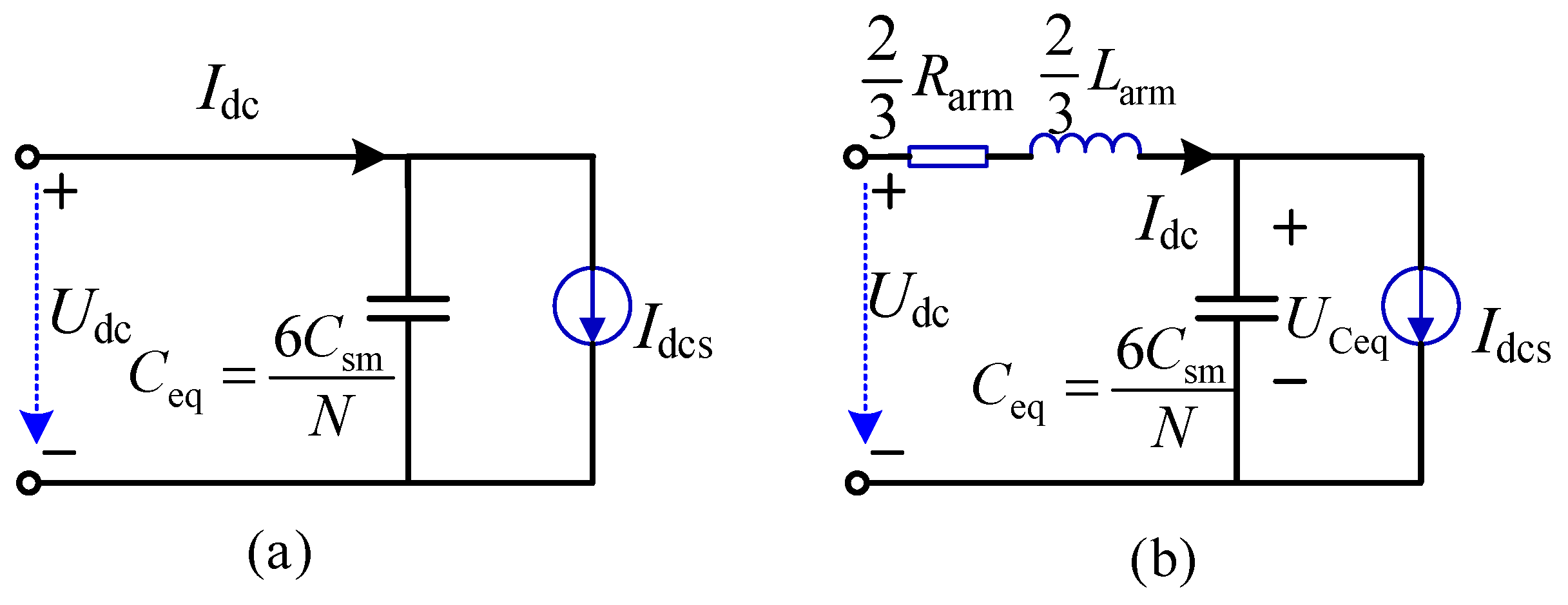
- An improved electromechanical model of LCC-MMC hybrid MTDC system is proposed. Specifically, the DC-side model of the MMC is established as a second-order model, which is more accurate than the conventional first-order DC-side model of the MMC.
- (2)
- Considering the firing angle limits of LCC, we propose a sequential power flow algorithm for the initialization of the LCC-MMC hybrid MTDC system.
2. Electromechanical Transient Modeling of LCC-MMC Hybrid Multi-Terminal HVDC System
2.1. General Idea of Modeling
- Establishing the AC-side and DC-side models of the LCC/MMC;
- Establishing the controller models of the LCC/MMC;
- Establishing the DC network with arbitrary topology.
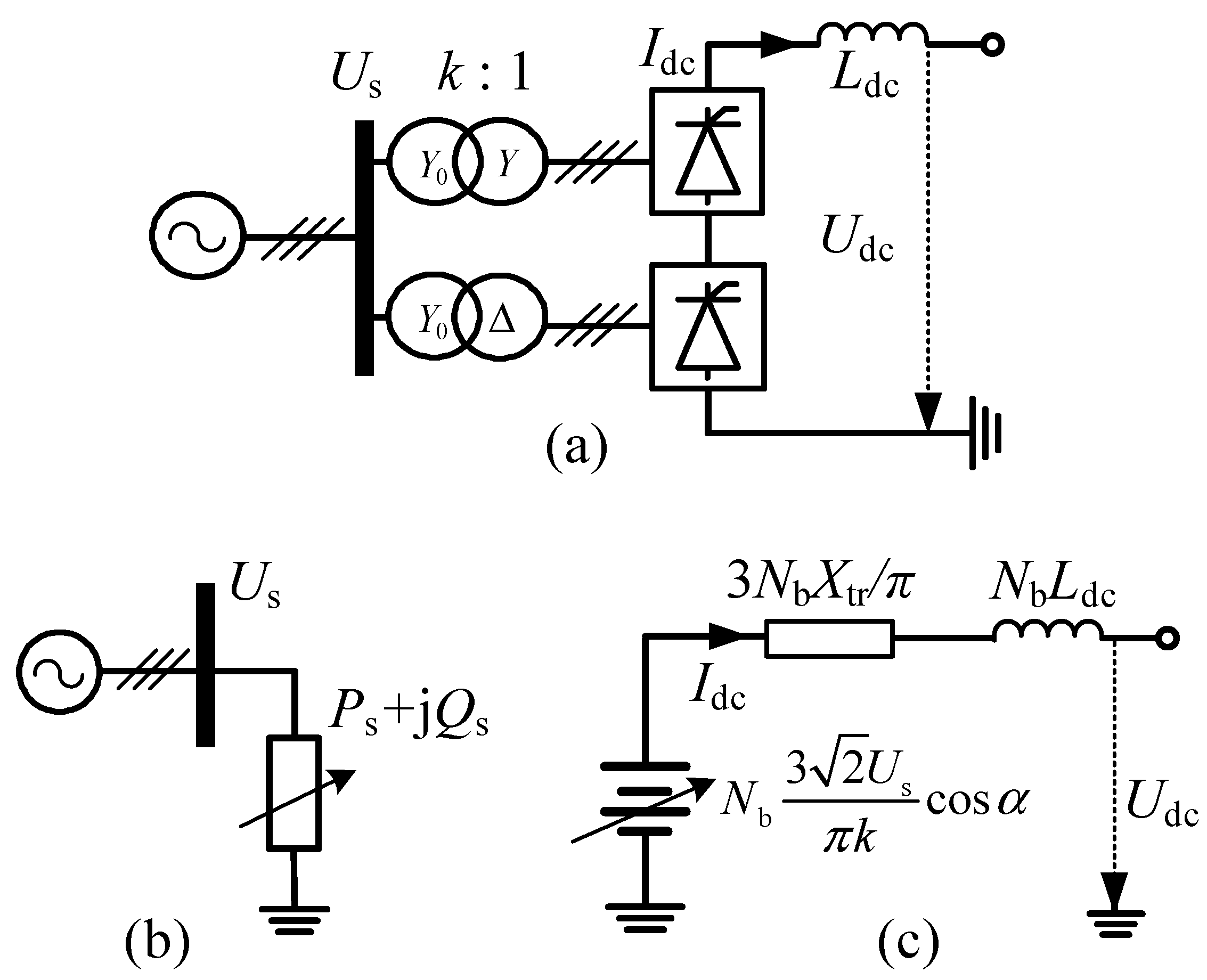
2.2. Modeling of LCC Station
2.2.1. AC-side Model of the LCC
2.2.2. DC-side Model of the LCC
2.2.3. Controller Modeling of the LCC
2.3. Modeling of MMC Station
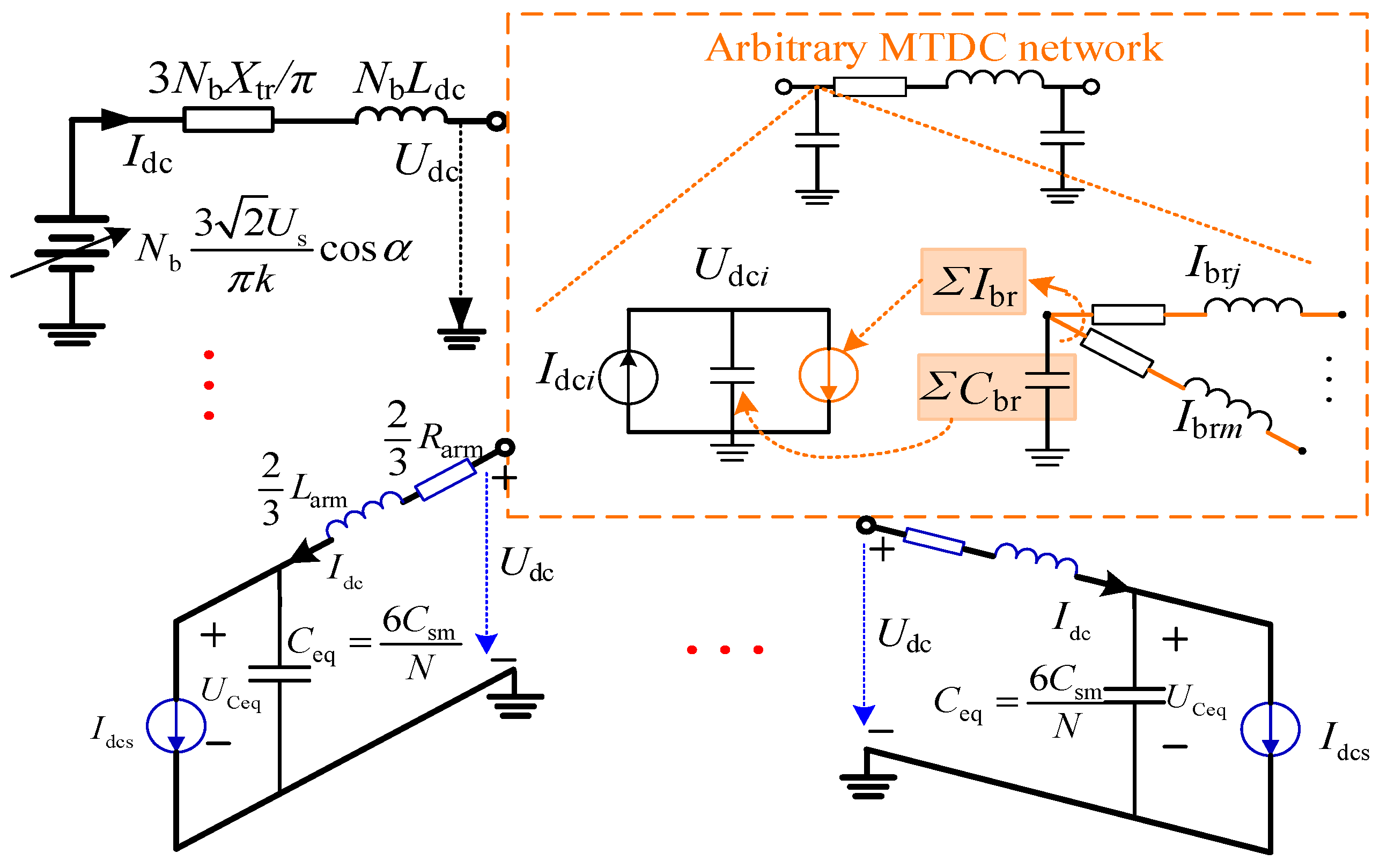
2.4. Modeling of the Hybrid MTDC Network
- For the i-th DC node:where Cbrk and Ibrk are the capacitance and current of the kth DC branch associated with node i; Udci is the DC voltage of the i-th node; if node i belongs to a converter node, Idci is the DC current source fed from LCC/MMC station, otherwise Idci is zero for the i-th intermediate node in a DC network.
- For the k-th DC branch between node i and node v:where Rbrk and Lbrk are the resistance and inductance of the kth DC branch, respectively; Udcv is the DC voltage of the v-th node.
2.5. Summary of the Differential Algebraic Equations of the LCC-MMC Hybrid MTDC System
3. Initialization of the LCC-MMC Hybrid MTDC Systems
3.1. Determination of Converter Bus Types
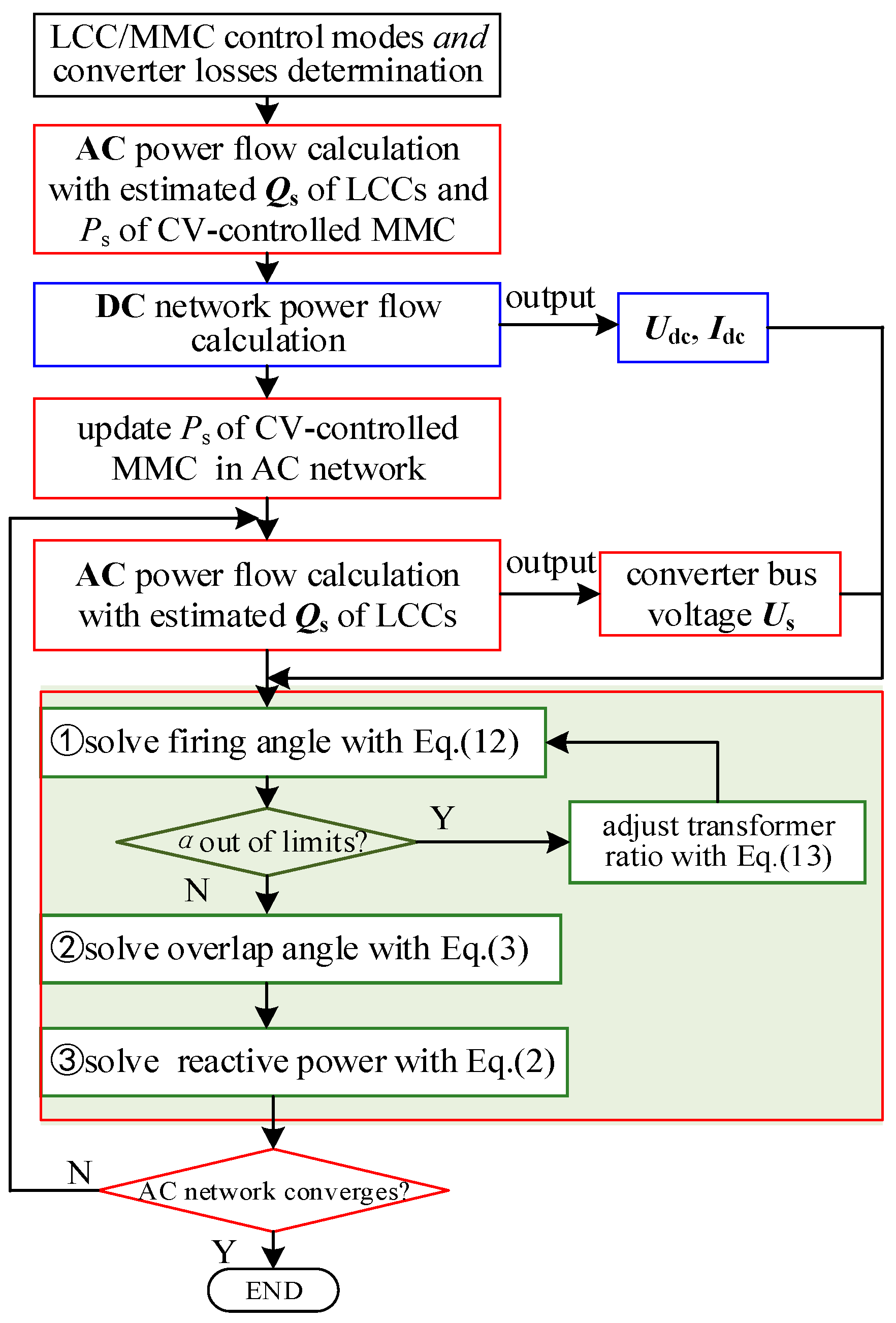
3.2. Implementation of the Sequential Power Flow Algorithm
- Solving the AC network with focus on AC/DC interfaces.
- Solving the DC network solution.
- Solving the internal variables such as firing angles and overlap angles of the LCCs.
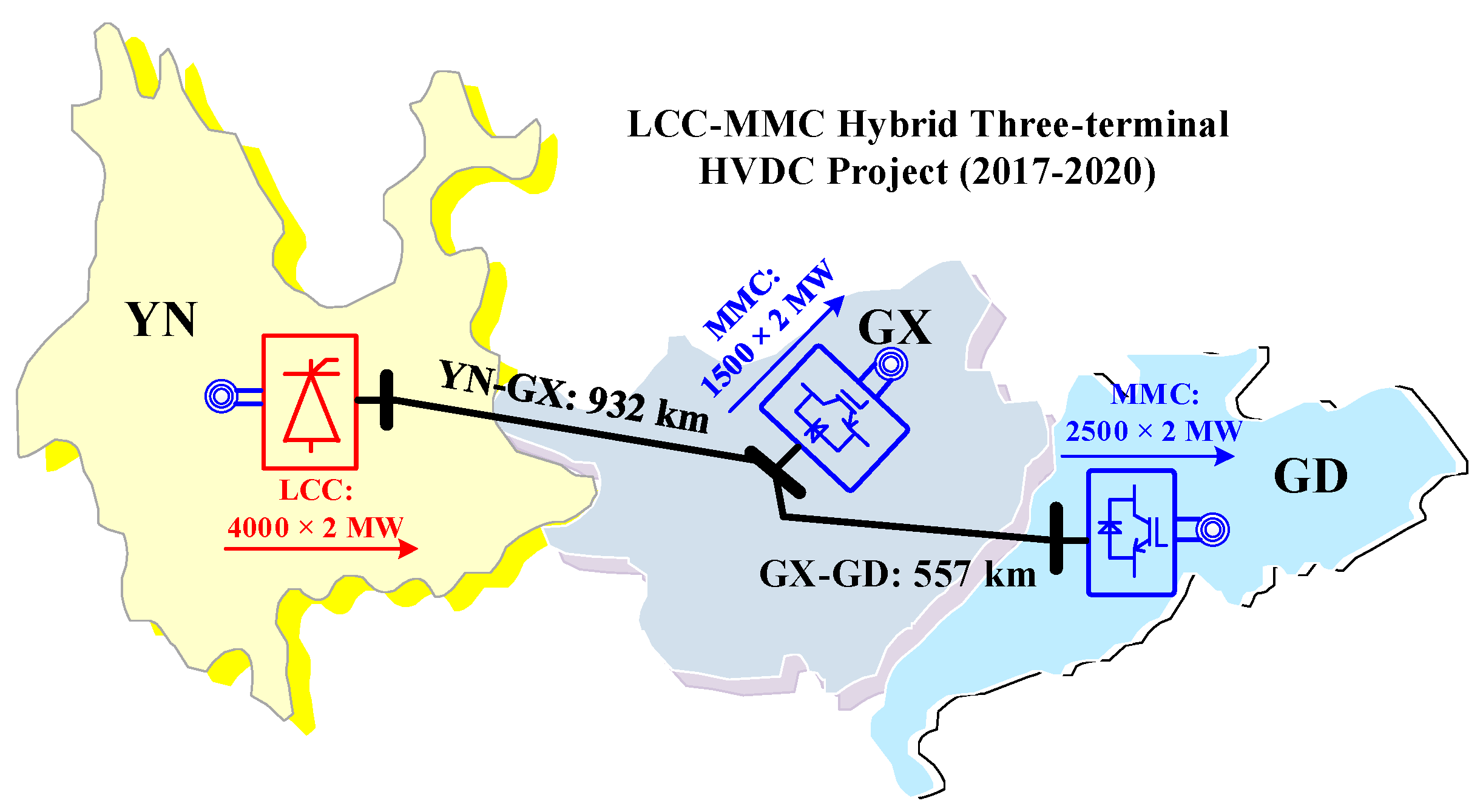
4. Case Study
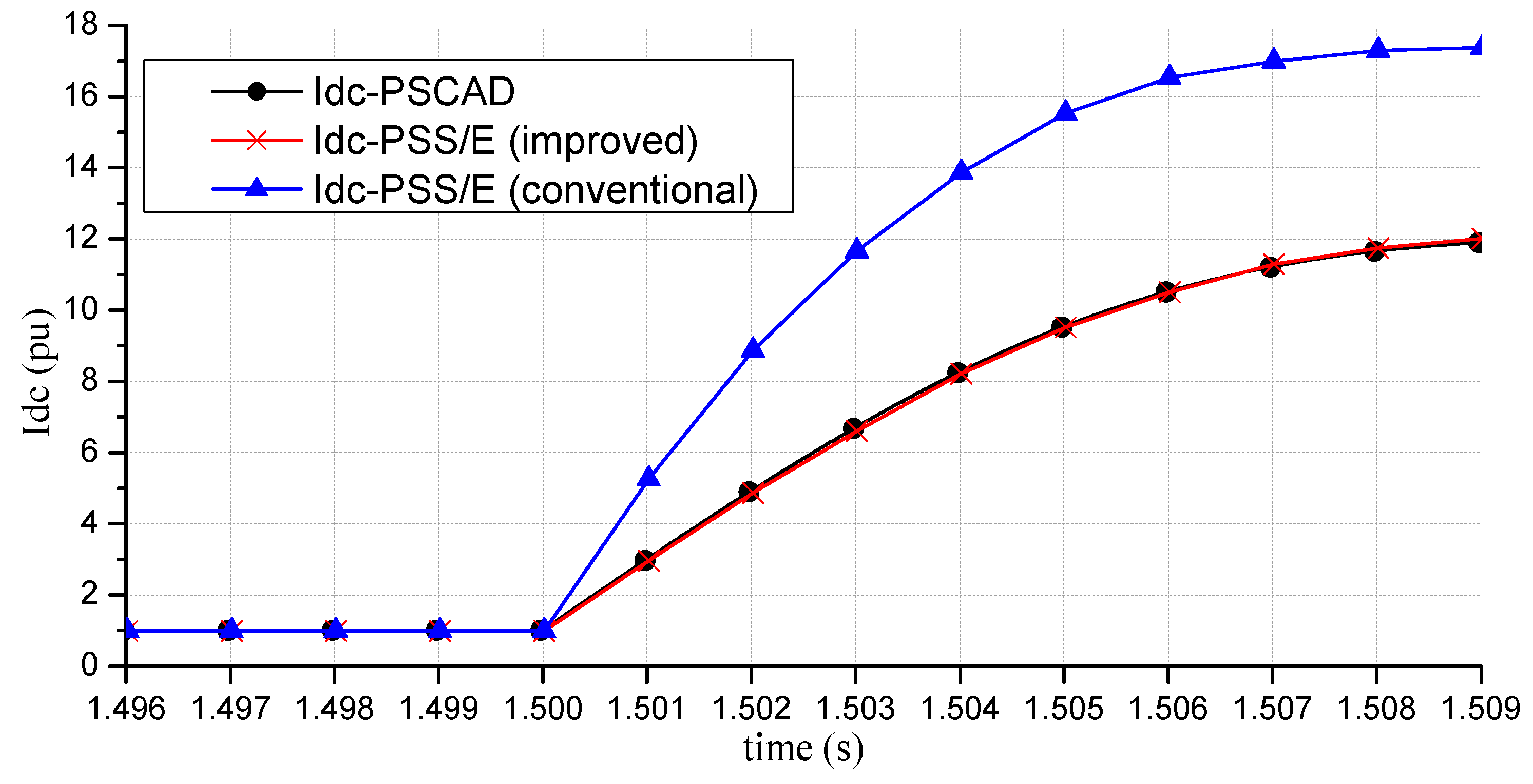
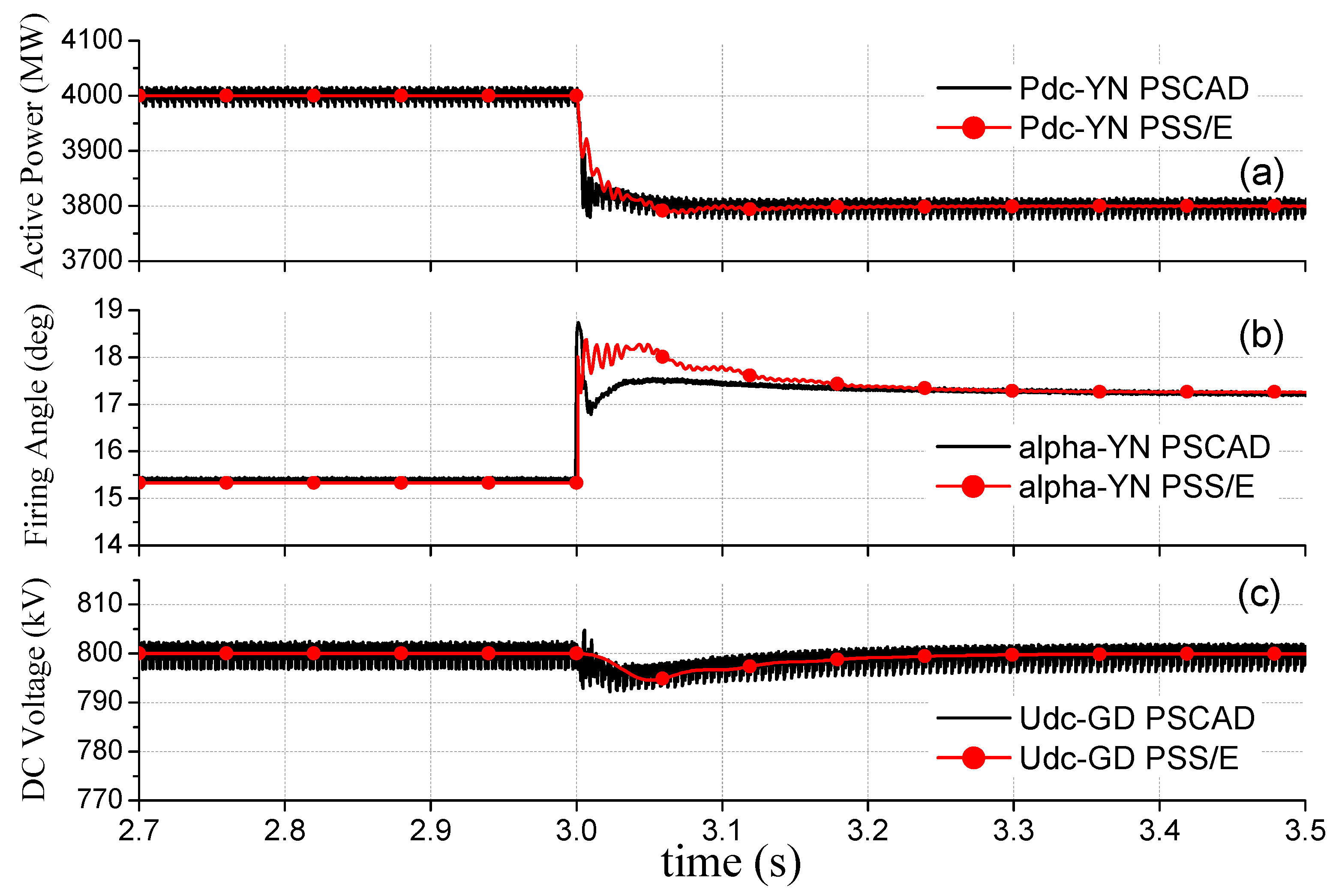
4.1. Case 1: Validation of the Electromechanical Model of the LCC-MMC Hybrid MTDC System
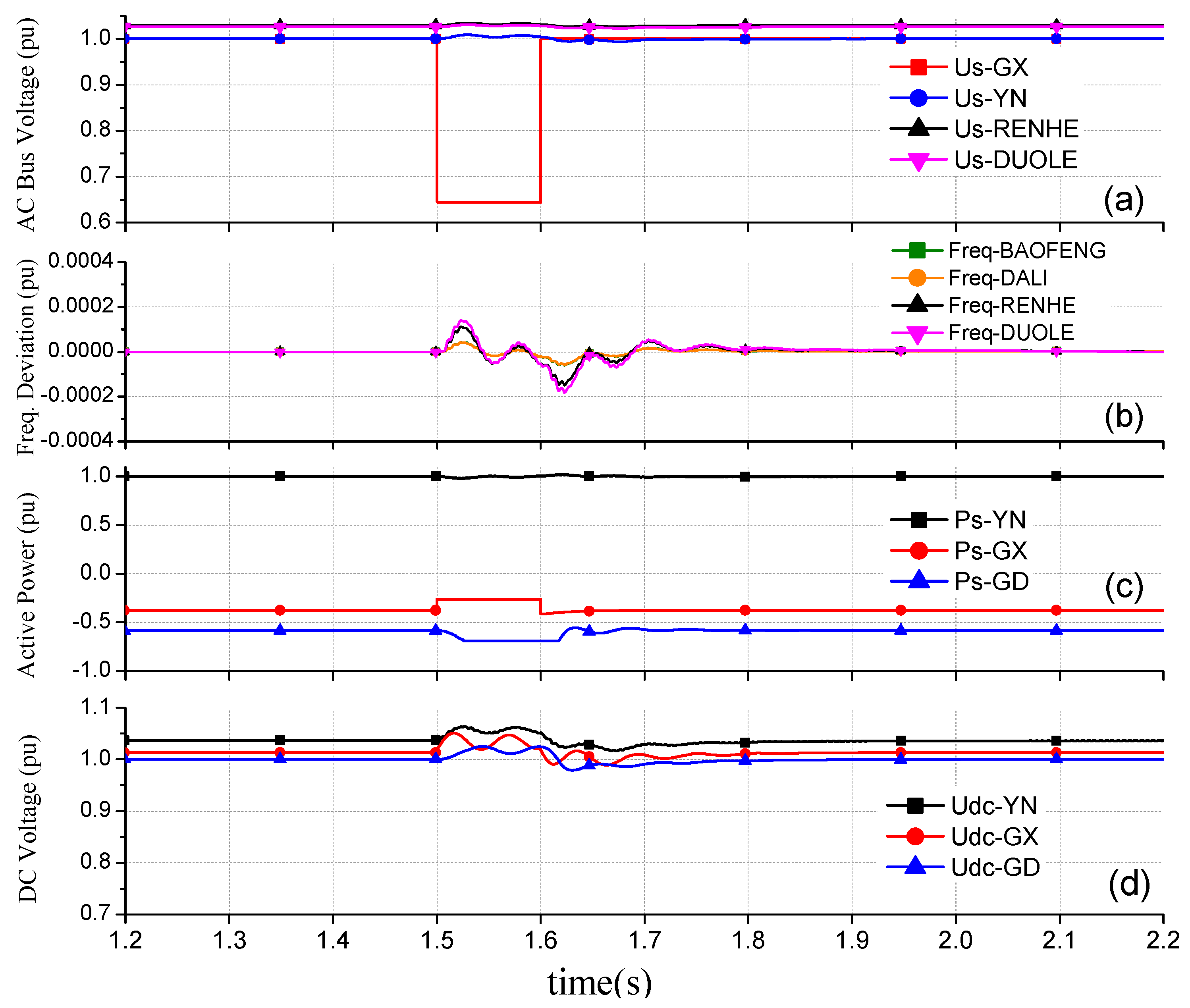
4.2. Case 2: Dynamic Analysis of the Large-Scale AC/DC System Embedded with a Hybrid MTDC System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Item | Retifier | Inverter |
|---|---|---|
| Rated L-L RMS voltage of AC system (kV) | 220 | 220 |
| Equivalent system impedance (Ω) | 0.484 + j4.84 | 0.484 + j4.84 |
| Rated capacity of MMC (MVA) | 400 | 400 |
| Rated DC voltage (kV) | 400 | 400 |
| Rated capacity of transformer (MVA) | 480 | 480 |
| Nominal ratio of transformer (kV) | 220:210 | 220:210 |
| Leakage inductance of transformer (mH) | 35 | 35 |
| Arm inductance of MMC (mH) | 76 | 76 |
| Arm resistance of MMC (Ω) | 0.48 | 0.48 |
| Number of sub module per arm | 200 | 200 |
| Capacitance of sub module (μF) | 6667 | 6667 |
| Smoothing reactor (mH) | 100 | 100 |
| Control mode | constant Ps + Qs | constant Udc + Qs |
| Reference (MW/Mvar/kV) | Ps*: 400, Qs*: 0 | U*dc: 400, Qs*: 0 |
| Item | LCC-YN | MMC-GX | MMC-GD |
|---|---|---|---|
| Converter rated capacity: SN (MVA) | 4000 | 1500 | 2500 |
| Rated DC voltage: UdcN (kV) | +800 | +800 | +800 |
| Nominal transformer ratio: kN (kV) | 525:178 | 525:440 | 525:440 |
| Step size of transformer tap: Ttap | 1.25% | / | / |
| Leakage reactance: Xtr(pu) | 0.2 | 0.16 | 0.18 |
| Arm inductance: Larm (mH) | / | 81 | 49 |
| Number of sub module per arm: N | / | 400 | 400 |
| Capacitance of sub module: Csm (μF) | / | 12500 | 20833 |
| Smoothing reactor: Ldc(mH) | 100 | 100 | 75 |
| Loss ratio: r (%) | 0 | 1 | 1 |
| Control mode | constant Idc | constant Ps + Qs | constant Udc + Qs |
| Reference (MW/Mvar/kV) | Pdc*: 4000 | P*s: 1500, Qs*: 0 | Udc*: 800, Qs*: 0 |
| Abbreviation | Description |
|---|---|
| LCC | line commutated converter |
| MMC | modular multilevel converter |
| HVDC | high voltage direct current transmission |
| VSC | voltage source converter |
| MTDC | multi-terminal HVDC |
| YN | Yunnan (Province of China) |
| GX | Guangxi (Province of China) |
| GD | Guangdong (Province of China) |
| CSPG | China Southern Power Grid |
| DAEs | differential-algebraic equations |
| CV-controlled | constant DC voltage controlled |
| PSS/E | Power System Simulation for Engineering, |
| PSASP | Power System Analysis Software Package |
| PSCAD | Power Systems Computer Aided Design |
References
- HVDC Grid Feasibility Study. Available online: http://eepublishers.co.za/wp-content/uploads/legacy/ Energize_2013/07_TT_05_HVDC.pdf (accessed on 1 July 2018).
- An, T.; Tang, G.; Wang, W. Research and application on multi-terminal and DC grids based on VSC-HVDC technology in China. High Volt. 2017, 2, 1–10. [Google Scholar] [CrossRef]
- Pierri, E.; Binder, O.; Hemdan, N.G.A.; Kurrata, M. Challenges and opportunities for a European HVDC grid. Renew. Sustain. Energy Rev. 2017, 70, 427–456. [Google Scholar] [CrossRef]
- Torres-Olguin, R.E.; Molinas, M.; Undeland, T. Offshore wind farm grid integration by VSC technology with LCC-based HVDC transmission. IEEE Trans. Sustain. Energy 2012, 3, 899–907. [Google Scholar] [CrossRef]
- Tang, G.; Xu, Z. A LCC and MMC hybrid HVDC topology with DC line fault clearance capability. Int. J. Electr. Power Energy Syst. 2014, 62, 419–428. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, S.; Xiao, H. Hybrid high-voltage direct current topology with line commutated converter and modular multilevel converter in series connection suitable for bulk power overhead line transmission. IET Power Electron. 2016, 9, 2307–2317. [Google Scholar] [CrossRef]
- Jung, J.J.; Cui, S.; Lee, J.H.; Sul, S.K. A new topology of multilevel VSC converter for a hybrid HVDC transmission system. IEEE Trans. Power Electron. 2017, 32, 4199–4209. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J.; Qiu, P.; Xiao, H.; Liu, G.; Xu, Z. Comparison of DC fault handling strategies for hybrid HVDC system. In Proceedings of the 43rd Annual Conference on the IEEE Industrial Electronic Society, Beijing, China, 29 October–1 November 2017; pp. 146–151. [Google Scholar]
- Dong, S.; Chi, Y.; Li, Y. Active voltage feedback control for hybrid multiterminal hvdc system adopting improved synchronverters. IEEE Trans. Power Deliv. 2016, 31, 445–455. [Google Scholar] [CrossRef]
- Zeng, R.; Xu, L.; Yao, L.; Finney, S.J.; Wang, Y. Hybrid HVDC for integrating wind farms with special consideration on commutation failure. IEEE Trans. Power Deliv. 2016, 31, 789–797. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.; Xue, Y.; Tang, G. DC-Side harmonic currents calculation and DC-Loop resonance analysis for an LCC–MMC hybrid HVDC transmission system. IEEE Trans. Power Deliv. 2015, 30, 642–651. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, Z.; Xiao, L.; Zhang, Z.; Xiao, H. Analysis of coupling effect on LCC-MCC hybrid HVDC from parallel AC lines in close proximity. In Proceedings of the Sower & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Kotb, O.; Ghandhari, M.; Eriksson, R.; Sood, V.K. On small signal stability of an AC/DC power system with a hybrid MTDC network. Electr. Power Syst. Res. 2016, 136, 79–88. [Google Scholar] [CrossRef]
- Guo, C.; Yin, Z.; Zhao, C.; Iravani, R. Small-signal dynamics of hybrid LCC-VSC HVDC systems. Electr. Power Energy Syst. 2018, 98, 362–372. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Teng, Y.; Qian, S.; Cheng, R. Optimal integration of a hybrid solar-battery power source into smart home nanogrid with plug-in electric vehicle. J. Power Sources 2017, 363, 277–283. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Barnes, M.; Hertem, D.V.; Teeuwsen, S.P.; Callavik, M. HVDC systems in smart grids. Proc. IEEE 2017, 105, 2082–2098. [Google Scholar] [CrossRef]
- Prabna, K. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Hahn, C.; Andreas, G.; Matthias, L. Modelling and Control Design of Hybrid-LCC and VSC based-HVDC Systems. In Proceedings of the Transmission and Distribution Conference and Exposition on the IEEE Power & Energy Society, Dallas, TX, USA, 3–5 May 2016; pp. 1–6. [Google Scholar]
- Zi, P.; Zhao, Z.; Chen, X.; Zhou, X.; Wan, L.; Shi, H.; An, N.; Tian, F. Electromechanical transient modeling of hybrid DC grid based on LCC and VSC converter. Proc. CSEE 2015, 35, 6265–6274. (In Chinese) [Google Scholar]
- Lei, J.; An, T.; Du, Z.; Yuan, Z. A General Unified AC/DC Power Flow Algorithm with MTDC. IEEE Trans. Power Syst. 2017, 32, 2837–2846. [Google Scholar] [CrossRef]
- Chai, R.; Zhang, B.; Dou, J.; Hao, Z.; Zheng, T. Unified power flow algorithm based on the nr method for hybrid AC/DC grids incorporating VSCs. IEEE Trans. Power Syst. 2016, 31, 4310–4318. [Google Scholar] [CrossRef]
- Bandaru, T. Newton-Raphson load flow model for hybrid multi-terminal HVDC systems consisting of voltage sourced converters and line commutated converters. In Proceedings of the IEEE Students Conference on Engineering and Systems, Allahabad, India, 6–8 November 2015; pp. 1–6. [Google Scholar]
- Beerten, J.; Cole, S.; Belmans, R. Generalized steady-state VSC mtdc model for sequential AC/DC power flow algorithms. IEEE Trans. Power Syst. 2012, 27, 821–829. [Google Scholar] [CrossRef]
- Liang, H.; Zhao, X.; Yu, X.; Gao, Y.; Yang, J. Study of power flow algorithm of AC/DC distribution system including VSC-MTDC. Energies 2015, 8, 8391–8405. [Google Scholar] [CrossRef]
- Dou, J.; Zhang, B.; Chai, R. A sequential power flow algorithm for AC/DC networks incorporating hybrid HVDC. In Proceedings of the Power and Energy Engineering Conference on the IEEE Power & Energy Society, Xi’an, China, 25–28 October 2016; pp. 773–779. [Google Scholar]
- Khan, M.O.; Jamali, S.Z.; Noh, C.H.; Gwon, G.H.; Kim, C.H. A load flow analysis for AC/DC hybrid distribution network incorporated with distributed energy resources for different grid scenarios. Energies 2018, 11, 367. [Google Scholar] [CrossRef]
- Guide for the Development of Models for HVDC Converters in a HVDC Grid. Available online: http://b4.cigre.org/Publications/Technical-Brochures/TB-604-2014-B4-57-Guide-for-the-Development-of-Models-for-HVDC-Converters-in-a-HVDC-Grid (accessed on 13 August 2018).
- Liu, S.; Xu, Z.; Hua, W.; Tang, G.; Xue, Y. Electromechanical transient modelling of modular multilevel converter based multi-terminal HVDC systems. IEEE Trans. Power Syst. 2014, 29, 72–83. [Google Scholar] [CrossRef]
- Trinh, N.T.; Zeller, M.; Wuerflinger, K.; Erlich, I. Generic model of MMC-VSC-HVDC for interaction study with AC power system. IEEE Trans. Power Syst. 2016, 31, 27–34. [Google Scholar] [CrossRef]
- Kou, L.; Zhu, L.; Li, F. Electromechanical transient model of HVDC grids based on modular multilevel converter. In Proceedings of the Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–6. [Google Scholar]
- Saad, H.; Dennetière, S.; Mahseredjian, J.; Delarue, P.; Guillaud, X.; Peralta, J.; Nguefeu, S. Modular multilevel converter models for electromagnetic transients. IEEE Trans. Power Deliv. 2014, 29, 1481–1489. [Google Scholar] [CrossRef]


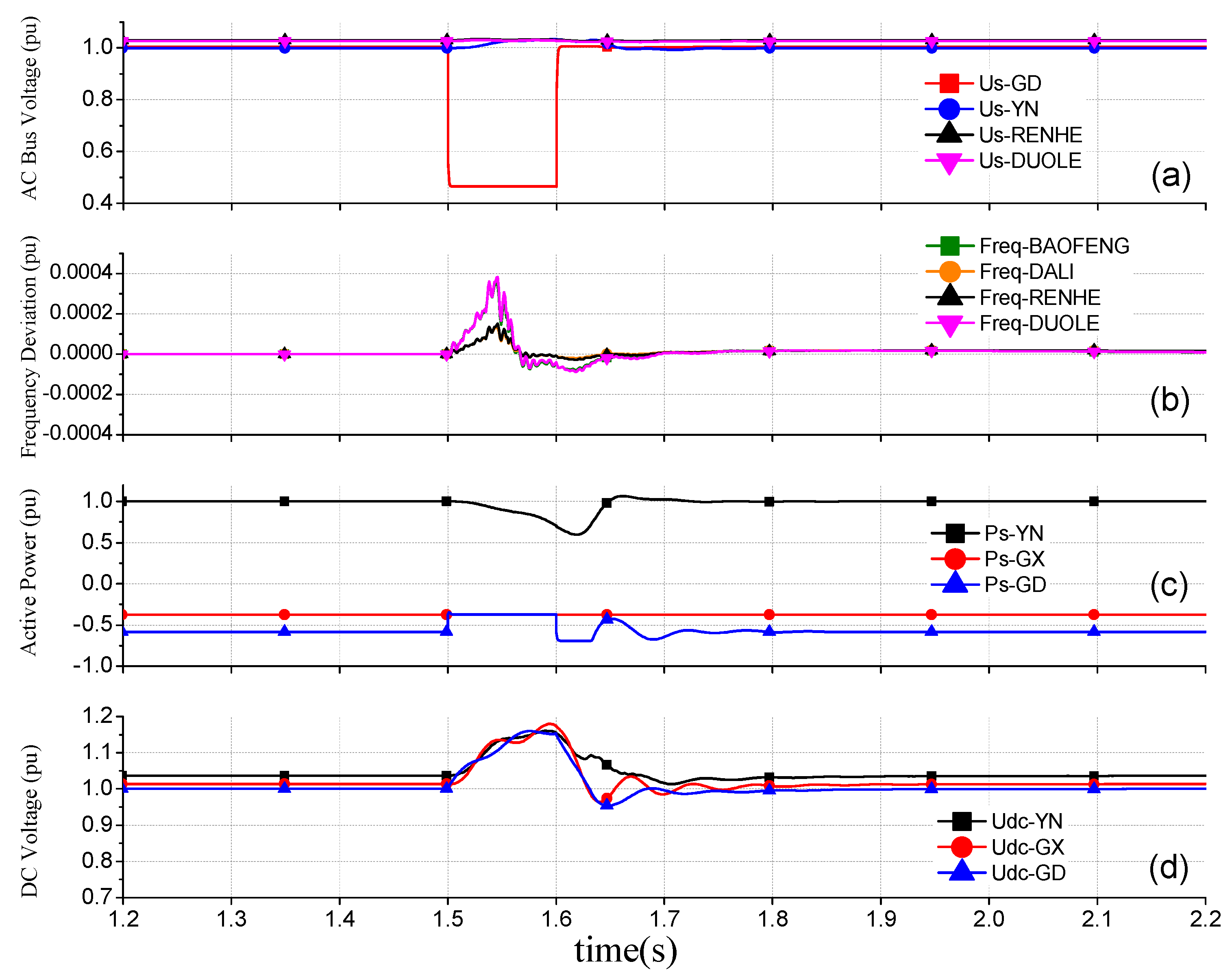
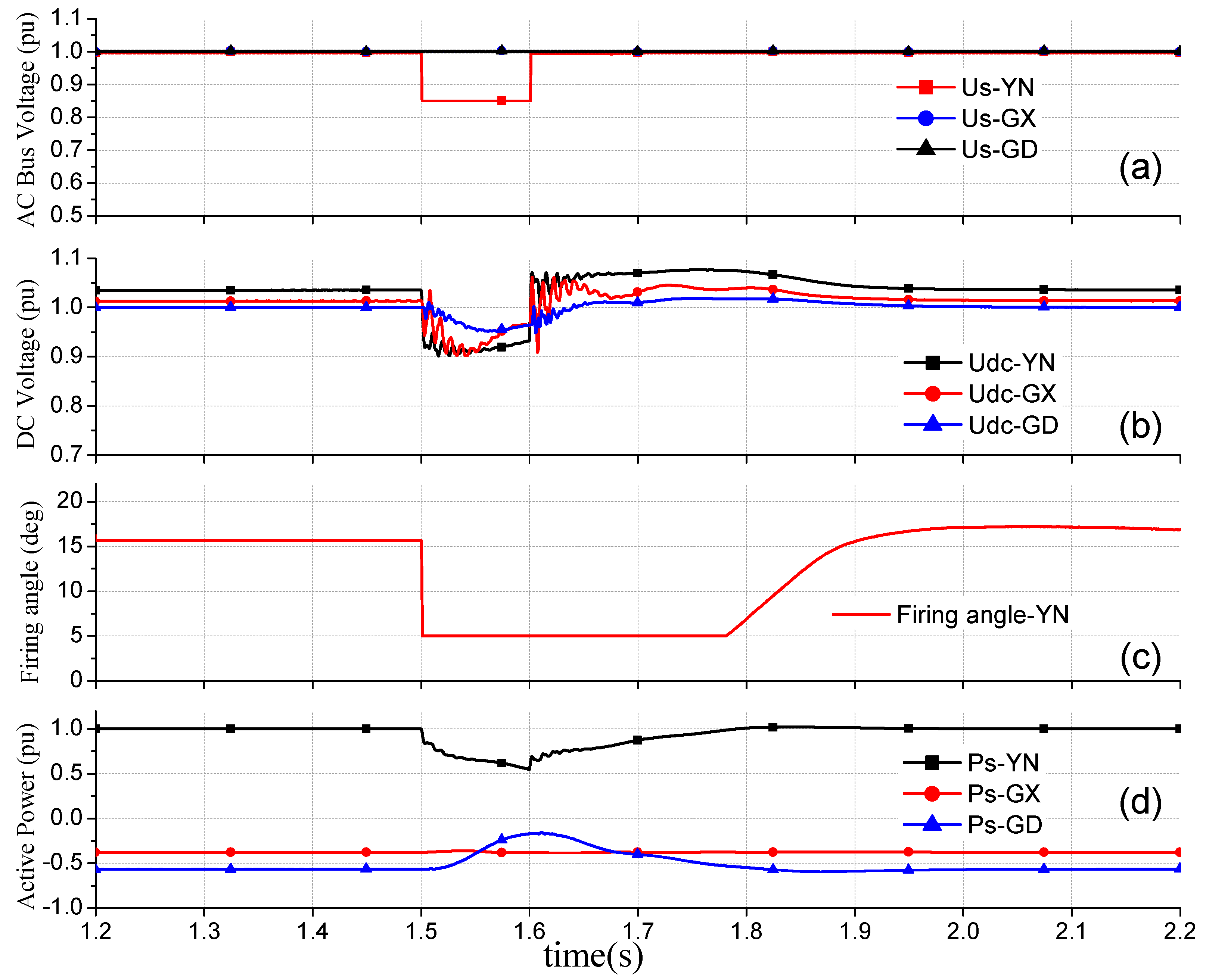
| Components | Differential-Algebraic Equations |
|---|---|
| LCC | AC-side model: Equation (4) + Equation (5) |
| DC-side model: Equation (6) | |
| controller model: Equation (7) | |
| MMC | AC-side model: reference [29] |
| DC-side model: Equation (8) | |
| controller model: reference [29] | |
| DC network | Equation (9) + Equation (10) |
| Converter | Control Mode | Bus Type |
|---|---|---|
| LCC | constant Idc | PQ |
| MMC | d axis: constant Udc + q axis: constant Qs | PQ |
| d axis: constant Udc + q axis: constant Us | PV | |
| d axis: constant Ps + q axis: constant Qs | PQ | |
| d axis: constant Ps + q axis: constant Us | PV |
| Item | LCC-YN | MMC-GX | MMC-GD | Max Error | |
|---|---|---|---|---|---|
| PSCAD | Ps (MW) | 4012.7 | −1499.8 | −2328.6 | / |
| Qs (Mvar) | 2280.3 | 0.0 | 0.0 | / | |
| Us (kV) | 518.3 | 528.3 | 528.2 | / | |
| α (°) | 15.4 | / | / | / | |
| Udc (kV) | 828.7 | 810.6 | 800.0 | / | |
| Idc (kA) | 4.83 | 1.88 | 2.94 | / | |
| PSS/E (considering firing angle limits) | Ps (MW) | 4000.0 | −1500.0 | −2342.5 | −0.6% |
| Qs (Mvar) | 2258.8 | 0.0 | 0.0 | 0.9% | |
| Us (kV) | 517.0 | 527.6 | 527.6 | 0.3% | |
| α (°) | 15.3 | / | / | 0.6% | |
| Udc (kV) | 828.8 | 810.7 | 800.0 | −0.01% | |
| Idc (kA) | 4.83 | 1.87 | 2.96 | −0.7% | |
| PSS/E (without considering firing angle limits) | Ps (MW) | 4000.0 | −1500.0 | −2342.5 | −0.6% |
| Qs (Mvar) | 2209.6 | 0.0 | 0.0 | 3.1% | |
| Us (kV) | 516.5 | 527.6 | 527.6 | 0.3% | |
| α (°) | 14.2 | / | / | 7.8% | |
| Udc (kV) | 828.8 | 810.7 | 800.0 | −0.01% | |
| Idc (kA) | 4.83 | 1.87 | 2.96 | −0.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, L.; Li, Y.; Xiao, H.; Zhang, Z.; Xu, Z. Electromechanical Transient Modeling of Line Commutated Converter-Modular Multilevel Converter-Based Hybrid Multi-Terminal High Voltage Direct Current Transmission Systems. Energies 2018, 11, 2102. https://doi.org/10.3390/en11082102
Xiao L, Li Y, Xiao H, Zhang Z, Xu Z. Electromechanical Transient Modeling of Line Commutated Converter-Modular Multilevel Converter-Based Hybrid Multi-Terminal High Voltage Direct Current Transmission Systems. Energies. 2018; 11(8):2102. https://doi.org/10.3390/en11082102
Chicago/Turabian StyleXiao, Liang, Yan Li, Huangqing Xiao, Zheren Zhang, and Zheng Xu. 2018. "Electromechanical Transient Modeling of Line Commutated Converter-Modular Multilevel Converter-Based Hybrid Multi-Terminal High Voltage Direct Current Transmission Systems" Energies 11, no. 8: 2102. https://doi.org/10.3390/en11082102
APA StyleXiao, L., Li, Y., Xiao, H., Zhang, Z., & Xu, Z. (2018). Electromechanical Transient Modeling of Line Commutated Converter-Modular Multilevel Converter-Based Hybrid Multi-Terminal High Voltage Direct Current Transmission Systems. Energies, 11(8), 2102. https://doi.org/10.3390/en11082102








