1. Introduction
A Sodium-cooled Fast Reactor (SFR) is one of the Generation IV (Gen-IV) nuclear fission reactors [
1]. The Gen-IV reactors are particularly categorized to achieve a number of design goals: improved safety, sustainability, efficiency, cost, and proliferation resistance [
2,
3]. SFR is a fast neutron reactor, utilizing sodium as a coolant. The inherent passive safety of fast reactors, safely shutting itself down, is one of the advantages expected by the Gen-IV reactors. Further, sodium is known as a very efficient means of heat transfer. Sodium melts at a low temperature (98
C), and the boiling temperature is greater than 800
C. This property fits very well in a typical operating range of SFRs (300∼550
C).
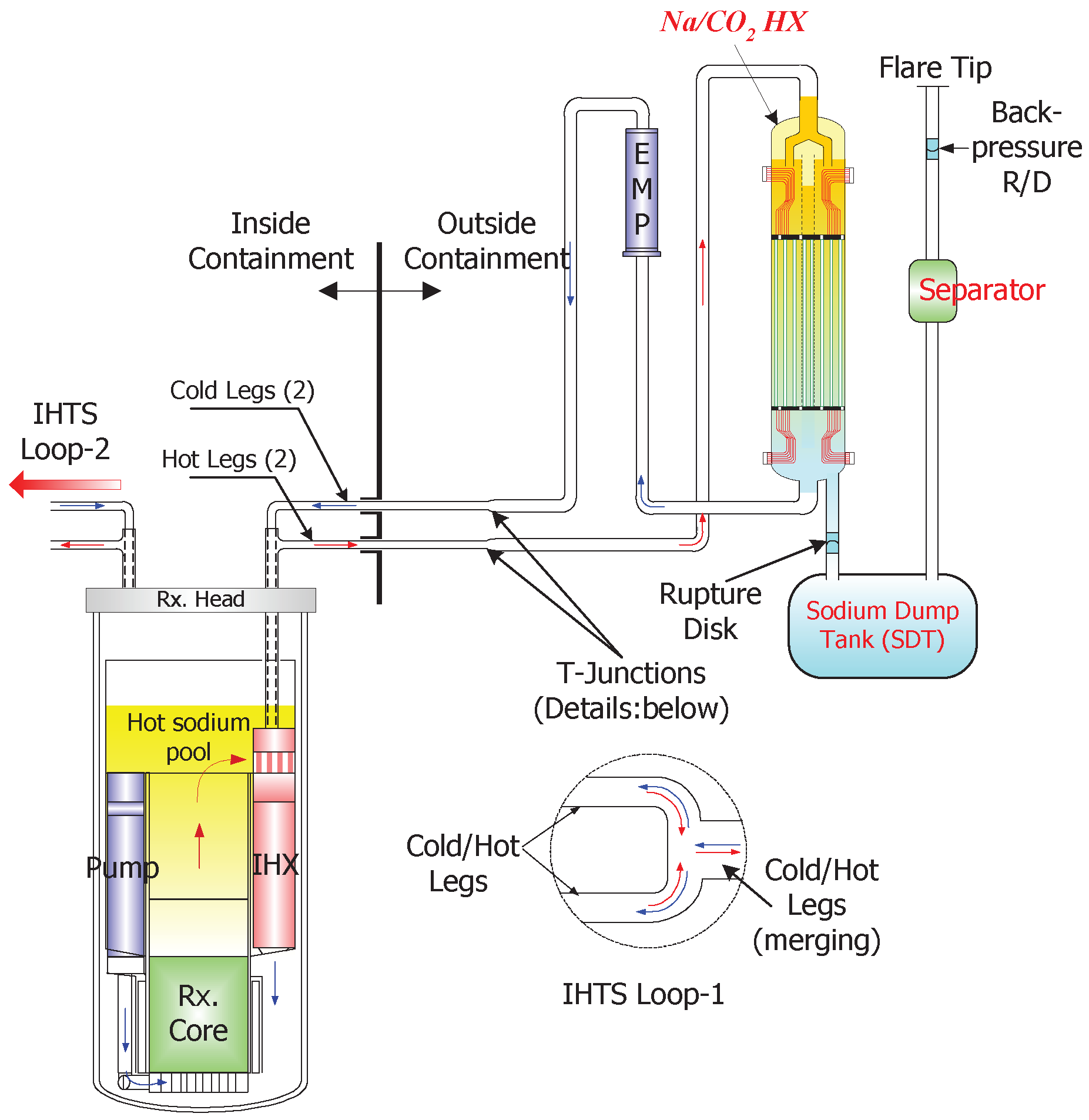
Contrary to the benefits of SFRs, sodium, which is a highly reactive metal, can cause a fire when it reacts with water. One of the critical accidents in Sodium-cooled Fast Reactors (SFRs) is a potential sodium fire or sodium-water reaction (SWR). SWR occurs in a steam generator (SG) unit where hot sodium coolant of the intermediate heat transport loop (IHTS) in an SFR exchanges heat with water to generate steam for the turbine input (refer to
Figure 1). Sodium reacts rapidly with steam/water, generating heat and pressure impulses that can lead to the catastrophic failure of an SG unit and intermediate sodium loop by over-pressure and temperature transients.
Some major SWR accidents have been reported in literature. The first SWR in PHENIX was 30 kg of water reacted [
4]. The worst tube leak event in SGs of PFR (Prototype Fast Reactor) occurred in 1987 [
5]. Thirty-nine tubes around the initial tube within 10 s were broken through during the time required for the pressure decrease on the steam side (rupture disk was broken). Significant SWR events occurred in BN-350 (detected by a satellite) and BN-600 (the most important reaction took place in January 1981 with 40 kg of water injected) [
6].
To detect SWR events at its early stage, hydrogen detection is used, because hydrogen as SWR byproducts is created and transported in a sodium loop [
7,
8]. However, an indispensable reliability and quick response of the hydrogen detection system is challenging, for hydrogen byproducts tend to travel along with the coolant in the loop, and are not relatively easy to measure. The design of a wrapper around the free-standing SG, which is capable of withstanding the most violent SWR, was proposed. This will eventually increase design and manufacturing costs, and large SWR accidents are in any case undesirable regardless of wrapper features. Rupture Disk (R/D) membranes are designed to limit pressure accumulations to avoid high internal pipe pressure in the loop and its consequential ruptures. When a rupture disk is broken, however, the secondary sodium coolant will be immediately drained from the loop. At the time of the rupture break burst, which is the last measure to protect the reactor from an SWR, the damage may have already developed, and this leads to a long-term shutdown. This is a huge economic loss in terms of operation and plant management.
Employing supercritical CO
(S-CO
) gas as an alternative matter replacing steam/water in an SG, the sodium-CO
heat exchangers as a Sodium-to-Gas Heat Exchanger (SGHX) are used instead of steam generators in the S-CO
Brayton cycle to generate electric power. The SGHX with the S-CO
Brayton cycle shown in
Figure 1 is advantageous in a couple of ways compared with the conventional Rankine cycle SG [
9]. In addition to its high thermal efficiency and its potential compactness of the heat-exchanger system with the S-CO
Brayton cycle [
9,
10], it can be a safer system than conventional SFR SGs. A sodium-CO
reaction is claimed to be milder than an SWR [
10,
11,
12]. Referring to [
13], the liquid sodium and CO
gas is categorized as a rate-controlled process, because its reaction rate strongly depends on the reaction condition, and the chemical reaction speed between sodium and CO
gas is consequently much slower than that of an SWR.
However, it is a contradiction that a scrupulous operation of the plant is required due to the reaction characteristics of CO. Moderate chemical interactions between CO and sodium imply that detecting CO ingress accidents, which may not be like conspicuous physical indications in Rankine SWRs, such as noisy wastage, makes it hard to detect at its early stage. In other words, the damaged sodium-CO heat exchanger can run for an extended period of time, and degrade further until the rupture disk breaks.
Roine [
14] studied sodium and carbon dioxide (CO
) chemical interactions. Among a couple of reactions, C-CO
and Na-CO
interactions produce a gaseous byproduct, carbon monoxide (CO). CO byproducts and unreacted portion of CO
ingress gases increase the pipe internal pressure. Eventually, as the pressure reaches a certain design level (approximately 1∼2 MPa, which is 10 times greater than the cover-gas pressure), R/D is broken to evacuate the sodium coolant in a loop to the sodium dump tank (SDT). As shown in Eoh et al. [
12], this study is based on the conservative assumption that sodium atoms simultaneously react with CO
molecules and produce CO gas for a simplified and unified modeling of sodium-CO
interactions. Though sequential chemical reactions between CO and sodium result in a mass loss of gaseous byproducts or even potential self-plugging issue on micro channels (or leak holes) due to accumulations of solid reaction products, the complicated reaction mechanism of sodium-CO
interactions is yet to be fully comprehended [
15]. Thus, the simplified interaction modeling described in a previous study [
12] has been adopted for this pilot monitoring study.
Before the R/D is torn apart by the CO ingress accident, an automatic shutdown accompanied with a quick depressurization in the CO gas side is desirable. Stopping the CO gas supply to SGHXs is a better strategy to mitigate SGHX damage than relying solely on R/Ds. Draining sodium may not be necessary, when the failure is detected early, and CO can be quickly injected once the damage is repaired. However, it is a general question whether the CO ingress can be detected by pressure measurements alone before R/D is broken and how the measurements can be used. Moreover, the way to calculate the threshold level and time to trigger the CO mitigation at an early damage stage is required.
The condition based monitoring (CBM), which consists of monitoring and diagnosis, describes a suite of activities for estimating system states and providing early warning of anomalous behaviour. The monitoring methods can be largely categorized into two groups: physics- and data-based models. Data based models without first principles are built on historical operation data with no explicitly defined understanding of the underlying physical mechanisms. In general, the data based-model is less time consuming to develop. For the sensors, monitoring techniques were proposed to assess the calibration of sensors using data collected during a plant operation. The U.S. NRC accepted the generic concept of monitoring for sensor calibration assessment and calibration interval extension [
16]. In addition, the sensor signal reconstruction was performed by using the Principal Component Analysis (PCA) [
17]. Induction motors are commonly monitored online through vibration testing, electrical signature analysis, and temperature monitoring. The Motor Current Signature Analysis (MCSA) is used to monitor specific frequencies for a sign of impending anomalies and faults [
18,
19,
20]. In addition, vibration monitoring can detect and diagnose mechanical issues in reactor components including the Reactor Coolant Pump (RCP) and mechanical valves. The degradation and failure of RCPs are commonly monitored through the RCP Vibration Monitoring System (RCPVMS) [
21,
22]. Lee et al. [
23] had looked at using acoustic emission signals for valve health monitoring. A check valve monitoring system using ultrasonic transducers coupled to a pipe was developed and patented [
24].
The downside of the data-based method is the difficulty to track undesirable decisions and to estimate for unexpected conditions [
25,
26]. Even though it is also argued that physics-based monitoring systems can be difficult to be constructed with considerable amounts of costs and time in particularly complex systems [
27,
28], physics-based techniques can address faults more accurately with traceable outcomes. The first principles can describe the expected nominal behavior based on measured system features or operating conditions with reasonable assumptions on disturbances and perturbation. Thus, the physics-based models can estimate a wide variety of conditions. For example, the remote testing methods that rely on accurate physics-based models of the induction machine were patented (the on-line diagnostic monitoring system for motor operating valves) [
29]. For SFR SGHX systems, the physical relations were extensively studied by Eoh et al. [
30]. In the study, the generated hydrogen amount increases the internal loop pressure in a fairly short period of time, and this pressure surge is less dependent on the loop flow rate or disturbed flow by an in-flow obstacle. Thus, a less intrusive monitoring approach using only global metrics in pressure can monitor more than 1400 tubes for two SGHXs, and this scheme is very effective.
Based on the previous studies on the physics relations, a physics-based framework is proposed here, and this makes it available to estimate the detection time of a CO
ingress due to the target damage size of micro or small leak rates (self-wastage level of approximately 10
1 g/s). The goal of this study is to bring about a mathematical framework, introduced in
Section 3, for a CBM system based on physics to automatically depressurize the steam side, and disconnect the CO
gas supply by detecting localized sodium-CO
events in SGHXs. The proposed algorithm is also compared to the data-based method described in
Section 4. For this pilot study, experimental results from the simplified mass and energy transfer (SMET) model were adopted to evaluate the proposed mathematical framework. Calculation results of the achievable minimum time for given in-let flow rates and discussion are presented in
Section 5. Concluding remarks follow in the final section.
2. Problem Formulation
Since the intermediate heat transport system connecting the reactor to SGHXs is a closed loop, the pressure and temperature transients in the cover gas area of an expansion tank of the loop represent the dynamic behaviour of the loop as a whole [
30]. Therefore, once a relationship between the cover-gas pressure and mass flow rate into the loop due to the CO
ingress is determined, the SGHX failure can be monitored by cover-gas pressure measurements. The description of the relation can be proceeded from the energy balance between the cover gas and the shell-side sodium as a simplified mass and energy transfer (SMET) model (
Figure 2) developed in [
12].
For the SMET model, the authors of [
12] developed a mathematical representation and have shown its validity [
12]. Referring to the thermo-dynamic relation for the pressure
in the cover gas region from the same paper, it is expressed as
The full derivation of the above Equation (1) is described in [
12]. In Equation (1), the subscripts
p and
g stand for byproducts due to the reactions and cover gas, respectively.
and
t represent the molecular weight, universal gas constant (8.314 [kJ/kmol/K]), temperature [K], volume [m
], mass [kg], and time [s], respectively.
is the accumulated byproducts in the cover gas, and the superscript 0 means an initial or reference state. During the process, the cover gas volume changes little relatively in the early stage of reactions, and thus the time derivative of
is taken to be zero. Molecular weights do not change over time, and the cover-gas mass is assumed to be conserved (
=
all the time).
Thus, Equation (1) can be approximated in discrete time
j with a very small sampling time
in a forward difference-equation form as
where
In early times of the reaction,
can be relatively negligible to the cover-gas mass
. Equation (2) can be re-organized, having
neglected, as follows:
Define the damage term
as a multiplicative constant for a limited period of time as
where
is the byproduct generation rate in g/s due to the CO
ingress. Thus, Equation (3) can be further simplified into
In the equation, the subscript g was dropped for convenience, because only the cover gas region is of interest.
3. Model-Based Pressure Monitoring Algorithm
The method for the pressure monitoring algorithm is derived by the first principles of damage propagation with a probabilistic analysis. From Equation (7), the cover gas pressure as a time propagation model can be constructed as
where
and
is the cover gas pressure compensation term due to the temperature variation at time step
j.
A scheme to monitor CO ingress accidents is to compare the pressure measurements of two identical heat exchangers at the same time. This strategy assumes that two identical steam generators, which appear in a general power plant, are deployed. It is also grounded upon other assumptions that two heat transport systems are under a similar working condition, and it is very unlikely that two systems will fail at the same time with the same degree of damage. These assumptions are reasonable, because two systems are designed to be identical, are connected to one nuclear reactor, and work at the same site, but a typical breakage failure between a shell and tube sides may be caused by manufacturing faults that are random.
A residual
r is defined for the comparison between 1 and 2 heat transport systems. For
r, pressure measurements from two target devices are subtracted from each other as follows:
The difference between sensor measurements, considering its noise factor and variations due to slight different working environment, can be modeled as a random variable
in a normal distribution function. Also, for this initial study, the difference between temperature propagation terms
and
is regarded as a system variation which is included in
. The measurement variation
is between two healthy systems, and the damage term has to be accumulated in time. Suppose only the system 1 is damaged from time
until
. Then, Equation (8) can be expressed from Equation (5) as
where
The inspection is carried out after every decision time interval as of the following statements.
Statement 1. If at , no failure is declared.
Statement 2. If or at , a detection of a failure due to ingress accidents is declared.
Inspections are performed at every time (s). In other words, to detect the failure, it has to be waited for seconds, and even if high (or low) r value is found in between, it is not declared as being “detected”, for it is highly likely to be a noise. This scheme is strongly dependent on the hydro-dynamic behavior of the cover-gas region expressed in Equation (1) and its damage model in Equation (9).
A constant mass flow rate from reactions was assumed, and an average temperature
is taken. When a reaction starts from time
j = 1 to
, Equation (9) becomes
When there is no damage in a system
, the residual
r for monitoring is centered around its average 0 as a bell-curve shape shown in
Figure 3. The figure shows two curves with small and large variances
. The probability of false alarming is the integral of the probability density curve in the outside of the threshold level
.
L is solved for by having an allowable false alarm rate, which should be very small. For the same false alarm rate, the threshold range for greater variance should be wider as in the figure
.
However, when there is a fault in a system
, the bell-curve is shifted as much as the mean-value contribution
as shown in
Figure 4. The figure shows two different detection times
. The probability of a true detection for this scenario is the area under the density function curve in the outside the threshold level
. Therefore, with longer waiting to detect the same amount of a fault, the probability of detection increases as illustrated in the figure (the area for
is greater than for
).
To design the monitoring system (mainly for the threshold level
L and detection time
), parameters of the statistics information of sensors and target damage size should be determined with probability inputs
and
(maximum allowed false alarm and least required true detection probabilities). The least
L and soonest
are calculated based on the probability model in Equation (11) and descriptions given earlier as follows in Equations (12) and (13).
Again, is a very small number such as one in 1000 inspections, and is close to 1 such as 99.99%.
4. Comparison with the Data-Based Method
To assess the performance of the proposed monitoring algorithm in this paper, Auto-Associative Kernel Regression and Sequential Probability Ratio Test (AAKR-SPRT) as one of the most widely employed on-line monitoring methods [
16] is taken for comparison. From historical data, AAKR can calculate estimated values with which SPRT detects a fault comparing sensor measurements. AAKR is the combination concept of auto associative and kernel as a regression method. The general regression assumes that dependent and independent variables are taken to be true. On the contrary, the auto associative concept assumes noise in variables (not to be true always). Therefore, AAKR controls variable values through weighting by correlations of variables. To calculate weights, a kernel function such as Gaussian distribution is used.
For a simple AAKR example, let virtual training data be
as below. In the matrix, the row and column indicates
m historical values and
p state variables, respectively.
A
query vector
from measurements is represented as
AAKR is composed of three steps. The first step calculates the distance between measured values and training data. Using
as
m memory vectors (
) as training data, the distance-Euclidean
L norm-is used to calculate the distance between measured values and training data in AAKR, as expressed below:
becomes an
vector with
s.
for
has
m historical sets and each element in
is calculated repeatedly for each set by Equation (16).
Second, the weight
calculation is performed by the Gaussian kernel
K and
as
where
h is the kernel bandwidth and is obtained by performing optimization according to the data set. The estimates
are obtained by the weighted average equation expressed as follows:
and
pth
element
can be written as
Or, simply,
can be expressed as
where
and
The Sequential Probability Ratio Test (SPRT) is a statistical test by the sequence of residuals being generated by a random process with a mean of zero or from a process with a nonzero mean due to some fault condition. With SPRT, the simplest method of fault detection is thresholding, which compares a residual with a designated (and fixed in general) level, and a fault is registered when the residual exceeds this level. When the distribution which represents normal and fault behavior is given, the difference between nominal and abnormal states can be detected using a mean and standard deviation of each distribution function. The normal distribution is used in SPRT due to the residuals’ random nature. The log-likelihood ratio
at a
k sampling time is expressed below, given a sequence of consecutive
p observations of a residual
s.
The cumulative sum
of
as a recurrent form is updated at every sampling time
k as
And the residuals are assumed to be normally distributed with a zero mean and variance of
. Thus,
In the above equations,
is the residual at time
k, and
is the mean variance under the hypothesis 0 (normal) or 1 (fault). For a normal condition, the mean of the residual
can be zero, and
is derived as of the following.
The decision boundaries follow the Wald’s two-sided rule. The decision boundaries of A and B with
(false probability) and
(missing probability) are expressed as
If
,
is accepted (a normal operating condition), while a fault is registered with
, when
. The results are validated by SPRT as well.
5. Experiments and Simulation
The monitoring strategy was verified for the first time with the water mock-up test facility introduced in [
12]. With using this facility and data, the sodium/CO
reaction by CO
ingress accidents was simulated with an air injected into the water loop that corresponds to the sodium heat transport system. For the verification, the monitoring system is to detect the air injection. The design of the system is explained with the results for the air detection.
For the data acquisition setting, the sampling time
is set to 0.2 s. Given the byproduct (injected air), the cover gas are air and the cover gas volume is 5.38 liters, the environmental constants,
and
in [J/m
·g·K], are
The average temperature
of the cover gas region is 286 K. In order to take advantage of the test facility, the monitoring scheme is constructed to compare the cover-gas pressure with its statistical mean
, and from Equation (11) the residual becomes
and
5.1. Threshold L Determination
In
Figure 5, pressure measurements for a dry run of 90 s without air injection are given. The data are used for extracting the statistics information of the loop (system) including the sensor dynamics: statistical mean
and standard deviation
.
To minimize false alarms when no fault occurs, the threshold level was set by the above statistics information and allowable false positive rate of 0.1%.
and the calculated threshold level
L is obtained as
5.2. Decision-Time Determination
The decision time
is calculated by the target damage level
converted from the air injection flow rate. The air is injected in a rate of 30 cc/s. Thus, the air mass flow rate, converted from its density at a 286 K temperature, and the damage factor becomes
With the mass flow rate of the air, an equivalent fault level of CO
ingress can be estimated. It is reported that the generation rate of CO gas is far less than 30% of the total of the released CO
gas [
12]. However, conservatively,
is divided by 0.3, as
is a substitute of CO gas. Then, an equivalent mass flow rate of CO
gas for 0.03675 g/s in Equation (36) becomes 0.12 g/s.
Substituting the obtained parameters:
L in Equation (35),
in Equation (32),
in Equation (37),
= 286 K, and the minimum required detection probability of 99.99%; the detection time
is solved for from Equation (38).
and
A range of various leak rates including the air mass flow value in Equation (36) is simulated from the relation in Equation (38). The plot in
Figure 6 gives the results of the decision time for the leak-rate range. As expected, a longer detection time is required for a small leak rate (damage) than a large one. In other words, for a large damage, the detection time required is very short. Furthermore, for a comparison, the figure contains three cases of
: 80%, 99.9%, and 99.99%. For the same amount of damage, a longer detection is required for a higher probability as depicted in the figure. A sample value, for example, of a leak rate of 0.0372 g/s is marked, having a 67 s detection time in the figure.
As demonstrated, the inspection timing is determined by the damage size (or a leak rate) with the detection probability. The operator can tweak the alarming level by the detection probability () based on the operational guidance or regulatory rules. An operator also knows how much the damage size should be to be identified. Then, the algorithm yields the best timing for the inspection with a known false alarm setting (). With the time integration until the determined inspection time, the noise becomes less sensitive, having the constant damage effect–in case the CO ingress occurs-stand out.
Its decreasing pattern of
Figure 6 is exponential, meaning very small damage less than 0.01 g/s is almost impossible to detect, considering the plant operation and other extraneous effects. It also takes too long (such as five minutes) to run a system effectively. This long interval is not able to find an incipient failure, and thus a very small amount of damage is not an appropriate target.
5.3. Case Study
A sample case study of air-injection tests performed in [
31] was considered. The residual by pressure measurement data as a black curve of
Figure 7 was compared with the calculated
L (green dashed line) at
(blue dashed line) time. The mean
MPa was subtracted from the pressure to yield a residual as in Equation (30). As shown in
Figure 7, at the calculated
of 67.8 s, 30 cc/s of air injection into the water mock-up test facility was able to be detected with a 99.99% detection probability. The measured pressure is 0.1249 MPa at 67.8 s, and the residual (
MPa) is greater than the upper threshold
L of 0.014 MPa.
The results by the model-based method as the proposed approach in this paper and data-based method explained in
Section 4 were compared.
Figure 8 shows the results by AAKR-SPRT for the same case. In this case, the kernel bandwidth
h was selected as 0.01. An
of 0.01 and
of 0.1 were chosen, as these values were assumed by a generic sensor calibration in nuclear grade devices.
Figure 8 displays the cover gas pressure measurements with no air injected as a normal operation mode (black solid curve), AAKR estimation for the normal mode (blue solid curve), and fault mode with the injection of air as simulated CO
gas (yellow dashed curve). Due to the sensor noise, high spikes are observed in the normal mode measurements (black). The AAKR cut out sharp peaks in measurements, and yielded smoother estimates as shown in the blue curve compared to the black curve, while the estimates have some drift. As expected, the yellow curve as the heat exchanger failure simulation is going upward with some fluctuations (sensor noises), while the black as a healthy system is simply fluctuating without a moving average. At about 20 s, the pressure of the fault mode exceeds visibly the normal operation values. Even though an early detection of failure is highly desirable, many false alarms due to measurement fluctuations (even with the AAKR estimates) deteriorate the reliability on the system. Thus, 10 consecutive detections with hypothesis 1 (the fault condition) were counted for the final decision, and the detect time was determined as 75.8 s (indicated by a bold dashed green line in the figure) in this case by AAKR-SPRT.
It is noted that the AAKR-SPRT method gives a detection time eight seconds slower than the model-based approach proposed here. It seemed that AAKR-SPRT gives a faster detection time, because the SPRT monitoring inspects the condition at every sampling time nearly continuously, but it was the opposite in this case. The proposed model-based algorithm calculates the inspection time (67.8 s here) a priori, and the inspection to make a decision for a healthy or faulty mode is made only at this time. This observation implies the AAKR estimation and the number of true detections to trigger the alarm (for the fault) made the monitoring less sensitive to the fault. If is set to 0.001 (0.1% setting for the model-based method), it will take more time to detect the fault than 75.8 s.
There are also other disadvantages of the data-based method including subjective choices of the kernel bandwidth h, , , and the number of consecutive detections with hypothesis 1. These parameters are not based on the first principles of the system under consideration, and they can be chosen inappropriately for any particular power plant. The data-based method takes the state-variable mean and variance from historical data at normal operations, but h, , and are typically set by nominal values. Therefore, data-based method has some intrinsic uncertainties in choosing the parameters.
6. Conclusions
A pressure monitoring algorithm to detect a structural failure due to CO ingress accidents was developed by the first principles, given two identical systems to be inspected. The monitoring scheme was analyzed based on the probabilities. The scheme, comparing the cover gas pressure measurements with two redundant systems, could detect anomalies of a sodium-CO heat exchanger due to a CO ingress accident.
The threshold and decision time parameters for this pressure monitoring algorithm were probabilistically calculated from statistics information of measurements by setting a false alarm and true detection rate. The threshold allows statistical variations of measurements to minimize false alarming, when there is no fault. The decision time is chosen to be sufficiently long to detect a particular damage level with a high probability of detection, when there is a fault in one system.
To verify the algorithm, water mock-up experimental results were studied. In verification, the by-products due to CO ingress were simulated by the air injection. The scheme was modified into comparing pressure values with the average of measurements at times when the air is not injected. To allow signal noise, the threshold level of 0.014 MPa was calculated to minimize the false alarm rate down to 0.1% (one false alarm out of 1000 inspection times). With 0.065 MPa sensor noise (standard deviation), the 30 cc/s air injection, which is equivalent to the CO ingress rate of 0.12 g/s, was able to be detected at the detection time of 67.8 s with a 99.99% detection probability.
Furthermore, the proposed physics-based approach was compared to the data-based method, AAKR-SPRT, the data-based monitoring method. The detection time was 75.8 s, a eight seconds longer detection time than using the proposed model-based method. The time could be faster than 75.8 s by tweaking monitoring settings such as and . However, many false alarms can be anticipated, because it inspects the state at every sampling time once noisy signals exceed the threshold for a small amount of time. Also, SPRT demands greater computation burdens compared to the proposed approach. With SPRT, an operator does not know how much the damage can be, when an alarm rings a bell.
The first-principle models are not always available; even operations will degrade or change the system from its design basis. These issues could be effectively addressed by comparing two identical heat exchanger systems incorporating thermal-hydraulic relations into the monitoring algorithm, because natural degradations of two systems are common, but a CO ingress accident can occur most likely at only one equipment at the first time. By the first principles, the model-based approach determines the threshold level and detection time based on the given false alarm rate, detection probability, and damage degree. It inspects the condition at only this designated time. The threshold level is calculated by the given false alarm rate, and thus it will give more or less false alarms as specified (the plant operator can have a sense of the possible false alarm number from the system). The false alarm rate and detection probability can be logically drawn from the nuclear regulations or requirements. More importantly, the proposed approach uses a damage level which is converted from damage degradation modeling specified by the CO ingress rate (it was calculated by 30 cc/s air ingress). Using the damage level in the monitoring, this physics method is very helpful in both plant operation and design, because it can estimate a certain damage level (or ingress rate) that should be detected to the system, reflecting former experiences. In other words, the monitoring system informs an operator on how much the damage can be, when an alarm is triggered. If the critical accident level is to be 30 cc/s ingress, then the 67.8 s detection time is required at least. Again, the proposed algorithm can be used for the nuclear power plant (NPP) design as well.
In the future, a comprehensive operation and monitoring system with multiple levels of accidents (or alarms) can be designed for any NPP, since it is typical that a plant employs two identical steam generators. Also, a more rigorous test bed with two heat exchanger mock-ups is to be built for validating the proposed methodology with various accident scenarios to make NPPs more safe.