A New Transient Frequency Acceptability Margin Based on the Frequency Trajectory
Abstract
:1. Introduction
- (1)
- The TFAI proposed in this paper can use frequency deviation information to quantitatively evaluate frequency acceptability.
- (2)
- By comparing real-time parameters and the parameters obtained by off-line simulation, the TFAM proposed in this paper directly provides the distance between the current operating point and the critical boundary. This facilitates the dispatcher to judge the frequency acceptability and take measures.
- (3)
- The TFAM proposed in this paper is expressed in power space and considers the power mismatch. Compared with other frequency margins, the TFAM is more convenient to formulate security control measures.
- (4)
- The TFAM proposed in this paper can be used to compare the transient frequency deviation acceptability under different faults.
2. The Construction of the TFAM
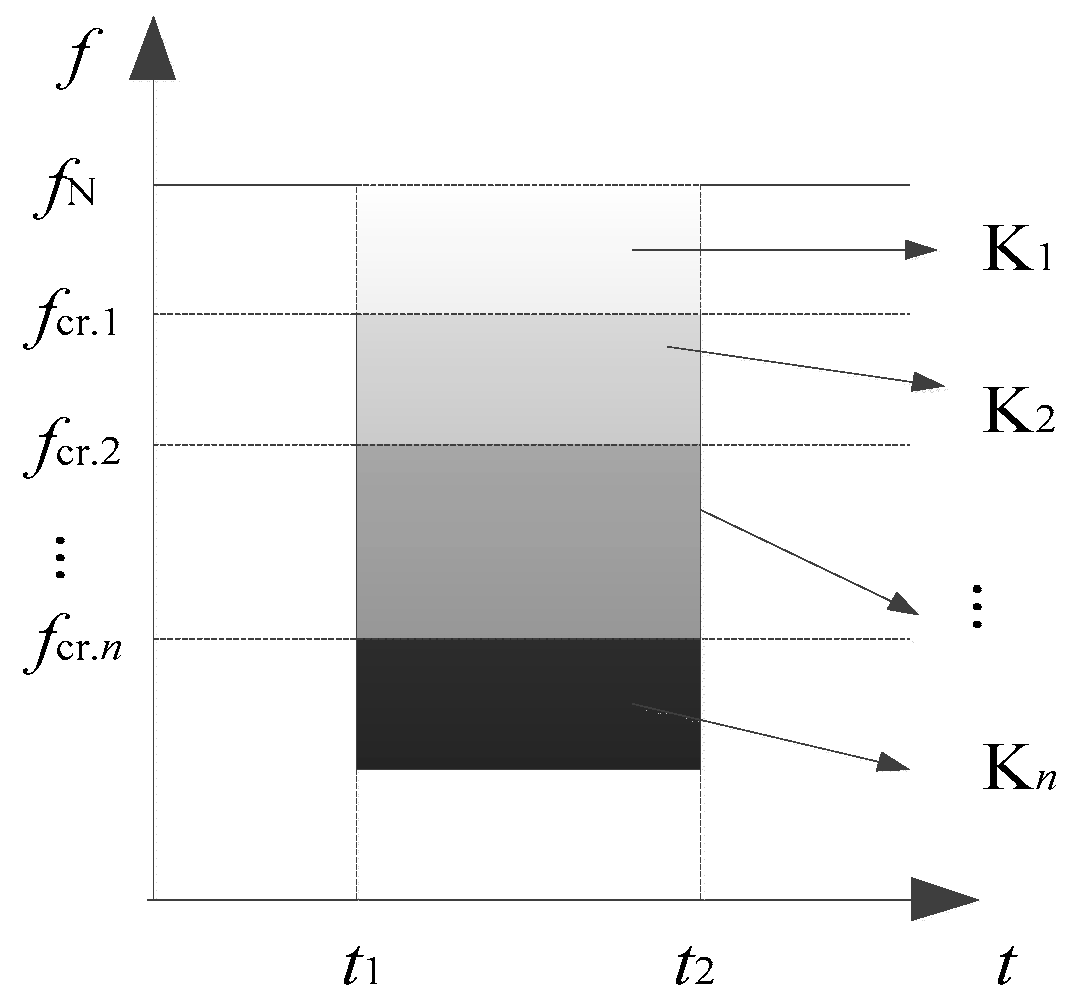
2.1. Transient Frequency Acceptability Index
2.2. Transient Frequency Acceptability Margin
2.2.1. Power Disturbance with Single Parameter
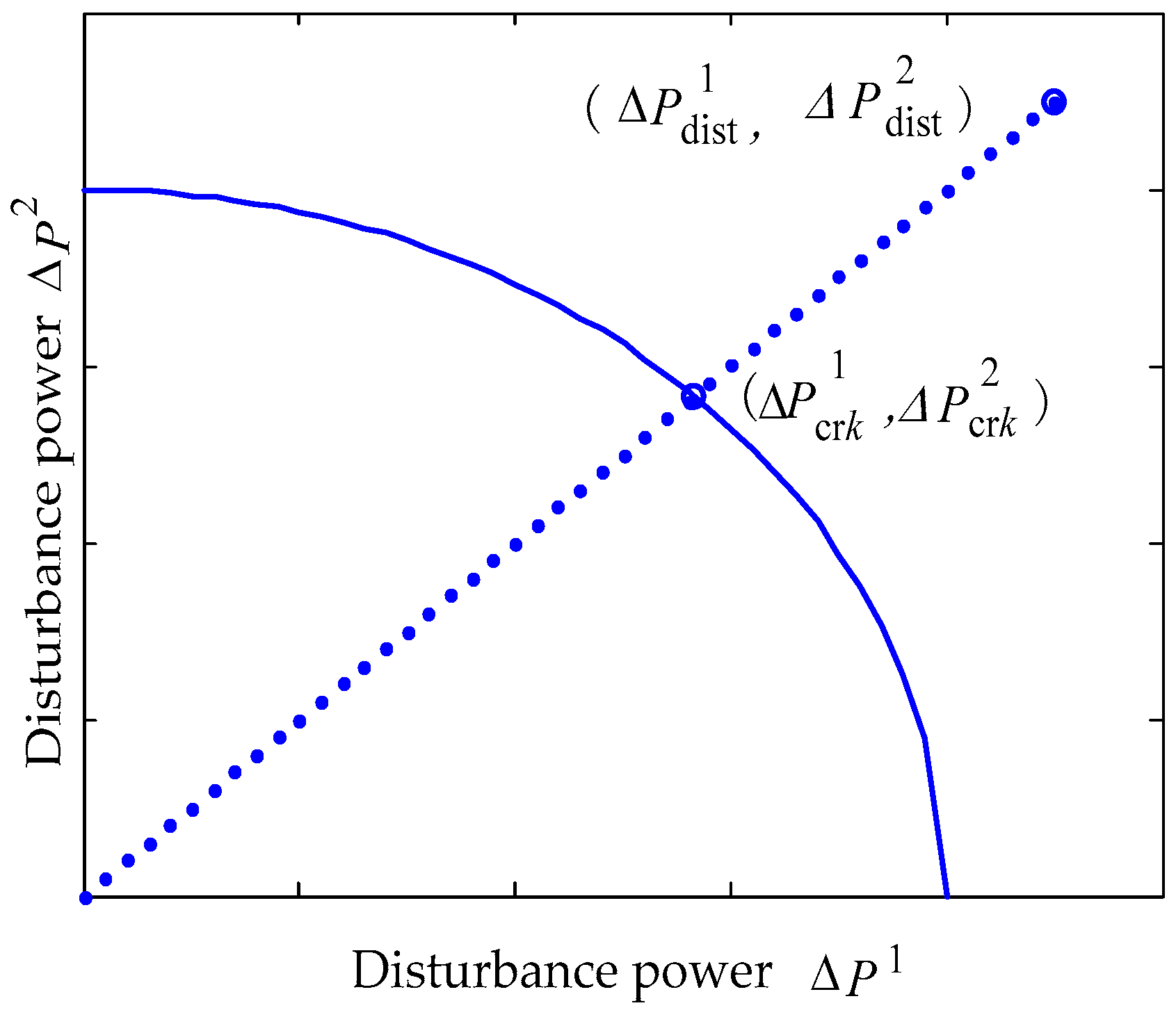
2.2.2. Power Disturbance with Multiple Parameters
2.2.3. Increase of the Disturbance Parameters in the Fixed Direction
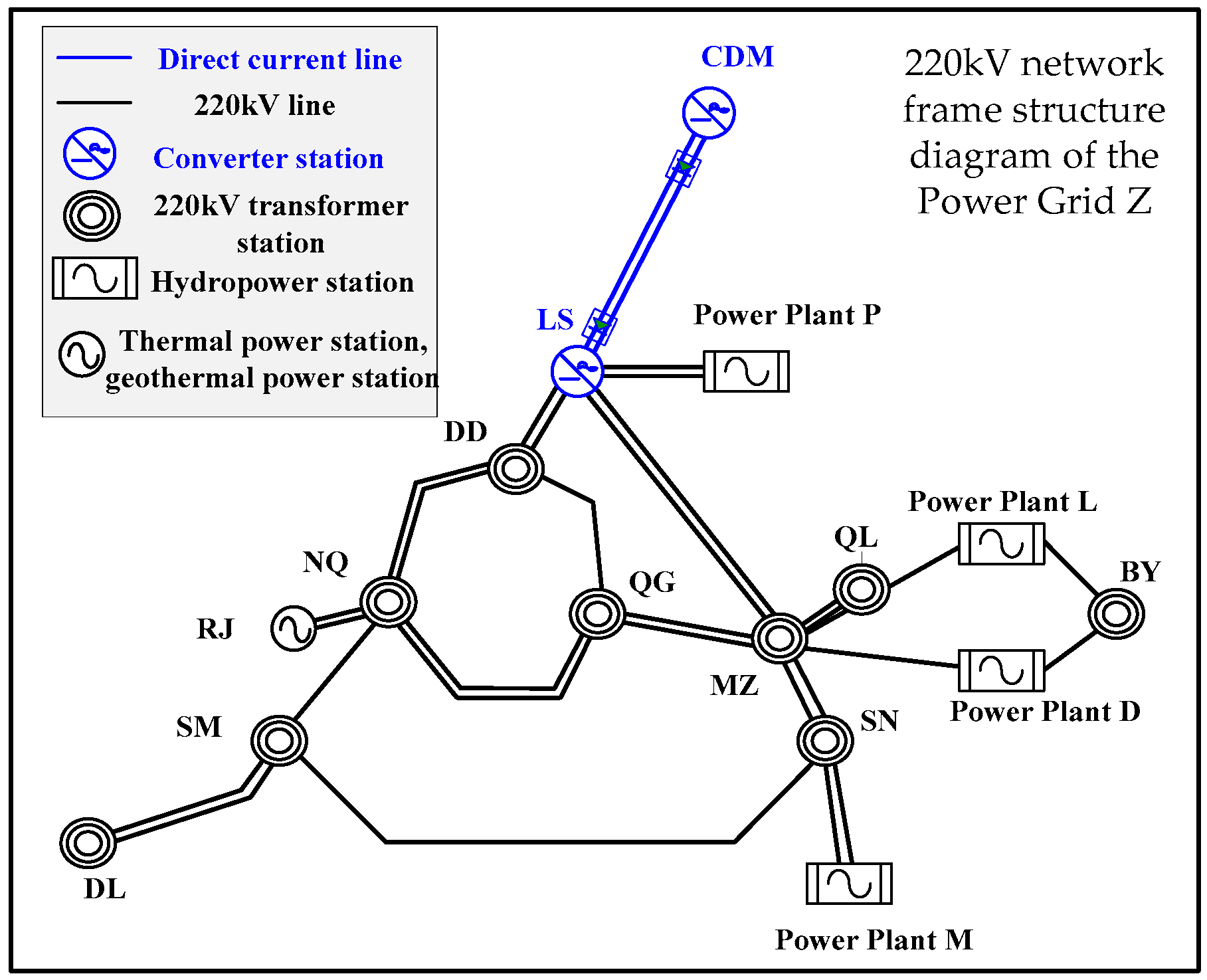
3. TFAI for the Small Power Grid Z
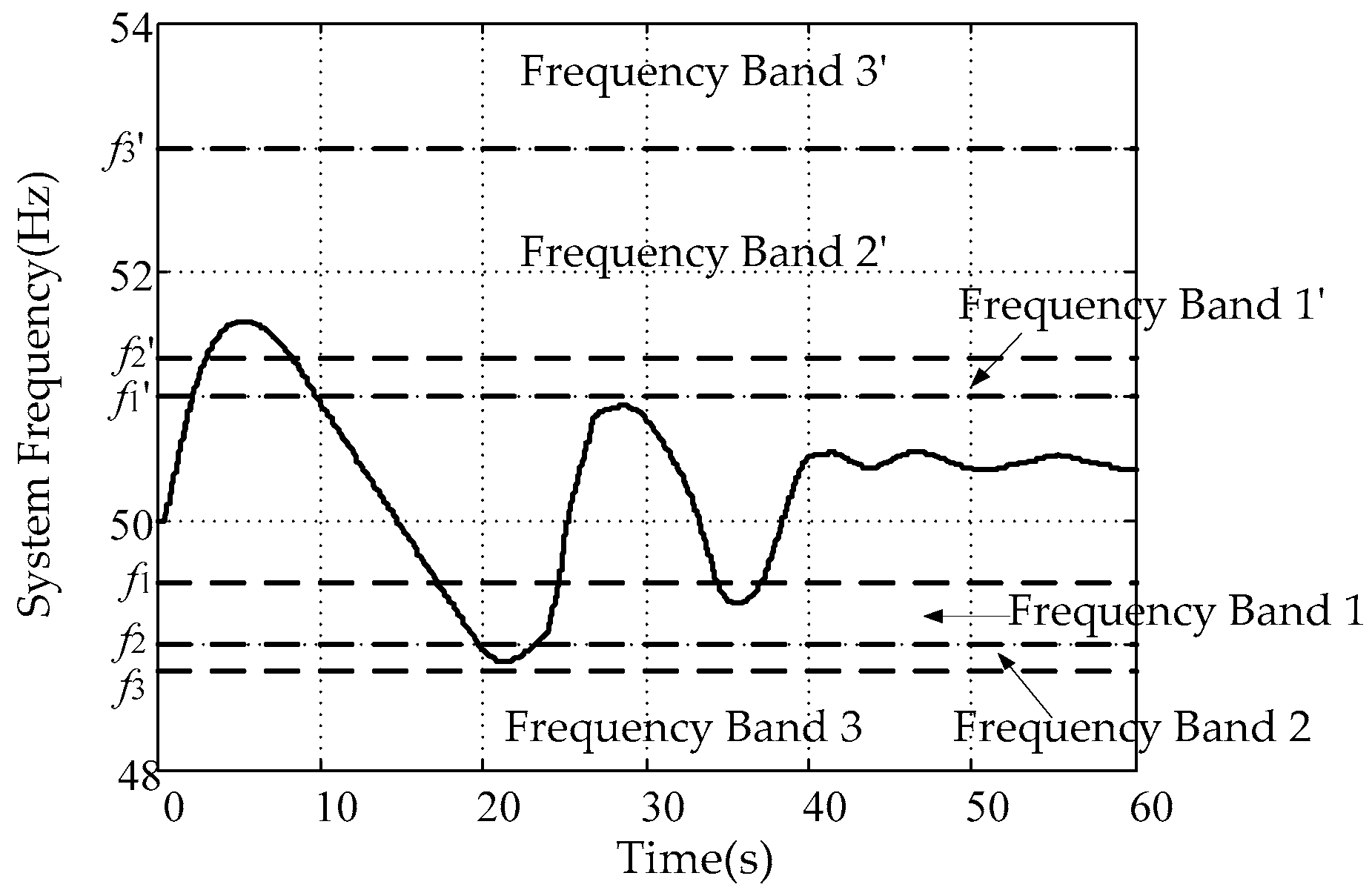
3.1. Frequency Bands and Time Duration Limits
3.2. Determination of Weight Factors
3.3. Determination of Sampling Interval
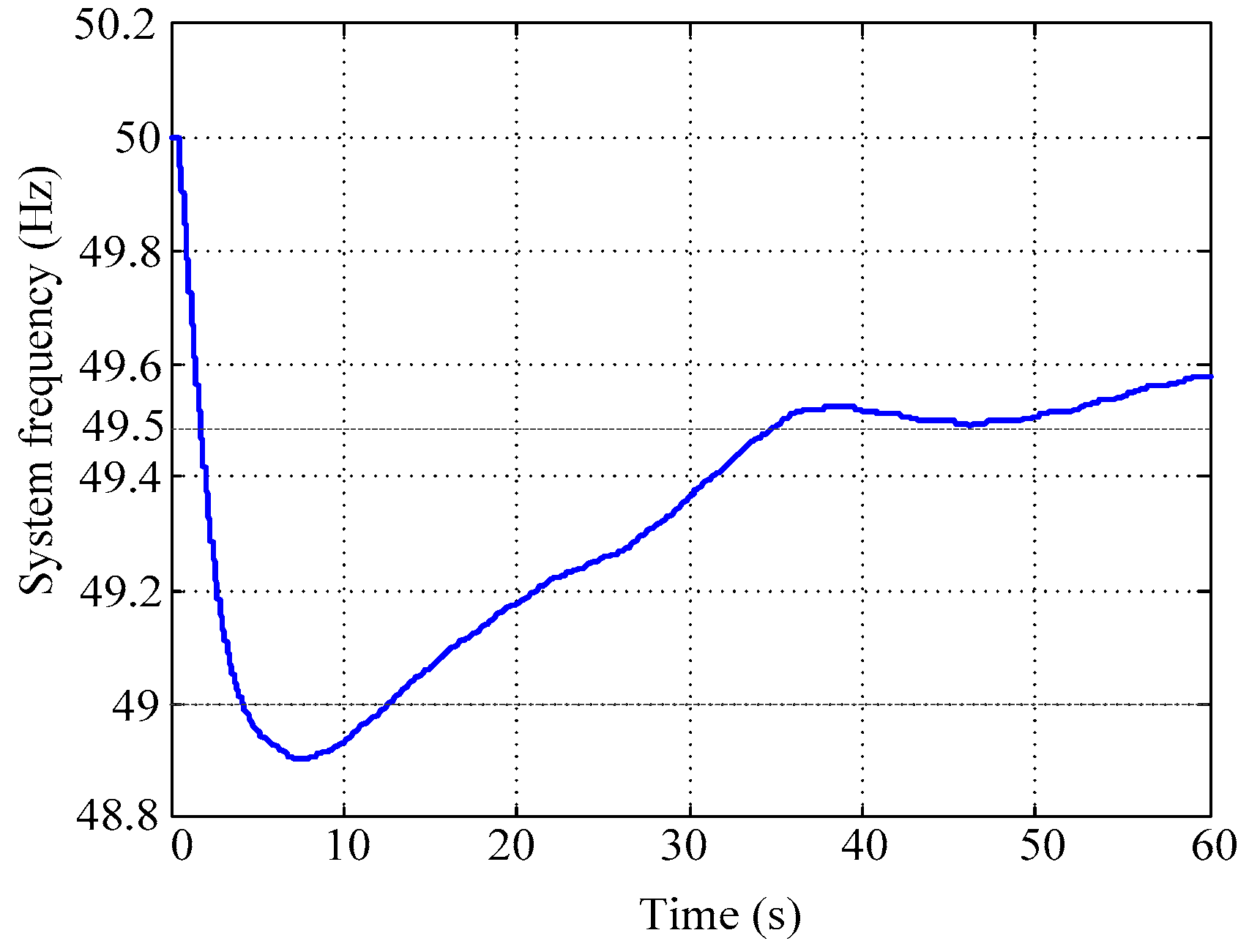
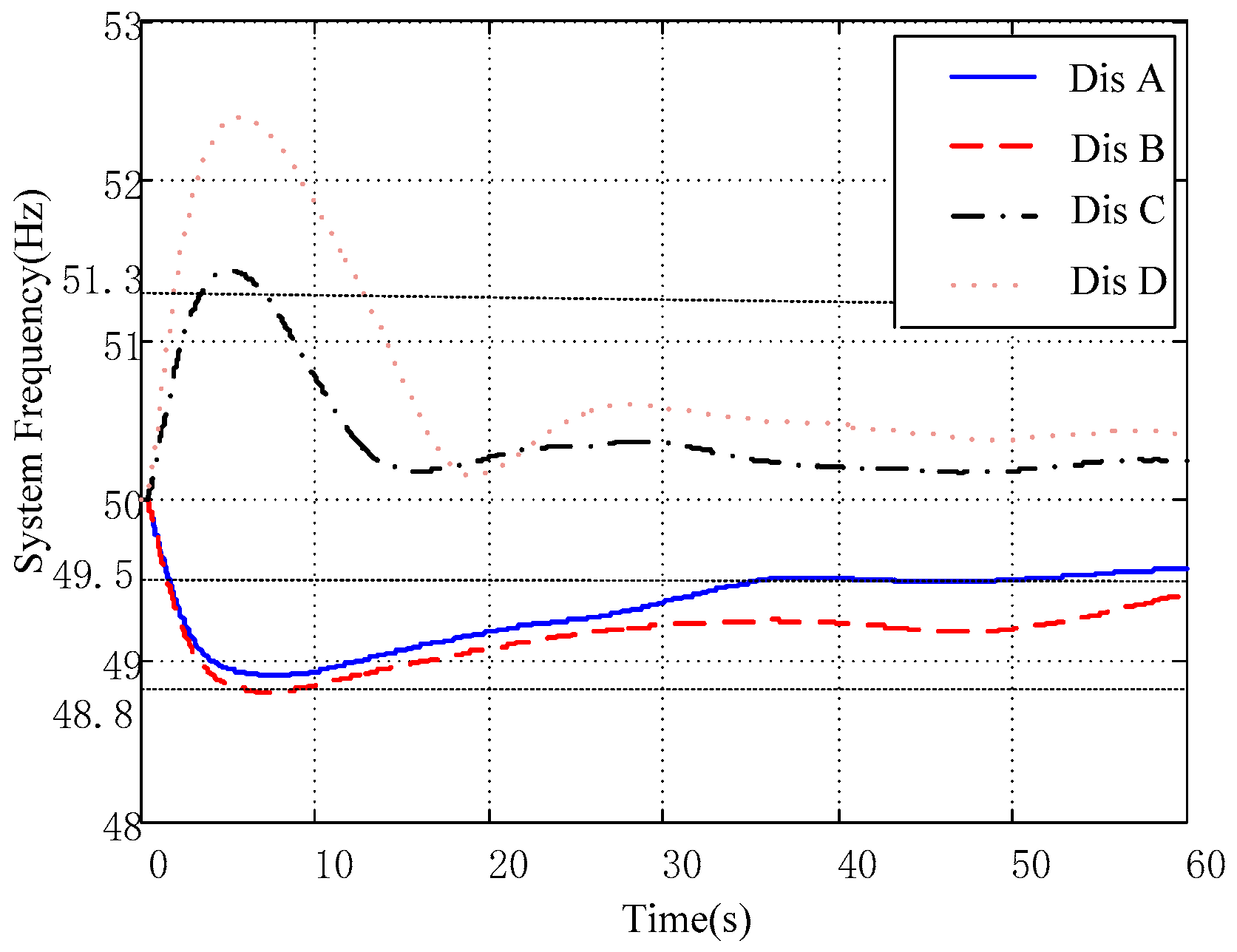
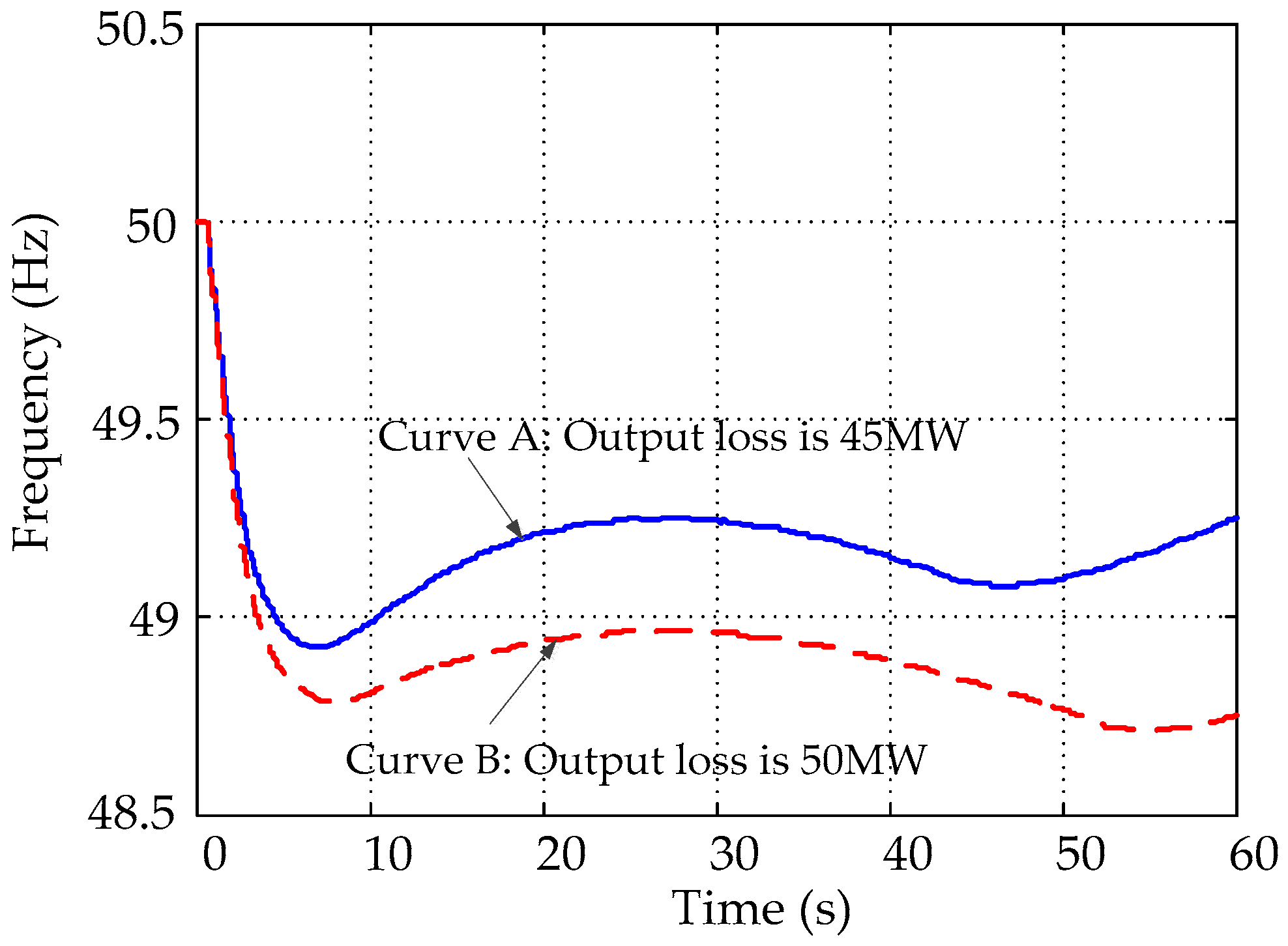
3.4. Effectiveness of the Proposed TFAI
- (1)
- Dis A: the load at bus ZD increases 50 MW.
- (2)
- Dis B: the load at bus ZD increases 55 MW.
- (3)
- Dis C: the load at bus H decreases 60 MW.
- (4)
- Dis D: the load at bus H decreases 130 MW, the load at bus DG decreases 15 MW.
4. Validation for the TFAM
4.1. Disturbance with Single Parameter
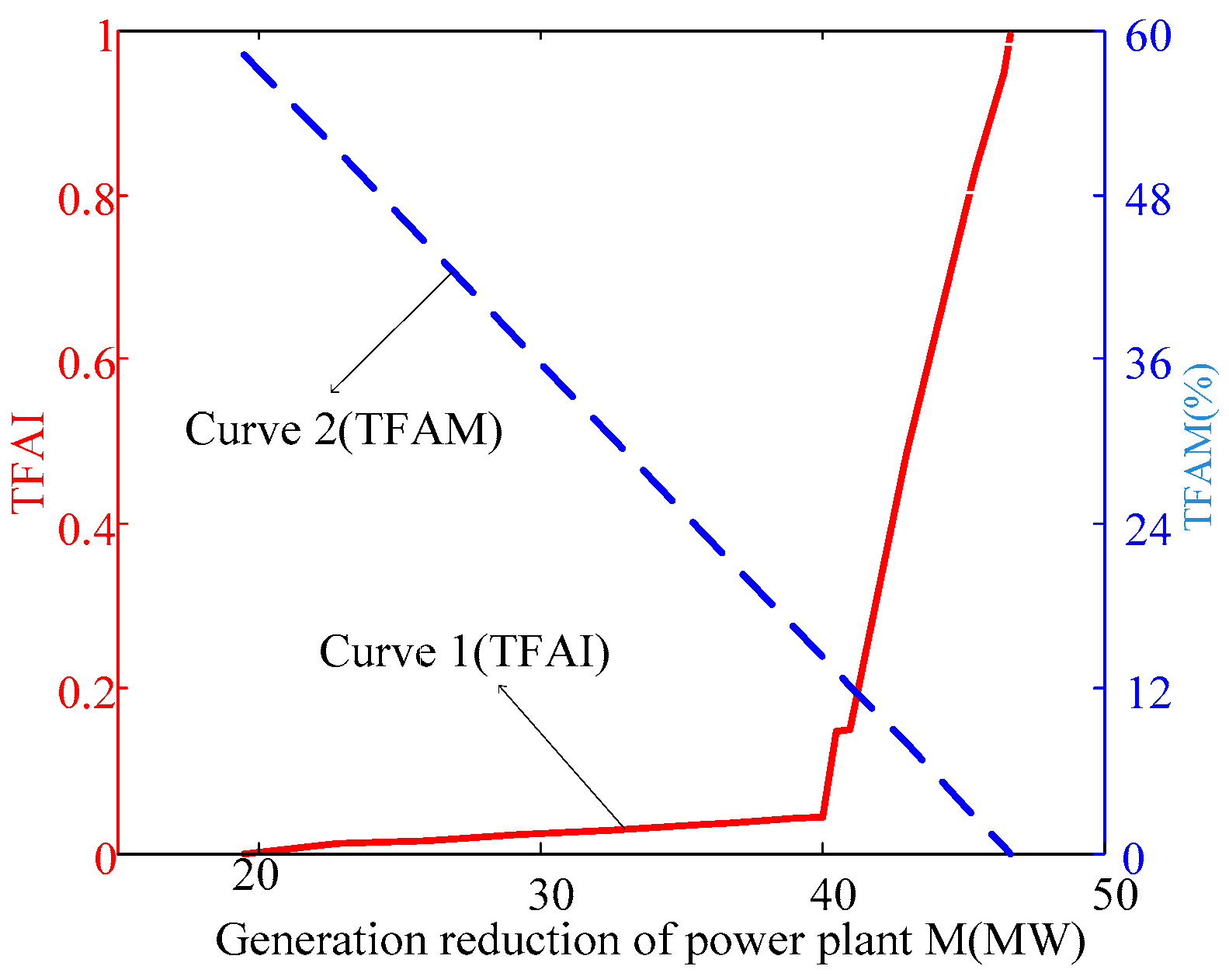
4.1.1. Case 1: Generation Reduction in Power Plant M
4.1.2. Case 2: Load Shedding at Bus H
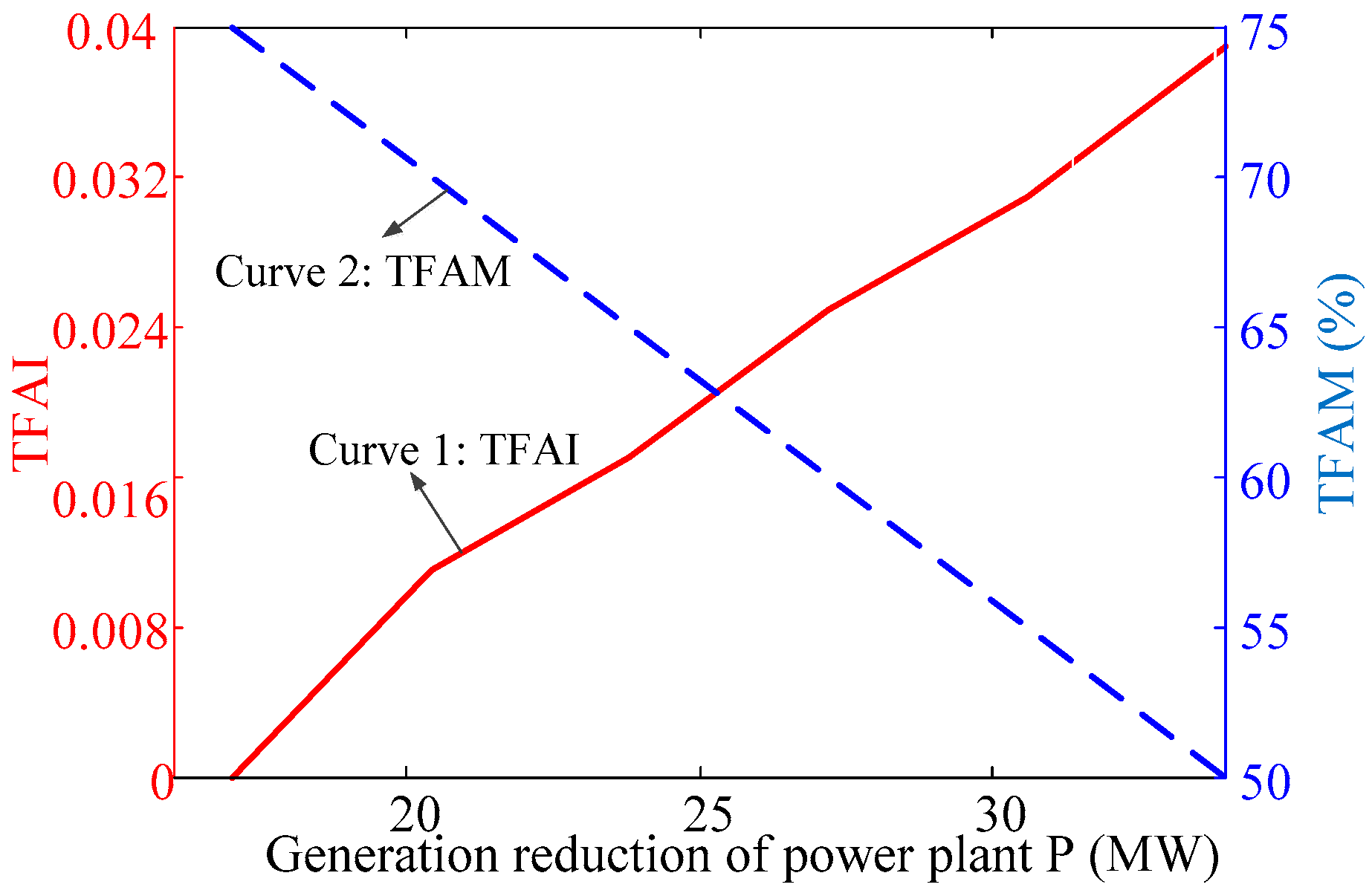
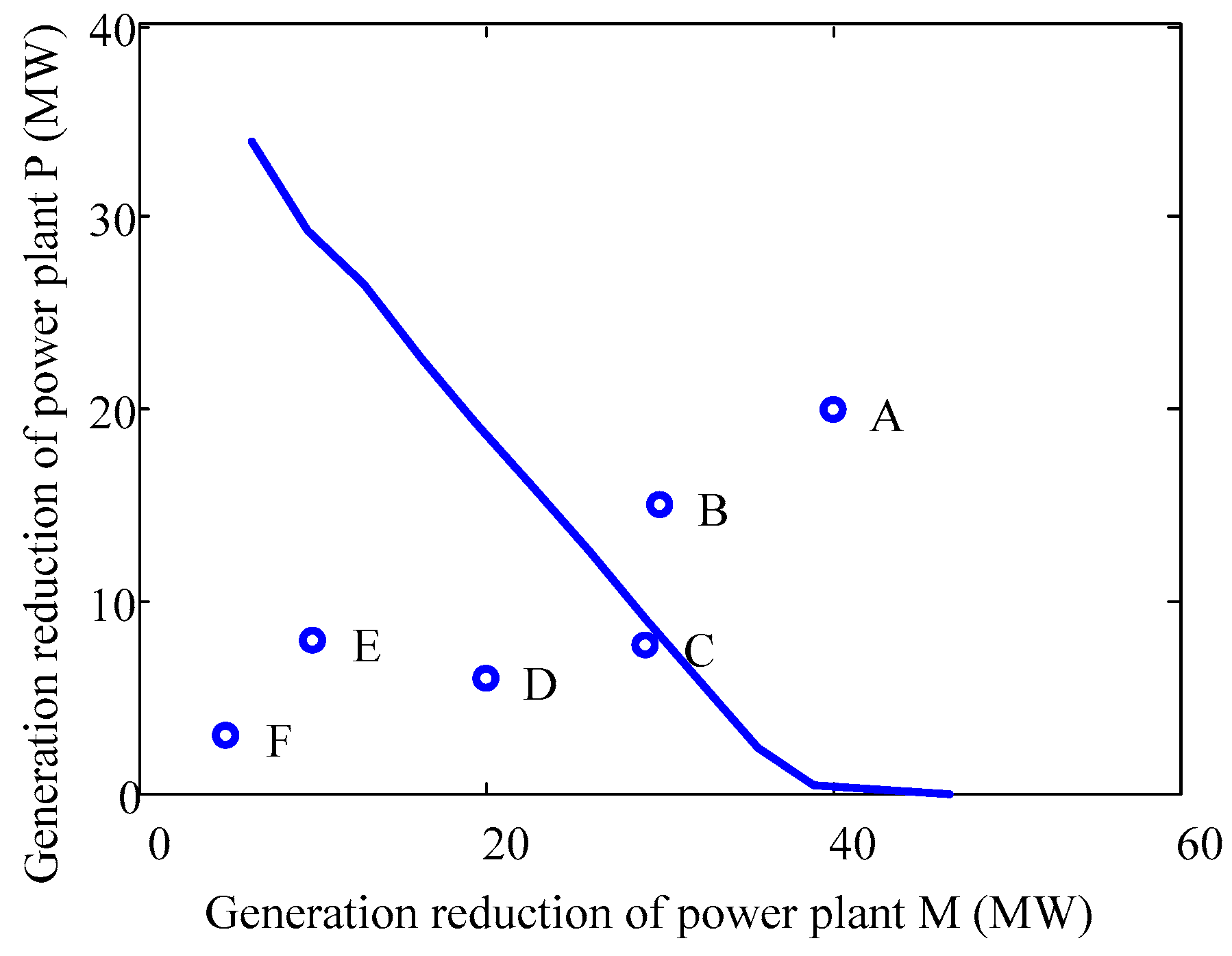
4.1.3. Case 3: Generation Reduction in Power Plant P
4.2. Disturbance with Multiple Parameters
4.3. Comparison of TFAM and Other Indexes
5. Conclusions and Discussions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chan, M.L.; Dunlop, R.D.; Schweppe, F. Dynamic equivalents for average system frequency behavior following major disturbances. IEEE Trans. Power Appar. Syst. 1972, 91, 1637–1642. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
- Han, Y.D.; Min, Y.; Hong, S.B. Analysis of power-frequency dynamics in large scale multi-machine power systems. Autom. Electr. Power Syst. 1992, 1, 28–33. [Google Scholar]
- Brazil, T.J. Accurate and efficient incorporation of frequency-domain data within linear and non-linear time-domain transient simulations. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, USA, 17 June 2005; pp. 797–800. [Google Scholar]
- Tavakkoli, M.; Arabi, J.; Zabihi, S.; Godina, R.; Pouresmaeil, E. Reserve Allocation of Photovoltaic Systems to Improve Frequency Stability in Hybrid Power Systems. Energies 2018, 11, 2583. [Google Scholar] [CrossRef]
- Tavakkoli, M.; Pouresmaeil, E.; Arabi, J.; Godina, R.; Catalao, J.P.S. Load-frequency control in a multi-source power system connected to wind farms through multi terminal HVDC systems. Comput. Oper. Res. 2018, 96, 305–315. [Google Scholar] [CrossRef]
- Shehadeh, H.; Favuzza, S.; Sanseverino, E.R. Electrostatic synchronous generator model of an inverter-based distributed generators. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015. [Google Scholar]
- Thong, V.V.; Driesen, J.; Belmans, R. Transmission system operation concerns with high penetration level of distributed generation. In Proceedings of the 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007. [Google Scholar]
- Sapari, N.M.; Mokhlis, H.; Bakar, A.H.A.; Dahalan, M.R.M. Online stability index monitoring for load shedding scheme in islanded distribution network. In Proceedings of the 2014 IEEE 8th International Power Engineering and Optimization Conference (PEOCO2014), Langkawi, Malaysia, 24–25 March 2014; pp. 445–449. [Google Scholar]
- Zhang, H.T.; Lai, C.S.; Lai, L.L. A novel load shedding strategy for distribution systems with distributed generations. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Zhao, Z.L.; Yang, P.; Guerrero, J.M.; Xu, Z.R.; Green, T.C. Multiple-Time-Scales Hierarchical Frequency Stability Control Strategy of Medium-Voltage Isolated Microgrid. IEEE Trans. Power Electron. 2015, 31, 5974–5991. [Google Scholar] [CrossRef]
- Velez, F.G.; Centeno, V.A.; Phadke, A.G. Multiple swing transient stability assessment with phasor measurements. In Proceedings of the IEEE Manchester Power Tech, Manchester, UK, 18–22 June 2017. [Google Scholar]
- Wu, Z.Y.; Zora, L.T.; Phadke, A.G. Simultaneous transmission line parameter and PMU measurement calibration. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Abdal-Rahman, K.; Mill, L.; Phadke, A.G.; De La Ree, J.; Liu, Y.L. Internet based wide area information sharing and its roles in power system state estimation. In Proceedings of the IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001. [Google Scholar]
- Larsson, M.; Christian, R. Predictive frequency stability control based on wide-area phase measurements. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; Volume 1, pp. 233–238. [Google Scholar]
- Thorp, J.S.; Wang, X.R.; Hopkinson, K.M. Agent technology applied to the protection of power systems. In Autonomous Systems and Intelligent Agents in Power System Control and Operation; Springer: Berlin, Germany, 2003; pp. 115–154. ISBN 978-3540402022. [Google Scholar]
- Zhang, W.; Wang, X.R.; Liao, G.D. Automatic load shedding emergency control algorithm of power system based on wide-area measurement data. Power Syst. Technol. 2009, 33, 69–73. [Google Scholar] [CrossRef]
- Chen, C.R.; Liu, C.C. Dynamic stability assessment of power system using a new supervised clustering algorithm. In Proceedings of the 2000 Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000; pp. 1851–1854. [Google Scholar]
- Rahmann, C.; Ortiz-Villalba, D.; Alvarez, R.; Salles, M. Methodology for selecting operating points and contingencies for frequency stability studies. In Proceedings of the 2017 IEEE Power and Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- YatendraBabu, G.V.N.; Naguru, N.R.; Sarkar, V. Real-Time Transient Instability Detection Using Frequency Trend Vector in Wide Area Monitoring System. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–4. [Google Scholar]
- Seethalekshmi, K.; Singh, S.N.; Srivastava, S.C. WAMS assisted frequency and voltage stability based adaptive load shedding scheme. In Proceedings of the 2009 IEEE Power and Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Ye, H.; Qi, Z.P.; Pei, W. Modeling and evaluation of short-term frequency control for participation of wind farms and energy storage in power systems. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 2647–2654. [Google Scholar]
- Xu, T.S.; Xue, Y.S. Quantitative analysis of acceptability of transient frequency offset. Autom. Electr. Power Syst. 2002, 19, 7–10. [Google Scholar]
- Xu, T.S.; Li, B.J.; Bao, Y.H. Global optimization of UFLS and UVLS quantity considering transient safety. Autom. Electr. Power Syst. 2003, 22, 12–15. [Google Scholar]
- Liu, H.T.; Zeng, Y.G.; Li, J.S. UFLS scheme based on frequency security quantitative analysis for China Southern Power Grid. Electr. Power 2007, 40, 28–32. [Google Scholar]
- Zhang, H.X.; Liu, Y.T. New index for frequency deviation security assessment. In Proceedings of the 2010 Conference Proceedings IPEC, Singapore, 27–29 October 2010; pp. 1031–1034. [Google Scholar]
- Iessa, A.; Wahab, N.I.A.; Mariun, N.; Hizam, H. Method of estimating the maximum penetration level of wind power using transient frequency deviation index based on COI frequency. In Proceedings of the 2016 IEEE International Conference on Power and Energy (PECon), Melaka, Malaysia, 28–29 November 2016; pp. 274–279. [Google Scholar]
- Zhang, H.X.; Hou, Z.Y.; Liu, Y.T. Online Security Assessment of Power System Frequency Deviation. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar]
- Liu, Y.T.; Li, C.G. Impact of large-scale wind penetration on transient frequency stability. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–5. [Google Scholar]
- Sun, Y.K. Study on the Third Line Defense of Frequency Stability Coordinating Control for Sending-End Power System. Master’s Dissertation, North China Electrical Power University, Beijing, China, 11 March 2014. [Google Scholar]
- Tan, F. Study on Frequency Stability Coordinating Control for Sending-End Power System with the Integration of Large-Scale Wind Power. Master’s Dissertation, North China Electrical Power University, Beijing, China, 11 March 2014. [Google Scholar]
- Yue, L.; Xue, A.C.; Cui, J.H. Study on the influence of transient frequency Evaluation Index and governor parameter of small power grid. Power Syst. Technol. 2018, 42, 4031–4036. [Google Scholar] [CrossRef]
- Xue, A.C.; Wu, F.F.; Lu, Q.; Mei, S.W. Power system dynamic security region and its approximation. IEEE Trans. Circuits Syst. I Regul. Papers 2006, 53, 2849–2859. [Google Scholar] [CrossRef]
- Kaye, R.J.; Wu, F.F. Dynamic security regions of power systems. IEEE Trans. Circuits Syst. 1982, 29, 612–623. [Google Scholar] [CrossRef]
- Chinese National Energy Administration. DL/T 1234-2013 Technique Specification of Power System Security and Stability Calculation; China Electric Power Press: Beijing, China, 2013; pp. 15–16.



| Threshold-delay parameter | (49.5, 600) | (49, 10) | (48.8, 0.3) |
| Weight factor | K1 | K2 | K3 |
| Value of weight factor | 0.0033 | 0.1000 | 2.7778 |
| Threshold-delay parameter | (51, 180) | (51. 3,10) | (53, 0.3) |
| Weight factor | H1 | H2 | H3 |
| Value of weight factor | 0.0056 | 0.0769 | 1.1111 |
| Sampling interval/s | 0.02 | 0.04 | 0.1 |
| TFAI | 0.9616 | 6.0280 | 126.1728 |
| Disturbance | TFAI | Transient Frequency Acceptability |
|---|---|---|
| Dis A | 0.9616 | Acceptable |
| Dis B | 1.5620 | Unacceptable (The time duration of the frequency lower than 49 Hz is 13.01 s, more than 10 s) |
| Dis C | 0.4025 | Acceptable |
| Dis D | 1.6752 | Unacceptable (The time duration of the frequency higher than 51.3 Hz is 11.3 s, more than 10 s) |
| Point Nomenclature | Generation Reduction of Power Plant M ΔPdistM/MW | Generation Reduction of Power Plant P ΔPdistP/MW | TFAM η/% |
|---|---|---|---|
| A | 40 | 20 | −46.59 |
| B | 30 | 15 | −14.34 |
| C | 29.25 | 7.718 | 4.56 |
| D | 20 | 6 | 31.18 |
| E | 10 | 8 | 53.75 |
| F | 5 | 3 | 79.21 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, A.; Cui, J.; Wang, J.; Chow, J.H.; Yue, L.; Bi, T. A New Transient Frequency Acceptability Margin Based on the Frequency Trajectory. Energies 2019, 12, 12. https://doi.org/10.3390/en12010012
Xue A, Cui J, Wang J, Chow JH, Yue L, Bi T. A New Transient Frequency Acceptability Margin Based on the Frequency Trajectory. Energies. 2019; 12(1):12. https://doi.org/10.3390/en12010012
Chicago/Turabian StyleXue, Ancheng, Jiehao Cui, Jiawei Wang, Joe H. Chow, Lei Yue, and Tianshu Bi. 2019. "A New Transient Frequency Acceptability Margin Based on the Frequency Trajectory" Energies 12, no. 1: 12. https://doi.org/10.3390/en12010012




