Robust Design Optimization with Penalty Function for Electric Oil Pumps with BLDC Motors
Abstract
:1. Introduction
2. EOP System and BLDC Motor
2.1. EOP System
2.2. BLDC Motor
3. Methods
3.1. RDO Process
- (1)
- Define noise factors caused by control factors and design variable uncertainties.
- (2)
- Configure experimental combinations according to an orthogonal array table and perform experiments.
- (3)
- Calculate the SNR to which the penalty function is added considering the constraint condition.
- (4)
- Determine the optimal experimental combination based on the design factor levels estimated through analysis of variance.
- (5)
- If the SNR does not converge to the set value, repeat steps (2) through (4) using the new levels identified in the optimal level search.
- (6)
- When the SNR converges to the set value, the design process is complete.
3.2. DDO Process
3.3. RDO Definition
4. Verification
4.1. Simulation Results
4.2. Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- He, H.; Liu, Z.; Zhu, L.; Liu, X. Dynamic Coordinated Shifting Control of Automated Mechanical Transmissions without a Clutch in a Plug-In Hybrid Electric Vehicle. Energies 2012, 5, 3094–3109. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.-S. Energy Efficiency Comparison between Hydraulic Hybrid and Hybrid Electric Vehicles. Energies 2015, 8, 4697–4723. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Xiong, R.; Wang, K.; Jiao, B. Optimal Energy Management Strategy of a Plug-in Hybrid Electric Vehicle Based on a Particle Swarm Optimization Algorithm. Energies 2015, 8, 3661–3678. [Google Scholar] [CrossRef] [Green Version]
- Xia, C.; DU, Z.; Zhang, C. A Single-Degree-of-Freedom Energy Optimization Strategy for Power-Split Hybrid Electric Vehicles. Energies 2017, 10, 896. [Google Scholar] [CrossRef]
- Capata, R. Urban and Extra-Urban Hybrid Vehicles: A Technological Review. Energies 2018, 11, 2924. [Google Scholar] [CrossRef]
- Doikin, A.; Habib Zadeh, E.; Campean, F.; Priest, M.; Brown, A.; Sherratt, A. Impact of Duty Cycle on Wear Progression in Variable-displacement Vane Oil Pumps. Procedia Manuf. 2018, 16, 115–122. [Google Scholar] [CrossRef]
- Rostek, E.; Babiak, M.; Wróblewski, E. The Influence of Oil Pressure in the Engine Lubrication System on Friction Losses. Procedia Eng. 2017, 192, 771–776. [Google Scholar] [CrossRef]
- Podevin, P.; Clenci, A.; Decombes, G. Influence of the lubricating oil pressure and temperature on the performance at low speeds of a centrifugal compressor for an automotive engine. Appl. Therm. Eng. 2011, 31, 194–201. [Google Scholar] [CrossRef] [Green Version]
- Miyachi, E.; Ishiguro, M.; Mizumoto, K. Development of Electric Oil Pump; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, J.; Jo, C.; Kim, Y.; Song, M.; Kim, J.; Kim, H. Development and Control of an Electric Oil Pump for Automatic Transmission-Based Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2011, 60, 1981–1990. [Google Scholar] [CrossRef]
- Kim, H.; Wi, J.; Yoo, J.; Son, H.; Park, C.; Kim, H. A Study on the Fuel Economy Potential of Parallel and Power Split Type Hybrid Electric Vehicles. Energies 2018, 11, 2103. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.-T.; Kum, D.; Peng, H. Prius+ and Volt−: Configuration Analysis of Power-Split Hybrid Vehicles with a Single Planetary Gear. IEEE Trans. Veh. Technol. 2012, 61, 3544–3552. [Google Scholar] [CrossRef]
- Zhao, Z.; He, L.; Yang, Y.; Wu, C.; Li, X.; Karl Hedrick, J. Estimation of torque transmitted by clutch during shifting process for dry dual clutch transmission. Mech. Syst. Signal Process. 2016, 75, 413–433. [Google Scholar] [CrossRef]
- Della Gatta, A.; Iannelli, L.; Pisaturo, M.; Senatore, A.; Vasca, F. A survey on modeling and engagement control for automotive dry clutch. Mechatronics 2018, 55, 63–75. [Google Scholar] [CrossRef]
- Song, M.; Oh, J.; Kim, J.; Kim, Y.; Yi, J.; Kim, Y.; Kim, H. Development of an electric oil pump control algorithm for an automatic-transmission-based hybrid electric vehicle considering the gear shift characteristics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 228, 21–36. [Google Scholar] [CrossRef]
- Tu, J.; Choi, K.; Park, Y.H. A New Study on Reliability-Based Design Optimization. J. Mech. Des. 1999, 121, 557–564. [Google Scholar] [CrossRef] [Green Version]
- Kim, N.; Kim, D.; Kim, D.; Kim, H.; Lowther, D.; Sykulski, J. Robust Optimization Utilizing the Second-Order Design Sensitivity Information. IEEE Trans. Magn. 2010, 46, 3117–3120. [Google Scholar] [CrossRef]
- Lagaros, N.D.; Papadrakakis, M. Robust seismic design optimization of steel structures. Struct. Multidisc. Optim. 2007, 33, 457–469. [Google Scholar] [CrossRef]
- Liu, C.; Lei, G.; Ma, B.; Guo, Y.; Zhu, J. Robust Design of a Low-Cost Permanent Magnet Motor with Soft Magnetic Composite Cores Considering the Manufacturing Process and Tolerances. Energies 2018, 11, 2025. [Google Scholar] [CrossRef]
- Jun, C.-S.; Kwon, B.-I.; Kwon, O. Tolerance Sensitivity Analysis and Robust Optimal Design Method of a Surface-Mounted Permanent Magnet Motor by Using a Hybrid Response Surface Method Considering Manufacturing Tolerances. Energies 2018, 11, 1159. [Google Scholar] [CrossRef]
- Zhan, S.; Li, Z.; Hu, J.; Liang, Y.; Zhang, G. Model Order Identification for Cable Force Estimation Using a Markov Chain Monte Carlo-Based Bayesian Approach. Sensors 2018, 18, 4187. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, F.; Chen, J.; Li, J. Risk Analysis for Reservoir Real-Time Optimal Operation Using the Scenario Tree-Based Stochastic Optimization Method. Water 2018, 10, 606. [Google Scholar] [CrossRef]
- Choi, S.-H.; Hussain, A.; Kim, H.-M. Adaptive Robust Optimization-Based Optimal Operation of Microgrids Considering Uncertainties in Arrival and Departure Times of Electric Vehicles. Energies 2018, 11, 2646. [Google Scholar] [CrossRef]
- Pervez, M.N.; Shafiq, F.; Sarwar, Z.; Jilani, M.M.; Cai, Y. Multi-Response Optimization of Resin Finishing by Using a Taguchi-Based Grey Relational Analysis. Materials 2018, 11, 426. [Google Scholar] [CrossRef] [PubMed]
- Hong, G.; Wei, T.; Ding, X.; Duan, C. Multi-Objective Optimal Design of Electro-Hydrostatic Actuator Driving Motors for Low Temperature Rise and High Power Weight Ratio. Energies 2018, 11, 1173. [Google Scholar] [CrossRef]
- Hendershot, J.R.; Miller, T.J.E. Design of Brushless Permanent-Magnet Machines, 2nd ed.; Motor Design Books LLC: Venice, FL, USA, 2010. [Google Scholar]
- Tseng, K.-H.; Shiao, Y.-F.; Chang, R.-F.; Yeh, Y.-T. Optimization of Microwave-Based Heating of Cellulosic Biomass Using Taguchi Method. Materials 2013, 6, 3404–3419. [Google Scholar] [CrossRef] [Green Version]
- Solehati, N.; Bae, J.; Sasmito, A.P. Optimization of Wavy-Channel Micromixer Geometry Using Taguchi Method. Micromachines 2018, 9, 70. [Google Scholar] [CrossRef] [PubMed]






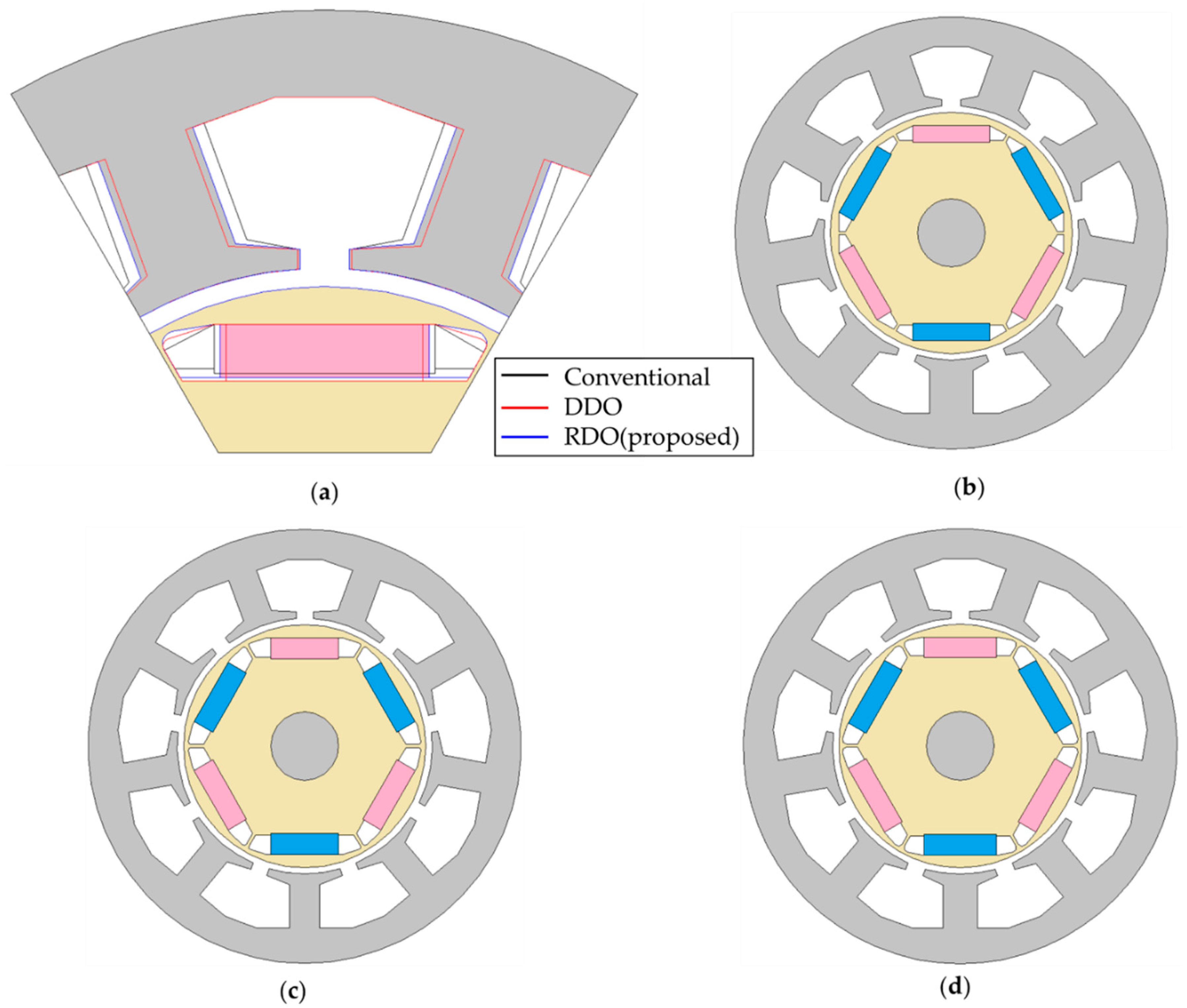





| Items | Value | Unit | |
|---|---|---|---|
| Stator | Outer/Inner diameter | 51/30 | mm |
| Slots | 9 | - | |
| Number of turns | 14 | turns | |
| Rotor | Outer/Inner diameter | 29/8 | mm |
| Pole | 6 | - | |
| Magnet grade | N42EH | NdFeB | |
| Rated | Speed | 4000 | rpm |
| Output power | 150 | W | |
| Efficiency | 70 | % | |
| Torque | 0.358 | Nm | |
| Stack length | 35 | mm | |
| Air-gap length | 0.5 | mm | |
| Maximum speed | 6000 | rpm | |
| Cogging torque (peak to peak) | 0.037 | Nm | |
| Torque ripple (peak to peak) | 0.06 | Nm | |
| Items | Description | |
|---|---|---|
| Case #1 | When X1 is determined as the optimal level | X1 = X1prev − Δ1 |
| X2 = X1prev | ||
| X3 = X2prev | ||
| Case #2 | When X2 is determined as the optimal level | X1 = X2prev − Δ1/2 |
| X2 = X2prev | ||
| X3 = X2prev + Δ2/2 | ||
| Case #3 | When X3 is determined as the optimal level | X1 = X2prev |
| X2 = X3prev | ||
| X3 = X2prev + Δ2 | ||
| Items | Parameters | Level 1 | Level 2 | Level 3 | Unit | XL | XU |
|---|---|---|---|---|---|---|---|
| Lower | Upper | ||||||
| Design factor | X1 | 2.1 | 2.2 | 2.3 | mm | 1.5 | 2.5 |
| X2 | 5.0 | 5.1 | 5.2 | mm | 4.5 | 5.5 | |
| X3 | 3.44 | 3.54 | 3.64 | mm | 3.0 | 4.0 | |
| X4 | 8.9 | 9.0 | 9.1 | mm | 8.0 | 10.0 | |
| X5 | 18.9 | 19.0 | 19.1 | degree | 10 | 60 | |
| Noise factor | - | Level 1 | Level 1 | Level 1 | - | - | - |
| Tolerance | - | −0.1 | 0 | 0.1 | - | - | - |
| Items | Conventional | DDO | RDO | Unit |
|---|---|---|---|---|
| X1 | 2.2 | 2.2 | 2.0 | mm |
| X2 | 5.1 | 3.5 | 4.1 | mm |
| X3 | 3.54 | 3.84 | 3.7 | mm |
| X4 | 9.0 | 8.0 | 8.5 | mm |
| X5 | 19.0 | 33.0 | 42.0 | degree |
| Tcog | 0.037 | 0.019 | 0.011 | Nm |
| Tripple | 0.087 | 0.052 | 0.017 | Nm |
| σcog | - | 0.0484 | 0.0315 | - |
| Iterative designs | - | 9 | 15 | - |
| Required simulations | - | 124 | 336 | - |
| Items | Conventional | DDO | RDO | Unit | |
|---|---|---|---|---|---|
| Simulation | Cogging torque | 0.037 | 0.019 | 0.011 | Nm |
| Torque ripple | 0.087 | 0.052 | 0.017 | Nm | |
| Rated efficiency | 70.0 | 71.2 | 72.2 | % | |
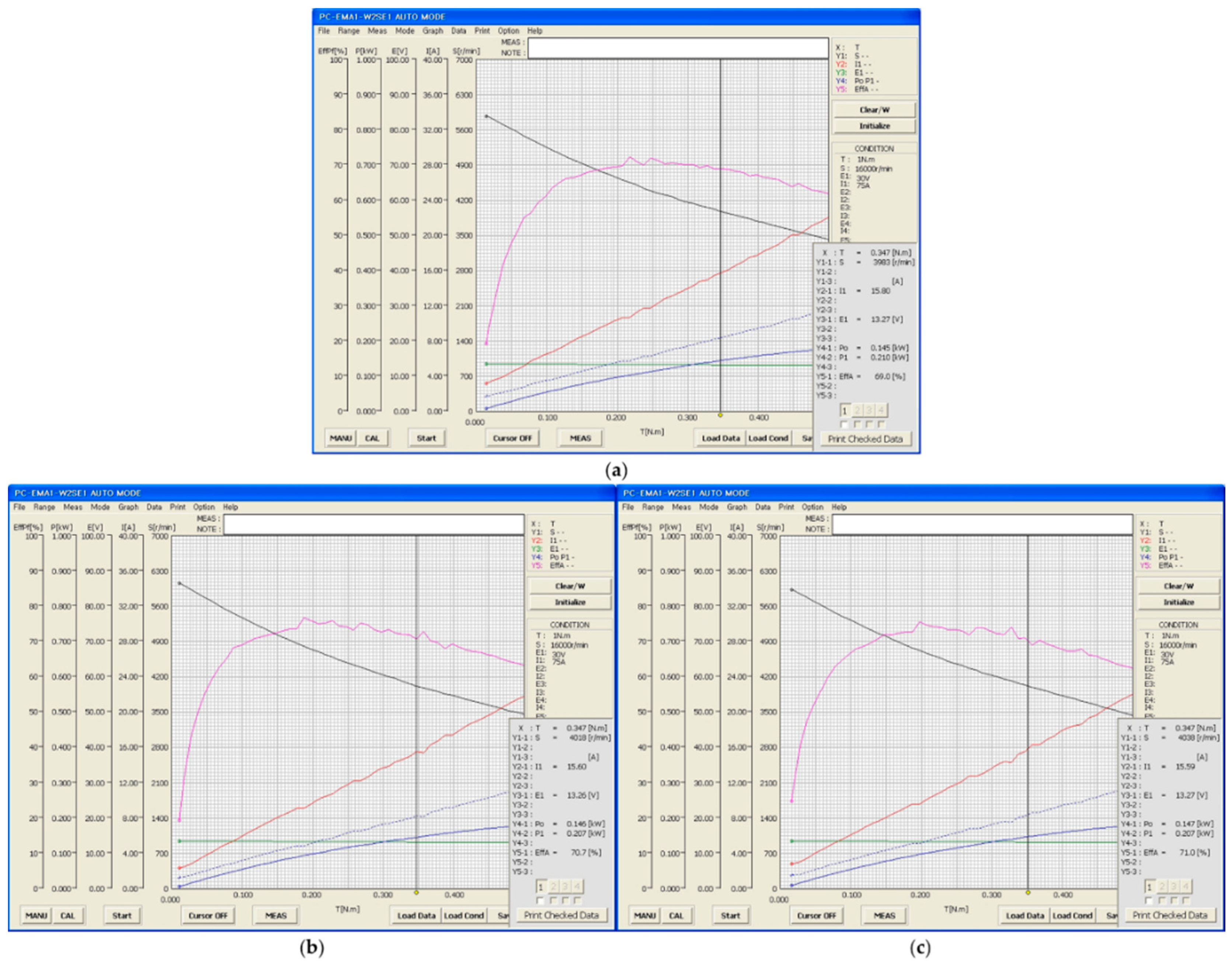
| Experiment | Cogging torque | 0.071 | 0.046 | 0.014 | Nm |
| Torque ripple | 0.155 | 0.097 | 0.055 | Nm | |
| Rated efficiency | 69.0 | 70.7 | 71.0 | % | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, K.-Y.; Baek, S.-W. Robust Design Optimization with Penalty Function for Electric Oil Pumps with BLDC Motors. Energies 2019, 12, 153. https://doi.org/10.3390/en12010153
Yoon K-Y, Baek S-W. Robust Design Optimization with Penalty Function for Electric Oil Pumps with BLDC Motors. Energies. 2019; 12(1):153. https://doi.org/10.3390/en12010153
Chicago/Turabian StyleYoon, Keun-Young, and Soo-Whang Baek. 2019. "Robust Design Optimization with Penalty Function for Electric Oil Pumps with BLDC Motors" Energies 12, no. 1: 153. https://doi.org/10.3390/en12010153
APA StyleYoon, K.-Y., & Baek, S.-W. (2019). Robust Design Optimization with Penalty Function for Electric Oil Pumps with BLDC Motors. Energies, 12(1), 153. https://doi.org/10.3390/en12010153




