Torque Analysis of a Flat Reconfigurable Magnetic Coupling Thruster for Marine Renewable Energy Systems Maintenance AUVs

Abstract

The concept of reconfigurable magnetic coupling thrusters (RMCT) applied to the vectorial thrust of autonomous underwater vehicles (AUV) has been recently developed and presented. This technology ensures greater robot watertightness with enhanced maneuvering capabilities, which are desired features in agile AUVs for marine renewable energy (MRE) system maintenance. It is possible since in RMCTs the driving torque is magnetically transmitted to the propeller, which has its orientation changed. This work is focused on the coupling and control torque calculation and further analysis of the latest prototype version (Flat-RMCT), in the static condition for the full thrust vector range. For this purpose, a numerical model is implemented and validated with experimental results. The numerical model is based on the finite volume integral method. The results indicate that the minimum magnetic reluctance propensity creates not only the expected magnetic spring effect but also an auto-driving torque due to the non-axial symmetry of coupling rotors, which exists only for reconfigurable couplings. Mathematical functions are proposed to model these effects and they are used to extend the understanding of the coupling. These models can be used to compose a full and accurate dynamic model for a better RMCT simulation, identification, and control.

1. Introduction

Since the end of the 20th century, autonomous robots have been used in tasks where the presence of divers is costly, dangerous, or even impossible. There is an important interest in these robots for the maintenance of marine renewable energy (MRE) systems (underwater devices such as offshore wind turbines, tidal turbines, or hydroelectric dam underwater structures). Moreover, there are also interests in military applications (mine warfare, sensitive areas protection) and for offshore industry activity (pipelines or telecommunication cables).

For these missions, underwater interventions on complex structures (hostile environment) require autonomous underwater vehicles (AUVs) with enhanced maneuvering capabilities [1]. These more stringent demands imply the need to expand the capabilities of AUVs such as speed, power, control, and perception. However, the propulsion and control systems for this robot kind have not improved as quickly as their needs, which restricts their performance and thus their autonomy. According to [2], it is necessary to give long range and maneuvering capabilities to AUVs to advance to a new generation of underwater robots able to perform a more extensive set of operations. What refers to two design aspects of these vehicles: hull shape and propulsion system. [1] observes that investigations and developments have been conducted about underwater vehicles locomotion, but few are dedicated to the propulsion system. Therefore, this is our research focus.

The propulsion systems of underwater vehicles can be divided into three categories [2]:

• Classical rear propeller with control surface architectures, as in large conventional submarine equipped with rudders;
• Biomimetic propulsion, i.e., inspired by natural propulsion mechanisms present in marine life, e.g., dolphin and whale fins;
• Vectorial thrust (VT), which can be achieved with one or a set of propellers, whose thrust vectors drive and steer the vehicle without the need for control surfaces.

It is immediate that the propulsion architecture of a vehicle determines its set of possible motion directions as well as influences the ability to control the movement. The first category of propulsion systems offers low maneuverability and the second one is difficult to implement or control [3,4,5,6].

In VT propulsion systems, it is possible to drive and steer the vehicle only using thrusters through various strategies. One possibility is to use a set of fixed thrusters (FT) [7]. A single FT endows the robot with only a thrust vector which does not allow trajectory tracking. This issue is solved with the combination of several FTs acting in different directions and with different thrust, e.g., water-jet thrusters. Another possibility is to use a few or a single reconfigurable thruster (RT), since they may have their thrust vectors redirected, which involves more than one degree of freedom (DOF) [8,9].

One of the RT systems advantages over FT ones is the possibility of reducing the number of thrusters to the minimum, which reduces the total vehicle mass. Another advantage is the reduced consumption of energy when changing directions [2]. However, to guarantee a greater maneuverability and increased controllability of AUVs, an RT must be endowed with the greatest possible capability to reorient its thrust vector [10].

Recently, researches have been carried out to advance in the development of different RT types. A research team developed spherical-shaped underwater vehicles with three [11] and four [12] reconfigurable water-jet thrusters, with 2-DOF of reconfiguration each, but using waterproof servomotors (IP67 protection). Ref. [13] developed a small underwater vehicle with an RT based on nozzle orientation that redirects the propeller exhaust flow with 2-DOF, keeping the propeller without contact with marine life, and not requiring any shaft reorientation. Ref. [14] also developed an RT with 2-DOF of propeller and duct reconfiguration using a spherical parallel mechanism. In [15], authors analyzed the state-of-the-art in key technologies for AUVs and indicate that the VT technologies are not yet mature and due it, they propose an orientable motor-to-propeller transmission mechanism, based on ball gear, with wide range wrist rotation. However, their review did not take into account the advances in RMCTs [1], since they analyzed only mechanical transmission systems. Excluding [11], all these projects indicate that:

• They do not need to reorient their motor axis to reconfigure the thrust vector. Only their propeller, duct or nozzle must be reoriented. Thus, reduced power and torque values are required in the maneuvers.
• They need three actuators to ensure 2-DOF of VT reconfiguration.
• They need mechanical seals, since the movement is transmitted through shafts or rods, which implies frictions and likely watertightness issues.

The watertightness issue is more critical in deep-water tasks, due to high pressure. Also due to this, we proposed a new vectorial thruster based on reconfigurable magnetic couplings, which is named reconfigurable magnetic coupling thruster (RMCT) [10]. In this thruster, the motor shaft movement is transmitted to the propeller one at a distance, without any material medium, through a magneto-mechanical device which works as a coupling and/or joint allowing the propeller driving and orientation. This brings benefits [16] such as:

• Movement transmission between insulated environments
• Complex and unsure mechanical seals are no longer needed
• Robot watertightness is not jeopardized by a hull breach
• It eliminates the friction inherent to mechanical seals and joints
• The magnetic coupling also works as a mechanical fuse (torque limiter) to protect the motor in case of severe load peaks (where a gearbox would break)
• Eventual vibrations are mitigated (spring effect)
• Low maintenance when it is compared to a mechanical coupling or a universal joint

The challenge in this proposal lies in difficulty of implementing two mechanical functions, jointly: the transmission torque function (coupling) at the distance with the hull in between, and the 3D rotational freedom (spherical joint). Seeking it, we have proposed the first RMCT, the spherical one [1], with magnets just in one side of the coupling (motor), which results in a low transmitted torque. Recently, we have started to develop a new RMCT version, the radial one [17]. 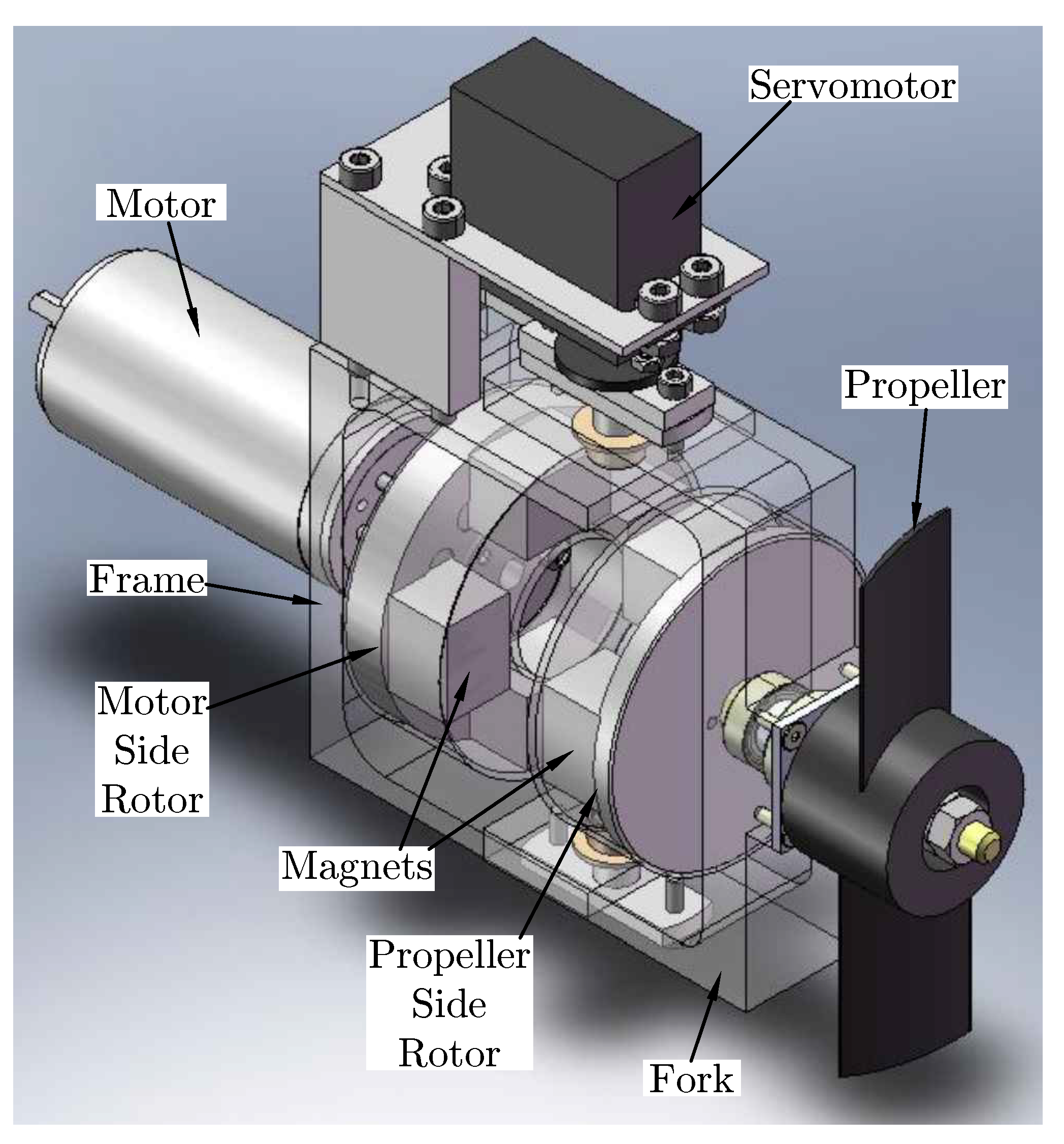In [18], we presented the flat reconfigurable magnetic coupling thruster (Flat-RMCT, see Figure 1), modeling the magnetic torque using partial domain simulation results with a commercial software (Flux3D) achieved by TE2M. TE2M (www.te2m.fr) is a French company based in Brest specialized on solutions for magnetic systems in high value products industry.

As the Flat-RMCT technology needs a detailed presentation, the present work aims at a further understanding on its coupling torque mechanism. Since this coupling is based on permanent magnets attraction, it has a steady-state synchronous behavior and its causes can be analyzed in detail using a magnetostatic model. In transient-state, besides small oscillations, the coupling can also be considered synchronous. These small oscillations do not generate significant losses, which do not generate a damping effect [19]. The magnetic torque behavior is fully described using analytical and numerical models validated with real-world experiments on our prototype (Figure 1). The numerical magnetostatic model adopted is the finite volume integral method [20] implemented in the RADIA 3D tool [21] for Mathematica^TM Wolfram language [22]. It is expected to be able to answer the bellow RMCT questions:

• What is the complete reconfigurable magnetic coupling torque behavior, and how does it depend on all angles?
• What torque must the servomotor apply to control the propeller orientation?

Once its characteristics are precisely known, it will be possible to simulate, design, and control a Flat-RMCT for AUVs.

This work is organized as follows. In Section 2 the studied magnetic coupling is discussed. In Section 3, the magnetostatic numerical model is presented. In Section 4, the numerical model is validated experimentally, simulated to investigate the RMCT torques behavior, and the results are discussed. The last section gives the conclusion, ongoing works, and perspectives.

2. The Flat Reconfigurable Magnetic Coupling Thruster or Flat-RMCT

The RMCT design has been improving. These improvements have focused on increasing the magnetic coupling torque in intensity and quality. First, we developed the Spherical-RMCT [1] and then the Flat-RMCT [18] (Figure 1) with a better torque transmission. The Flat-RMCT uses two parts of conventional axial permanent magnetic couplings but using flat shaped magnets (parallelepipedic), which makes easier its fabrication.

The conventional axial permanent magnetic couplings are not new [23,24], and were also denominated face type couplings [25]. Often, an axial magnetic coupling has two rotors with magnets assembled on soft-iron yokes, which concentrates the magnetic flux and increases the air gap magnetic energy density [26]. Usually, others magnetic couplings, besides axial ones, have their driving and driven axes parallels. However, since magnetic gears are also magnetic couplings, there are some couplings with nonparallel axes, e.g., the bevel gear [27]. Even so, they were always using fixed axes before we have proposed reconfiguring their output axis orientation [10,28], disregarding the permanent-magnet spherical actuators [29], which have other applications not transmitting output shaft torque or speed, but controlling a multidegree-of-freedom joint orientation.

Figure 2 shows the Flat-RMCT. For more details about the mechanical model see [18]. The figure shows the magnetic parts without their nonmagnetic protection cover against water (jackets). Naturally, the quantity and material type of magnets affect the coupling torque values. We have eight equal samarium cobalt magnets ($S{m}_{2}C{o}_{17}$) placed 90 degrees between each other, with the remnant magnetization $B_r=1.05\pm$ $0.02$ $\mathrm{T}$, made by TE2M company. The magnets colored in blue have their south pole facing the air gap, and the red ones are in the other way. Both soft-iron yokes of rotors are made of steel Z8C17 (magnetic stainless steel), with their diameter equal to 62 mm and thickness equivalent to $4.76$ mm. The blues lines indicate the two more important magnetic induction lines: the circuit between two magnets in the same part (e.g., magnets (1) and (2)), and a bigger circuit including four magnets, two on each side (e.g., magnets (1), (5), (6) and (2)). There are four frames. The global frame 0 ($x_0,y_0,z_0$) is linked to the robot (frame fixed). Frame 1 ($x_1,y_1,z_1$) is linked to the motor side rotor, rotating ${\theta }_m$ (motor rotor angle) around $z_0$. Frame 2 ($x_2,y_2,z_2$) is linked to the fork, rotating $\alpha$ (reconfiguration angle) around $y_0$. In addition, frame 3 ($x_3,y_3,z_3$) is linked to the propeller side rotor, rotating ${\theta }_h$ (propeller rotor angle) around $z_2$. In any configuration the frames origins are in O.

In Figure 2 and Figure 3a, the coupling is showed with its maximum reconfiguration angle, $\alpha =+30.5$°, when magnets (4) and (8) are closest and magnets (2) and (6) are farthest, and with ${\theta }_m={\theta }_h=0$°, i.e., when the magnets on motor side are aligned with those on propeller side: stable state with the minimum magnetic reluctance (MMR). The distance between the reconfiguration axis $y_2$ and the plane that contains the magnets faces is equal to $11.22\pm$ $0.17$ mm, which defines a variable air gap with height equal to $22.44\pm$ $0.33$ mm when $\alpha =0$°. It is important to point out that the torque transmission capacity is highly sensible to any air gap change.

In practice, the magnetic reluctance principle implies that the system always seeks the more aligned configuration (north pole with south pole) with lowest air gaps (if possible, with contact between north and south pole), reducing the reluctance and thus increasing the magnetic flux. This principle makes the coupling to work as a rotational nonlinear spring driven by the magnetic spring angle $\theta$, generating the magnetic spring torque $T_z$:

$$\theta ={\theta }_m-{\theta }_h$$

(1)

We should have a stable configuration when $\theta =0$° (with the magnets alignments (1)–(5), (2)–(6), (3)–(7) and (4)–(8)) and also for $\theta =\pm 180$° (with the magnets alignments (1)–(7), (2)–(8), (3)–(5) and (4)–(6)), due the coupling symmetry. These stable positions ($\theta =0(mod\pi )$) with no spring effect should present a magnetic spring torque $T_z=0$ [18]. There are other configurations where $T_z$ should be null but completely unstable. It occurs when the equals poles are aligned (closest), i.e., when $\theta =0(mod\frac{\pi }{2})$. It is expected $T_z\ne 0$ in all other configurations when $\theta \ne 0$°, being maximum when $\theta$ is between 0° and 90°, i.e., 45° ($\theta =0(mod\frac{\pi }{4})$). Thus, the operative range is $\theta =[-45°,45°]$ since after the extreme torque values the coupling decouples. Moreover, due to the device symmetry $T_z\left(\theta \right)=-T_z(-\theta )$. Therefore, it would be enough to explore the coupling with $\theta \in [0,45°]$.

The magnetic torque between rotors is a vector which can be projected in different axes: ${\mathbf{T}}_{\mathbf{m}}$ is the torque on the motor side rotor due to the interaction with the propeller side rotor, as well as ${\mathbf{T}}_{\mathbf{h}}$ is the torque on the propeller side rotor due to the interaction with the motor side rotor. Thus, ${\mathbf{T}}_{\mathbf{m}}=-{\mathbf{T}}_{\mathbf{h}}$ since they are the action and reaction vectors. The projections of ${\mathbf{T}}_{\mathbf{m}}$ in the axes $x_1,y_1,z_1$ (motor side rotor frame) are $T_{m_x},T_{m_y},T_{m_z}$ respectively, as well as the projections of ${\mathbf{T}}_{\mathbf{h}}$ in the axes $x_3,y_3,z_3$ (propeller side rotor frame) are $T_{h_x},T_{h_y},T_{h_z}$ respectively.

In our last work [18], it was assumed that for all angle $\alpha$ values, the output (transmitted) torque $T_{h_z}$ had the same intensity than the input torque $T_{m_z}$, as well as than the magnetic spring torque $T_z$, i.e., $|T_{h_z}|=|T_{m_z}|=|T_z|$. Now, this will be studied in detail. When $\alpha =0$° we have classical magnetic couplings (parallel rotors axes), where $|T_{h_z}|=|T_{m_z}|=|T_z|$ is true. In this condition, if $\theta =0$° (null magnetic spring torque), the magnet faces of a rotor are parallels to those of the other rotor, with the same air gap between all exposed faces of magnets. Hence, the attraction and repulsion forces between magnets around the reconfiguration axis $y_2$ (servomotor axis) are balanced, and there is no torque around this axis. However, the $\alpha =0$° configuration is completely unstable because if $\alpha >0$° (even with a small $\alpha$) the attraction force between magnets (4) and (8) is greater than the force between magnets (2) and (6), thus there is a torque around axis $y_2$, which tends to increase $\alpha$. In this case, to keep and control $\alpha$, the servomotor (Figure 1) has to apply a counter torque, which is called restoring torque $T_{Rest}$ in Figure 2 (${\Gamma }_{Rest}$ in [18]), defined by Equation (2). Finally, due the symmetry around $y_2$ axis, it is enough to calculate it with positive values of $\alpha$ since $T_{Rest}\left(\alpha \right)=-T_{Rest}(-\alpha )$.

$$T_{Rest}=-{\mathbf{T}}_{\mathbf{h}}·{\mathbf{y}}_{\mathbf{2}}={\mathbf{T}}_{\mathbf{m}}·{\mathbf{y}}_{\mathbf{2}}$$

(2)

3. Magnetostatic Numerical Modeling

The magnetostatic numerical model is implemented using the finite volume integral method [20], from the RADIA [21] tool. RADIA works as a library (add-on) for the Mathematica^TM [22] software, which calls the solver, receives the results, and manages the optimization process if necessary.

The main idea of the method is to represent a magnetic body by polyhedrons (finite volumes) where the magnetization is considered uniform. Both hard (magnets) and soft (iron) magnetic bodies are represented by these volumes, and their magnetization vectors $\mathbf{M}$ are determined as a function of the magnetic field strength $\mathbf{H}$. This relation can be linear for isotropic (e.g., paramagnetic and diamagnetic) and anisotropic (e.g., permanent magnets) materials, or nonlinear for other isotropic materials (e.g., ’iron’). Thus, as happens in the real world, the magnets, coils and other determined external fields (the sources of $\mathbf{H}$) magnetize the soft magnetic bodies (reorienting their magnetic domains) $\mathbf{M}\left(\mathbf{H}\right)$, which interact mutually since more magnetization generates more magnetic field $\mathbf{H}\left(\mathbf{M}\right)$. Therefore, an iterative relaxation procedure is needed to evaluate how every volume magnetization affects, and is affected by, each other volume, until a stable state be achieved: $\mathbf{M}\left(\mathbf{H}\right)\leftrightarrow \mathbf{H}\left(\mathbf{M}\right)$. After this step, the magnetic field and field integrals can be calculated by summing the field generated by every discrete volume with its stabilized magnetization vector. The magnetic field is calculated by analytic expressions (surface integral). Using analytical formulas, it is not necessary to apply a mesh outside the bodies to know the magnetic field in free space, which reduces the processing time. This is an important difference compared to the finite element method and justifies our choice since the Flat-RMCT analysis requires many simulations.

Figure 4a presents the Flat-RMCT RADIA discretized model. Each magnet is discretized in 64 parts (parallelepipeds) with constant magnetization, and each soft-iron yoke is divided into 384 elements (polyhedrons). The soft-iron yokes made of steel Z8C17 are modeled with a nonlinear magnetization behavior, using another equivalent material: 430 stainless steel. Its $B\left(H\right)$ curve is available at FEMM materials library [30]. Figure 4b shows the magnetizations vectors for every polyhedron after the relaxation process.

Finally, the magnetic torque is calculated by the RADIA virtual work approach.

4. Numerical and Experimental Investigation

4.1. Numerical Model Validation from Experimental Results

Firstly, the numerical model is validated experimentally on our Flat-RMCT prototype (see Figure 5). The validation process is performed comparing numerical results with experimental ones obtained measuring the propeller side torque $T_{h_z}$, when the prototype is configured in the neutral configuration ($\alpha =0$°), and for the maximum reconfiguration angle ($\alpha =30.5$°). Figure 5a shows the experimental setup for $\alpha =30.5$°, but the method is the same and even simpler for $\alpha =0$° (Figure 5b). The cable and the propeller shaft are linked by a pulley with radius $R_p=51.39\pm 0.3$ mm. On its other end, the cable is linked to a mass which is placed on a precision balance ($\pm 0.5\mathrm{g}$). The mass is heavy enough to stay always in contact with the balance plate. The experimental procedure is to rotate the motor side rotor, changing and measuring ${\theta }_m$ ($\pm 0.5$°) while the propeller side rotor is locked by the cable (${\theta }_h=0$°, thus $\theta ={\theta }_m$), and to record weights measured by the balance, i.e., the mass weight minus the maximum cable force due to $T_{h_z}$.

Forty-two real-world experiments were carried out: 21 $\theta$ values $[0°,90°]$ for neutral ($\alpha =0°$) and extreme ($\alpha =30.5°$) configurations. The experiments were performed with two magnets configuration: when the magnets (1) and (5) start aligned for $\theta =0°$ (Config.1), or when the magnets (1) and (7) do it (Config.2). Four measurements were taken for each point. These experimental results are shown in Figures 8–10 in comparison with numerical ones. In

Table 1. Torque values comparison between numerical and experimental results.

${\mathit{T}}_{{\mathit{h}}_{\mathit{z}}}$ [mNm]		Experiments	Numerical Model
		${\mathit{T}}_{{\mathit{h}}_{\mathit{z}}}$	${\mathit{T}}_{{\mathit{h}}_{\mathit{z}}}$	Rel. Error
$\theta =0°$	$\alpha =\{0°,30.5°\}$	0.0	0.0	0%
$\theta =45°$	$\alpha =0°$	373.1 ± 3.3	371.6	0.4%
	$\alpha =30.5°$	607.1 ± 5.3	595.6	1.9%

maximum values of each curve are compared.

In conclusion, the numerical model can be considered validated, and can be used to analyze the Flat-RMCT torques behavior.

4.2. Magnetic Coupling Torques: Spring and Auto-Driving Rotors Effects

After model validation, numerical experiments are performed to determine and analyze how the torques behave according to the angles $\theta$, ${\theta }_m$, ${\theta }_h$, and $\alpha$. Firstly, we examine how the propeller and the motor torques $T_{h_z}$ and $T_{m_z}$ behave for a fixed $\theta$ (when ${\theta }_m$ and ${\theta }_h$ (see Equation (1)) are changing together), for $\alpha \ne 0°$, because in this configuration the magnets do not maintain the same distance between them. Therefore, the question is whether $T_{h_z}$ and $T_{m_z}$ are the same for a fixed $\theta$ no matter the ${\theta }_m$ and ${\theta }_h$ values.

Since $\theta$ is considered the genuine angle that generates the magnetic spring torque, if it is null the torque on the rotors should be null. It is true only if this configuration ensures always an MMR position, which always happens for all ${\theta }_m$ and ${\theta }_h$ only in the neutral configuration, i.e., when $\alpha =0°$ (known for classical, or non-reconfigurable magnetic couplings). To verify if it occurs for $\alpha \ne 0$, from simulations with the numerical model, the middle curve of Figure 6 shows the torque $T_{h_z}$ when $\theta =0°$ (no spring effect), with ${\alpha }_{max}$, and with ${\theta }_m$ and ${\theta }_h$ increasing together being always equal.

It is possible to see that $T_{h_z}$ is null only if ${\theta }_h={\theta }_m=0(mod\frac{\pi }{2})$, i.e., when the magnets are closest, e.g., as presented in Figure 2 (stable), or in the midway with ${\theta }_h={\theta }_m=\frac{\pi }{4}(mod\frac{\pi }{2})$ (unstable). Out of these points for $\theta =0°$, the Flat-RMCT presents not null torques because rotors are not completely geometrically axisymmetric and the system always tends towards MMR positions. These torque values are extreme for ${\theta }_h={\theta }_m=\frac{\pi }{8}(mod\frac{\pi }{4})$ (since 22.5° is a midpoint between two MMR positions), with a sinusoidal variation which has an amplitude equal to $7.5$ $\mathrm{mNm}$ (for ${\alpha }_{max}$) and argument equal to $4{\theta }_m$ (or $4{\theta }_h$, since $\theta =0°$), due to the four magnets pairs. This torque variation $\Delta T_z(\alpha ,{\theta }_{m\mathrm{or}h})$ can be named auto-driving effect (Equation (3)), which is identical for both rotors when $\theta$ is null, i.e., $T_{m_z}(\theta =0)=T_{h_z}(\theta =0)$ (Equation (4)), driving them in the same direction. Its amplitude is the same for other $\theta$ angles, depending only on $\alpha$, thus named $A_{\Delta T_z}\left(\alpha \right)$. For this condition we can write Equations (3) and (4).

$$\Delta T_z(\alpha ,{\theta }_{m\mathrm{or}h})=-A_{\Delta T_z}\left(\alpha \right)sin\left(4{\theta }_{m\mathrm{or}h}\right)$$

(3)

$$T_{h_z}(\alpha ,0°,{\theta }_h)=T_{m_z}(\alpha ,0°,{\theta }_m)=\Delta T_z(\alpha ,{\theta }_{m\mathrm{or}h})$$

(4)

Figure 6 also shows the propeller torque $T_{h_z}$ for $\theta =\pm 0.5°$. In these cases, besides auto-driving torque $\Delta T_z$, there is also an offset in the mean value (constant amplitude) equal to 11.2 $\mathrm{mNm}$, which is caused by $\theta$ angle, and changes with $\alpha$ as well. This is the expected magnetic spring torque $T_z(\alpha ,\theta )$, which is the most important component in the total magnetic coupling torque, and the only one when coupling parallel axes. This value has opposite signs in $T_{m_z}$ and $T_{h_z}$ since there are the action and the reaction. Moreover, now there is a phase angle equal to $\theta$ between $T_{m_z}$ and $T_{h_z}$ in the $\Delta T_z$ contribution, since now $\theta \ne 0°$ and so ${\theta }_m\ne {\theta }_h$, as they are connected in Equation (1). Performing the same simulations for others $\alpha$ angles and $\theta$ angles, in the operative range $\theta =[-45°,45°]$, it is possible to obtain analytical functions (by regression analysis) to represent $T_{m_z}$ and $T_{h_z}$, depending on ${\theta }_m$ and ${\theta }_h$, with a good accuracy. Therefore, Equation (4) is extended to $\theta$ variations with Equations (5) and (6), which are valid only within this operative range:

$$T_{m_z}(\alpha ,\theta ,{\theta }_m)=-T_z(\alpha ,\theta )-A_{\Delta T_z}\left(\alpha \right)sin\left(4{\theta }_m\right)$$

(5)

$$T_{h_z}(\alpha ,\theta ,{\theta }_h)=T_z(\alpha ,\theta )-A_{\Delta T_z}\left(\alpha \right)sin\left(4{\theta }_h\right)$$

(6)

Equations (5) and (6) have analogous forms, which is natural since rotors are identical. If we want to analyze $T_{m_z}$ and $T_{h_z}$ together according to only one rotation variable (${\theta }_m$, for example), we could rewrite Equation (6) in function of ${\theta }_m$ instead of ${\theta }_h$, leading to

$$T_{h_z}(\alpha ,\theta ,{\theta }_m)=T_z(\alpha ,\theta )-A_{\Delta T_z}\left(\alpha \right)sin\left(4({\theta }_m-\theta )\right)$$

(7)

4.3. Auto-Driving Effect Amplitude Model

Equation (3) models the auto-driving effect $\Delta T_z$. To complete it, Figure 7 shows numerical results for the amplitude $A_{\Delta T_z}$ of $\Delta T_z$. In addition, Equation (8) presents an analytical function, which models the relation $A_{\Delta T_z}\left(\alpha \right)$. This equation is a result of a Wolfram Mathematica function called FindFormula that combines nonlinear regression with optimization algorithms.

In Figure 7 it is possible to see that the auto-driving effect becomes relevant when $\alpha >9°$.

$$A_{\Delta T_z}\left(\alpha \right)=0.002773-2467\alpha +1623sin\left(\alpha \right)+843.5tan\left(\alpha \right)$$

(8)

4.4. Magnetic Spring Effect $T_z$ Results and Model

According to Figure 6 (where $\theta$ is small), it is expected that the spring effect torque $T_z$ values are considerably higher than those related to the auto-driving effect $\Delta T_z$. To obtain them, the adopted model (Equation (6), for example) shows that the magnetic spring torque is equal to the propeller torque for ${\theta }_h=0°$, where ${\theta }_m$ becomes equal to $\theta$: $T_z(\alpha ,\theta )=T_{h_z}(\alpha ,{\theta }_m=\theta )$. Thus, Figure 8 presents the $T_z(\alpha ,\theta )$ simulations with 252 configuration points computed, which are the black dots. Taking into account the coupling symmetry (Section 2), the numerical experiments are performed with $\alpha \in [0°,30.5°]$ and $\theta \in [0°,90°]$. The colored surface is obtained by automatic interpolation, using a Mathematica^TM software function.

Looking from the lower right side ($\theta$ axis) of Figure 8, we see what is presented in Figure 9, and from the lower left side ($\alpha$ axis) what is presented in Figure 10.

It is possible to see that the maximum torques occur when $\theta =45°$ whatever the $\alpha$ angle. For $\theta =0°$ or 90°, $T_z$ is always null.

From the above results, a regression analysis is performed in order to find an analytical function to calculate the magnetic spring torque according to the angles, which is presented in Equation (9), and is valid for $\theta =[-90°,90°]$ and $\alpha =[-{\alpha }_{max},{\alpha }_{max}]$. This $\theta$ range as well as Equation (9) periodicity (equal to $2\theta$) comes from the Flat-RMCT rotors symmetry, since there is a magnet with the same orientation every 180° (Figure 2), as discussed in Section 2.

Table 2. Approximated function parameters.

${\mathit{A}}_{\mathbf{0}}$	${\mathit{A}}_{\mathbf{1}}$	${\mathit{A}}_{\mathbf{2}}$	${\mathit{A}}_{\mathbf{3}}$	${\mathit{B}}_{\mathbf{0}}$	${\mathit{B}}_{\mathbf{1}}$	${\mathit{B}}_{\mathbf{2}}$
14.057	1.1654	14.676	26.306	20.578	14.461	−9.1914

shows the approximated function parameters.

$$T_z(\alpha ,\pm \theta )=\pm \sum _{i=0}^3{A}_i{\left|\alpha \right|}^i\left(B_{0}sin\left(2\right|\theta \left|\right)+\sum _{i=1}^2{B}_i{\left|\theta \right|}^i\right)$$

(9)

Equation (9) was obtained from the magnetic torque analysis according to its periodicity (with respect to $\theta$) and its magnitude (with respect to $\alpha$ and $\theta$), using sinusoidal and polynomial functions. Its parameters were obtained by numerical fitting tools.

Figure 11 shows the error for this approximated magnetic spring torque function compared with numerical results.

The torque approximation error can be considered acceptable since the biggest difference ($5\mathrm{mNm}$ for ${\alpha }_{max}$) represents less than $1\%$ of the maximum magnetic spring torque (around $600\mathrm{mNm}$).

4.5. Restoring Torque $T_{Rest}$

As defined above, the restoring torque $T_{Rest}$ is the static torque that the servomotor must apply to maintain the reconfiguration angle $\alpha$ (Section 2). Figure 12 shows the restoring torque results in function of $\theta$ and $\alpha$ angles, $T_{Rest}(\alpha ,\theta )$.

The restoring torque is extreme for $\theta =0(mod\frac{\pi }{2})$, close to zero for $\theta =\frac{\pi }{4}(mod\frac{\pi }{2})$, and its intensity increases with $\alpha$. For $\alpha =0°$ and for $\theta <45°$ the rotors equilibrium is unstable, since when $\alpha$ changes, the attractive magnetic forces increase this variation. Conversely, when $\theta >45°$ the equilibrium is stable, since the repulsive magnetic forces counteract the variation of $\alpha$. However, for $\theta =45°$ the attractive and repulsive effects are balanced. Moreover, it is important to note that the extreme values of $T_{Rest}$ is around $600\mathrm{mNm}$, which is equivalent to the maximum magnetic spring torque.

5. Discussion

Equations (5) and (6) with Equations (8) and (9) give us the complete model for $T_{m_z}$ and $T_{h_z}$, taking into account magnetic spring and auto-driving effects. With this model, we can study the impact of the auto-driving effect on the rotors torque (when $\alpha >9°$, see Figure 7). In work [18], we assumed that the rotors torque was depending only on the relative position between rotors (i.e., $\theta$) from the well-known magnetic spring effect $T_z\left(\theta \right)$. Now, the auto-driving effect ${\Delta }_{T_z}$ depends on the absolute position of rotors (i.e., ${\theta }_m$ and ${\theta }_h$ in Equations (5) and (6)). The consequence of ${\Delta }_{T_z}$ can be analyzed from the rotors torque absolute difference $|T_{h_z}|-|T_{m_z}|$. 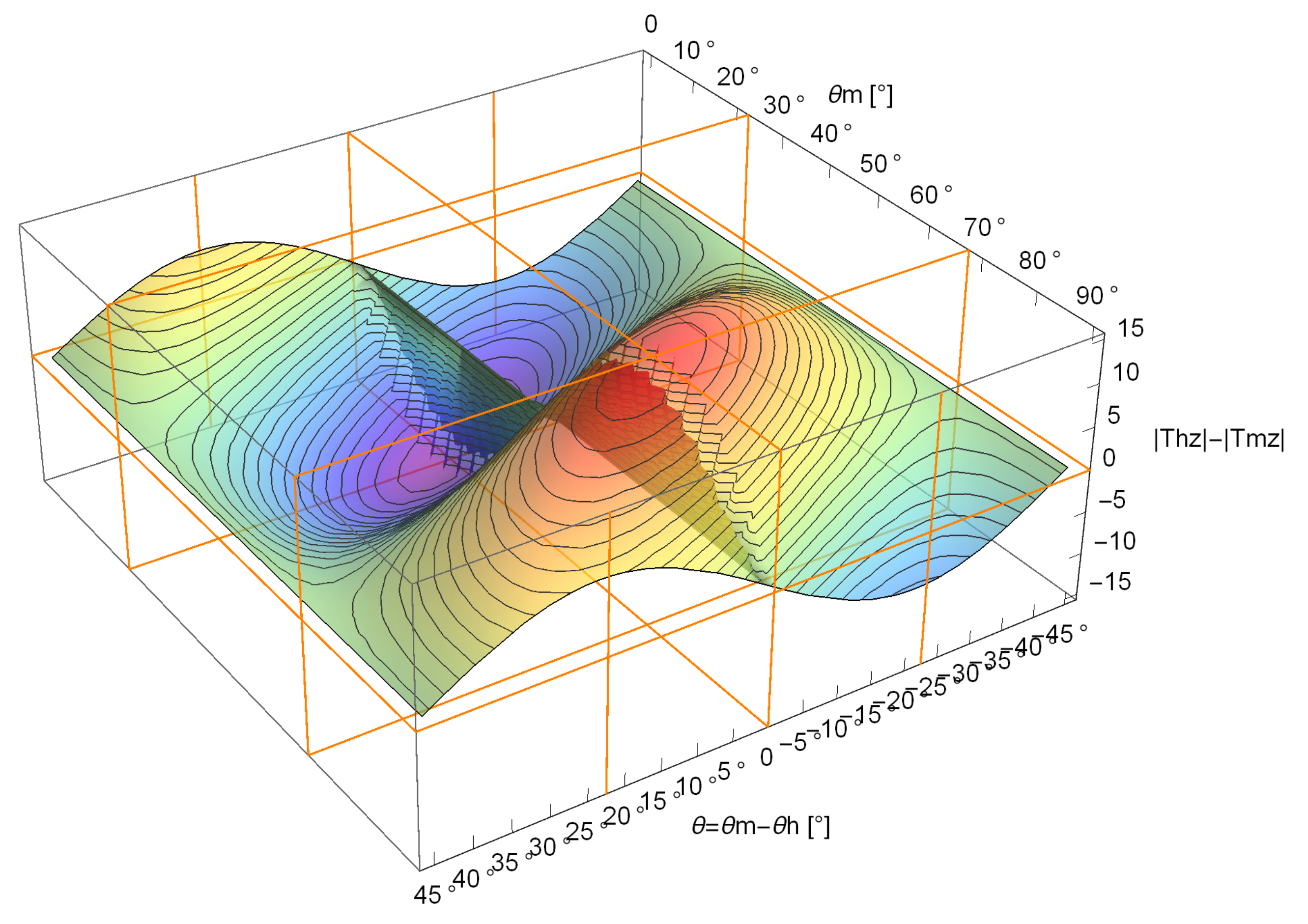Figure 13 shows it for ${\alpha }_{max}$, in the $\theta$ operative range and for one cycle of ${\theta }_m$. Firstly, we see that the difference has an oscillatory behavior according to $\theta$ and ${\theta }_m$, it is equal to zero for $\theta =0°$ and decreases when $\theta$ tends towards $\pm 45°$.

Looking into Equations (5) and (6) it is possible to see that $|T_{m_z}|$ is equal to $|T_{h_z}|$ if ${\theta }_m=-{\theta }_h$, where the symmetrical rotors have their magnets oppositely equidistant from the symmetric plan. It happens also for other ${\theta }_m$ and ${\theta }_h$ when $sin\left(4{\theta }_m\right)=-sin\left(4{\theta }_h\right)$. This observation has been verified with the numerical model. For example, for ${\theta }_m=10°$ and ${\theta }_h=-10°$ ($\theta =20°$) the simulation results are $T_{m_z}=-398.3\mathrm{mNm}$ and $T_{h_z}=398.4\mathrm{mNm}$. In addition, for ${\theta }_m=55°$ and ${\theta }_h=35°$ (also with $\theta =20°$ but with ${\theta }_m$ and ${\theta }_h$ shifted by 45°) the simulation results are $T_{m_z}=-387.8\mathrm{mNm}$ and $T_{h_z}=387.7\mathrm{mNm}$. In both cases we can consider that $|T_{m_z}|=|T_{h_z}|$, since $0.1\mathrm{mNm}$ is the torque calculation error of our numerical model. It validates our analytical model.

Still noting in Equations (5) and (6) that auto-driving and magnetic spring effects have same signs for $T_{m_z}$ and opposite ones for $T_{h_z}$, the biggest difference between $|T_{h_z}|$ and $|T_{m_z}|$ ($15.1\mathrm{mNm}$, see Figure 13) happens when the auto-driving effect absolute value is maximum and equal to the magnetic spring effect absolute value $|{\Delta }_{T_z}|=|T_z|=7.55\mathrm{mNm}$. We have observed it for a small magnetic spring angle $\theta =\pm 0.342°$, with ${\theta }_m=\frac{\pi }{8}(mod\frac{\pi }{4})+\frac{\theta }{2}$. We have compared this analytical model result with simulations. Where for $\theta =0.342°$ the analytical model gives us $T_{m_z}=-15.1\mathrm{mNm}$ and $T_{h_z}=0\mathrm{mNm}$, simulations give $T_{m_z}=-15.2\mathrm{mNm}$ and $T_{h_z}=0.12\mathrm{mNm}$. The difference of $0.1\mathrm{mNm}$ is again equal to the torque calculation error of our numerical model. It also validates our analytical model.

Normally, a difference of $15.1\mathrm{mNm}$ between motor and propeller side rotors should not be a problem. For example, if we consider that the coupling is working with ${\alpha }_{max}$ and with $80\%$ of its torque transmission capacity (i.e., $480\mathrm{mNm}$ with $\theta =26.3°$—see Figure 9), $15.1\mathrm{mNm}$ means only $3.1\%$ of the transmitted torque. $80\%$ is considered since the magnetic coupling should be designed to work close to the maximum transmissible torque, to be able to uncouple in case of load peak.

Recently, we have proposed a new reconfigurable magnetic coupling [17], which is at least geometrically axisymmetric (i.e., composed by arc shaped magnets), tending to remove the auto-driving effect.

6. Conclusion and Perspectives

A detailed presentation and static torque analysis was performed on a Flat-RMCT, making possible to understand its complex and intrinsic behavior. This was possible from numerical and analytical models that were validated with experiments using the prototype.

Besides the expected rotational magnetic spring effect (common in parallel axes coupling), it was identified another effect due to non-completely axisymmetric rotors. This effect implies an auto-driving torque (oscillatory) in the system and can make motor and propeller torques different when the magnetic spring angle in non-null. The auto-driving effect is small in comparison to the magnetic spring effect ($3\%$ when transmitting a torque with a value equal to $80\%$ of the maximum magnetic coupling capacity). However, this effect is important at low-load conditions. Finally, it was explored the restoring torque necessary to keep the propeller orientation angle, which is especially important for the control of the Flat-RMCT. The maximum restoring torque for this Flat-RMCT is considered high compared to the maximum transmissible torque ($600\mathrm{mNm}$ for both).

Next steps include the use of the improved torque model in a more accurate vectorial thruster dynamic model.