Hybrid Model Predictive Control Strategy of Supercapacitor Energy Storage System Based on Double Active Bridge
Abstract
:1. Introduction
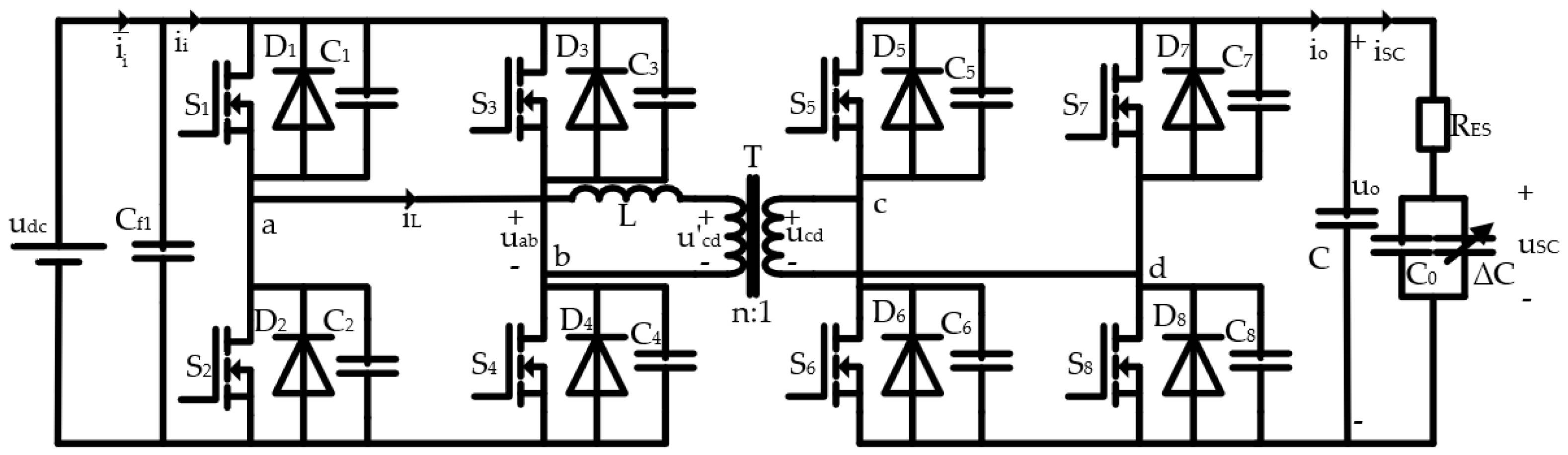
2. Working Principle of the DAB-SC System
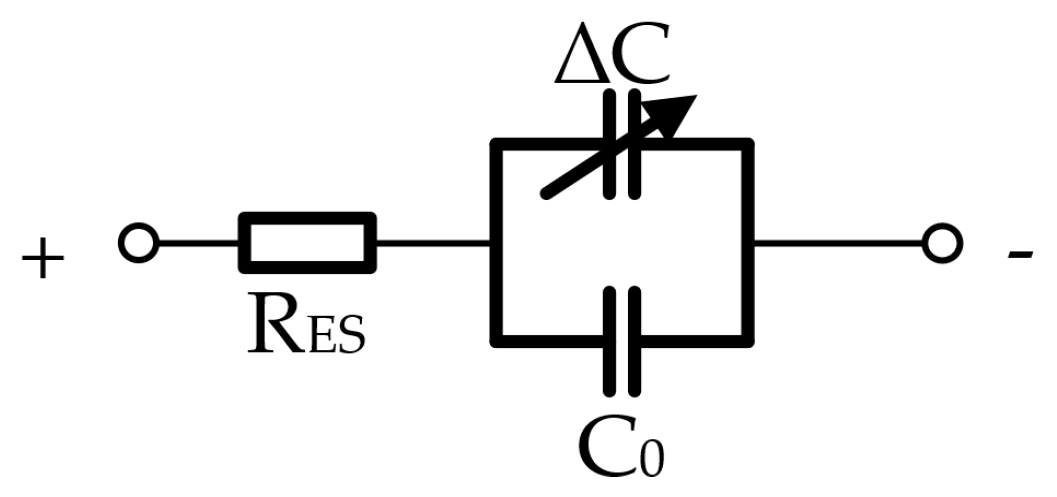
2.1. SC Model
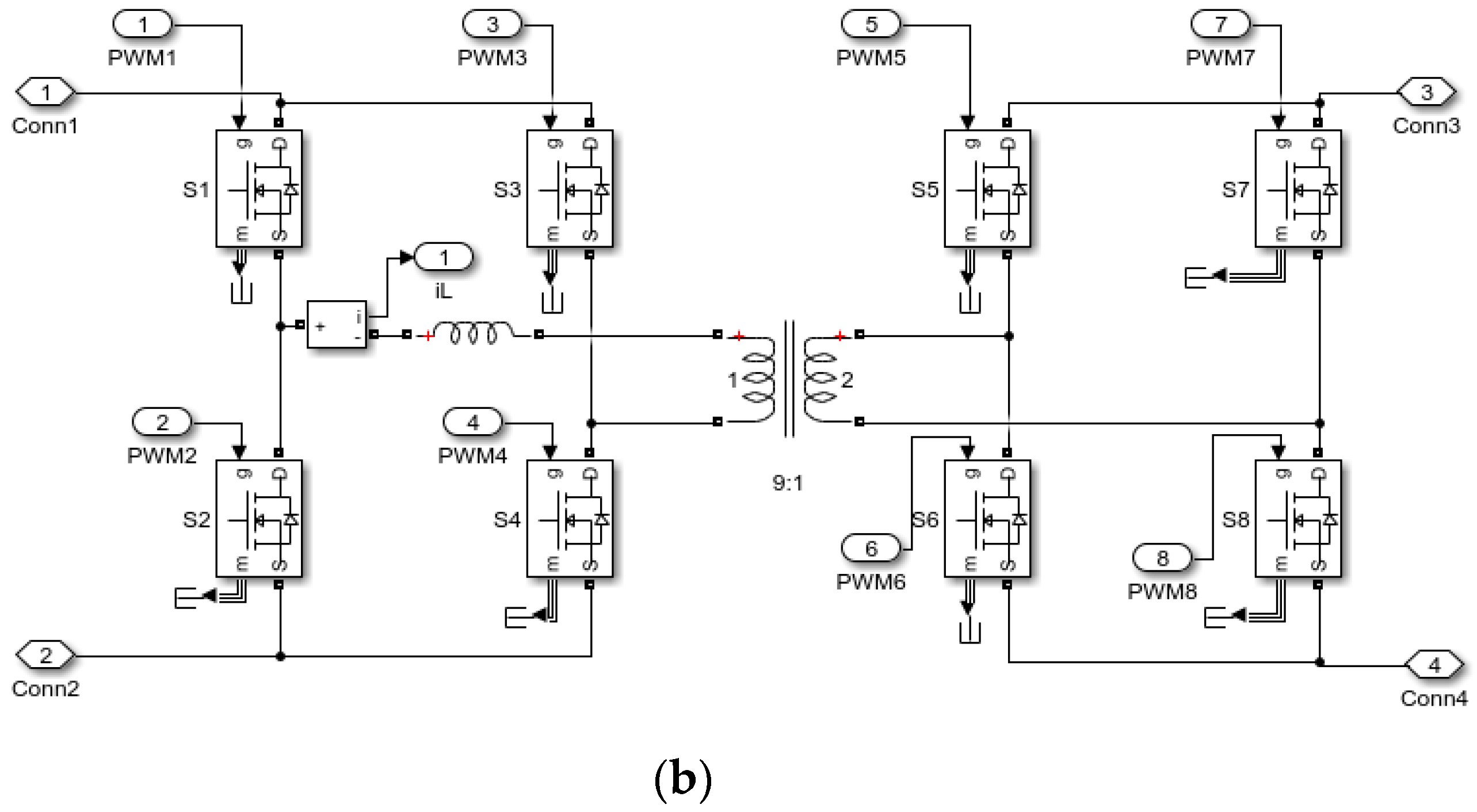
2.2. Principle Analysis of DAB
2.3. State Space Average Model of DAB-SC
3. Management Strategy
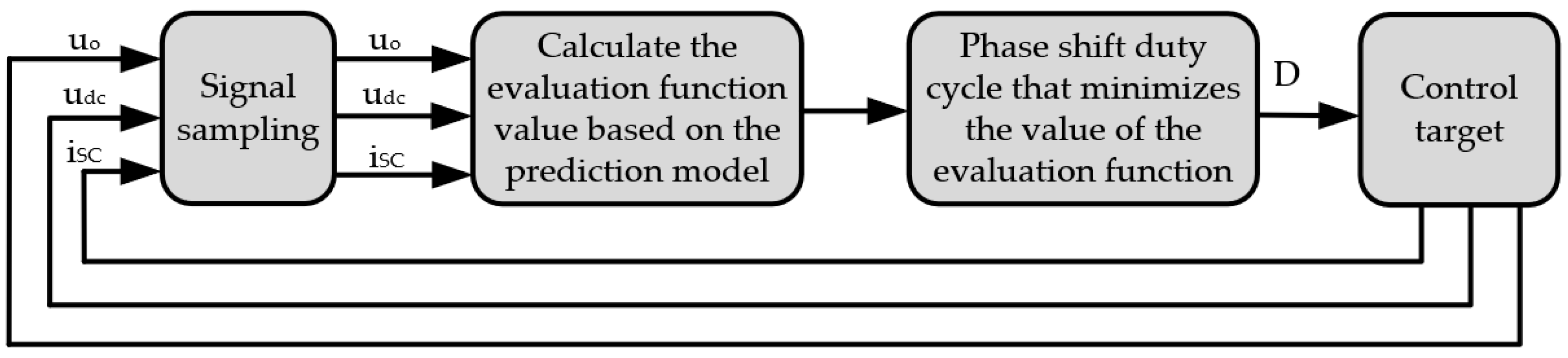
4. Model Predictive Control
4.1. Establishment of the Prediction Model for the DAB-SC System
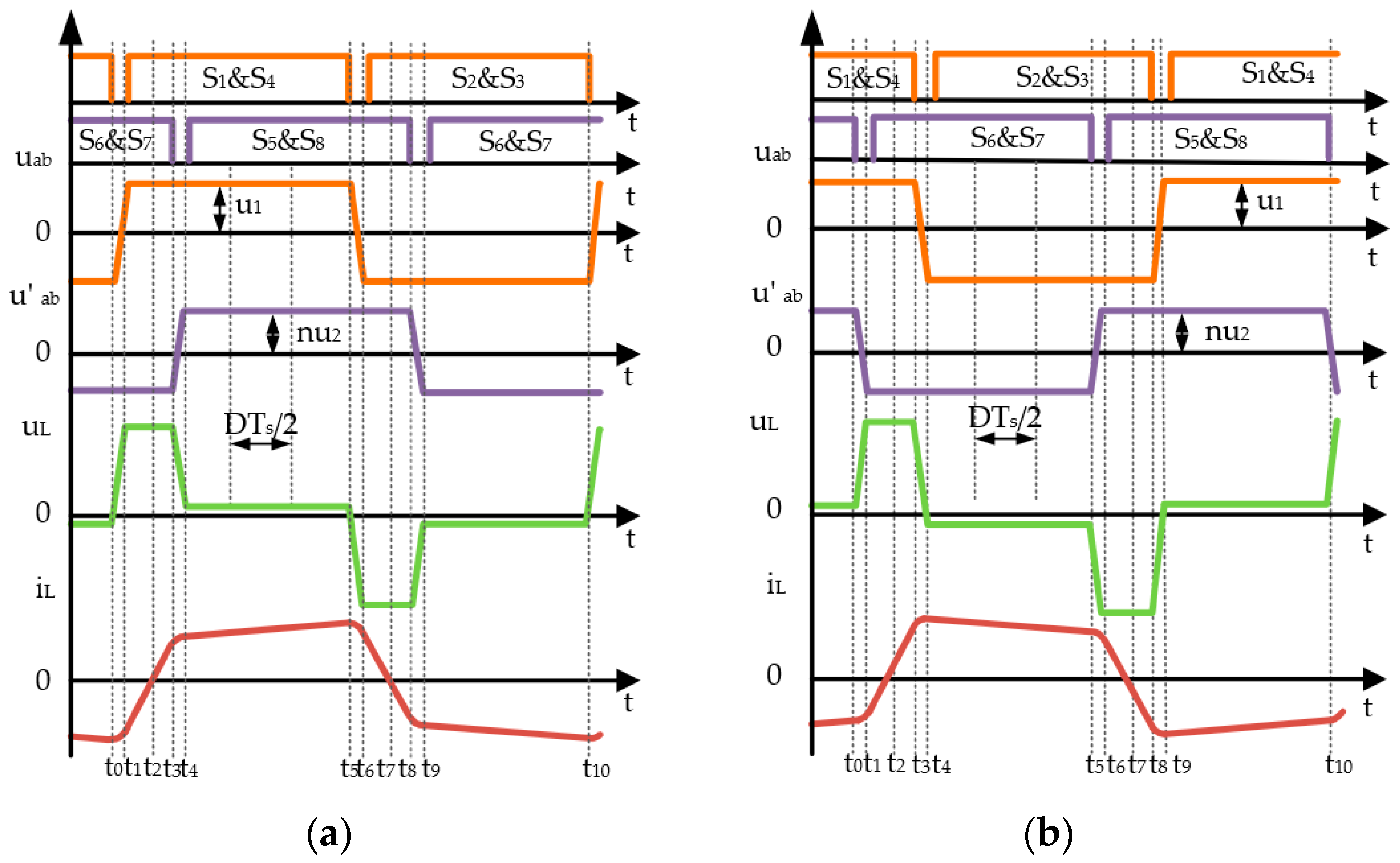
4.2. Phase Shift Optimization Calculation and Analysis
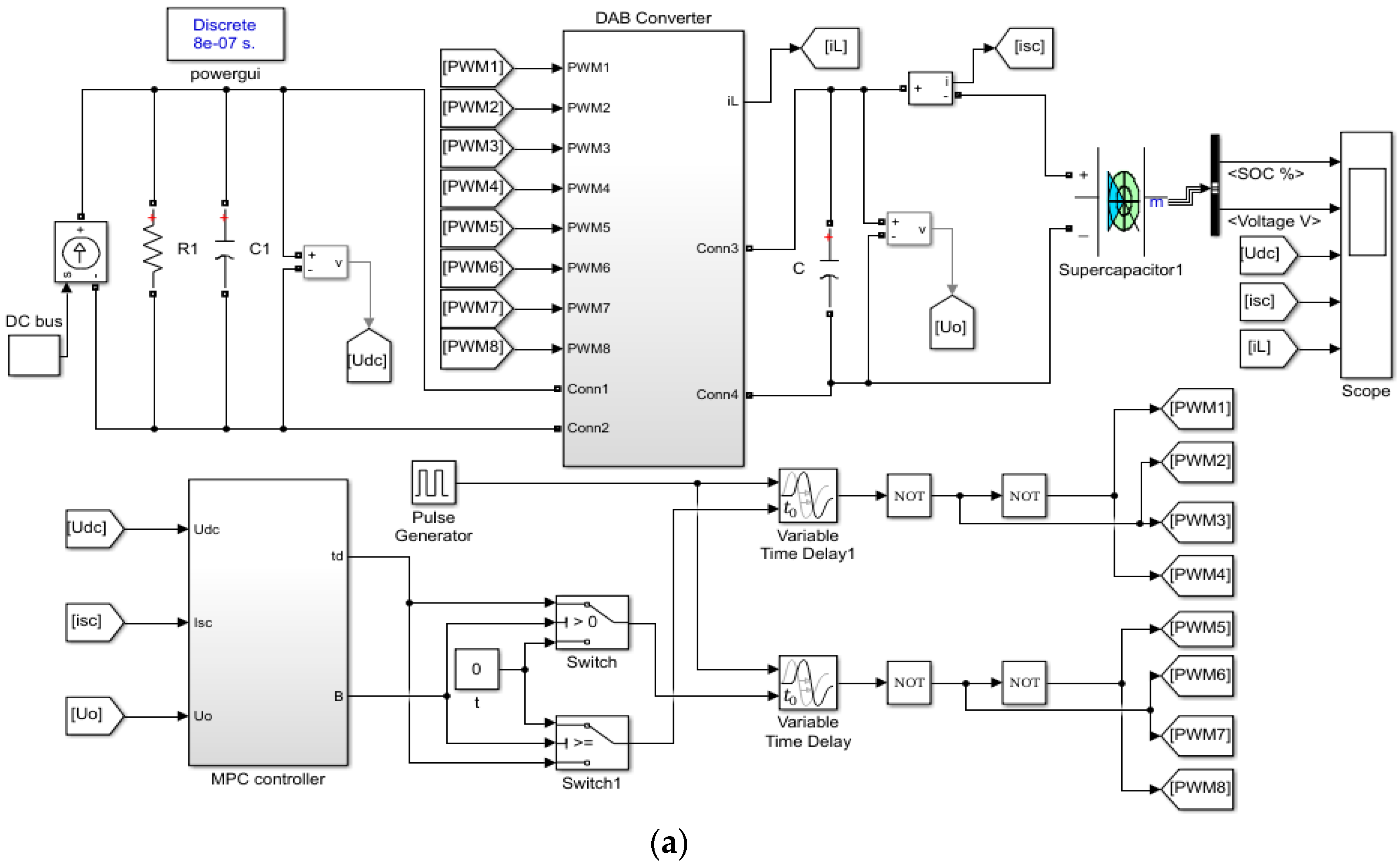
5. Simulation Analysis
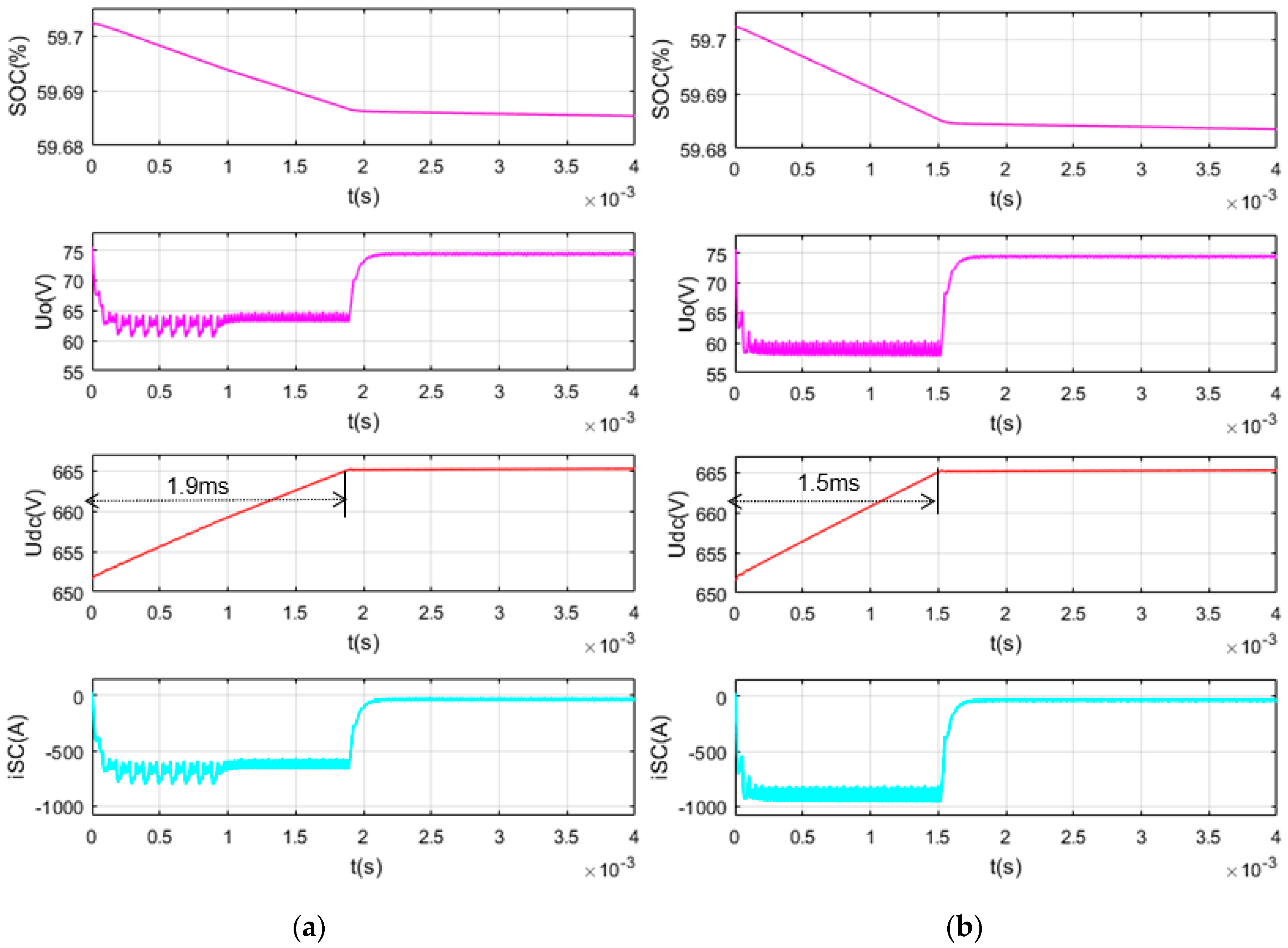
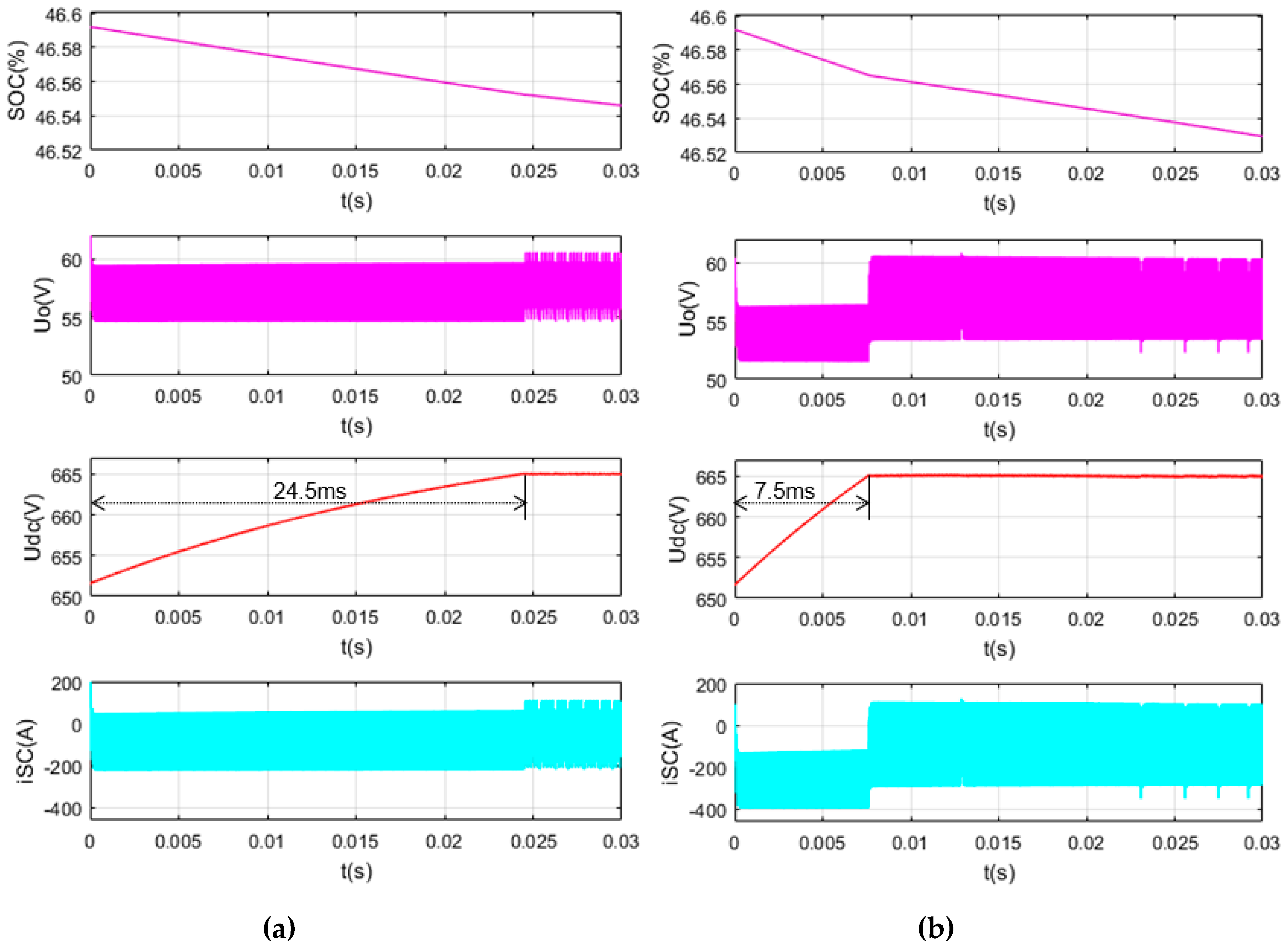
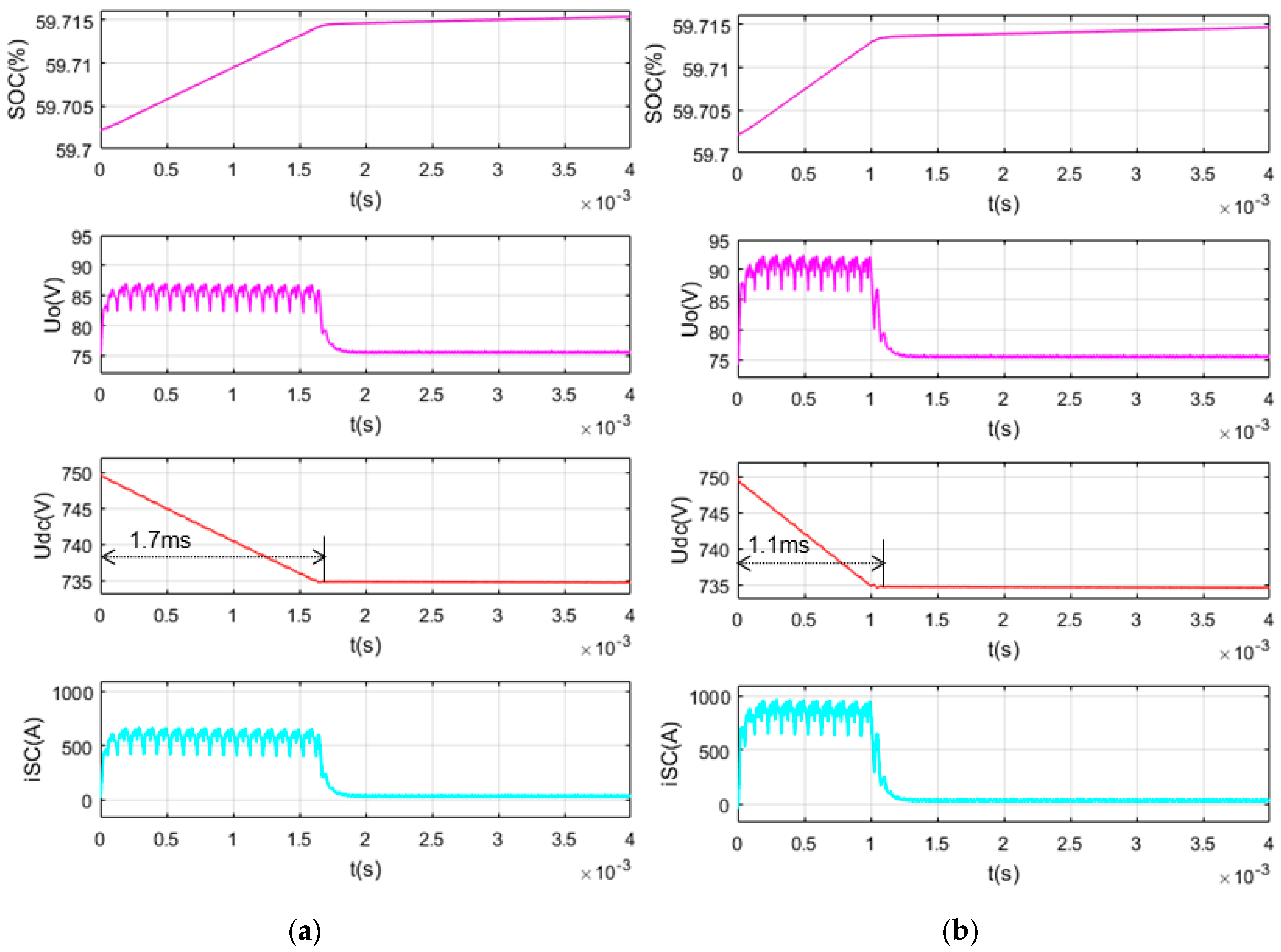
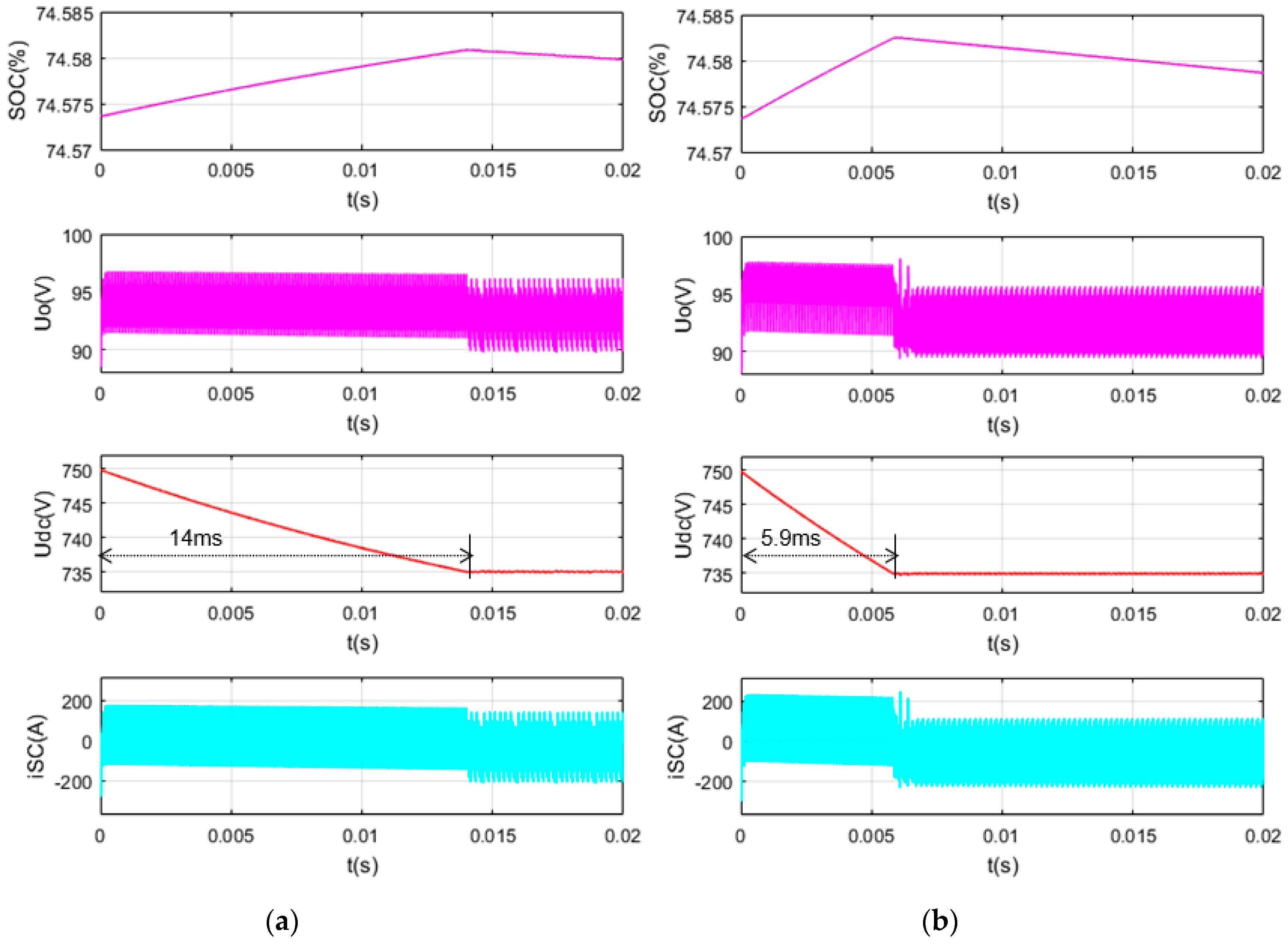
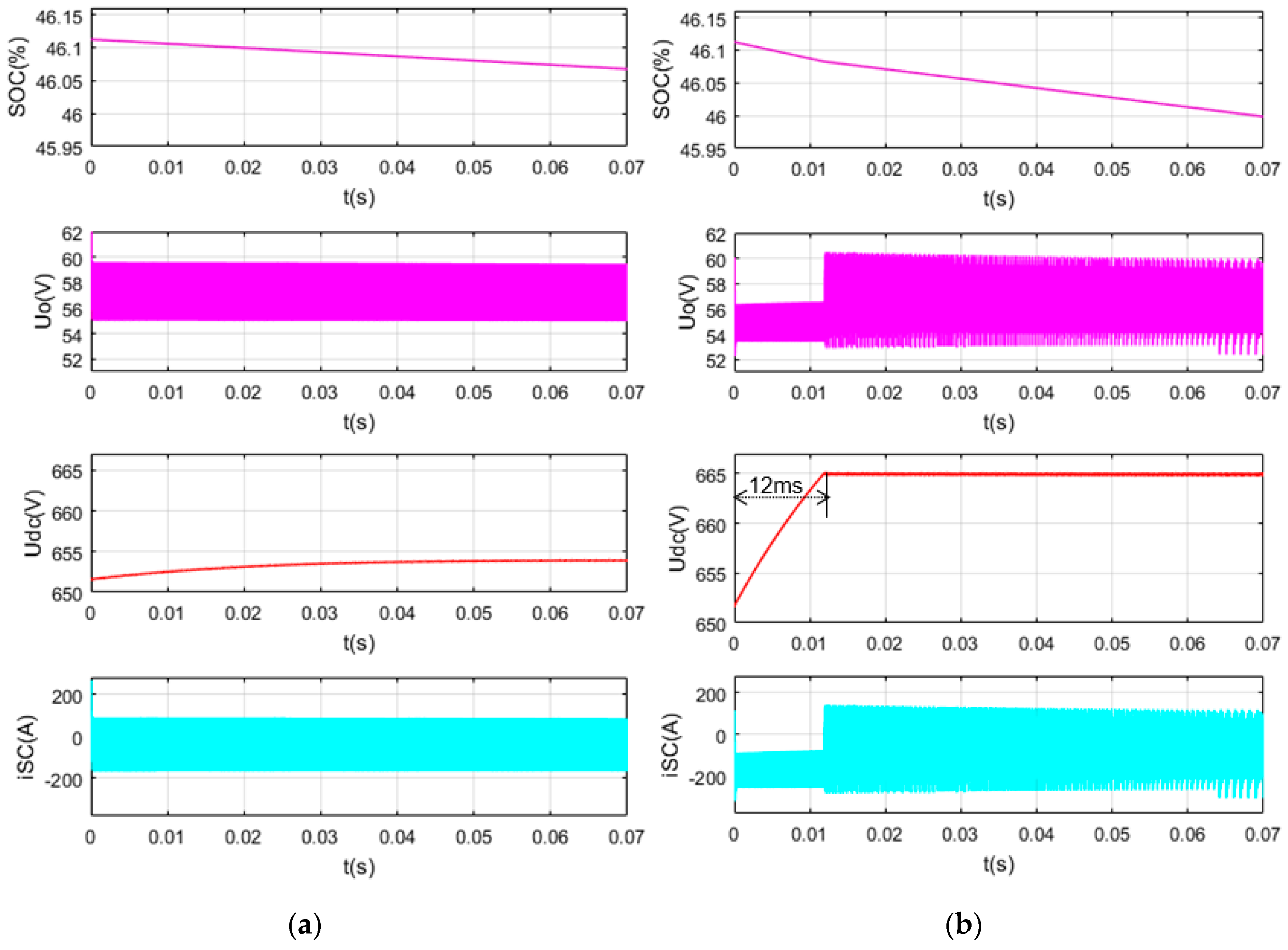
5.1. SC Discharge in the Normal Working Range
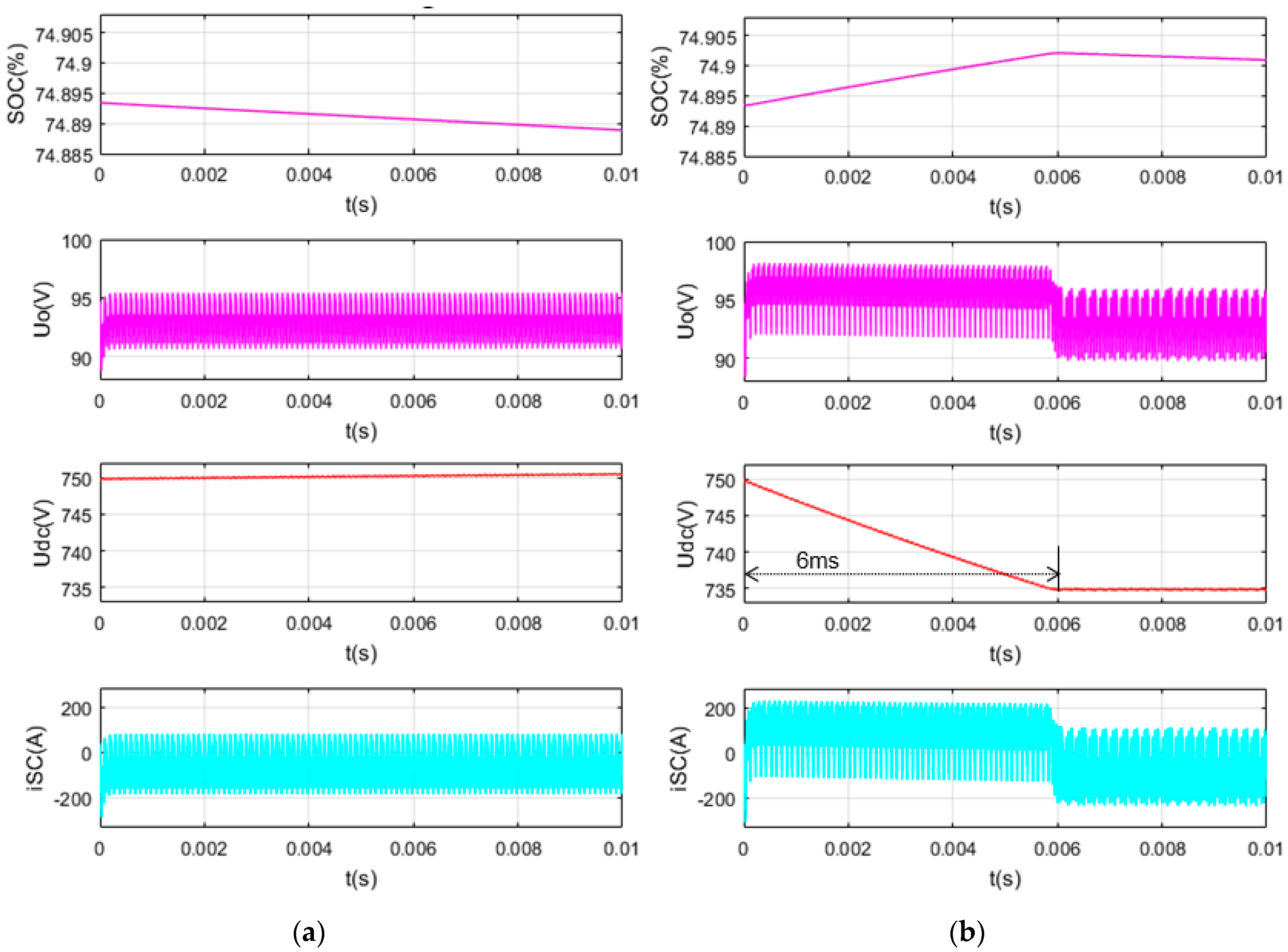
5.2. SC Charge in the Normal Working Range
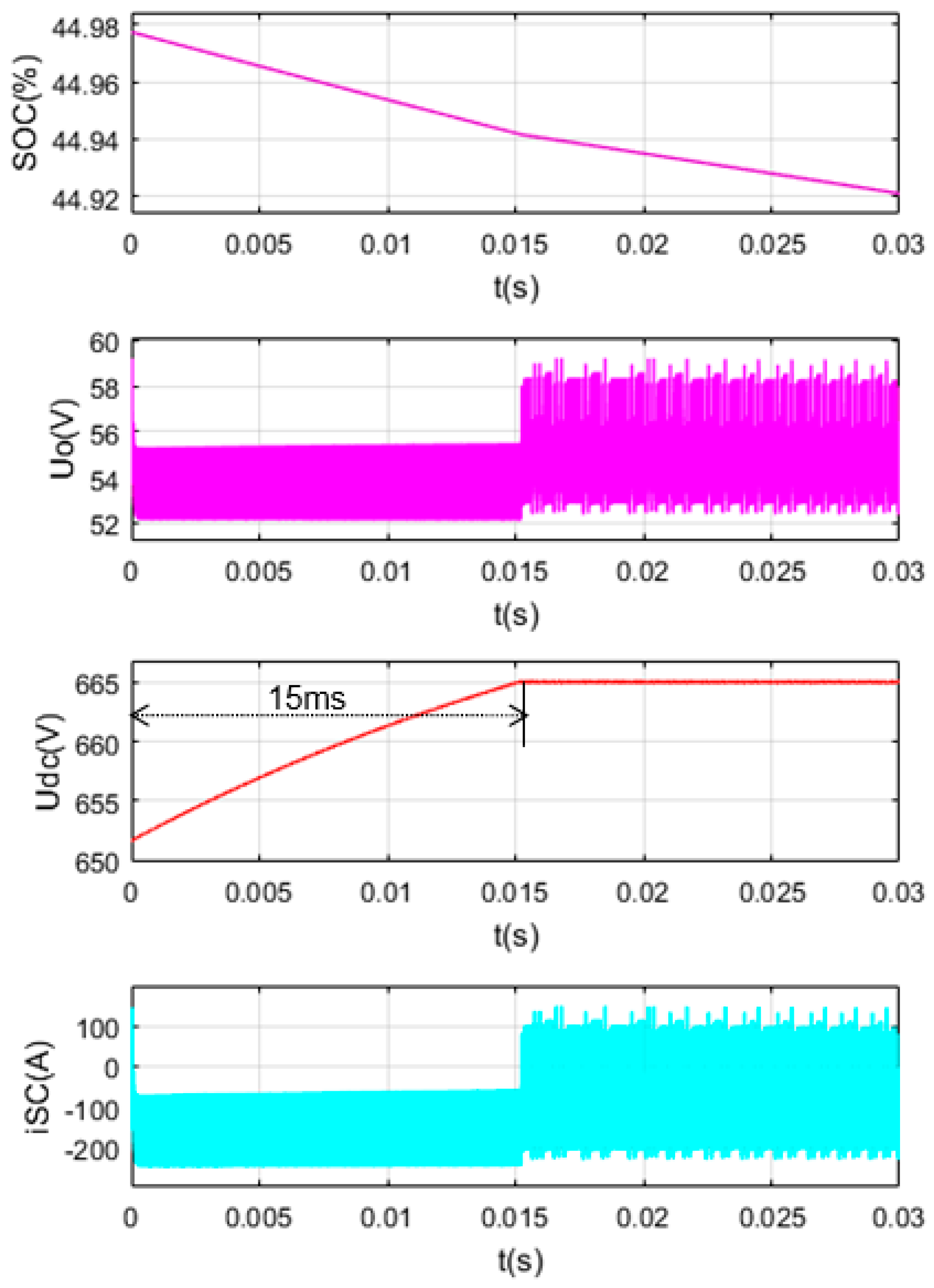
5.3. SC Discharge Closer to the Lower Limit
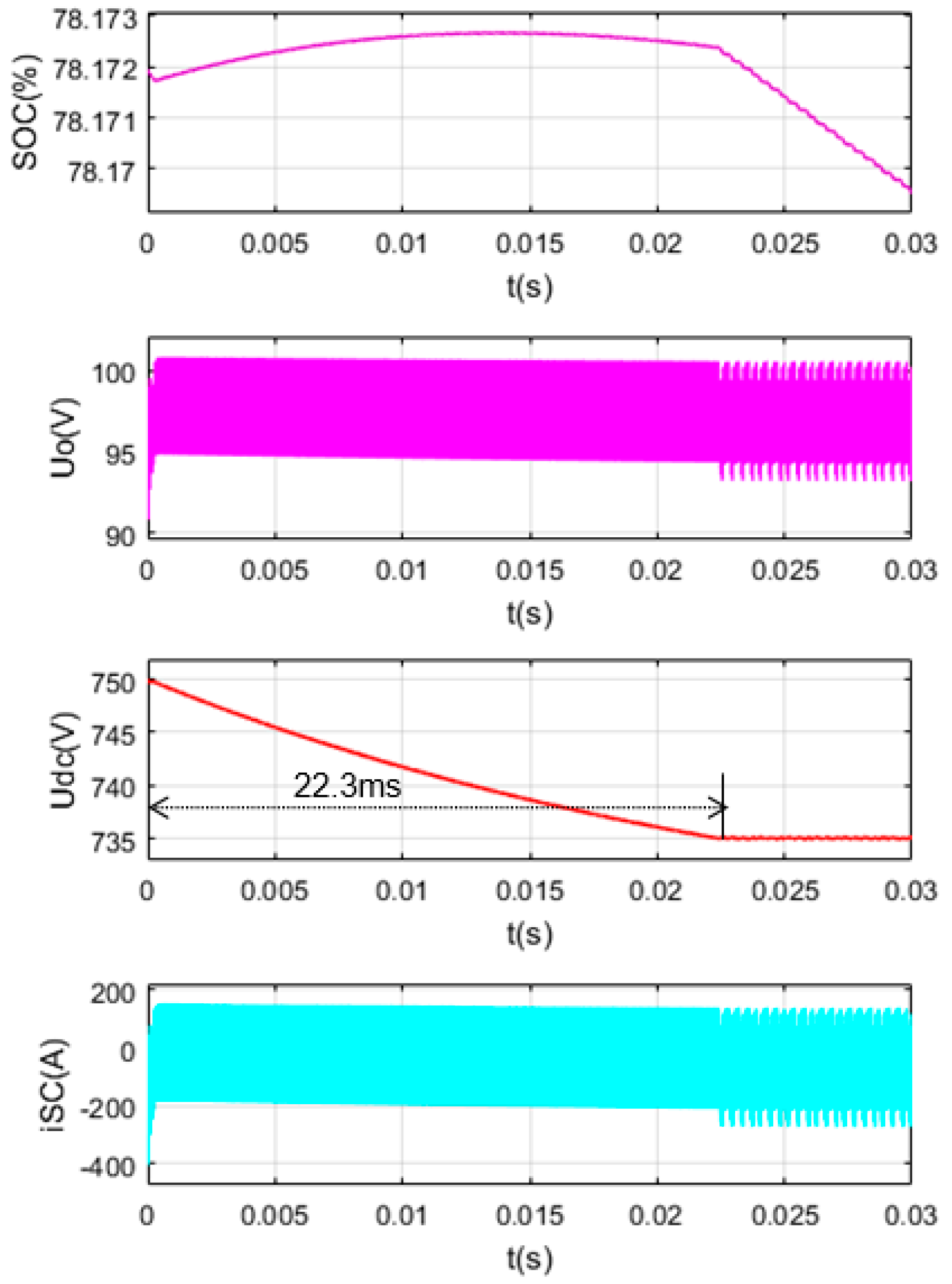
5.4. SC Charge Closer to the Upper Limit
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviation
| SC | Supercapacitor |
| DAB | Dual active bridge |
| RC | Resistor-capacitor |
| ANN | Artificial neural network |
| DC | Direct current |
| ZVS | Zero voltage switch |
| AC | Alternative current |
| MPC | Model predictive control |
| SOC | State of charge |
Appendix A
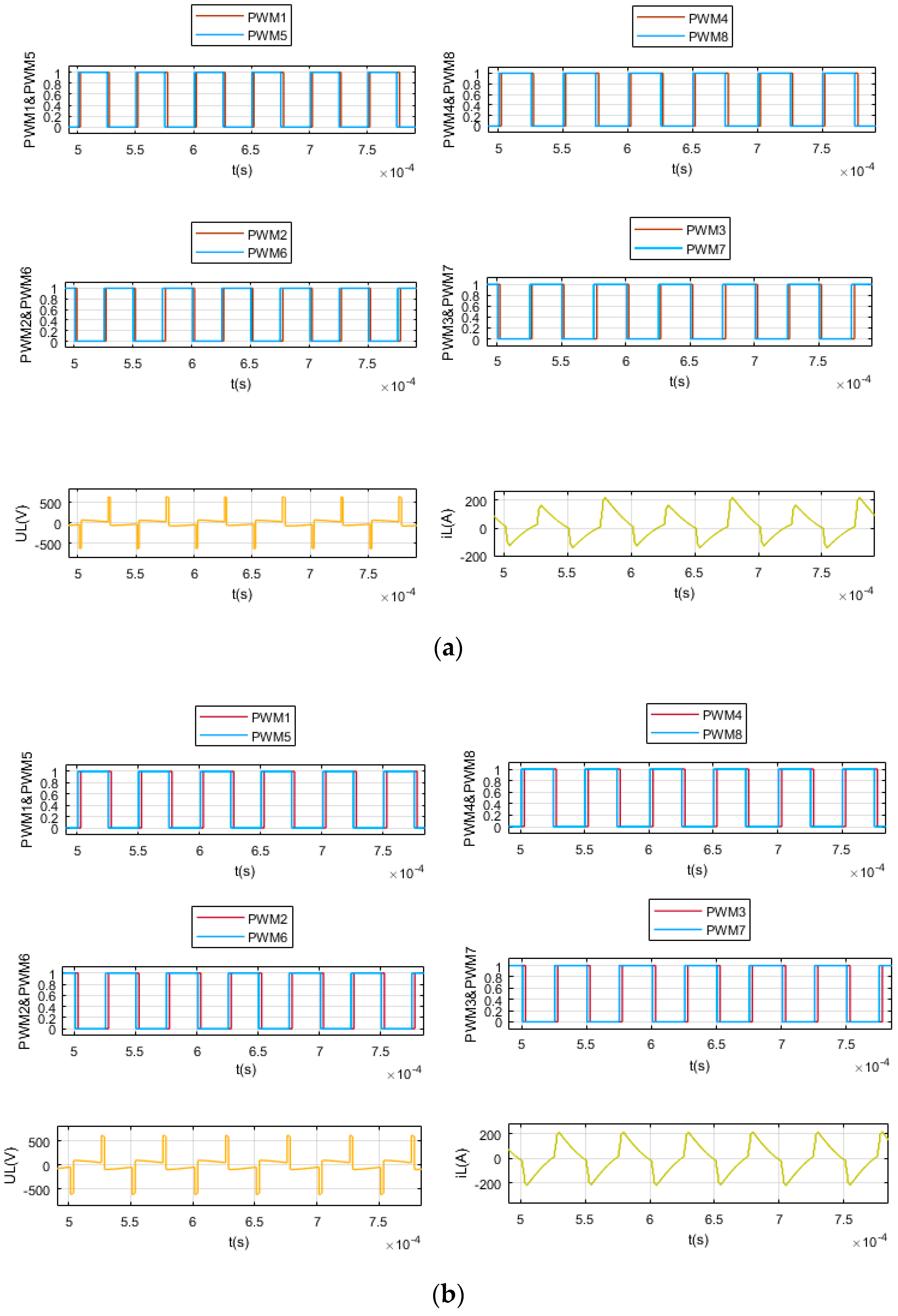
Appendix B
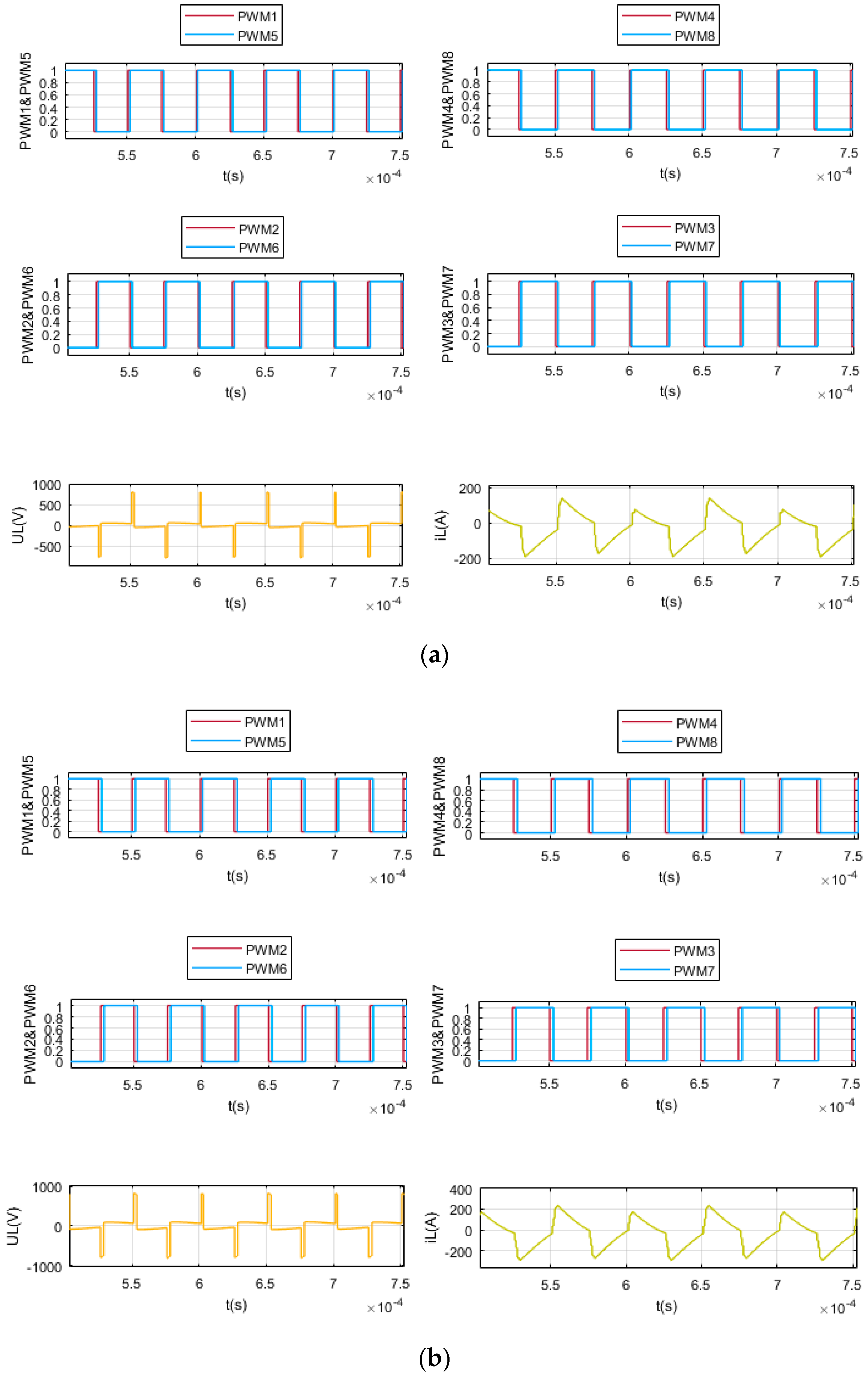
References
- Liu, J.; Zhang, L. Strategy Design of Hybrid Energy Storage System for Smoothing Wind Power Fluctuations. Energies 2016, 9, 991. [Google Scholar] [CrossRef]
- Wang, L. Research of Converter Topology Based on Super Capacitor Energy Storage System. Electron. Des. Eng. 2018, 26, 29–133. [Google Scholar]
- Xun, Q.; Wang, P.; Quan, L.; Xu, Y. Voltage Balancing Strategy Based on Cooperative Control for Super Capacitor. Power Electron. 2017, 51, 113–116. [Google Scholar]
- Han, W.; Huang, S.; Dai, Q.; Wan, J. Modeling and Simulation of an Elevator Energy-saving System Based on Isolated Bidirectional DC/DC Converter. Electr. Autom. 2015, 37, 7–9. [Google Scholar]
- Lv, X.; Liu, C.; Wang, Y.; Li, Z. Research of Bidirectional DC-DC Converter in Distributed Wind-photovoltaic-storage System. Electr. Meas. Instrum. 2017, 54, 16–20, 41. [Google Scholar]
- Choi, W.; Rho, K.M.; Cho, B.H. Fundamental Duty Modulation of Dual-Active-Bridge Converter for Wide Range Operation. IEEE Trans. Power Electron. 2016, 31, 4048–4064. [Google Scholar] [CrossRef]
- Sha, D.; Wang, X.; Chen, D. High Efficiency Current-Fed DAB DC–DC Converter with ZVS Achievement throughout Full Range of Load Using Optimized Switching Patterns. IEEE Trans. Power Electron. 2018, 33, 1347–1357. [Google Scholar] [CrossRef]
- Takagi, K.; Fujita, H. Dynamic Control and Performance of a Dual-Active-Bridge DC-DC Converter. IEEE Trans. Power Electron. 2018, 33, 7858–7866. [Google Scholar] [CrossRef]
- Yi, L.; Chen, Y.; Zhang, H.; Guo, Z. Unified Control for Mode Swap of Bidirectional DC/DC Converter in Distributed Generation System. Power Electron. 2017, 51, 4–7. [Google Scholar]
- Oggier, G.; Ordonez, M.; Galvez, J.; Luchino, F. Fast Transient Boundary Control and Steady-state Operation of the DAB Converter Using the Natural Switching Surface. IEEE Trans. Power Electron. 2014, 29, 946–957. [Google Scholar] [CrossRef]
- Hou, N.; Song, W.; Wu, M. A Load Current Feedforward Control Scheme of DAB DC/DC Converters. Proc. Csee 2016, 36, 2478–2485. [Google Scholar]
- Song, W.; Hou, N.; Wu, M. Virtual Direct Power Control Scheme of DAB DC-DC Converters for Fast Dynamic Response. IEEE Trans. Power Electron. 2018, 33, 1750–1759. [Google Scholar] [CrossRef]
- Yang, K.; Song, W.; An, F.; Hou, N. Rapid Dynamic Response Control Method of Dual-active-bridge DC-DC Converters in Current Source Mode. Proc. Csee 2018, 38, 2439–2447, S23. [Google Scholar]
- An, F.; Song, W.; Yang, K. Model Predictive Control and Power Balance Scheme of Dual-active-bridge DC-DC Converters in Power Electronic Transformer. Proc. Csee 2018, 38, 3921–3929, S22. [Google Scholar]
- Wang, X.; Han, M.; Gao, F.; Wang, M.; Wang, K. A Review of Modeling in New Energy Research on Super-capacitor. World Power Supply 2016, 1, 37–40, S28. [Google Scholar]
- Yu, P.; Jing, T.; Yang, R. Capacitance Measurement and Parameter Estimation Method for SCs with Variable Capacitance. Trans. Chin. Soc. Agric. Eng. 2016, 32, 169–174. [Google Scholar]
- Hu, B.; Yang, Z.; Lin, F.; Zhao, K.; Zhao, Y. Equivalent Circuit Model of Super Capacitor Group for Urban Rail Transit Application. Electr. Drive Locomot. 2013, 5, 65–68, 74. [Google Scholar]
- Feng, J.; Xu, F.; Li, L.; Qin, Y.; Shi, X. Capacitance Measurement of SCs Based on Discharge Procedure with Constant Load. Electron. Compon. Mater. 2016, 35, 88–91. [Google Scholar]
- Yuan, X. A Research on Phase-shift-control of the Full-bridge-isolated DC/DC Converter. Electr. Autom. 2017, 39, 7–10. [Google Scholar]
- Kan, J.; Wu, Y.; Xie, S.; Tang, Y.; Xue, Y.; Yao, Z.; Zhang, B. Dual-active-bridge Bidirectional DC/DC Converter Based on High-frequency AC Buck-Boost Theory. Proc. Csee 2017, 37, 1797–1807, S24. [Google Scholar]
- Xue, Y.; Zhou, J.; Cui, Y. Simulation Research on Coordinated Control Strategy of Hybrid Energy Storage Based on DC Microgrid. Electr. Mach. Control Appl. 2017, 44, 19–25, 37. [Google Scholar]

| Symbol | Quantity |
|---|---|
| fs | 20 kHz |
| Udc | 700 V |
| C | 3 × 10−3 F |
| L | 6.815 × 10−6 H |
| n | 9 |
| RES | 0.018 Ω |
| Kv | 0.1127 |
| C0 | 81.384 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Guo, J.; Xu, C.; Wu, T.; Lin, H. Hybrid Model Predictive Control Strategy of Supercapacitor Energy Storage System Based on Double Active Bridge. Energies 2019, 12, 2134. https://doi.org/10.3390/en12112134
Wang L, Guo J, Xu C, Wu T, Lin H. Hybrid Model Predictive Control Strategy of Supercapacitor Energy Storage System Based on Double Active Bridge. Energies. 2019; 12(11):2134. https://doi.org/10.3390/en12112134
Chicago/Turabian StyleWang, Lujun, Jiong Guo, Chen Xu, Tiezhou Wu, and Huipin Lin. 2019. "Hybrid Model Predictive Control Strategy of Supercapacitor Energy Storage System Based on Double Active Bridge" Energies 12, no. 11: 2134. https://doi.org/10.3390/en12112134
APA StyleWang, L., Guo, J., Xu, C., Wu, T., & Lin, H. (2019). Hybrid Model Predictive Control Strategy of Supercapacitor Energy Storage System Based on Double Active Bridge. Energies, 12(11), 2134. https://doi.org/10.3390/en12112134




