Representation of Balancing Options for Variable Renewables in Long-Term Energy System Models: An Application to OSeMOSYS
Abstract
1. Introduction
1.1. Literature Background
1.2. Scope and Structure of the Paper
2. Materials and Methods
- Energy balances;
- Capacity balances;
- Storage balances;
- Reserve balances and operational constraints;
- Computation of emissions;
- Computation of costs.
- The configuration of OSeMOSYS as a linear program restricts the possible code modifications to linear formulations;
- Given that the models created through OSeMOSYS are, in most cases, regional or national, the spatial resolution is coarse. Therefore, in this case the authors will not talk about capacity of a technology referring to single power plants, but rather to the cumulative installed capacity of a family of similar power plants (such as CCGTs, coal fired steam cycles, photovoltaic, etc.). This capacity is allowed to vary continuously, as if small power plants could be installed.
2.1. Cost of the Starts
2.2. Cost of Fuel at Partial Load Operation
2.3. Refurbishment Option
- The first set of constraints defines the withdrawn capacity of the old version of the technology as the sum of the one fictitiously retired to be replaced by the refurbished capacity, and the one actually decommissioned;
- The second set of constraints defines the refurbished capacity as a capacity of the new technology equalling that of the old technology that is fictitiously retired;
- Finally, the third set of constraints only consists of a number of equations of the original code, updated to account for the refurbished capacity and the cost of the refurbishment.
2.4. Test Case Study
- REF: a reference scenario where no target is imposed.
3. Results and Discussion
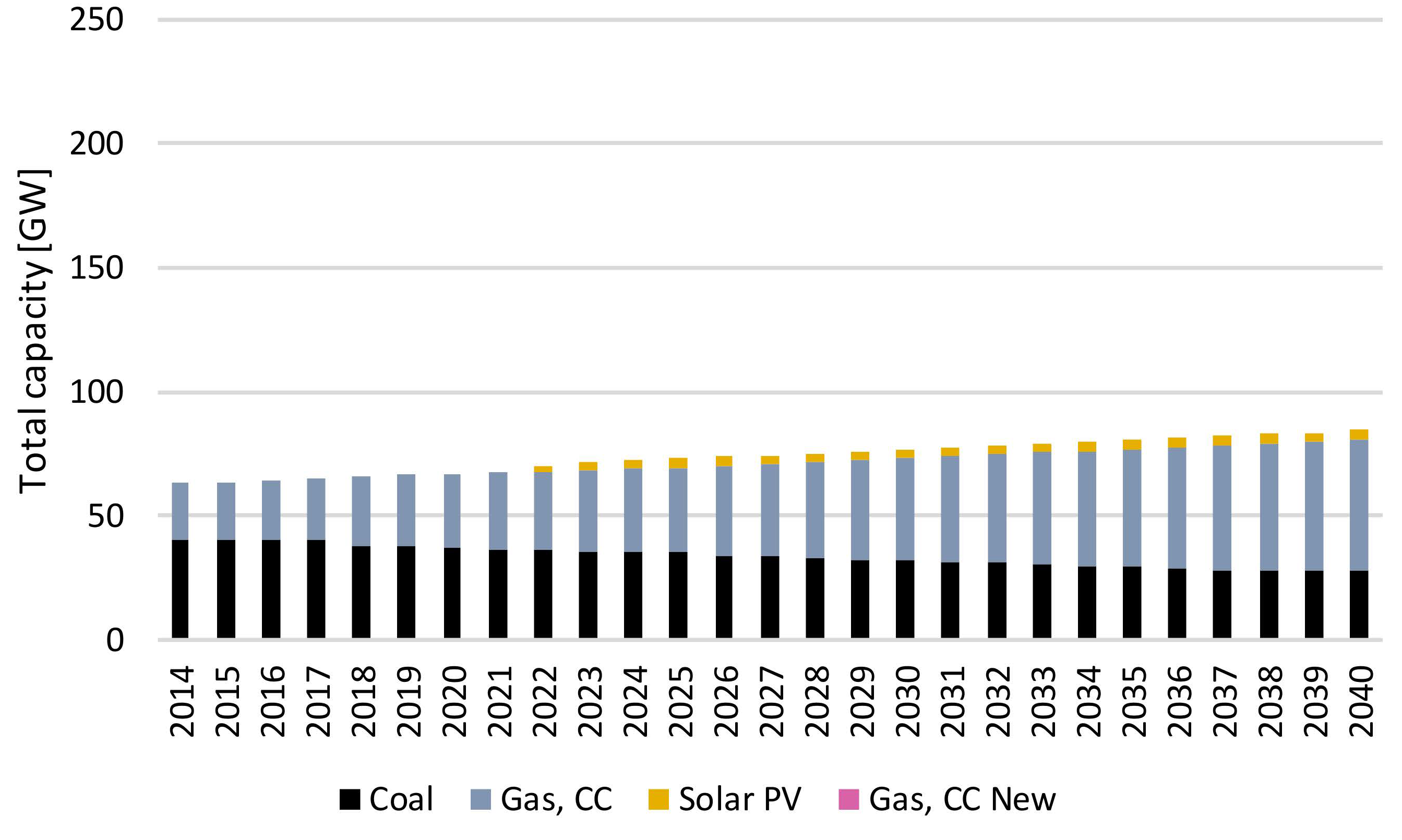
3.1. Without Code Modifications
3.2. With Code Modifications
4. Conclusions
- They are highly accessible to the modelling community, including non-expert modellers: they are open source licensed, documented at several levels (plain description, algebraic formulation, and code) and explained step by step in the supplementary materials. This contributes to the establishment of standards for the development of an open source modelling tool and the creation of benchmarks. Building on practices initiated in previous studies, it provides a proof of concept for open source incremental changes to OSeMOSYS, including code and model documentation, licenses, and metadata, and a retrievable, reproducible, reusable, interoperable, and auditable case study.
- They are simple to use: they consist of a limited number of additional equations and input parameters, thus requiring minimum additional effort on the user’s side regarding their integration into a model.
- They are linear: yet they allow the introduction of non-linear behaviour, such as when modelling the cost of fuel at partial load operation (see Figure 1 and Equation (6)). This enables a realistic representation with limited computational requirements.
supplementary materials
Author Contributions
Funding
Conflicts of Interest
Acronyms and Nomenclature
| NGCC | Natural Gas Combined Cycle |
| Coal PP | Coal Power Plants |
| RES | Reference Energy System |
| WN | Winter night |
| WM | Winter morning |
| WA | Winter afternoon |
| WE | Winter evening |
| SN | Spring night |
| SM | Spring morning |
| SA | Spring afternoon |
| SE | Spring evening |
| SuN | Summer night |
| SuM | Summer morning |
| SuA | Summer afternoon |
| SuE | Summer evening |
| AN | Autumn night |
| AM | Autumn morning |
| AA | Autumn afternoon |
| AE | Autumn evening |
| REF | Reference scenario |
| RETarget | Renewable Energy Target scenario |
References
- European Commission. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee, the Committee of the Regions and the European Investment Bank on ’A Framework Strategy for a Resilient Energy Union with a Forward-Looking Climate Change Policy; European Commission: Brussels, Belgium, 2015. [Google Scholar]
- International Energy Agency (IEA). World Energy Outlook 2017; International Energy Agency (IEA): Paris, France, 2017. [Google Scholar]
- International Renewable Energy Agency. Renewable Power Generation Costs in 2017; International Renewable Energy Agency: Abu Dhabi, UAE, 2018. [Google Scholar]
- OECD/IEA; IRENA. Perspectives for the Energy Transition: Investment Needs for a Low-Carbon Energy System; IRENA: Abu Dhabi, UAE, 2017. [Google Scholar]
- Shivakumar, A.; Taliotis, C.; Deane, P.; Gottschling, J.; Pattupara, R.; Kannan, R.; Jakšić, D.; Stupin, K.; Hemert, R.V.; Normark, B.; et al. Need for Flexibility and Potential Solutions. In Europe’s Energy Transition—Insights for Policy Making; Elsevier: Amsterdam, The Netherlands, 2017; pp. 149–172. [Google Scholar]
- Falchetta, M. Fonti Rinnovabili e rete Elettrica in Italia. Considerazioni di Base e Scenari di Evoluzione delle Fonti Rinnovabili Elettriche in Italia; ENEA: Rome, Italy, 2014. [Google Scholar]
- Terna. Dati Statistici 2015. Available online: https://www.terna.it/it-it/sistemaelettrico/statisticheeprevisioni/datistatistici.aspx (accessed on 14 May 2019).
- European Commission. Consultation Paper on Generation Adequacy, Capacity Mechanisms and the Internal Market in Electricity; European Commission: Brussels, Belgium, 2012. [Google Scholar]
- Welsch, M.; Howells, M.; Hesamzadeh, M.; OGallachoir, B.; Deane, P.; Strachan, N.; Bazilian, M.; Kammen, D.M.; Jones, L.; Strbac, G.; et al. Supporting security and adequacy in future energy systems: The need to enhance long-term energy system models to better treat issues related to variability. Int. J. Energy Res. 2015, 39, 377–396. [Google Scholar] [CrossRef]
- PLEXOS® Simulation Software. Energy Ex n.d. Available online: https://energyexemplar.com/products/plexos-simulation-software/ (accessed on 11 October 2018).
- Prina, M.G.; Cozzini, M.; Garegnani, G.; Manzolini, G.; Moser, D.; Filippi Oberegger, U.; Pernettia, R.; Vaccaroa, R.; Sparber, W. Multi-objective optimization algorithm coupled to EnergyPLAN software: The EPLANopt model. Energy 2018, 149, 213–221. [Google Scholar] [CrossRef]
- Prina, M.G.; Fanali, L.; Manzolini, G.; Moser, D.; Sparber, W. Incorporating combined cycle gas turbine flexibility constraints and additional costs into the EPLANopt model: The Italian case study. Energy 2018, 160, 33–43. [Google Scholar] [CrossRef]
- Hörsch, J.; Hofmann, F.; Schlachtberger, D.; Brown, T. PyPSA-Eur: An open optimisation model of the European transmission system. Energy Strategy Rev. 2018, 22, 207–215. [Google Scholar] [CrossRef]
- Brinkerink, M.; Shivakumar, A. System dynamics within typical days of a high variable 2030 European power system. Energy Strategy Rev. 2018, 22, 94–105. [Google Scholar] [CrossRef]
- Schrattenholzer, L. The Energy Supply Model MESSAGE; IIASA: Laxenburg, Austria, 1981. [Google Scholar]
- Loulou, R.; Remme, U.; Kanudia, A.; Lehtila, A.; Goldstein, G. Documentation for the TIMES Model Part I; IEA-ETSAP: Paris, France, 2005. [Google Scholar]
- The Balmorel Open Source Project—Home n.d. Available online: http://www.balmorel.com/ (accessed on 11 October 2018).
- Howells, M.; Rogner, H.; Strachan, N.; Heaps, C.; Huntington, H.; Kypreos, S.; Hughes, A.; Silveira, S.; DeCarolis, J.; Bazillian, M.; et al. OSeMOSYS: The Open Source Energy Modeling System: An introduction to its ethos, structure and development. Energy Policy 2011, 39, 5850–5870. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Ludig, S.; Haller, M.; Schmid, E.; Bauer, N. Fluctuating renewables in a long-term climate change mitigation strategy. Energy 2011, 36, 6674–6685. [Google Scholar] [CrossRef]
- Welsch, M.; Deane, P.; Howells, M.; OGallachoir, B.; Rogan, F.; Bazilian, M.; Rogner, H. Incorporating flexibility requirements into long-term energy system models—A case study on high levels of renewable electricity penetration in Ireland. Appl. Energy 2014, 135, 600–615. [Google Scholar] [CrossRef]
- Gardumi, F. Personal GitHub. Gardumi OSeMOSYS Repos n.d. Available online: https://github.com/FraGard/OSeMOSYS/tree/master/addons (accessed on 14 May 2019).
- Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions: European Cloud Initative—Building a Competitive Data and Knowledge Economy in Europe; European Commission: Brussels, Belgium, 2016.
- Taliotis, C.; Rogner, H.; Ressl, S.; Howells, M.; Gardumi, F. Natural gas in Cyprus: The need for consolidated planning. Energy Policy 2017, 107, 197–209. [Google Scholar] [CrossRef]
- Taliotis, C.; Shivakumar, A.; Ramos, E.P.; Howells, M.; Mentis, D.; Sridharan, V.; Broad, O.; Mofor, L. An indicative analysis of investment opportunities in the African electricity supply sector—Using TEMBA (The Electricity Model Base for Africa). Energy Sustain. Dev. 2016, 31, 50–66. [Google Scholar] [CrossRef]
- Pinto de Moura, G.N.; Loureiro Legey, L.F.; Balderrama, G.P.; Howells, M. South America power integration, Bolivian electricity export potential and bargaining power: An OSeMOSYS SAMBA approach. Energy Strategy Rev. 2017, 17, 27–36. [Google Scholar] [CrossRef]
- Henke, H. The Open Source Energy Model Base for the European Union (OSEMBE). 2017. Available online: https://aaltodoc.aalto.fi/bitstream/handle/123456789/27115/master_Henke_Hauke_2017.pdf?sequence=1&isAllowed=y (accessed on 14 June 2019).
- Huntington, H.; Weyant, J.; Sweeney, J. Modeling for insights, not numbers: The experiences of the energy modeling forum. Omega 1982, 10, 449–462. [Google Scholar] [CrossRef]
- OSeMOSYS Community of Practice. OSeMOSYS.org n.d. Available online: http://www.osemosys.org/ (accessed on 14 May 2019).
- Gardumi, F.; Shivakumar, A.; Morrison, R.; Taliotis, C.; Broad, O.; Beltramo, A.; Sridharan, V.; Howells, M.; Hörsch, J.; Niet, T.; et al. From the development of an open-source energy modelling tool to its application and the creation of communities of practice: The example of OSeMOSYS. Energy Strategy Rev. 2018, 20, 209–228. [Google Scholar] [CrossRef]
- Kumar, N.; Besuner, P.; Lefton, S.; Agan, D.; Hilleman, D. Power Plant Cycling Costs; National Renewable Energy Laboratory: Sunnyvale, CA, USA, 2012.
- IEA. Power Generation from Coal Measuring and Reporting Efficiency Performance and CO2 Emissions; IEA: Paris, France, 2010. [Google Scholar]
- Lucquiaud, M.; Fernandez, E.; Chalmers, H.; Mac Dowell, N.; Gibbins, J. Enhanced operating flexibility and optimised off-design operation of coal plants with post-combustion capture. Energy Procedia 2014, 63, 7494–7507. [Google Scholar] [CrossRef]
- Kim, T. Comparative analysis on the part load performance of combined cycle plants considering design performance and power control strategy. Energy 2004, 29, 71–85. [Google Scholar] [CrossRef]
- Gardumi, F. A Multi-Dimensional Approach to the Modelling of Power Plant Flexibility. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2016. [Google Scholar]
- Terna S.p.A. Piano di Sviluppo 2015 n.d. Available online: https://www.arera.it/allegati/operatori/pds/PdS%202015_Gennaio%202015.pdf (accessed on 14 May 2019).
- Venkataraman, S.; Jordan, G.; O’Connor, M. Cost-Benefit Analysis of Flexibility Retrofits for Coal and Gas-Fueled Power Plants; NREL: Golden, CO, USA, 2013.
- European Commission. Report from the Commission to the European Parliament and the Council: Report on the Functioning of the European Carbon Market; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Energetico, R.S. Energia Elettrica, Anatomia dei Costi: Aggiornamento Dati al 2015; Editrice Alkes: Milano, Italy, 2015. [Google Scholar]
- IEA-ETSAP. Energy Supply Technologies Data 2015. Available online: http://109.73.233.125/~ieaetsap/index.php/energy-technology-data/energy-supply-technologies-data (accessed on 14 May 2019).
- Meibom, P.; Barth, R.; Brand, H.; Hasche, B.; Swider, D.; Ravn, H. Final Report for All Island Grid Study Work-stream 2 (b): Wind Variability Management Studies; Riso National Laboratory: Roskilde, Denmark, 2007. [Google Scholar]
- Di Rete, C. Capitolo 4: Regole per il Dispacciamento; Terna S.p.A.: Rome, Italy, 2015. [Google Scholar]
- International Energy Agency (IEA). Country Statistics. Stat Glob Energy Data Your Fingertips 2017. Available online: https://www.iea.org/statistics/statisticssearch/report/?country=Mozambique&product=balances (accessed on 14 May 2019).
- Ministero dello Sviluppo Economico. Strategia Energetica Nazionale: Per Un’energia Più Competitiva E Sostenibile; Italian Government: Rome, Italy, 2013.
- Dhakouani, A.; Gardumi, F.; Znouda, E.; Bouden, C.; Howells, M. Long-term optimisation model of the Tunisian power system. Energy 2017, 141, 550–562. [Google Scholar] [CrossRef]
- International Energy Agency. Nuclear Power in a Clean Energy System; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Maggi, C. Accounting for the Long Term Impact of High Renewable Shares through Energy System Models: A Novel Formulation and Case Study. Master’s Thesis, Politecnico di Milano, Milano, Italy, 2016. [Google Scholar]


















| Time Domain | 2014–2040 |
|---|---|
| Time split | 16 time slices: night, morning, afternoon, evening-4 seasons 1 |
| Electricity demand | 291 TWh in 2014, then increasing at constant rate of 1% |
| Upward reserve capacity demand | 4.61 GW in 2014, then increasing at constant rate of 1% |
| Downward reserve capacity demand | 2.17 GW in 2014, then increasing at constant rate of 1% |
| Taxations | 4 €/ton CO2, constant |
| Price of coal | 2.63 €/GJ, constant |
| Price of gas | 8.08 €/GJ, constant |
| Discount rate | 5% |
| Parameter | PV | Coal PP | NGCC | NGCCupg |
|---|---|---|---|---|
| Capital Costs [M€/GW] | 1200 | 1750 | 650 | 653 |
| Variable Costs [M€/PJ] | 6.420 | 0.694 | 0.875 | 0.875 |
| Fixed Costs [M€/GW] | 20 | 35 | 10.5 | 10.5 |
| Fuel Cost [M€/PJ] | 0 | 2.6 | 8.1 | 8.1 |
| Efficiency at full load [%] | 100 | 41.1 | 56 | 56 |
| CO2 emission factor [Mton/PJ] | 0 | 0.219 | 0.103 | 0.103 |
| Operational life (years) | 30 | 35 | 30 | 30 |
| Parameter | PV | Coal PP | NGCC | NGCCupg |
|---|---|---|---|---|
| Minimum Stable Operation [% of full load] | 0 | 45 | 42 | 42 |
| Efficiency at min stable operation [%] | 0 | 37 | 44 | 48 |
| Max ramping rate [MW/min] | 0 | 8 | 11 | 11 |
| Cost of starts [M€/GW] | 0 | 0.050 | 0.043 | 0.034 |
| Cost of retrofit [M€/GW] | 0 | 0 | 0 | 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gardumi, F.; Welsch, M.; Howells, M.; Colombo, E. Representation of Balancing Options for Variable Renewables in Long-Term Energy System Models: An Application to OSeMOSYS. Energies 2019, 12, 2366. https://doi.org/10.3390/en12122366
Gardumi F, Welsch M, Howells M, Colombo E. Representation of Balancing Options for Variable Renewables in Long-Term Energy System Models: An Application to OSeMOSYS. Energies. 2019; 12(12):2366. https://doi.org/10.3390/en12122366
Chicago/Turabian StyleGardumi, Francesco, Manuel Welsch, Mark Howells, and Emanuela Colombo. 2019. "Representation of Balancing Options for Variable Renewables in Long-Term Energy System Models: An Application to OSeMOSYS" Energies 12, no. 12: 2366. https://doi.org/10.3390/en12122366
APA StyleGardumi, F., Welsch, M., Howells, M., & Colombo, E. (2019). Representation of Balancing Options for Variable Renewables in Long-Term Energy System Models: An Application to OSeMOSYS. Energies, 12(12), 2366. https://doi.org/10.3390/en12122366




