Impacts of an Increased Substitution of Fossil Energy Carriers with Electricity-Based Technologies on the Swiss Electricity System
Abstract
:1. Introduction
2. Methodology
2.1. Current Swiss Electricity Production and Consumption
2.2. Electrification of the Heat Demand in Switzerland
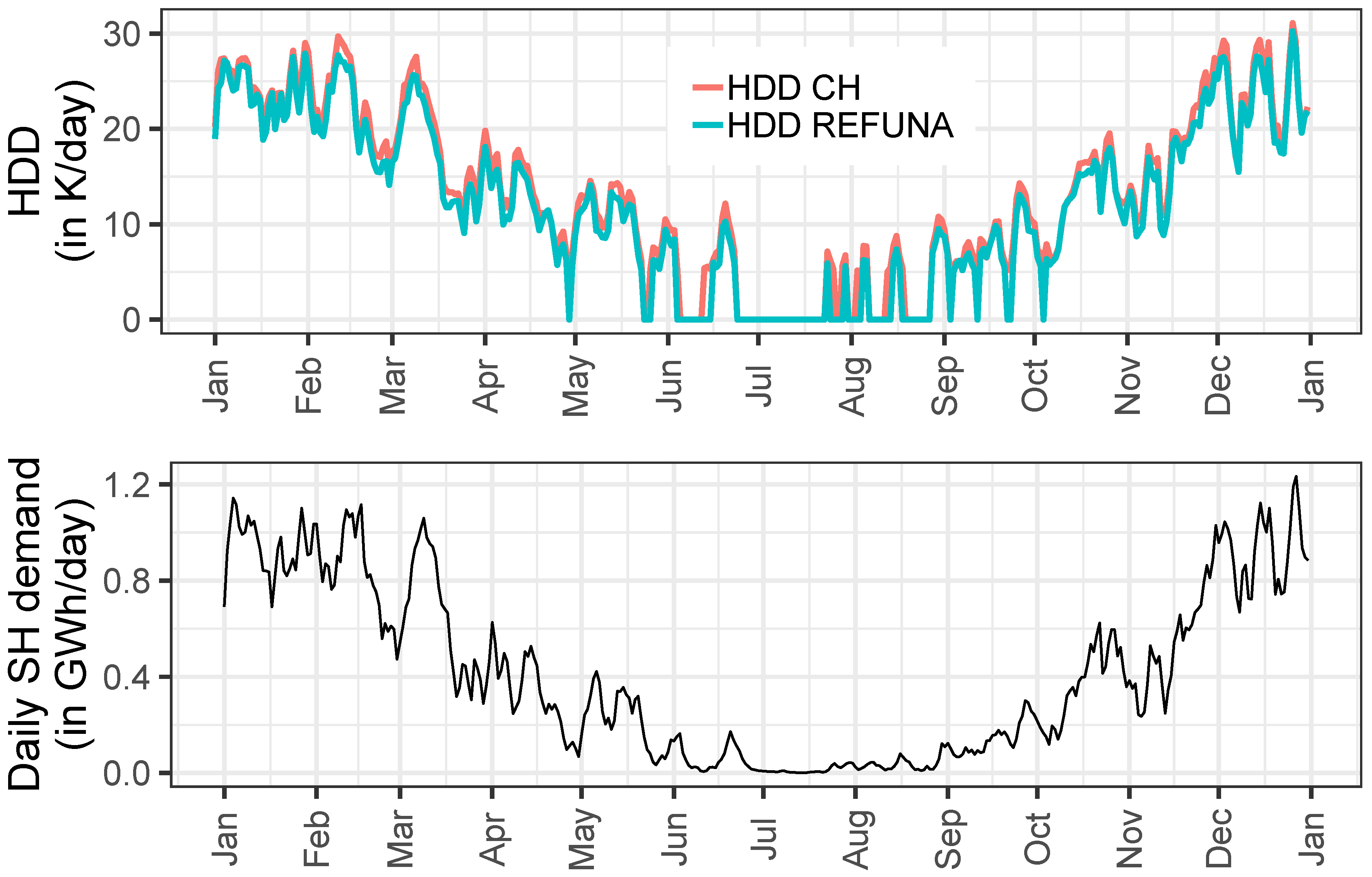
2.2.1. Total Heat Demand
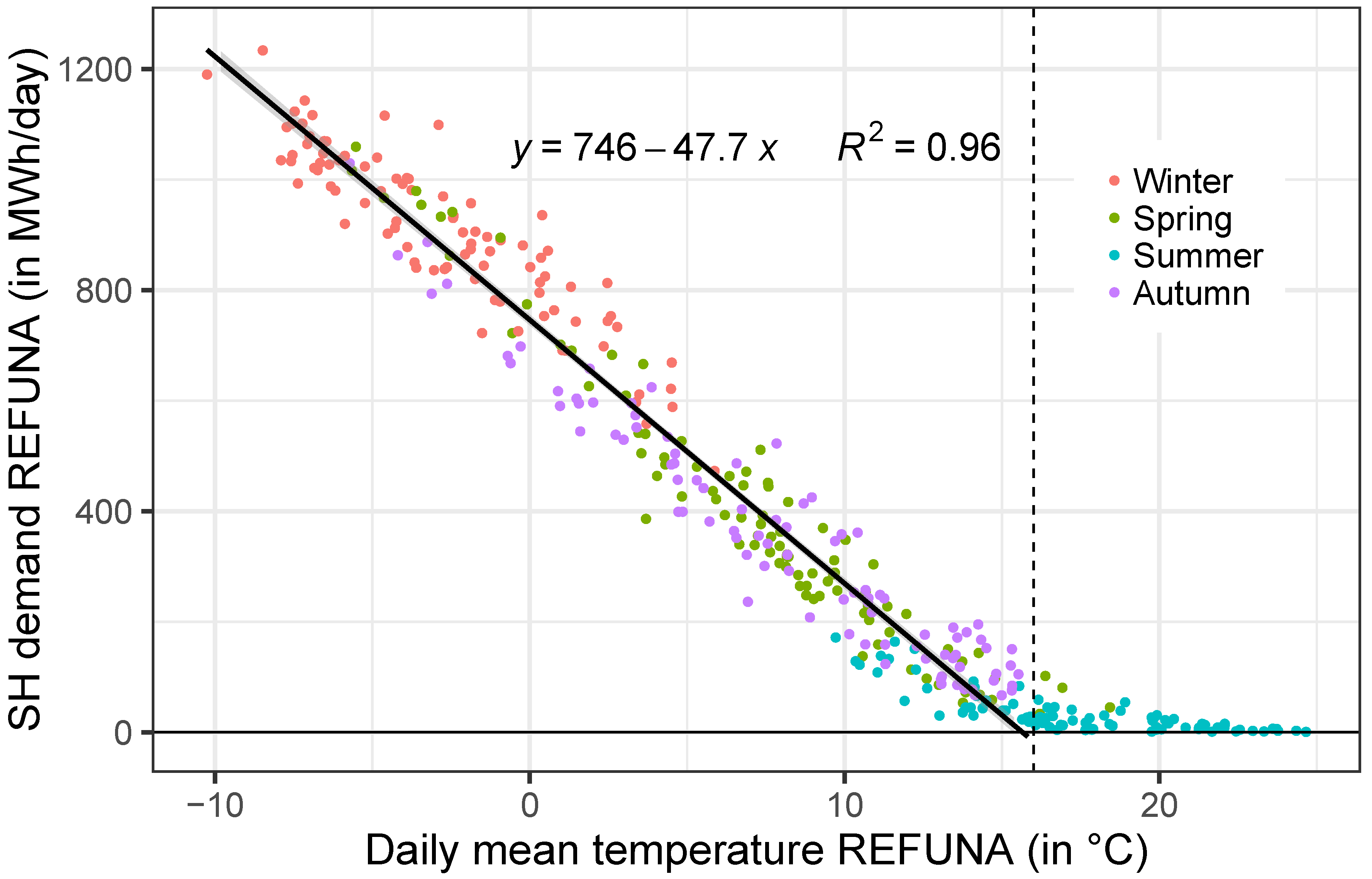
2.2.2. Hourly Heat Demand in a District Heating Grid
2.2.3. Domestic Hot Water and Space Heating Demand
2.2.4. Extrapolation to National-Scale
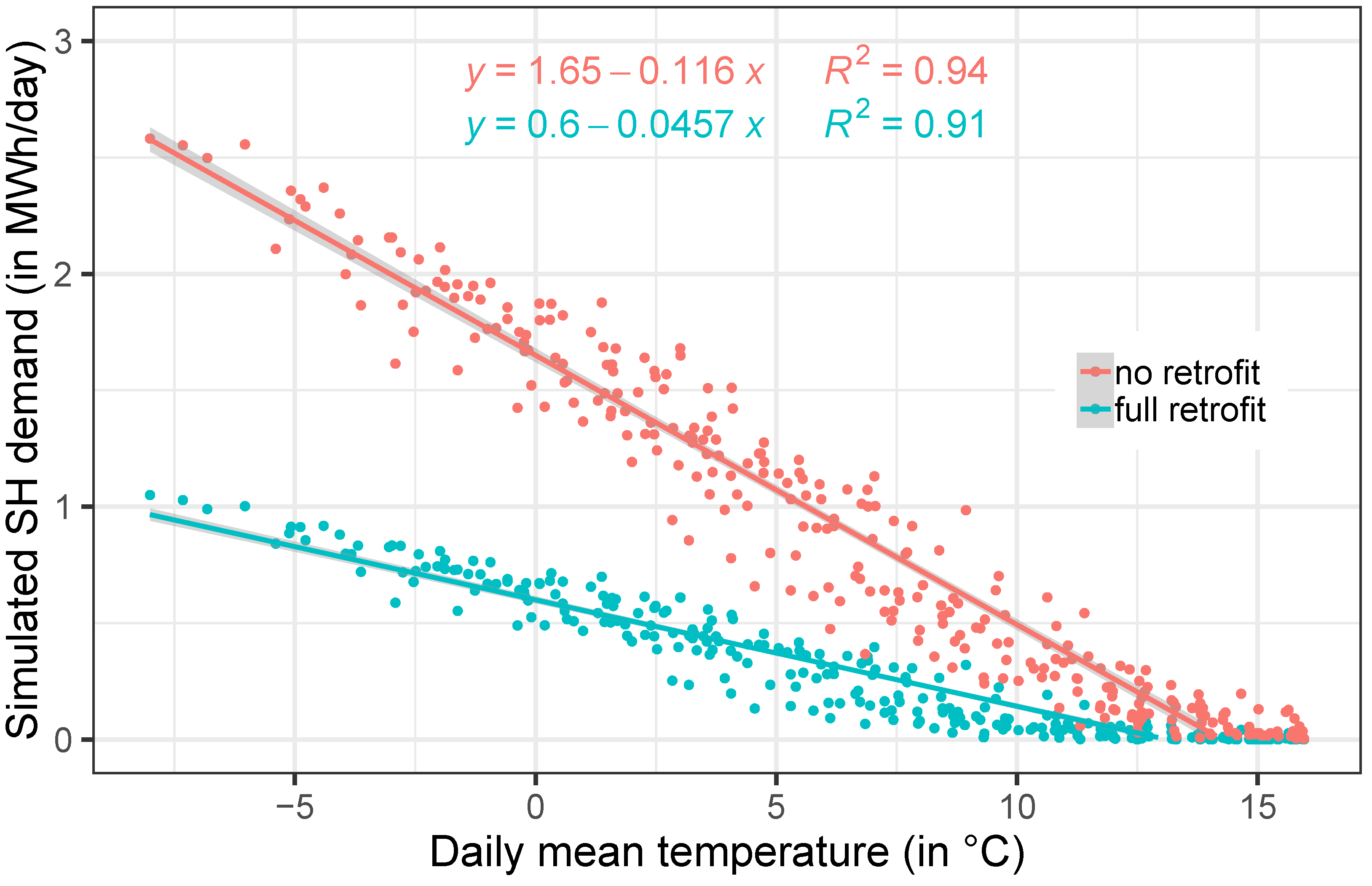
2.2.5. Influence of Building Retrofitting
2.2.6. Heat Pumps
2.3. Electrification of Mobility in Switzerland
2.3.1. Energy Demand
2.3.2. Recharging
2.4. Denuclearization of Electricity in Switzerland
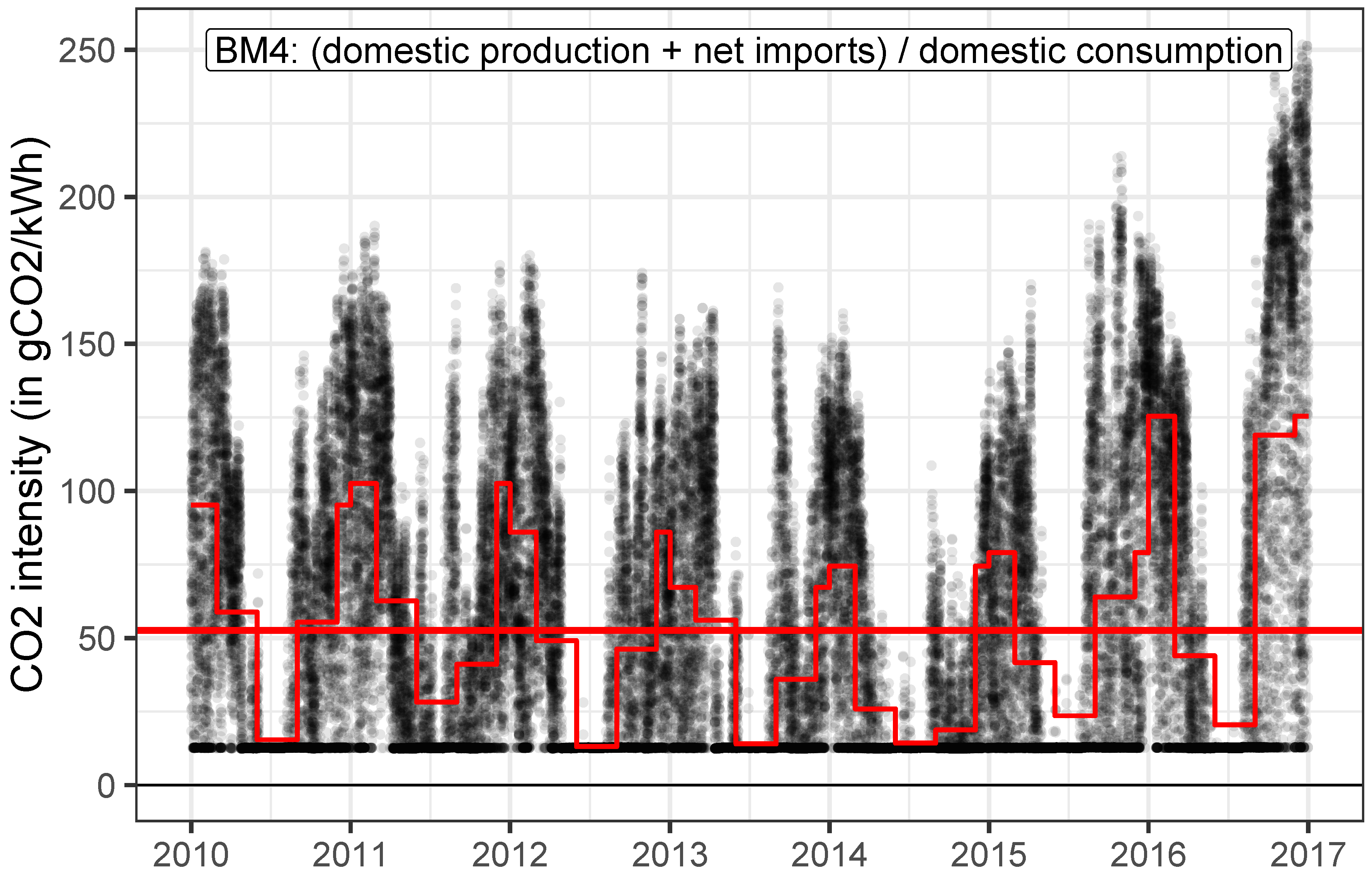
2.5. CO2 Intensities
2.5.1. Fossil Energy Carriers
2.5.2. Electricity
- Hydro (13 g/kWh): This is a weighted average according to the Swiss production expectation of run-of-river (4.3 g/kWh, weight 48%), dam (6.9 g/kWh, weight 48%) and PHS (196 g/kWh, weight 4%) [53,61]. For PHS, 86% of the CO2 emissions are attributed to the electricity needed to pump water into the reservoir. Wernet et al. [61] assume that the average Swiss electricity mix at 112 g/kWh (domestic production plus imports) is used and that PHS has a 70% round-trip efficiency. Only 11% of the CO2 intensity is attributed to direct CO2 and CH4 emissions of the reservoir.
- PV (50 g/kWh): The 2018 CO2 emissions based on LCA of single-Si PV electricity produced on roofs of European residences is approximately 90 g/kWh [61]. In the future (2030 to 2050), for a scenario with “realistic” improvements, these CO2 emissions could be reduced to 25 g/kWh because of projected changes in key parameters and the background system [65]. Therefore, in this study, a reasonable intermediate value of 50 g/kWh is used.
- NPP (12 g/kWh): This is a weighted average according to the Swiss production expectation of all pressurised water reactors (PWR) with 11.9 g/kWh and boiling water reactors (BWR) with 12.6 g/kWh [61].
- Imports (443 g/kWh): The CO2 intensity of imported electricity is set to 443 g/kWh, which is the CO2 intensity of modern CCGT power plants and is substantially less than the 2017 Swiss import mix with a share of 67% from Germany (679 g/kWh), 8% from France (109 g/kWh) and 25% from Austria (389 g/kWh) for a weighted average CO2 intensity of 560 g/kWh [53,61]. The CO2 intensity of imported electricity is assumed to be constant throughout the year. That is, no variability with regard to surplus production of e.g., wind electricity (with 18 g/kWh) in other countries is considered. In addition, not considered is the fact that most electricity is imported in winter and the CO2 intensity in winter is higher due to a higher overall demand in Europe—as well as the fact that within a day, imports usually are higher during high demand hours with higher CO2 intensities. Another reasoning behind taking the CO2 intensity of CCGT for imports is that instead of importing electricity (at deficit hours), it could also be produced in Switzerland by newly built CCGT power plants (running mostly on imported natural gas). This corresponds to variant “C” in ES2050.
2.6. Sensitivity Analysis
3. Results and Discussion
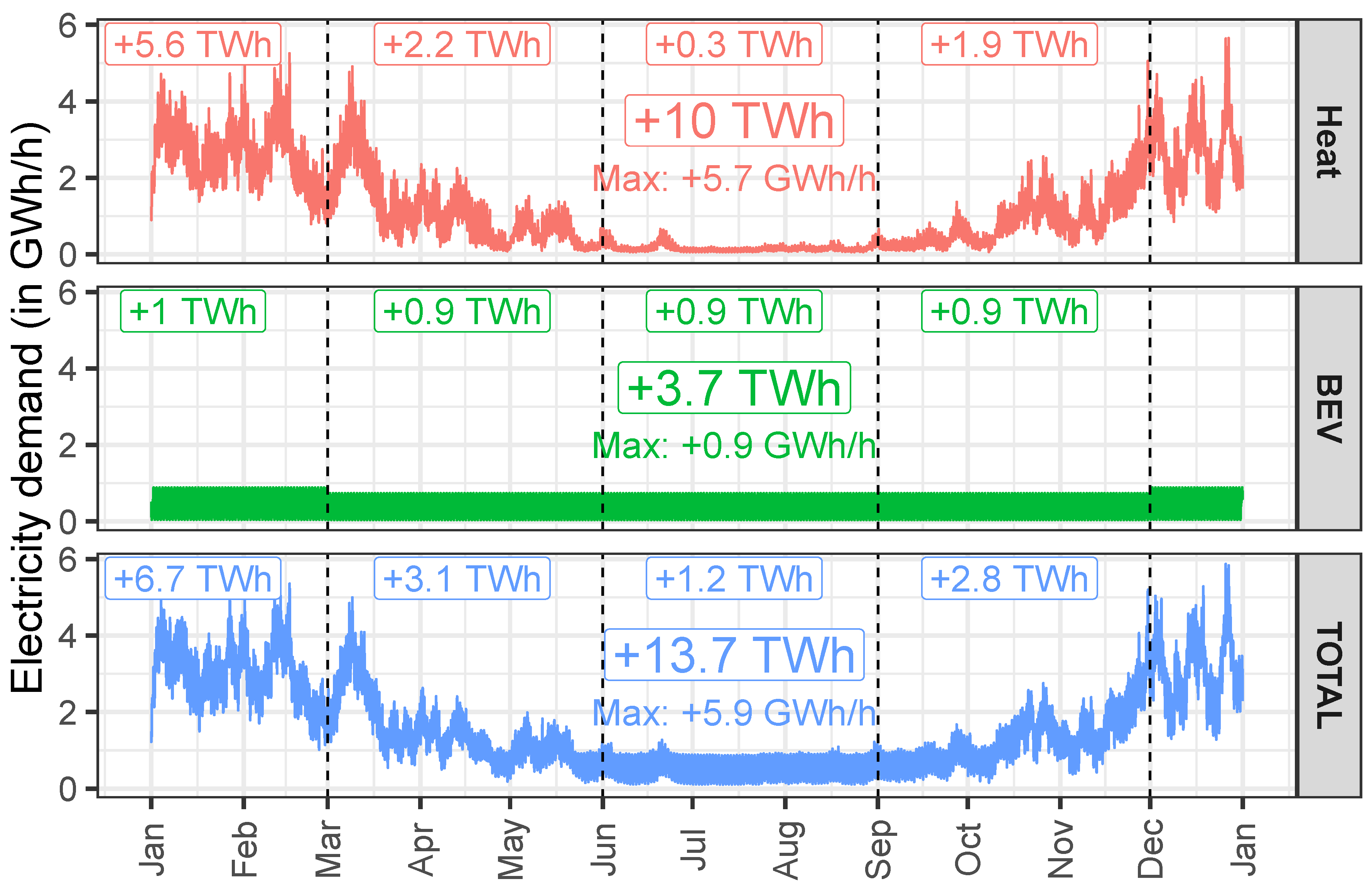
3.1. Additional Electricity Demand by Heat Pumps and BEV
3.1.1. Total Electricity Demand
3.1.2. Maximum Power Demand
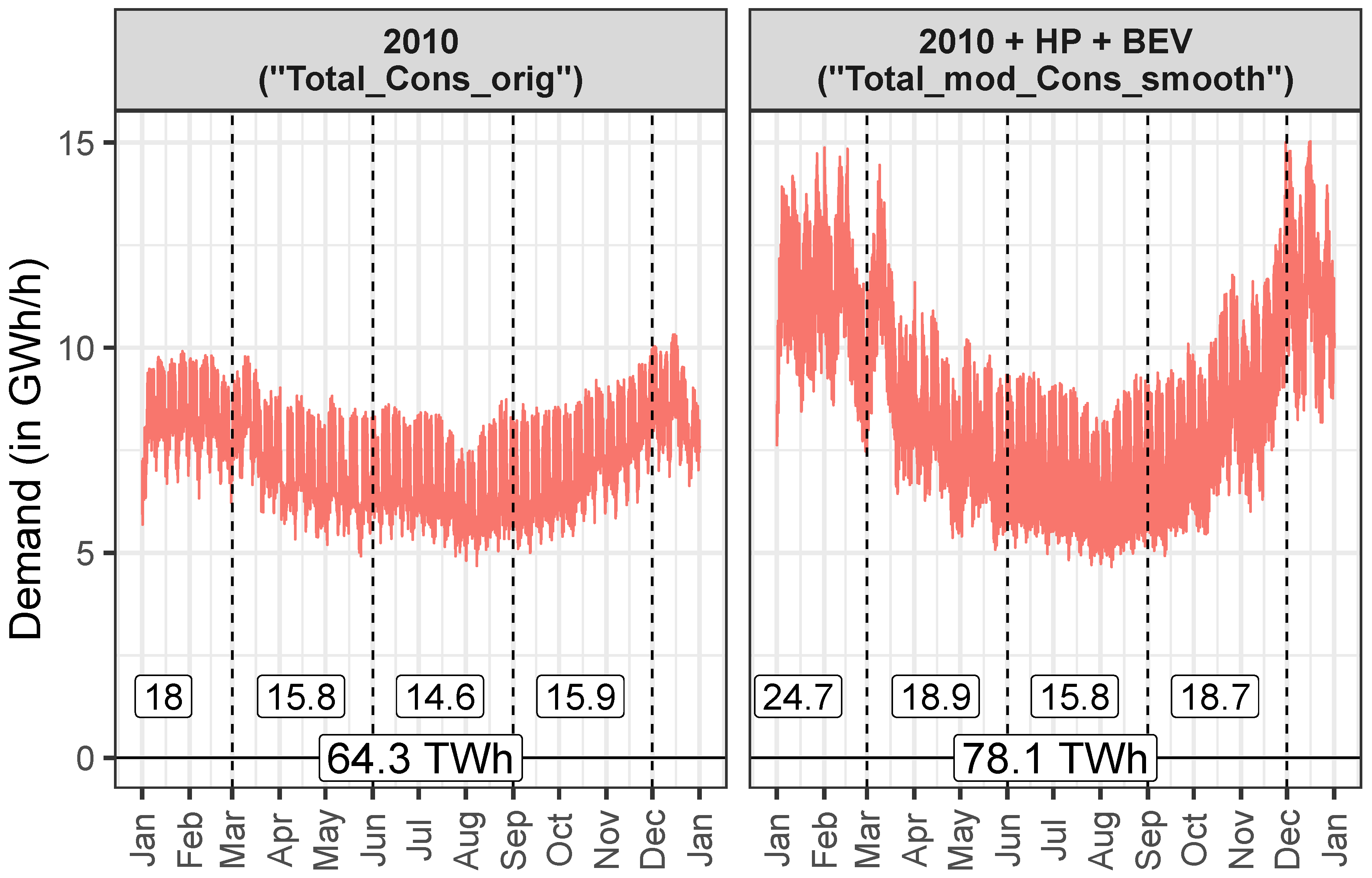
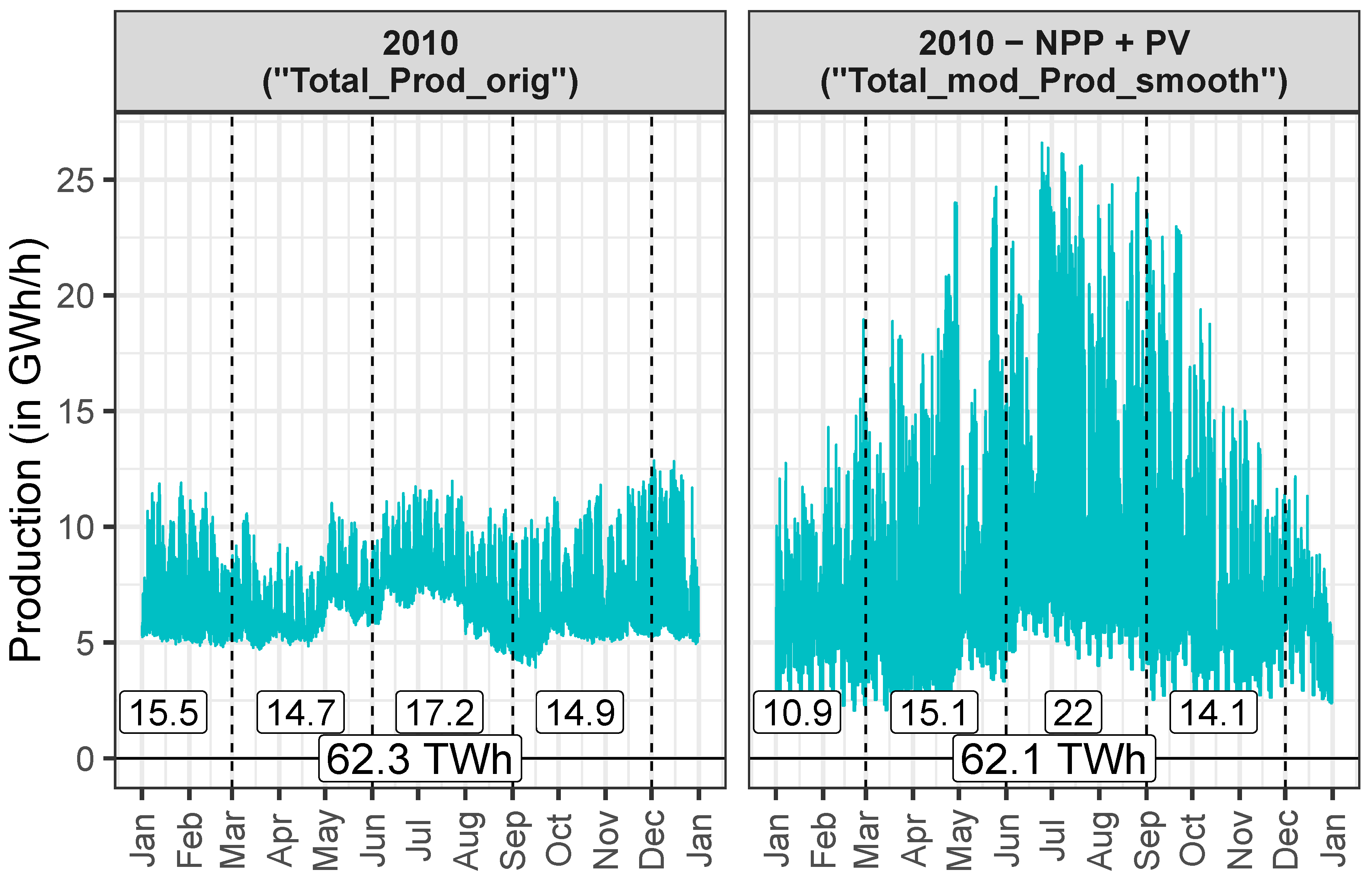
3.2. Total Swiss Electricity Demand and Production
3.2.1. Demand
- Nuclear 3.3
- Run-of-river 4.0
- Dam 8.7
- PHS 2.0 (as of 2020: 4.0 )
- PV 1.7
- Others 1.1
- TOTAL: 20.8
3.2.2. Production
3.3. Deficits and Surpluses
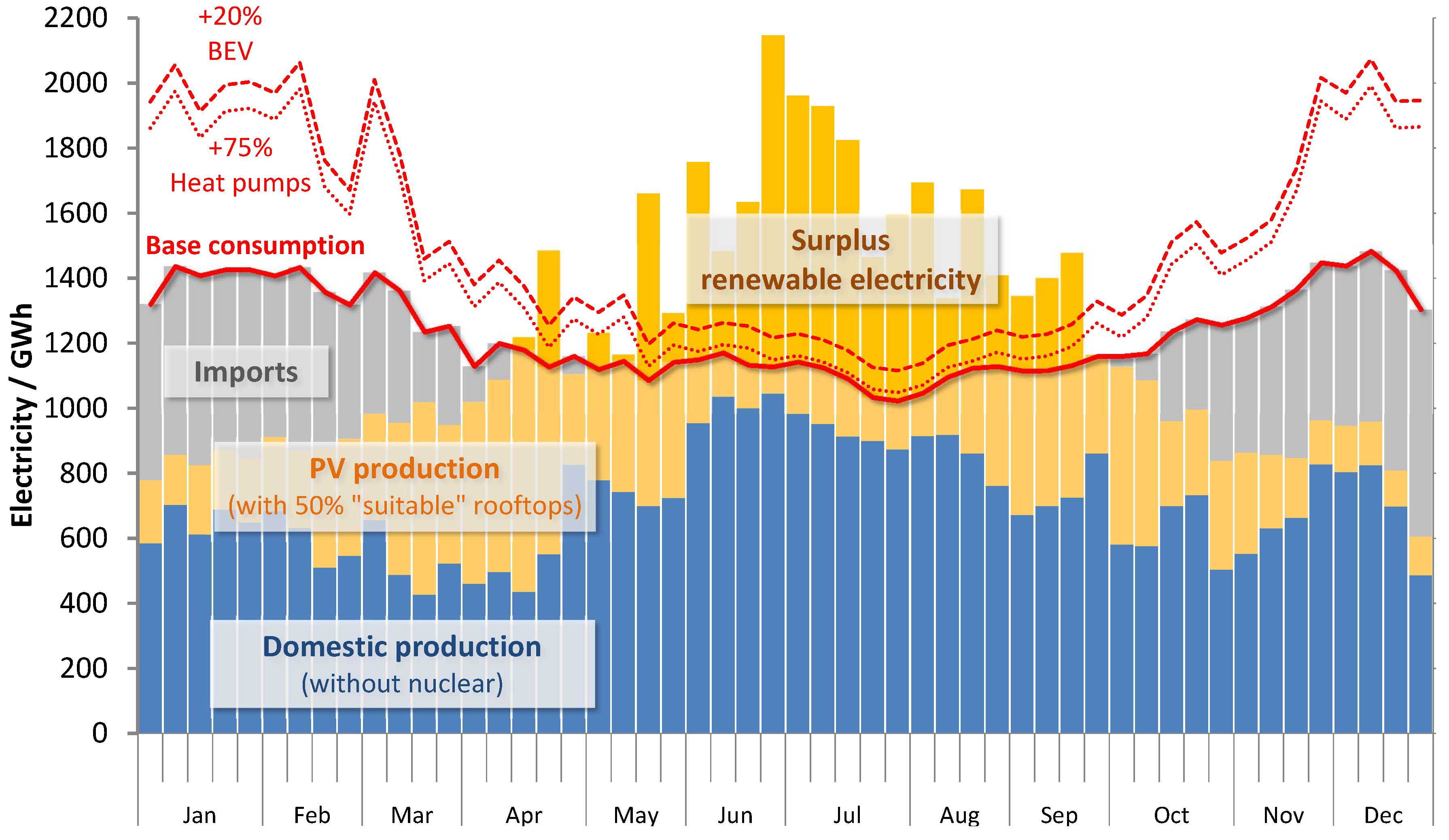
3.3.1. Hourly Values
3.3.2. Weekly Aggregation
3.3.3. Summary
3.4. CO2 Mitigation
3.4.1. Hourly CO2 Intensities
3.4.2. CO2 Savings
3.4.3. General Discussion
3.5. Imports from Neighbouring Countries
4. Conclusions
- Production side:
- (a)
- Investigations on the effective potentials to manage hydro and pumped-hydro storage in the various scenarios and along with other storage technologies (e.g., batteries, etc.)
- (b)
- Investigations on the impacts of varying nuclear phase-out scenarios (in time and intensity) on CO2 mitigation and electricity supply
- Demand side:
- (a)
- Investigations on tangible building flexibility options such as local and district heat storage, storage options on both sides of heat pumps (electricity or heat), etc.
- (b)
- Investigations on tangible demand side control strategies for mobility (e.g., recharging scheduling, vehicle-to-grid, etc.)
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. Adoption of the Paris Agreement. Framework Convention on Climate Change; Technical Report; United Nations: Paris, France, 2015. [Google Scholar]
- Prognos. Die Energieperspektiven für die Schweiz bis 2050. Energienachgefrage und Elektrizitätsangebot in der Schweiz 2000–2050; Technical Report; Prognos AG: Basel, Switzerland, 2012. [Google Scholar]
- Sugiyama, M. Climate change mitigation and electrification. Energy Policy 2012, 44, 464–468. [Google Scholar] [CrossRef]
- Williams, J.H.; DeBenedictis, A.; Ghanadan, R.; Mahone, A.; Moore, J.; Morrow, W.R.; Price, S.; Torn, M.S. The technology path to deep greenhouse gas emissions cuts by 2050: The pivotal role of electricity. Science 2012, 335, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, D.; Bielen, D.; Eichman, J.; Eurek, K.; Logan, J.; Mai, T.; McMillan, C.; Parker, A.; Vimmerstedt, L.; Wilson, E. Electrification & Decarbonization: Exploring U.S. Energy Use and Greenhouse Gas Emissions in Scenarios with Widespread Electrification and Power Sector Decarbonization; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2017.
- Ruhnau, O.; Bannik, S.; Otten, S.; Praktiknjo, A.; Robinius, M. Direct or indirect electrification? A review of heat generation and road transport decarbonisation scenarios for Germany 2050. Energy 2019, 166, 989–999. [Google Scholar] [CrossRef]
- BFS. Treibhausgasemissionen in der Schweiz. Entwicklung in CO2-Äquivalente und Emissionen nach Sektoren; Technical Report; BFS: Neuchâtel, Switzerland, 2018. [Google Scholar]
- Tarroja, B.; Chiang, F.; AghaKouchak, A.; Samuelsen, S.; Raghavan, S.V.; Wei, M.; Sun, K.; Hong, T. Translating climate change and heating system electrification impacts on building energy use to future greenhouse gas emissions and electric grid capacity requirements in California. Appl. Energy 2018, 225, 522–534. [Google Scholar] [CrossRef] [Green Version]
- Love, J.; Smith, A.Z.; Watson, S.; Oikonomou, E.; Summerfield, A.; Gleeson, C.; Biddulph, P.; Chiu, L.F.; Wingfield, J.; Martin, C.; et al. The addition of heat pump electricity load profiles to GB electricity demand: Evidence from a heat pump field trial. Appl. Energy 2017, 204, 332–342. [Google Scholar] [CrossRef]
- McCollum, D.; Krey, V.; Kolp, P.; Nagai, Y.; Riahi, K. Transport electrification: A key element for energy system transformation and climate stabilization. Clim. Chang. 2014, 123, 651–664. [Google Scholar] [CrossRef]
- Singh, B.; Ellingsen, L.A.W.; Strømman, A.H. Pathways for GHG emission reduction in Norwegian road transport sector: Perspective on consumption of passenger car transport and electricity mix. Transp. Res. Part D Transp. Environ. 2015, 41, 160–164. [Google Scholar] [CrossRef]
- Moro, A.; Lonza, L. Electricity carbon intensity in European Member States: Impacts on GHG emissions of electric vehicles. Transp. Res. Part D Transp. Environ. 2018, 64, 5–14. [Google Scholar] [CrossRef]
- Guminski, A.; Böing, F.; Murmann, A.; Von Roon, S. System effects of high demand-side electrification rates: A scenario analysis for Germany in 2030. Wiley Interdiscip. Rev. Energy Environ. 2018. [Google Scholar] [CrossRef]
- Densing, M.; Hirschberg, S.; Turton, H. Review of Swiss Electricity Scenarios 2050; Technical Report; Paul Scherrer Institute (PSI): Villigen, Switzerland, 2014. [Google Scholar]
- Bauer, C.; Bäuerle, Y.; Biollaz, S.; Calbry-Muzyka, A.; Cox, B.; Heck, T.; Hirschberg, S.; Lehnert, M.; Meier, A.; Prasser, H.M.; et al. Potentials, Costs and Environmental Assessment of Electricity Generation Technologies; Technical Report; Paul Scherrer Institute (PSI): Villigen, Switzerland, 2017. [Google Scholar]
- Díaz Redondo, P.; van Vliet, O. Modelling the Energy Future of Switzerland after the Phase Out of Nuclear Power Plants. Energy Procedia 2015, 76, 49–58. [Google Scholar] [CrossRef] [Green Version]
- Bartlett, S.; Dujardin, J.; Kahl, A.; Kruyt, B.; Manso, P.; Lehning, M. Charting the course: A possible route to a fully renewable Swiss power system. Energy 2018, 163, 942–955. [Google Scholar] [CrossRef]
- Sousa, T.; Soares, T.; Pinson, P.; Moret, F.; Baroche, T.; Sorin, E. Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 104, 367–378. [Google Scholar] [CrossRef] [Green Version]
- Barmettler, F.; Beglinger, N.; Zeyer, C. Cleantech Energiestrategie—Richtig rechnen und wirtschaftlich profitieren, auf CO2-Zielkurs; Technical Report; Foundation for Global Sustainability: Bern, Switzerland, 2013. [Google Scholar]
- Andersson, G.; Boulouchos, K.; Bretschger, L. Energiezukunft Schweiz; Technical Report; ETH Zürich: Zürich, Switzerland, 2011. [Google Scholar]
- Greenpeace. Energieszenario Schweiz 2013—Energy [r]evolution—Eine nachhaltige Energieversorgung für die Schweiz; Technical Report; Greenpeace International: Zürich, Switzerland, 2013. [Google Scholar]
- Gunzinger, A. Kraftwerk Schweiz—Plädoyer für eine Energiewende mit Zukunft; Zytglogge: Zürich, Switzerland, 2015. [Google Scholar]
- Berntsen, P.B.; Trutnevyte, E. Ensuring diversity of national energy scenarios: Bottom-up energy system model with Modeling to Generate Alternatives. Energy 2017, 126, 886–898. [Google Scholar] [CrossRef] [Green Version]
- Schlecht, I.; Weigt, H. SwissMod—A Model of the Swiss Electricity Market; Technical Report; University of Basel: Basel, Switzerland, 2013. [Google Scholar]
- Codina Gironès, V.; Moret, S.; Maréchal, F.; Favrat, D. Strategic energy planning for large-scale energy systems: A modelling framework to aid decision-making. Energy 2015, 90, 173–186. [Google Scholar] [CrossRef]
- Moret, S. Strategic Energy Planning under Uncertainty Stefano MORET. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2017. [Google Scholar]
- Kannan, R.; Turton, H. Switzerland Energy Transistion Scenarios-Devlopment and Application of Swiss TIMES Energy System Model (STEM); Technical Report; Paul Scherrer Institut (PSI): Villigen, Switzerland, 2014. [Google Scholar]
- Pfenninger, S. Dealing with multiple decades of hourly wind and PV time series in energy models: A comparison of methods to reduce time resolution and the planning implications of inter-annual variability. Appl. Energy 2017, 197, 1–13. [Google Scholar] [CrossRef]
- Trutnevyte, E. EXPANSE methodology for evaluating the economic potential of renewable energy from an energy mix perspective. Appl. Energy 2013, 111, 593–601. [Google Scholar] [CrossRef]
- Kannan, R.; Hirschberg, S. Interplay between electricity and transport sectors—Integrating the Swiss car fleet and electricity system. Transp. Res. Part A Policy Pract. 2016, 94, 514–531. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Delucchi, M.A.; Bauer, Z.A.; Goodman, S.C.; Chapman, W.E.; Cameron, M.A.; Bozonnat, C.; Chobadi, L.; Clonts, H.A.; Enevoldsen, P.; et al. 100% Clean and Renewable Wind, Water, and Sunlight All-Sector Energy Roadmaps for 139 Countries of the World. Joule 2017, 1, 108–121. [Google Scholar] [CrossRef] [Green Version]
- Swissgrid. Aggregated Energy Data of the Control Block Switzerland, 2019. Available online: https://www.swissgrid.ch/en/home/customers/topics/energy-data-ch.html (accessed on 18 June 2019).
- Begert, M.; Frei, C. Long-term area-mean temperature series for Switzerland—Combining homogenized station data and high resolution grid data. Int. J. Climatol. 2018, 38, 2792–2807. [Google Scholar] [CrossRef]
- Prognos. Analyse des Schweizerischen Energieverbrauchs 2000–2017—Auswertung nach Verwendungszwecken; Technical Report; BFE: Bern, Switzerland, 2018. [Google Scholar]
- REFUNA. Geschäftsbericht 2010/2011; Technical Report; REFUNA: Döttingen, Switzerland, 2011. [Google Scholar]
- REFUNA. Technische Anschlussvorschrift (TAV); Technical Report; REFUNA: Döttingen, Switzerland, 2005. [Google Scholar]
- Prognos. Witterungsbereinigung auf Basis von Gradtagen und Solarstrahlung—Aufarbeitung und Dokumentation; Technical Report; Prognos AG: Basel, Switzerland, 2015. [Google Scholar]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Christenson, M.; Manz, H.; Gyalistras, D. Climate warming impact on degree-days and building energy demand in Switzerland. Energy Convers. Manag. 2006, 47, 671–686. [Google Scholar] [CrossRef]
- SIA. SIA Standard 381/3: Heating Degree-Days In Switzerland; Technical Report; Swiss Association of Engineers and Architects (SIA): Zürich, Switzerland, 1982. [Google Scholar]
- Schneider, S.; Hollmuller, P.; Le Strat, P.; Khoury, J.; Patel, M.; Lachal, B. Spatial–Temporal Analysis of the Heat and Electricity Demand of the Swiss Building Stock. Front. Built Environ. 2017, 3, 1–17. [Google Scholar] [CrossRef]
- Wang, D.; Landolt, J.; Mavromatidis, G.; Orehounig, K.; Carmeliet, J. CESAR: A bottom-up building stock modelling tool for Switzerland to address sustainable energy transformation strategies. Energy Build. 2018, 169, 9–26. [Google Scholar] [CrossRef]
- Murray, P.; Niffeler, M.; Mavromatidis, G.; Orehounig, K. Optimal retrofitting measures for residential buildings at large scale: A multi-objective approach. In Proceedings of the International Building Simulation Conference, Rome, Italy, 2–4 September 2019. [Google Scholar]
- Effiziento. Performance Diagrams; Effiziento: Güglingen, Germany, 2019. [Google Scholar]
- Roost, M.; Ménard, M.; Lehmann, M.; Ott, W.; Sitzmann, B. WP-GAP: Performance Gap bei Mehrfamilienhäusern mit Wärmepumpe—Die Rolle der Betreiber; Technical Report; BFE: Bern, Switzerland, 2018. [Google Scholar]
- Maivel, M.; Kurnitski, J. Low temperature radiator heating distribution and emission efficiency in residential buildings. Energy Build. 2014, 69, 224–236. [Google Scholar] [CrossRef]
- Küng, L.; Bütler, T.; Georges, G.; Boulouchos, K. Decarbonizing passenger cars using different powertrain technologies: Optimal fleet composition under evolving electricity supply. Transp. Res. Part C Emerg. Technol. 2018, 95, 785–801. [Google Scholar] [CrossRef]
- Weber, C.; Figenbaum, E. Transition from ICEV to BEV: How do personal usage patterns change? In Proceedings of the EVS32 International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium, Lyon, France, 19–22 May 2019. [Google Scholar]
- Hänggi, S.; Elbert, P.; Bütler, T.; Cabalzar, U.; Teske, S.L.; Bach, C.; Onder, C. A Review of Synthetic Fuels for Passenger Vehicles. Energy Rep. J. 2019, 5, 555–569. [Google Scholar] [CrossRef]
- Kohle, U.; Pfister, W.; Apfelbeck, R. Bioethanol Heater for the Passenger Compartments of Electric Cars; Technical Report 1; ATZ live: Wiesbaden, Germany, 2012; Volume 114. [Google Scholar]
- Robinson, A.; Blythe, P.; Bell, M.; Hübner, Y.; Hill, G. Analysis of electric vehicle driver recharging demand profiles and subsequent impacts on the carbon content of electric vehicle trips. Energy Policy 2013, 61, 337–348. [Google Scholar] [CrossRef] [Green Version]
- EBP. Elektromobilität—Studie Ladeinfrastruktur Region Basel; Technical Report; EBP, Sustainserv: Zürich, Switzerland, 2014. [Google Scholar]
- BFE. Schweizerische Elektrizitätsstatistik 2017; Technical Report; BFE: Bern, Switzerland, 2017. [Google Scholar]
- Portmann, M.; Galvagno-Erny, D.; Lorenz, P.; Schacher, D. Sonnendach.ch: Berechnung von Potenzialen in Gemeinden; Technical Report; BFE: Bern, Switzerland, 2016. [Google Scholar]
- Klauser, D. Solarpotentialanalyse für Sonnendach.ch. Schlussbericht; Technical Report; Meteotest: Bern, Switzerland, 2016. [Google Scholar]
- Plum, C.; Olschewski, R.; Jobin, M.; van Vliet, O. Public preferences for the Swiss electricity system after the nuclear phase-out: A choice experiment. Energy Policy 2019, 130, 181–196. [Google Scholar] [CrossRef]
- Thees, O.; Burg, V.; Erni, M.; Bowman, G.; Lemm, R. Biomassepotenziale der Schweiz für die energetische Nutzung, Ergebnisse des Schweizerischen Energiekompetenzzentrums SCCER BIOSWEET; Technical Report; WSL: Birmensdorf, Switzerland, 2017. [Google Scholar]
- Hostettler, T. Bericht zur Markterhebung Sonnenenergie 2017—Deutsche Fassung; Technical Report; Swisssolar: Zürich, Switzerland, 2018. [Google Scholar]
- Kaufmann, U. Schweizerische Statistik der Erneuerbaren Energien—Ausgabe 2017; Technical Report; BFE: Bern, Switzerland, 2018. [Google Scholar]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef] [Green Version]
- Wernet, G.; Bauer, C.; Steubing, B.; Reinhard, J.; Moreno-Ruiz, E.; Weidema, B. The ecoinvent database version 3 (part I): Overview and methodology. Int. J. Life Cycle Assess. 2016, 21, 1218–1230. [Google Scholar] [CrossRef]
- Messmer, A.; Frischknecht, R. Umweltbilanz Strommix Schweiz 2014; Technical Report; treeze Ltd.: Uster, Switzerland, 2016. [Google Scholar]
- KBOB. KBOB Ökobilanzdatenbestand v2.2:2016; Grundlage für die KBOB-Empfehlung 2009/1:2016: Ökobilanzdaten im Baubereich, Stand 2016; KBOB: Bern, Switzerland, 2016. [Google Scholar]
- Flury, K.; Frischknecht, R. Ökobilanz Erdgasauto; Technical Report; ESU-Services Ltd.: Uster, Switzerland, 2012. [Google Scholar]
- Frischknecht, R.; Itten, R.; Wyss, F.; Blanc, I.; Heath, G.; Raugei, M.; Sinha, P.; Wade, A. Subtask 2.0 “LCA”, IEA-PVPS Task 12; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2014.
- TEP. CO2-Intensität des Stromabsatzes an Schweizer Endkunden—Schlussbericht; Technical Report; TEP Energy GmbH: Zürich, Switzerland, 2009. [Google Scholar]
- Marshall, H.E. Sensitivity analysis. In Technology Management Handbook; CRC Press: Boca Raton, FL, USA, 1999; pp. 59–63. [Google Scholar]
- ElCom. Stromversorgungssicherheit der Schweiz 2018; Technical Report; ElCom: Bern, Switzerland, 2018. [Google Scholar]
- Dujardin, J.; Kahl, A.; Kruyt, B.; Bartlett, S.; Lehning, M. Interplay between photovoltaic, wind energy and storage hydropower in a fully renewable Switzerland. Energy 2017, 135, 513–525. [Google Scholar] [CrossRef]
- Beer, M. Abschätzung des Potenzials der Schweizer Speicherseen zur Lastdeckung bei Importrestriktionen. Zeitschrift für Energiewirtschaft 2018, 42, 1–12. [Google Scholar] [CrossRef]
- EKZ. NEC Installs Switzerland’s Largest Battery; EKZ: Zürich, Switzerland, 2019. [Google Scholar]
- Guttinger, M.; Ahcin, P. The potential of Demand Side Management and Vehicle-to-Grid for the city of Bern, Switzerland. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Teske, S.L.; Rüdisüli, M.; Bach, C.; Schildhauer, T.J. Potentialanalyse Power-to-Gas in der Schweiz; Technical Report; Empa: Dübendorf, Switzerland, 2019. [Google Scholar]
- Kober, T.; Bauer, C.; Bach, C.; Beuse, M.; Georges, G.; Held, M.; Heselhaus, S.; Korba, P.; Küng, L.; Malhotra, A.; et al. White Paper “Power-to-X: Perspectives in Switzerland”; Technical Report; Paul Scherrer Institut (PSI): Villigen, Switzerland, 2019. [Google Scholar]
- Romano, E.; Hollmuller, P.; Patel, M.K. Real-time carbon emission due to electricity consumption—A marginal approach for an open economy: The case of Switzerland. In Proceedings of the 3rd AIEE Energy Symposium—Current and Future Challenges to Energy Security, Milano, Italy, 10–12 December 2018; pp. 26–27. [Google Scholar]
- Climate Action Tracker. Country Assessments 2018. Available online: https://climateactiontracker.org/countries/switzerland (accessed on 18 June 2019).
- Sarsfield-Hall, R.; Unger, B. Fully Decarbonising Europe’s Energy System by 2050; Technical Report; Pöyry Point of View: London, UK, 2018. [Google Scholar]
- Kaya, Y. Impact of Carbon Dioxide Emission Control on GNP Growth: Interpretation of Proposed Scenarios. Paper presented at the IPCC Energy and Industry Subgroup, Response Strategies Working Group, Paris, France, 1990; Available online: https://www.ipcc.ch/report/emissions-scenarios/?idp=50 (accessed on 21 June 2019).
- Mavromatidis, G.; Orehounig, K.; Richner, P.; Carmeliet, J. A strategy for reducing CO2 emissions from buildings with the Kaya identity—A Swiss energy system analysis and a case study. Energy Policy 2016, 88, 343–354. [Google Scholar] [CrossRef]
- Díaz, P.; Vliet, O.V.; Patt, A.; Díaz, P.; Van Vliet, O.; Patt, A. Do We Need Gas as a Bridging Fuel? A Case Study of the Electricity System of Switzerland. Energies 2017, 10, 861. [Google Scholar] [CrossRef]
- IEA. World Energy Balances; Technical Report; International Energy Agency: Paris, France, 2016. [Google Scholar]






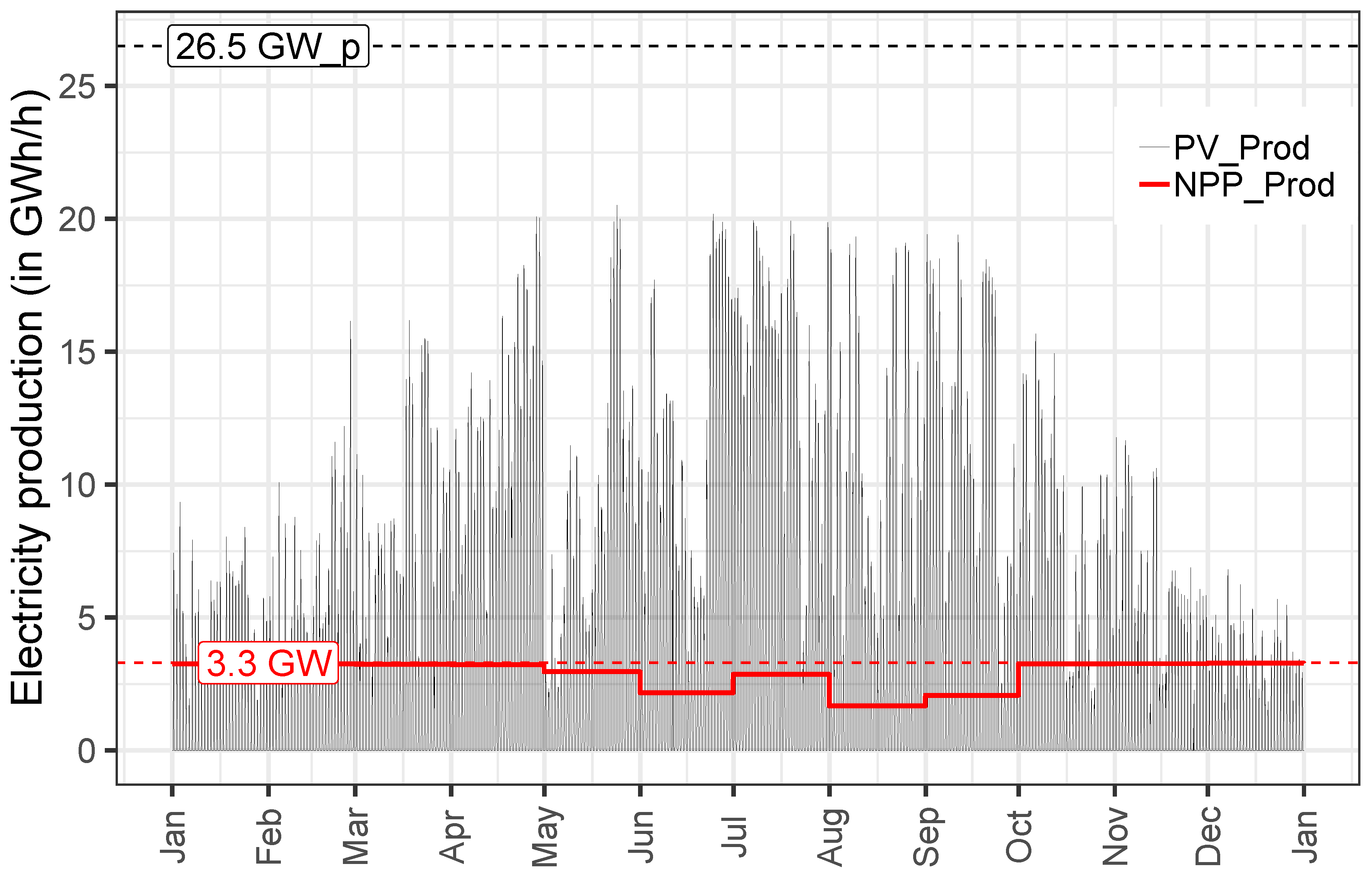













| Type | Profile | Notes/Sources |
|---|---|---|
| Production | Total_Prod_orig | Swissgrid: Total production control block CH 2010 |
| Production | NPP_Prod | BFE: monthly nuclear production CH 2010 |
| Production | PV_Prod | Renewables.ninja: hourly PV production CH 2010 at 26.5 GW |
| Production | Hydro_Prod_orig | Total_Prod_orig - NPP_Prod |
| Production | Hydro_Prod_smooth | smooth(Hydro_Prod_orig) |
| Production | Total_mod_Prod_orig | Hydro_Prod_orig + PV_Prod |
| Production | Total_mod_Prod_smooth | Hydro_Prod_smooth + PV_Prod |
| Demand | Total_Cons_orig | Swissgrid: Total end-use consumption control block CH 2010 |
| Demand | Enduse_Cons_orig | Swissgrid: Total consumption control block CH 2010 |
| Demand | LossPump_orig | Total_Cons_orig - Enduse_Cons_orig |
| Demand | LossPump_smooth | smooth(LossPump_orig) |
| Demand | Total_Cons_smooth | Enduse_Cons_orig + LossPump_smooth |
| Demand | HP_Cons | Heat pump electricity consumption |
| Demand | BEV_Cons | BEV electricity consumption |
| Demand | Total_mod_Cons_smooth | Total_Cons_smooth + HP_Cons + BEV_Cons |
| Scenario | Production Profile | Consumption Profile | Notes |
|---|---|---|---|
| “Status quo” | Total_Prod_orig | Total_Cons_orig | “Original” electricity production and demand of Swissgrid for 2010 |
| “PV-NPP” | Total_mod_Prod_smooth | Total_Cons_smooth | “Smoothed” electricity production with PV instead of NPP; “smoothed” electricity demand without additional heat pumps and BEV |
| “PV-NPP-HP-BEV” | Total_mod_Prod_smooth | Total_mod_Cons_smooth | Electricity production as in “PV-NPP”; electricity demand of “PV-NPP” plus additional electricity demand of heat pumps and BEV |
| Parameter | Default | Plausible Range | Notes [Sources] |
|---|---|---|---|
| HP share SH | 80% | [50–90%] | - |
| HP share DHW | 50% | [25–75%] | - |
| BEV km share | 20% | [10–50%] | - |
| PV prod. | 25 TWh | [12 *–50 **] | * POM [2]; ** Portmann et al. [54] |
| eta BEV | 85% | [80–90%] | - |
| HP flow temp. | 45 °C | [35, 50] | Effiziento [44] |
| SH savings | −42% * | [−20%, −64% **] | * BAU [2]; ** NEP [2] |
| CO2 int. nuc. | 12 g/kWh | [10–15] | Wernet et al. [61] |
| CO2 int. hydro | 13 g/kWh | [10–20] | Wernet et al. [61] |
| CO2 int. PV | 50 g/kWh | [15 *–92 **] | * OPT [65]; ** current [61] |
| CO2 int. imp. | 443 * g/kWh | [109 **–679 ***] | * CCGT [61]; ** France import mix [61]; |
| *** Germany import mix [61] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rüdisüli, M.; Teske, S.L.; Elber, U. Impacts of an Increased Substitution of Fossil Energy Carriers with Electricity-Based Technologies on the Swiss Electricity System. Energies 2019, 12, 2399. https://doi.org/10.3390/en12122399
Rüdisüli M, Teske SL, Elber U. Impacts of an Increased Substitution of Fossil Energy Carriers with Electricity-Based Technologies on the Swiss Electricity System. Energies. 2019; 12(12):2399. https://doi.org/10.3390/en12122399
Chicago/Turabian StyleRüdisüli, Martin, Sinan L. Teske, and Urs Elber. 2019. "Impacts of an Increased Substitution of Fossil Energy Carriers with Electricity-Based Technologies on the Swiss Electricity System" Energies 12, no. 12: 2399. https://doi.org/10.3390/en12122399
APA StyleRüdisüli, M., Teske, S. L., & Elber, U. (2019). Impacts of an Increased Substitution of Fossil Energy Carriers with Electricity-Based Technologies on the Swiss Electricity System. Energies, 12(12), 2399. https://doi.org/10.3390/en12122399






