Exergy and Exergoeconomic Analysis of a Combined Cooling, Heating, and Power System Based on Solar Thermal Biomass Gasification
Abstract
:1. Introduction
2. System Description and Modelling
2.1. System Description
2.2. Thermodynamic Models
- (1)
- It is assumed that the system is based on the steady state.
- (2)
- The pressure descends of the whole heat exchangers and pipeline can be neglected.
- (3)
- In the heat transfer models, all heat exchangers are considered to be countercurrent heat transfer.
- (4)
- In the AC/H model, it is assumed that the steam, water, and solution at the outlet of evaporator, condenser, absorber, and high and low pressure generator are all saturated.
- (5)
- In the heat transfer model of the solar dish collector, the heat exchange in the inner wall of the component is heat conduction, and the heat exchange between the component and the surrounding environment includes convection heat transfer and radiation heat transfer.
3. Methodology
3.1. Exergy Analysis
3.2. Exergoeconomic Analysis
4. Results and Discussion
4.1. Initialization
4.2. Results
4.2.1. Exergy Performances
4.2.2. Exergoeconomic Performances
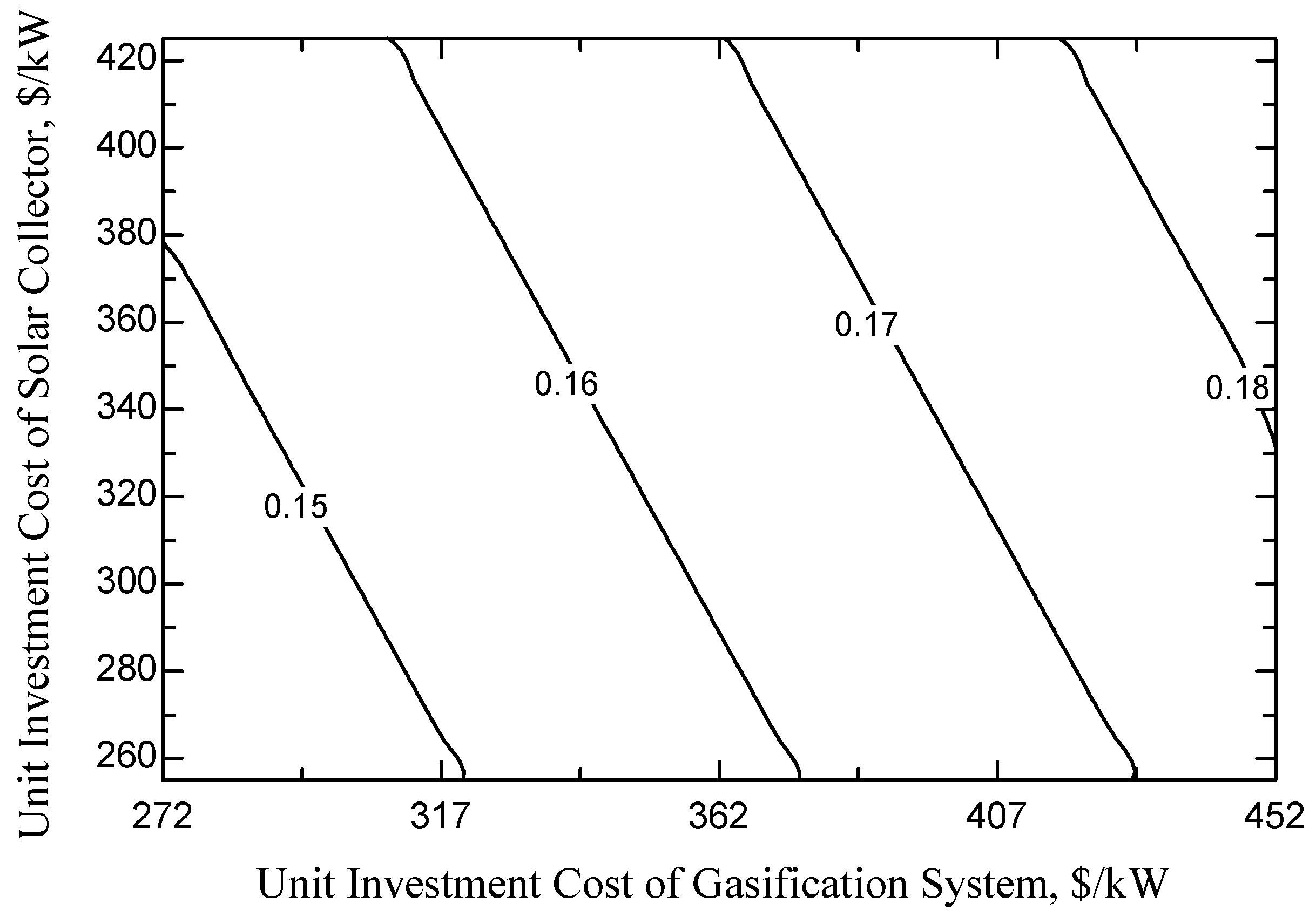
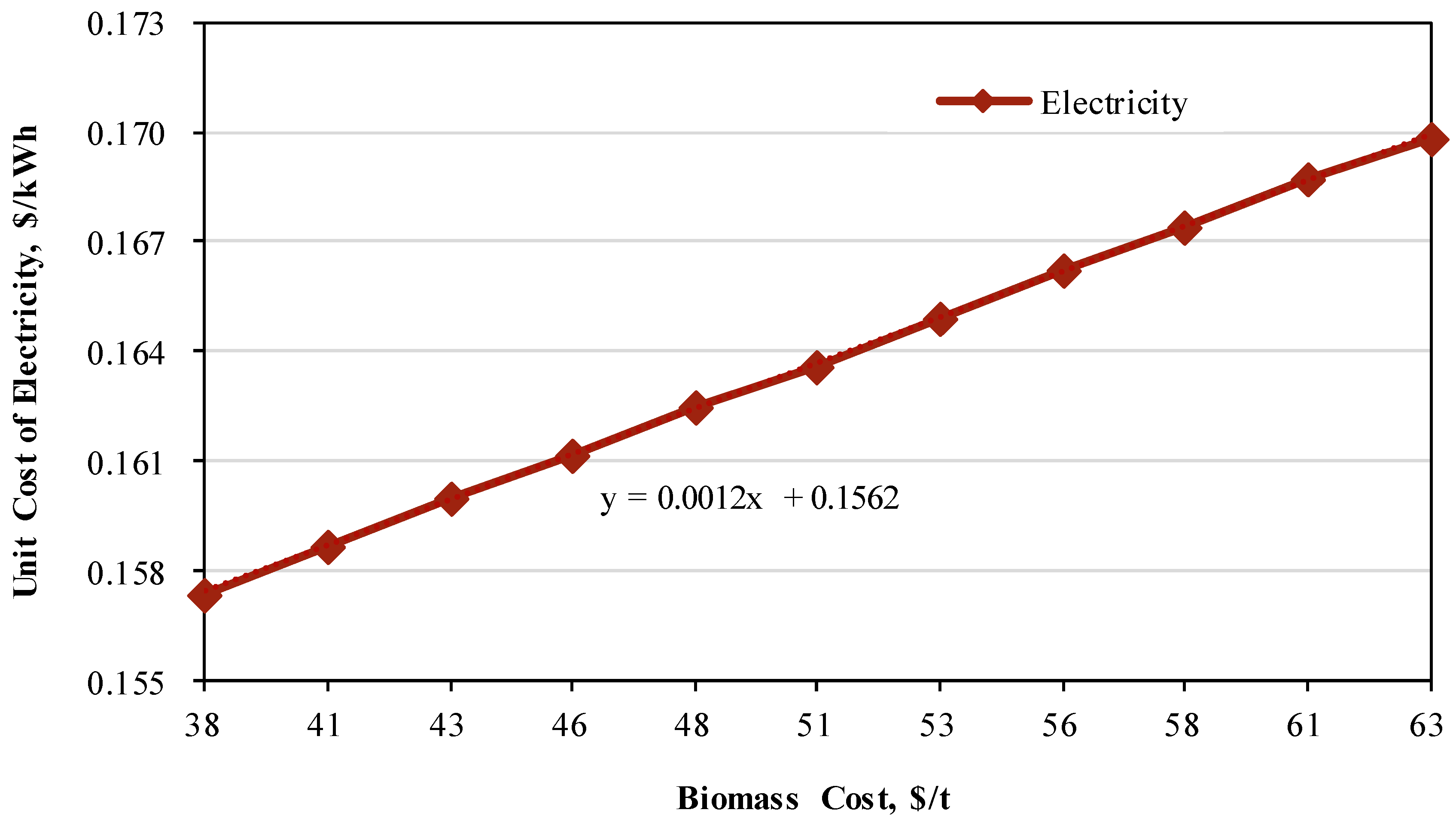
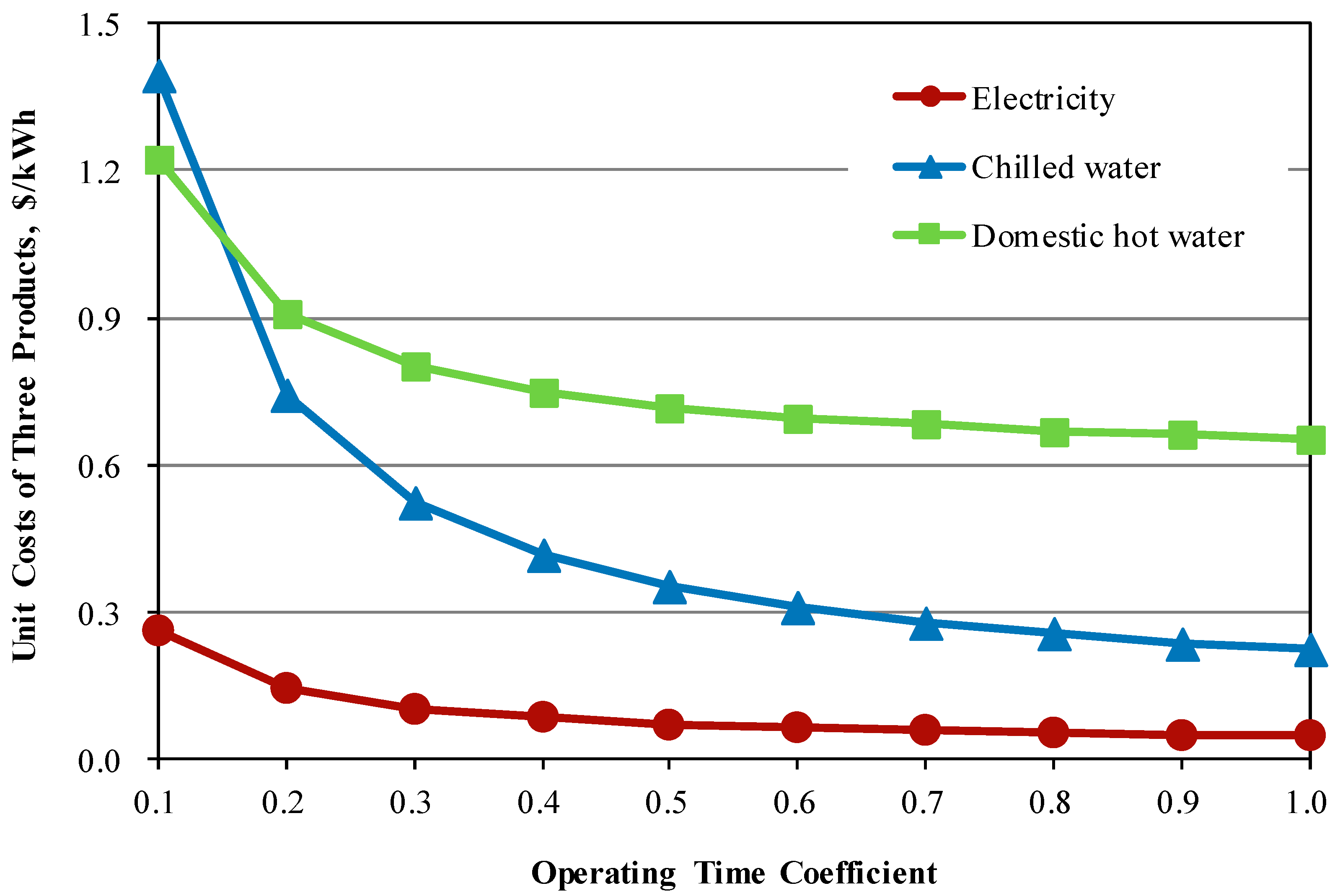
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| surface area of the parabolic dish mirror (m2) | |
| A | ash |
| C | exergy cost ($/h) |
| c | unit exergy cost ($/kWh) |
| average specific heat (kJ/(kg·K)) | |
| DNI | solar radiation illuminance (W/m2) |
| Ex | exergy (kW) |
| specific exergy (kJ/kg) | |
| exergoeconomic factor | |
| FC | fixed carbon |
| H | enthalpy (kJ) |
| h | specific enthalpy (kJ/kg) |
| LHV | low heat value (MJ/Nm3) |
| m | mass flow (kg/s) |
| M | moisture |
| maximum power generation capacity (kW) | |
| n | service life (year) |
| p | product |
| Q | heat transfer (kW) |
| R | universal gas constant (kJ/((kmol·K)) |
| S | entropy (kJ/K) |
| s | specific entropy (kJ/(kg·K)) |
| i | interest rate |
| T | temperature (°C or K) |
| x | molar ratio |
| V | volatile |
| Z | investment cost ($) |
| Greek symbols | |
| reflectivity of the parabolic dish mirror | |
| operating hours (h) | |
| interception factor | |
| shading factor | |
| efficiency (%) | |
| exergy efficiency | |
| capital recovery coefficient | |
| fixed cost as a percentage of initial investment cost | |
| ratio of exergy to energy | |
| Subscripts and superscripts | |
| a | ambient |
| Abs | absorber |
| b | biomass |
| C | carbon |
| ch | chemical |
| cond | conduction |
| conv | convection |
| cw | cooling water |
| des | destruction |
| dw | domestic hot water |
| exh | exhaust gas |
| Eva | evaporator |
| f | fuel |
| H | hydrogen |
| HG | high pressure generator |
| HX | heat exchanger |
| in | inlet |
| jw | jacket water |
| k | species |
| l | loss |
| LG | low pressure generator |
| N | nitrogen |
| 0 | standard reference state |
| O | oxygen |
| out | outlet |
| p | product |
| ph | physical |
| rad | radiation |
| rw | chilled water |
| sol | solar |
| sw | space heating water |
| W | mechanical power |
| w | tap water |
References
- Liu, T.; Liu, Q.; Lei, J.; Sui, J. A new solar hybrid clean fuel-fired distributed energy system with solar thermochemical conversion. J. Clean. Prod. 2019, 213, 1011–1023. [Google Scholar] [CrossRef]
- No, S.-Y. Application of bio-oils from lignocellulosic biomass to transportation, heat and power generation—A review. Renew. Sustain. Energy Rev. 2014, 40, 1108–1125. [Google Scholar] [CrossRef]
- Wang, J.-J.; Yang, K.; Xu, Z.-L.; Fu, C. Energy and exergy analyses of an integrated CCHP system with biomass air gasification. Appl. Energy 2015, 142, 317–327. [Google Scholar] [CrossRef]
- Wang, J.; Sui, J.; Jin, H. An improved operation strategy of combined cooling heating and power system following electrical load. Energy 2015, 85, 654–666. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y. Energy, exergy and environmental analysis of a hybrid combined cooling heating and power system utilizing biomass and solar energy. Energy Convers. Manag. 2016, 124, 566–577. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Liu, L.; Zeng, R.; Zhang, G. Exergy and environmental assessments of a novel trigeneration system taking biomass and solar energy as co-feeds. Appl. Therm. Eng. 2016, 104, 697–706. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Liu, L.; Zeng, R.; Zhang, G. Analysis of a feasible trigeneration system taking solar energy and biomass as co-feeds. Energy Convers. Manag. 2016, 122, 74–84. [Google Scholar] [CrossRef]
- Kalinci, Y.; Hepbasli, A.; Dincer, I. Performance assessment of hydrogen production from a solar-assisted biomass gasification system. Int. J. Hydrog. Energy 2013, 38, 6120–6129. [Google Scholar] [CrossRef]
- Li, R.; Zeng, K.; Soria, J.; Mazza, G.; Gauthier, D.; Rodriguez, R.; Flamant, G. Product distribution from solar pyrolysis of agricultural and forestry biomass residues. Renew. Energy 2016, 89, 27–35. [Google Scholar] [CrossRef]
- Molino, A.; Larocca, V.; Chianese, S.; Musmarra, D. Biofuels Production by Biomass Gasification: A Review. Energies 2018, 11, 811. [Google Scholar] [CrossRef]
- Chang, K.-H.; Lou, K.-R.; Ko, C.-H. Potential of bioenergy production from biomass wastes of rice paddies and forest sectors in Taiwan. J. Clean. Prod. 2019, 206, 460–476. [Google Scholar] [CrossRef]
- Rahbari, A.; Venkataraman, M.B.; Pye, J. Energy and exergy analysis of concentrated solar supercritical water gasification of algal biomass. Appl. Energy 2018, 228, 1669–1682. [Google Scholar] [CrossRef]
- Xu, W.D.; Duan, J.; Mao, W.J. Process Study and Exergy Analysis of a Novel Air Separation Process Cooled by LNG Cold Energy. J. Therm. Sci. 2014, 23, 77–84. [Google Scholar] [CrossRef]
- Liu, J.C.; Zhang, X.J.; Xu, Y.J.; Chen, Z.Y.; Chen, H.S.; Tan, C.Q. Economic Analysis of using Above Ground Gas Storage Devices for Compressed Air Energy Storage System. J. Therm. Sci. 2014, 23, 535–543. [Google Scholar] [CrossRef]
- Han, C.H.; Kim, K.H. Entransy and Exergy Analyses for Optimizations of Heat-Work Conversion with Carnot Cycle. J. Therm. Sci. 2016, 25, 242–249. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, N.; Ding, Y.; Chang, C.; Wang, D.; Yuan, T. Exergy and exergoeconomic analyses of a combined cooling, heating, and power (CCHP) system based on dual-fuel of biomass and natural gas. J. Clean. Prod. 2019, 206, 893–906. [Google Scholar] [CrossRef]
- Seyyedi, S.M.; Hashemi-Tilehnoee, M.; Rosen, M.A. Exergy and exergoeconomic analyses of a novel integration of a 1000 MW pressurized water reactor power plant and a gas turbine cycle through a superheater. Ann. Nucl. Energy 2018, 115, 161–172. [Google Scholar] [CrossRef]
- Kohl, T.; Teles, M.; Melin, K.; Laukkanen, T.; Järvinen, M.; Park, S.W.; Guidici, R. Exergoeconomic assessment of CHP-integrated biomass upgrading. Appl. Energy 2015, 156, 290–305. [Google Scholar] [CrossRef]
- Wang, J.; Li, M.; Ren, F.; Li, X.; Liu, B. Modified exergoeconomic analysis method based on energy level with reliability consideration: Cost allocations in a biomass trigeneration system. Renew. Energy 2018, 123, 104–116. [Google Scholar] [CrossRef]
- Wang, Z.; Han, W.; Zhang, N.; Su, B.; Liu, M.; Jin, H. Assessment of off-design performance of a combined cooling, heating and power system using exergoeconomic analysis. Energy Convers. Manag. 2018, 171, 188–195. [Google Scholar] [CrossRef]
- Wang, J.; Mao, T. Cost allocation and sensitivity analysis of multi-products from biomass gasification combined cooling heating and power system based on the exergoeconomic methodology. Energy Convers. Manag. 2015, 105, 230–239. [Google Scholar] [CrossRef]
- Soltani, S.; Mahmoudi, S.M.S.; Yari, M.; Morosuk, T.; Rosen, M.A.; Zare, V. A comparative exergoeconomic analysis of two biomass and co-firing combined power plants. Energy Convers. Manag. 2013, 76, 83–91. [Google Scholar] [CrossRef]
- Wang, J.; Mao, T.; Wu, J. Modified exergoeconomic modeling and analysis of combined cooling heating and power system integrated with biomass-steam gasification. Energy 2017, 139, 871–882. [Google Scholar] [CrossRef]
- Ma, Y.J.; Dang, X.G.; Shan, Z.H. Thermal Analysis and Identification of Potential Fire-proof Energy Building Material Based on Artificial Leather. J. Therm. Sci. 2019, 28, 88–96. [Google Scholar] [CrossRef]
- Lazzaretto, A.; Tsatsaronis, G. SPECO: A systematic and general methodology for calculating efficiencies and costs in thermal systems. Energy 2006, 31, 1257–1289. [Google Scholar] [CrossRef]
- Xu, L.; Yan, P.; Huang, H.Y.; Han, W.J. Effects of Hot Steam Injection from the Slot at the Trailing Edge on Turbine Nozzle Vane Flow Field. J. Therm. Sci. 2008, 17, 298–304. [Google Scholar] [CrossRef]
- Erlach, B.; Tsatsaronis, G.; Cziesla, F. A new approach for assigning costs and fuels to cogeneration products. Int. J. Thermodyn. 2001, 4, 145–156. [Google Scholar]
- Peng, Q.; Zhang, S.; Guo, J. Resonable structure of supplementary equation used for cost analysis in thermal economics. Therm. Power Gener. 2003, 1, 29–31. [Google Scholar]
- Wang, Z.; Han, W.; Zhang, N.; Liu, M.; Jin, H. Exergy cost allocation method based on energy level (ECAEL) for a CCHP system. Energy 2017, 134, 240–247. [Google Scholar] [CrossRef]
- Wang, J.; Ma, C.; Wu, J. Thermodynamic analysis of a combined cooling, heating and power system based on solar thermal biomass gasification. Appl. Energy 2019, 247, 102–115. [Google Scholar] [CrossRef]
- Klein, S.A. Software, Engineering Equation Solver (EES)(6.883-3D); F-Chart Software: Madison, WI, USA, 2012; Available online: http://www.fchart.com/ees/ (accessed on 30 April 2019).
- Yang, Y. Study of Solar-Hybrid Combined Cooling Heating and Power System Drvien by Natural Gas; North China Electric Power University: Baoding, China, 2017. [Google Scholar]
- Wang, J.; Mao, T.; Sui, J.; Jin, H. Modeling and performance analysis of CCHP (combined cooling, heating and power) system based on co-firing of natural gas and biomass gasification gas. Energy 2015, 93, 801–815. [Google Scholar] [CrossRef]
- Wang, J.; Xie, X.; Lu, Y.; Liu, B.; Li, X. Thermodynamic performance analysis and comparison of a combined cooling heating and power system integrated with two types of thermal energy storage. Appl. Energy 2018, 219, 114–122. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Chu, S.X.; Liu, L.H. Analysis of terrestrial solar radiation exergy. Sol. Energy 2009, 83, 1390–1404. [Google Scholar] [CrossRef]
- Ptasinski, K.J.; Prins, M.J.; Pierik, A. Exergetic evaluation of biomass gasification. Energy 2007, 32, 568–574. [Google Scholar] [CrossRef]
- Yue, T.; Lior, N. Exergo economic analysis of solar-assisted hybrid power generation systems integrated with thermochemical fuel conversion. Appl. Energy 2017, 191, 204–222. [Google Scholar] [CrossRef]
- Yue, T.; Lior, N. Exergo-economic competitiveness criteria for hybrid power cycles using multiple heat sources of different temperatures. Energy 2017, 135, 943–961. [Google Scholar] [CrossRef]
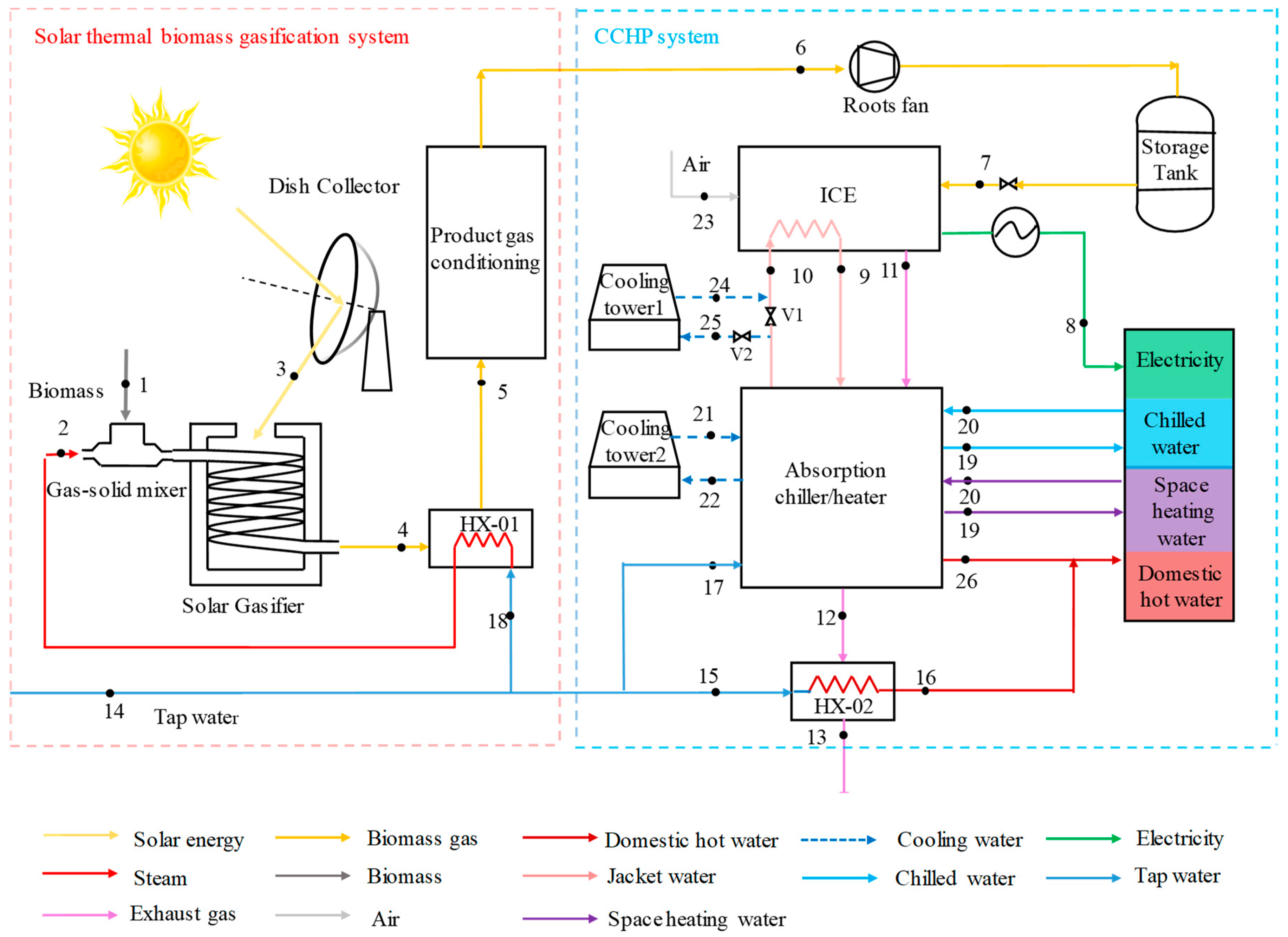
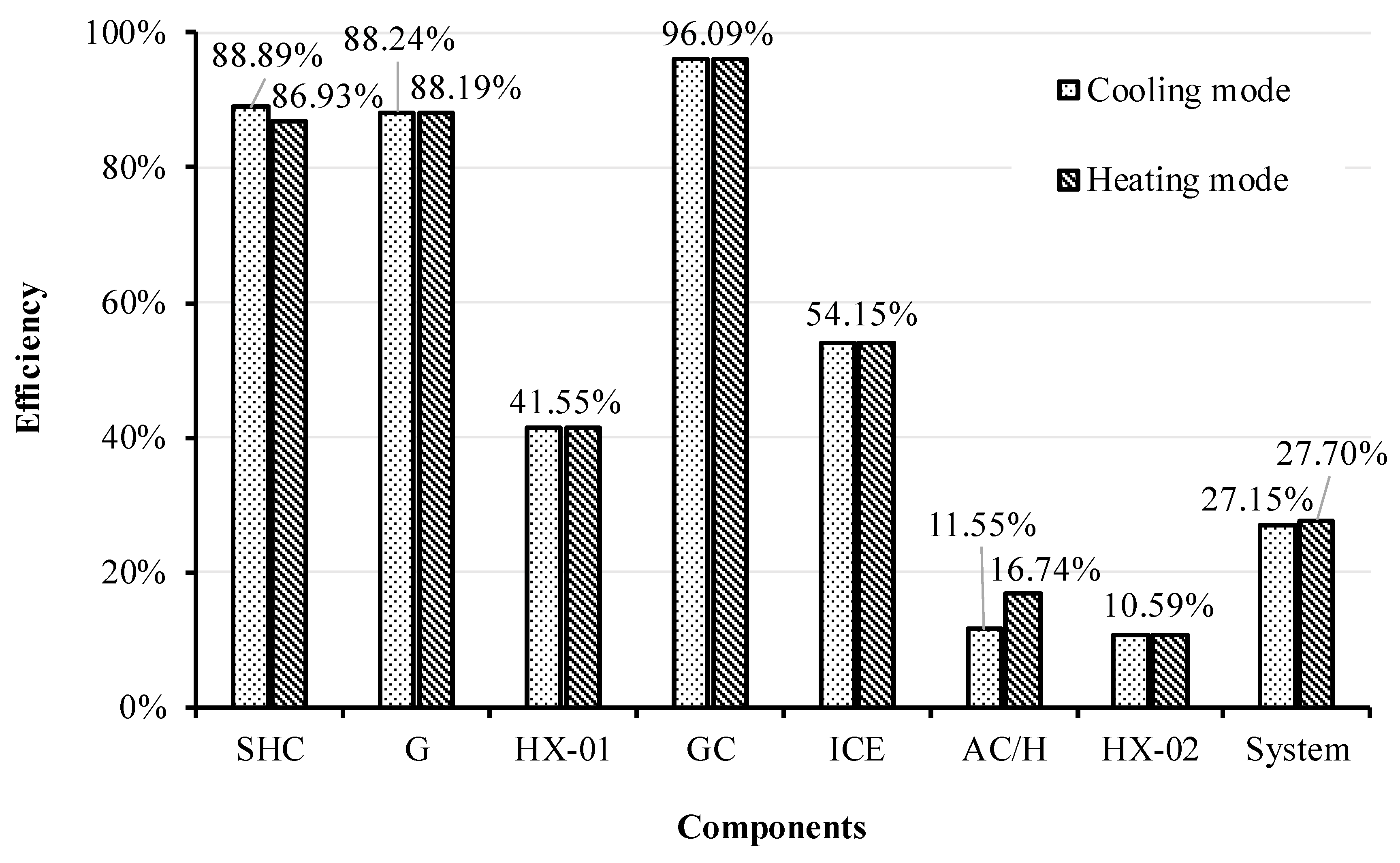
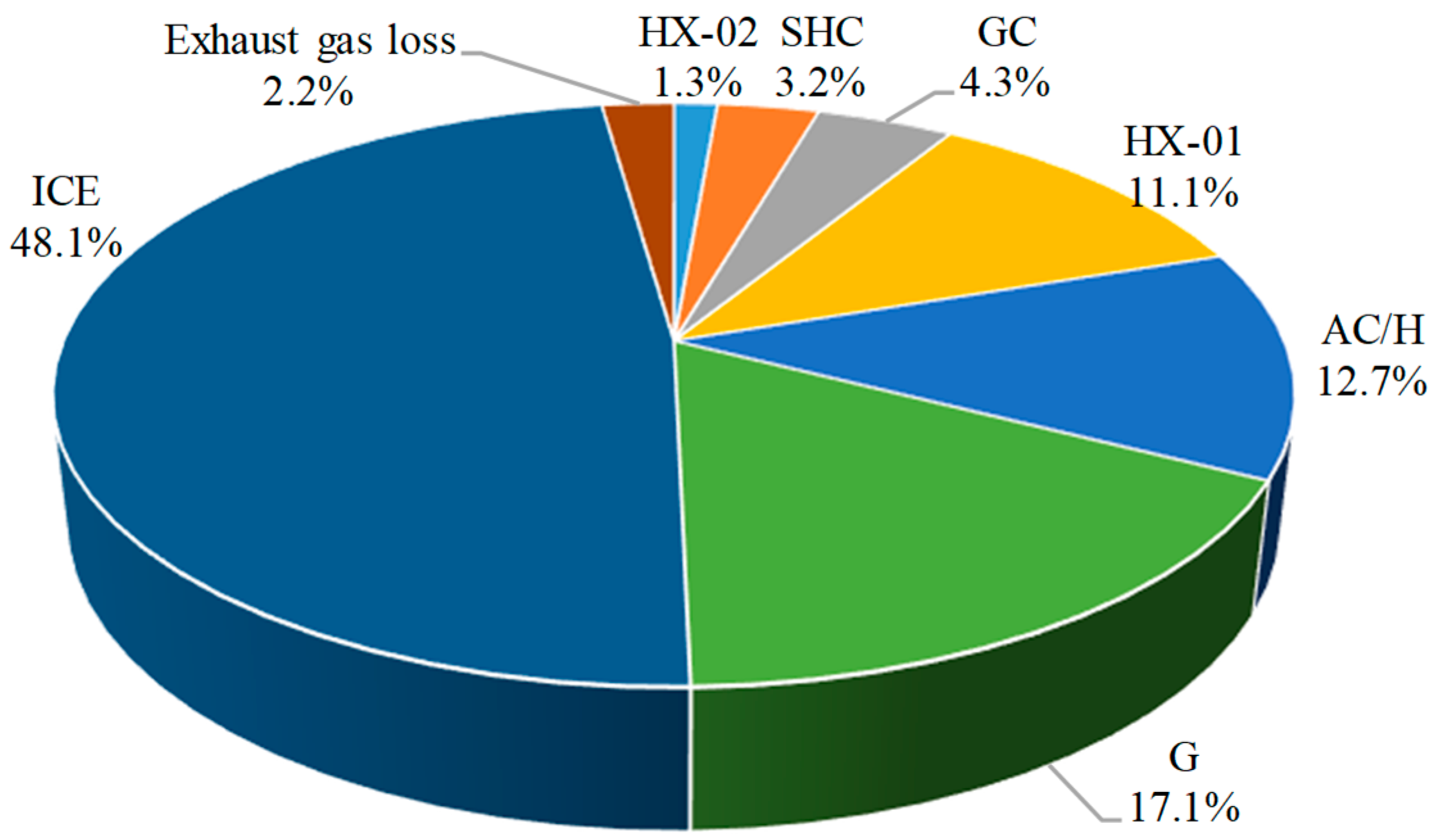
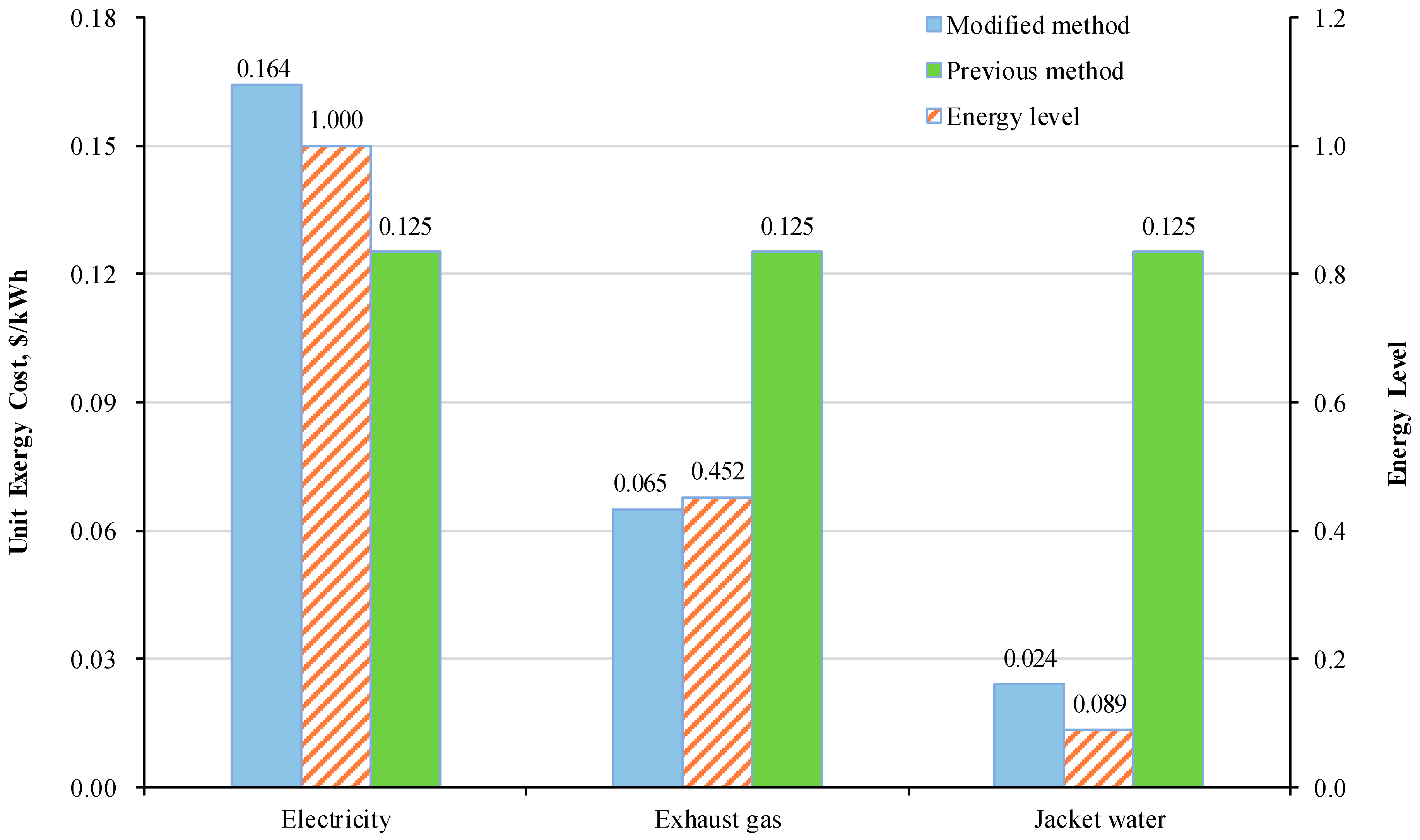

| Components | Parameters | Value |
|---|---|---|
| Biomass steam subsystem | Heat collecting area (m2) | 115.6 |
| Radiation intensity(W/m2) | Winter 600/Summer 800 | |
| Steam temperature (°C) | 450 (state 2) | |
| Tap water temperature (°C) | 25 (state 18, 17, and 15) | |
| HX-01 inlet temperature (°C) | 800 (state 4) | |
| HX-01 outlet temperature (°C) | 43 (state 5) | |
| ICE | ICE inlet (°C) | 25 (state 7) |
| Exhaust gas heat (kW) | 47.16 | |
| Jacket water heat (kW) | 50.31 | |
| Exhaust gas thermal efficiency (%) | 15.94 | |
| power generation (kW) | 100 | |
| AC/H | Exhaust gas temperature (°C) | 478/170 (state 11/12) |
| Jacket water temperature (°C) | 85/70 (state 9/10) | |
| Chilled water temperature (°C) | 14/7 (state 20/19) | |
| Space heating water temperature (°C) | 50/60 (state 20/19) | |
| Cooling water temperature (°C) | 32/36 (state 21/22) | |
| HX-02 | Exhaust gas temperature (°C) | 120 (state 13) |
| Domestic hot water temperature (°C) | 60 (state 16) |
| Components | Energy Balance Equations | Auxiliary Equations |
|---|---|---|
| Solar dish collector | , , , Further detailed data for heat transfer can be found in Ref. [30]. | |
| Biomass gasification | Further detailed data for heat transfer can be found in Ref. [30]. | |
| ICE | , , Further detailed data for heat transfer can be found in Ref. [32,33,34] | |
| AC/H | (summer) (winter) Further detailed data for heat transfer can be found in Ref. [5] | |
| HX |
| Item | Parameters | |||||
|---|---|---|---|---|---|---|
| Wheat straw | Proximate Analysis (wt. %) | V | FC | A | M | - |
| 70.11 | 17.47 | 9.14 | 3.28 | - | ||
| Elemental analysis (wt. %) | C | H | O | N | S | |
| 45.17 | 5.75 | 35.66 | 0.86 | 0.14 | ||
| LHV (MJ/Nm3) | 17.4 | |||||
| Items | Component | Unit Cost | Capacity | Investment (103 $) |
|---|---|---|---|---|
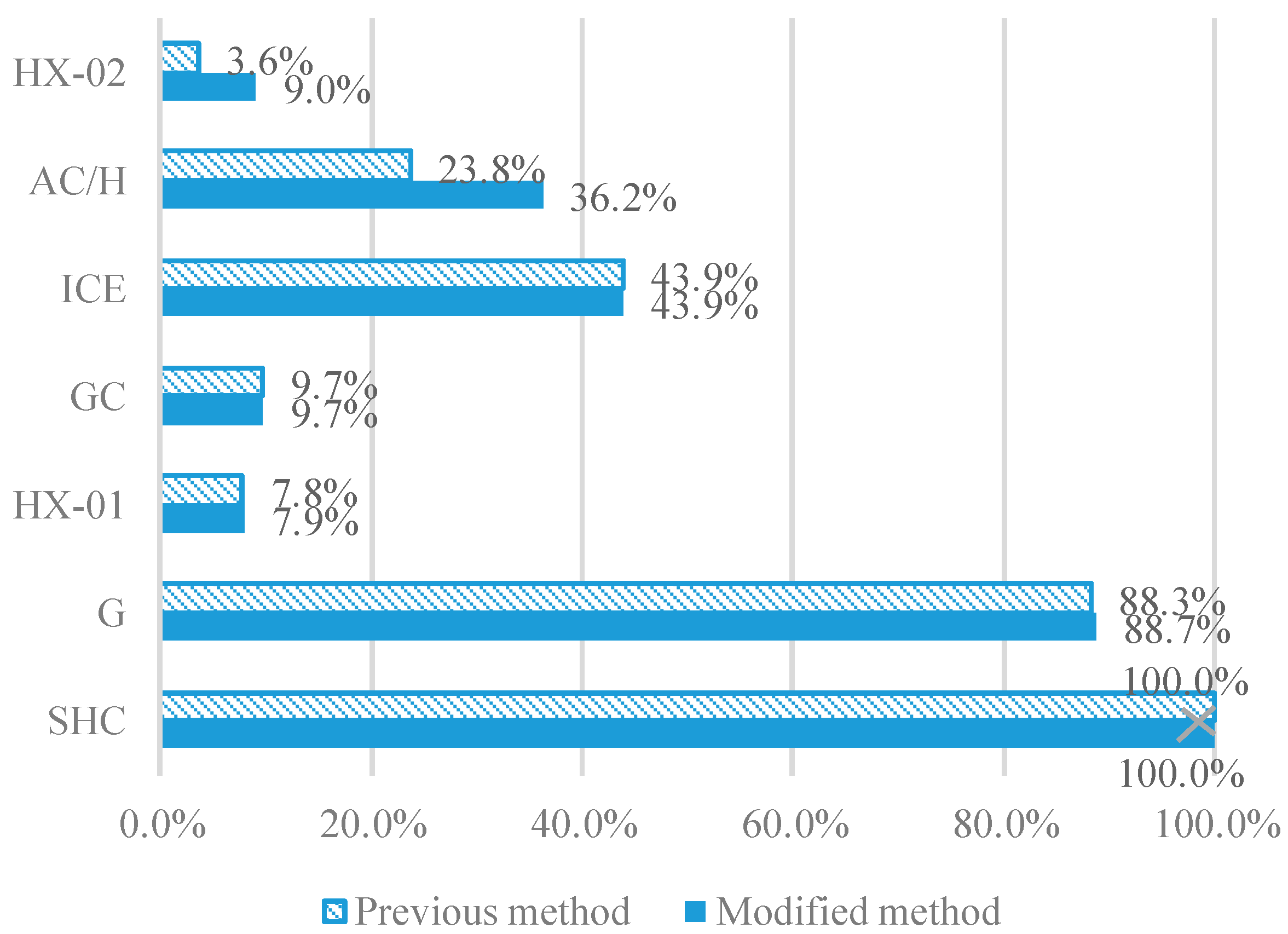
| Investment | G | 362 ($/kW) | 309.2 (kW) | 111.93 |
| SHC | 340.28 ($/m2) | 115.6 (m2) | 39.39 | |
| ICE | 695.04 ($/kW) | 100 (kW) | 69.50 | |
| AC/H | 173.76 ($/kW) | 109.1 (kW) | 18.97 | |
| HX 01 | 30.408 ($/kW) | 54.3 (kW) | 1.59 | |
| HX 02 | 30.408 ($/kW) | 7.6 (kW) | 0.29 | |
| Cost parameter | Annual operating hours, h | 1500 | Service life, year | 20 |
| Maintenance cost coefficient | 2.5% | Interest rate | 6.15% | |
| Fuel price | Biomass ($/ton) | 50.68 | Tap water ($/ton) | 1.035 |
| Operation Mode | Project | Electricity | Chilled Water/Heating Water | Domestic Hot Water |
|---|---|---|---|---|
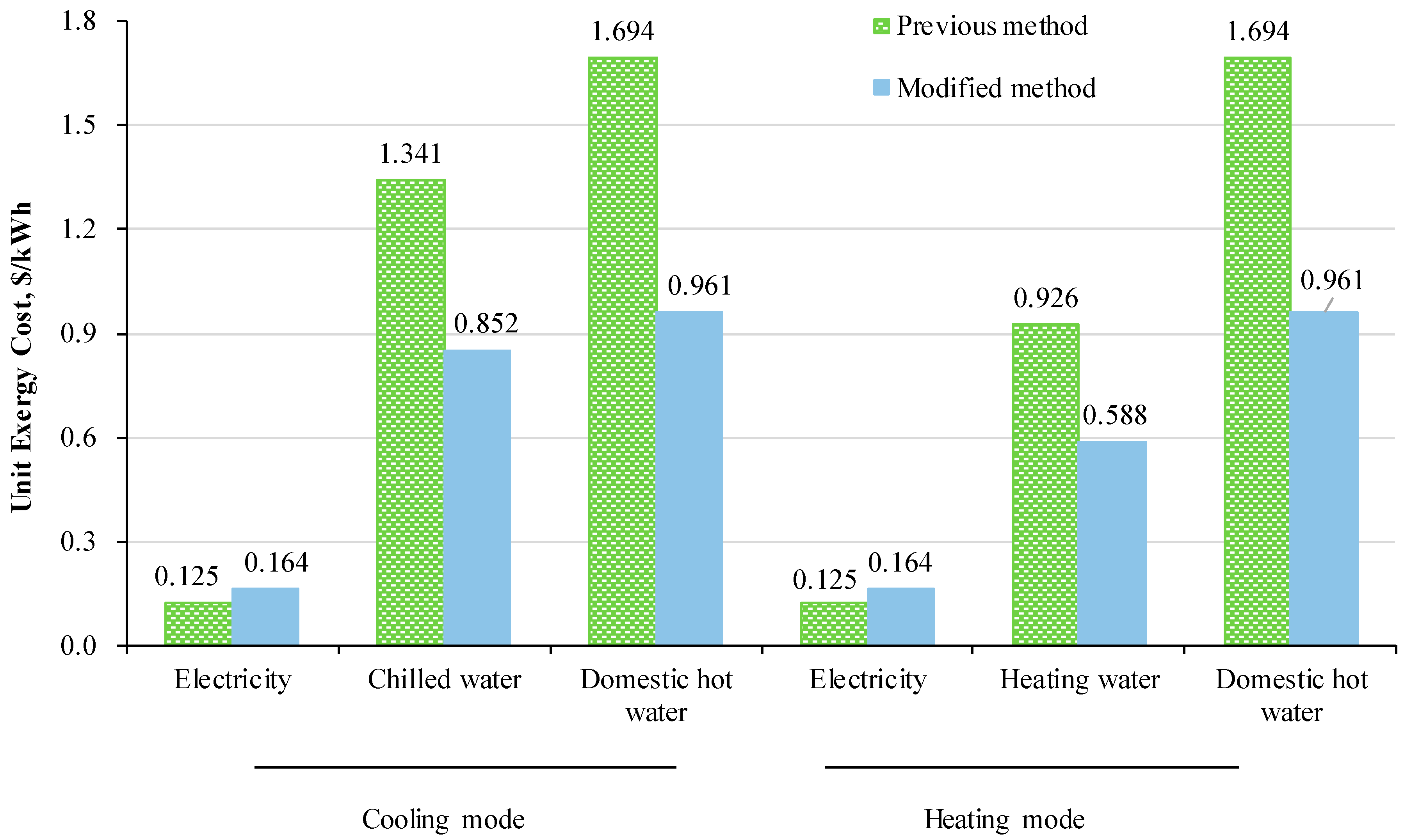
| Cooling mode | Energy cost ($/kWh) | 0.164 | 0.044 | 0.052 |
| Exergy cost ($/kWh) | 0.164 | 0.852 | 0.961 | |
| Heating mode | Energy cost ($/kWh) | 0.164 | 0.054 | 0.052 |
| Exergy cost ($/kWh) | 0.164 | 0.588 | 0.961 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wang, J.; Wu, J.; Ma, C. Exergy and Exergoeconomic Analysis of a Combined Cooling, Heating, and Power System Based on Solar Thermal Biomass Gasification. Energies 2019, 12, 2418. https://doi.org/10.3390/en12122418
Wu J, Wang J, Wu J, Ma C. Exergy and Exergoeconomic Analysis of a Combined Cooling, Heating, and Power System Based on Solar Thermal Biomass Gasification. Energies. 2019; 12(12):2418. https://doi.org/10.3390/en12122418
Chicago/Turabian StyleWu, Jin, Jiangjiang Wang, Jing Wu, and Chaofan Ma. 2019. "Exergy and Exergoeconomic Analysis of a Combined Cooling, Heating, and Power System Based on Solar Thermal Biomass Gasification" Energies 12, no. 12: 2418. https://doi.org/10.3390/en12122418
APA StyleWu, J., Wang, J., Wu, J., & Ma, C. (2019). Exergy and Exergoeconomic Analysis of a Combined Cooling, Heating, and Power System Based on Solar Thermal Biomass Gasification. Energies, 12(12), 2418. https://doi.org/10.3390/en12122418





