Decoupled Current Controller Based on Reduced Order Generalized Integrator for Three-Phase Grid-Connected VSCs in Distributed System
Abstract
:1. Introduction
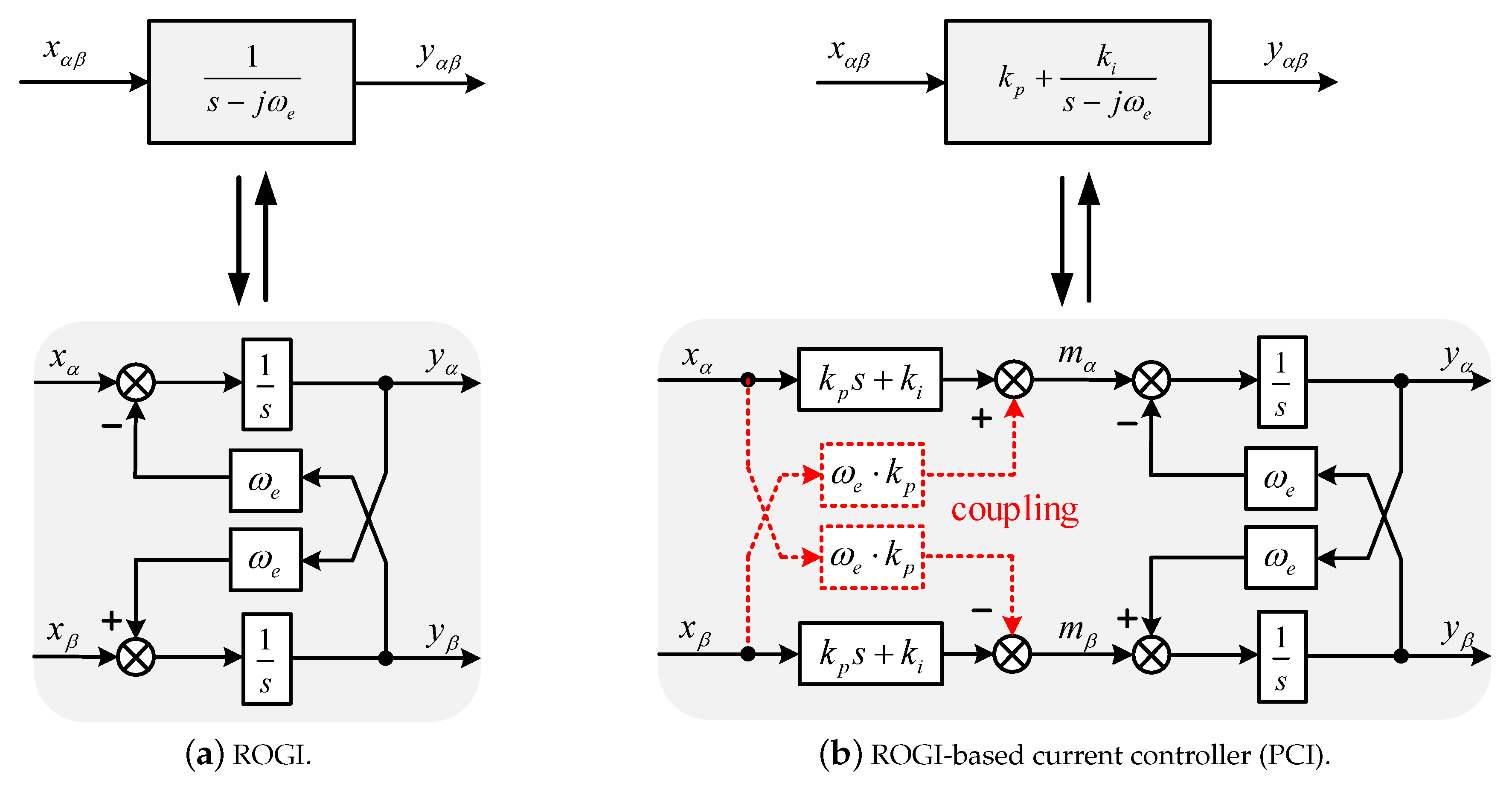
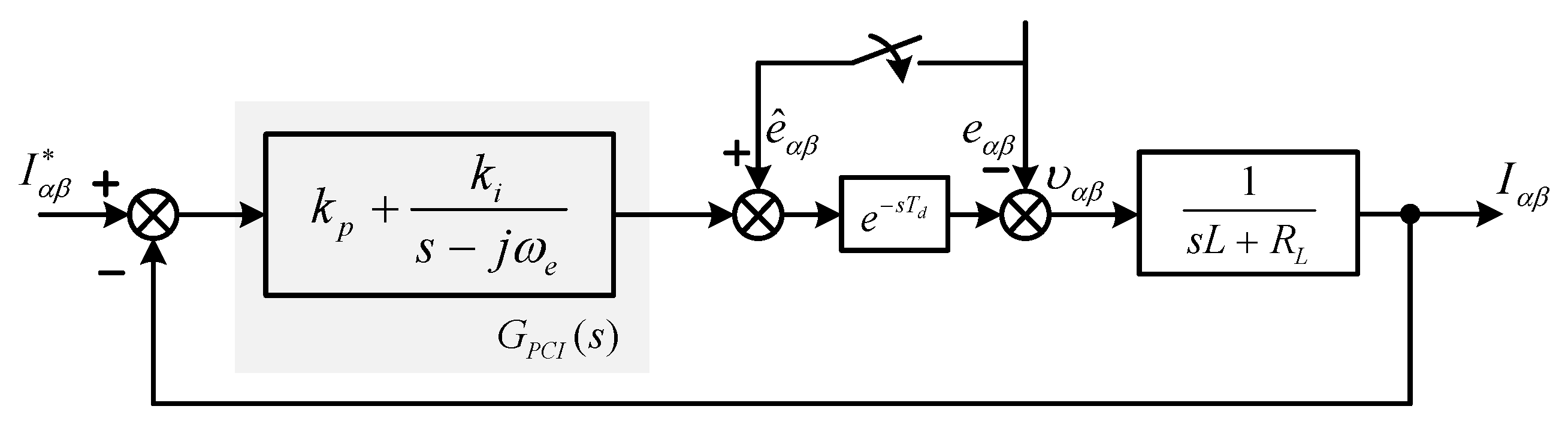
2. Coupling Analysis of ROGI-Based Current Controller
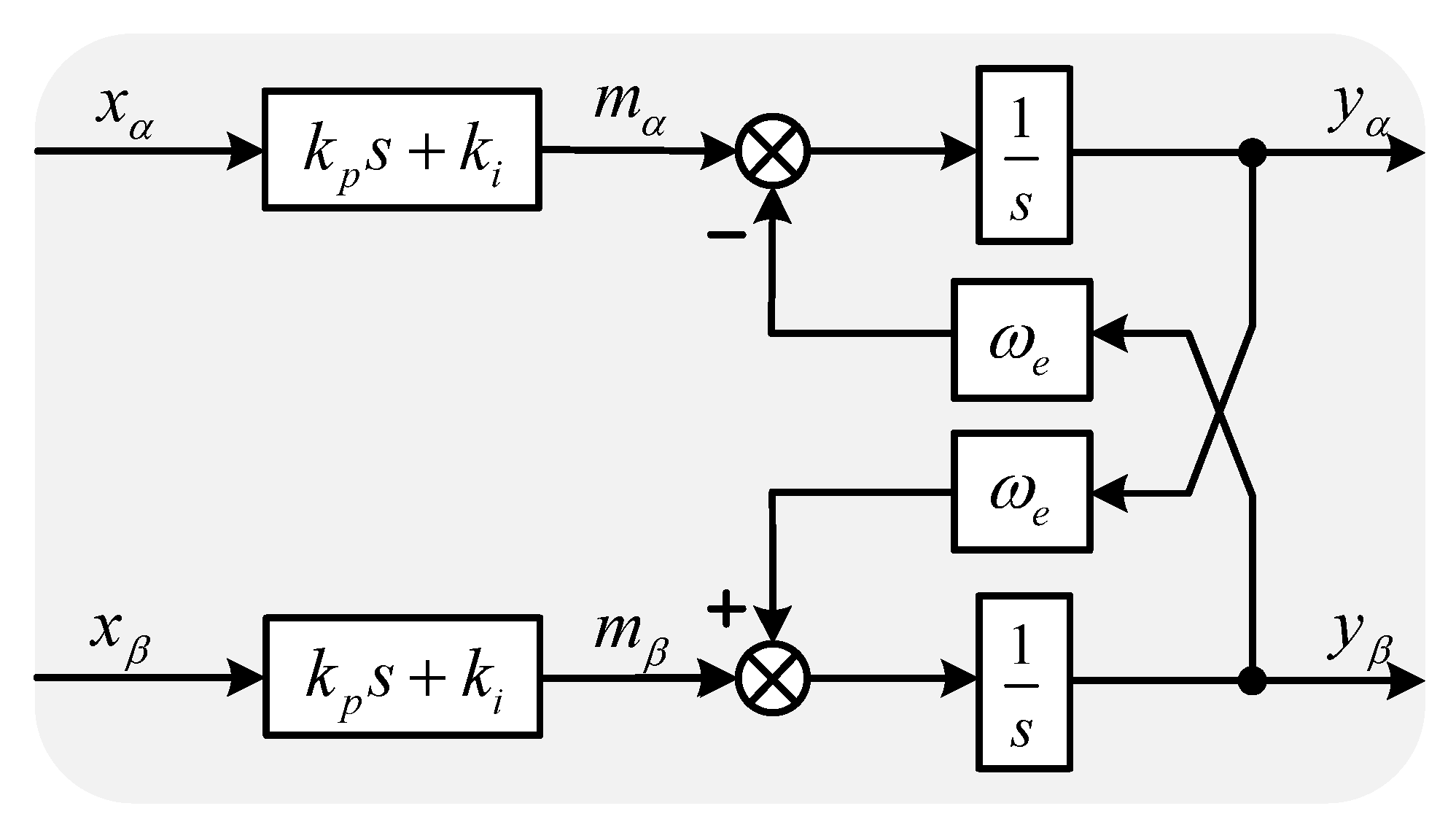
3. The Proposed ROGI-Based Decoupled Current Controller
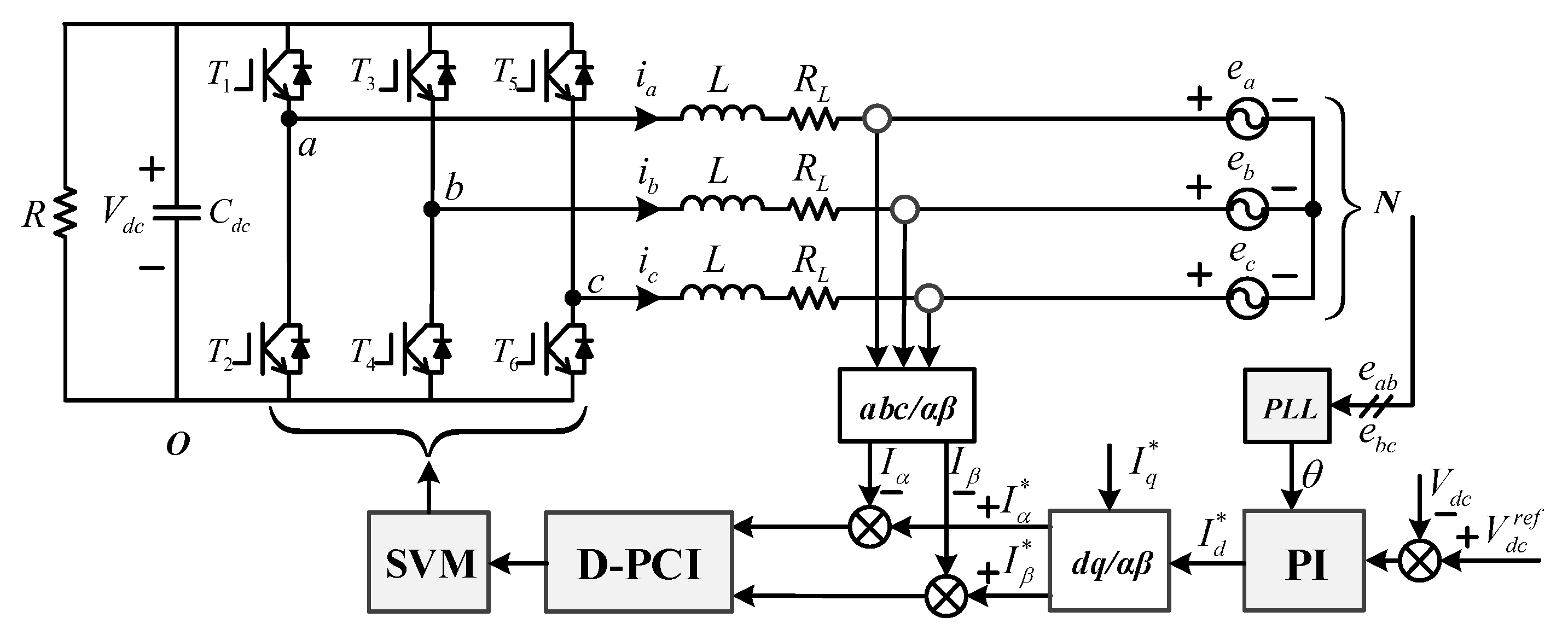
3.1. Structure of the D-PCI Controller
3.2. Performance Analysis of the D-PCI Controller
- (1)
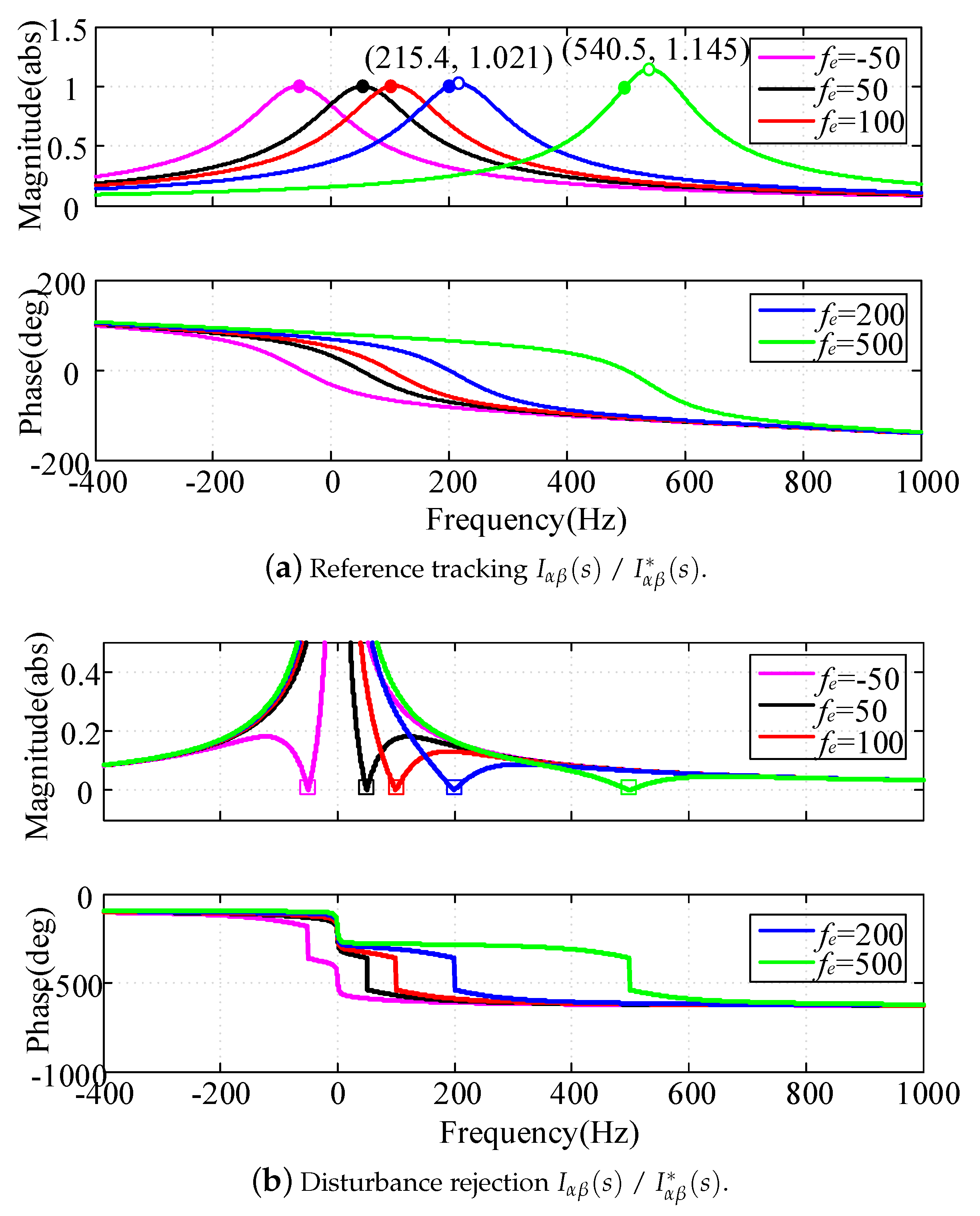
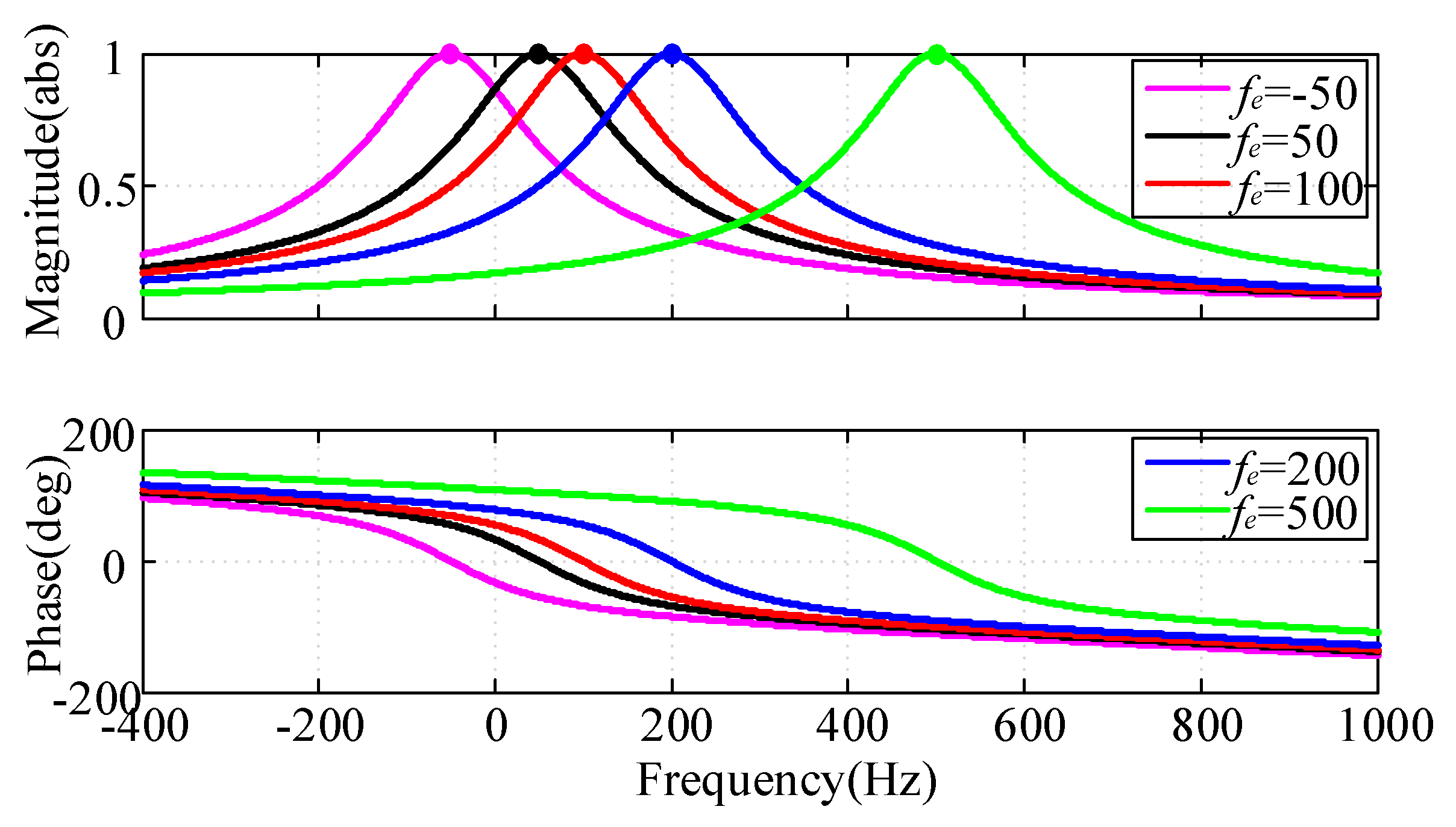
- Since the controller provides infinite gain at the interested control frequency (−50 Hz, 50 Hz, 100 Hz, 200 Hz and 500 Hz), unity gain and phase lag output current can be achieved, i.e., , the steady-state error is zero, as shown by “•” in Figure 8a.
- (2)
- As shown by “∘” in Figure 8a, a closed-loop anomalous peak (amplification phenomenon of output current) appears near the control frequency, and, as the control frequency increases, the peak value becomes larger, e.g., no obvious amplification appears at 50 Hz or 100 Hz, while the peak value is 1.02 (1.145) times of the unity gain at 215 Hz (540 Hz). It means that the closed-loop anomalous peak will aggravate the transient oscillation and increase the adjustment time and overshoot with the abrupt change of reference signal. Besides, if phase lock angle is inaccurate, the steady-state output current would be amplified.
- (3)
- As shown in Figure 8b, the disturbance signal at the interested control frequency is completely suppressed, i.e., the magnitude is zero (as shown by “□”).
3.3. Parameter Tuning for the D-PCI Controller
4. Simulation and Experimental Results
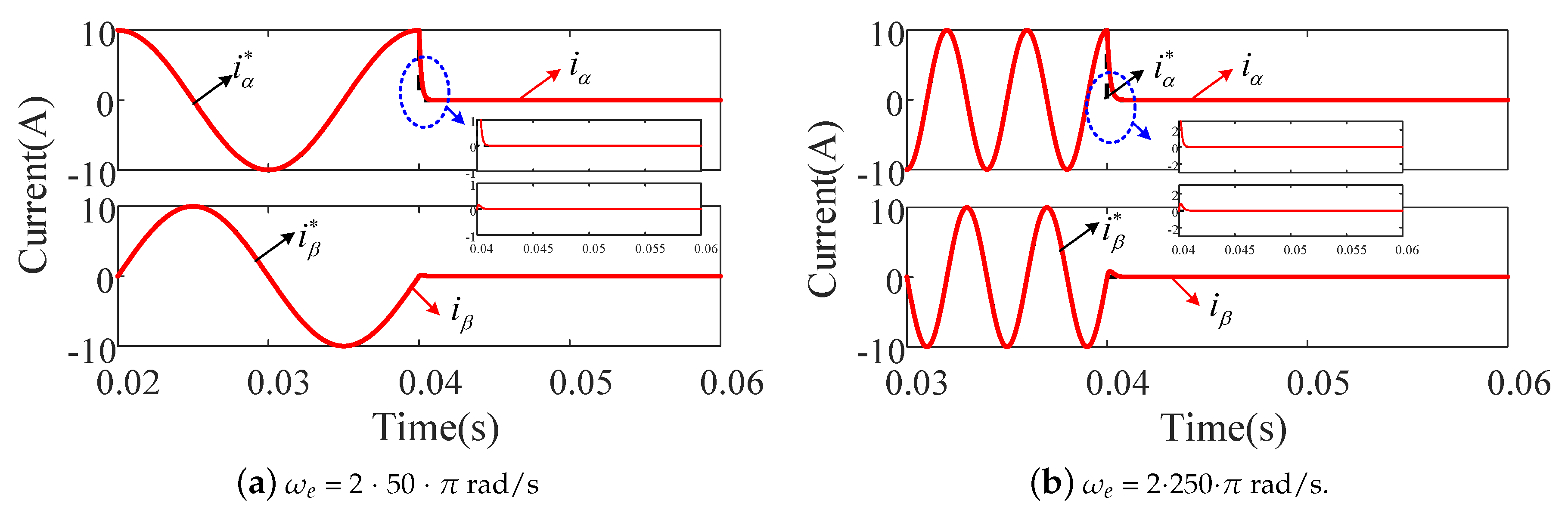
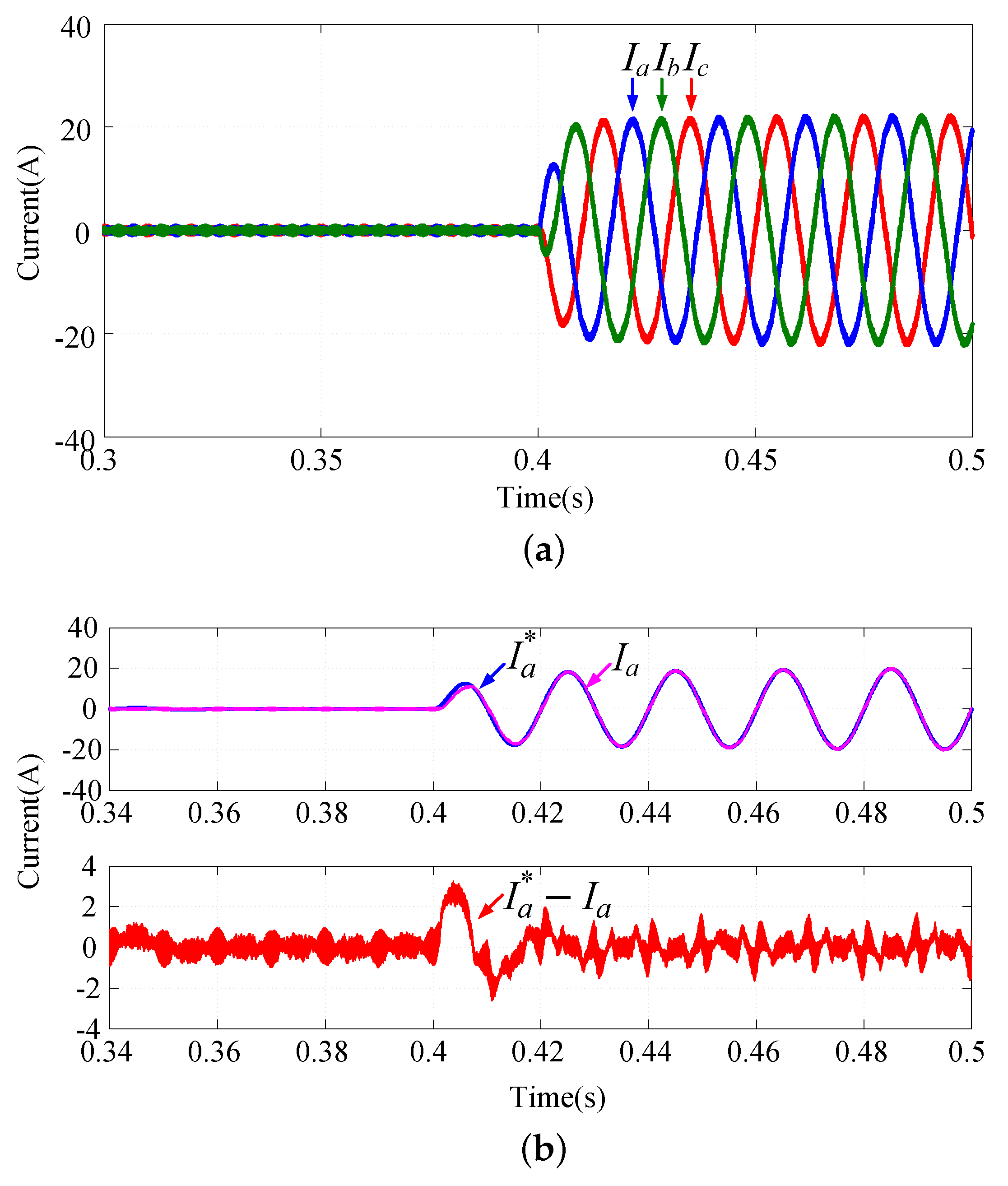
4.1. Simulation Results
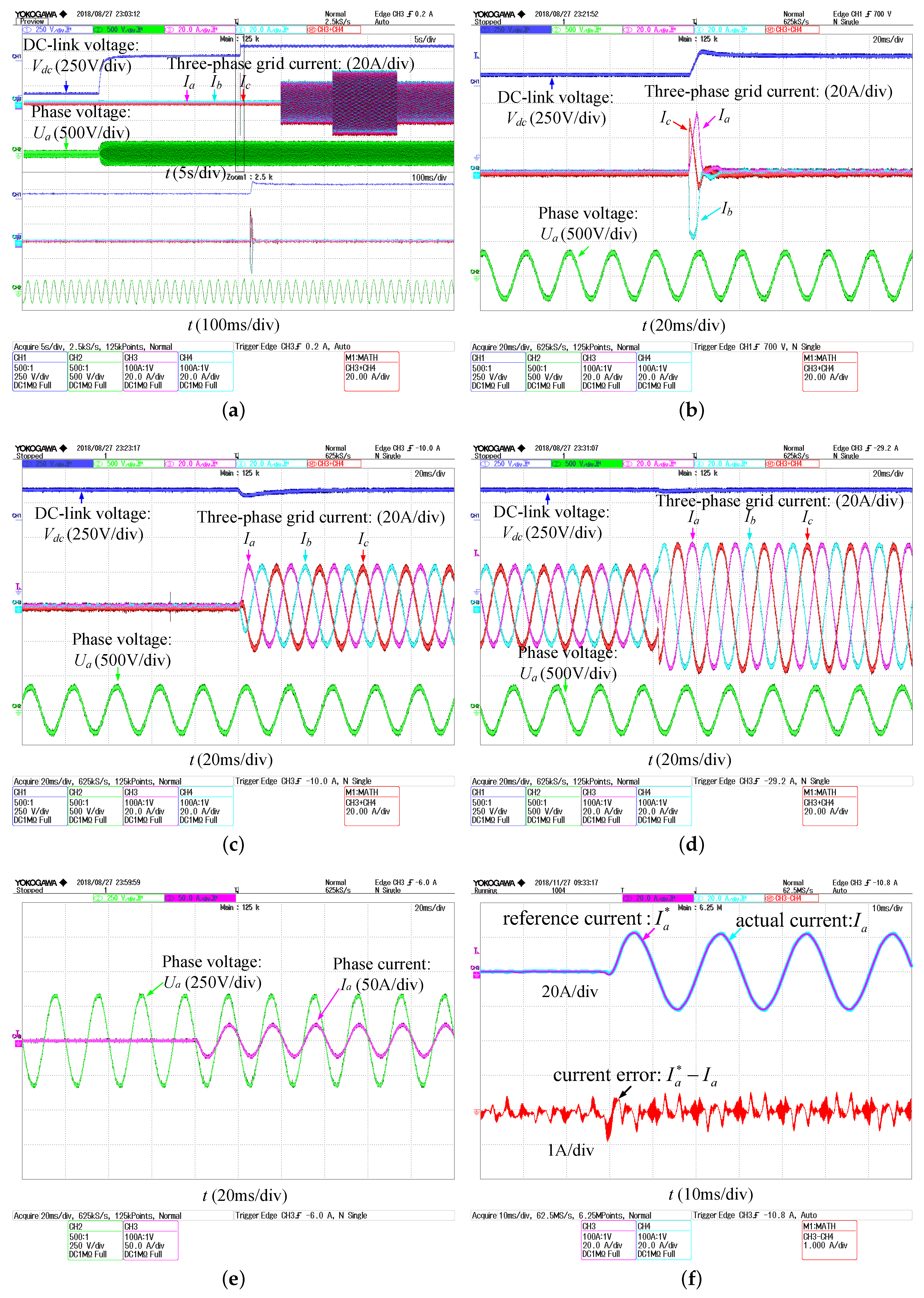
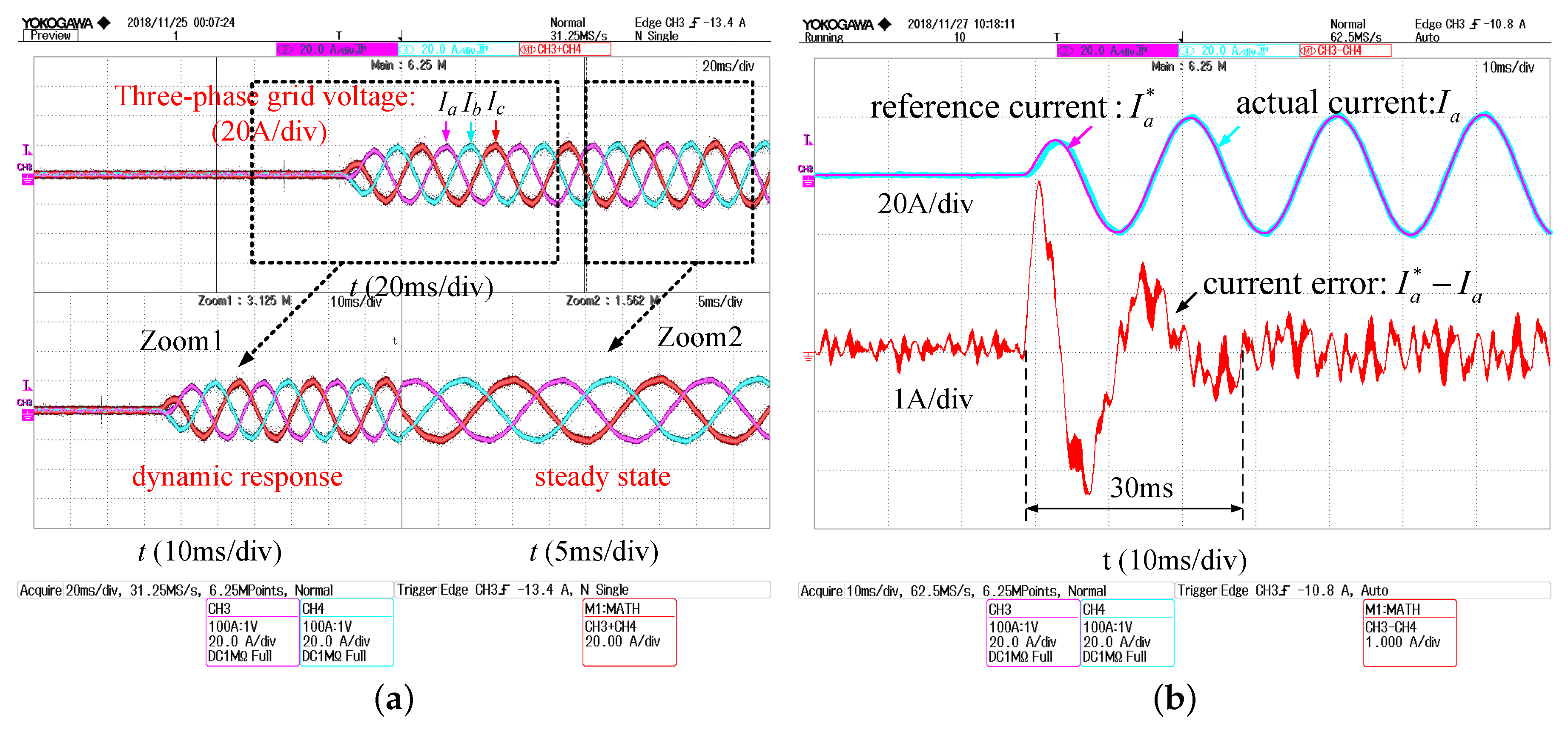
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bose, B. Global Energy Scenario and Impact of Power Electronics in 21st Century. IEEE Trans. Ind. Electron. 2013, 60, 2638–2651. [Google Scholar] [CrossRef]
- Arbab-Zavar, B.; Palacios-Garcia, E.; Vasquez, J.; Guerrero, J. Smart Inverters for Microgrid Applications: A Review. Energies 2019, 12, 840. [Google Scholar] [CrossRef]
- Molina, M. Energy Storage and Power Electronics Technologies: A Strong Combination to Empower the Transformation to the Smart Grid. Proc. IEEE. 2017, 105, 2191–2219. [Google Scholar] [CrossRef]
- Bose, B. Power Electronics, Smart Grid, and Renewable Energy Systems. Proc. IEEE. 2017, 105, 2011–2018. [Google Scholar] [CrossRef]
- Pang, B.; Nian, H. Improved Operation Strategy with Alternative Control Targets for Voltage Source Converter under Harmonically Distorted Grid Considering Inter-Harmonics. Energies 2019, 12, 1236. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, X.; Li, K.; Zou, J.; Guerrero, J.M. A New Tuning Method of Multi-Resonant Current Controllers for Grid-Connected Voltage Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 458–466. [Google Scholar] [CrossRef]
- Busada, C.A.; Jorge, S.G.; Solsona, J.A. Resonant Current Controller With Enhanced Transient Response for Grid-Tied Inverters. IEEE Trans. Ind. Electron. 2018, 65, 2935–2944. [Google Scholar] [CrossRef]
- Nie, C.; Wang, Y.; Lei, W.; Li, T.; Yin, S. Modeling and Enhanced Error-Free Current Control Strategy for Inverter with Virtual Resistor Damping. Energies 2018, 11, 2499. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A.; McGrath, B.P.; Kong, W.Y. Optimized Design of Stationary Frame Three Phase AC Current Regulators. IEEE Trans. Power Electron. 2009, 24, 2417–2426. [Google Scholar] [CrossRef]
- Guo, X.; Guerrero, J.M. General Unified Integral Controller With Zero Steady-State Error for Single-Phase Grid-Connected Inverters. IEEE Trans. Smart Grid. 2016, 7, 74–83. [Google Scholar] [CrossRef]
- Guo, X.Q.; Wu, W.Y. Improved current regulation of three-phase grid-connected voltage-source inverters for distributed generation systems. IET Renew. Power Gener. 2010, 4, 101–115. [Google Scholar] [CrossRef]
- Yuan, X.M.; Merk, W.; Stemmler, H.; Allmeling, J. Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions. IEEE Trans. Ind. Appl. 2002, 38, 523–532. [Google Scholar] [CrossRef]
- Harnefors, L.; Nee, H. Model-based current control of AC machines using the internal model control method. IEEE Trans. Ind. Appl. 1998, 34, 133–141. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. Frequency Response Analysis of Current Controllers for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Ind. Electron. 2009, 56, 337–347. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. High Performance Current Controller for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Power Electron. 2007, 22, 1826–1835. [Google Scholar] [CrossRef]
- Vidal, A.; Freijedo, F.D.; Yepes, A.G. Assessment and Optimization of the Transient Response of Proportional-Resonant Current Controllers for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2013, 60, 1367–1383. [Google Scholar] [CrossRef]
- Briz, F.; Degner, M.W.; Lorenz, R.D. Analysis and design of current regulators using complex vectors. IEEE Trans. Ind. Appl. 2000, 36, 817–825. [Google Scholar] [CrossRef] [Green Version]
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Bae, B.; Sul, S. A compensation method for time delay of full-digital synchronous frame current regulator of PWM AC drives. IEEE Trans. Ind. Appl. 2003, 39, 802–810. [Google Scholar] [CrossRef]
- Pérez-Estévez, D.; Doval-Gandoy, J.; Yepes, A.G.; López, Ó. Positive- and Negative-Sequence Current Controller With Direct Discrete-Time Pole Placement for Grid-Tied Converters With LCL Filter. IEEE Trans. Power Electron. 2017, 32, 7207–7221. [Google Scholar] [CrossRef]
- Busada, C.A.; Jorge, S.G.; Leon, A.E.; Solsona, J.A. Current Controller Based on Reduced Order Generalized Integrators for Distributed Generation Systems. IEEE Trans. Ind. Electron. 2012, 59, 2898–2909. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, X.; Li, K.; Liu, D.; Guerrero, J.M.; Vasquez, J.C. Phase Compensated Reduced Order Generalized Integrators for Grid-Tied VSCs With Harmonics Compensation Capability. IEEE Trans. Ind. Appl. 2018, 54, 2568–2578. [Google Scholar] [CrossRef]
- Hwang, J.G.; Lehn, P.W.; Winkelnkemper, M. A Generalized Class of Stationary Frame-Current Controllers for Grid-Connected AC–DC Converters. IEEE Trans. Power Del. 2010, 25, 2742–2751. [Google Scholar] [CrossRef]
- Jorge, S.G.; Busada, C.A.; Solsona, J.A. Frequency-Adaptive Current Controller for Three-Phase Grid-Connected Converters. IEEE Trans. Ind. Electron. 2013, 60, 4169–4177. [Google Scholar] [CrossRef]
- Jorge, S.G.; Busada, C.A.; Solsona, J. Reduced order generalised integrator-based current controller applied to shunt active power filters. IET Power Electron. 2013, 7, 1083–1091. [Google Scholar] [CrossRef]
- Yepes, A.G.; Vidal, A.; Malvar, J.; López, O.; Doval-Gandoy, J. Tuning Method Aimed at Optimized Settling Time and Overshoot for Synchronous Proportional-Integral Current Control in Electric Machines. IEEE Trans. Power Electron. 2014, 29, 3041–3054. [Google Scholar] [CrossRef]




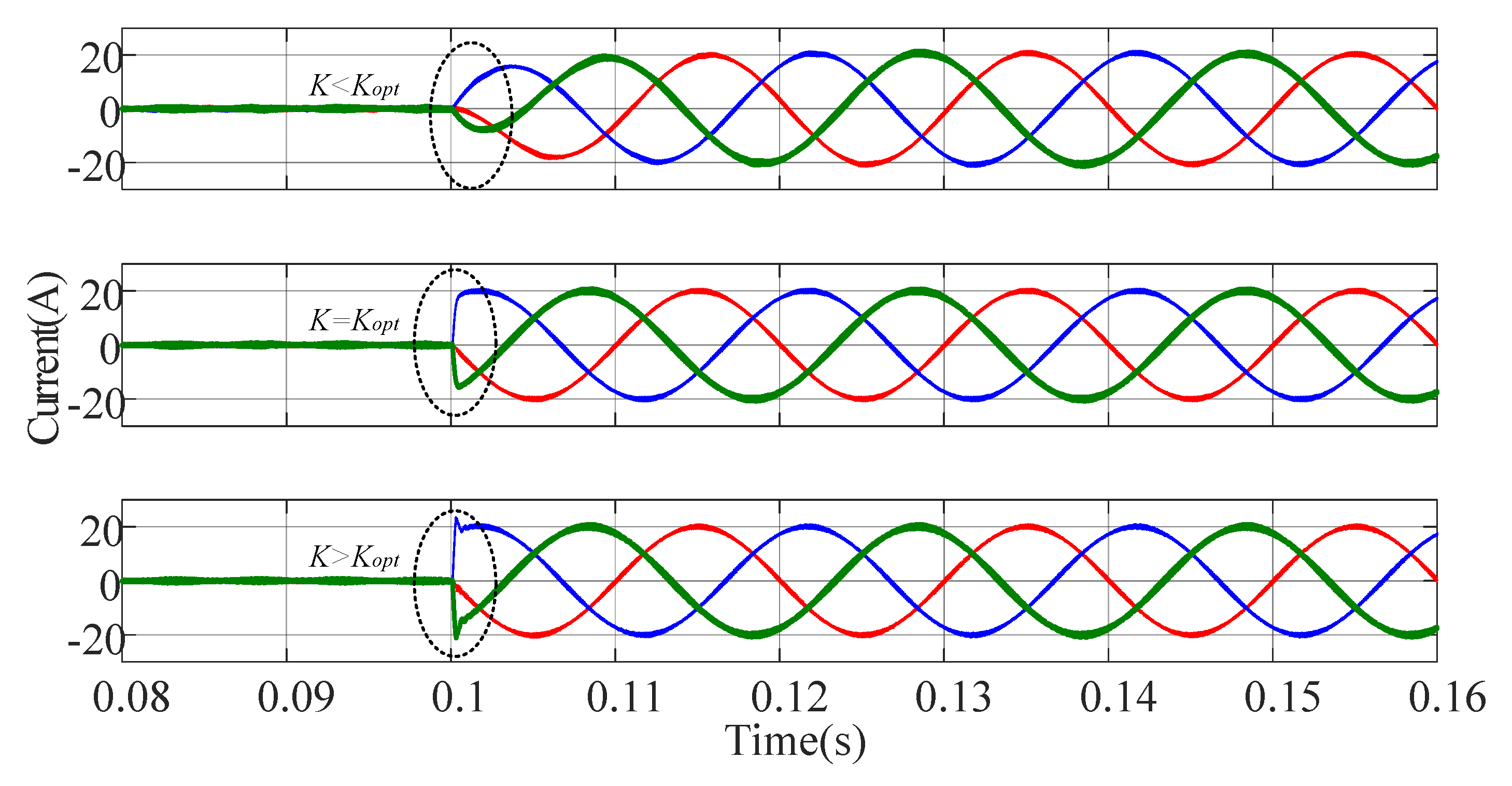


| Gain (K) | Damping Ratio | Overshoot | Response Speed |
|---|---|---|---|
| no | slow | ||
| no | fast | ||
| have | fast |
| Symbol | Parameters | Value | Unit |
|---|---|---|---|
| Phase-to-phase voltage | 380 | V | |
| f | Grid frequency | 50 | Hz |
| DC-link voltage | 700 | V | |
| L | Inductance of the L filter | 5 | mH |
| Equivalent resistance of the L filter | 0.05 | ||
| Capacitor of DC-link | 4000 | uF | |
| Active power Load | 50(10) | (kW) | |
| (Q) | Reactive power Load | 21.5(10) | A(kvar) |
| Switching frequency | 10 | kHz | |
| Sampling frequency | 10 | kHz | |
| Bandwidth of the current loop | 600 | Hz | |
| Proportional gain of the current loop | 12.3 | / | |
| Integral gain of the current loop | 123 | / | |
| Proportional gain of the voltage loop | 0.5 | / | |
| Integral gain of the voltage loop | 29.87 | / |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhao, J.; Zhao, Z.; Liu, K.; Wang, P.; Yang, B. Decoupled Current Controller Based on Reduced Order Generalized Integrator for Three-Phase Grid-Connected VSCs in Distributed System. Energies 2019, 12, 2426. https://doi.org/10.3390/en12122426
Zhang S, Zhao J, Zhao Z, Liu K, Wang P, Yang B. Decoupled Current Controller Based on Reduced Order Generalized Integrator for Three-Phase Grid-Connected VSCs in Distributed System. Energies. 2019; 12(12):2426. https://doi.org/10.3390/en12122426
Chicago/Turabian StyleZhang, Sen, Jianfeng Zhao, Zhihong Zhao, Kangli Liu, Pengyu Wang, and Bin Yang. 2019. "Decoupled Current Controller Based on Reduced Order Generalized Integrator for Three-Phase Grid-Connected VSCs in Distributed System" Energies 12, no. 12: 2426. https://doi.org/10.3390/en12122426
APA StyleZhang, S., Zhao, J., Zhao, Z., Liu, K., Wang, P., & Yang, B. (2019). Decoupled Current Controller Based on Reduced Order Generalized Integrator for Three-Phase Grid-Connected VSCs in Distributed System. Energies, 12(12), 2426. https://doi.org/10.3390/en12122426





