On the Determination of the Aerodynamic Damping of Wind Turbines Using the Forced Oscillations Method in Wind Tunnel Experiments
Abstract
:1. Introduction
2. State-of-the-Art and Previous Studies
2.1. Aerodynamic Damping of Wind Turbines
2.2. Aerodynamic Damping in Civil Engineering Structures
3. Wind Turbine Model and Measurement Equipment
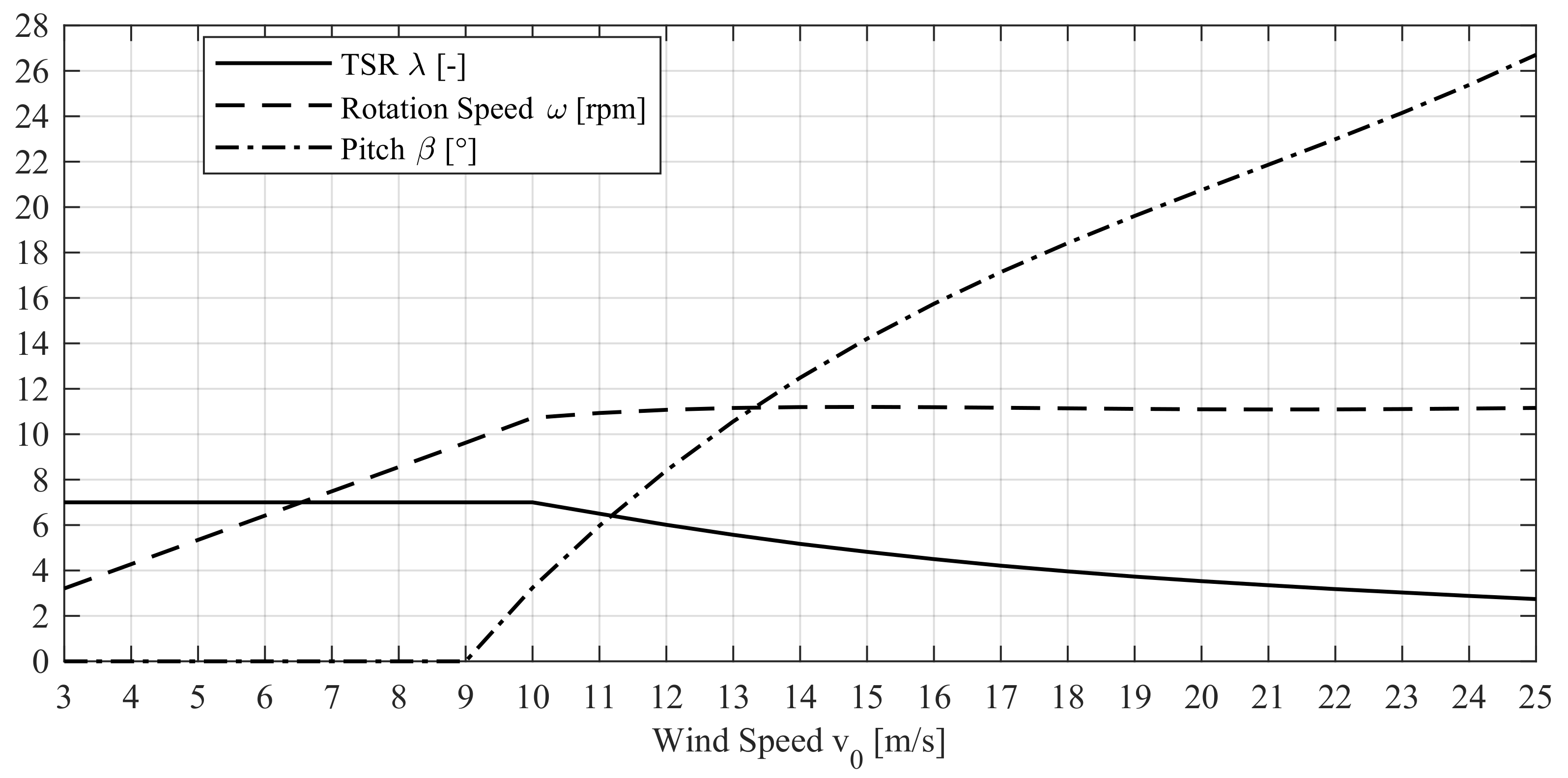
3.1. Wind Turbine Model
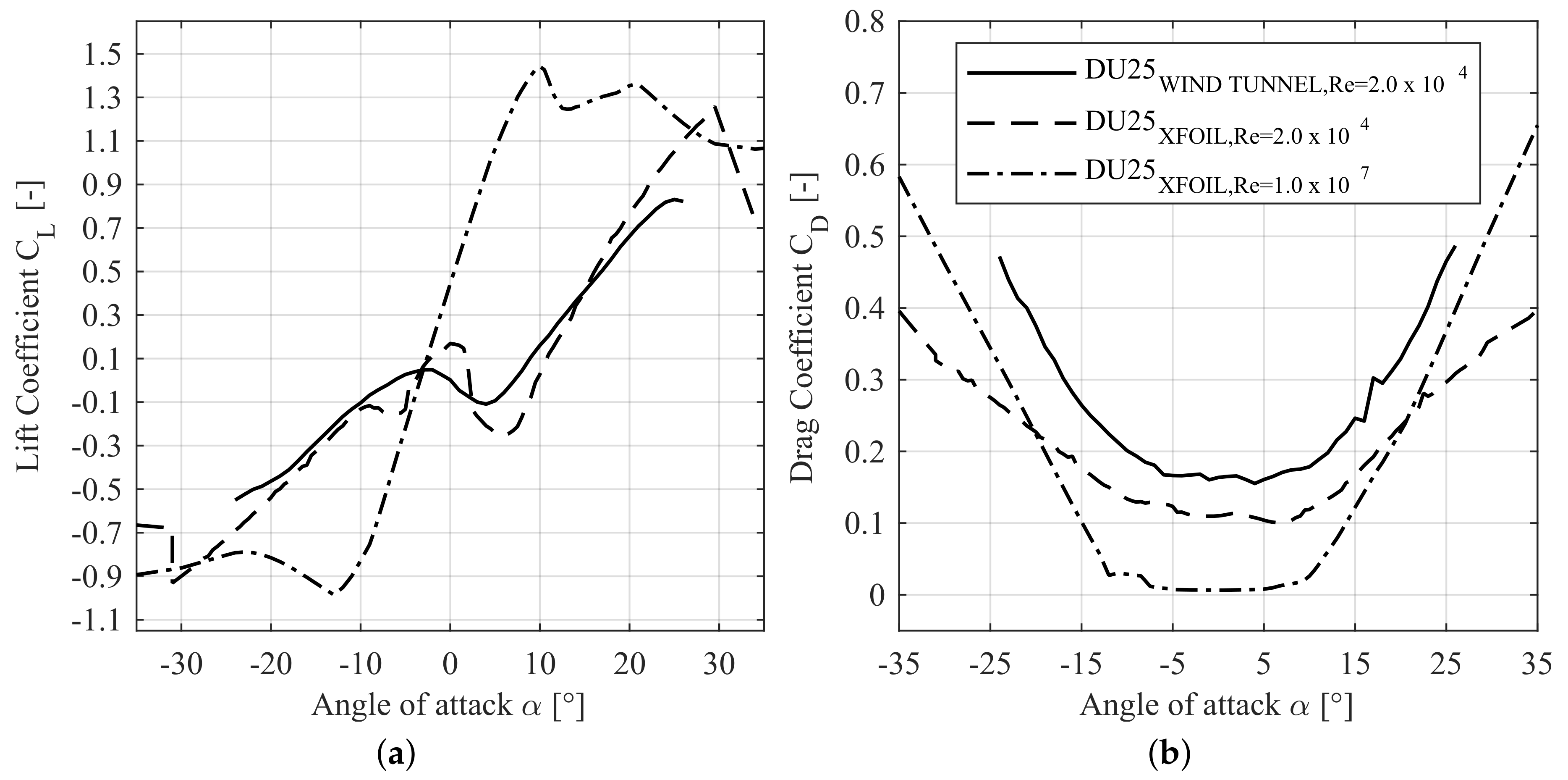
3.2. Scale Effects
3.3. Test Rig and Wind Tunnel
4. Wind Tunnel Measurements and Evaluation
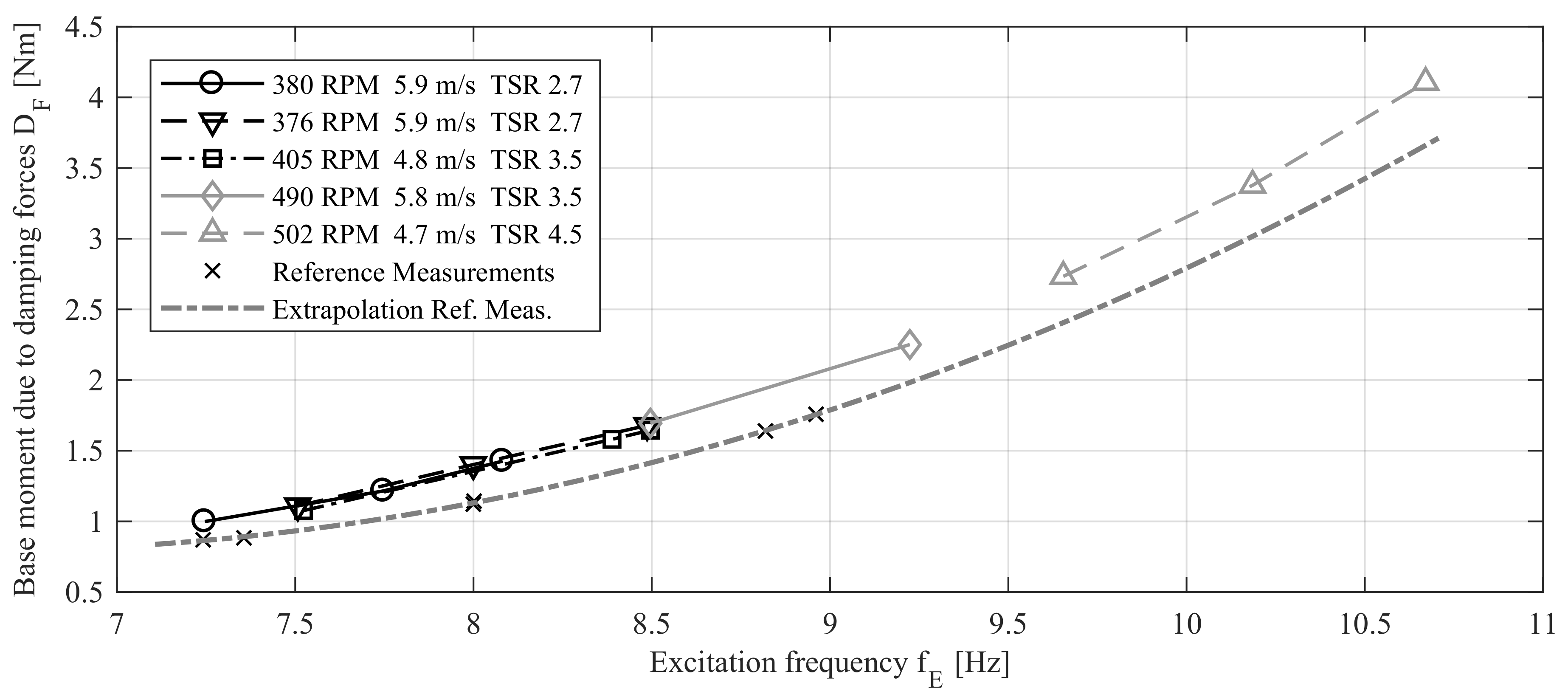
4.1. Forced Oscillation Measurements of the Tower Model
4.2. Forced Oscillation Measurements of the Wind Turbine Model
5. Results
5.1. Aerodynamic Damping of Wind Turbine Tower
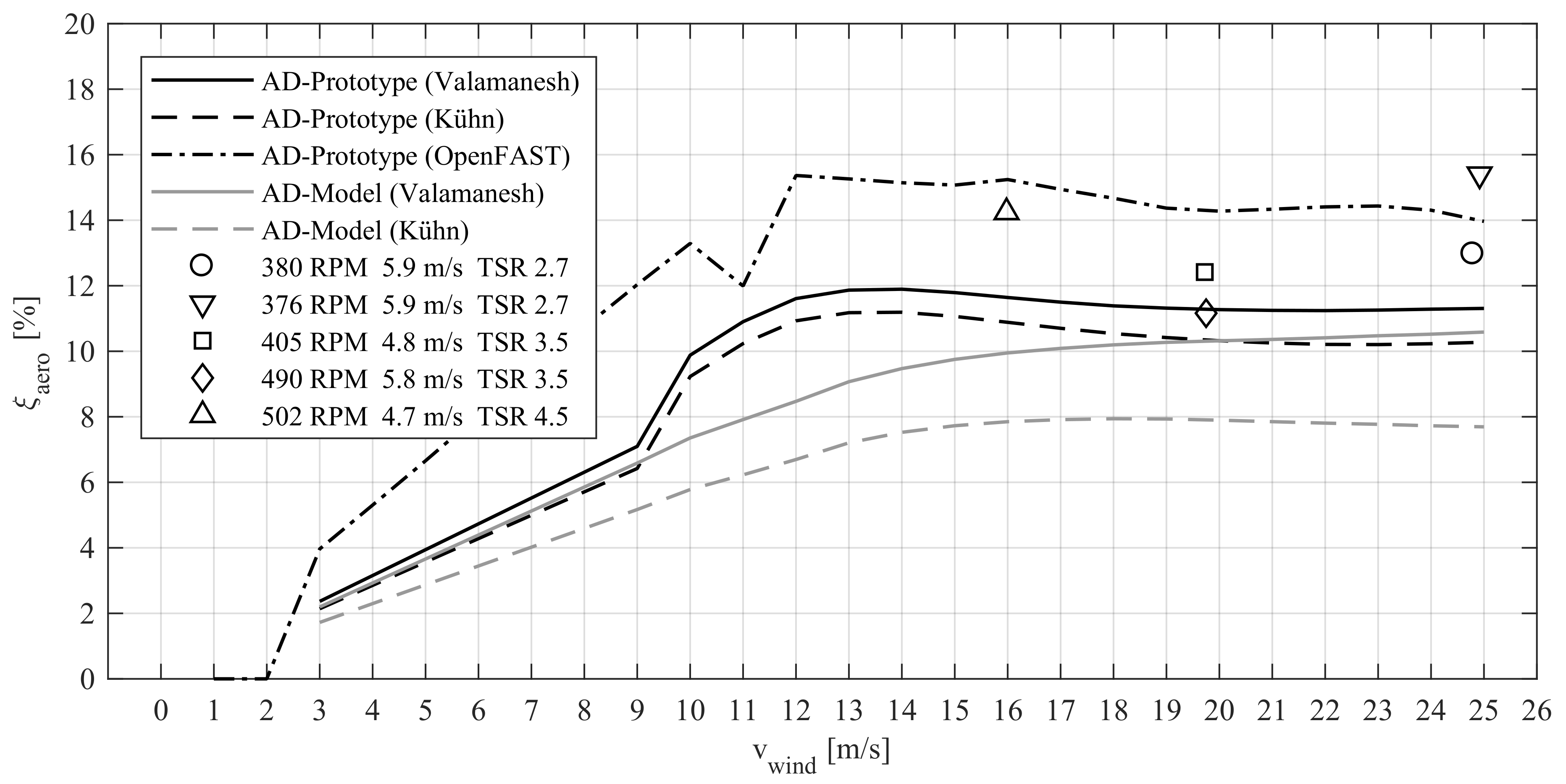
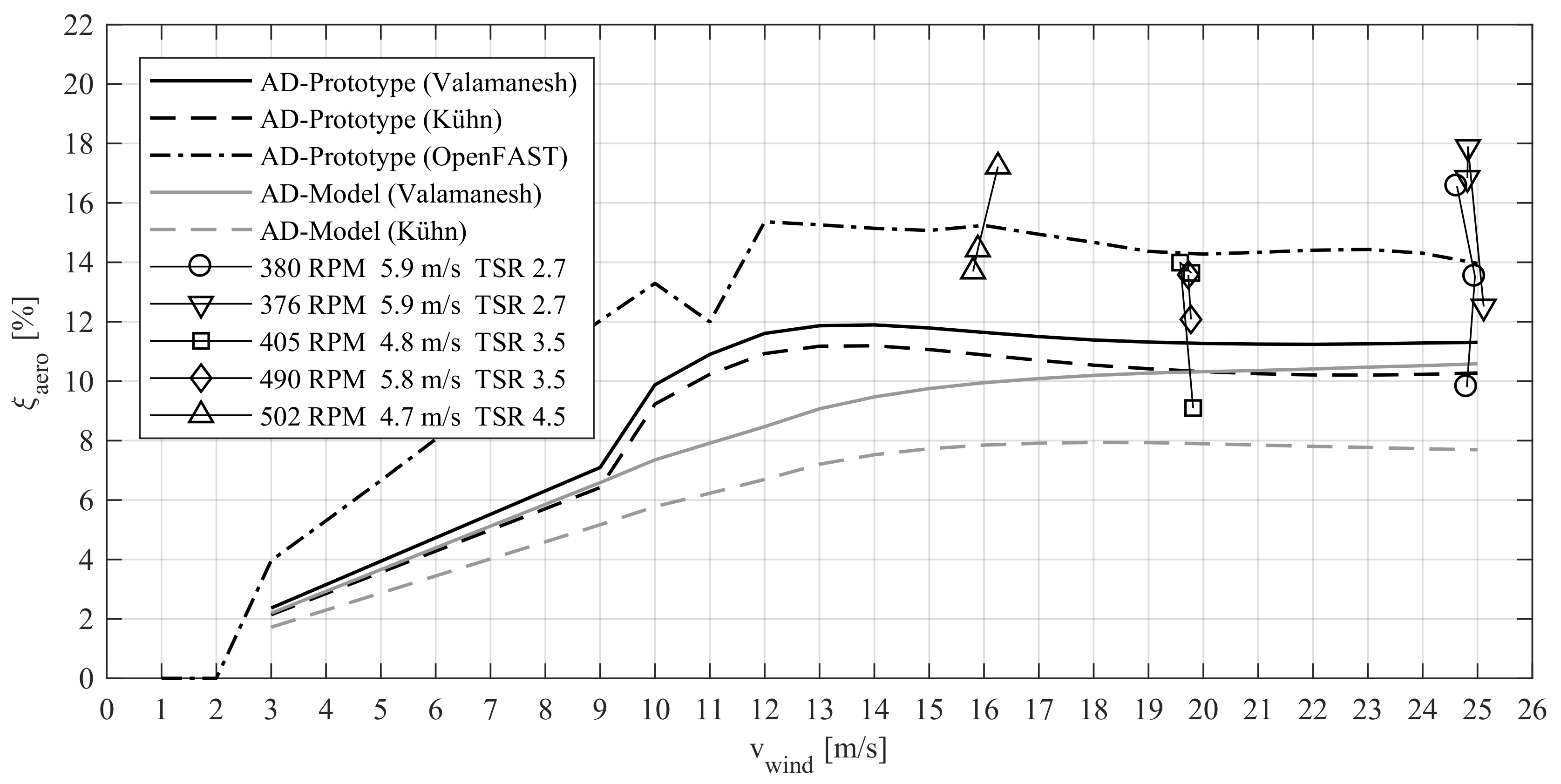
5.2. Aerodynamic Damping of Wind Turbine
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wind Europe. Wind in Power: 2016 European Statistics; Wind Europe: Brussels, Belgium, 2016. [Google Scholar]
- Gasch, R. Windkraftanlagen: Grundlagen, Entwurf, Planung Und Betrieb, 9th ed.; Vieweg + Teubner Verlag: Berlin, Germany, 2016. [Google Scholar]
- Devriendt, C.; Jordaens, P.J.; Sitter, G.D.; Guillaume, P. Damping Estimation of an Offshore Wind Turbine on a Monopile Foundation. ET Renew. Power Generat. 2013, 7, 401. [Google Scholar] [CrossRef]
- Devriendt, C.; Weijtjens, W. The overall damping of an offshore wind turbine during different operating conditions. In Proceedings of the EWEA Offshore 2015, Copenhagen, Denmark, 10–12 March 2015. [Google Scholar]
- Devriendt, C.; Weijtjens, W. Damping of offshore wind turbines. In Proceedings of the Offshore Wind Energy 2017, London, UK, 6–8 June 2017. [Google Scholar]
- Hansen, M.H.; Thomsen, K.; Fuglsang, P.; Knudsen, T. Two methods for estimating aeroelastic damping of operational wind turbine modes from experiments. Wind Energy 2006, 9, 179–191. [Google Scholar] [CrossRef] [Green Version]
- Garrad, A.D. Forces and Dynamics of horizontal axis wind turbines. In Wind Energy Conversion Systems; Freris, L.L., Ed.; Prentice Hall: New York, NY, USA, 1990; pp. 119–142. [Google Scholar]
- Kühn, M.J. Dynamics and Design Optimisation of Offshore Wind Energy Conversion Systems; Report; DUWIND Delft University Wind Energy Research Institute: Delft, The Netherlands, 2001; Volume 2. [Google Scholar]
- Cerda Salzmann, D.J.; van der Tempel, J. Aerodynamic damping in the design of support structures for offshore wind turbines. In Proceedings of the Copenhagen Offshore Wind Conference, Delft, The Netherlands, 26–28 October 2005. [Google Scholar]
- Valamanesh, V.; Myers, A.T. Aerodynamic Damping and Seismic Response of Horizontal Axis Wind Turbine Towers. J. Struct. Eng. 2014, 140, 04014090. [Google Scholar] [CrossRef]
- Van der Tempel, J. Design of Support Structures for Offshore Wind Turbines; Report; DUWIND Delft University Wind Energy Research Institute: Delft, The Netherlands, 2006; Volume 29. [Google Scholar]
- Van der Tempel, J. Lifetime Fatigue of an Offshore Wind Turbine Support Structure, Section Offshore Technology & Section Wind Energy; Delft University of Technology: Delft, The Netherlands, 2000. [Google Scholar]
- Larsen, A. (Ed.) Aerodynamics of Large Bridges. In Proceedings of the 1st International Symposium on Aerodynamics of Large Bridges, Copenhagen, Denmark, 19–21 February 1992; Balkema: Rotterdam, The Netherlands, 1992. [Google Scholar]
- Svensson, H. Cable-Stayed Bridges: 40 Years of Experience Worldwide; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Alan, G.; Davenport Wind Engineering Group. Wind Tunnel Testing: A General Outline; Western: London, ON, Canada, 2007. [Google Scholar]
- Tanaka, H. Similitude and modelling in wind tunnel testing of bridges. J. Wind Eng. Indust. Aerodyn. 1990, 33, 283–300. [Google Scholar] [CrossRef]
- Scanlan, R.H. Aeroelastic Simulation of Bridges. J. Struct. Eng. 1983, 109, 2829–2837. [Google Scholar] [CrossRef]
- Hortmanns, M. Zur Identifikation und Berücksichtigung Nichtlinearer Aeroelastischer Effekte; Stahlbau; Shaker: Aachen, Germany, 1997; Volume H.34. [Google Scholar]
- Fontecha, R. Determination of Flutter Derivatives of Bridge Sections Determination of Flutter Derivatives of Bridge Sections based on Wind Tunnel Experiments Under Forced Excitation. Master’s Thesis, RWTH Aachen, Aachen, Germany, 2012. [Google Scholar]
- Scanlan, R.H.; Sabzevari, A. Experimental Aerodynamic Coefficients in the Analytical Study of Suspension Bridge Flutter. J. Mech. Eng. Sci. 1969, 11, 234–242. [Google Scholar] [CrossRef]
- Steckley, A. Motion-induced Wind Forces on Chimneys and Tall Buildings; Canadian theses = Thèses canadiennes; National Library of Canada: Ottawa, ON, Canada, 1990. [Google Scholar]
- Steckley, A.; Vickery, B.J.; Isyumov, N. On the measurement of motion induced forces on models in turbulent shear flow. J. Wind Eng. Indust. Aerodyn. 1990, 36, 339–350. [Google Scholar] [CrossRef]
- Feldmann, M.; Jakobs, G.; Klinkel, S.; Butenweg, C.; Kemper, F.; Schelenz, R. Boden-Bauwerk-Triebstrang- Interaktion von Windenergieanlagen: Abschlussbericht; Final Report: 01.01.2015–12.31.2017; RWTH Aachen University: Aachen, Germany, 2018. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab.: Lakewood, CO, USA, 2009. [Google Scholar]
- Lindenburg, C. Aeroelastic Modelling of the LMH64-5 Blade. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.475.7675rep=rep1type=pdf (accessed on 25 June 2019).
- Tschanz, T. The Base Balance Measurement Technique And Applications to Dynamic Wind Loading to Structures. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, July 1982. [Google Scholar]
- Tschanz, T.; Davenport, A.G. The base balance technique for the determination of dynamic wind loads. J. Wind Eng. Indust. Aerodyn. 1983, 13, 429–439. [Google Scholar] [CrossRef]
- Davenport, A.G. The Application of statistical concepts to the wind loading of stuctures. Proc. Inst. Civ. Eng. 1961, 19, 449–472. [Google Scholar] [CrossRef]
- Davenport, A.G. The Treatment of Wind Loading on Tall Buildings. In Tall Buildings; Elsevier: Amsterdam, The Netherlands, 1967; pp. 3–45. [Google Scholar] [CrossRef]
- Baniotopoulos, C.C.; Borri, C.; Stathopoulos, T. Environmental Wind Engineering And Design Of Wind Energy Structures; CISM Courses and Lectures; Springer: Vienna, Austria; New York, NY, USA, 2011; Volume 531. [Google Scholar]
- Burdett, T.A.; van Treuren, K.W. Scaling Small-Scale Wind Turbines for Wind Tunnel Testing. In Proceedings of the ASME Turbo Expo 2012, Copenhagen, Denmark, 11–15 June 2012; ASME: New York, NY, USA, 2012; p. 811. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 8th ed.; McGraw-Hill: New York, NY, USA, 2016. [Google Scholar]
- Irwin, P.A. Full Aeroelastic Model Tests. In Aerodynamics of Large Bridges; Larsen, A., Ed.; Balkema: Rotterdam, The Netherlands, 1992; pp. 125–135. [Google Scholar]
- Tanaka, H. Similitude and Modelling in Bridge Aerodynamics. In Aerodynamics of Large Bridges; Larsen, A., Ed.; Balkema: Rotterdam, The Netherlands, 1992; pp. 83–93. [Google Scholar]
- Fontecha, R. Determination of aerodynamic Damping and vortex-shedding Correlation Length of Wind Turbine Towers based on Wind Tunnel Experiments with the High Fre-quency Force Balance (HFFB) and Forced-Oscillations Methods. In Proceedings of the EACWE 2017, Liege, Belgium, 4–7 July 2017. [Google Scholar]
- Fontecha, R.; Henneke, B.; Kemper, F.; Feldmann, M. Aerodynamic properties of Wind Turbine Towers based on Wind Tunnel Experiments. Proc. Eng. 2017, 199, 3121–3126. [Google Scholar] [CrossRef]
- Van Treuren, K.W.; Burdett, T.A. Experimental Testing of Wind Turbines Using Wind Tunnels With an Emphasis on Small-Scale Wind Turbines Under Low Reynolds Numbers. In Aerodynamics of Wind Turbines; Amano, R., Sundén, B., Eds.; WIT Transactions on State of the Art in Science and Engineering; WIT Press: Ashurst, UK, 2014; Volume 1, pp. 67–110. [Google Scholar]
- Van Treuren, K.W. Small-Scale Wind Turbine Testing in Wind Tunnels Under Low Reynolds Number Conditions. J. Energy Res. Technol. 2015, 137, 051208. [Google Scholar] [CrossRef]
- Evangelista, R.; McGhee, R.J.; Walker, B.S. Correlation of Theory to Wind-Tunnel Data at Reynolds Numbers below 500,000. In Low Reynolds Number Aerodynamics; Mueller, T.J., Ed.; Lecture Notes in Engineering; Springer: Berlin/Heidelberg, Germany, 1989; Volume 54, pp. 146–160. [Google Scholar]
- Gao, X.; Hu, J. Numerical research of Reynolds number impact on scale model of wind turbine. In Proceedings of the 2009 World Non-Grid-Connected Wind Power and Energy Conference (WNWEC 2009), Nanjing, China, 24–26 September 2009; pp. 1–4. [Google Scholar] [CrossRef]
- XFOIL: Subsonic Airfoil Developement System. 2017. Available online: http://web.mit.edu/drela/Public/web/xfoil/ (accessed on 25 June 2019).
- Van Treuren, K.W.; Hays, A. Designing and Testing Small-Scale Horizontal Ais Wind Turbines for the Urban Environment. In Proceedings of the 1st Global Power and Propulsion Forum, Shangai, China, 31 October–1 November 2017. [Google Scholar]
- Deutsches Institut für Normung e. V. Eurocode 1: Actions on Structures—Part 1-4: General Actions—Wind Actions; Technical Committee: Brussels, Belgium, 2010. [Google Scholar]
- Bottasso, C.L.; Campagnolo, F.; Petrović, V. Wind tunnel testing of scaled wind turbine models: Beyond aerodynamics. J. Wind Eng. Indust. Aerodyn. 2014, 127, 11–28. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Bernini, L.; Mikkelsen, R.; Zasso, A. On the aero-elastic design of the DTU 10MW wind turbine blade for the LIFES50+ wind tunnel scale model. J. Phys. Conf. Ser. 2016, 753, 022028. [Google Scholar] [CrossRef]
- Selig, M.S.; Guglielmo, J.J.; Broeren, A.P.; Giguère, P. Summary of Low-Speed Airfoil Data; SoarTech Publications; SoarTech: Virginia Beach, VA, USA, 1995; Volume 1. [Google Scholar]
- Selig, M.S.; Lyon, C.A.; Giguère, P.; Ninham, C.N.; Guglielmo, J.J. Summary of Low-Speed Airfoil Data; SoarTech Publications; SoarTech: Virginia Beach, VA, USA, 1995; Volume 2. [Google Scholar]
- Lyon, C.A.; Broeren, A.P.; Giguère, P.; Gopalarathnam, A.; Selig, M.S. Summary of Low-Speed Airfoil Data; SoarTech Publications; SoarTech: Virginia Beach, VA, USA, 1995; Volume 3. [Google Scholar]
- Selig, M.S.; McGranahan, B.D. Wind Tunnel Aerodynamic Tests of Six Airfoils for Use on Small Wind Turbines; Techical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2004. [Google Scholar]







| [-] | [-] | [m/s] | [min−1] | [Hz] | [m/s] | [min−1] | [Hz] | ||
|---|---|---|---|---|---|---|---|---|---|
| 2.8 | 33.7 | 24.8 | 11 | 0.21 | 26.4 | 6 | 387 | 7.6 | 8.0 |
| 3.5 | 27.4 | 20.2 | 11 | 0.21 | 20.9 | 5/6 | 408/490 | 7.8/9.3 | 4.0 |
| 4.3 | 16.9 | 16.8 | 11 | 0.21 | 16.9 | 5 | 497 | 9.4 | 0.0 |
| [-] | [-] | [-] | [m/s] | [Hz] | [Nm] | [m/s] | [Hz] | [MNm] |
|---|---|---|---|---|---|---|---|---|
| 2.8 | 33.7 | –3.15 | 6 | 7.6 | 0.007 | 24.8 | 0.21 | 0.42 |
| 3.5 | 27.4 | –2.55 | 5/6 | 7.8/9.3 | 0.006/0.009 | 20.2 | 0.21 | 0.34 |
| 4.3 | 16.9 | –1.45 | 5 | 9.4 | 0.005 | 16.8 | 0.21 | 0.19 |
| [-] | [m/s] | [min−1] | [Hz] | [m] | [kg/s] | [kg/s] | [kN] | [MNm] |
|---|---|---|---|---|---|---|---|---|
| 2.8 | 24.8 | 11 | 0.21 | 0.75 | 1.30 × 104 | 1.05 × 105 | 101.1 | 11.3 |
| 3.5 | 20.2 | 11 | 0.21 | 0.75 | 1.30 × 104 | 0.85 × 105 | 84.1 | 9.4 |
| 4.3 | 16.8 | 11 | 0.21 | 0.75 | 1.31 × 104 | 1.03 × 105 | 101.5 | 11.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fontecha, R.; Kemper, F.; Feldmann, M. On the Determination of the Aerodynamic Damping of Wind Turbines Using the Forced Oscillations Method in Wind Tunnel Experiments. Energies 2019, 12, 2452. https://doi.org/10.3390/en12122452
Fontecha R, Kemper F, Feldmann M. On the Determination of the Aerodynamic Damping of Wind Turbines Using the Forced Oscillations Method in Wind Tunnel Experiments. Energies. 2019; 12(12):2452. https://doi.org/10.3390/en12122452
Chicago/Turabian StyleFontecha, Robert, Frank Kemper, and Markus Feldmann. 2019. "On the Determination of the Aerodynamic Damping of Wind Turbines Using the Forced Oscillations Method in Wind Tunnel Experiments" Energies 12, no. 12: 2452. https://doi.org/10.3390/en12122452
APA StyleFontecha, R., Kemper, F., & Feldmann, M. (2019). On the Determination of the Aerodynamic Damping of Wind Turbines Using the Forced Oscillations Method in Wind Tunnel Experiments. Energies, 12(12), 2452. https://doi.org/10.3390/en12122452






