Structural Analysis of Large-Scale Vertical-Axis Wind Turbines, Part I: Wind Load Simulation
Abstract
1. Introduction
2. Wind Load Simulation Framework for VAWTs
2.1. Straight-Bladed VAWT
2.2. Wind Conditions
2.3. Strip Analysis Method
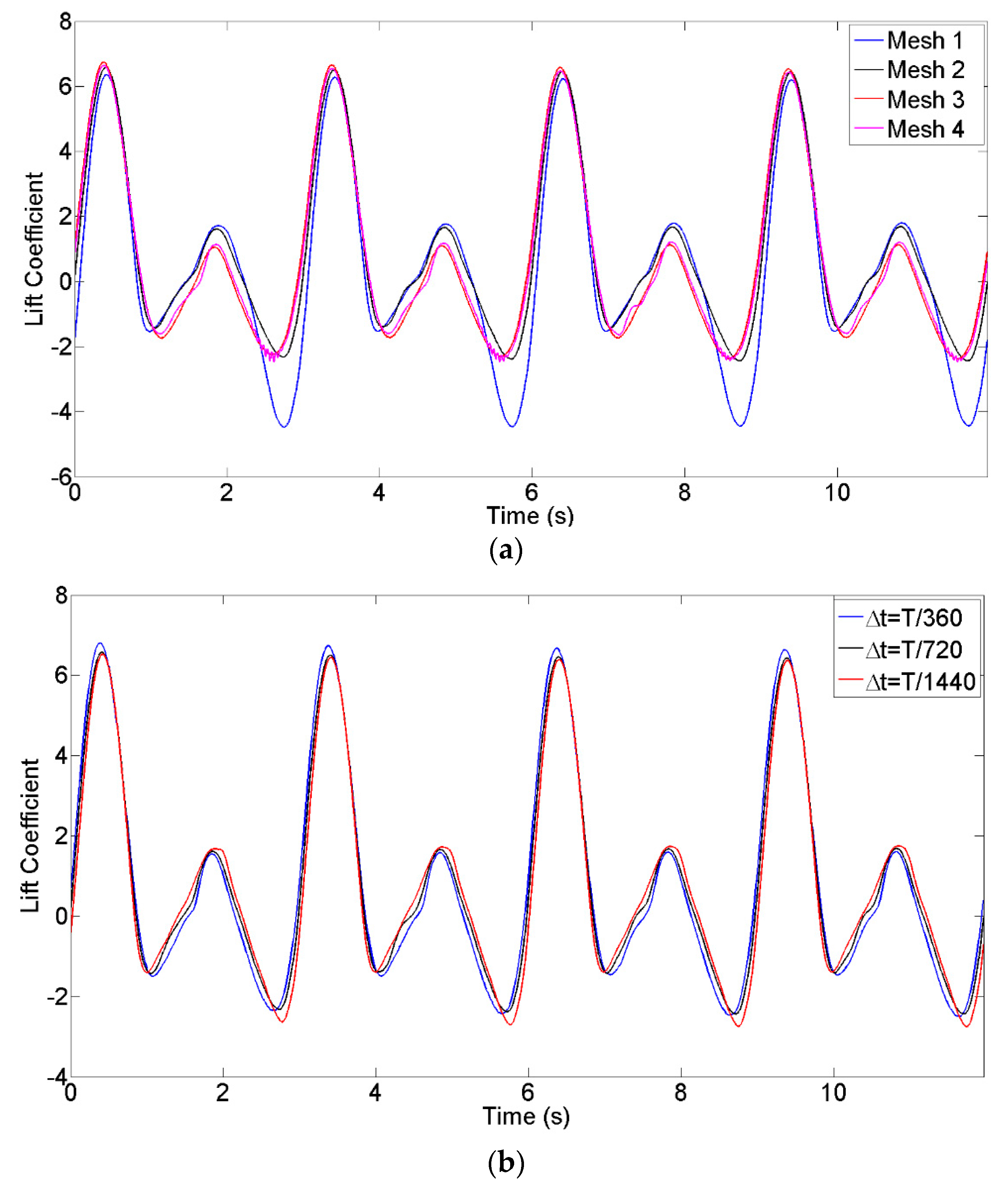
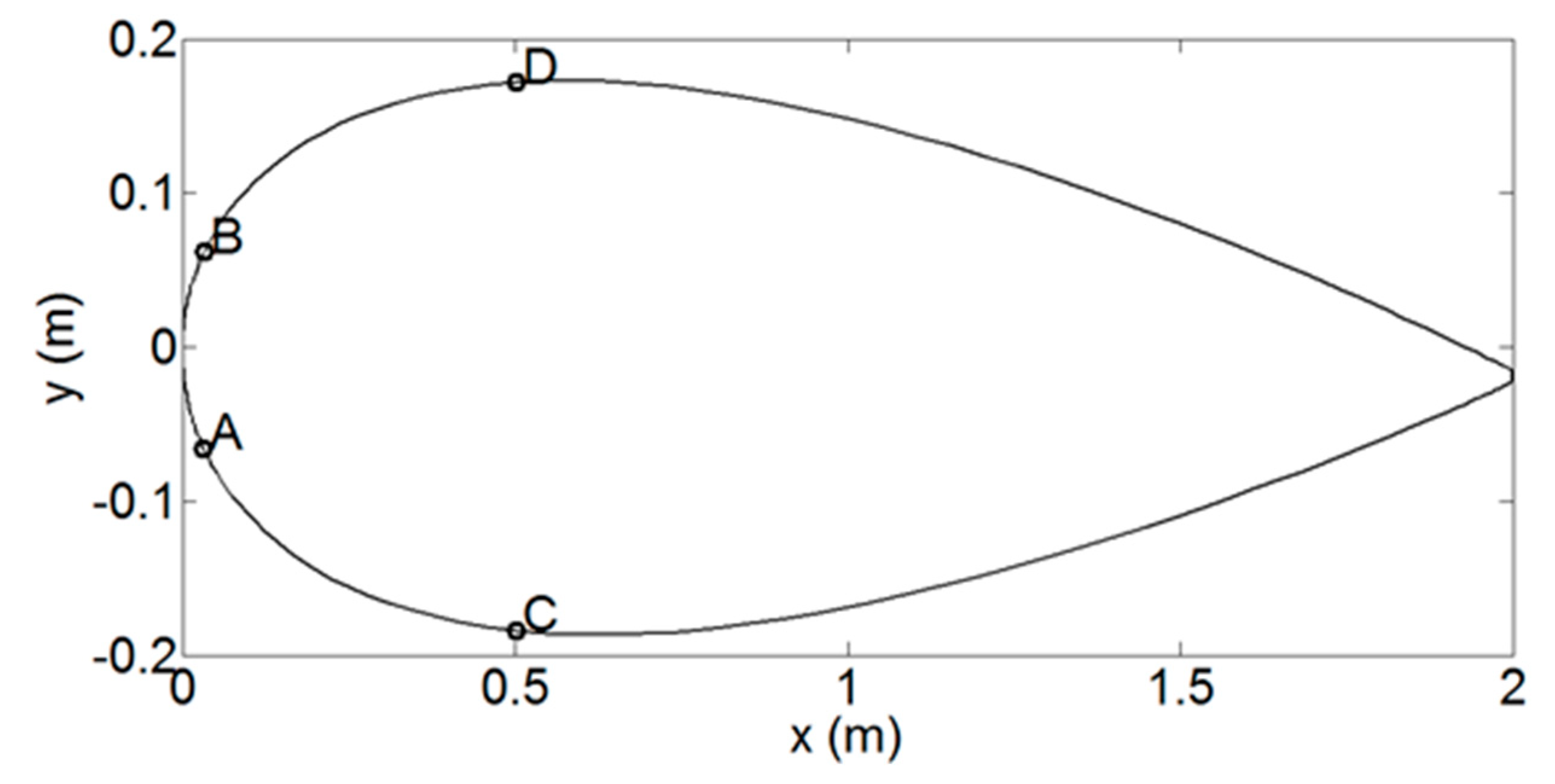
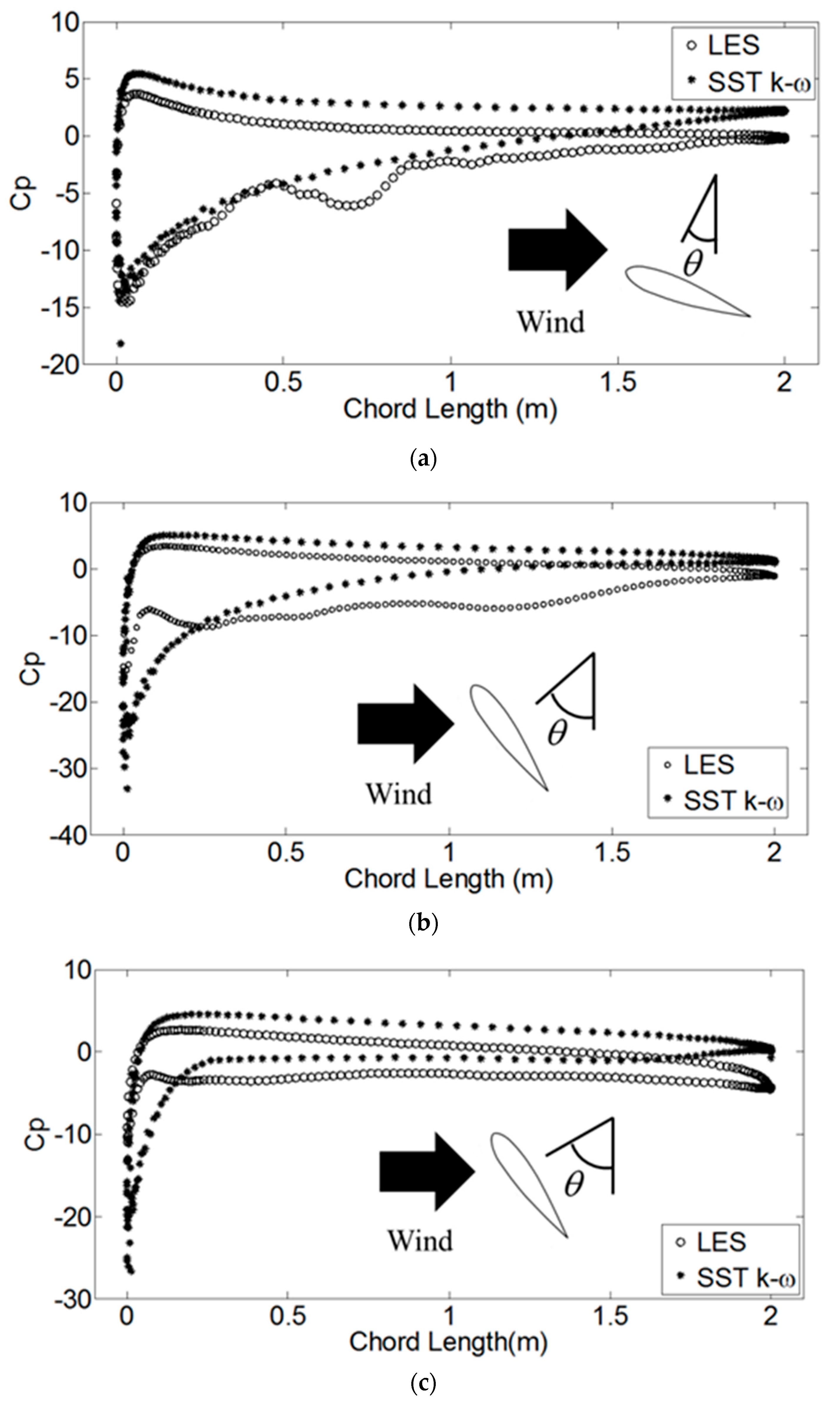
3. Validity of SST k-ω for Wind Load Simulation
3.1. CFD Simulation Strategy
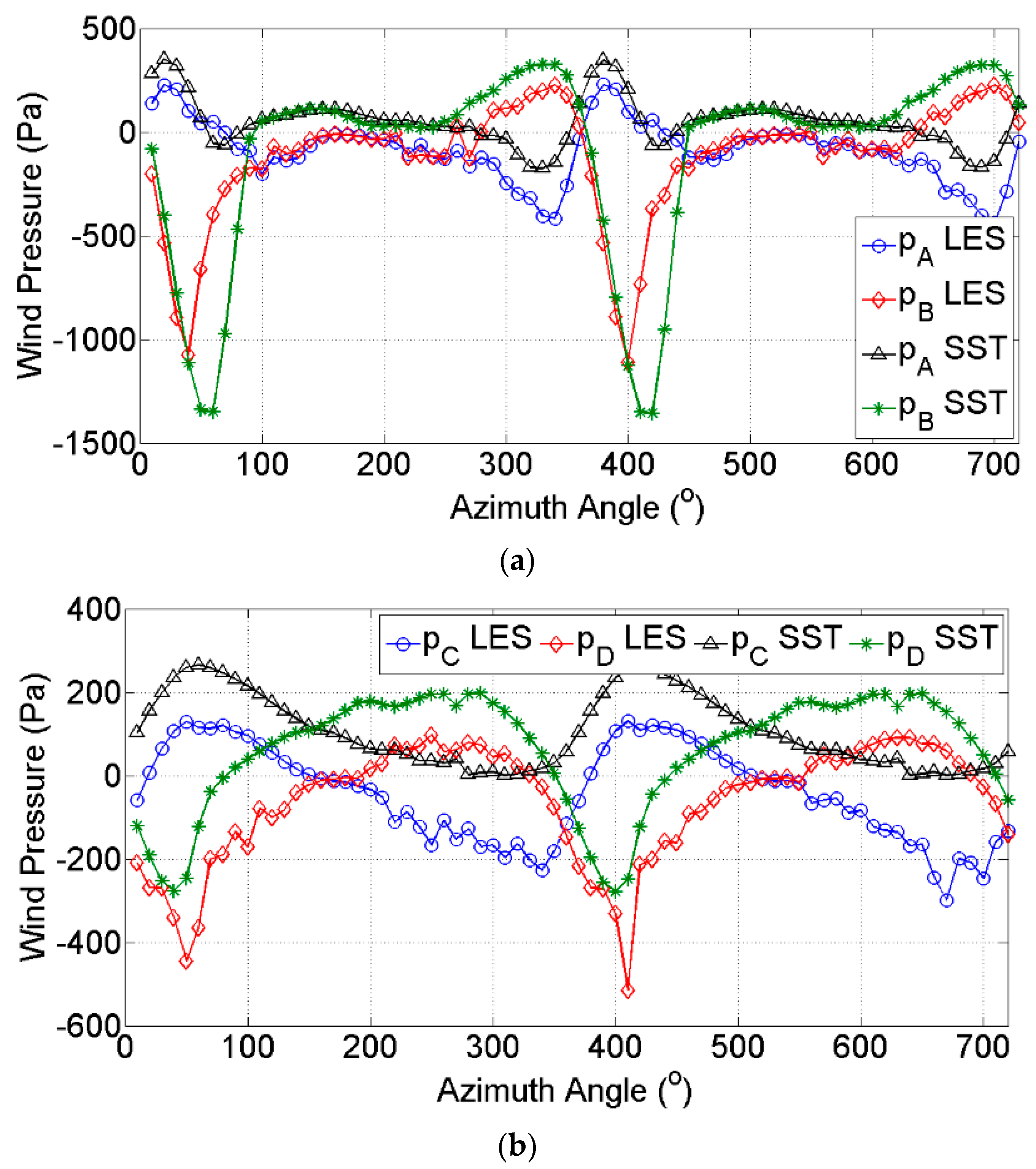
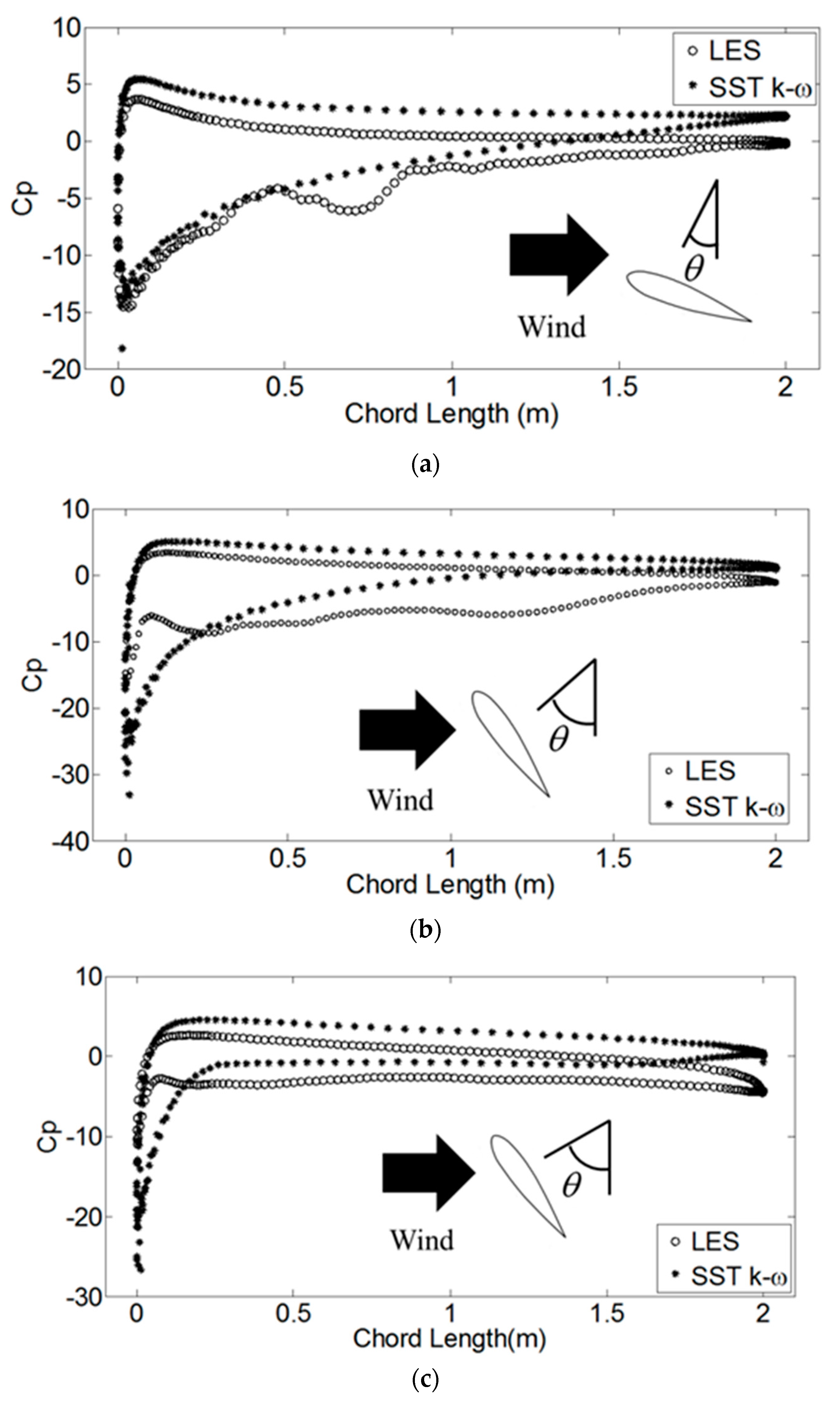
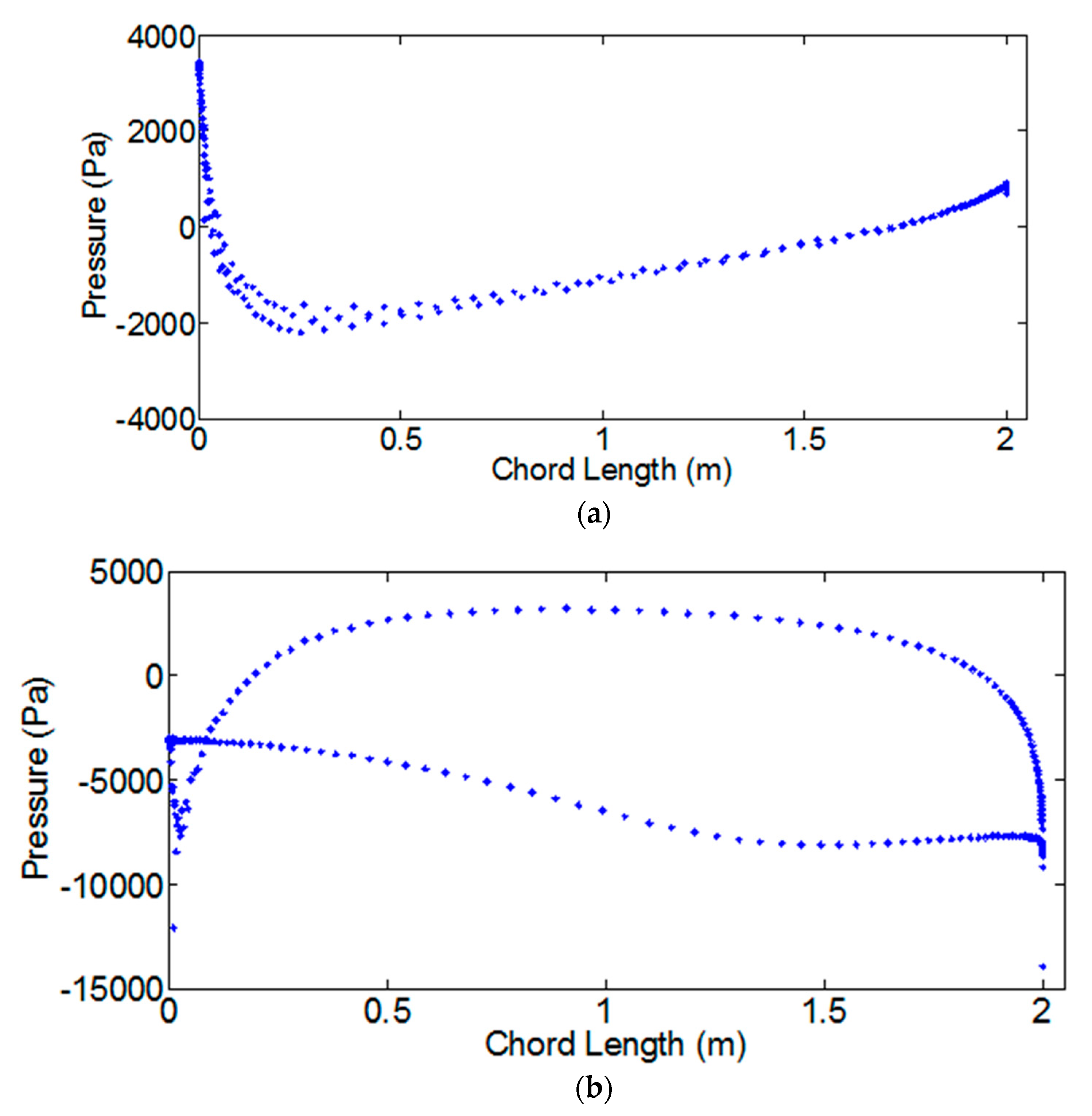
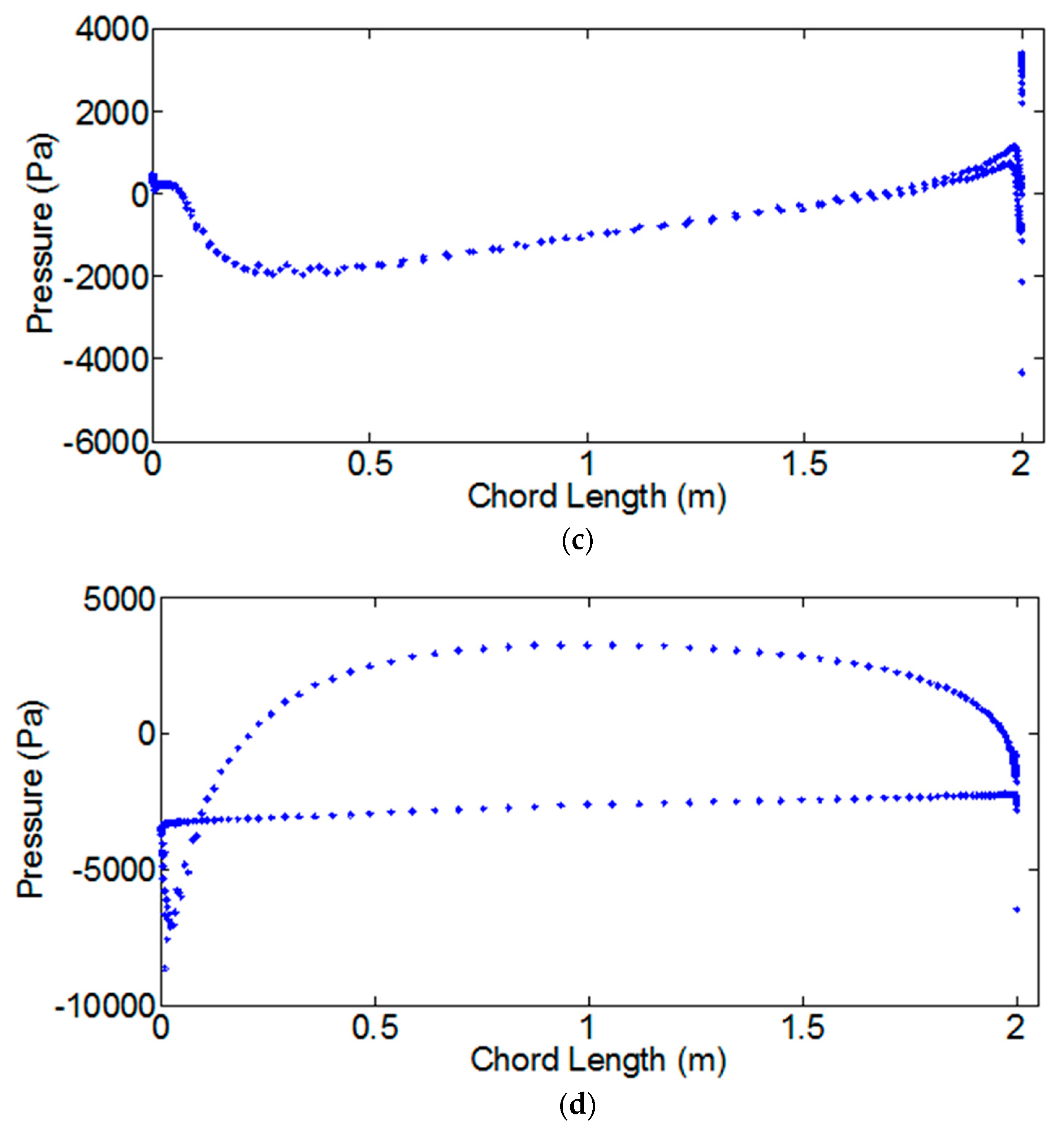
3.2. Wind Load Simulation Result
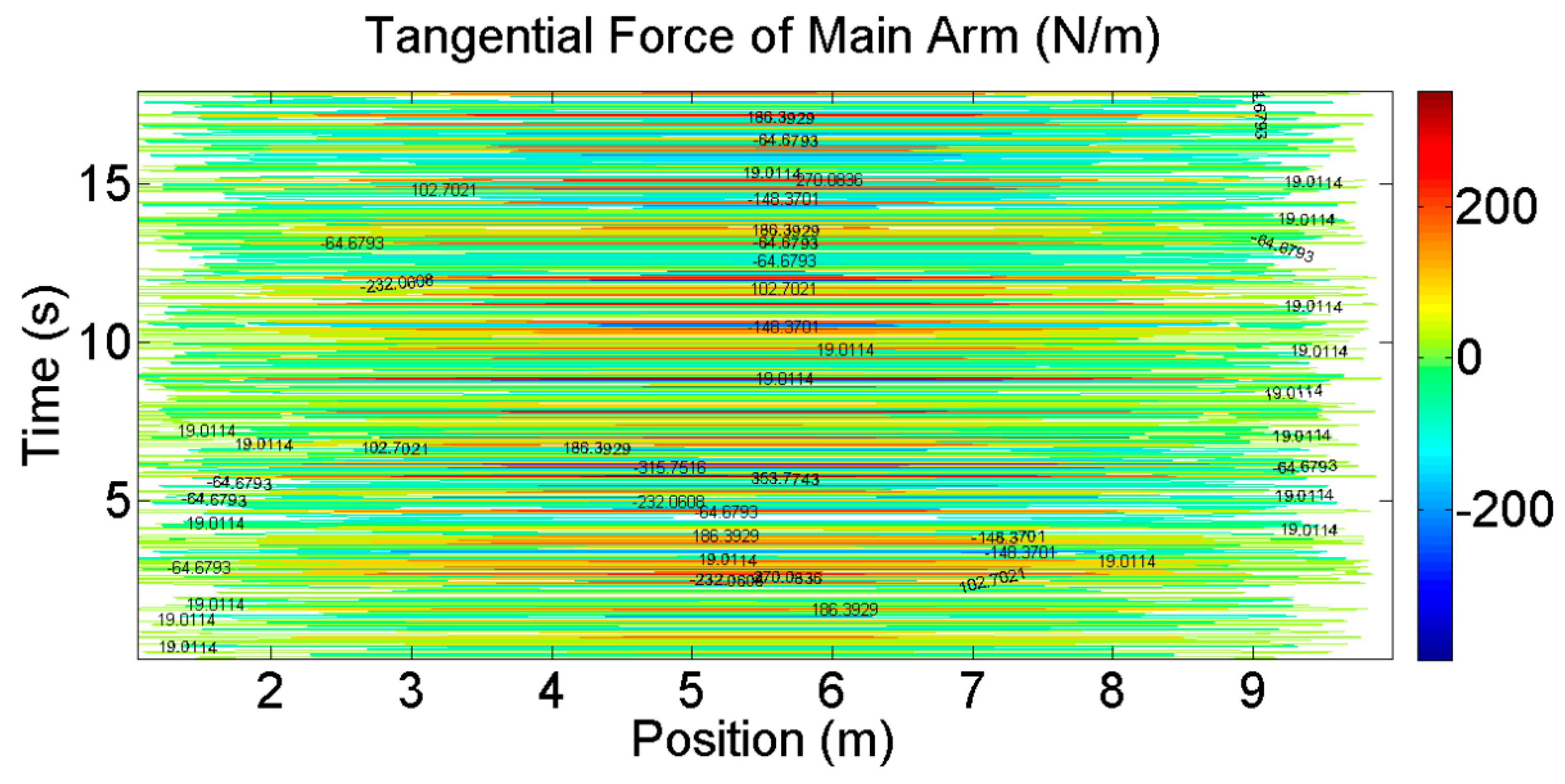
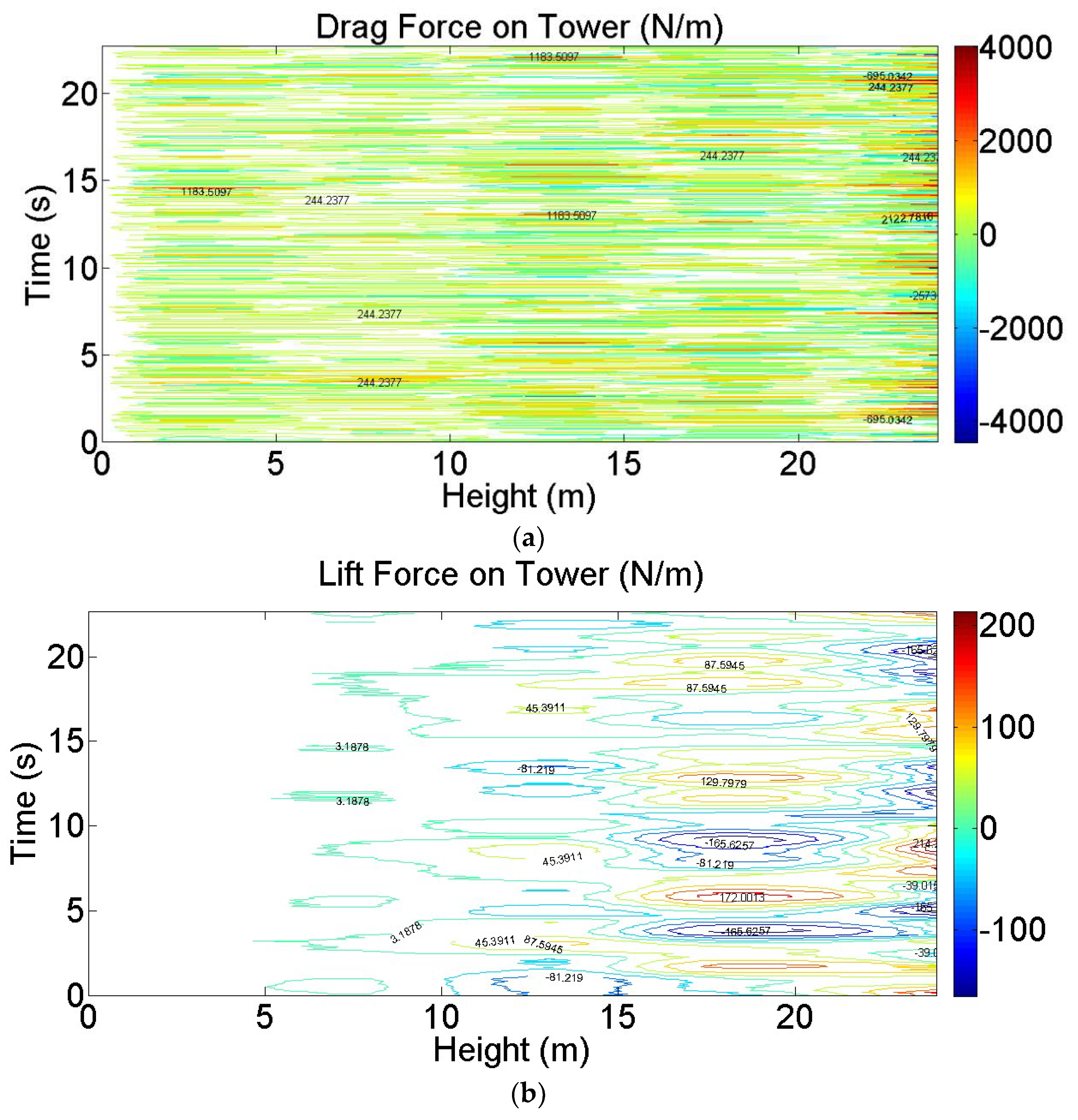
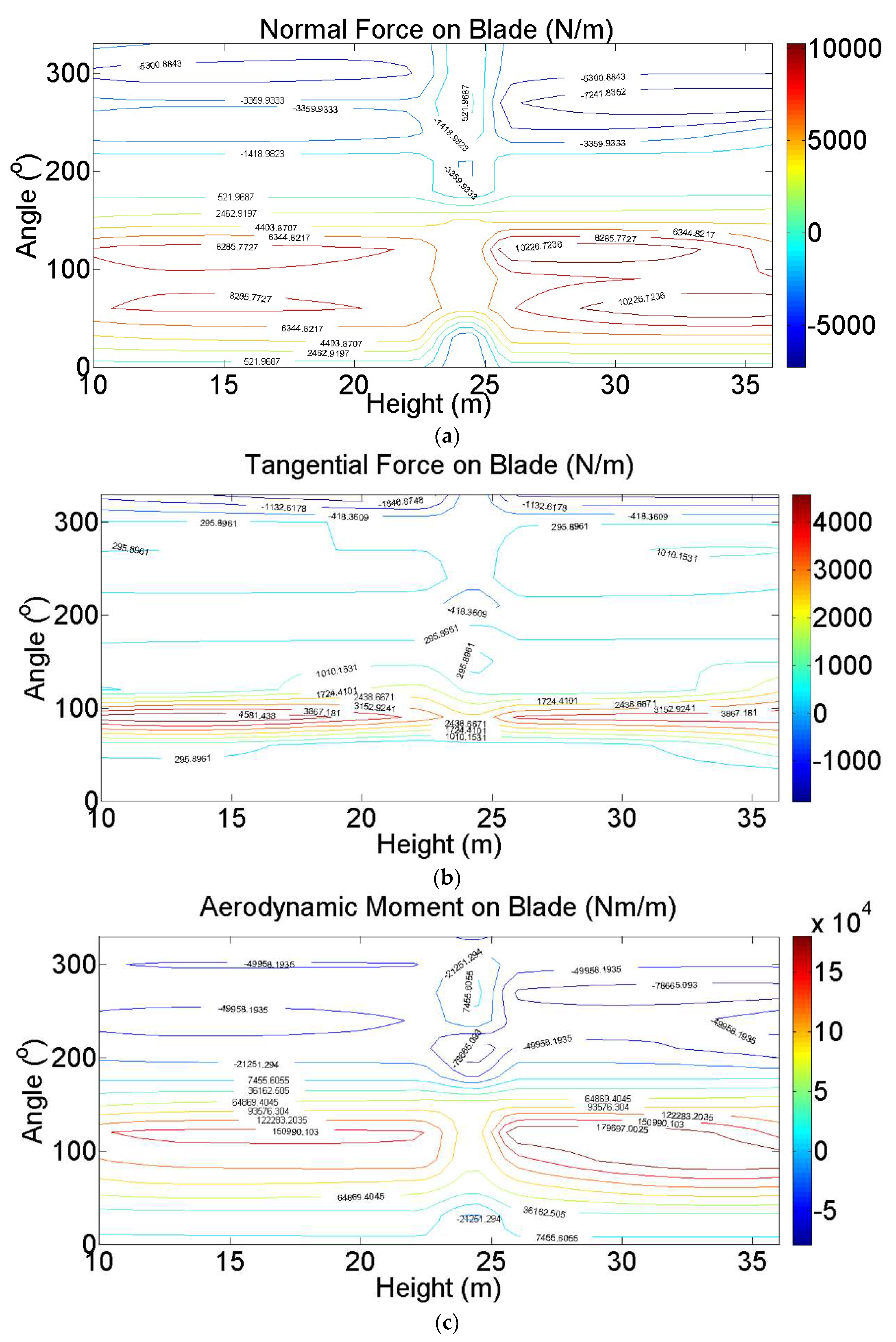
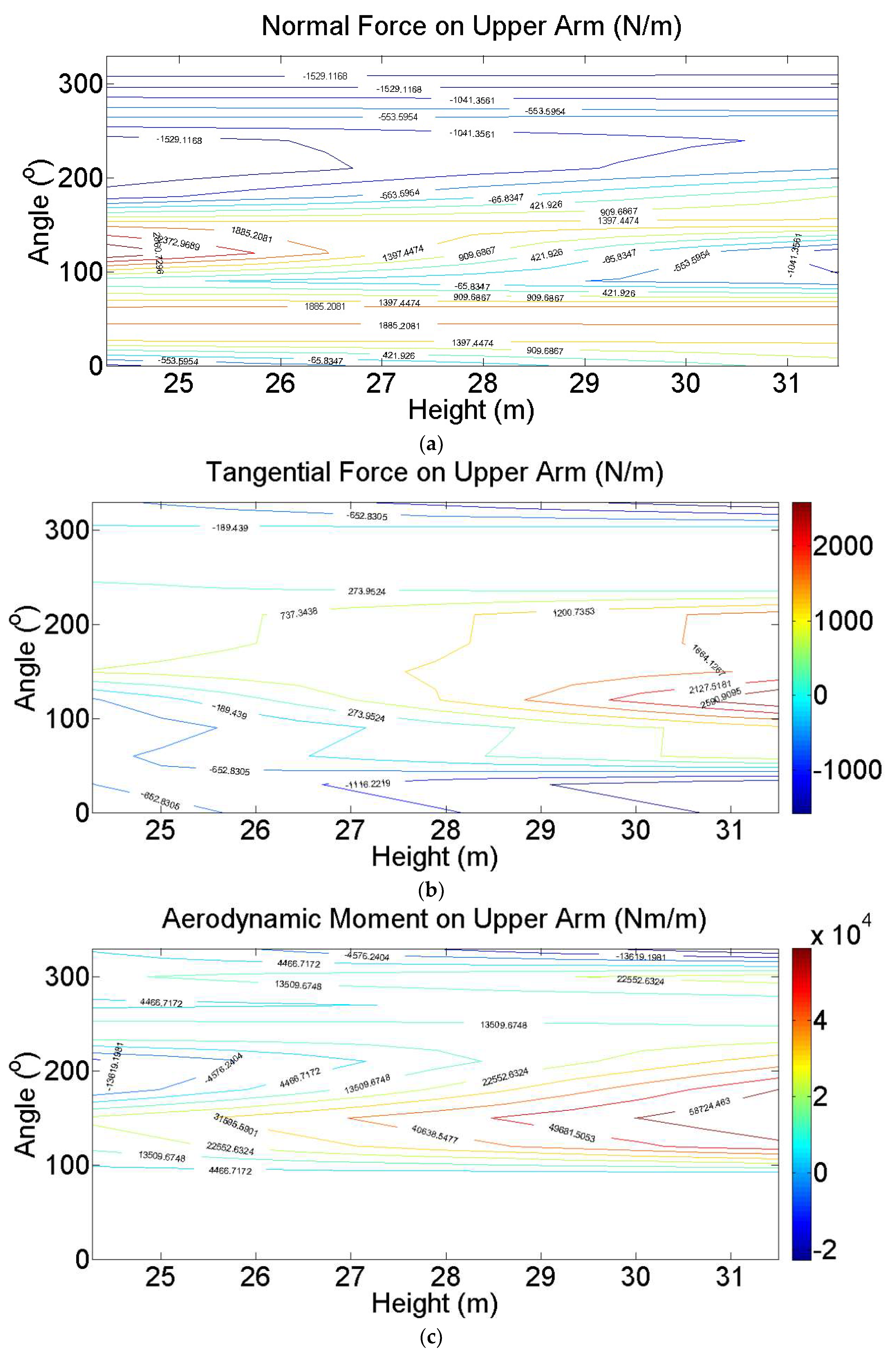
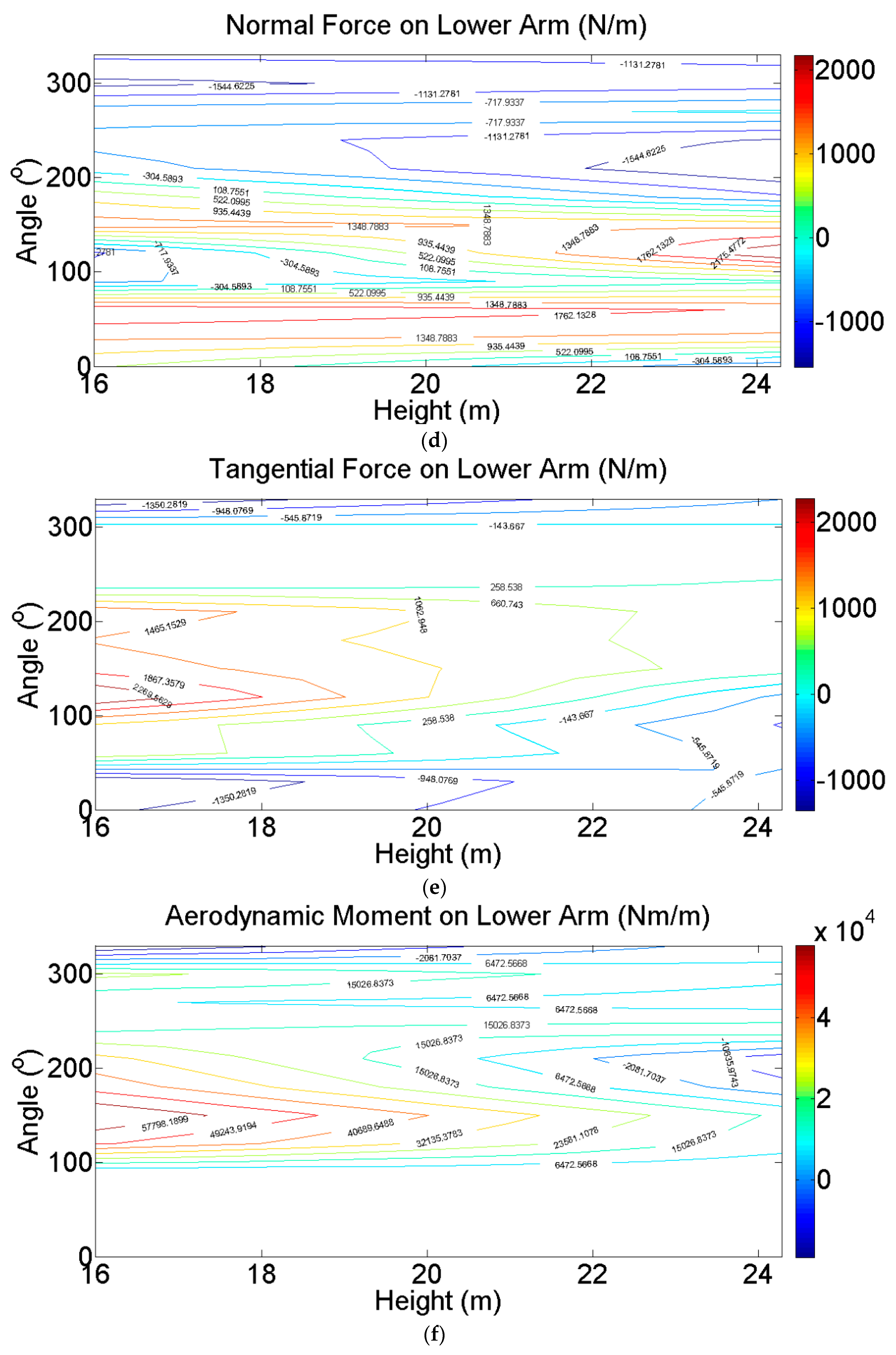
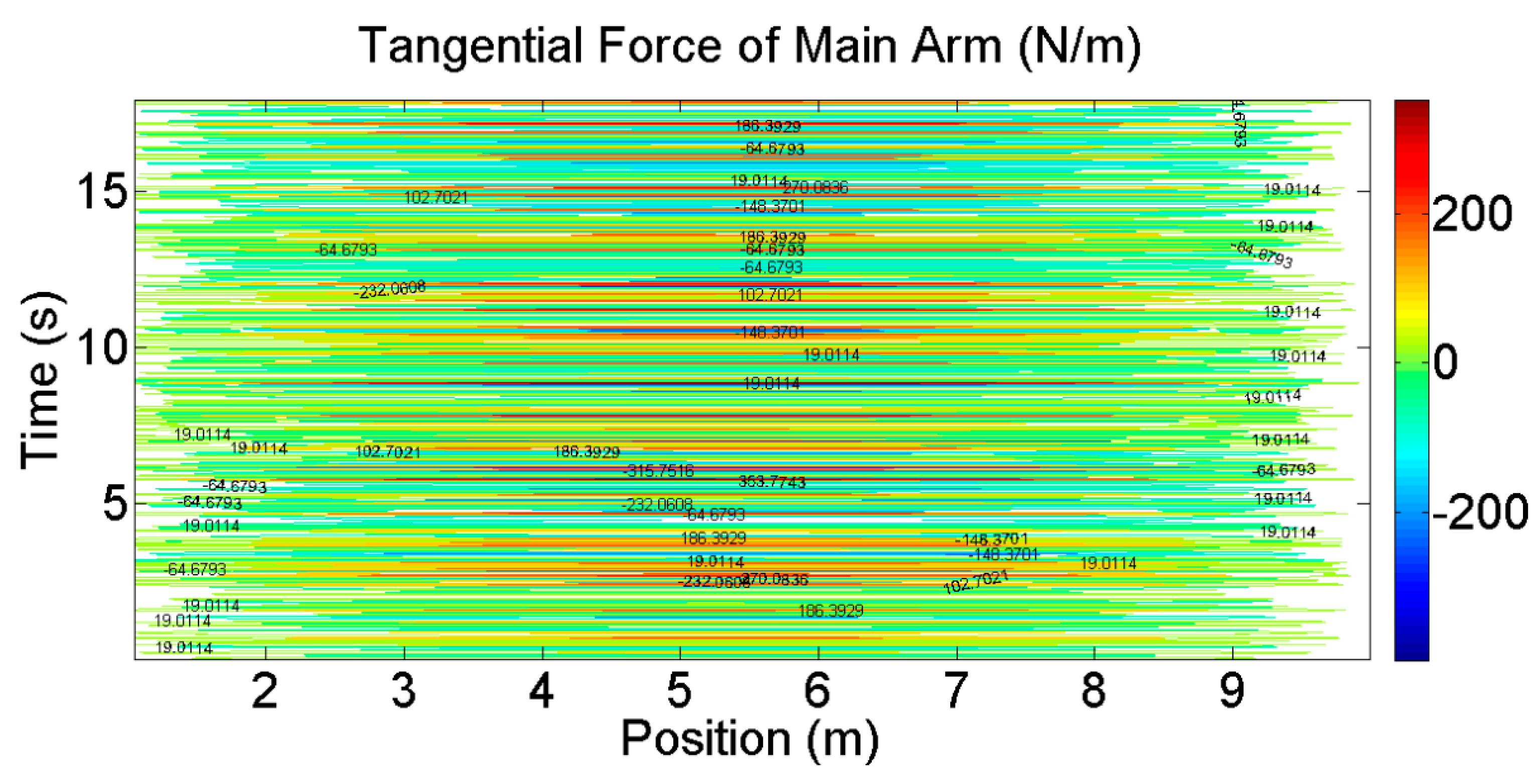
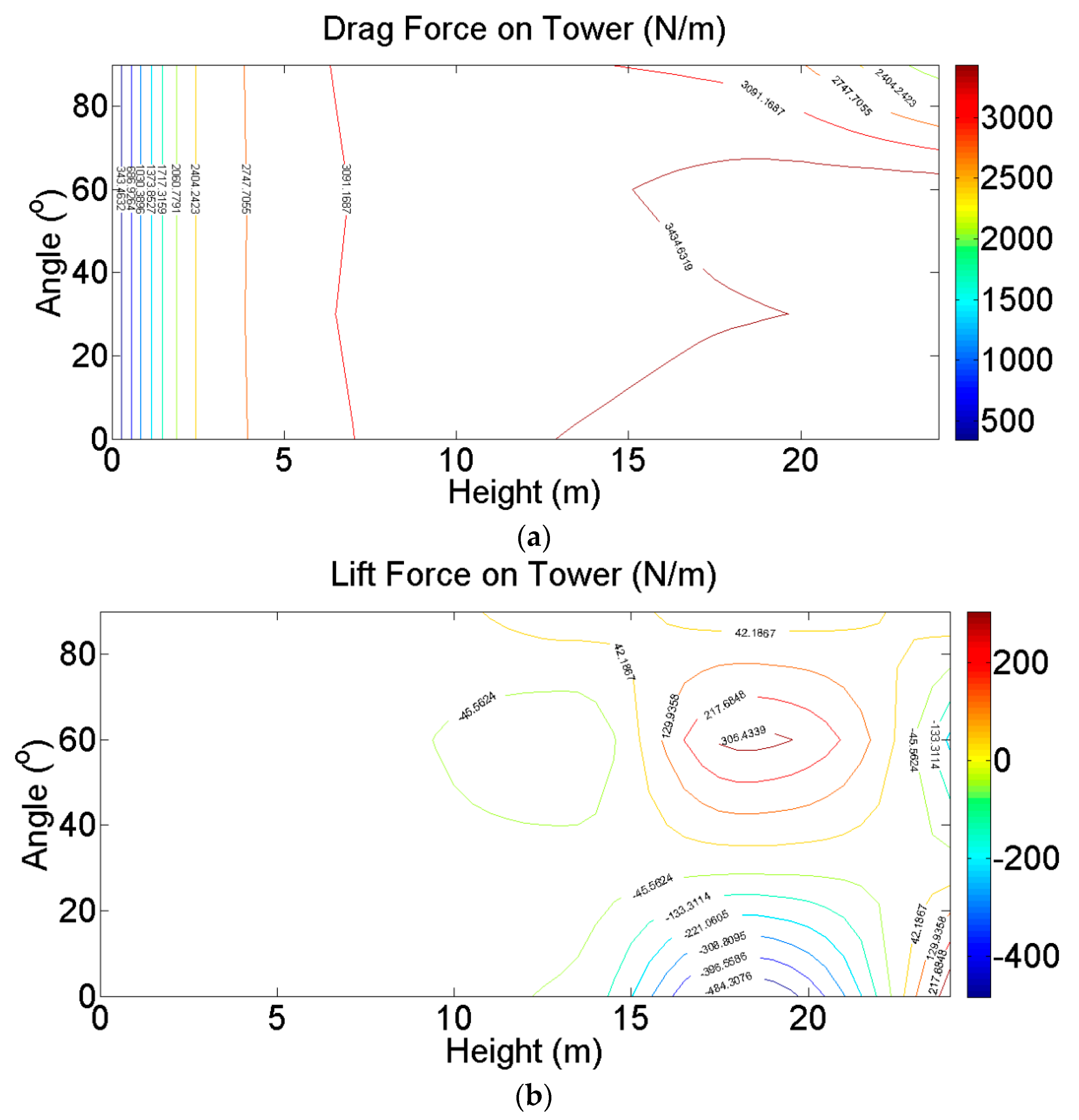
4. Wind Loads on the Entire VAWT
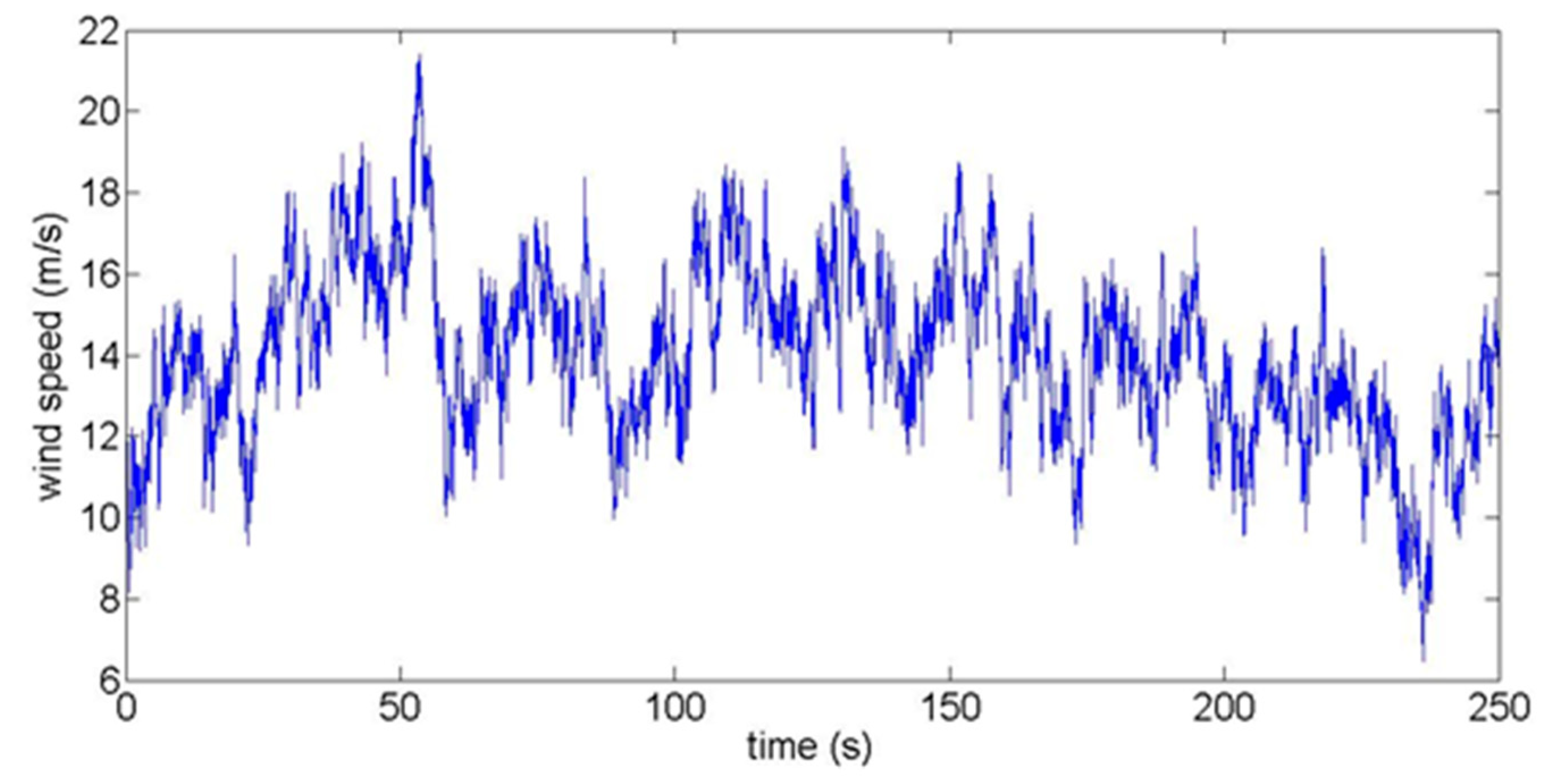
4.1. Wind Speed Simulations
4.2. CFD Simulation Strategy
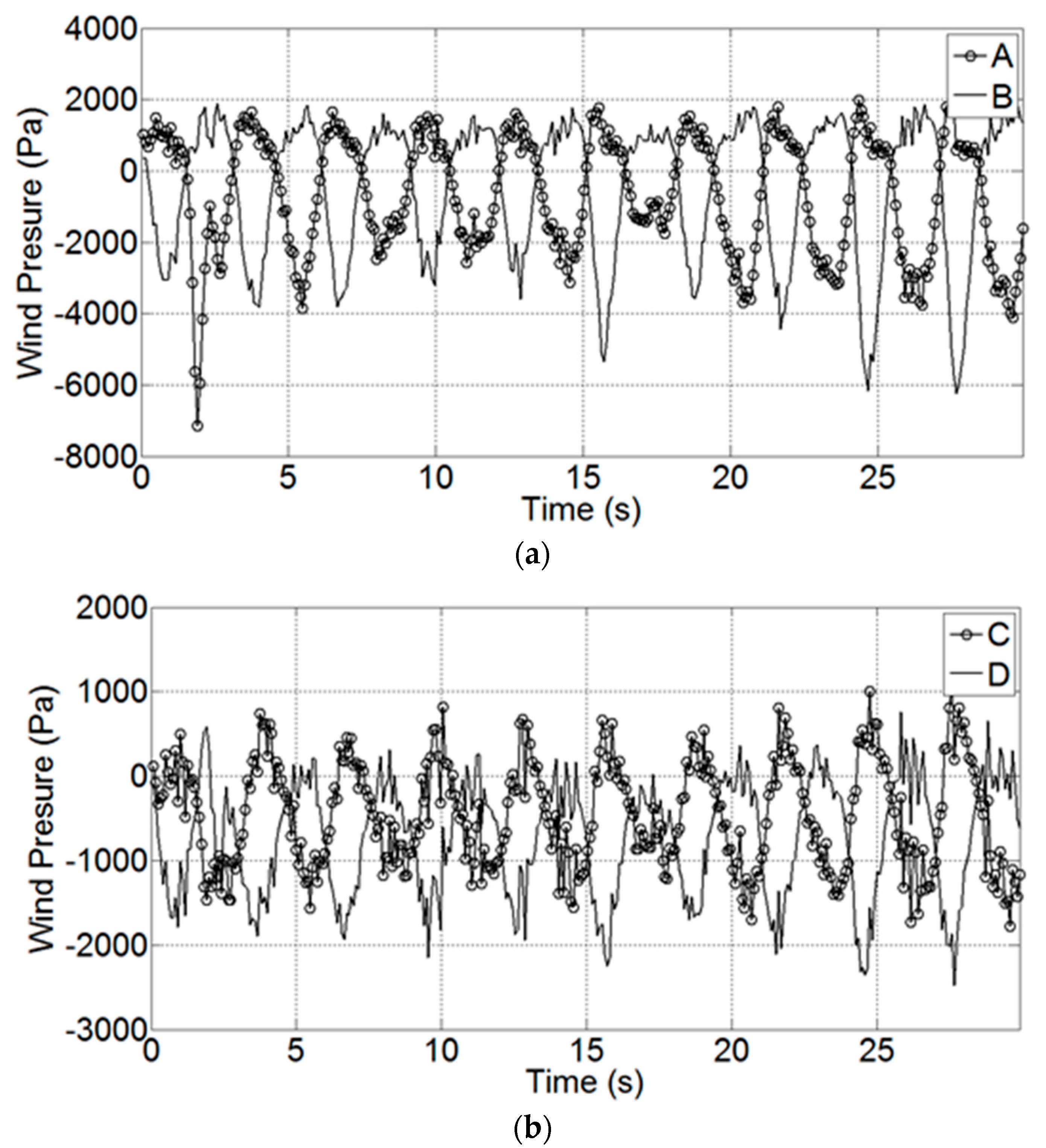
4.3. Wind Loads in Normal Wind Speed
4.4. Wind Loads in the Extreme Wind Speed
5. Conclusions
- (1)
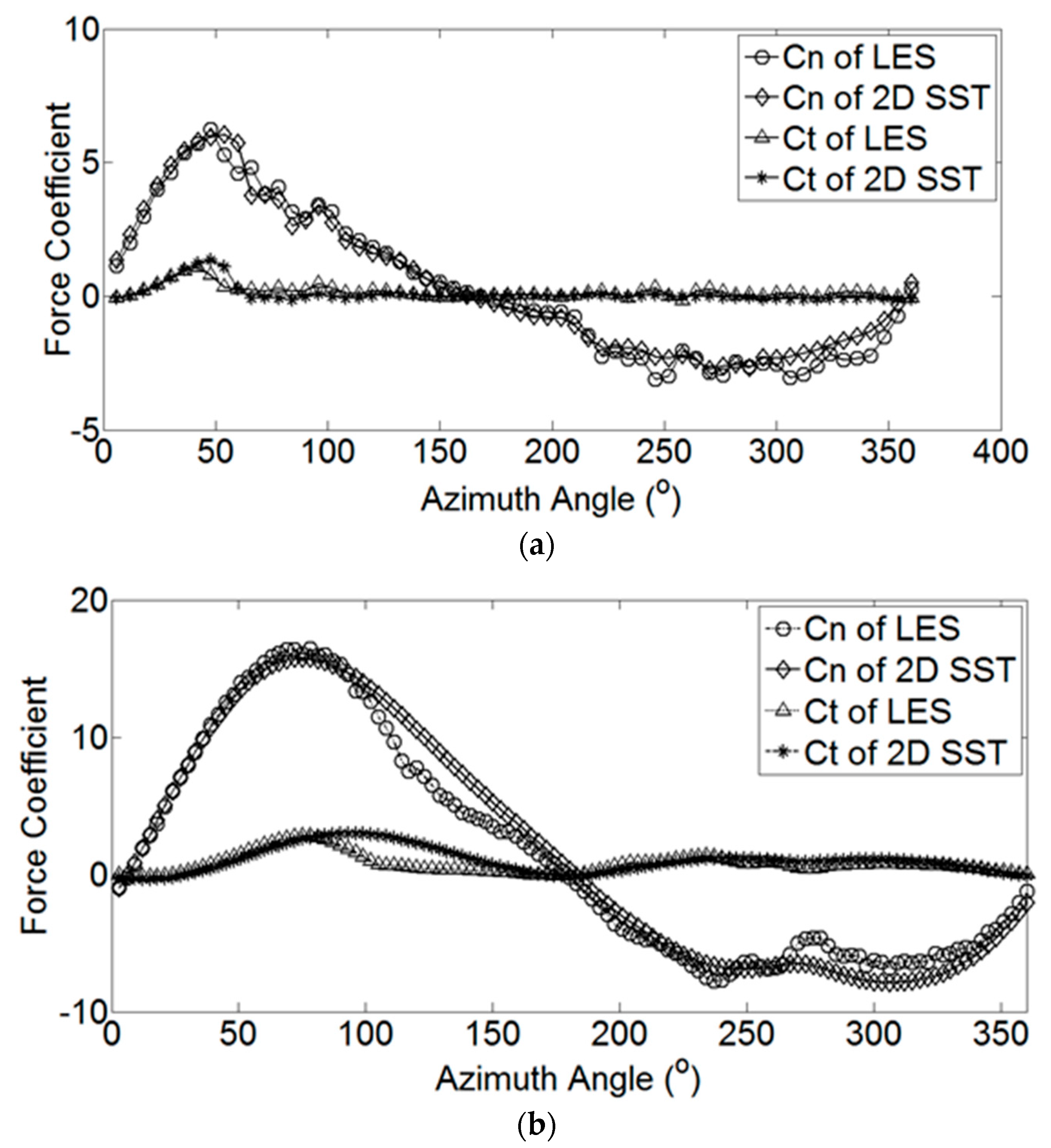
- The results from the 2.5D LES and the 2D SST simulations were compared. The two methods could obtain similar results for the cases of λ = 1 and λ = 3. In the case of λ = 1, the slight difference in the tangential force was because of the different predictions of flow separation. The 2D SST can be used as a proper model for determining the wind loads on VAWTs.
- (2)
- Using the 2D SST simulation, the wind pressures on blades and aerodynamic forces on the whole VAWT were obtained. The influences of turbulent inflow, tower, and arms on the aerodynamic forces on the blade were investigated. The tower of this large VAWT was far from the blades. Thus, the tower had a slight effect on the wind load of the blade and only caused a small reduction in the aerodynamic forces in the downwind side. The arms caused a considerable reduction in the tangential force and power coefficient.
- (3)
- Using the strip analysis method with a series of 2D SST k-ω simulations offers VAWT designers an engineering approach, which can obtain more detailed information of aerodynamics compared with DMST, while avoiding the intensive computational cost of 3D simulation.
- (4)
- Further quantifying the influence of support structure, such as arms and tower, and the accuracy of the proposed framework requires a high-fidelity 3D CFD simulation. More efforts should be directed toward this topic in the future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paraschivoiu, I. Wind Turbine Design—With Emphasis on Darrieus Concept; Presses Internationales Polytechnique: Montreal, QC, Canada, 2002. [Google Scholar]
- Almohammadi, K.M.; Ingham, D.B.; Ma, L.; Pourkashan, M. Computational fluid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine. Energy 2013, 58, 483–493. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Ferrara, G.; Ferrari, L. Dimensionless numbers for the assessment of mesh and timestep requirements in CFD simulations of Darrieus wind turbines. Energy 2016, 97, 246–261. [Google Scholar] [CrossRef]
- Li, C.; Xiao, Y.; Xu, Y.; Peng, Y.; Hu, G.; Zhu, S. Optimization of blade pitch in h-rotor vertical axis wind turbines through computational fluid dynamics simulations. Appl. Energy 2018, 212, 1107–1125. [Google Scholar] [CrossRef]
- Meana-Fernández, A.; Oro, J.M.F.; Díaz, K.M.A.; Velarde-Suárez, S. Turbulence-Model Comparison for Aerodynamic-Performance Prediction of a Typical Vertical-Axis Wind-Turbine Airfoil. Energies 2019, 12, 488. [Google Scholar] [CrossRef]
- Lanzafame, R.; Mauro, S.; Messina, M. Wind turbine CFD modeling using a correlation-based transitional model. Renew. Energy 2013, 52, 31–39. [Google Scholar] [CrossRef]
- Li, C.; Zhu, S.; Xu, Y.L.; Xiao, Y. 2.5 D large eddy simulation of vertical axis wind turbine in consideration of high angle of attack flow. Renew. Energy 2013, 51, 317–330. [Google Scholar] [CrossRef]
- Ismail, M.F.; Vijayaraghavan, K. The effects of aerofoil profile modification on a vertical axis wind turbine performance. Energy 2015, 80, 20–31. [Google Scholar] [CrossRef]
- Amet, E.; Maître, T.; Pellone, C.; Achard, J.L. 2D numerical simulations of blade-vortex interaction in a darrieus turbine. J. Fluids Eng. 2009, 131, 111103. [Google Scholar] [CrossRef]
- Castelli, M.R.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Danao, L.A.; Edwards, J.; Eboibi, O.; Howell, R. A numerical investigation into the influence of unsteady wind on the performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2014, 116, 111–124. [Google Scholar] [CrossRef]
- Mcintosh, S.C.; Babinsky, H.; Bertenyi, T. Unsteady Power Output of Vertical Axis Wind Turbines Operating within a Fluctuating Free-Stream. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 7–10 January 2008. [Google Scholar]
- Scheurich, F.; Brown, R.E. Modelling the aerodynamics of vertical-axis wind turbines in unsteady wind conditions. Wind Energy 2013, 16, 91–107. [Google Scholar] [CrossRef]
- Ferreira, C.J.; Bijl, H.; van Bussel, G.; van Kuik, G. Simulating dynamic stall in a 2D VAWT: Modeling strategy, verification and validation with particle image velocimetry data. J. Phys. Conf. Ser. 2007, 75, 012–023. [Google Scholar] [CrossRef]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Numerical investigations on dynamic stall of low Reynolds number flow around oscillating airfoils. Comput. Fluids 2010, 39, 1529–1541. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. Characterization of aerodynamic performance of vertical axis wind turbines: Impact of operational parameters. Energy Convers. Manag. 2018, 169, 45–77. [Google Scholar] [CrossRef]
- Hand, B.; Kelly, G.; Cashman, A. Numerical simulation of a vertical axis wind turbine airfoil experiencing dynamic stall at high Reynolds numbers. Comput. Fluids 2017, 149, 12–30. [Google Scholar] [CrossRef]
- Nini, M.; Motta, V.; Bindolino, G.; Guardone, A. Three-dimensional simulation of a complete vertical axis wind turbine using overlapping grids. J. Comput. Appl. Math. 2014, 270, 78–87. [Google Scholar] [CrossRef]
- Elkhoury, M.; Kiwata, T.; Aoun, E. Experimental and numerical investigation of a three-dimensional vertical-axis wind turbine with variable-pitch. J. Wind Eng. Ind. Aerod. 2015, 139, 111–123. [Google Scholar] [CrossRef]
- Omar, D.L.M.; Jhon, J.Q.; Santiago, L. RANS and Hybrid RANS-LES Simulations of an H-Type Darrieus Vertical Axis Water Turbine. Energies 2018, 11, 2348. [Google Scholar]
- Balduzzi, F.; Drofelnik, J.; Bianchini, A.; Ferrara, G.; Ferrari, L.; Campobasso, M.S. Darrieus Wind Turbine Blade Unsteady Aerodynamics: A Three-Dimensional Navier-Stokes CFD assessment. Energy 2017, 128, 550–563. [Google Scholar] [CrossRef]
- MacPhee, D.W.; Beyene, A. Fluid–structure interaction analysis of a morphing vertical axis wind turbine. J. Fluids Struct. 2016, 60, 143–159. [Google Scholar] [CrossRef]
- Yang, P.; Xiang, J.; Fang, F.; Pain, C.C. A fidelity fluid-structure interaction model for vertical axis tidal turbines in turbulence flows. Appl. Energy 2019, 236, 465–477. [Google Scholar] [CrossRef]
- Liu, K.; Yu, M.; Zhu, W. Enhancing wind energy harvesting performance of vertical axis wind turbines with a new hybrid design: A fluid-structure interaction study. Renew. Energy 2019, 140, 912–927. [Google Scholar] [CrossRef]
- Cachafeiro, H.; de Arevalo, L.; Vinuesa, R.; Goikoetxea, J.; Barriga, J. Impact of solar selective coating ageing on energy cost. Energy Procedia 2015, 69, 299–309. [Google Scholar] [CrossRef]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Snel, H.; Schepers, J.G. Joint Investigation of Dynamic Inflow Effects and Implementation of an Engineering Method; ECN: Sint Maartensvlotbrug, The Netherlands, 1995. [Google Scholar]
- Wendler, J.; Marten, D.; Pechlivanoglou, G.; Nayeri, C.; Paschereit, C. An unsteady aerodynamics model for lifting line free vortex wake simulations of HAWT and VAWT in QBlade. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Lei, H.; Zhou, D.; Bao, Y.; Chen, C.; Ma, N.; Han, Z. Numerical simulations of the unsteady aerodynamics of a floating vertical axis wind turbine in surge motion. Energy 2017, 127, 1–17. [Google Scholar] [CrossRef]
- Wekesa, D.W.; Wang, C.; Wei, Y.; Kamau, J.N.; Danao, L.A.M. A numerical analysis of unsteady inflow wind for site specific vertical axis wind turbine: A case study for Marsabit and Garissa in Kenya. Renew. Energy 2015, 76, 648–661. [Google Scholar] [CrossRef]
- Danao, L.A.; Eboibi, O.; Howell, R. An experimental investigation into the influence of unsteady wind on the performance of a vertical axis wind turbine. Appl. Energy 2013, 107, 403–411. [Google Scholar] [CrossRef]
- Mcintosh, S.C.; Babinsky, H.; Bertenyi, T. Optimizing the Energy Output of Vertical Axis Wind Turbines for Fluctuating Wind Conditions. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 8–11 January 2007. [Google Scholar]
- Simiu, E.; Scanlan, R.H. Wind Effects on Structures: An Introduction to Wind Engineering; John Wiley: New York, NY, USA, 1986. [Google Scholar]
- Xu, Y.L. Wind Effects on Cable-Supported Bridges; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- International Electrotechnical Commission. IEC 61400-1: Wind Turbines Part 1: Design Requirements, 3rd ed.; IEC: Geneva, Switzerland, 2015. [Google Scholar]
- Vinuesa, R.; Nagib, H. Enhancing the accuracy of measurement techniques in high Reynolds number turbulent boundary layers for more representative comparison to their canonical representations. Eur. J. Mech. B Fluid. 2016, 55, 300–312. [Google Scholar] [CrossRef]
- Shinozuka, M.; Jan, C.M. Digital simulation of random processes and its applications. J. Sound Vib. 1972, 25, 111–128. [Google Scholar] [CrossRef]
- Chen, X.; Kareem, A. Equivalent static wind loads on buildings: New model. J. Struct. Eng. ASCE 2004, 130, 1425–1435. [Google Scholar] [CrossRef]
- Vinuesa, R.; Hosseini, S.; Hanifi, A.; Henningson, D.; Schlatter, P. Pressure-gradient turbulent boundary layers developing around a wing section. Flow Turbul. Combust. 2017, 99, 613–641. [Google Scholar] [CrossRef] [PubMed]
- Chattot, J.; Hafez, M. Wind Turbine and Propeller Aerodynamics—Analysis and Design. In Theoretical and Applied Aerodynamics; Springer: Berlin, Germany, 2015; pp. 327–372. [Google Scholar]
- Davenport, A.G. The use of taut-strip models in the prediction of the response of long span bridges to turbulent wind. In Proceedings of the IUTAM/IAHR Symposium on Flow-Induced Structural Vibrations, Karlsruhe, Germany, 14–16 August 1972. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Turbulence, Heat and Mass Transfer 4; Begell House, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Barnes, W.; McCormick, W. Aerodynamics, Aeronautics, and Flight Mechanics (Volume 2); Wiley: New York, NY, USA, 1995. [Google Scholar]
- ANSYS. 12.0 User’s Guide; Ansys Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Lin, J.H.; Xu, Y.L.; Xia, Y. Structural Analysis of Large-scale Vertical Axis Wind Turbines, Part II: Fatigue and Ultimate Strength Analyses. Energies 2019. accepted for publication. [Google Scholar]

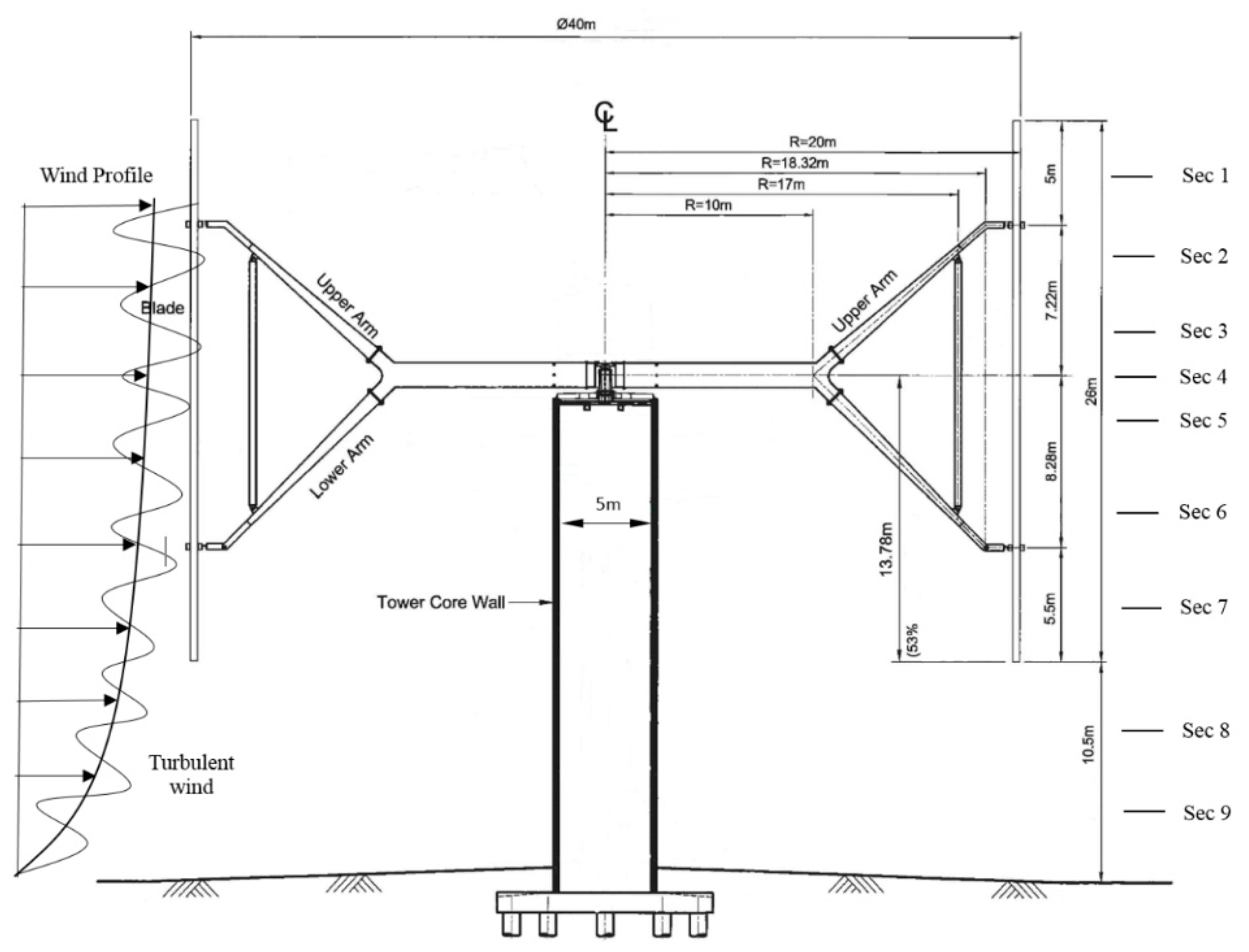
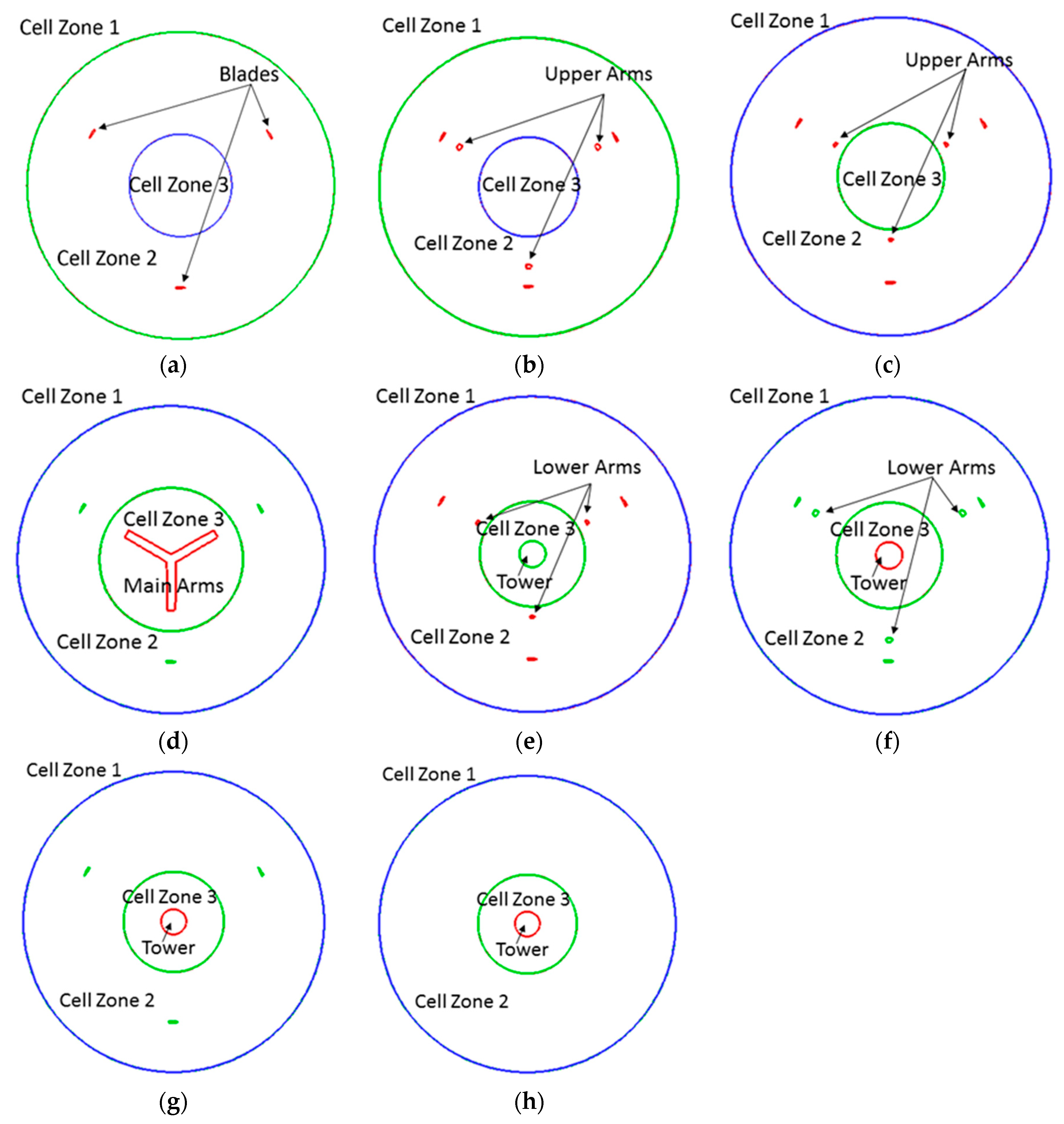
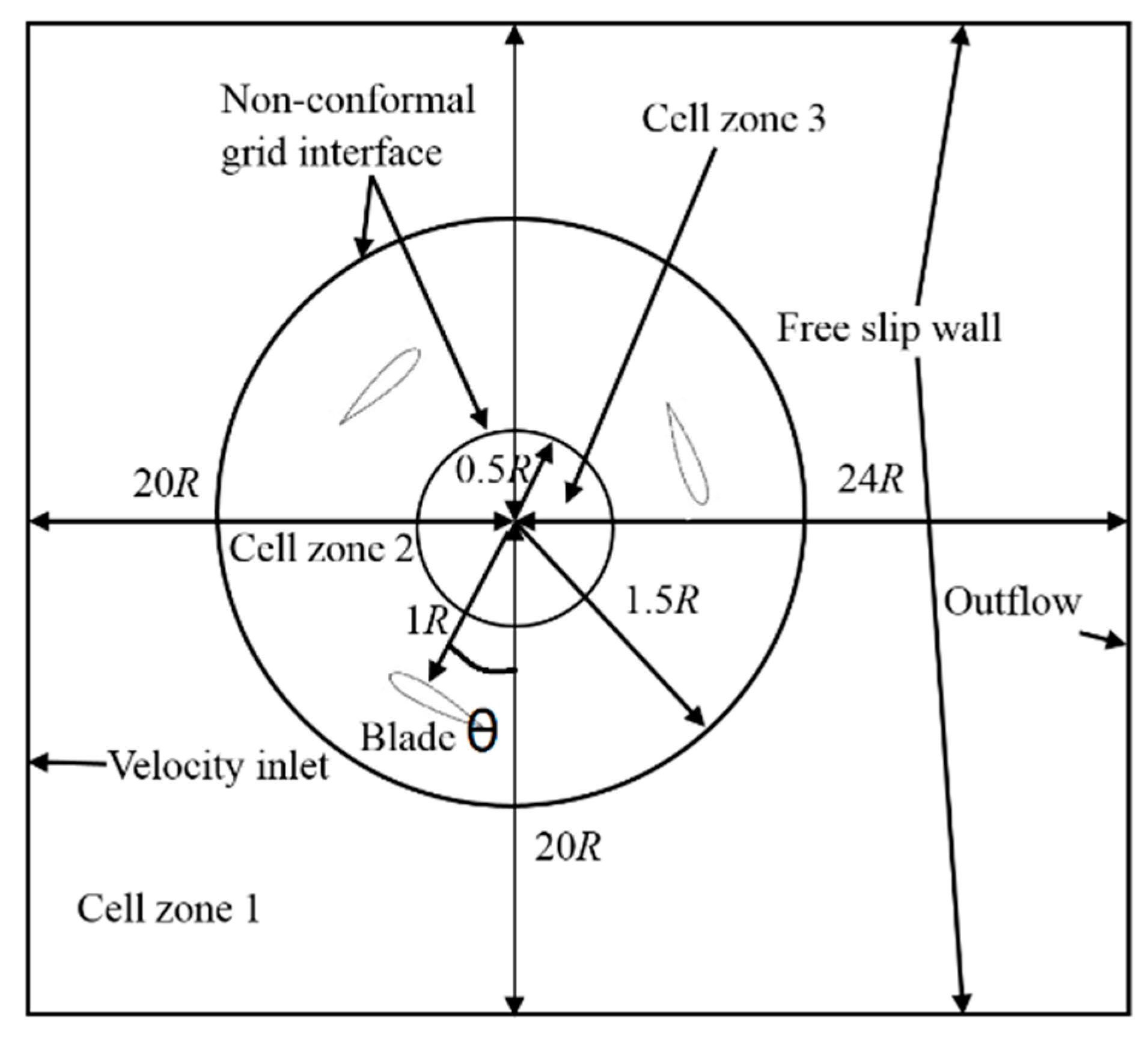
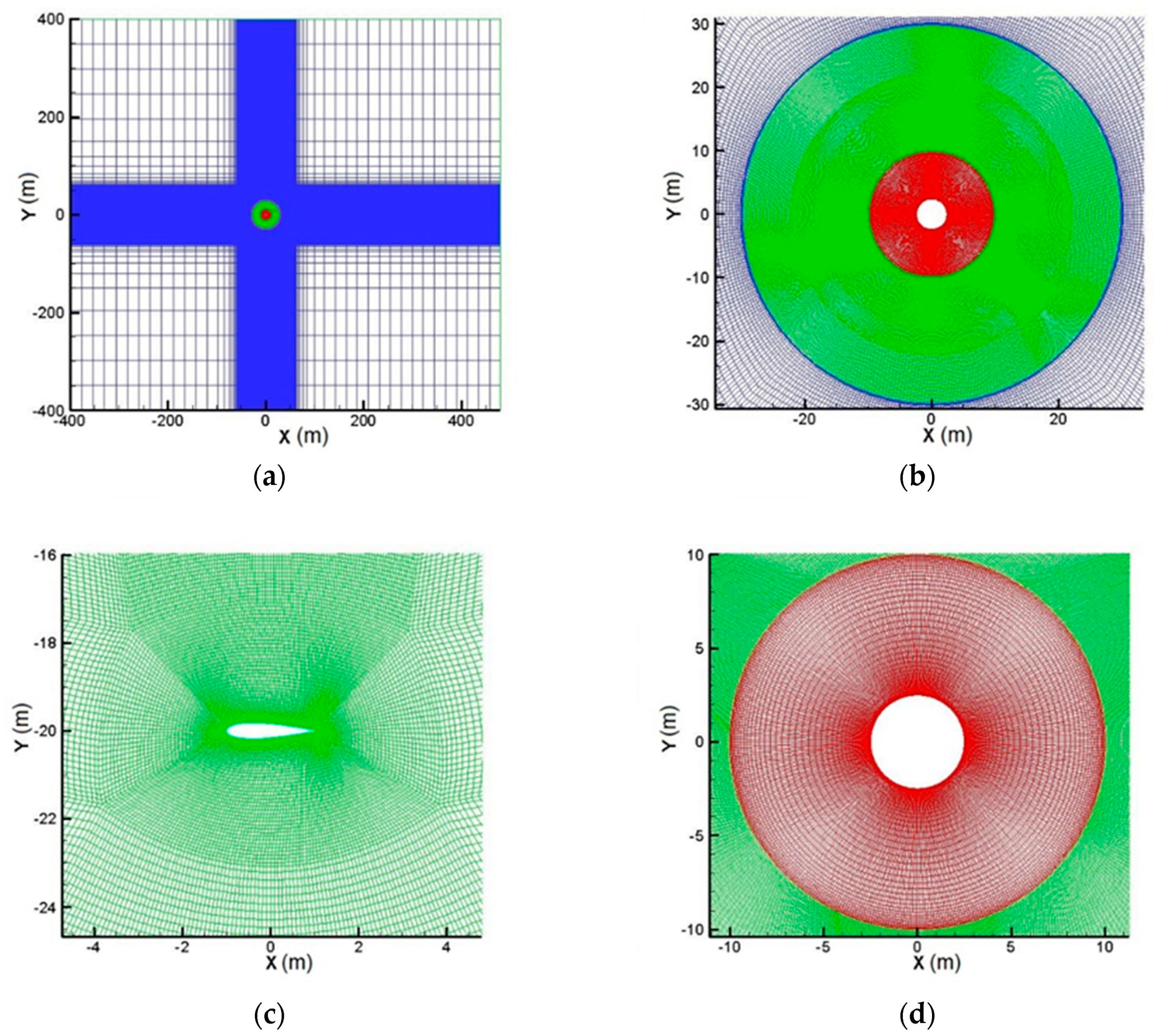


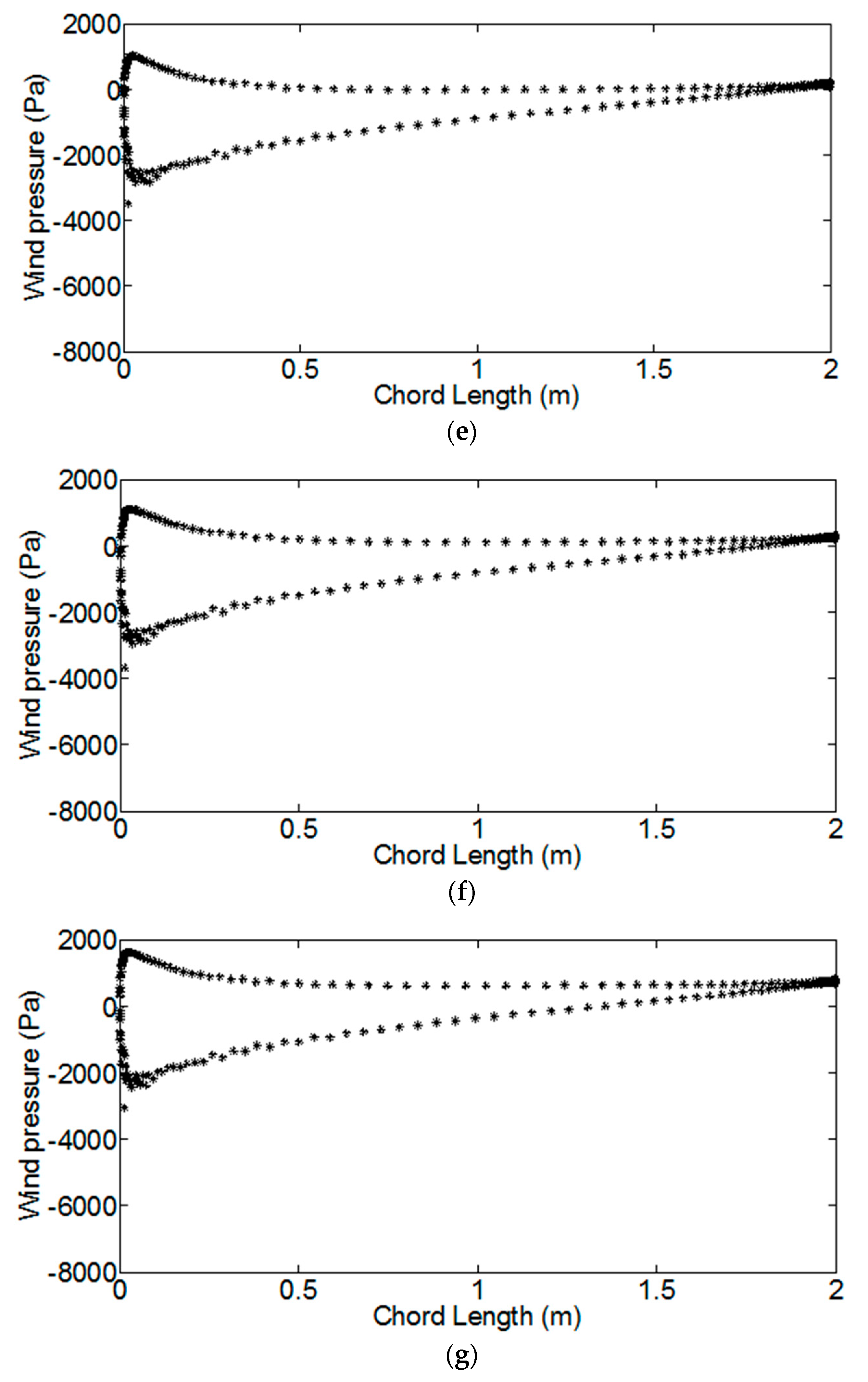
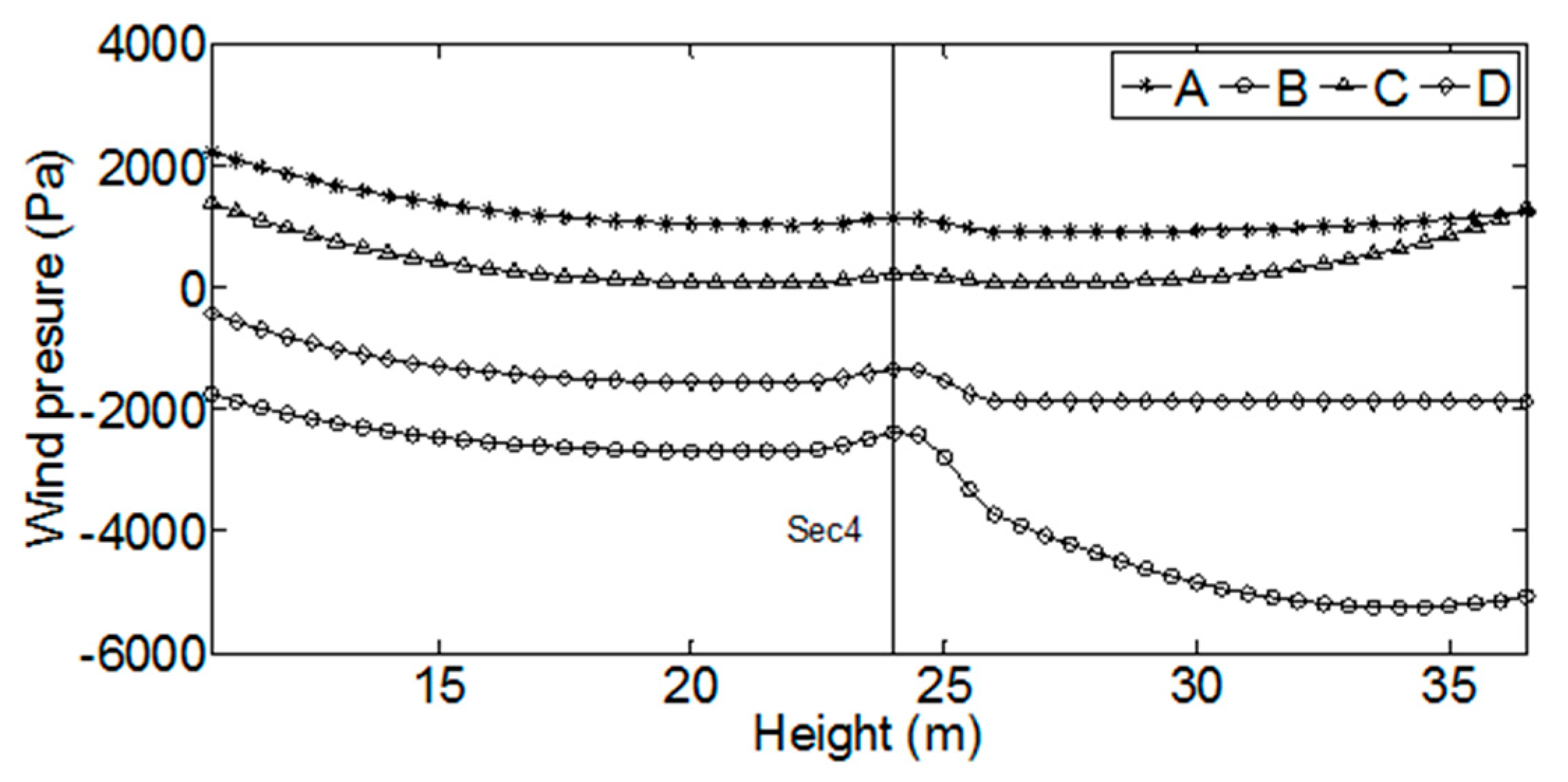
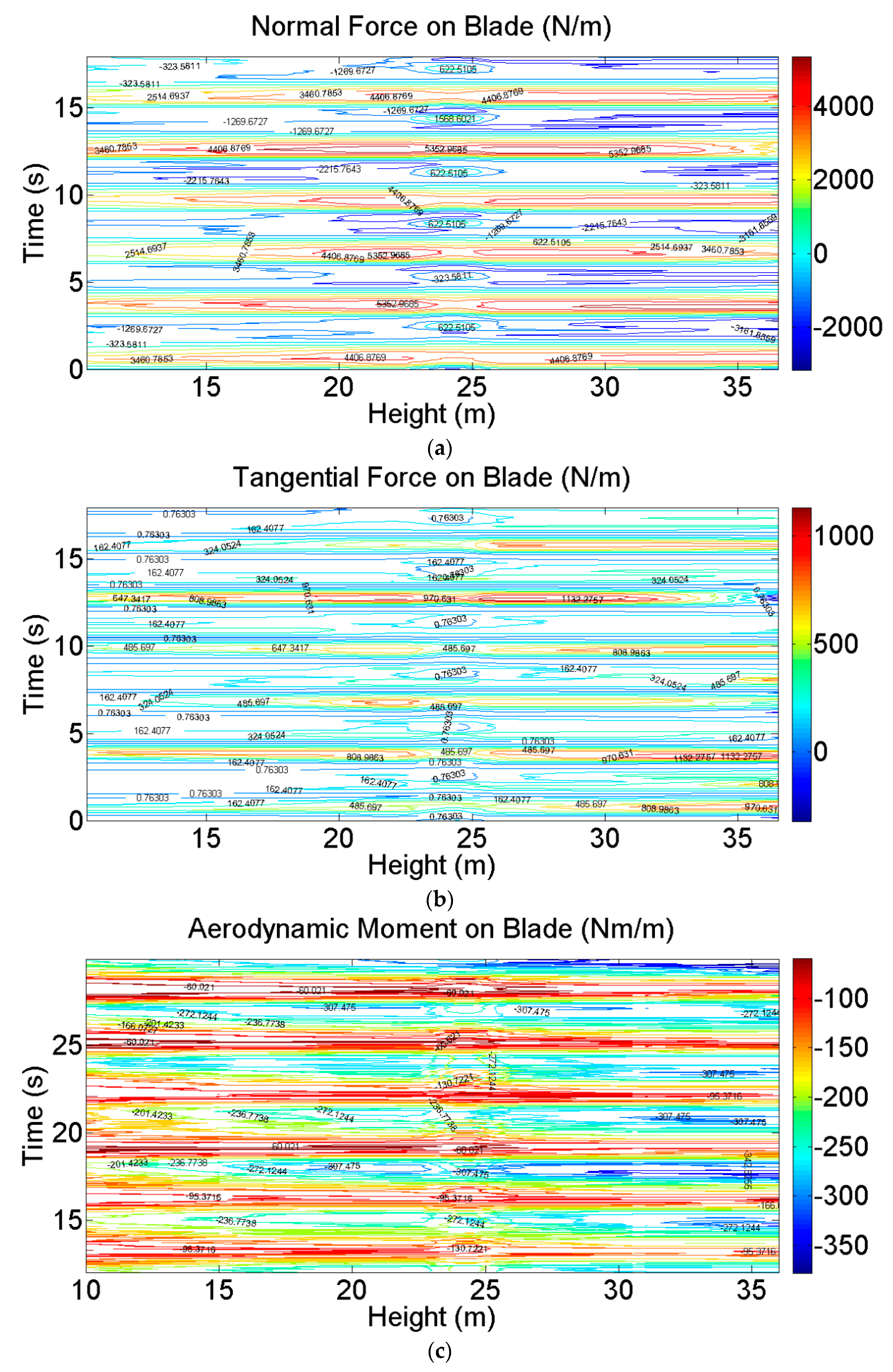

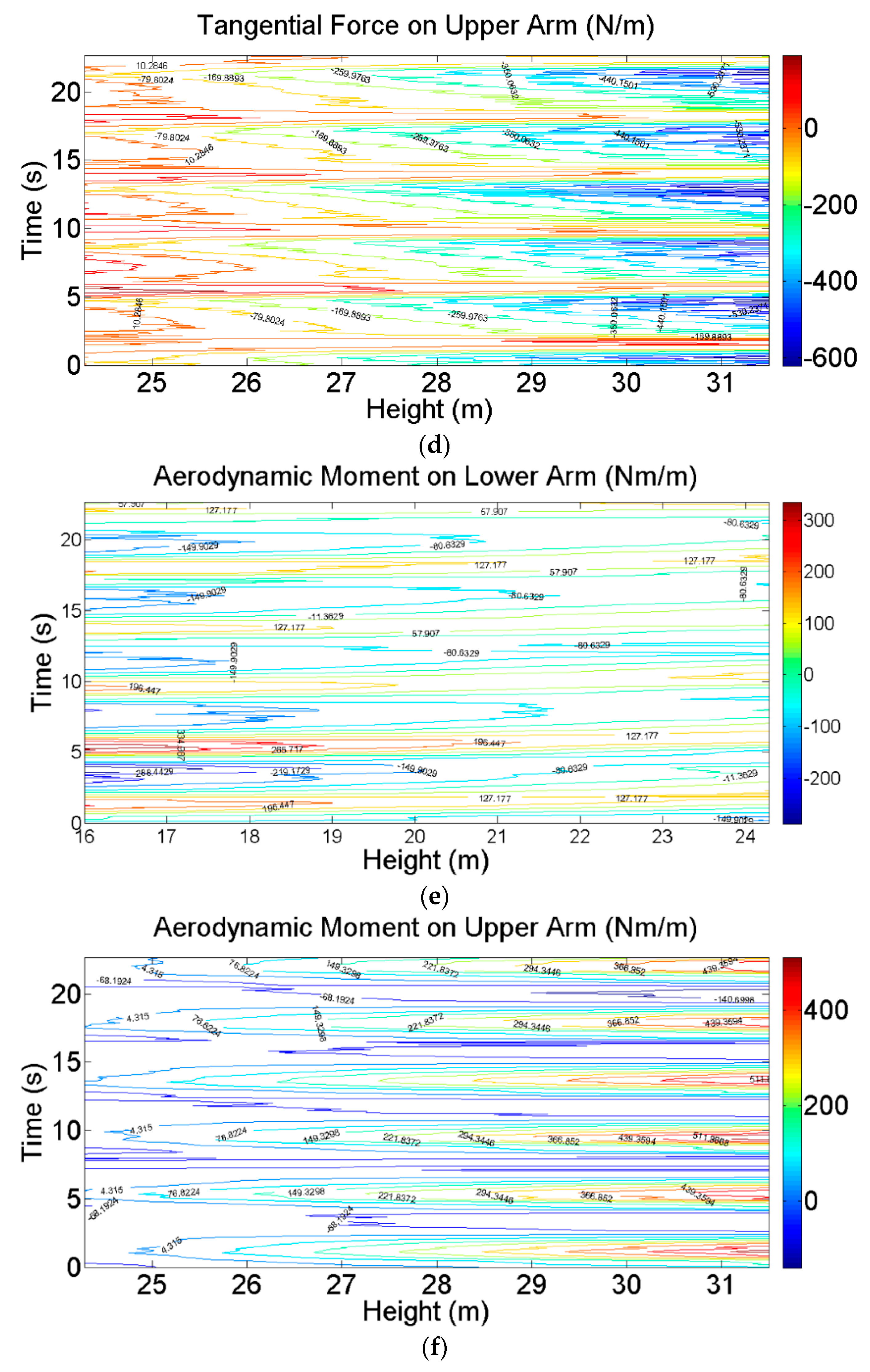
| Section | Sec 1 | Sec 2 | Sec 3 | Sec 4 | Sec 5 | Sec 6 | Sec 7 | Sec 8 | Sec 9 |
|---|---|---|---|---|---|---|---|---|---|
| Elevation above ground (m) | 34.0 | 29.7 | 26.1 | 24.3 | 22.2 | 18.1 | 13.3 | 7.9 | 2.6 |
| Section | Sec 1 | Sec 2 | Sec 3 | Sec 4 | Sec 5 | Sec 6 | Sec 7 | Sec 8 | Sec 9 |
|---|---|---|---|---|---|---|---|---|---|
| Grid Number | 217,432 | 299,032 | 279,832 | 238,232 | 277,832 | 277,832 | 231,032 | 88,432 | 88,432 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Xu, Y.-L.; Xia, Y.; Li, C. Structural Analysis of Large-Scale Vertical-Axis Wind Turbines, Part I: Wind Load Simulation. Energies 2019, 12, 2573. https://doi.org/10.3390/en12132573
Lin J, Xu Y-L, Xia Y, Li C. Structural Analysis of Large-Scale Vertical-Axis Wind Turbines, Part I: Wind Load Simulation. Energies. 2019; 12(13):2573. https://doi.org/10.3390/en12132573
Chicago/Turabian StyleLin, Jinghua, You-Lin Xu, Yong Xia, and Chao Li. 2019. "Structural Analysis of Large-Scale Vertical-Axis Wind Turbines, Part I: Wind Load Simulation" Energies 12, no. 13: 2573. https://doi.org/10.3390/en12132573
APA StyleLin, J., Xu, Y.-L., Xia, Y., & Li, C. (2019). Structural Analysis of Large-Scale Vertical-Axis Wind Turbines, Part I: Wind Load Simulation. Energies, 12(13), 2573. https://doi.org/10.3390/en12132573






