Abstract
This paper presents a sector subdivision based space vector pulse width modulation (SVPWM) strategy with reduced current ripple for a three-level inverter. Using the output current ripple theory, closed-form expressions of average current ripple vectors for both continuous and discontinuous switching sequences are derived. Based on the sector and triangle distributions of conventional SVPWM strategy, each triangle is further divided into three small-regions. Then the switching sequence with the lowest magnitude of the average current ripple vector is applied in every small-region, so that the advantages of continuous pulse width modulation (CPWM) and discontinuous pulse width modulation (DPWM) under different modulation index conditions are combined to reduce the current ripple in the whole modulation range. The output performance of the proposed strategy is compared with the conventional CPWM and DPWM strategy, and experimental results verify that the proposed strategy could reduce the current ripple of three-level inverters effectively.
1. Introduction
Three-level inverters are possible to generate five-level-step-shaped line to line voltage and three-level-step-shaped phase voltage. So the harmonics of the output voltage and current are reduced compared with conventional two-level inverters. Additionally, the emitter-collector voltage is only one half of that of conventional two-level inverters. Due to the low stress to switching devices, switching loss and switching noise are reduced [1,2,3]. The topology of three-level inverters can be divided into three categories: cascade H-bridge (CHB) [4], flying capacitor (FC) [5], and neutral-point-clamped (NPC) [6]. Among them, NPC three-level inverters are the most widely used in medium-voltage high-power industrial applications, such as traction drive, mine hoister, and wind power generation [7,8,9].
The research of three-level inverter has been focused on output current ripple reduction [10], neutral-point potential fluctuation restraint [8,11,12], common mode voltage reduction [13], switching loss suppression [14], and low switching frequency operation [15]. With these strategies, basic vectors used to synthesize the reference vector or dwell times of redundant switching states are changed to meet the requirement of a certain aspect of performance. When three-level inverters are applied in medium-voltage high-power motor drives, the output current ripple is increased because of the limitation of the switching frequency. Furthermore, with the increase of current harmonics and torque ripple, the additional loss and noise are introduced in both the inverter and the motor. As a result, how to evaluate and reduce the output current ripple of three-level inverters has been attracting attention from researchers all over the world.
In recent years, various evaluation methods, such as weighted total harmonic distortion (WTHD) [15,16], root-mean-square (RMS) value of stator flux ripple, [17], and magnitude of the average current ripple vector [10,18], are proposed to evaluate the output ripple of the three-level inverter. If WTHD is regarded as the evaluation indicator of the output current ripple, the expression of each harmonic needs to be obtain by using a double-fourier transform of the output voltage. Unfortunately, the computational process is very complicated. And in most cases, it is convenient to compare PWM strategies based on the overall quality of output waveform rather than the individual harmonic produced by them. Thus, the RMS value of stator flux ripple and the magnitude of the average current ripple vector could be adopted to evaluate the output current ripple. Compared with WTHD, the computational burdens are lower.
Based on the above evaluation methods, lots of modulation strategies are presented to reduce the output current ripple of three-level inverters [10,16,18], which can be divided into CPWM strategies and DPWM strategies. In reference [18], the magnitude of the average current ripple vector is used as the indicator, and the dwell times of the two redundant switching states in continuous switching sequences are redistributed to reduce the output current ripple. DPWM methods for three-level inverters are proposed in reference [16], and WTHD of the output voltage for both the CPWM and DPWM strategies are compared with each other. The concept of stator flux ripple is proposed in reference [17], and the closed-form expressions of stator flux ripple for different switching sequences are obtained, and then the output performance of different switching sequences are compared with each other.
According to the above modulation strategies, it can be concluded that the current ripple of CPWM strategies is lower than that of DPWM strategies under a lower modulation index condition, while the conclusion is reversed under a higher modulation index condition. Thus, CPWM and DPWM strategies are both adopted in this paper. The closed-form expressions of the average current ripple vector for both the continuous and discontinuous switching sequences are derived. The sub-regions of different switching sequences are determined on the basis of the minimum value of magnitude of the average current ripple vector. Then a sector subdivision based SVPWM strategy with a reduced current ripple can be obtained.
2. Analysis of Switching Sequence in Space Vector Modulation Strategies
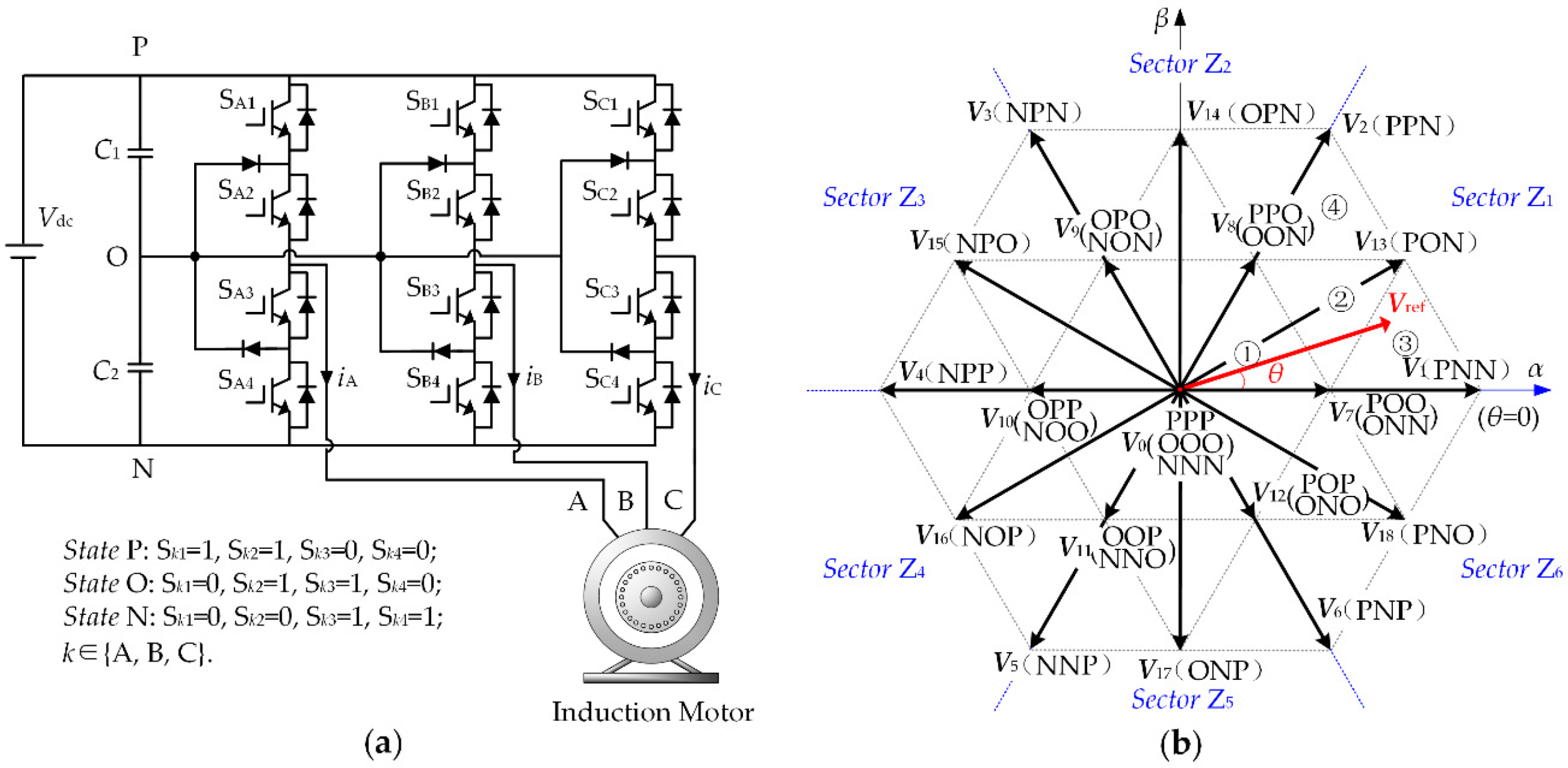
The topology of the NPC three-level inverter is shown in Figure 1a. Each of three phases (A, B, and C) has three switching states (P, O, and N), so there are 33 = 27 switching state combinations for the three-level inverter. According to Park transformation in Equation (1), each combination can be represented by a basic space voltage vector Vj, j = 0, 1, 2, …, 18, as shown in Figure 1b.
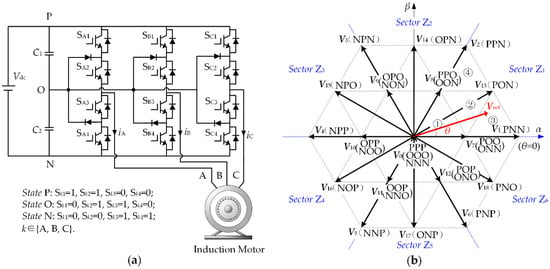
Figure 1.
The topology of NPC three-level inverter and the space vector hexagon: (a) topology; (b) space vector hexagon.
Based on the vector’s magnitude, 19 basic vectors can be divided into four categories, which are zero-voltage, small-voltage, medium-voltage and large-voltage. Zero vector V0 corresponds to three combinations, and each of small vectors V7 ~ V12 corresponds to two combinations. Different switching state combinations corresponding to the same voltage vector are defied as redundant switching states in this paper. The space vector hexagon could be symmetrically divided into six sectors Z1 ~ Z6, and every sector could be further divided into four triangles ① to ④.
The nearest three vectors are usually adopted to synthesize the reference voltage vector Vref in three-level space vector PWM strategies. The dwell time of each vector can be solved by the principle of voltage-second balance. For example, when Vref locates in triangle ③ of sector Z1, yields
where T1, T2, and T0 represent the dwell times of basic vector V7, V1, and V13 in each sample period Ts, respectively. The reference voltage vector Vref can be synthesized by using various switching sequences. That is because each switching state can be arranged at any arbitrary time interval of each sample period and there are redundant switching states for basic voltage vectors V0 and V7 ~ V12.
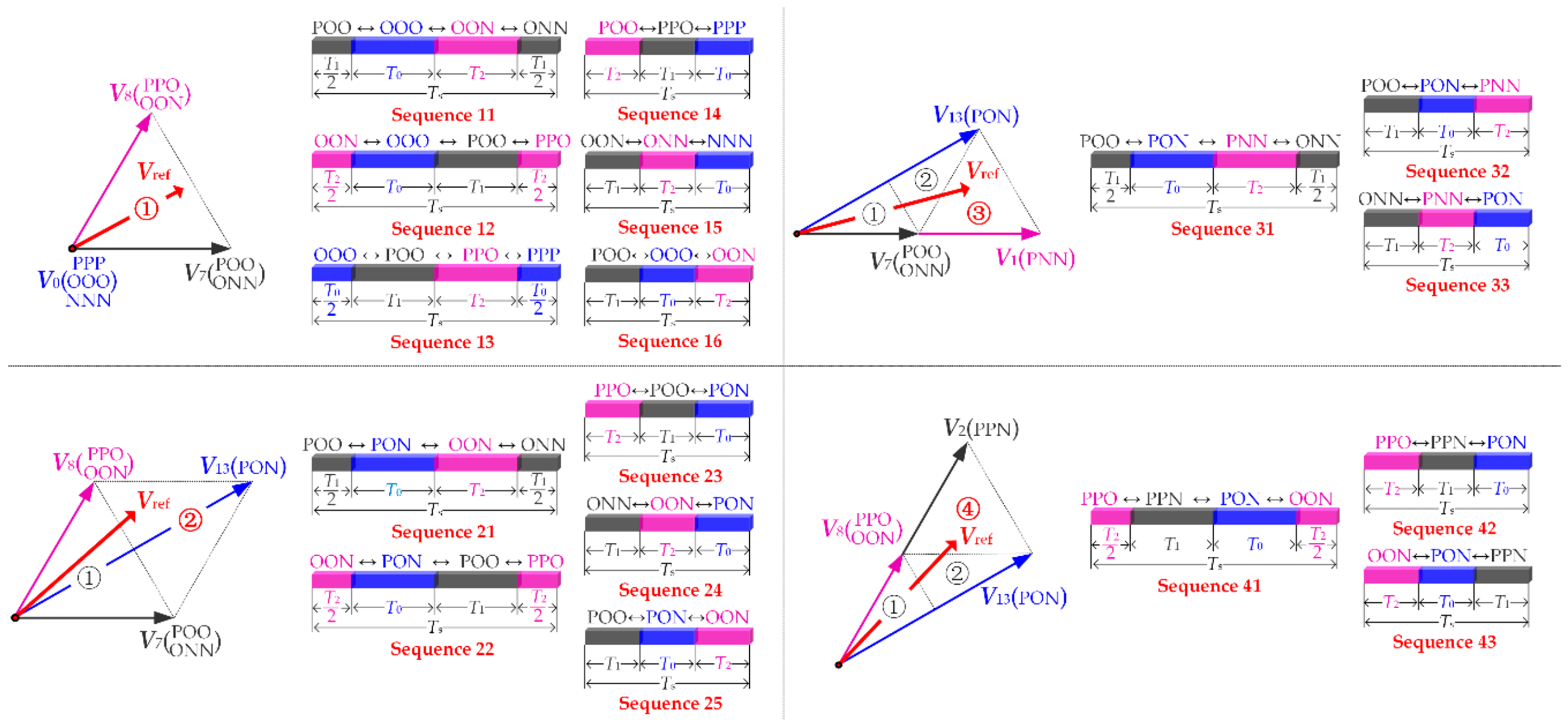
All the possible switching sequences synthesized the reference voltage vector Vref in triangle ①–④ of sector Z1 are shown in Figure 2. The conditions that keep the switching loss as low as possible are listed as follows [17]:
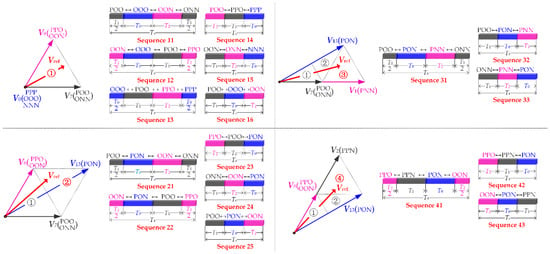
Figure 2.
All possible switching sequences in Triangle ①–④ of Sector Z1.
- The switching exists in at most one phase leg during each state transition.
- The total number of switching sequences in each sample period must be less or equal to three.
Based on the number of switching in each sample period, the switching sequences can be categorized into continuous switching sequences (Sequence 11, 12, 13, 21, 22, 31, and 41) and discontinuous switching sequences (Sequence 14, 15, 16, 23, 24, 25, 32, 33, 42, and 43). For discontinuous switching sequences, the switching only appears in two phase legs. Meanwhile for continuous switching sequences, the switching appears in all the three phase legs.
The switching sequences of space vector PWM strategies must be arranged symmetrically on both sides so that the switching sequence in a certain sample period is reversed in the next sample period. For example, if the switching sequence in one sample period is POO→PON→PNN→ONN, the sequence in the next sample period will be ONN→PNN→PON→POO, as shown in Figure 3b.
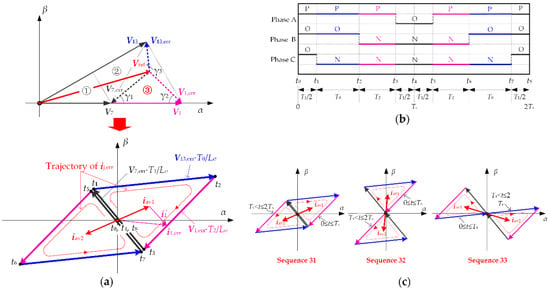
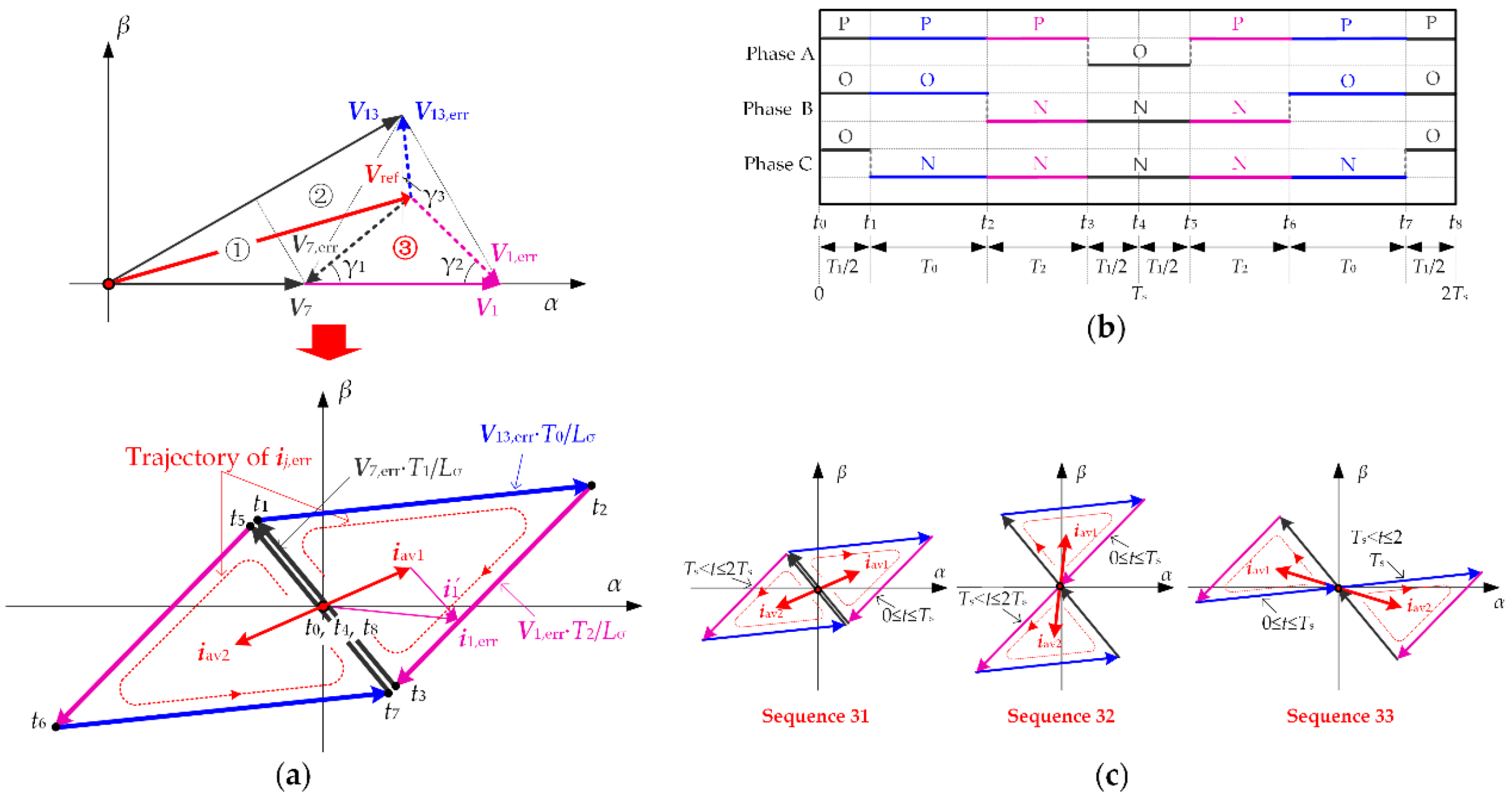
Figure 3.
The analysis of output current ripple: (a) voltage ripple vectors V1,err, V7,err, and V13,err, and trajectory of the current ripple vector ij,err in space vector plane; (b) switching states of Sequence 31 and corresponding time intervals; (c) trajectory of current ripple vector ij,err for Sequence 31–33 in Triangle ③ of Sector Z1.
Different arrangements of the switching sequence will inherently offer different behavior with regard to the performance indicators that can be used to assess the quality of the output waveform. Output current ripple of three-level inverters is used as the evaluation indicator and is analyzed in the next section.
3. Analysis of the Output Current Ripple
At any arbitrary instant in each sample period, there is always an error between the applied voltage and the reference voltage vector according to the principle of space vector PWM. The vector difference between Vj and Vref is defined as the voltage ripple vector Vj,err. As shown in Figure 3a, when Vref is located in triangle ③ of sector Z1, voltage ripple vectors corresponding to V7, V1, and V13 are V7,err, V1,err, and V13,err, respectively.
When the motor is driven by the voltage source inverter and the stator and rotor resistances are neglected, the voltage ripple vector Vj,err will generate the current ripple vector ij,err in the motor. The relationship of voltage and current ripple vectors in each Ts can be indicated as follows
where Lσ is the equivalent inductance of the motor. Take Sequence 31 as an example, as shown in Figure 3a, when t ∈ [0, T1/2], the switching state POO is applied, the start point of i7,err is at t0. The direction of current ripple vector ij,err lag the direction of voltage ripple vector Vj,err by π/2 so that the end point of i7,err travels from t0 to t1. When t = T1/2, |i7,err| equals to |V7,err·T1/2Lσ|. Similarly, the amplitude of current ripple vector are |V13,err·T0/Lσ|, |V1,err·T2/Lσ|, and |V7,err·T1/2Lσ| when the switching state PON, PNN, and ONN are applied alternatively. The instants t0~t8 shown in Figure 3a are corresponding to the instants shown in Figure 3b. The trajectory of ij,err during (0, Ts] is triangle t1–t2–t3–t1. And the trajectory during (Ts, 2Ts] is triangle t5–t6–t7–t5. The lengths of three sides are V7,err·T1/Lσ, V1,err·T2/Lσ, and V13,err·T0/Lσ, respectively.
The average current ripple vector in sample period (0, Ts] and (Ts, 2Ts] are defined as follows
As shown in Figure 3c, the shapes of triangle t1–t2–t3–t1 and t5–t6–t7–t5 are the same and are symmetrical about the origin. So iav1 and iav2 are equal in magnitude but opposite in direction. The conclusions derived in reference [18] are as follows:
Conclusion 1.
The terminal of the average current ripple vector is the mass center of the current ripple triangle.
In Figure 3b, point G and G′ are the mass center of triangle t1–t2–t3–t1 and t5–t6–t7–t5, respectively. So the terminals of iav1 and iav2 are point G and G′. The square RMS value of the output current ripple is normally introduced to estimate the performance of the inverter, which is defined as follows
In sample period (0, Ts], the current ripple vector can be divided into two parts
where auxiliary vector is the vector error between the current ripple vector ij,err and the average current ripple vector iav1. In time interval (0, Ts], averaging Equation (6), yields
Substituting Equations (6) and (7) into Equation (5), yields
The trajectories of current ripple vector during (0, 2Ts] corresponding to Sequence 31, 32, and 33 are shown in Figure 3c. As can be seen, for different switching sequences, the relative positions of the mass center and the origin are different from each other, which means magnitudes of the average current ripple vectors are different. While shapes of current ripple triangles are the same. So the second item in the right side of Equation (8) is not changed. Then the following conclusion can be drawn:
Conclusion 2.
The value of Irip_rms is determined by the value of |iav1|2. So the lower the value of |iav1|2 is, the better the output performance is.
4. The Expression of the Magnitude of the Average Current Ripple Vector
According to Conclusion 1 and Conclusion 2, the comparison of output performance for all the possible switching sequences can be replaced by the comparison of the distance between the mass center of current ripple triangle and the origin.
The modulation index m is defined as
where Vref is the amplitude of reference voltage vector, Vdc is the amplitude of dc-link voltage. As shown in Figure 3, the magnitudes of voltage ripple vector V7,err, V1,err, and V13,err can be derived as follows
where θ is the reference vector angle. According to Equation (2), the dwell time T1, T2, and T0 corresponding to V7, V1, and V13 during each sample period can be derived as follows
Based on Equations (10) and (11), and the geometric relationship in Figure 3c, the closed-form expression of |iav1| are listed in Table 1.

Table 1.
The expression of |iav1| in Triangle ③ of Sector Z1.
Similarly, the expressions of other switching sequences in Figure 2 also can be derived out. According to Equations (10) and (11), and Table 1, it can be concluded that expressions of the magnitude of the average current ripple vector are functions of variable Vdc, Ts, Lσ, m and θ. By developing expressions in Table 1, it can be deduced that VdcTs/Lσ is the common item so that expressions can be considered as a function of m and θ (The detailed derivation process of |iav1| is presented in Appendix A).
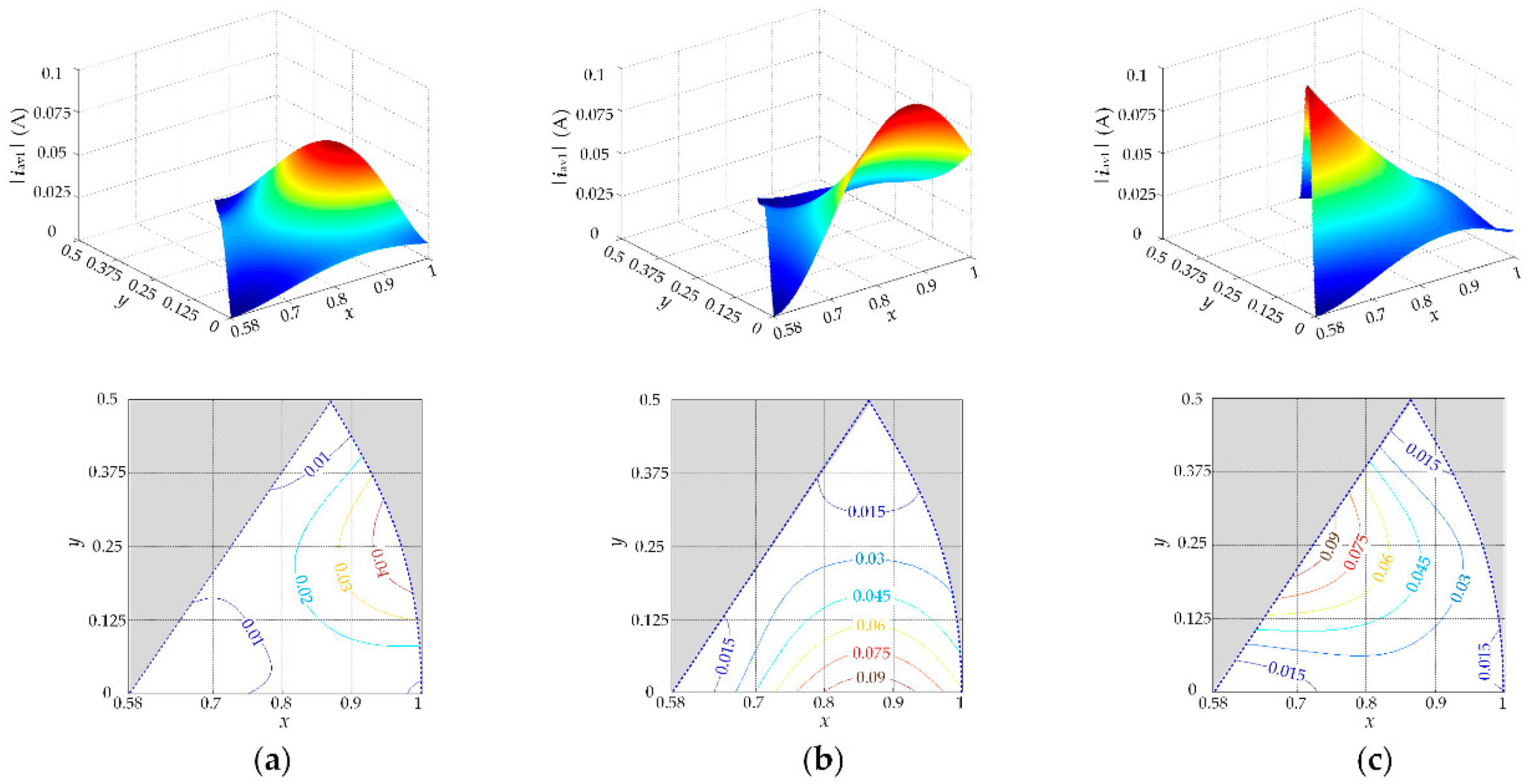
Let x and y to be m·cosθ and m·sinθ, respectively. The magnitude of the average current ripple vector |iav1| of sector Z1 in x-y rectangle coordinate system and the contour lines of |iav1| in x-y plane corresponding to Sequence 31–33 are shown in Figure 4. From Figure 4, variation trends of |iav1| corresponding to different sequences are not the same. If the switching sequence with the lowest |iav1| is adopted at any arbitrary position, the output current ripple of the inverter will be minimized.
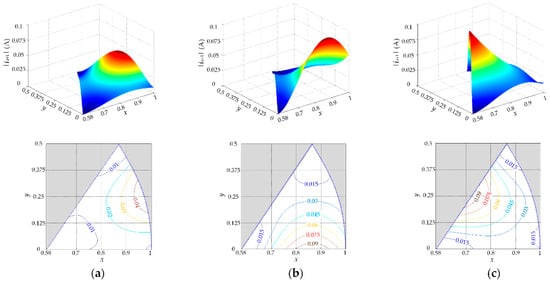
Figure 4.
Dependency of |iav1| on the modulation index m and reference vector angle θ in Triangle ③ of Sector Z1: (a) Sequence 31; (b) Sequence 32; (c) Sequence 33.
5. The Proposed Sector Subdivision Based SVPWM
5.1. The Boundaries of Different Switching Sequences
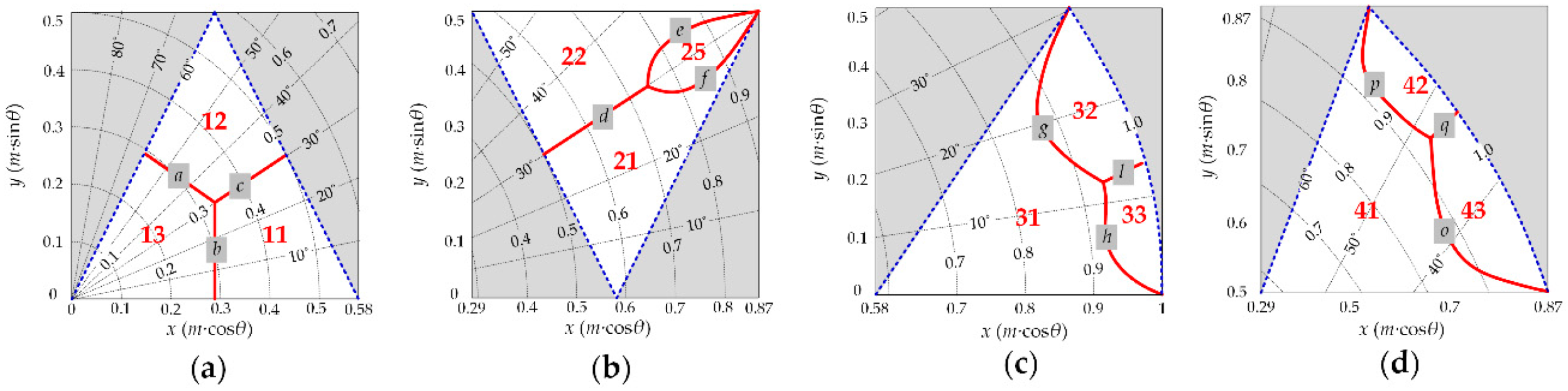
In order to obtain the boundary of the active area for Sequence 31 and 32, the intersection |iav1|(sequence 31) = |iav1|(sequence 32) need to be solved and the result is curve g in Figure 5c. Similarly, curve h is the intersection of |iav1|(sequence 31) = |iav1|(sequence 33) and curve l is the intersection of |iav1|(sequence 32) = |iav1|(sequence 33). When Vref is located in small triangle ①, ②, or ④, expressions of |iav1| can be derived out and the intersections can also be solved in the same manner. The distribution of sub-region for each switching sequence in small triangle ①–④ corresponding to the minimum value of |iav1| are shown in Figure 5a–d, respectively.
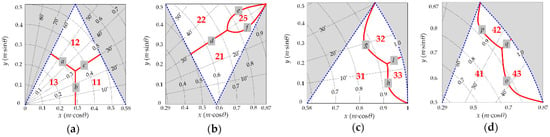
Figure 5.
The optimal distribution of sub-regions for different switching sequences in Sector Z1: (a) Triangle ①; (b) Triangle ②; (c) Triangle ③; (d) Triangle ④.
Each triangle is subdivided into three small-regions. In Figure 5a–d, the curve a–q are the boundaries of each sub-region. Equations of the boundaries can be solved off-line by the expressions of |iav1| of the two adjacent sub-regions. Omitting the tedious derivation process, the equation of a–q in x-y rectangle coordinate system are listed in Appendix B. Furthermore, the equations in Equation (A5) are independent of motor parameters, fundamental frequency, and dc bus voltage.
5.2. The Proposed Sector Subdivision Based SVPWM Strategy
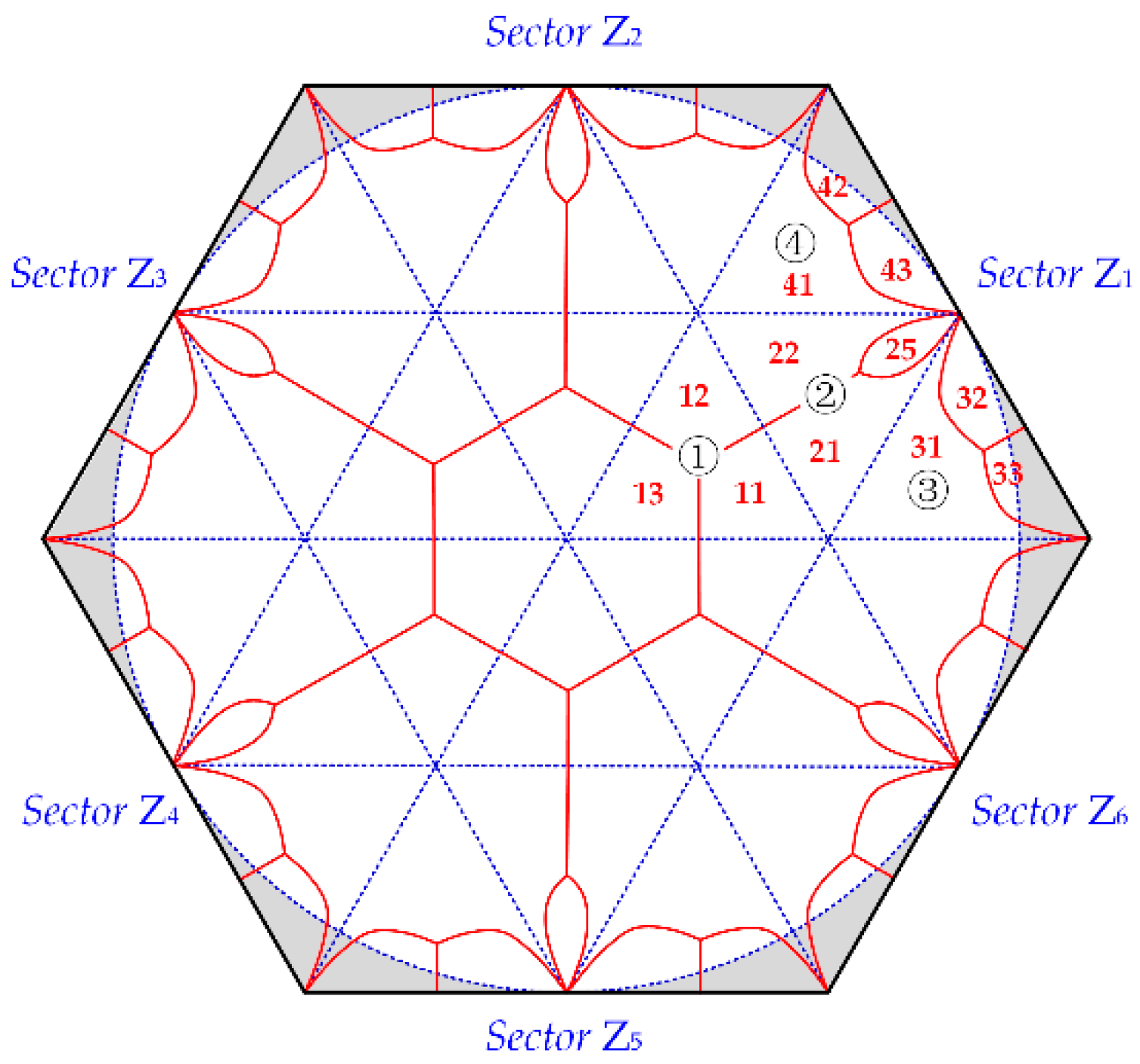
According to Figure 5a–d, the sub-region of each switching sequence in the whole space vector diagram is shown in Figure 6. The sub-regions are different because the types of switching sequences (continuous and discontinuous) adopted in each triangle are different.
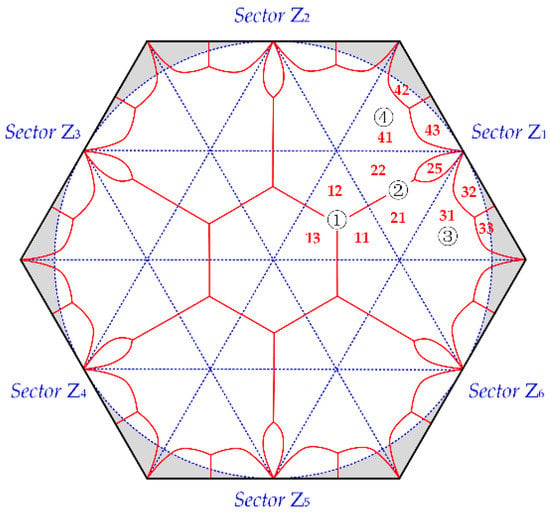
Figure 6.
The optimal distribution of switching sequences for the proposed sector subdivision based SVPWM strategy in space vector diagram (all six sectors).
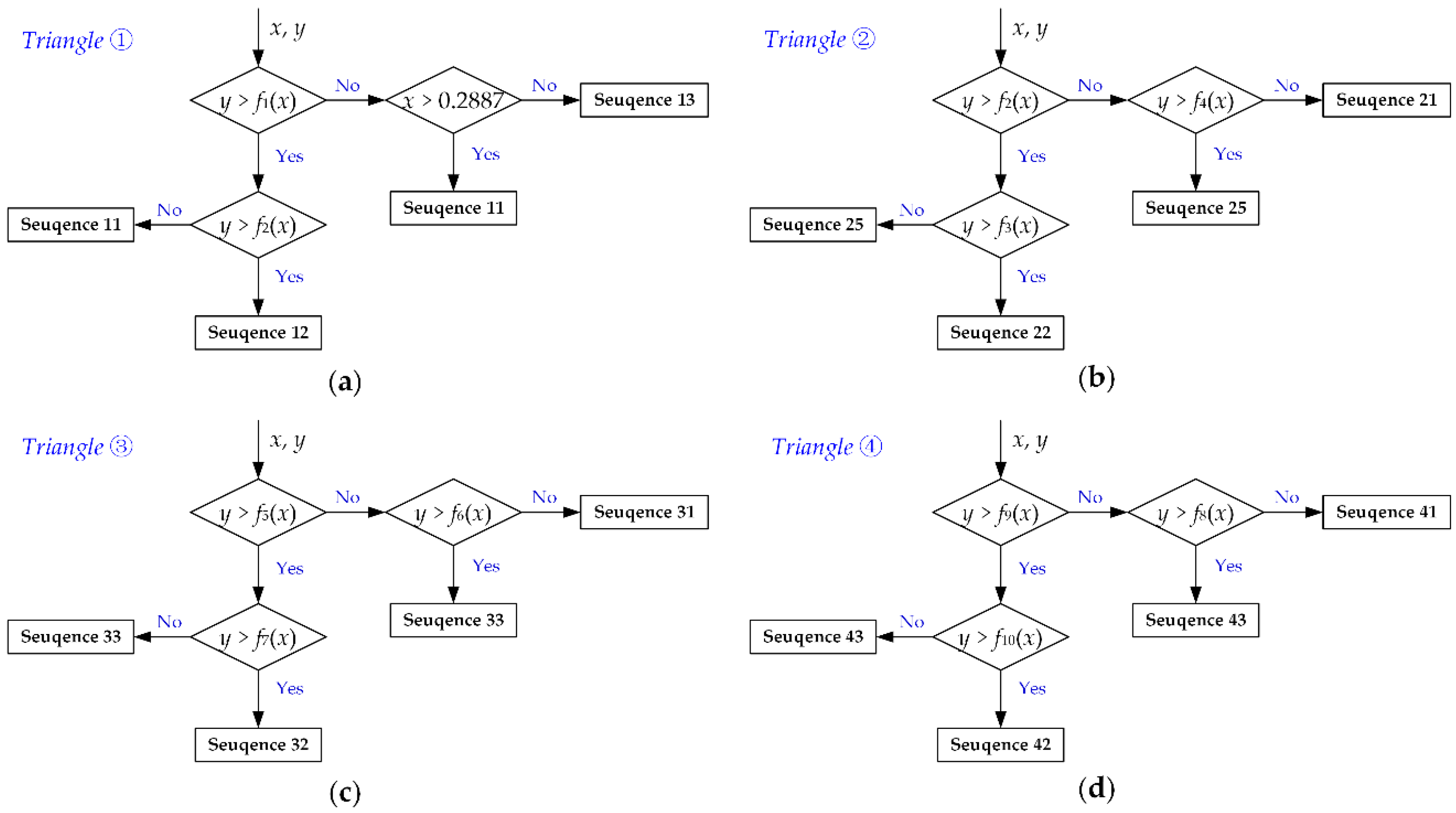
Generally, the determination process of sub-regions for different switching sequences in sector Z1 are taken as an example. The flowchart to find out the spatial region and switching sequence are shown in Figure 7.
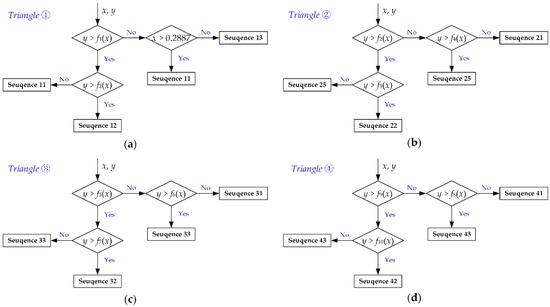
Figure 7.
The flowchart to find out the spatial sub-region and switching sequence of the proposed modulation strategy in Sector Z1: (a) Triangle ①; (b) Triangle ②; (c) Triangle ③; (d) Triangle ④.
Based on the sub-region and switching sequence distributions in Figure 6, a sector subdivision based SVPWM strategy combined of both continuous and discontinuous switching sequences can be presented to improve the output current performance. It is worth to be mentioned that the switching sequences adopted in the proposed strategy are all selected from Figure 2. And the switching sequence adopted in a certain sample period will be reversed in the next sample period so that the strategy is arranged symmetrically on both sides.
6. Experimental Verification
The proposed strategy, CPWM [19] and DPWM3 (with the lowest distortion among DPWM0–DPWM3) [20] are tested on the experimental prototype of three-level inverter fed induction motor shown in Figure 8. Parameters of the experimental prototype are listed in Table 2. The induction motor is driven with a constant V/f control.

Figure 8.
The experimental prototype of neutral-point-clamped three-level inverter.

Table 2.
Parameters of the experimental prototype.
6.1. The Proposed Sector Subdivision Based SVPWM Strategy
Instead of total harmonic distortion (THD), total demand distortion (TDD) is usually used as the output performance indicator of the inverter in a wide range of modulation index m [21], which is defined as follows
where Ih is the hth component of the output current and IN is the rated current. Ih and IN are both RMS values.
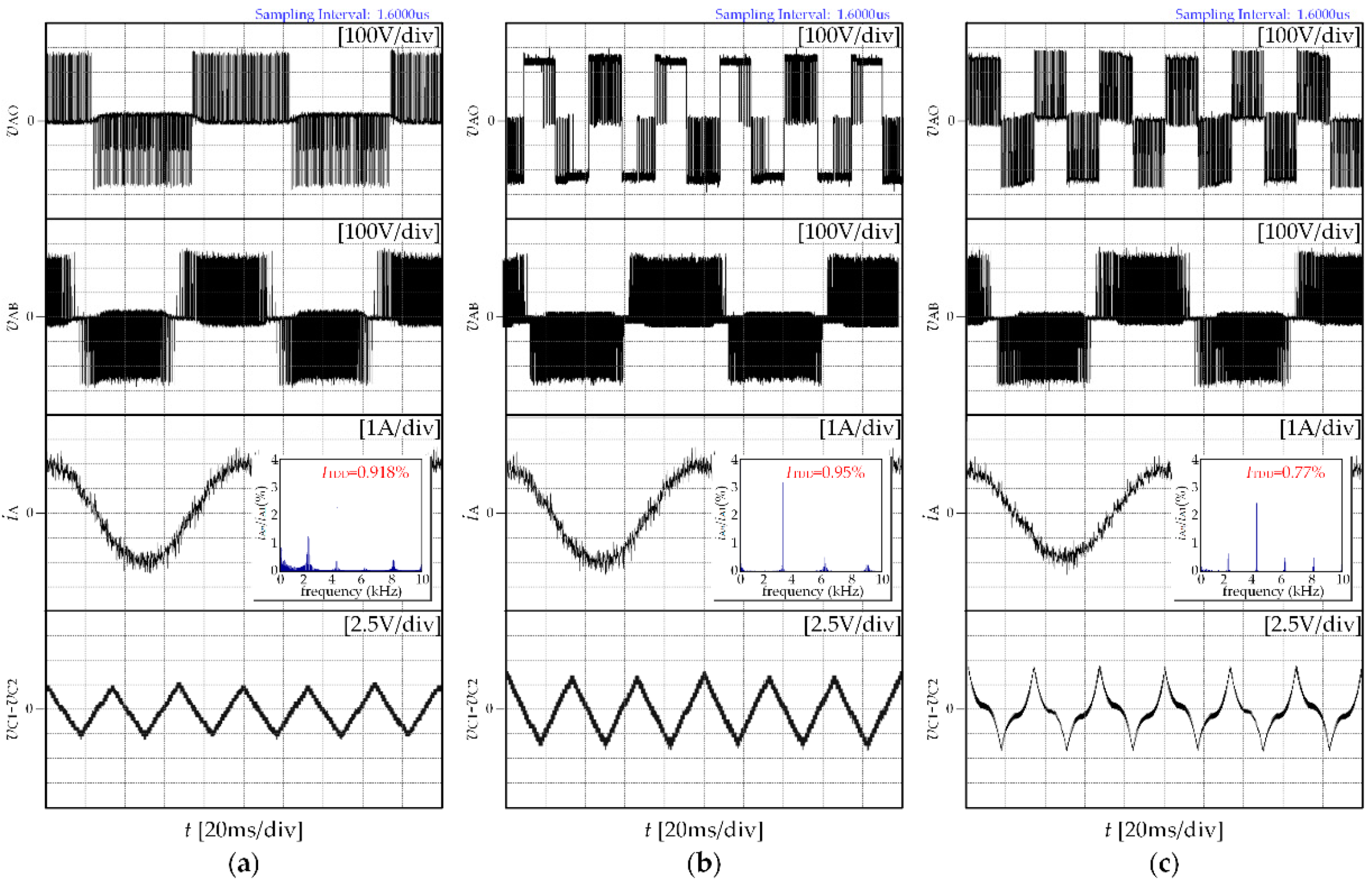
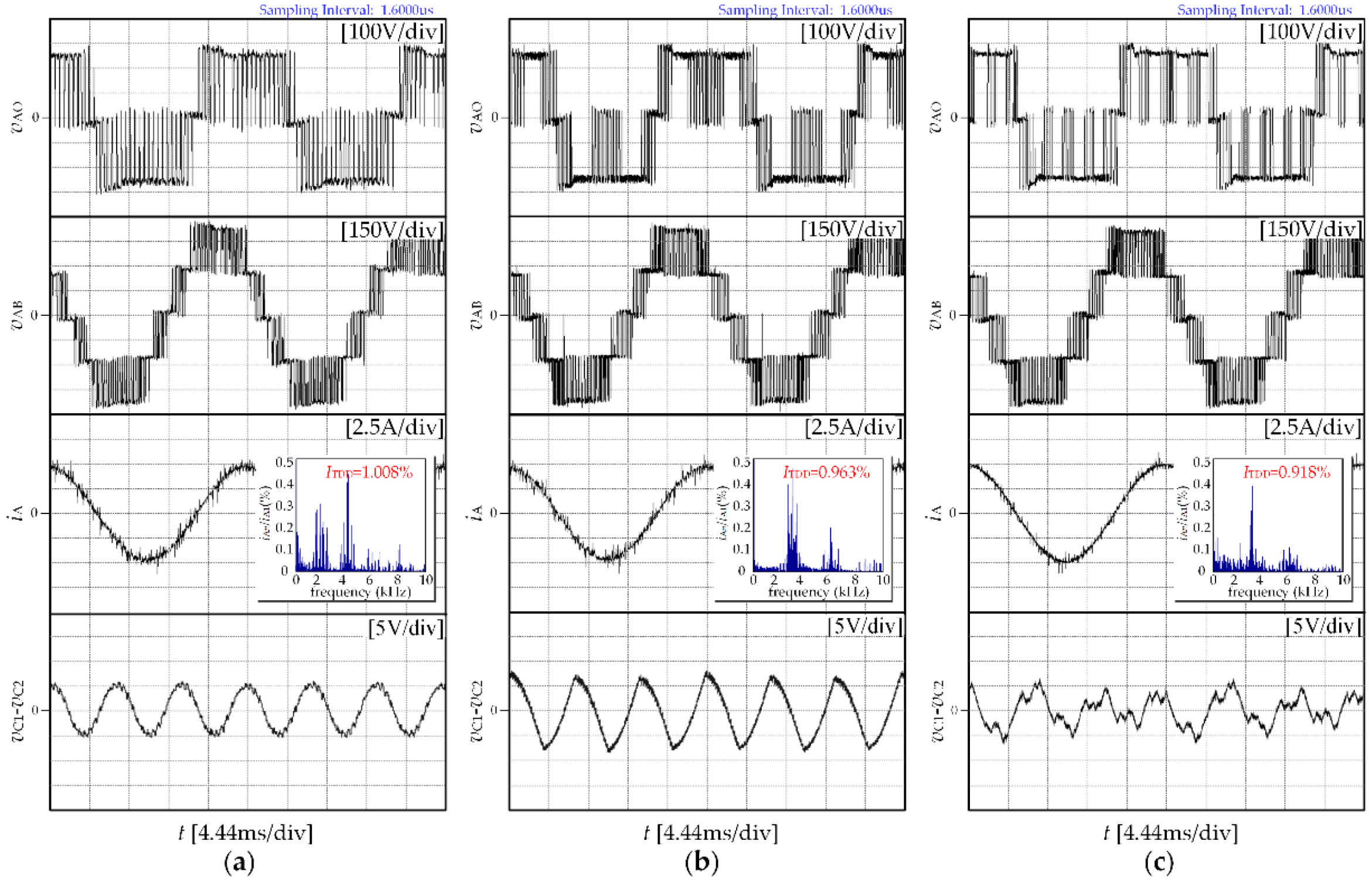
Experimental waveforms of output voltage vAO and vAB, output current iA for CPWM, DPWM3, and the proposed strategy under conditions of m = 0.2 and m = 0.9 are presented in Figure 9 and Figure 10, respectively. From Figure 9 and Figure 10, ITDD of the proposed strategy is lower than that of CPWM and DPWM3.
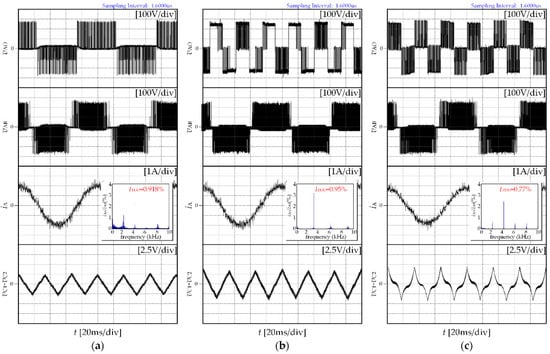
Figure 9.
Experimental results for CPWM, DPWM3, and the proposed strategy when m = 0.2: (a) CPWM; (b) DPWM3; (c) the proposed strategy.
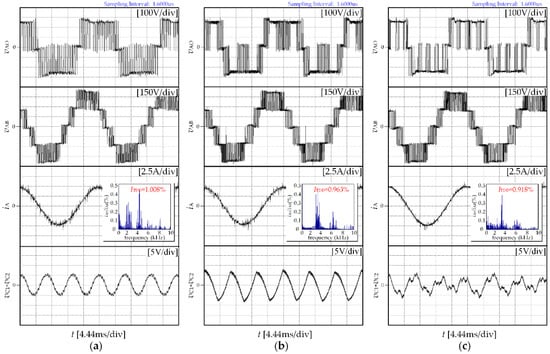
Figure 10.
Experimental results for CPWM, DPWM3, and the proposed strategy when m = 0.9: (a) CPWM; (b) DPWM3; (c) the proposed strategy.
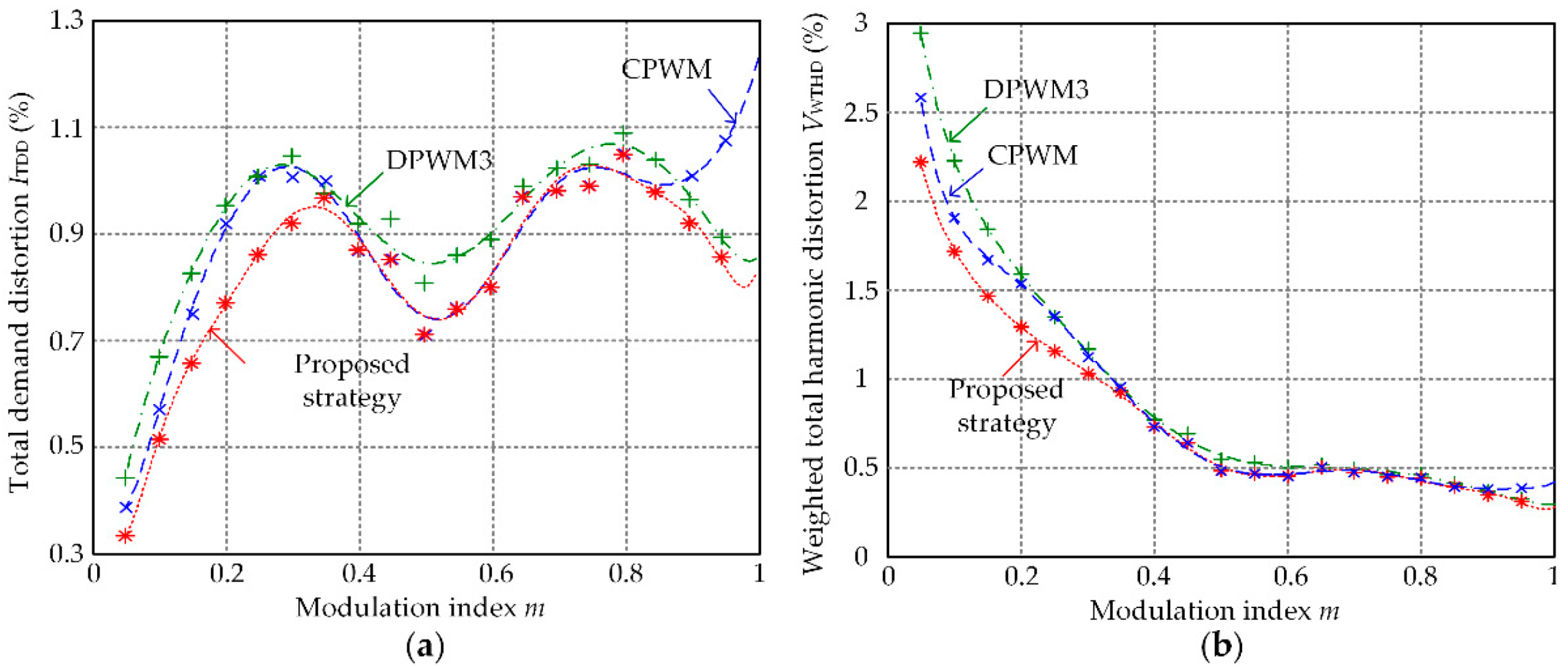
According to experimental results, the fast fourier transformation (FFT) analysis tool in Matlab is used to calculate the ITDD and VWTHD under different modulation index conditions. Then variations of ITDD and VWTHD with the change of modulation index m for CPWM, DPWM3, and the proposed strategy can be obtained, which is illustrated in Figure 11a,b.
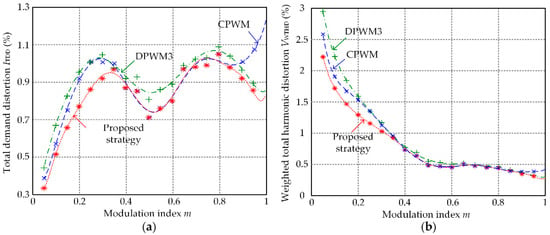
Figure 11.
Variations of ITDD and VWTHD with the change of m for CPWM, DPWM3, and the proposed strategy: (a) ITDD; (b) VWTHD.
The weighted total harmonic distortion of output voltage VWTHD is defined as
where V1 and Vh are the rms value of fundamental and hth component of output voltage.
As shown in Figure 11a, for the modulation index m < 0.38 and m ≥ 0.8, ITDD of the proposed strategy is lower than that of CPWM and DPWM3. For the modulation index 0.38 ≤ m < 0.8, output waveform quality of the proposed strategy and CPWM are the same, which is still better than that of DPWM3. The same conclusion can be obtained from Figure 11b. The percentage improvement of proposed strategy versus CPWM and DPWM3 is shown in Figure 12.
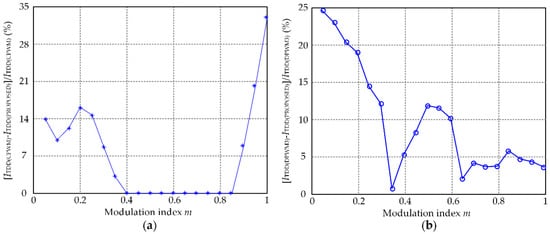
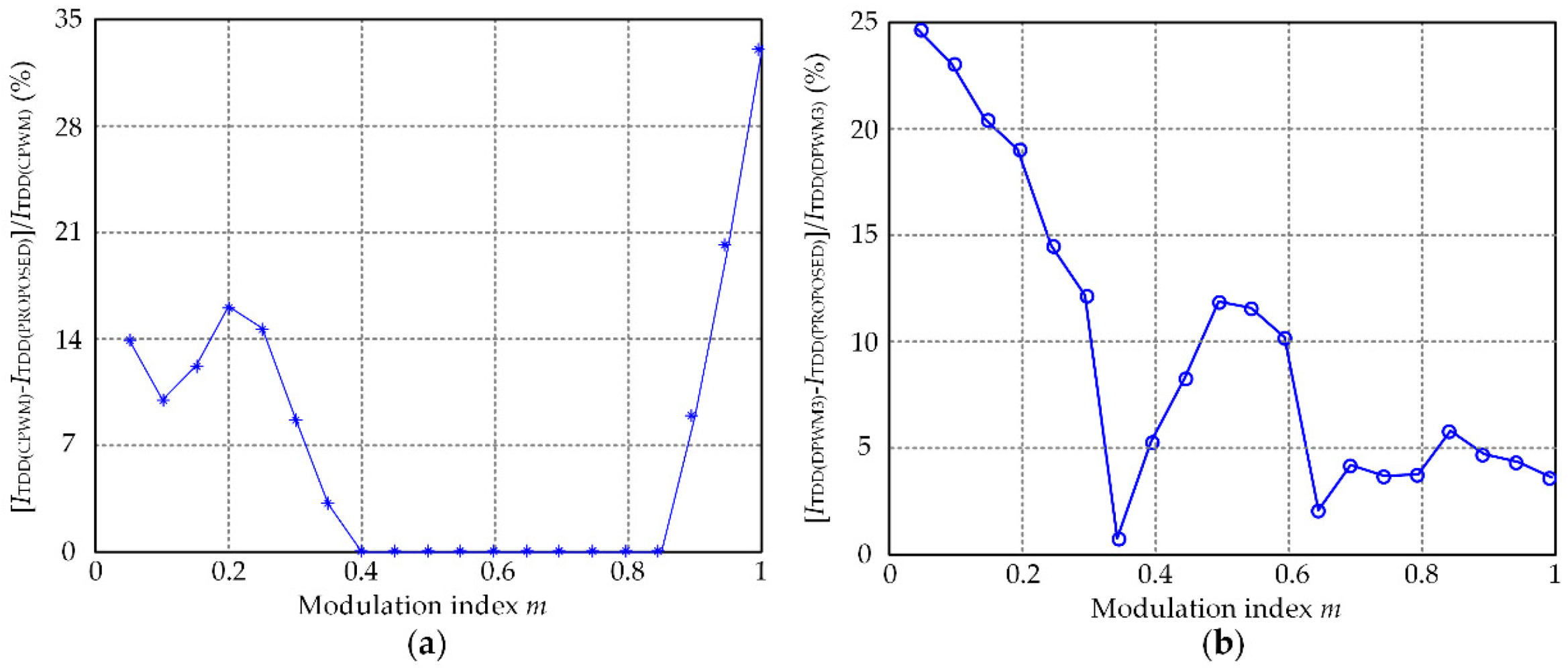
Figure 12.
The percentage improvement of proposed method versus CPWM and DPWM3: (a) proposed strategy versus CPWM (b) proposed strategy versus DPWM3.
At the rated frequency (modulation index m = 1), ITDD of the proposed strategy drops 33% and 3.5%, respectively, compared with CPWM and DPWM3. Thus, the output waveform quality of the proposed strategy is improved.
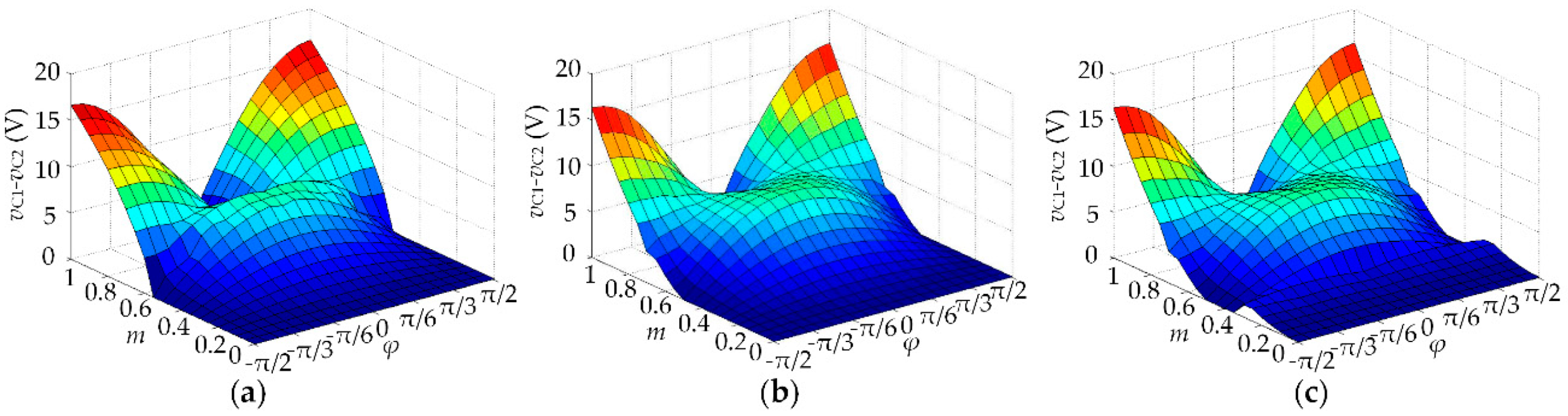
It is worth mentioning that the output waveform quality is also affected by the low frequency ripple in the neutral-point potential, as can be seen in Figure 9 and Figure 10. The dependence of neutral-point potential ripple vC1-vC2 on m and power factor angle φ for CPWM, DPWM3, and the proposed strategy can be calculated according to reference [22], as shown in Figure 13. The neutral-point potential ripple vC1-vC2 for CPWM, DPWM3, and the proposed strategy are approximately the same, so their effect on the output current ripple are the same, too.
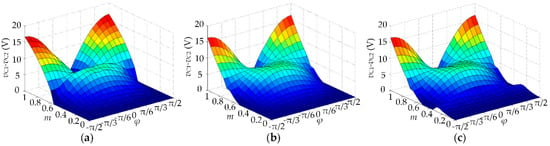
Figure 13.
The dependence of neutral point voltage ripple vC1-vC2 on m and φ: (a) CPWM; (b) DPWM3; (c) proposed strategy.
6.2. Comparison of Power Losses
The switching losses of CPWM, DPWM3 and proposed strategy are calculated according to the method in reference [23], and the dependence of switching loss on m and power factor angle φ are shown in Figure 14.
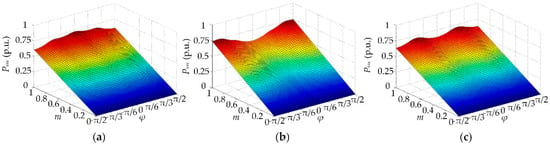
Figure 14.
The dependence of switching loss on m and power factor φ: (a) CPWM (b) DPWM3 (c) proposed strategy.
As can be seen, when the power factor is close to 1, the switching loss of proposed strategy is lower than CPWM and a little bit higher than DPWM3. However in other cases, the switching losses of these three strategies are approximately the same.
6.3. Comparison with Neutral Point Balancing Strategies
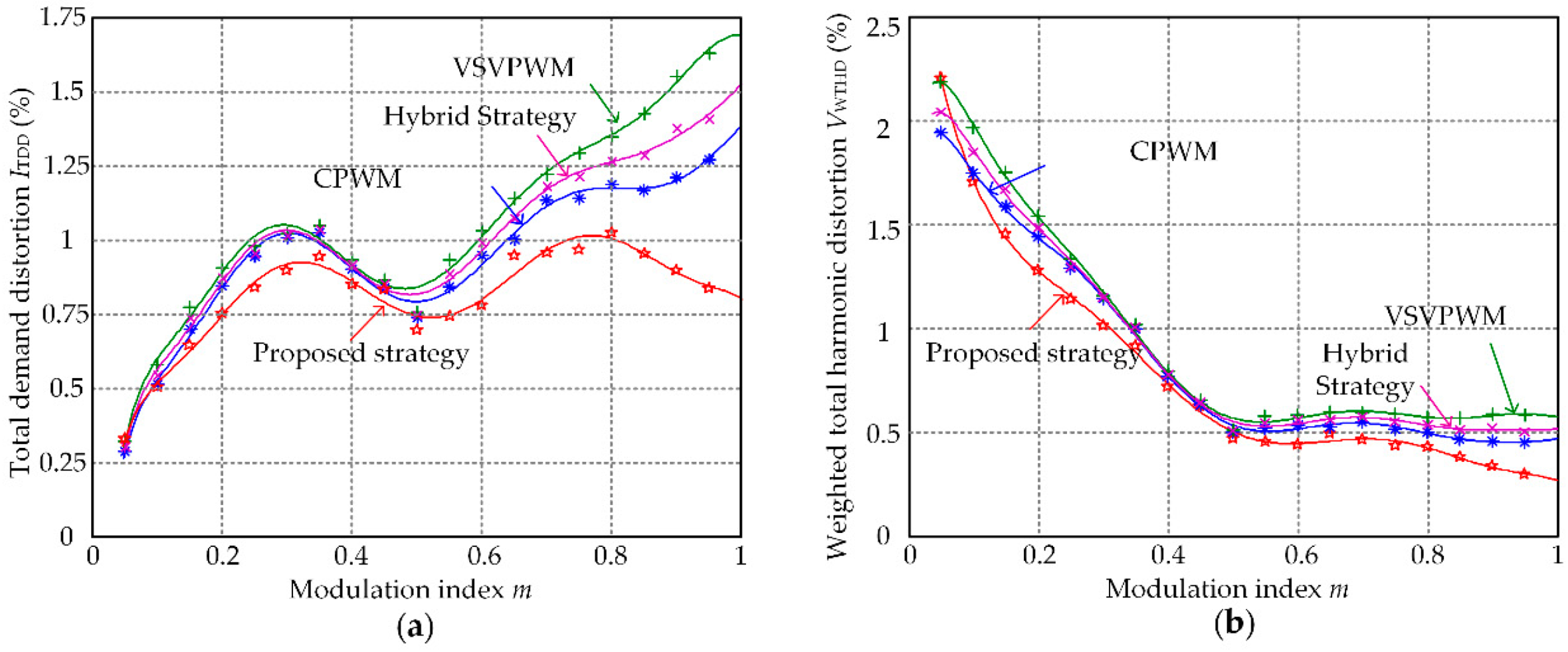
The dependence of ITDD and VWTHD on modulation index m for CPWM with a neutral-point balancing control [8], a virtual SVPWM (VSVPWM) [11], a hybrid strategy of these two methods [12] and the proposed method are shown in Figure 15. As can be seen, when the modulation index m > 0.1, ITDD and VWTHD of the proposed strategy is lower than the other three strategies. It can be concluded that the output performance of the proposed method is better than usual-adopted SVPWM with neutral-point potential balancing strategy and VSVPWM.
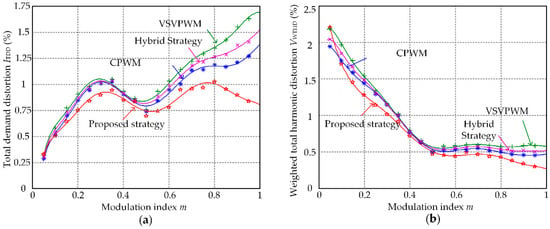
Figure 15.
The dependence of ITDD and VWTHD on m for CPWM with neutral-point balancing, VSVPWM, hybrid strategy and the proposed strategy: (a) ITDD; (b) VWTHD.
7. Conclusions
A sector subdivision based modulation strategy combined with continuous and discontinuous switching sequences has been presented to promote the output performance of three-level inverters. The magnitude of the average current ripple vector was introduced as the performance indicator of the output current ripple. Then the optimal distribution of switching sequences has been derived. Compared with CPWM and DPWM3, the output current ripple of the proposed strategy was reduced. It can be concluded that the output current ripple are reduced significantly under the condition of m < 0.38 and m ≥ 0.8. At the rated frequency, ITDD of the proposed strategy drops by 33% and 3.5%, respectively, compared with CPWM and DPWM3. The power loss of the proposed strategy was medium among those three strategies. Additionally, compared with neutral-point balancing strategies, the improvement of the output waveform quality was also significant.
Author Contributions
Conceptualization, X.G., X.L., Z.Z. and W.C.; methodology, G.Z.; software, X.L.; validation, G.Z., B.W. and X.L.; formal analysis, G.Z., B.W. and Z.Z.; writing—original draft preparation, G.Z.; writing—review and editing, B.W., X.G. and W.C.; funding acquisition, G.Z., X.L. and Z.Z.
Funding
This research was funded by “The Youth Fund Projects of National Natural Science Foundation of China, grant number 51807140 and 51807141” and “The Science & Technology Development Fund of Tianjin Education Commission for Higher Education, grant number 2018KJ207”.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
According to Conclusion 1, the terminal of the average current ripple vector is the mass center of the current ripple triangle. So the magnitude of the average current ripple vector iav1 is equal to the distance between the origin point and the mass center. The current ripple triangles and mass centers corresponding to Sequence 31–33 are shown in Figure A1.
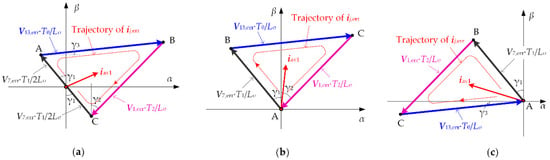
Figure A1.
Trajectory of current ripple vector ij,err for Sequence 31–33 in Triangle ③ of Sector Z1: (a) Sequence 31; (b) Sequence 32; (c) Sequence 33.
Figure A1.
Trajectory of current ripple vector ij,err for Sequence 31–33 in Triangle ③ of Sector Z1: (a) Sequence 31; (b) Sequence 32; (c) Sequence 33.
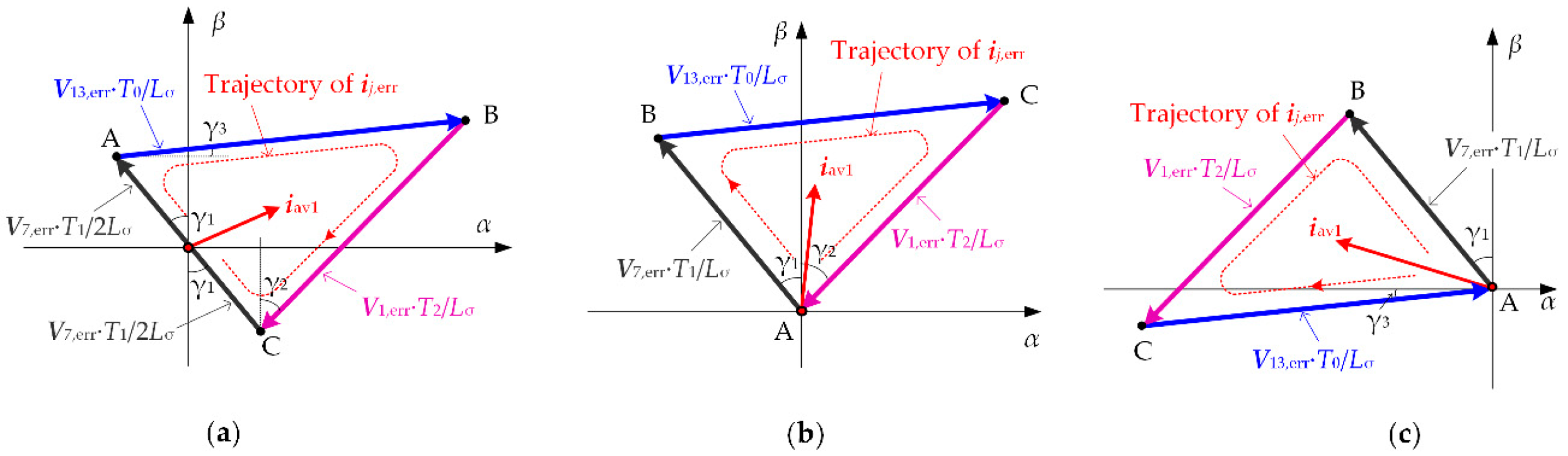
The coordinate of three vertexes A(α1, β1), B(α2, β2) and C(α3, β3) of current ripple triangle are shown in Table A1.

Table A1.
The coordinate of three vertexes of current ripple triangle.
Table A1.
The coordinate of three vertexes of current ripple triangle.
| Coordinate | Sequence 31 | Sequence 32 | Sequence 33 |
|---|---|---|---|
| α1 | −V7,errT1sinγ1/2Lσ | 0 | 0 |
| β1 | V7,errT1cosγ1/2Lσ | 0 | 0 |
| α2 | V7,errT1sinγ1/2Lσ+V1,errT2sinγ2/Lσ | −V7,errT1sinγ1/Lσ | −V7,errT1sinγ1/Lσ |
| β2 | −V7,errT1cosγ1/2Lσ+V1,errT2cosγ2/Lσ | V7,errT1cosγ1/Lσ | V7,errT1cosγ1/Lσ |
| α3 | V7,errT1sinγ1/2Lσ | V1,errT2sinγ2/Lσ | −V13,errT0cosγ3/Lσ |
| β3 | −V7,errT1cosγ1/2Lσ | V1,errT2cosγ2/Lσ | −V13,errT0sinγ3/Lσ |
The magnitude of iav1 can be expressed by the coordinate of three vertexes as follow
Substituting the coordinates in Table A1 into Equation (A1), the expressions of |iav1| corresponding to Sequence 31–33 are as follow:
The dwell time T1, T2, T3, the magnitude of voltage ripple vector V7,err, V1,err, V13,err and the expressions of γ1, γ2, γ3 are shown in Equations (10) and (11) and Table 1, respectively. According to Equation (10), the expressions ofγ1, γ2, γ3 can be further deduced as follow:
As can be seen, γ1, γ2, and γ3 are the function of m and θ. Substituting Equations (10), (11) and (A3) into (A2), yields
As can be seen, the expressions of |iav1| are the function of m, θ, Vdc, Ts, and Lσ. VdcTs/Lσ is the common item, and the value of VdcTs/Lσ doesn’t affect the comparison of |iav1|, so the expressions of |iav1| can be considered as the function of m and θ.
Appendix B
The equations of curve a–q in x-y rectangle coordinate system are shown as follows:
References
- Antonio, V.C.; Montero-Robina, P.; Umbría, F.; Cuesta, F.; Gordillo, F. Integrated control and modulation for three-level NPC rectifiers. Energies 2019, 12, 1641. [Google Scholar] [CrossRef]
- Li, P.; Zhang, L.; Ouyang, B.; Liu, Y. Nonlinear effects of three-level neutral-point clamped inverter on speed sensorless control of induction motor. Energies 2019, 8, 402. [Google Scholar] [CrossRef]
- Jun, E.; Kwak, S. A highly efficient single-phase three-level neutral point clamped (NPC) converter based on predictive control with reduced number of commutations. Energies 2018, 11, 3524. [Google Scholar] [CrossRef]
- Mao, W.; Zhang, X.; Hu, Y.; Zhao, T.; Wang, F.; Li, F.; Cao, R. A research on cascaded H-bridge module level photovoltaic inverter based on a switching modulation strategy. Energies 2018, 12, 1851. [Google Scholar] [CrossRef]
- Wei, C.; Yuan, X.; Zhou, J.; Wang, K.; Zhang, Y.; Wu, X. Voltage jump suppression and capacitor voltage fluctuation analysis for a four-level hybrid flying capacitor T-type converter. Energies 2018, 12, 698. [Google Scholar] [CrossRef]
- Hammami, M.; Rizzoli, G.; Mandrioli, R.; Grandi, G. Capacitors voltage switching ripple in three-phase three-level neutral point clamped inverters with self-balancing carrier-based modulation. Energies 2018, 11, 3244. [Google Scholar] [CrossRef]
- Son, Y.; Kim, J. A novel phase current reconstruction method for a three-level neutral point clamped inverter (NPCI) with a neutral shunt resistor. Energies 2018, 11, 2616. [Google Scholar] [CrossRef]
- Kang, K.; Cho, Y.; Ryu, M.; Baek, J. A harmonic voltage injection based DC-link imbalance compensation technique for single-phase three-level neutral-point-clamped (NPC) inverters. Energies 2018, 11, 1886. [Google Scholar] [CrossRef]
- In, H.; Kim, S.; Lee, K. Design and control of small DC-link capacitor-based three-level inverter with neutral-point voltage balancing. Energies 2018, 11, 1435. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, G.; Yan, Y.; Gu, X.; Shi, T.; He, X. Discontinuous space vector PWM strategy of neutral point clamped three level inverters for output current ripple reduction. IEEE Trans. Power Electron. 2017, 32, 5109–5121. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Bordonau, J.; Boroyevich, D.; Somavilla, S. The nearest three virtual space vector PWM—A modulation for the comprehensive neutral-point balancing in the three-level NPC inverter. IEEE Power Electron. Lett. 2004, 2, 11–15. [Google Scholar] [CrossRef]
- Jiang, W.; Du, S.; Chang, L.; Zhang, Y.; Zhao, Q. Hybrid PWM strategy of SVPWM and VSVPWM for NPC three-level voltage-source inverter. IEEE Trans. Power Electron. 2010, 25, 2607–2619. [Google Scholar] [CrossRef]
- Tsai, M.; Tsai, H.; Wang, M.; Cheng, P. Evaluation of carrier-based modulation techniques with common-mode voltage reduction for neutral point clamped converter. IEEE Trans. Power Electron. 2018, 33, 3268–3275. [Google Scholar] [CrossRef]
- Jiao, F.; Lee, C.; Lu, S. Space vector modulation for three-level NPC converter with neutral point voltage balance and switching loss reduction. IEEE Trans. Power Electron. 2014, 29, 5579–5591. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Gu, X.; Xia, C. Synchronized space vector PWM for three level VSI with lower harmonic distortion and switching frequency. IEEE Trans. Power Electron. 2016, 31, 6428–6441. [Google Scholar] [CrossRef]
- Brucker, T.; Holmes, D. Optimal pulse-width modulation for three-level inverters. IEEE Trans. Power Electron. 2005, 20, 82–89. [Google Scholar] [CrossRef]
- Das, S.; Narayanan, G. Analytical closed-form expressions for harmonic distortion corresponding to novel switching sequences for neutral-point-clamped inverters. IEEE Trans. Ind. Electron. 2014, 61, 4485–4497. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Theoretical and experimental analysis for the rms current ripple minimization in induction motor drives controlled by SVM technique. IEEE Trans. Ind. Electron. 2004, 51, 1056–1065. [Google Scholar] [CrossRef]
- Narendra, A.; Pramod, A. Nearest and non-nearest three vector modulations of npci using two-level space vector diagram—A novel approach. IEEE Trans. Ind. Appl. 2018, 54, 2400–2415. [Google Scholar] [CrossRef]
- Holmes, D.; Lipo, T. Pulse Width Modulation for Power Converter: Principle and Practice; Wiley-IEEE Press: Piscataway, NJ, USA, 2003. [Google Scholar]
- Geyer, T. A comparison of control and modulation schemes for medium-voltage drives: Emerging predictive control concepts versus PWM-based schemes. IEEE Trans. Ind. Appl. 2011, 47, 1380–1389. [Google Scholar] [CrossRef]
- Pou, J.; Pindado, R.; Boroyevich, D.; Rodriguez, P. Evaluation of the low-frequency neutral-point voltage oscillations in the three-level inverter. IEEE Trans. Ind. Electron. 2005, 52, 1582–1588. [Google Scholar] [CrossRef]
- Charumit, C.; Kinnares, V. Discontinuous SVPWM techniques of three-leg VSI-fed balanced two-phase loads for reduced switching losses and current ripple. IEEE Trans. Power Electron. 2015, 30, 2191–2204. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).