Observer-Based Sliding Mode FTC for Multi-Area Interconnected Power Systems against Hybrid Energy Storage Faults
Abstract
1. Introduction
2. Problem Formulation
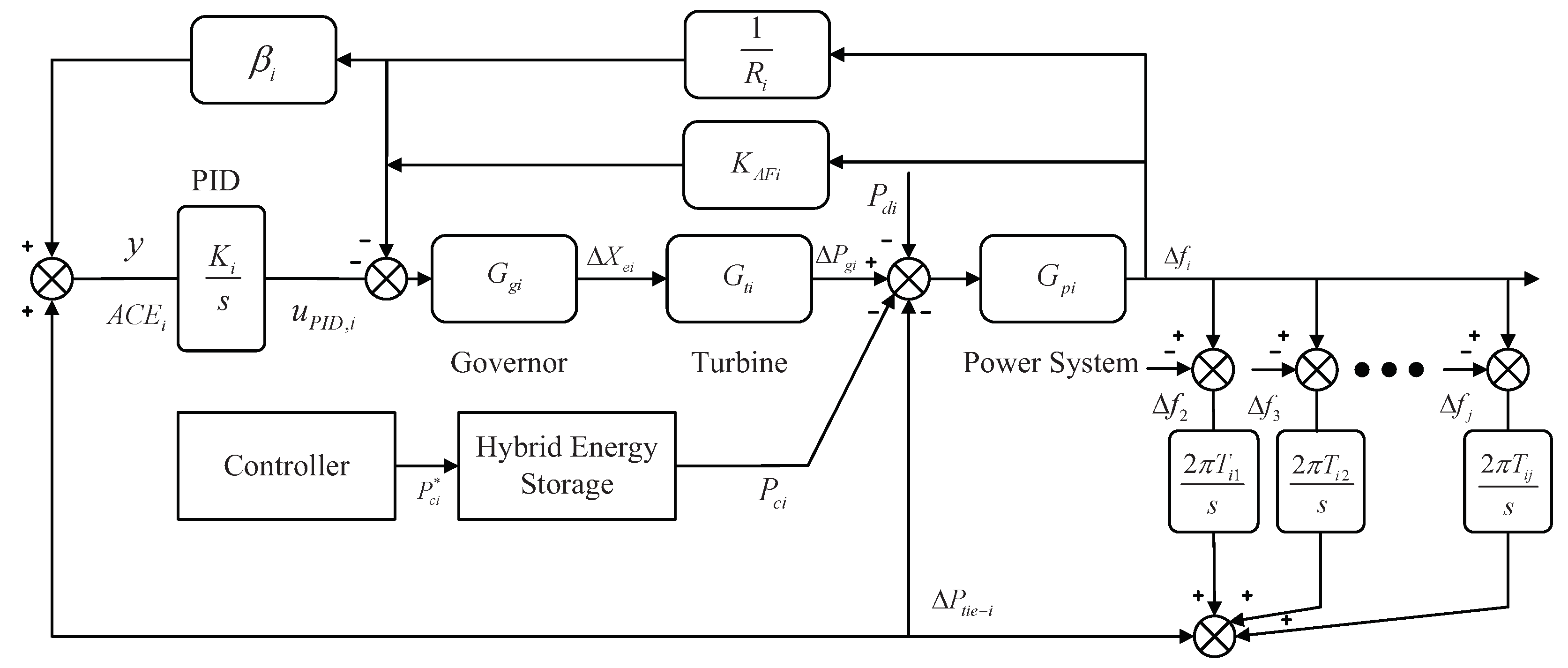
2.1. Mathematical Modeling
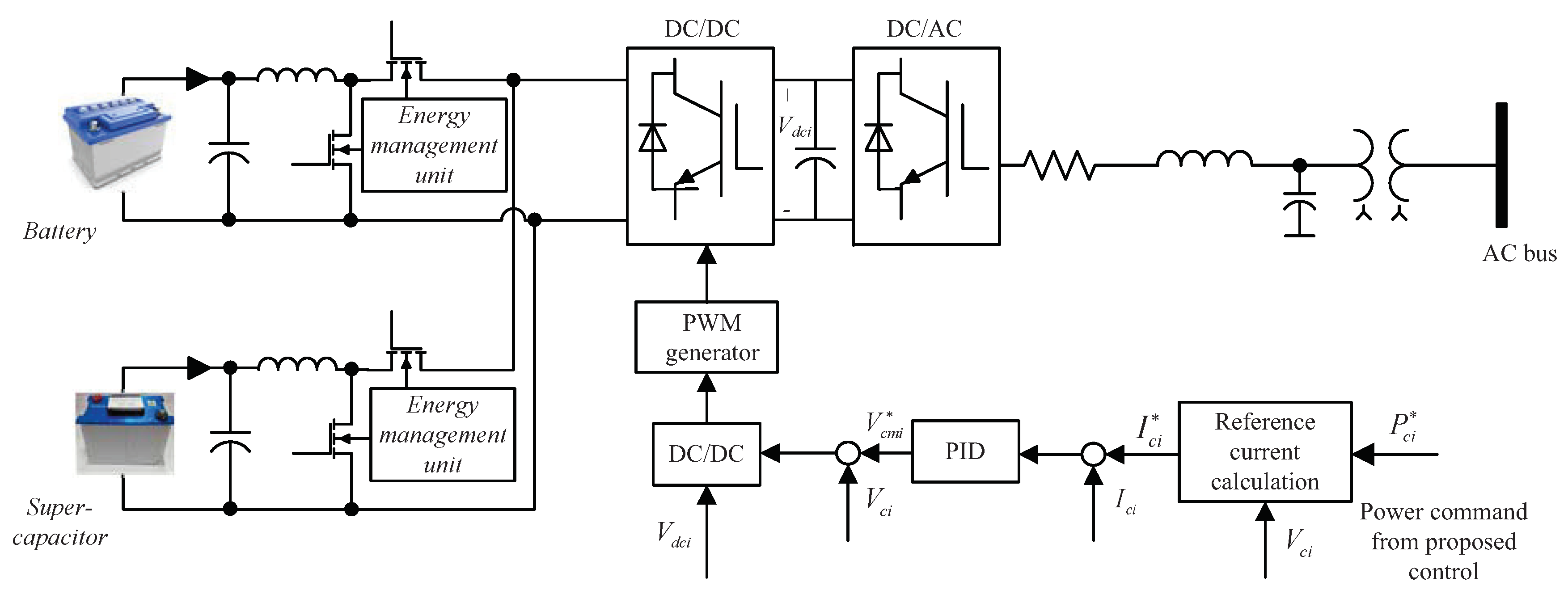
2.2. Hybrid Energy Storage System and Actuator Fault Modeling
3. Main Results
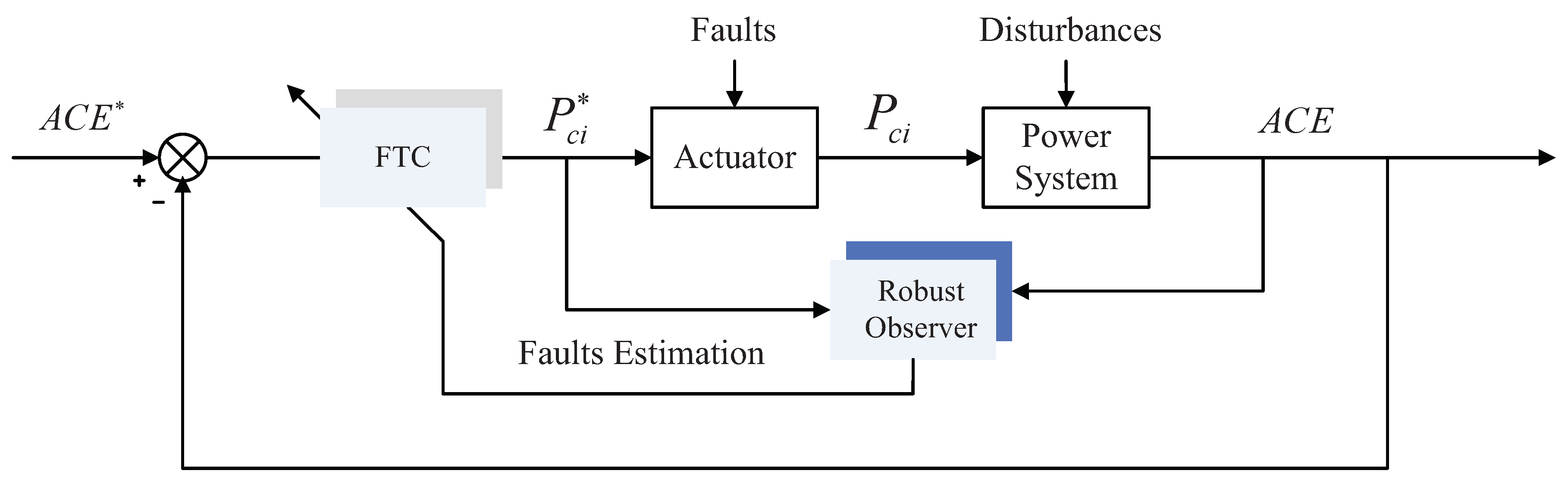
3.1. Observer Design
3.2. Fault-Tolerant Controller Design
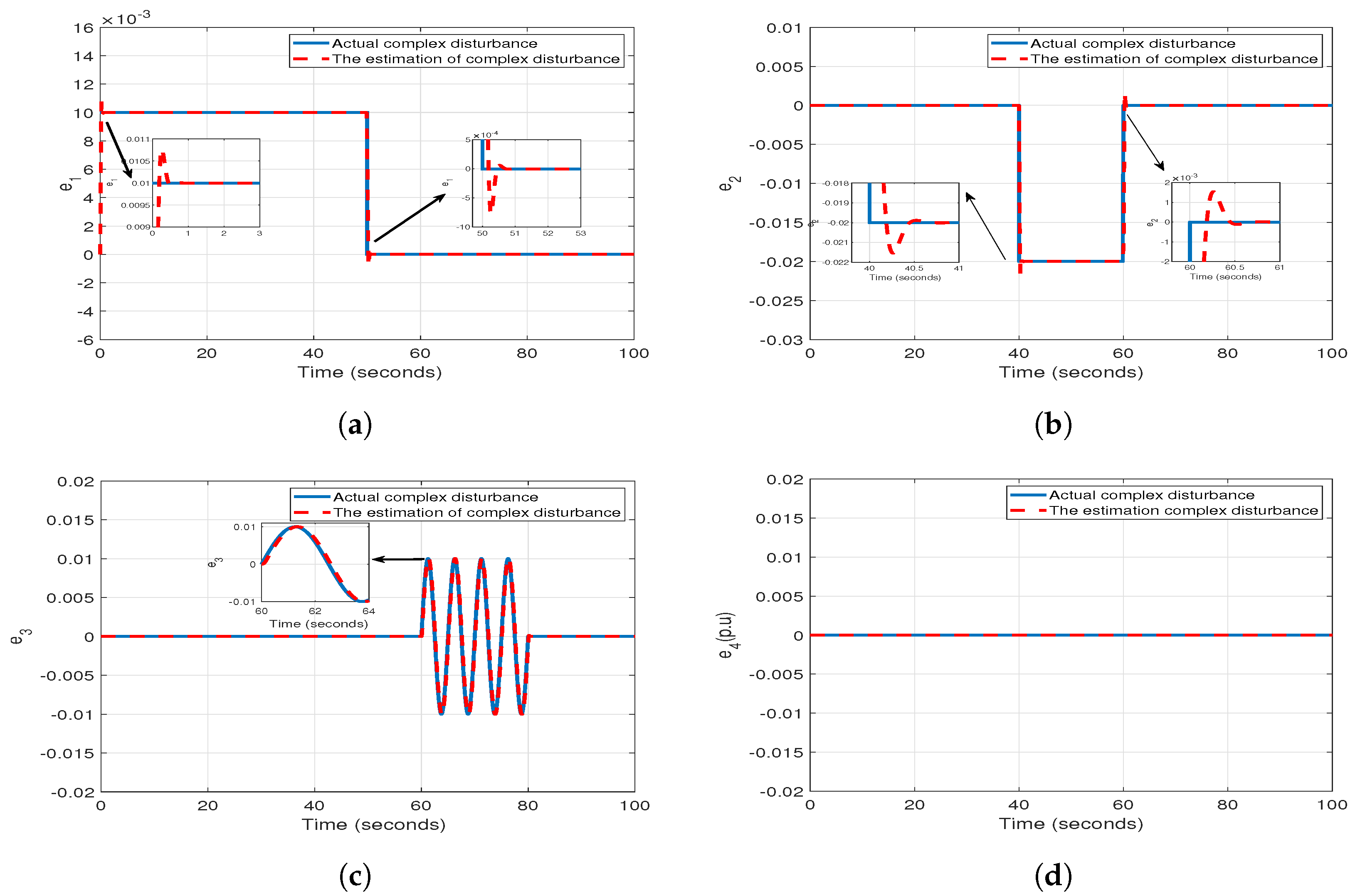
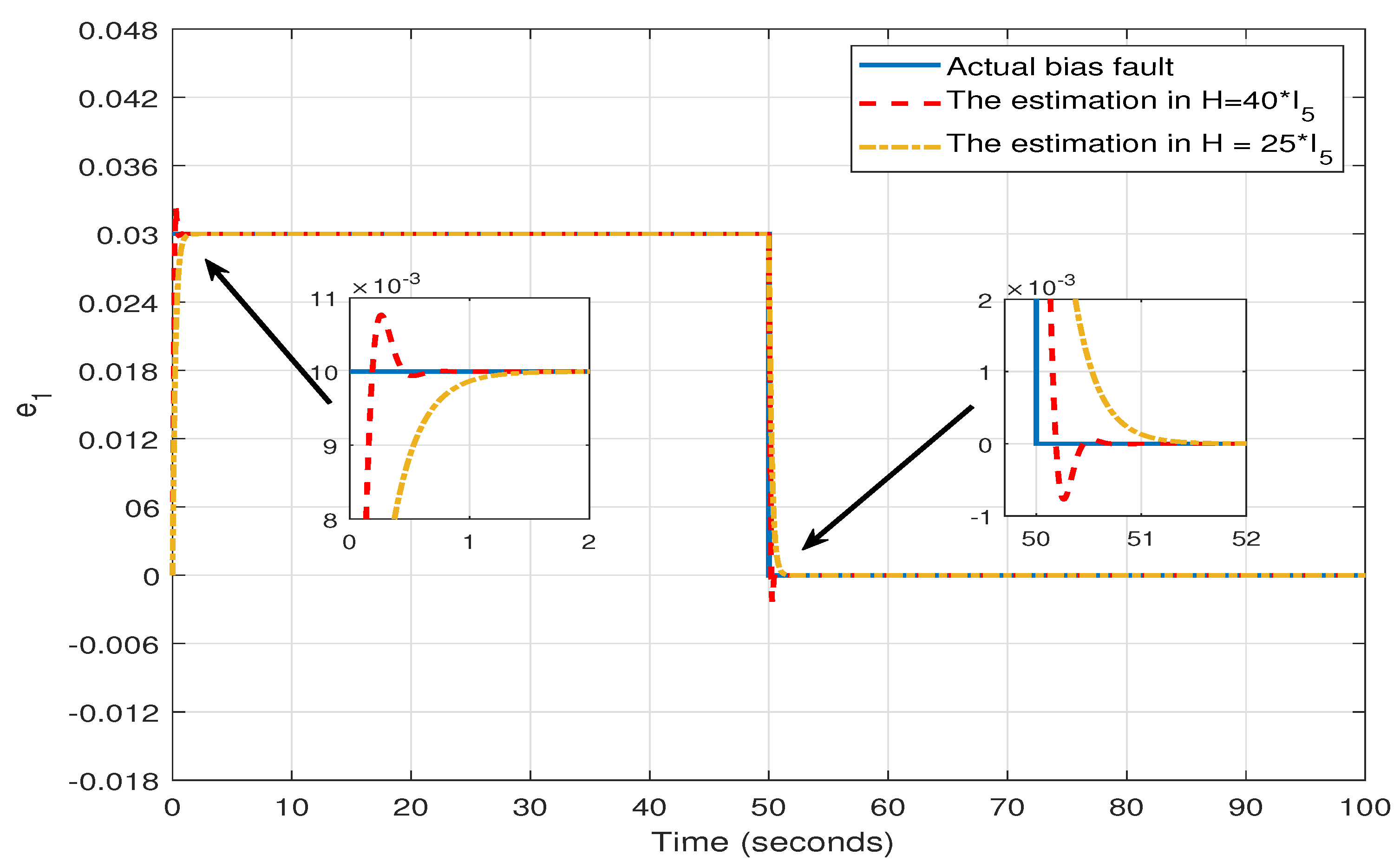
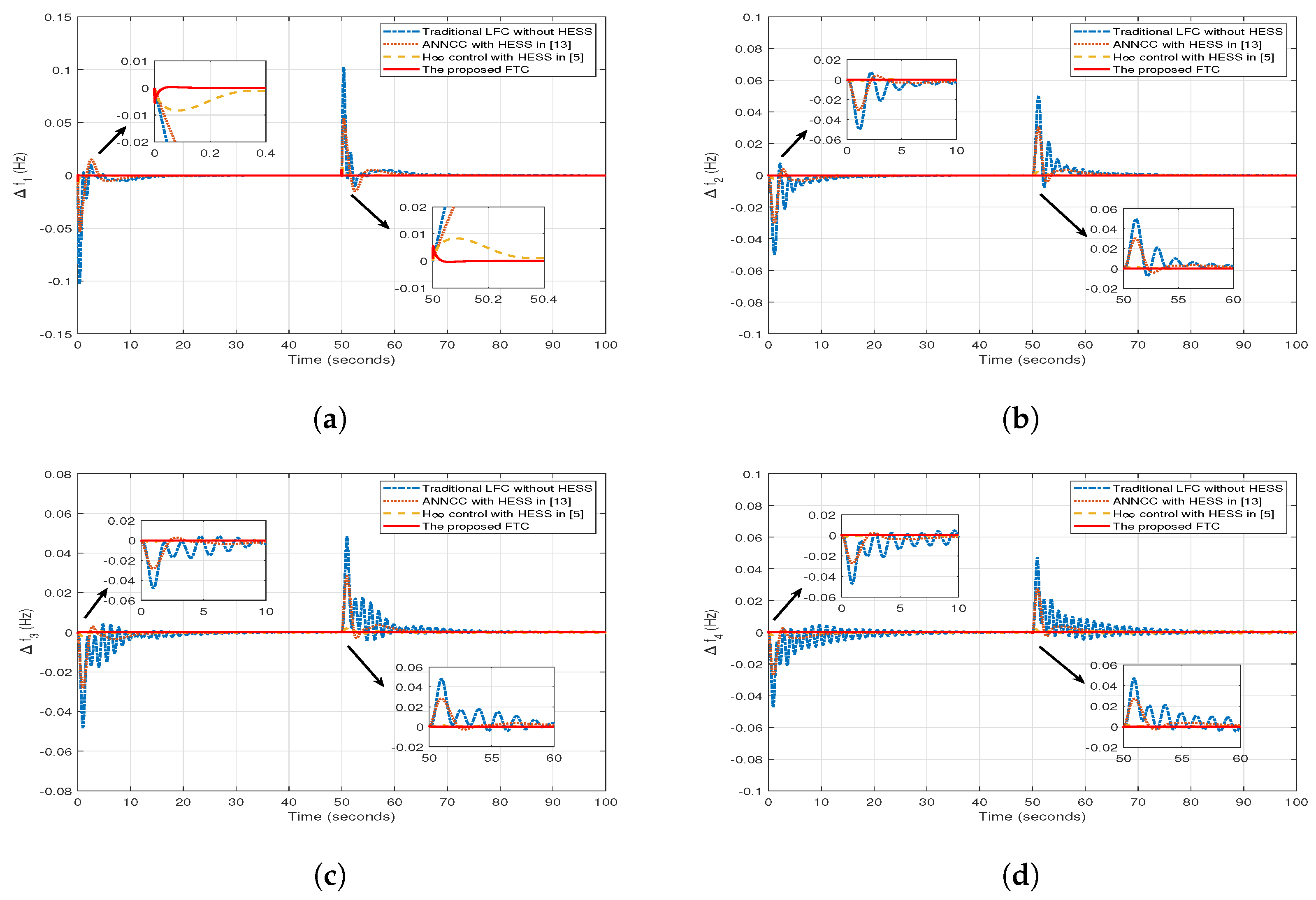
4. Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Dong, L.; Tang, Y.; He, H.; Sun, C. An event-triggered approach for load frequency control with supplementary ADP. IEEE Trans. Power Syst. 2017, 32, 581–589. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Load frequency control with communication topology changes in smart grid. IEEE Trans. Ind. Inform. 2016, 12, 1943–1952. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X.; Lee, K.Y. Distributed model predictive control for load frequency control with dynamic fuzzy valve position modelling for hydro–thermal power system. IET Control Theory Appl. 2016, 10, 1653–1664. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y.; Cao, Y.; She, J.; Wu, M. A two-layer active disturbance rejection controller design for load frequency control of interconnected power system. IEEE Trans. Power Syst. 2016, 31, 3320–3321. [Google Scholar] [CrossRef]
- Yan, W.; Sheng, L.; Xu, D.; Yang, W.; Liu, Q. H∞ Robust Load Frequency Control for Multi-Area Interconnected Power System with Hybrid Energy Storage System. Appl. Sci. 2018, 8, 1748. [Google Scholar] [CrossRef]
- Sabahi, K.; Sharifi, A.; Sh, M.A.; Teshnehlab, M.; Alisghary, M. Load frequency control in interconnected power system using multi-objective PID controller. J. Appl. Sci. 2008, 8, 3676–3682. [Google Scholar] [CrossRef]
- Rubaai, A.; Udo, V. An adaptive control scheme for load-frequency control of multiarea power systems Part I. Identification and functional design. Electr. Power Syst. Res. 1992, 24, 183–188. [Google Scholar] [CrossRef]
- Rahmani, M.; Sadati, N. Hierarchical optimal robust load-frequency control for power systems. IET Gener. Transm. Distrib. 2012, 6, 303–312. [Google Scholar] [CrossRef]
- Mi, Y.; Fu, Y.; Wang, C.; Wang, P. Decentralized sliding mode load frequency control for multi-area power systems. IEEE Trans. Power Syst. 2013, 28, 4301–4309. [Google Scholar] [CrossRef]
- Ersdal, A.M.; Cecílio, I.M.; Fabozzi, D.; Imsland, L.; Thornhill, N.F. Applying Model Predictive Control to Power System Frequency Control; IEEE PES ISGT Europe 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Qian, D.; Zhao, D.; Yi, J.; Liu, X. Neural sliding-mode load frequency controller design of power systems. Neural Comput. Appl. 2013, 22, 279–286. [Google Scholar] [CrossRef]
- ud din Mufti, M.; Lone, S.A.; Iqbal, S.J.; Ahmad, M.; Ismail, M. Super-capacitor based energy storage system for improved load frequency control. Electr. Power Syst. Res. 2009, 79, 226–233. [Google Scholar] [CrossRef]
- Xu, D.; Liu, J.; Yan, X.; Yan, W. A novel adaptive neural network constrained control for a multi-area interconnected power system with hybrid energy storage. IEEE Trans. Ind. Electron. 2018, 65, 6625–6634. [Google Scholar] [CrossRef]
- Mufti, M.D.; Iqbal, S.J.; Lone, S.A.; Ain, Q.U. Supervisory Adaptive Predictive Control Scheme for Supercapacitor Energy Storage System. IEEE Syst. J. 2014, 9, 1020–1030. [Google Scholar] [CrossRef]
- Shankar, R.; Chatterjee, K.; Bhushan, R. Impact of energy storage system on load frequency control for diverse sources of interconnected power system in deregulated power environment. Int. J. Electr. Power Energy Syst. 2016, 79, 11–26. [Google Scholar] [CrossRef]
- Shankar, R.; Bhushan, R.; Chatterjee, K. Small-signal stability analysis for two-area interconnected power system with load frequency controller in coordination with FACTS and energy storage device. Ain Shams Eng. J. 2016, 7, 603–612. [Google Scholar] [CrossRef]
- Molina, M.; Mercado, P. Modeling of a DSTATCOM with ultra-capacitor energy storage for power distribution system applications. In Proceedings of the 13th Eriac Decimo Tercer Encuentro Regional Iberoamericano De Cigre, Foz de Iguazu, Argentina, 24–28 May 2009; pp. 1–8. [Google Scholar]
- Attya, A.B.T.; Hartkopf, T. Utilising stored wind energy by hydro-pumped storage to provide frequency support at high levels of wind energy penetration. IET Gener. Transm. Distrib. 2015, 9, 1485–1497. [Google Scholar] [CrossRef]
- Gurumurthy, S.R.; Agarwal, V.; Sharma, A. High-efficiency bidirectional converter for flywheel energy storage application. IEEE Trans. Ind. Electron. 2016, 63, 5477–5487. [Google Scholar] [CrossRef]
- Bruno, S.; Dellino, G.; La Scala, M.; Meloni, C. A Microforecasting Module for Energy Management in Residential and Tertiary Buildings. Energies 2019, 12, 1006. [Google Scholar] [CrossRef]
- Liu, M.; Ho, D.W.; Shi, P. Adaptive fault-tolerant compensation control for Markovian jump systems with mismatched external disturbance. Automatica 2015, 58, 5–14. [Google Scholar] [CrossRef]
- Khalili, M.; Zhang, X.; Polycarpou, M.M.; Parisini, T.; Cao, Y. Distributed adaptive fault-tolerant control of uncertain multi-agent systems. Automatica 2018, 87, 142–151. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, B.; Staroswiecki, M.; Zhang, Y. Fault recoverability and fault tolerant control for a class of interconnected nonlinear systems. Automatica 2015, 54, 49–55. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z.; Zhang, A. Observer-based fault estimation and tolerant control for stochastic Takagi–Sugeno fuzzy systems with Brownian parameter perturbations. Automatica 2019, 102, 137–149. [Google Scholar] [CrossRef]
- Panagi, P.; Polycarpou, M.M. Distributed fault accommodation for a class of interconnected nonlinear systems with partial communication. IEEE Trans. Autom. Control 2011, 56, 2962–2967. [Google Scholar] [CrossRef]
- Polycarpou, M.M.; Panagi, P. A coordinated communication scheme for distributed fault tolerant control. IEEE Trans. Ind. Inform. 2013, 9, 386–393. [Google Scholar]
- Jin, X.; Yang, G. Distributed adaptive robust tracking and model matching control with actuator faults and interconnection failures. Int. J. Control. Autom. Syst. 2009, 7, 702. [Google Scholar] [CrossRef]
- Tong, S.; Huo, B.; Li, Y. Observer-based adaptive decentralized fuzzy fault-tolerant control of nonlinear large-scale systems with actuator failures. IEEE Trans. Fuzzy Syst. 2014, 22, 1–15. [Google Scholar] [CrossRef]
- Liu, T.; Hill, D.J.; Jiang, Z. Lyapunov formulation of ISS cyclic-small-gain in continuous-time dynamical networks. Automatica 2011, 47, 2088–2093. [Google Scholar] [CrossRef]
- Ibraheem; Kumar, P.; Kothari, D.P. Recent philosophies of automatic generation control strategies in power systems. IEEE Trans. Power Syst. 2005, 20, 346–357. [Google Scholar] [CrossRef]
- Gao, Z.; Jiang, B.; Shi, P.; Qian, M.; Lin, J. Active fault tolerant control design for reusable launch vehicle using adaptive sliding mode technique. J. Frankl. Inst. 2012, 349, 1543–1560. [Google Scholar] [CrossRef]
- Efimov, D.; Edwards, C.; Zolghadri, A. Enhancement of adaptive observer robustness applying sliding mode techniques. Automatica 2016, 72, 53–56. [Google Scholar] [CrossRef]
- Chiu, C.S. Derivative and integral terminal sliding mode control for a class of MIMO nonlinear systems. Automatica 2012, 48, 316–326. [Google Scholar] [CrossRef]
- Song, H.; Zhang, T. Fast robust integrated guidance and control design of interceptors. IEEE Trans. Control Syst. Technol. 2015, 24, 349–356. [Google Scholar] [CrossRef]
- Wang, X.; Luo, X.; Zhang, M.; Guan, X. Distributed detection and isolation of false data injection attacks in smart grids via nonlinear unknown input observers. Int. J. Electr. Power Energy Syst. 2019, 110, 208–222. [Google Scholar] [CrossRef]


| Parameters | Description |
|---|---|
| Tie-line power synchronization coefficient | |
| Time constant of power system | |
| Time constant of governor | |
| Time constant of turbine | |
| 1.00,0.00,0.00Control gain of PI controller in area i | |
| Load disturbance | |
| Tie-line deviation of power exchange between area i and others | |
| Incremental variation of governor valve positon | |
| Power delivered by the HESS to area i | |
| Power system gain | |
| Load frequency deviation of power system | |
| Set value of frequency deviation | |
| Control error of the i-th area. | |
| Speed regulation gain | |
| Proportional feedback coefficient of frequency deviation | |
| A diagonal matrix | |
| The euclidean norm | |
| N-dimensional unit matrix | |
| HESS | Hybrid energy storage system |
| LFC | Load frequency control |
| FTC | Fault-tolerant control |
| SMC | Sliding model control |
| ACE | Area control error |
| Parameters | Values |
|---|---|
| Observer parameters | |
| Controller parameters | |
| Area i | (s) | (s) | (Hz/p.u.Mw) | (s) | (Hz/p.u.Mw) | (s) | (Hz/p.u.Mw) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.08 | 0.3 | 2.4 | 0.0707 | 120 | 20 | 0.425 | 1.1 |
| 2 | 0.072 | 0.33 | 2.7 | 0.0707 | 112.5 | 25 | 0.425 | 1.1 |
| 3 | 0.07 | 0.35 | 2.5 | 0.0707 | 125 | 20 | 0.425 | 1.1 |
| 4 | 0.085 | 0.375 | 2 | 0.0707 | 115 | 15 | 0.425 | 1.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Yu, D.; Xu, D.; Zhang, Y. Observer-Based Sliding Mode FTC for Multi-Area Interconnected Power Systems against Hybrid Energy Storage Faults. Energies 2019, 12, 2819. https://doi.org/10.3390/en12142819
Yang W, Yu D, Xu D, Zhang Y. Observer-Based Sliding Mode FTC for Multi-Area Interconnected Power Systems against Hybrid Energy Storage Faults. Energies. 2019; 12(14):2819. https://doi.org/10.3390/en12142819
Chicago/Turabian StyleYang, Weilin, Dong Yu, Dezhi Xu, and Yiwei Zhang. 2019. "Observer-Based Sliding Mode FTC for Multi-Area Interconnected Power Systems against Hybrid Energy Storage Faults" Energies 12, no. 14: 2819. https://doi.org/10.3390/en12142819
APA StyleYang, W., Yu, D., Xu, D., & Zhang, Y. (2019). Observer-Based Sliding Mode FTC for Multi-Area Interconnected Power Systems against Hybrid Energy Storage Faults. Energies, 12(14), 2819. https://doi.org/10.3390/en12142819





