Exploring the Profitability and Efficiency of Variable Renewable Energy in Spot Electricity Market: Uncovering the Locational Price Disadvantages
Abstract
:1. Introduction
2. The Significance and Barriers of Bringing VRE to Market
2.1. Integration cost of VRE Power Generation and the Allocation Problem
2.1.1. Electricity Production Cost
2.1.2. The Integration Cost
2.2. VRE Market Participation as a Cost Allocation Approach
2.3. Several Unaddressed Problems of Bringing VRE to Market
- the profitability of VRE in a deregulated pool-based electricity market where integration cost is allocated;
- the influences of VRE market participation to system production efficiency;
- and the influences of learning and strategic behavior.
3. A VRE-Participated 2-Settlement Pool-Based Electricity Market
3.1. Production Model of Thermal and VRE GenCos
3.2. Day-Ahead forward Market Considering Reserve Services for Variability
3.3. Real Time Balance
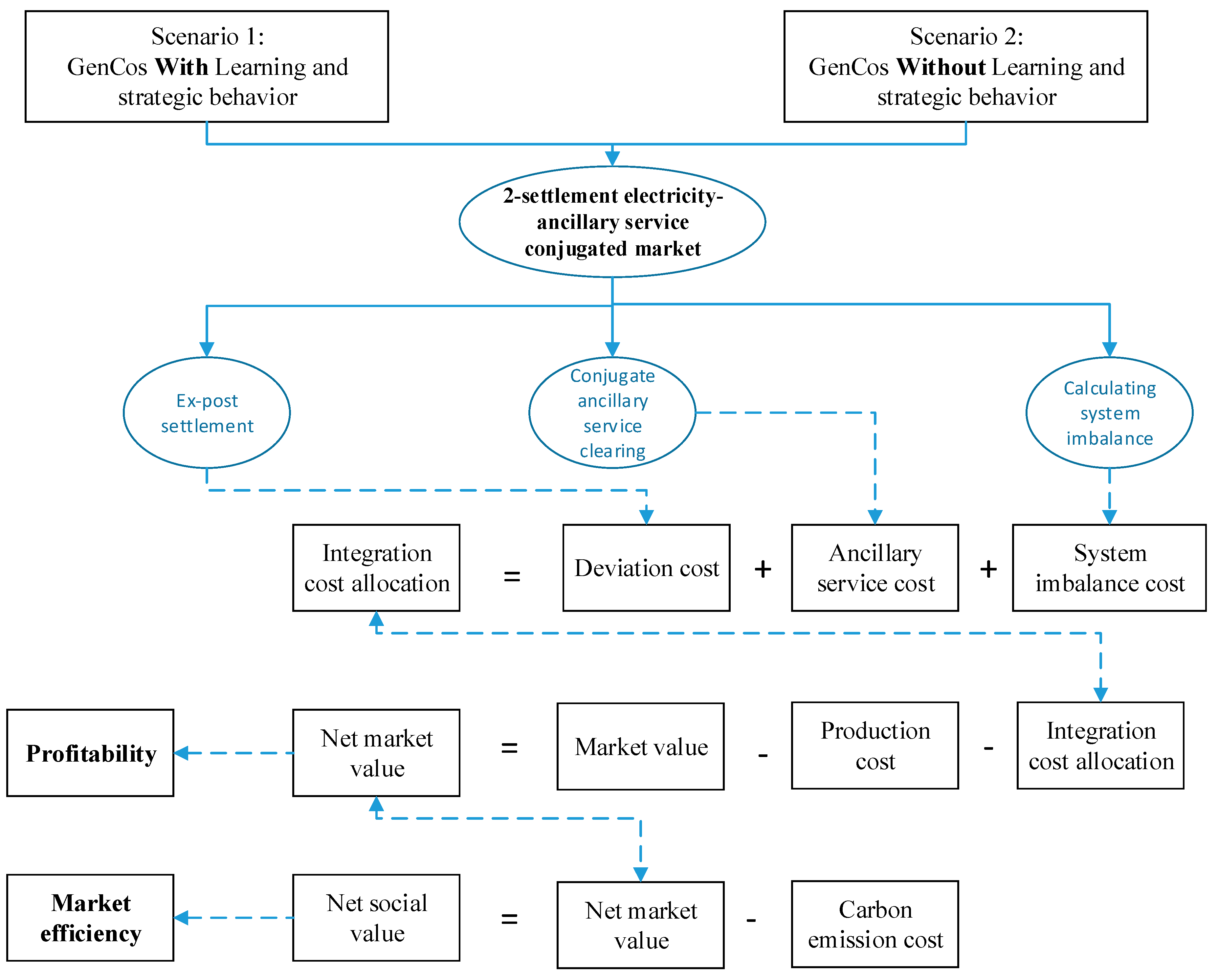
3.4. Ex-Post Settlement
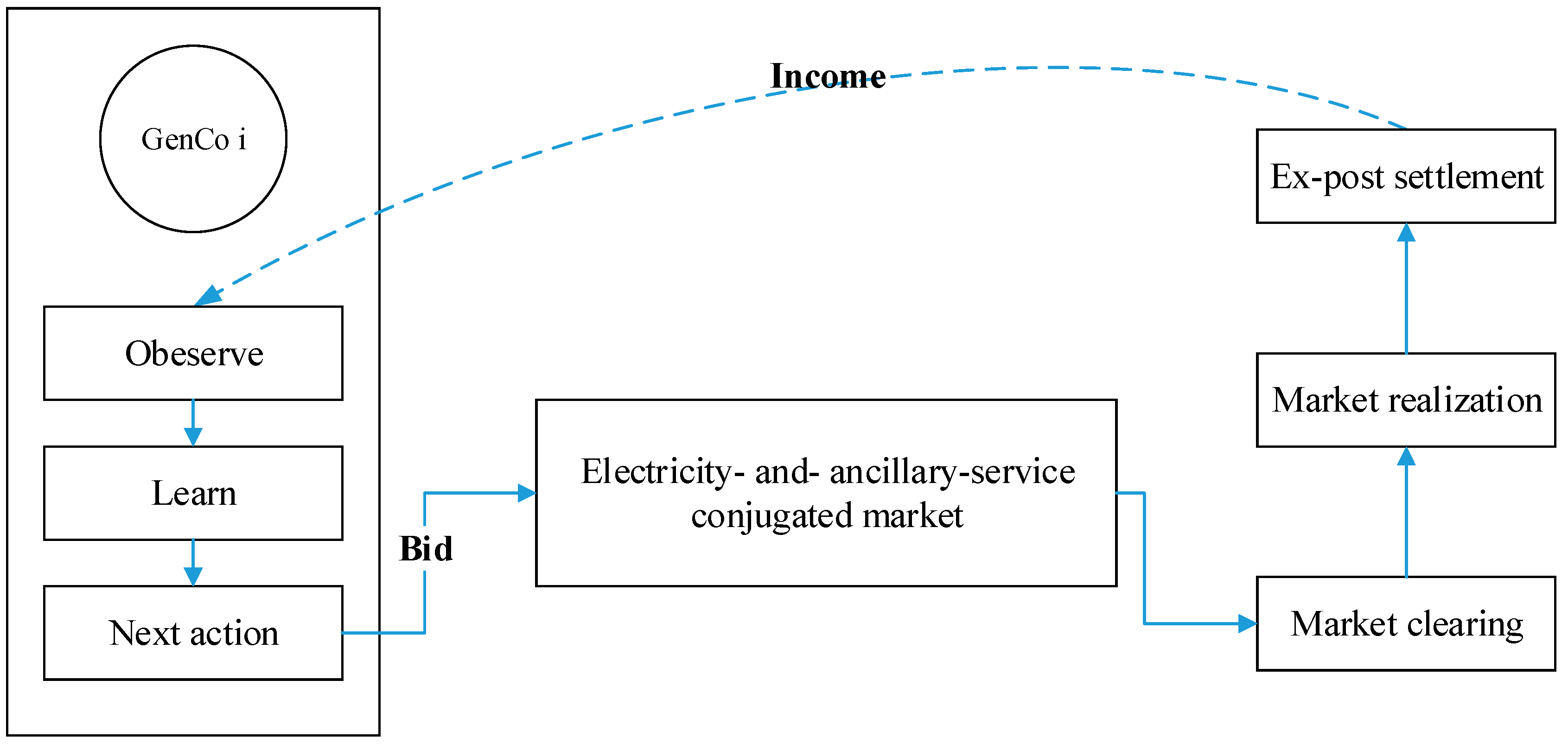
3.5. Learning and Strategic Behavior of GenCos
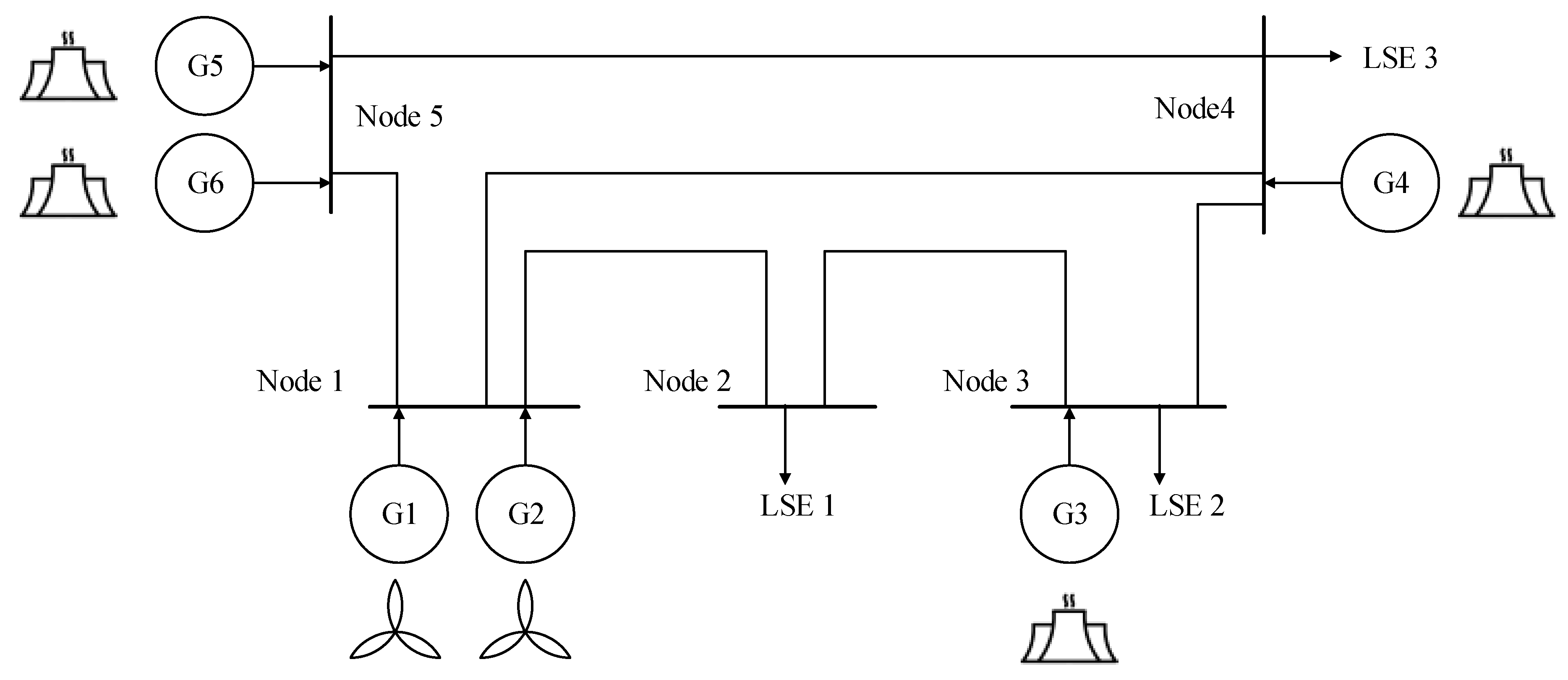
3.6. Case Design and Numerical Simulation
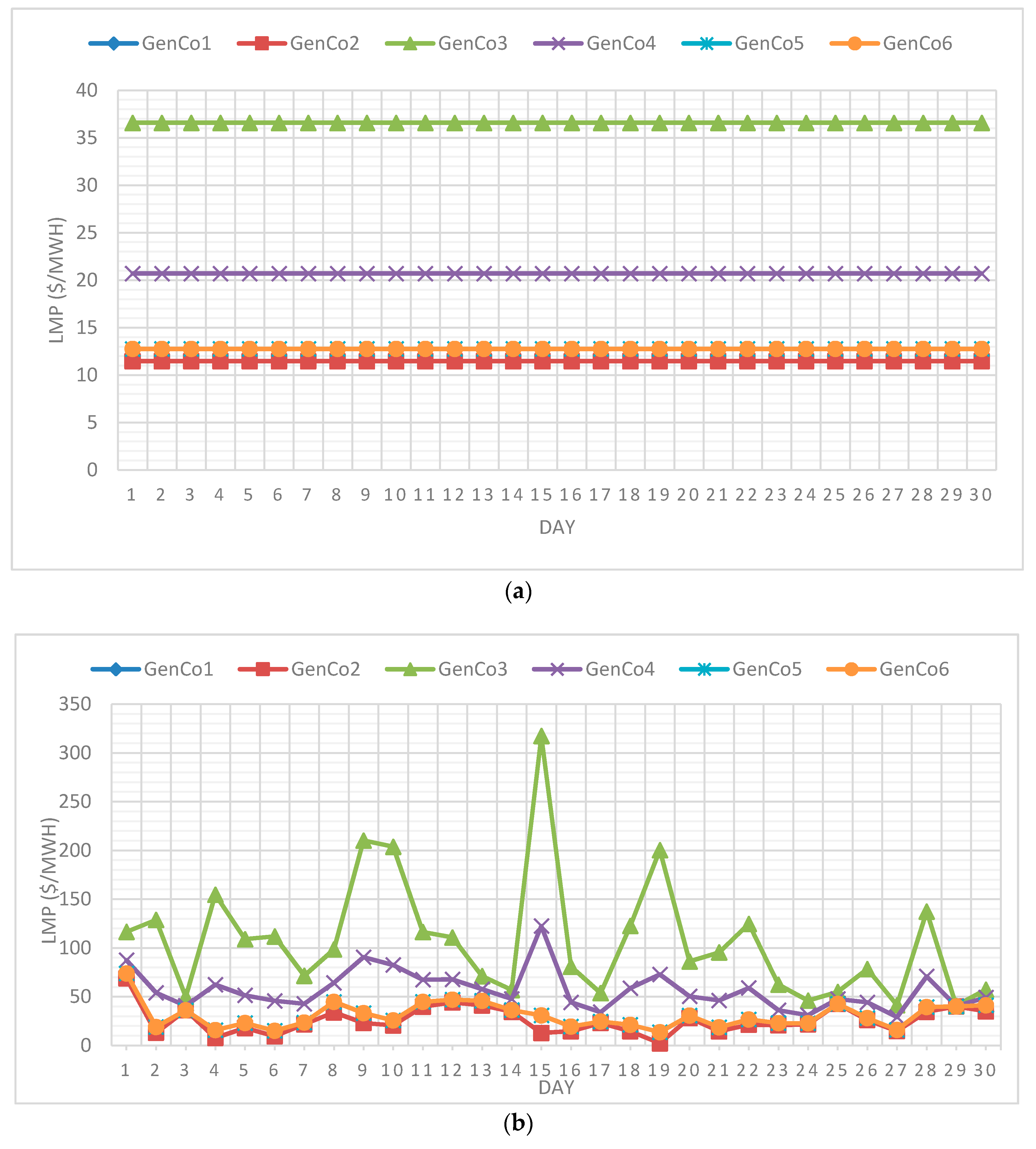
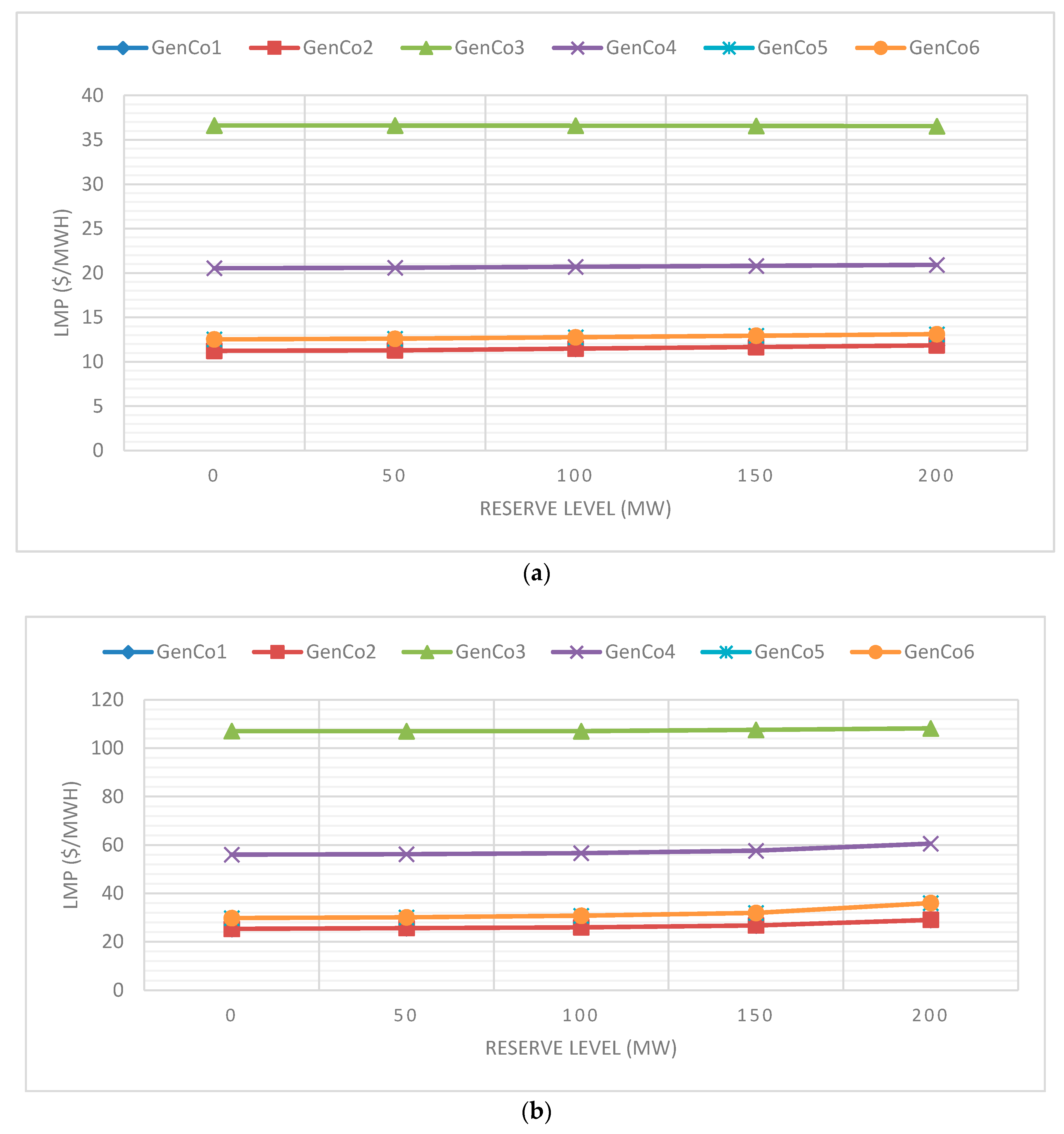
4. Results and Discussion
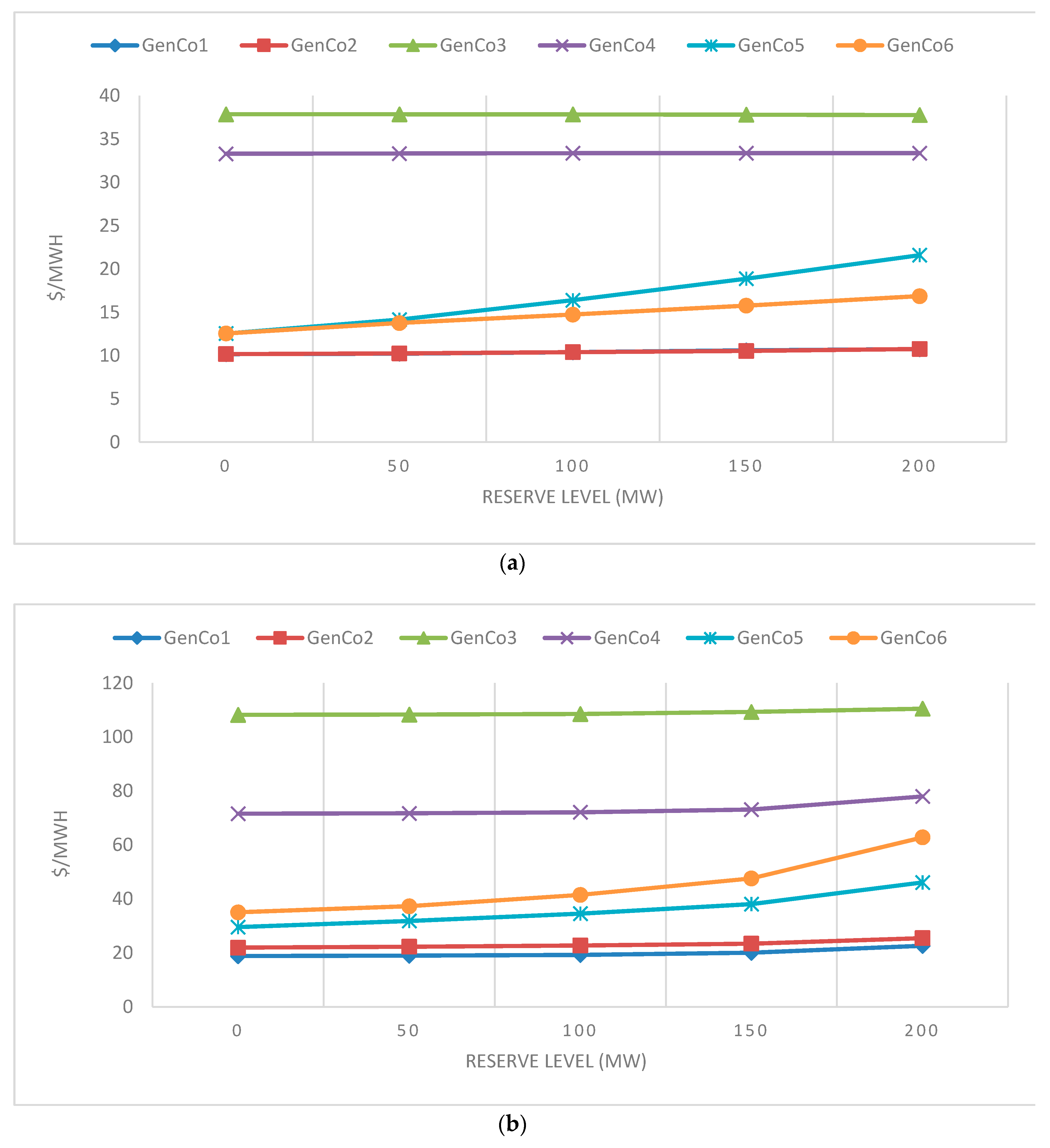
4.1. Profitability of VRE
4.2. Efficiency of VRE in Market
4.3. Discussions
4.3.1. Locational Marginal Price of VRE
4.3.2. The Market Value and LCOE of VRE
5. Conclusions and Suggestions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Rel | Reliability |
| pse | pseudo-max-cost |
| H | Upper limit for GenCo output |
| L | Lower limit for GenCo output |
| U | Upper limit for transmission line capacity |
| Hr | Realized Upper limit for a VRE GenCo |
| AS | Ancillary service |
| rep | Reported value |
| DA | Day ahead values |
| RT | Real time values |
| Exp | Ex-post values |
| Set | Settlement values |
| O | Operation |
| Subindices and superindices | |
| i,v,w | Subindices for GenCos |
| k,m | Subindices for nodes |
| km | Subindices for a transmission line from k to m |
| l | Subindices for transmission lines |
| P, Q | Subindices for conditions in SCED DA |
| j | Subindices for load-serving entities |
| t | Subindices for periods |
| Constants and variables | |
| Forecast error factor for VRE GenCos | |
| Active power output for a CenCo | |
| Reserve power for a thermal CenCo | |
| Reactance of line km | |
| Power flow | |
| Voltage angle | |
| , , | Lagrange multipliers |
| Penalty factor | |
| Locational marginal price (LMP) | |
| Day ahead ancillary service price | |
| Load demand of active power | |
| Price imbalance factor | |
| A, B, C, D | Cost coefficients |
| M | Market power |
| Ex-post settlement coefficients | |
| Settlement price | |
| Imbalance measurement factor | |
| Sets | |
| I | Set of thermal GenCos |
| V | Set of VRE GenCos |
| BR | Set of VRE transmission lines |
| J | Set of LSEs |
| N | Set of Nodes |
| Set of periods | |
| Functions | |
| Production function for a GenCo | |
| Ancillary service production function | |
| A penalty function | |
| A penalty function | |
| Operators | |
| Absolute value or set cardinality |
Appendix A
References
- Sawin, J.L.; Sverrisson, F.; Seyboth, K.; Adib, R.; Murdock, H.E.; Lins, C.; Edwards, I.; Hullin, M.; Nguyen, L.H.; Prillianto, S.S. Renewables 2017 Global Status Report; REN21: Paris, France, 2017. [Google Scholar]
- Shen, J.; Luo, C. Overall review of renewable energy subsidy policies in China–Contradictions of intentions and effects. Renew. Sustain. Energy Rev. 2015, 41, 1478–1488. [Google Scholar] [CrossRef]
- Kalkuhl, M.; Edenhofer, O.; Lessmann, K. Renewable energy subsidies: Second-best policy or fatal aberration for mitigation? Resour. Energy Econ. 2013, 35, 217–234. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Shi, H.; Cao, Y.; Wang, J.; Kuang, Y.; Tan, Y.; Wei, J. Comprehensive review of renewable energy curtailment and avoidance: A specific example in China. Renew. Sustain. Energy Rev. 2015, 41, 1067–1079. [Google Scholar] [CrossRef]
- Kane, L.; Ault, G. A review and analysis of renewable energy curtailment schemes and Principles of Access: Transitioning towards business as usual. Energy Policy 2014, 72, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Fink, S.; Mudd, C.; Porter, K.; Morgenstern, B. Wind Energy Curtailment Case Studies: May 2008–May 2009; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Denholm, P. Energy storage to reduce renewable energy curtailment. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–4. [Google Scholar]
- Hirth, L.; Ueckerdt, F.; Edenhofer, O. Integration costs revisited–An economic framework for wind and solar variability. Renew. Energy 2015, 74, 925–939. [Google Scholar] [CrossRef]
- Milligan, M.; Kirby, B. Calculating Wind Integration Costs: Separating Wind Energy Value from Integration Cost Impacts; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Koraki, D.; Strunz, K. Wind and solar power integration in electricity markets and distribution networks through service-centric virtual power plants. IEEE Trans. Power Syst. 2018, 33, 473–485. [Google Scholar] [CrossRef]
- Dragoon, K.; Milligan, M. Assessing Wind Integration Costs with Dispatch Models: A Case Study of PacifiCorp; Preprint; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2003. [Google Scholar]
- Ouyang, X.; Lin, B. Levelized cost of electricity (LCOE) of renewable energies and required subsidies in China. Energy Policy 2014, 70, 64–73. [Google Scholar] [CrossRef]
- Branker, K.; Pathak, M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2011, 15, 4470–4482. [Google Scholar] [CrossRef] [Green Version]
- IEA. Projected Costs of Generating Electricity; International Energy Agency (IEA): Paris, France, 2015. [Google Scholar]
- Bitar, E.Y.; Rajagopal, R.; Khargonekar, P.P.; Poolla, K.; Varaiya, P. Bringing wind energy to market. IEEE Trans. Power Syst. 2012, 27, 1225–1235. [Google Scholar] [CrossRef]
- Traber, T.; Kemfert, C. Gone with the wind?—Electricity market prices and incentives to invest in thermal power plants under increasing wind energy supply. Energy Econ. 2011, 33, 249–256. [Google Scholar] [CrossRef]
- Shin, H.; Baldick, R. Mitigating market risk for wind power providers via financial risk exchange. Energy Econ. 2018, 71, 344–358. [Google Scholar] [CrossRef]
- Lin, W.; Bitar, E. Forward electricity markets with uncertain supply: Cost sharing and efficiency loss. In Proceedings of the 2014 IEEE 53rd Annual Conference on Decision and Control (CDC), Los Angeles, CA, USA, 15–17 December 2014; pp. 1707–1713. [Google Scholar]
- Kirby, B.; Milligan, M.; Wan, Y. Cost-Causation-Based Tariffs for Wind Ancillary Service Impacts; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2006. [Google Scholar]
- Sotkiewicz, P.M.; Vignolo, J.M. Towards a Cost Causation-Based Tariff for Distribution Networks With DG. IEEE Trans. Power Syst. 2007, 22, 1051–1060. [Google Scholar] [CrossRef]
- Chakraborty, P.; Baeyens, E.; Khargonekar, P.P. Cost Causation Based Allocations of Costs for Market Integration of Renewable Energy. IEEE Trans. Power Syst. 2017, 33, 70–83. [Google Scholar] [CrossRef]
- Baeyens, E.; Bitar, E.Y.; Khargonekar, P.P.; Poolla, K. Coalitional aggregation of wind power. IEEE Trans. Power Syst. 2013, 28, 3774–3784. [Google Scholar] [CrossRef]
- Hernández-Moro, J.; Martínez-Duart, J.M. Analytical model for solar PV and CSP electricity costs: Present LCOE values and their future evolution. Renew. Sustain. Energy Rev. 2013, 20, 119–132. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, W.; Zhao, C.; Yuan, J. The Economics of Wind Power in China and Policy Implications. Energies 2015, 8, 1529–1546. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Sun, S.; Zhang, W.; Xiong, M. The economy of distributed PV in China. Energy 2014, 78, 939–949. [Google Scholar] [CrossRef]
- Xyu, R.; Song, Z.; Tang, Q.; Yu, Z. The cost and marketability of renewable energy after power market reform in China: A review. J. Clean. Prod. 2018, 204, 409–424. [Google Scholar]
- Yang, M.; Bewley, R. Integration of Variable Generation, Cost-Causation, and Integration Costs. Electr. J. 2011, 24, 51–63. [Google Scholar]
- Holttinen, H.; Meibom, P.; Orths, A.; O’Malley, M.; Ummels, B.; Tande, J.O.; Estanqueiro, A.; Gomez, E.; Smith, J.C.; Ela, E. Impacts of large amounts of wind power on design and operation of power systems, results of IEA collaboration. In Proceedings of the European Wind Energy Conference & Exhibition 2008, Brussels, Belgium, 31 March–3 April 2008. [Google Scholar]
- Ueckerdt, F.; Hirth, L.; Luderer, G.; Edenhofer, O. System LCOE: What are the costs of variable renewables? Soc. Sci. Electr. Publ. 2013, 63, 61–75. [Google Scholar]
- Dong, Y.L.; Shimada, K. Evolution from the renewable portfolio standards to feed-in tariff for the deployment of renewable energy in Japan. Renew. Energy 2017, 107, 590–596. [Google Scholar] [CrossRef]
- Wesseh, P.K., Jr.; Lin, B. A real options valuation of Chinese wind energy technologies for power generation: Do benefits from the feed-in tariffs outweigh costs? J. Clean. Prod. 2016, 112, 1591–1599. [Google Scholar] [CrossRef]
- Rodrigues, S.; Torabikalaki, R.; Faria, F.; Cafofo, N.; Chen, X.; Ivaki, A.R.; Mata-Lima, H.; Morgado-Dias, F. Economic feasibility analysis of small scale PV systems in different countries. Sol. Energy 2016, 131, 81–95. [Google Scholar] [CrossRef]
- Pyrgou, A.; Kylili, A.; Fokaides, P.A. The future of the Feed-in Tariff (FiT) scheme in Europe: The case of photovoltaics. Energy Policy 2016, 95, 94–102. [Google Scholar] [CrossRef]
- Merei, G.; Moshoevel, J.; Magnor, D.; Sauer, D.U. Optimization of self-consumption and techno-economic analysis of PV-battery systems in commercial applications. Appl. Energy 2016, 168, 171–178. [Google Scholar] [CrossRef]
- Javier Ramirez, F.; Honrubia-Escribano, A.; Gomez-Lazaro, E.; Pham, D.T. Combining feed-in tariffs and net-metering schemes to balance development in adoption of photovoltaic energy: Comparative economic assessment and policy implications for European countries. Energy Policy 2017, 102, 440–452. [Google Scholar] [CrossRef]
- Herrando, M.; Markides, C.N. Hybrid PV and solar-thermal systems for domestic heat and power provision in the UK: Techno-economic considerations. Appl. Energy 2016, 161, 512–532. [Google Scholar] [CrossRef] [Green Version]
- Razeghi, G.; Shaffer, B.; Samuelsen, S. Impact of electricity deregulation in the state of California. Energy Policy 2017, 103, 105–115. [Google Scholar] [CrossRef]
- Meyabadi, A.F.; Deihimi, M.H. A review of demand-side management: Reconsidering theoretical framework. Renew. Sustain. Energy Rev. 2017, 80, 367–379. [Google Scholar] [CrossRef]
- Polemis, M.L. Capturing the Impact of Shocks on the Electricity Sector Performance in the OECD. Energy Econ. 2017, 66, 99–107. [Google Scholar] [CrossRef]
- Ajayi, V.; Weyman-Jones, T.; Glass, A. Cost Efficiency and Electricity Market Structure: A Case Study of OECD Countries. Energy Econ. 2017, 65, 283–291. [Google Scholar] [CrossRef]
- Wang, N.; Mogi, G. Deregulation, market competition, and innovation of utilities: Evidence from Japanese electric sector. Energy Policy 2017, 111, 403–413. [Google Scholar] [CrossRef]
- Shi, X.; Sun, S. Energy price, regulatory price distortion and economic growth: A case study of China. Energy Econ. 2017, 63, 261–271. [Google Scholar] [CrossRef] [Green Version]
- Gawel, E.; Purkus, A. Promoting the market and system integration of renewable energies through premium schemes—A case study of the German market premium. Energy Policy 2013, 61, 599–609. [Google Scholar] [CrossRef]
- Zipp, A.; Kalogirou, S.A.; Christodoulides, P. The marketability of variable renewable energy in liberalized electricity markets—An empirical analysis. Renew. Energy 2017, 113, 1111–1121. [Google Scholar] [CrossRef]
- Wild, P. Determining commercially viable two-way and one-way “Contract-for-Difference” strike prices and revenue receipts. Energy Policy 2017, 110, 191–201. [Google Scholar] [CrossRef]
- Percebois, J.; Pommeret, S. Cross-subsidies Tied to the Introduction of Intermittent Renewable Electricity: An Analysis Based on a Model of the French Day-Ahead Market. Energy J. 2018, 39, 245–267. [Google Scholar] [CrossRef]
- Moutinho, V.F.; Moreira, A.C.; Bento, J.P.C. Strategic decisions on bilateral bidding behavior: Evidence from a wholesale electricity market. Empir. Econ. 2018, 54, 1353–1387. [Google Scholar] [CrossRef]
- Sheikhahmadi, P.; Bahramara, S.; Moshtagh, J.; Damavandi, M.Y. A risk-based approach for modeling the strategic behavior of a distribution company in wholesale energy market. Appl. Energy 2018, 214, 24–38. [Google Scholar] [CrossRef]
- Moutinho, V.; Moreira, A.C.; Mota, J. Do regulatory mechanisms promote competition and mitigate market power? Evidence from Spanish electricity market. Energy Policy 2014, 68, 403–412. [Google Scholar] [CrossRef]
- Aliabadi, D.E.; Kaya, M.; Sahin, G. An agent-based simulation of power generation company behavior in electricity markets under different market-clearing mechanisms. Energy Policy 2017, 100, 191–205. [Google Scholar] [CrossRef]
- Farashbashi-Astaneh, S.M.; Hu, W.; Chen, Z. Comparative study between two market clearing schemes in wind dominant electricity markets. IET Gener. Transm. Distrib. 2015, 9, 2215–2223. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, M.H.; Sheppard, J.W.; Kelly, N.C. Agent-Based Modeling in Electrical Energy Markets Using Dynamic Bayesian Networks. IEEE Trans. Power Syst. 2016, 31, 4744–4754. [Google Scholar] [CrossRef]
- Cramton, P. Electricity market design: The good, the bad, and the ugly. In Proceedings of the 36th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 6–9 January 2003. [Google Scholar]
- Hogan, W.W. On an “Energy Only” Electricity Market Design for Resource Adequacy; Working Paper; Harvard Kennedy School: Cambridge, MA, USA, 2005. [Google Scholar]
- Biskas, P.N.; Chatzigiannis, D.I.; Bakirtzis, A.G. European electricity market integration with mixed market designs—Part I: Formulation. IEEE Trans. Power Syst. 2014, 29, 458–465. [Google Scholar] [CrossRef]
- Martínez-Budría, E.; Jara-Díaz, S.; Ramos-Real, F.J. Adapting productivity theory to the quadratic cost function. An application to the Spanish electric sector. J. Product. Anal. 2003, 20, 213–229. [Google Scholar] [CrossRef]
- Tishler, A. Optimal production with uncertain interruptions in the supply of electricity: Estimation of electricity outage costs. Eur. Econ. Rev. 1993, 37, 1259–1274. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Xydas, E.; Qadrdan, M.; Marmaras, C.; Cipcigan, L.; Jenkins, N.; Ameli, H. Probabilistic wind power forecasting and its application in the scheduling of gas-fired generators. Appl. Energy 2017, 192, 382–394. [Google Scholar] [CrossRef] [Green Version]
- IEM. The Iowa Environmental Mesonet (IEM). Connecticut ASOS. Available online: https://mesonet.agron.iastate.edu/request/download.phtml?network=CT_ASOS (accessed on 10 May 2018).
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, J.; Li, C.; Fu, W.; Peng, T. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 143, 360–376. [Google Scholar] [CrossRef]
- Sun, J.; Tesfatsion, L. DC Optimal Power Flow Formulation and Solution Using QuadProgJ.; Working Paper No. 06014; Iowa State University: Ames, IO, USA, 2010. [Google Scholar]
- Martín, S.; Smeers, Y.; Aguado, J.A. A stochastic two settlement equilibrium model for electricity markets with wind generation. IEEE Trans. Power Syst. 2015, 30, 233–245. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, C.; Ding, Y.; Xydis, G.; Wang, J.; Østergaard, J. Review of real-time electricity markets for integrating distributed energy resources and demand response. Appl. Energy 2015, 138, 695–706. [Google Scholar] [CrossRef]
- Zheng, T.; Litvinov, E. On ex post pricing in the real-time electricity market. IEEE Trans. Power Syst. 2011, 26, 153–164. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D. Learning in games. Eur. Econ. Rev. 1998, 42, 631–639. [Google Scholar] [CrossRef]
- Erev, I.; Barron, G. On adaptation, maximization, and reinforcement learning among cognitive strategies. Psychol. Rev. 2005, 112, 912. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Tesfatsion, L. The AMES wholesale power market test bed: A computational laboratory for research, teaching, and training. In Proceedings of the PES’09 IEEE Power & Energy Society General Meeting, Calgary, AL, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Insider Co2 European Emission Allowance. Available online: https://markets.businessinsider.com/commodities/co2-emissionsrechte (accessed on 10 May 2018).
- Caramanis, M.C.; Bohn, R.E.; Schweppe, F.C. Optimal spot pricing: Practice and theory. IEEE Trans. Power Appar. Syst. 1982, 9, 3234–3245. [Google Scholar] [CrossRef]
- Frondel, M.; Ritter, N.; Schmidt, C.M.; Vance, C. Economic impacts from the promotion of renewable energy technologies: The German experience. Energy Policy 2010, 38, 4048–4056. [Google Scholar] [CrossRef] [Green Version]








| Minimum Capacity (MW) | Maximum Capacity (MW) | ||
|---|---|---|---|
| 14.00 | −0.02 | 0 | 100 |
| Fixed Cost | Ap | Bp | 1 | 1 | Initial Money 2 | AQ | BQ | 3 | Cv | Dv | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| GenCo1 | 0 | - | - | 0 | 100 | 1,000,000 | - | - | 2 | 14 | −0.02 |
| GenCo2 | 0 | - | - | 0 | 100 | 1,000,000 | - | - | 4 | 14 | −0.02 |
| GenCo3 | 0 | 25 | 0.010 | 0 | 520 | 1,000,000 | 2.5 | 0.0010 | - | - | - |
| GenCo4 | 0 | 30 | 0.012 | 0 | 200 | 1,000,000 | 3.0 | 0.0012 | - | - | - |
| GenCo5 | 0 | 10 | 0.007 | 0 | 400 | 1,000,000 | 1.0 | 0.0007 | - | - | - |
| GenCo6 | 0 | 10 | 0.007 | 0 | 200 | 1,000,000 | 1.0 | 0.0007 | - | - | - |
| From Node | To Node | 1 | Bkm 2 | |
|---|---|---|---|---|
| Branch1 | 1 | 2 | 250 | 0.0281 |
| Branch2 | 1 | 4 | 150 | 0.0304 |
| Branch3 | 1 | 5 | 400 | 0.0064 |
| Branch4 | 2 | 3 | 350 | 0.0108 |
| Branch5 | 3 | 4 | 240 | 0.0297 |
| Branch6 | 4 | 5 | 240 | 0.0297 |
| Scenario 1: No Learning and Strategic Behavior | ||
| Representative Test Case | Reserve Level 1 | Reliability Cost Level |
| All GenCos bid by true parameters and VREs spend High reliability cost | 0~200 | = 1 (High reliability) |
| All GenCos bid by true parameters and VREs spend Medium High reliability cost | 0~200 | = 2 (Medium High reliability) |
| All GenCos bid by true parameters and VREs spend Medium Low reliability cost | 0~200 | = 3 (Medium Low reliability) |
| All GenCos bid by true parameters and VREs spend Low reliability cost | 0~200 | = 4 (Low reliability) |
| Scenario 2: With Learning and Strategic Behavior | ||
| Representative Test Case | Reserve Level | Reliability Cost Level |
| All GenCos bid by learning and VREs adopt best reliability cost by learning | 0~200 | VREs adopt best reliability strategy by learning |
| Energy | Discount Rate | |||
|---|---|---|---|---|
| 3% | 7% | 10% | ||
| United States | Onshore wind | 32.71 * | 42.85 | 51.64 |
| Onshore wind | 39.60 | 52.23 | 63.20 | |
| Onshore wind | 49.46 | 65.32 | 79.08 | |
| Offshore wind—shallow | 102.95 | 137.19 | 166.87 | |
| Offshore wind—medium | 102.34 | 137.37 | 167.73 | |
| Offshore wind—deep | 155.58 | 154.58 | 188.38 | |
| PV—large, ground-mounted | 53.50 | 79.84 | 102.56 | |
| Supercritical pulverized coal | 82.64 | 93.79 | 104.00 | |
| CCGT 1 | 60.84 | 65.95 | 70.62 | |
| ALWR 2 | 54.34 | 77.71 | 101.76 | |
| China | Onshore wind | 45.96 | 59.92 | 71.91 |
| Onshore wind | 52.00 | 68.28 | 82.27 | |
| PV – large, ground-mounted | 54.84 | 72.64 | 87.98 | |
| Ultra-supercritical coal | 73.61 | 77.72 | 81.57 | |
| CCGT | 90.17 | 92.79 | 95.13 | |
| ALWR | 30.77 | 47.61 | 64.40 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Liu, Z.; Yu, Z. Exploring the Profitability and Efficiency of Variable Renewable Energy in Spot Electricity Market: Uncovering the Locational Price Disadvantages. Energies 2019, 12, 2820. https://doi.org/10.3390/en12142820
Xu R, Liu Z, Yu Z. Exploring the Profitability and Efficiency of Variable Renewable Energy in Spot Electricity Market: Uncovering the Locational Price Disadvantages. Energies. 2019; 12(14):2820. https://doi.org/10.3390/en12142820
Chicago/Turabian StyleXu, Ruhang, Zhilin Liu, and Zhuangzhuang Yu. 2019. "Exploring the Profitability and Efficiency of Variable Renewable Energy in Spot Electricity Market: Uncovering the Locational Price Disadvantages" Energies 12, no. 14: 2820. https://doi.org/10.3390/en12142820
APA StyleXu, R., Liu, Z., & Yu, Z. (2019). Exploring the Profitability and Efficiency of Variable Renewable Energy in Spot Electricity Market: Uncovering the Locational Price Disadvantages. Energies, 12(14), 2820. https://doi.org/10.3390/en12142820





