Thermodynamic Evaluation of LiCl-H2O and LiBr-H2O Absorption Refrigeration Systems Based on a Novel Model and Algorithm
Abstract
:1. Introduction
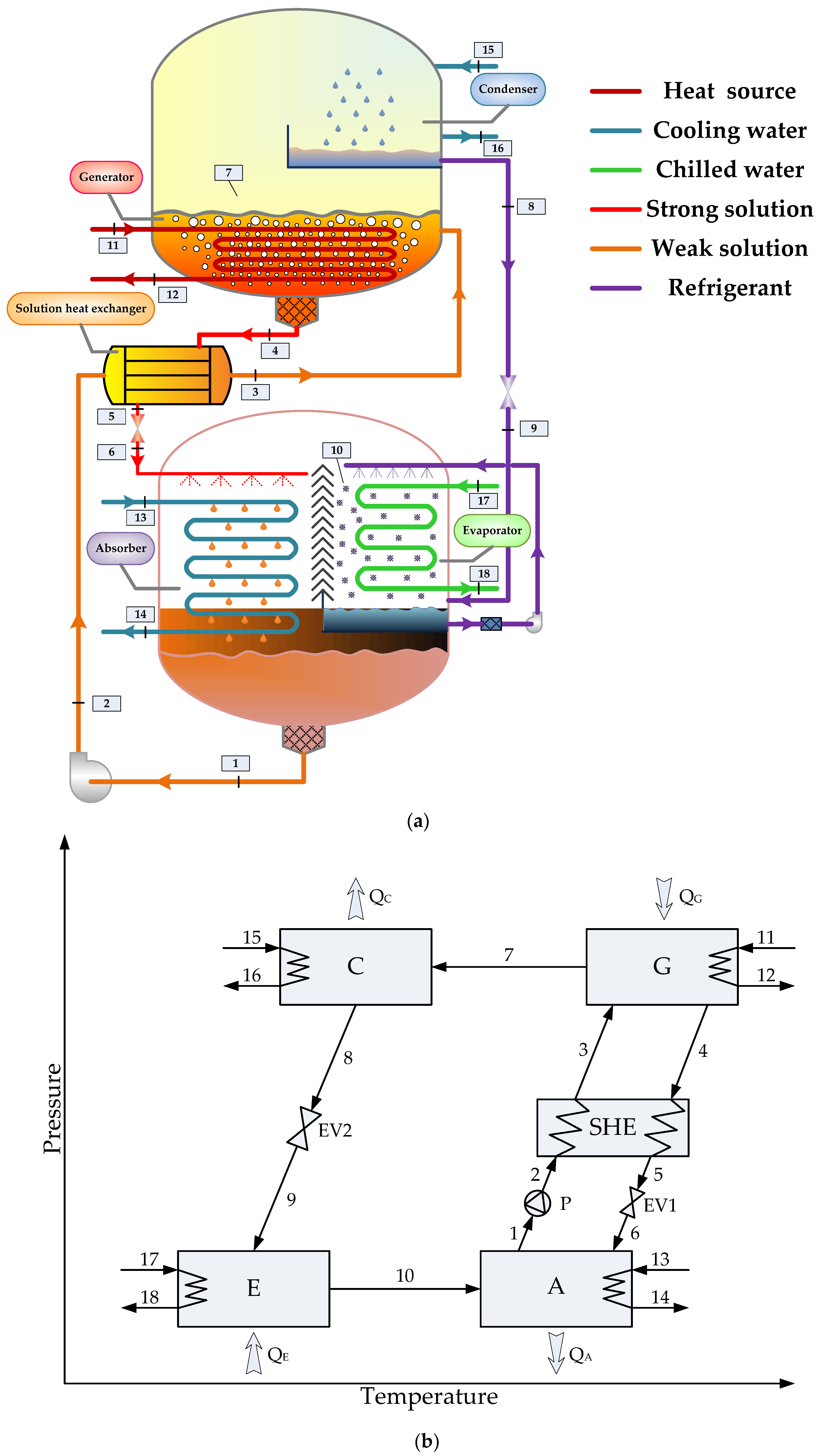
2. System Description
3. Mathematical Modeling
3.1. Model Assumptions
3.2. Thermodynamic Formulations
3.3. Standard Design of Absorption Chiller with LiBr-H2O/LiCl-H2O Working Pair
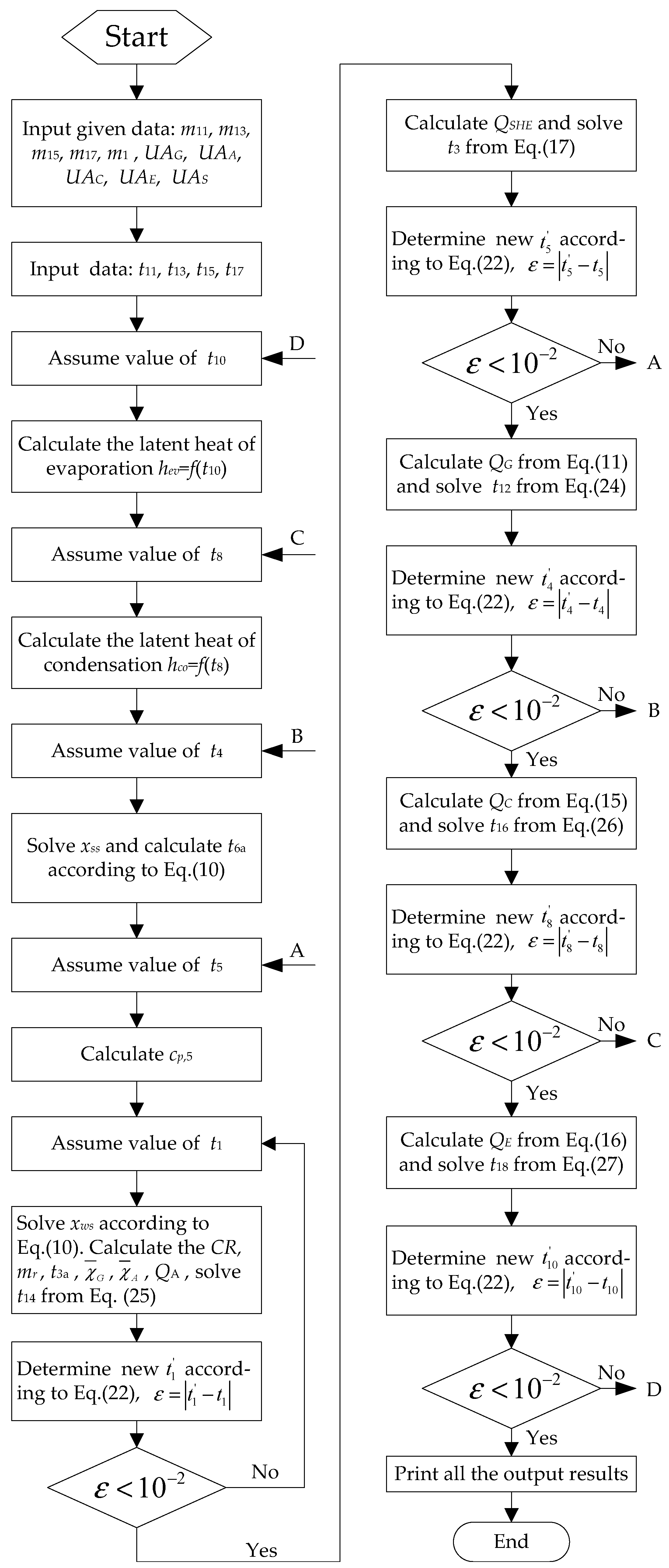
3.4. Calculation Procedure of Absorption Chiller under Design Features
4. Results and Discussion
4.1. Validation of the Model
4.2. Sensitivity Analysis of the Design Parameters
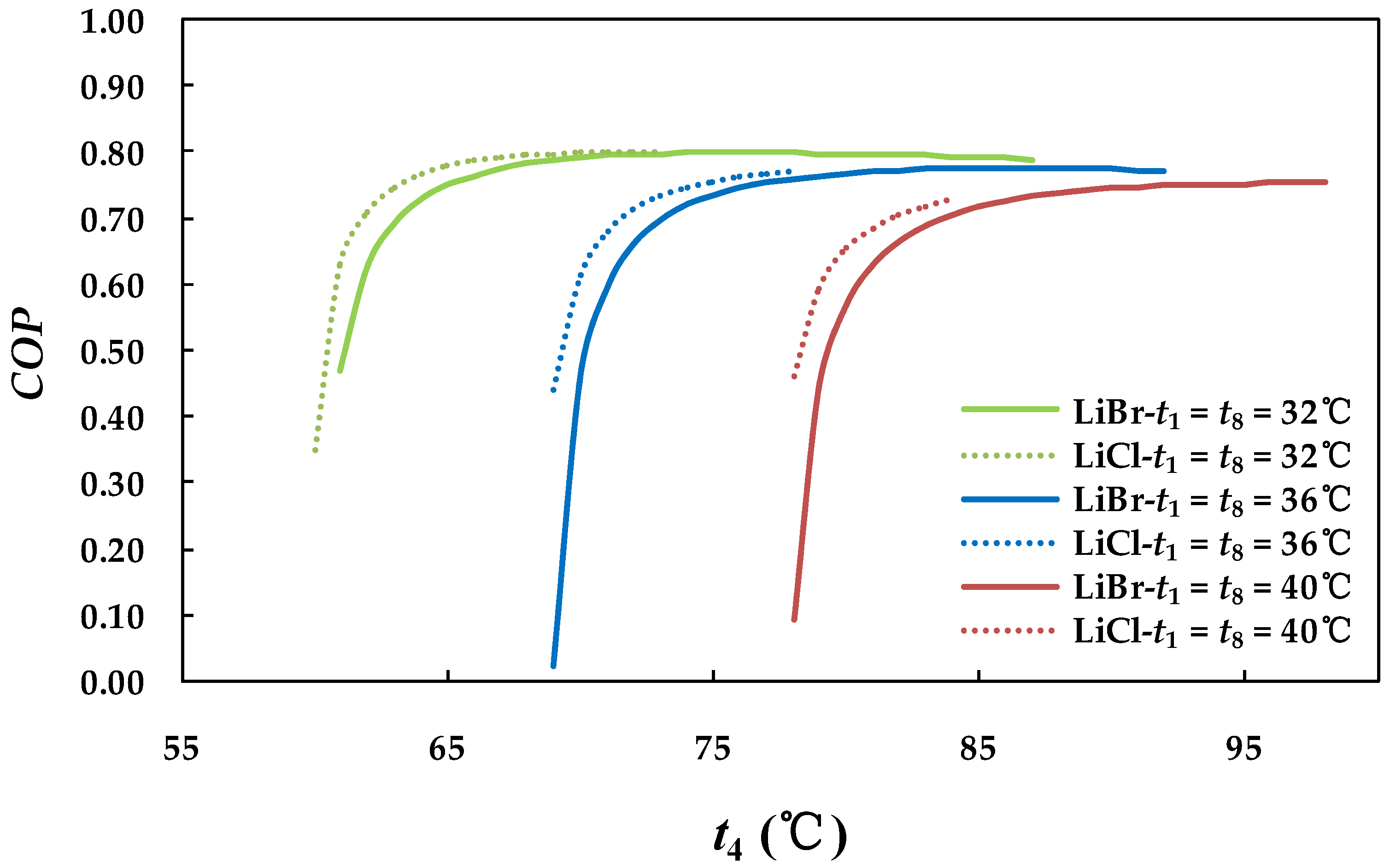
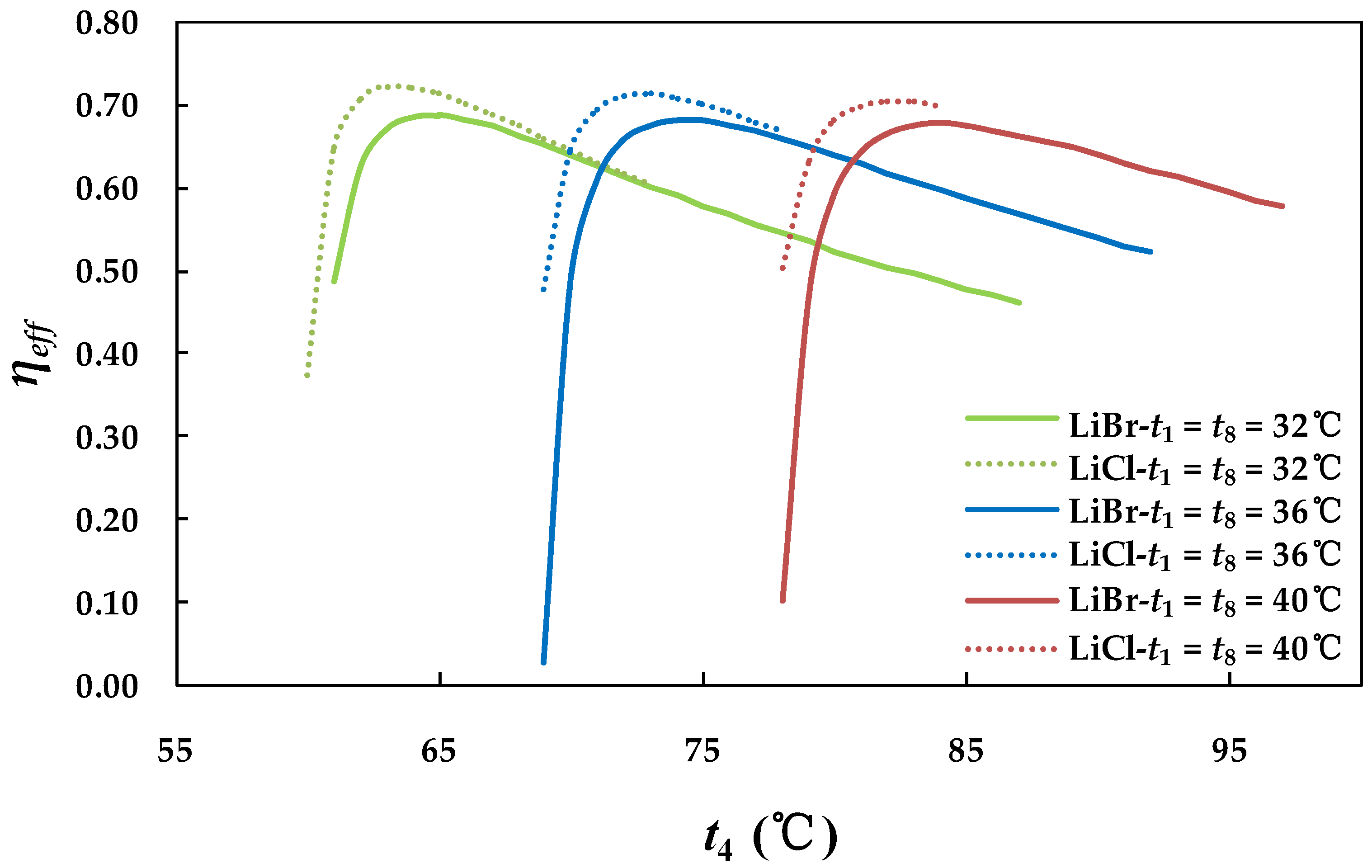
4.2.1. Effect of Generator Temperature on System
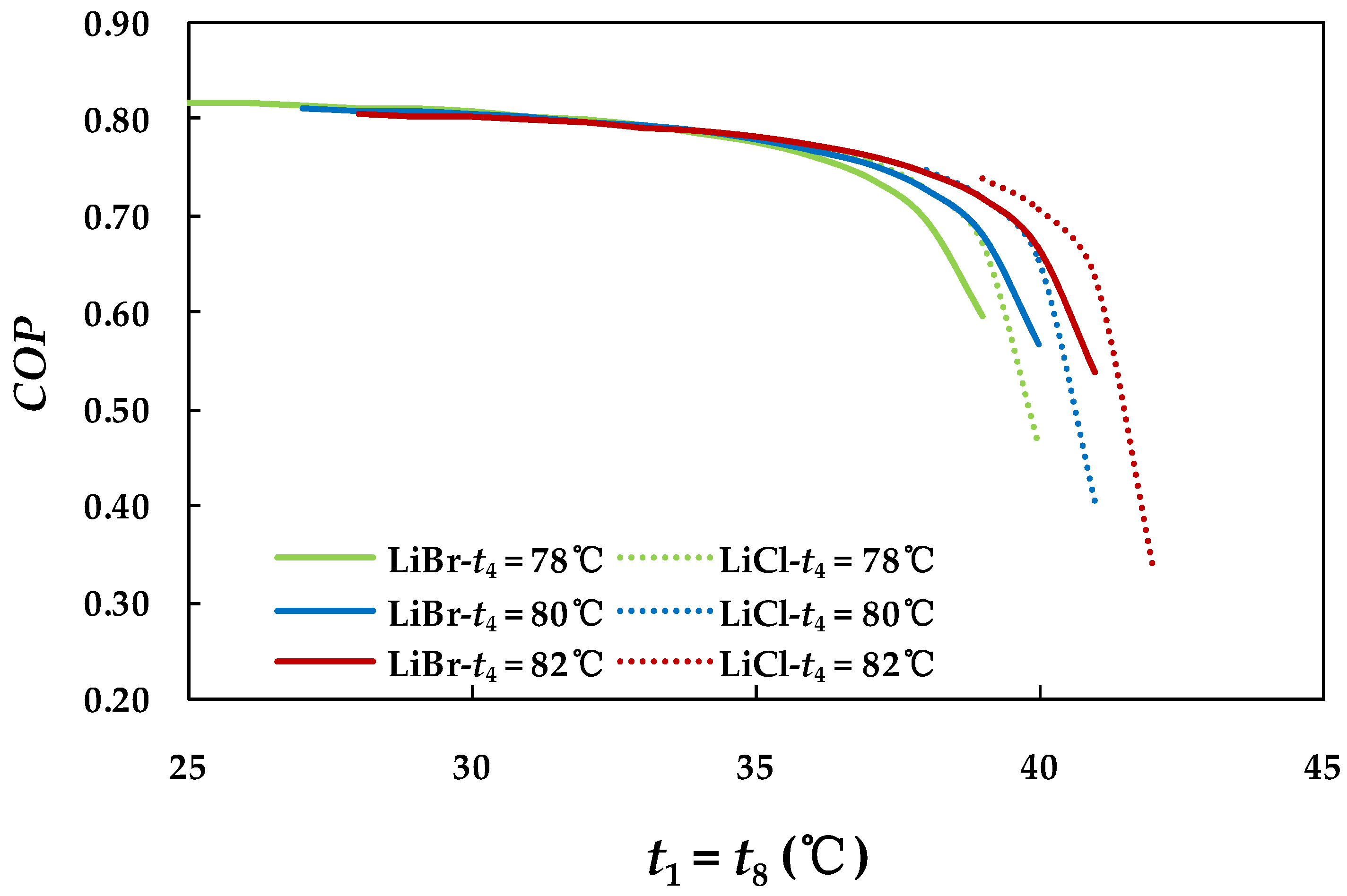
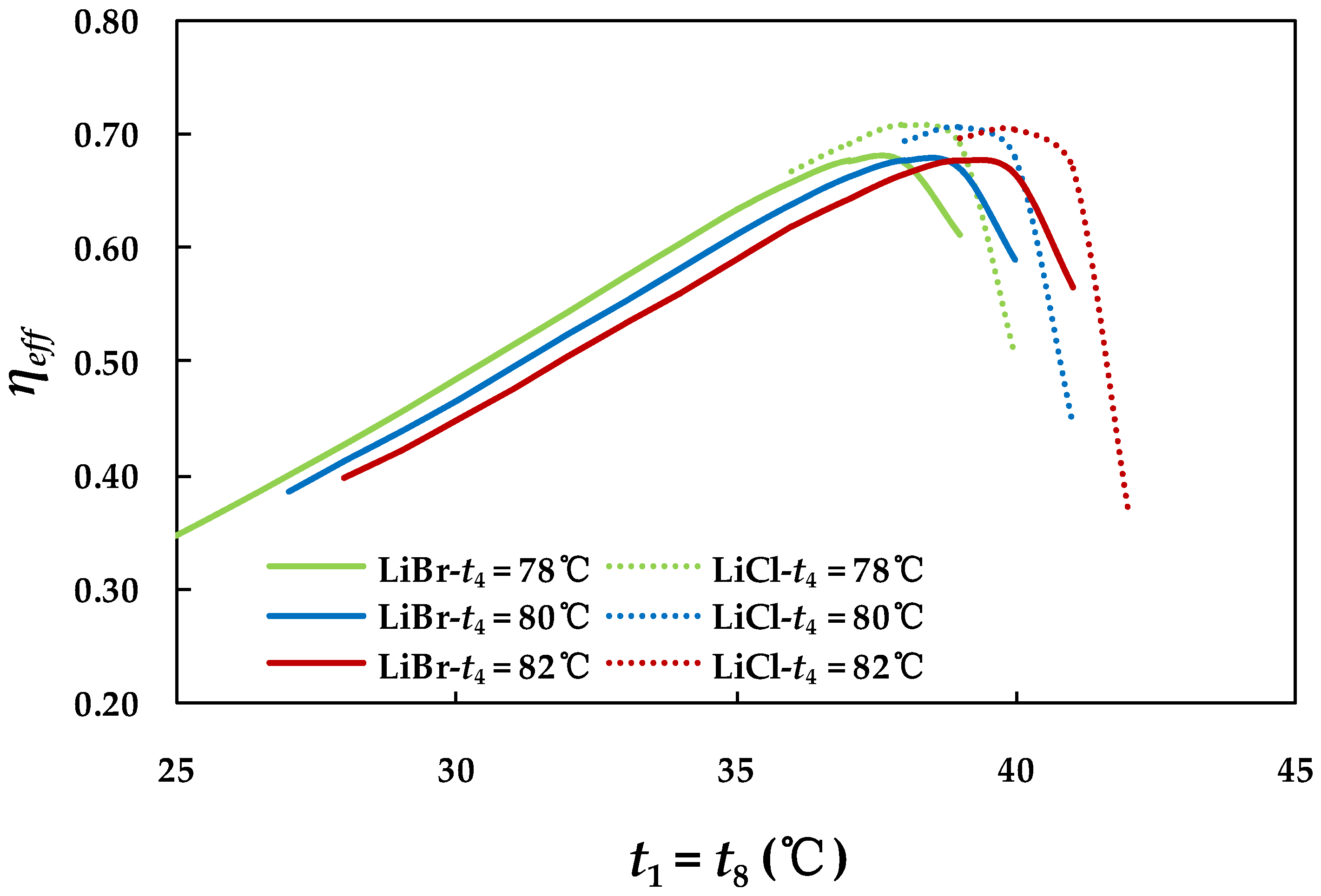
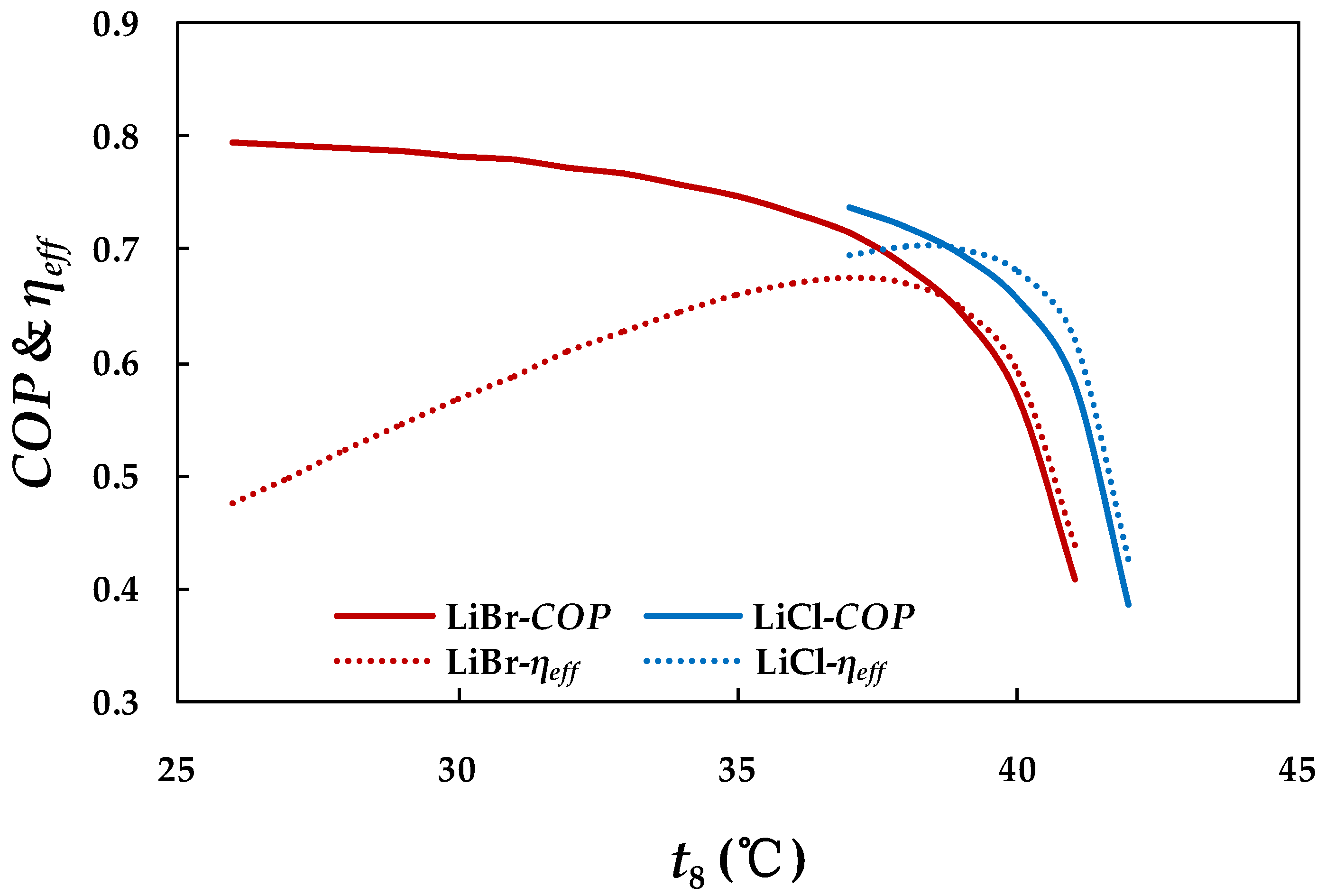
4.2.2. Effect of Absorber and Condenser Temperatures on System
4.2.3. Effect of Absorber and Condenser Temperatures on System
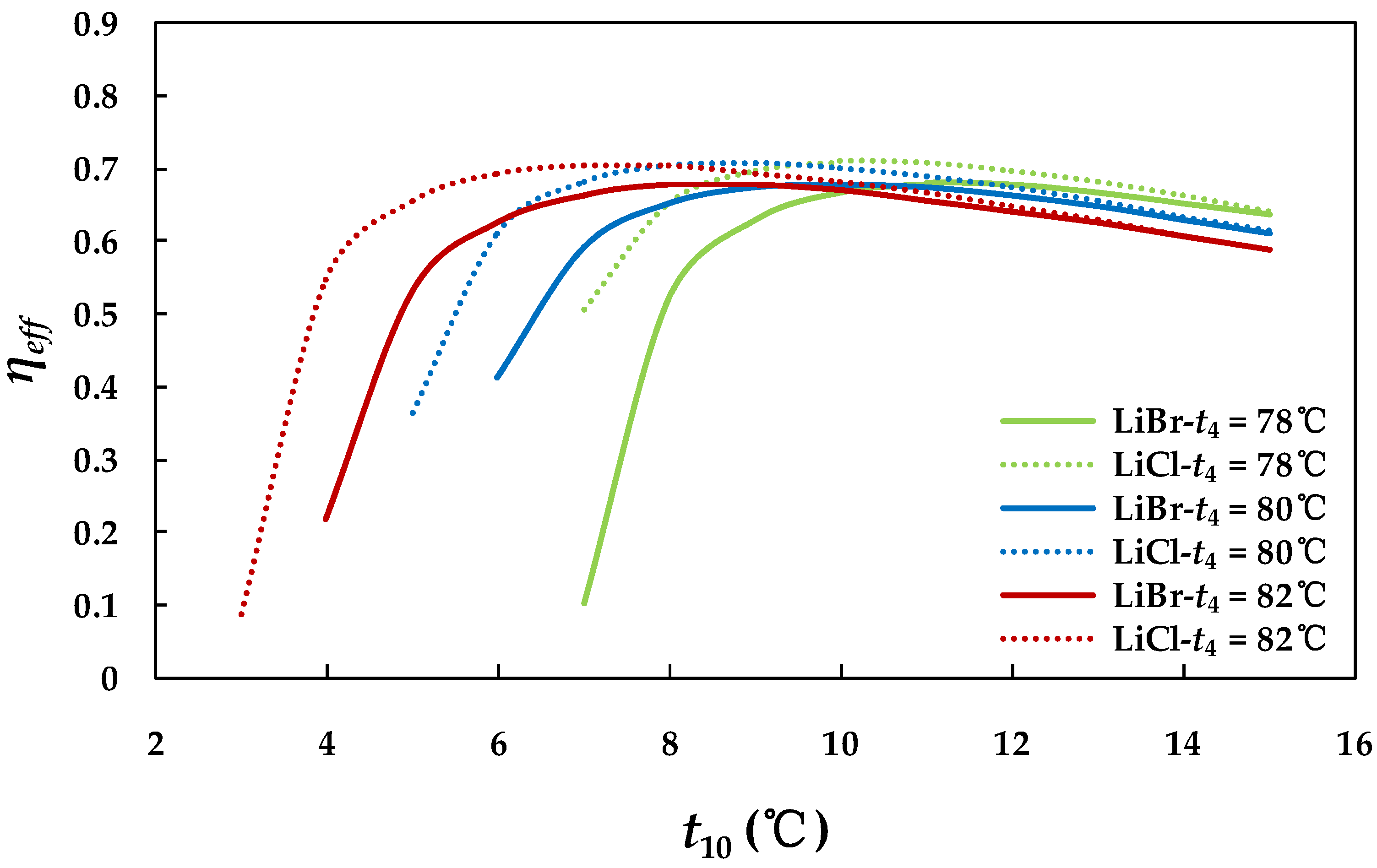
4.2.4. Effect of Evaporator Temperature on System
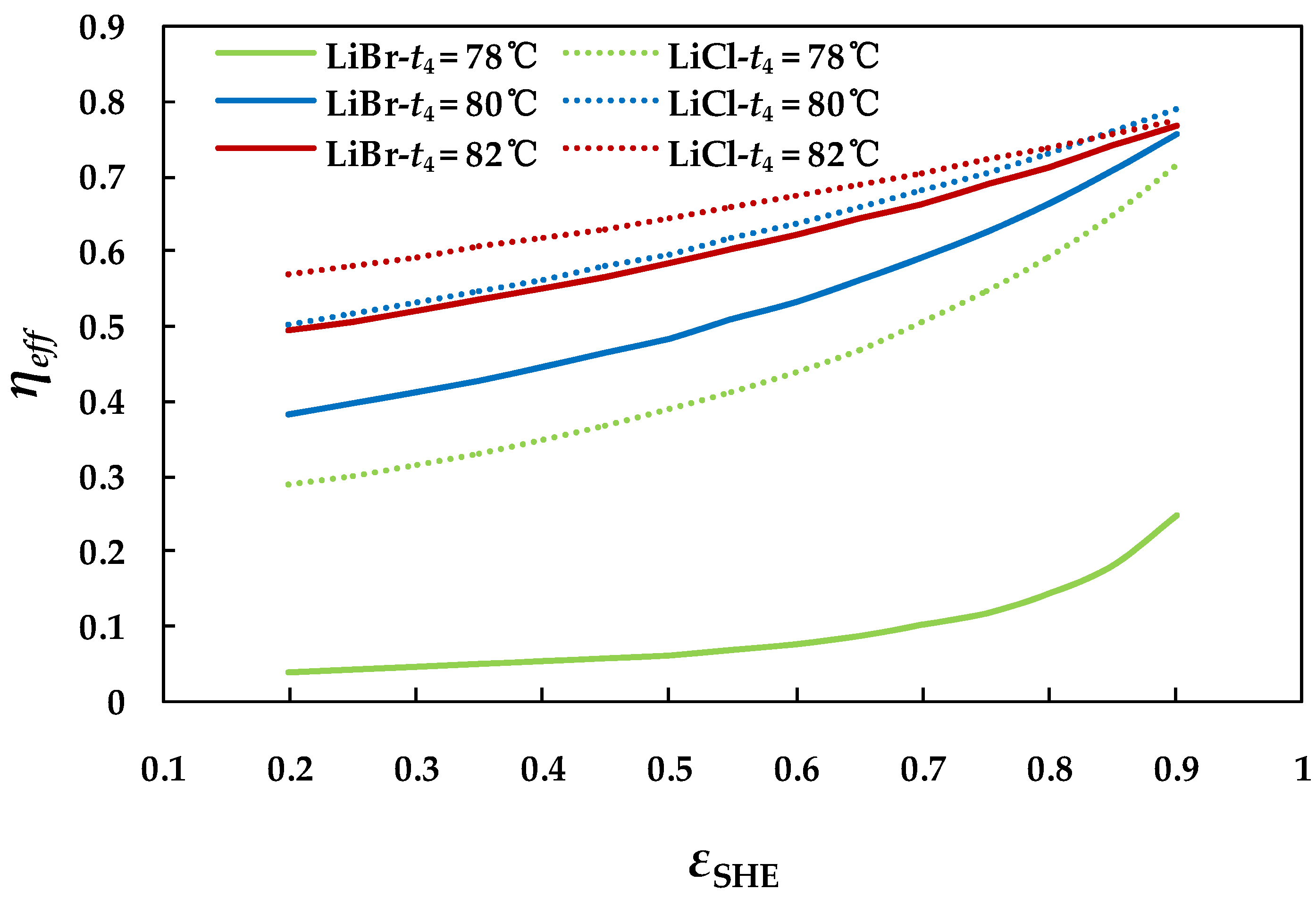
4.2.5. Effect of Effectiveness of Solution Heat Exchanger on System
4.3. Analysis of the Two Absorption Chillers at Off-design Conditions
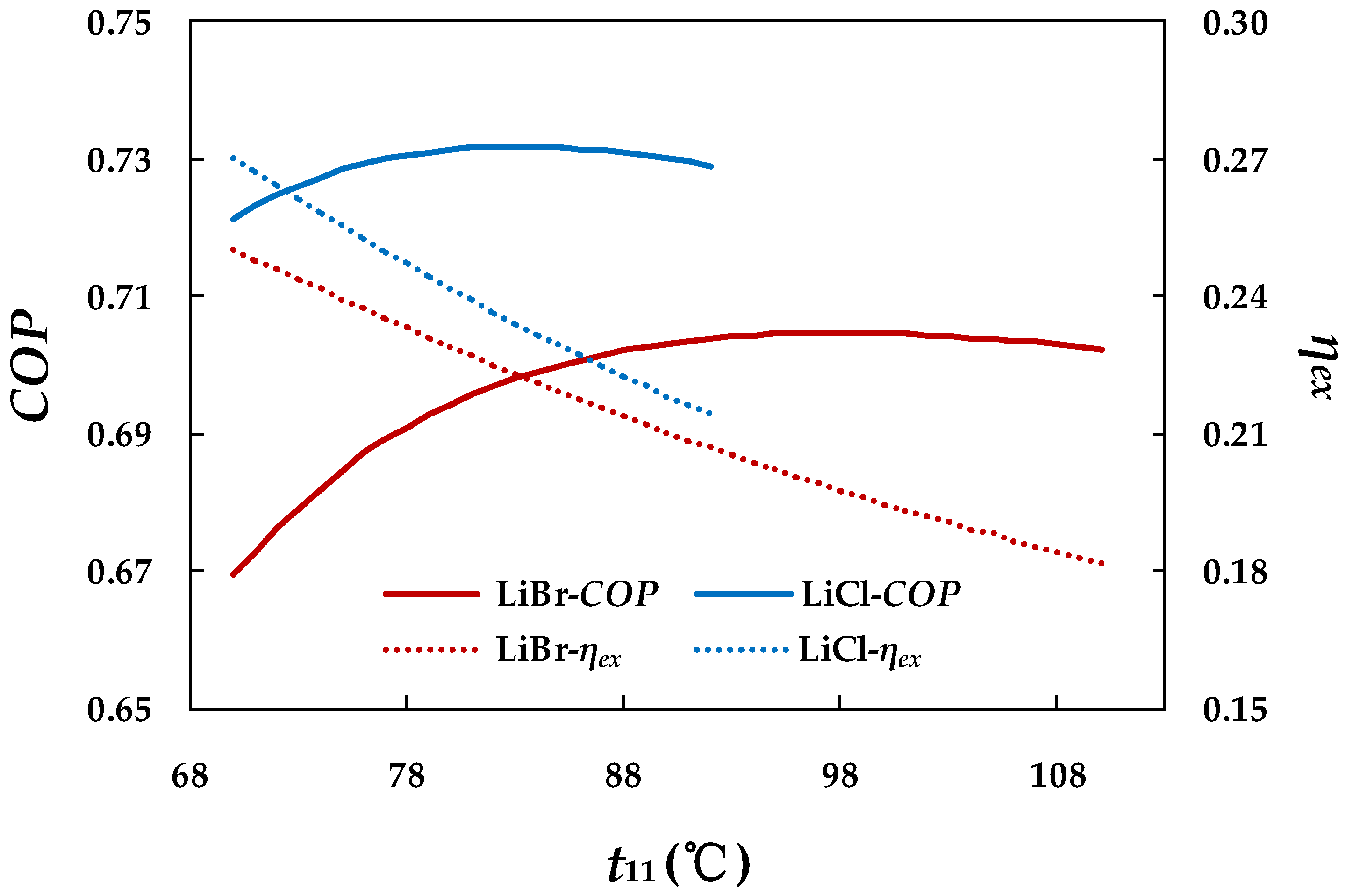
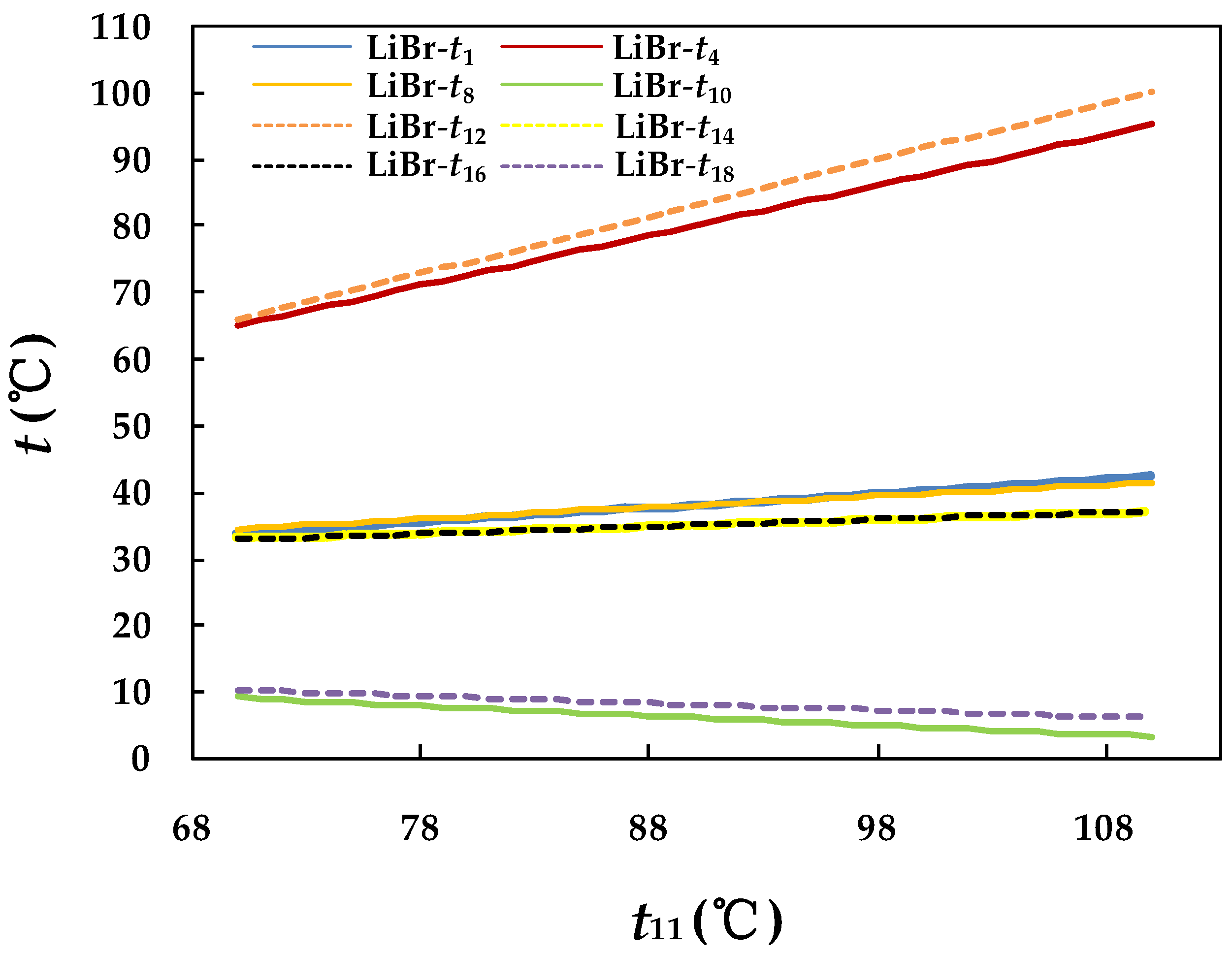
4.3.1. Effect of Hot Water Inlet Temperature in Generator
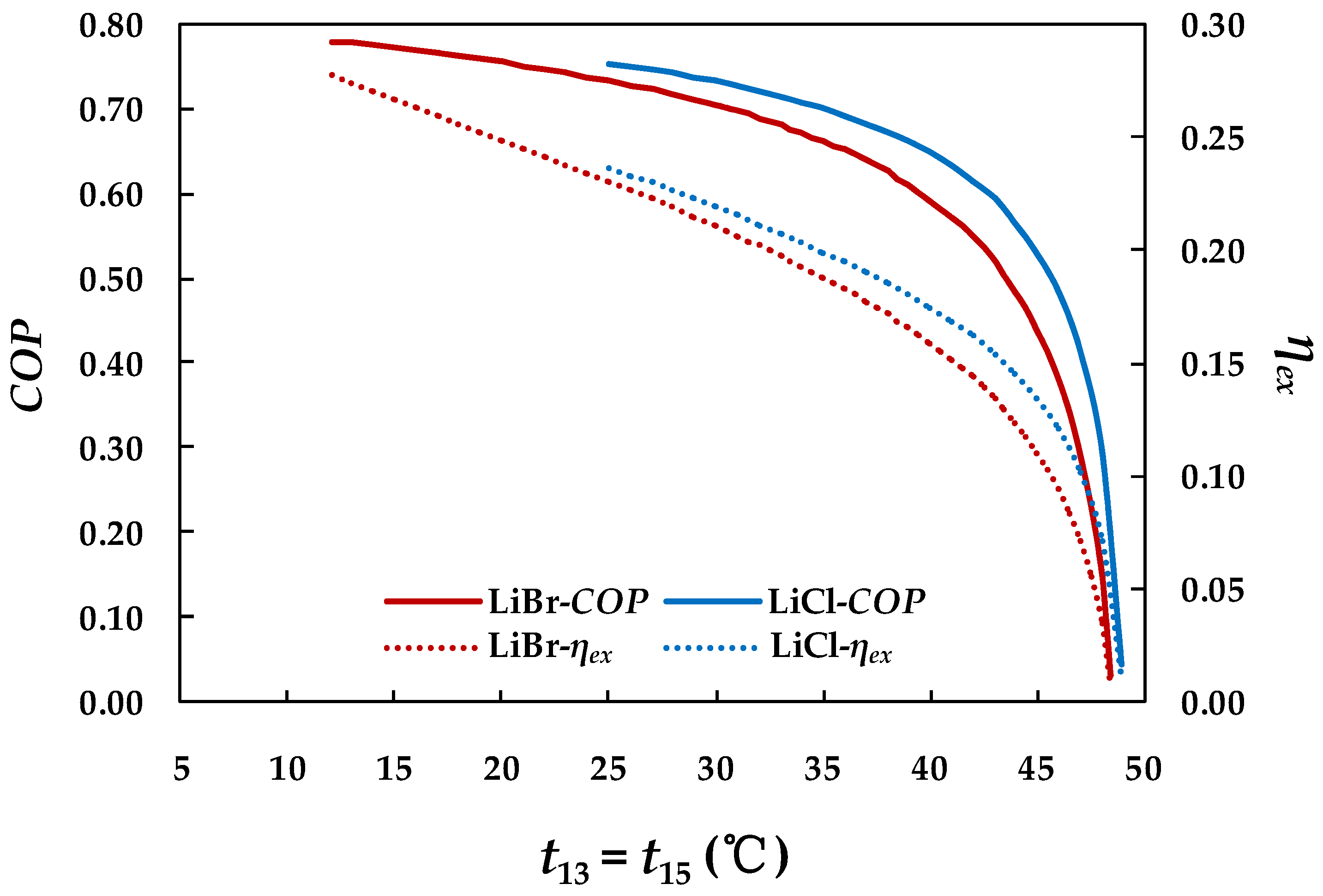
4.3.2. Effect of Cooling Water Inlet Temperature in Absorber and Condenser
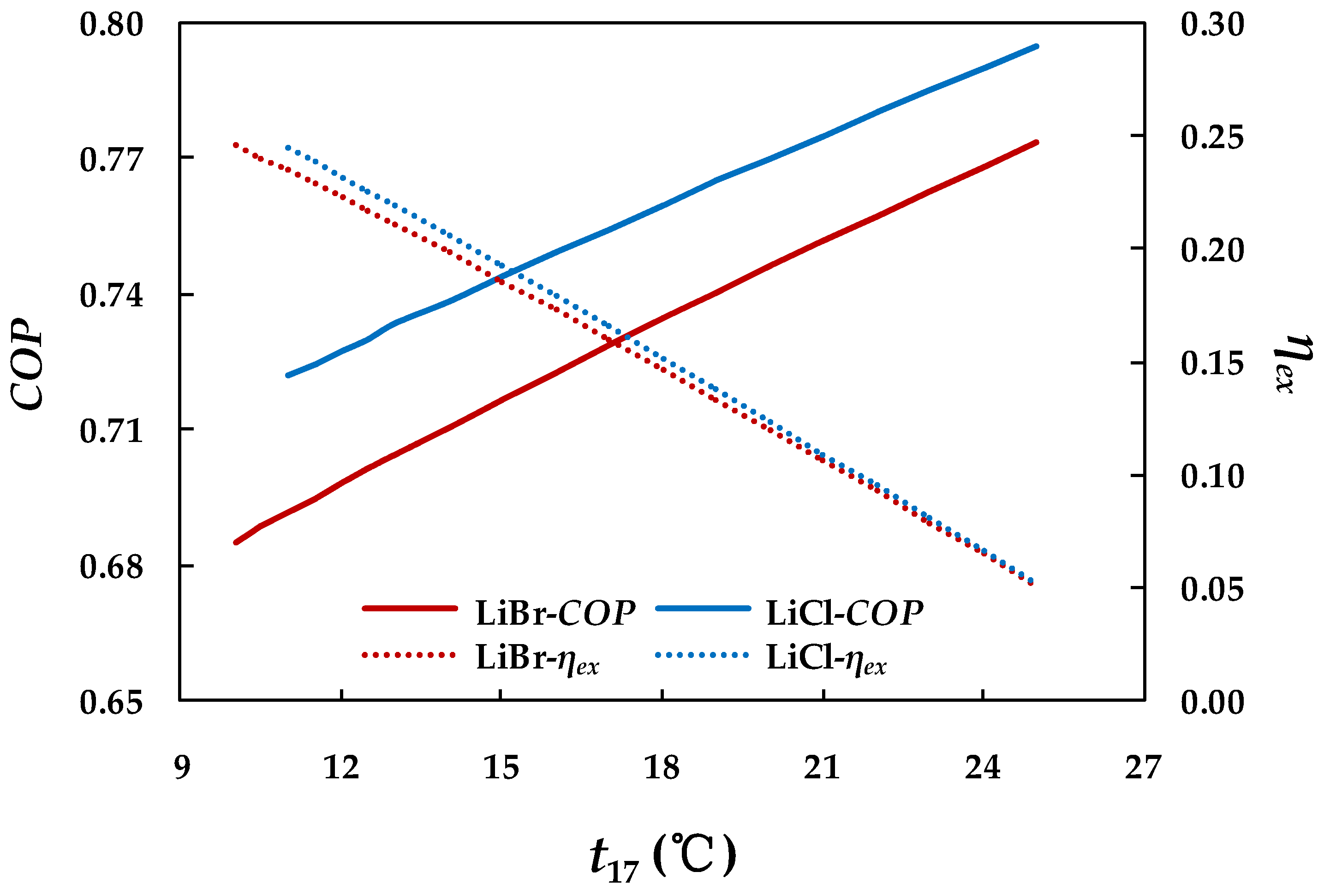
4.3.3. Effect of Chilled Water Inlet Temperature in Evaporator
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Subscripts and Superscripts | ||
| a | Dühring gradient | 0 | reference point |
| a0, a1 | constants | A | absorber |
| b | Dühring intercept | a | equilibrium state |
| b0, b1 | constants | C | condenser |
| cp | specific heat (kJ·kg−1∙K−1) | c | Carnot |
| H | energy flow rate (kW) | co | condensation |
| h | latent heat (kJ·kg−1) | E | evaporator |
| m | mass flow rate (kg·s−1) | eff | efficiency ratio |
| Q | heat load (kW) | ev | evaporation |
| t | temperature (°C) | ex | exergetic |
| W | power (kW) | G | generator |
| x | mass concentration of solution | K | Kelvin temperature scale |
| k | process unit | ||
| i | process stream | ||
| j | system substance (water, LiBr, LiCl) | ||
| Greek Letters | in | inlet | |
| ∆ | refers to the difference between two values | l | liquid |
| η | efficiency | lm | logarithmic mean temperature difference |
| ε | heat exchanger effectiveness | r | refrigerant |
| process quantity | out | outlet | |
| SHE | solution heat exchanger | ||
| s | dew point | ||
| ss | strong solution | ||
| Abbreviations | v | vapor | |
| COP | coefficient of performance | u | external utility (cooling water, chilled water, and hot water) |
| CR | circulation ratio | w | water |
| UA | heat transfer characteristics (kW·K−1) | ws | weak solution |
References
- Ebrahimi, K.; Jones, G.F.; Fleischer, A.S. A review of data center cooling technology, operating conditions and the corresponding low-grade waste heat recovery opportunities. Renew. Sustain. Energy Rev. 2014, 31, 622–638. [Google Scholar] [CrossRef]
- Mbikan, M.; Al-Shemmeri, T. Computational Model of a Biomass Driven Absorption Refrigeration System. Energies 2017, 10, 234. [Google Scholar] [CrossRef]
- Alobaid, M.; Hughes, B.; Calautit, J.K.; O’Connor, D.; Heyes, A. A review of solar driven absorption cooling with photovoltaic thermal systems. Renew. Sustain. Energy Rev. 2017, 76, 728–742. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudi, S.; Kordlar, M.A. A new flexible geothermal based cogeneration system producing power and refrigeration. Renew. Energy 2018, 123, 499–512. [Google Scholar] [CrossRef]
- Srikhirin, P.; Aphornratana, S.; Chungpaibulpatana, S. A review of absorption refrigeration technologies. Renew. Sustain. Energy Rev. 2001, 5, 343–372. [Google Scholar] [CrossRef]
- Sun, J.; Fu, L.; Zhang, S. A review of working fluids of absorption cycles. Renew. Sustain. Energy Rev. 2012, 16, 1899–1906. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Wang, M.; Dai, Y. Thermodynamic analysis and optimization of an ammonia-water power system with LNG (liquefied natural gas) as its heat sink. Energy 2013, 50, 513–522. [Google Scholar] [CrossRef]
- Günhan, T.; Ekren, O.; Demir, V.; Hepbasli, A.; Erek, A.; Şahin, A. Şencan Experimental exergetic performance evaluation of a novel solar assisted LiCl–H2O absorption cooling system. Energy Build. 2014, 68, 138–146. [Google Scholar] [CrossRef]
- Moreno-Quintanar, G.; Rivera, W.; Best, R. Comparison of the experimental evaluation of a solar intermittent refrigeration system for ice production operating with the mixtures NH3/LiNO3 and NH3/LiNO3/H2O. Renew. Energy 2012, 38, 62–68. [Google Scholar] [CrossRef]
- Cai, D.H.; Jiang, J.K.; He, G.G.; Li, K.Q.; Niu, L.J.; Xiao, R.X. Experimental evaluation on thermal performance of an air-cooled absorption refrigeration cycle with NH3-LiNO3 and NH3-NaSCN refrigerant solutions. Energy Conv. Manag. 2016, 120, 32–43. [Google Scholar] [CrossRef]
- Asfand, F.; Stiriba, Y.; Bourouis, M. Performance evaluation of membrane-based absorbers employing H2O/(LiBr + LiI + LiNO3 + LiCl) and H2O/(LiNO3+KNO3+NaNO3) as working pairs in absorption cooling systems. Energy 2016, 115, 781–790. [Google Scholar] [CrossRef]
- Alvarez, M.E.; Esteve, X.; Bourouis, M. Performance analysis of a triple-effect absorption cooling cycle using aqueous (lithium, potassium, sodium) nitrate solution as a working pair. Appl. Therm. Eng. 2015, 79, 27–36. [Google Scholar] [CrossRef]
- Gommed, K.; Grossman, G.; Ziegler, F. Experimental Investigation of a LiCl-Water Open Absorption System for Cooling and Dehumidification. J. Sol. Energy Eng. 2004, 126, 710–715. [Google Scholar] [CrossRef]
- Conde, M.R. Properties of aqueous solutions of lithium and calcium chlorides: Formulations for use in air conditioning equipment design. Int. J. Therm. Sci. 2004, 43, 367–382. [Google Scholar] [CrossRef]
- Kim, D.; Ferreira, C.I. A Gibbs energy equation for LiBr aqueous solutions. Int. J. Refrig. 2006, 29, 36–46. [Google Scholar] [CrossRef]
- Pátek, J.; Klomfar, J. Solid–liquid phase equilibrium in the systems of LiBr–H2O and LiCl–H2O. Fluid Phase Equilibria 2006, 250, 138–149. [Google Scholar] [CrossRef]
- Pátek, J.; Klomfar, J. A computationally effective formulation of the thermodynamic properties of LiBr–H2O solutions from 273 to 500K over full composition range. Int. J. Refrig. 2006, 29, 566–578. [Google Scholar] [CrossRef]
- Pátek, J.; Klomfar, J. Thermodynamic properties of the LiCl–H2O system at vapor–liquid equilibrium from 273 K to 400 K. Int. J. Refrig. 2008, 31, 287–303. [Google Scholar] [CrossRef]
- Parham, K.; Atikol, U.; Yari, M.; Agboola, O.P. Evaluation and optimization of single stage absorption chiller using (LiCl+H2O) as the working pair. Adv. Mech. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Patel, J.; Pandya, B.; Mudgal, A. Exergy Based Analysis of LiCl-H2O Absorption Cooling System. Energy Procedia 2017, 109, 261–269. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A. Exergetic and energetic comparison of LiCl-H2O and LiBr-H2O working pairs in a solar absorption cooling system. Energy Convers. Manag. 2016, 123, 453–461. [Google Scholar] [CrossRef]
- Gogoi, T.; Konwar, D. Exergy analysis of a H2O–LiCl absorption refrigeration system with operating temperatures estimated through inverse analysis. Energy Convers. Manag. 2016, 110, 436–447. [Google Scholar] [CrossRef]
- She, X.H.; Yin, Y.G.; Xu, M.F.; Zhang, X.S. A novel low-grade heat-driven absorption refrigeration system with LiCl-H2O and LiBr-H2O working pairs. Int. J. Refrig. 2015, 58, 219–234. [Google Scholar] [CrossRef]
- Ochoa, A.; Dutra, J.; Henríquez, J.; Dos Santos, C. Dynamic study of a single effect absorption chiller using the pair LiBr/H2O. Energy Convers. Manag. 2016, 108, 30–42. [Google Scholar] [CrossRef]
- Ochoa, A.; Dutra, J.; Henríquez, J.; Dos Santos, C.; Rohatgi, J. The influence of the overall heat transfer coefficients in the dynamic behavior of a single effect absorption chiller using the pair LiBr/H2O. Energy Convers. Manag. 2017, 136, 270–282. [Google Scholar] [CrossRef]
- Marc, O.; Sinama, F.; Praene, J.-P.; Lucas, F.; Castaing-Lasvignottes, J. Dynamic modeling and experimental validation elements of a 30 kW LiBr/H2O single effect absorption chiller for solar application. Appl. Therm. Eng. 2015, 90, 980–993. [Google Scholar] [CrossRef]
- Kohlenbach, P.; Ziegler, F. A dynamic simulation model for transient absorption chiller performance. Part I: The model. Int. J. Refrig. 2008, 31, 217–225. [Google Scholar] [CrossRef]
- Kohlenbach, P.; Ziegler, F. A dynamic simulation model for transient absorption chiller performance. Part II: Numerical results and experimental verification. Int. J. Refrig. 2008, 31, 226–233. [Google Scholar] [CrossRef]
- Hellmann, H.M.; Schweigler, C.; Ziegler, F. A Simple Method for Modelling the Operating Characteristics of Absorption Chillers. In Proceedings of the Thermodynamics Heat and Mass Transfers of Refrigeration Machines and Heat Pumps Seminar Eurotherm No. 59, Nancy, France, 6–7 July 1998; pp. 219–226. [Google Scholar]
- Arnavat, M.P.; López-Villada, J.; Bruno, J.C.; Coronas, A. Analysis and parameter identification for characteristic equations of single- and double-effect absorption chillers by means of multivariable regression. Int. J. Refrig. 2010, 33, 70–78. [Google Scholar] [CrossRef]
- Gutiérrez-Urueta, G.; Rodríguez, P.; Ziegler, F.; Lecuona, A.; Rodríguez-Hidalgo, M. Extension of the characteristic equation to absorption chillers with adiabatic absorbers. Int. J. Refrig. 2012, 35, 709–718. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Ferreira, C.I. Analytic modelling of steady state single-effect absorption cycles. Int. J. Refrig. 2008, 31, 1012–1020. [Google Scholar] [CrossRef]
- Wagner, W.; Cooper, J.R.; Dittmann, A.; Kijima, J.; Kretzschmar, H.J.; Kruse, A.; Mareš, R.; Oguchi, K.; Sato, H.; Stöcker, I.; et al. The IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam. J. Eng. Gas Turbines Power 2000, 122, 150–184. [Google Scholar] [CrossRef]
- Patel, H.A.; Patel, L.; Jani, D.; Christian, A. Energetic Analysis of Single Stage Lithium Bromide Water Absorption Refrigeration System. Procedia Technol. 2016, 23, 488–495. [Google Scholar] [CrossRef] [Green Version]
- Edgar, T.F.; Himmelblau, D.M.; Lasdon, L.S. Optimization of Chemical Processes; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Gebreslassie, B.H.; Groll, E.A.; Garimella, S.V. Multi-objective optimization of sustainable single-effect water/Lithium Bromide absorption cycle. Renew. Energy 2012, 46, 100–110. [Google Scholar] [CrossRef] [Green Version]
- Martínez, J.C.; Martinez, P.; Bujedo, L.A. Development and experimental validation of a simulation model to reproduce the performance of a 17.6 kW LiBr–water absorption chiller. Renew. Energy 2016, 86, 473–482. [Google Scholar] [CrossRef]
- Kerme, E.D.; Chafidz, A.; Agboola, O.P.; Orfi, J.; Fakeeha, A.H.; Al-Fatesh, A.S. Energetic and exergetic analysis of solar-powered lithium bromide-water absorption cooling system. J. Clean. Prod. 2017, 151, 60–73. [Google Scholar] [CrossRef]
- Kaita, Y. Simulation results of triple-effect absorption cycles. Int. J. Refrig. 2002, 25, 999–1007. [Google Scholar] [CrossRef]
- Anand, D.; Kumar, B. Absorption machine irreversibility using new entropy calculations. Sol. Energy 1987, 39, 243–256. [Google Scholar] [CrossRef]
- Kaushik, S.; Arora, A. Energy and exergy analysis of single effect and series flow double effect water–lithium bromide absorption refrigeration systems. Int. J. Refrig. 2009, 32, 1247–1258. [Google Scholar] [CrossRef]








| Component | State Point | Symbol | Value |
|---|---|---|---|
| Generator | Inlet temperature of hot water (°C) | t11 | 90 |
| Outlet temperature of hot water (°C) | t12 = t11 − 7 | 83 | |
| Outlet solution temperature from generator (°C) | t4 = t12 − 3 | 80 | |
| Absorber | Inlet temperature of cooling water (°C) | t13 | 30 |
| Outlet temperature of cooling water (°C) | t14 = t13 + 5 | 35 | |
| Outlet solution temperature from absorber (°C) | t1 = t14 + 3 | 38 | |
| Condenser | Inlet temperature of cooling water (°C) | t15 | 30 |
| Outlet temperature of cooling water (°C) | t16 = t15 + 5 | 35 | |
| Condensation temperature (°C) | t8 = t16 + 3 | 38 | |
| Evaporator | Inlet temperature of chilled water (°C) | t17 | 13 |
| Outlet temperature of chilled water (°C) | t18 = t17 − 5 | 8 | |
| Evaporation temperature (°C) | t10 = t17 − 7 | 6 |
| LiBr-H2O | LiCl-H2O | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Name | Symbol | Anand [40] | Kaushik [41] | Present Work | Difference Percentage (%) with Anand | Difference Percentage (%) with Kaushik | Patel [20] | Present Work | Difference Percentage (%) with Patel |
| Heat capacity of generator (kW) | QG | 3073.11 | 3095.70 | 3074.45 | 0.04 | −0.69 | 4.465 | 4.519 | 1.21 |
| Heat capacity of absorber (kW) | QA | 2922.39 | 2945.27 | 2945.90 | 0.80 | 0.02 | 4.268 | 4.379 | 2.6 |
| Heat capacity of condenser (kW) | QC | 2507.89 | 2505.91 | 2504.22 | −0.15 | −0.07 | 3.705 | 3.691 | −0.38 |
| Heat capacity of evaporator (kW) | QE | 2357.17 | 2355.45 | 2355.93 | −0.05 | 0.02 | 3.517 | 3.505 | −0.34 |
| Coefficient of performance | COP | 0.7670 | 0.7609 | 0.7663 | −0.09 | 0.71 | 0.7877 | 0.7758 | −1.51 |
| Point | LiBr-H2O | LiCl-H2O | ||||
|---|---|---|---|---|---|---|
| t (°C) | m (kg·s−1) | x (%) | t (°C) | m (kg·s−1) | x (%) | |
| 1 | 38.0 | 0.50039 | 55.858 | 38.0 | 0.25584 | 43.874 |
| 2 | 38.0 | 0.50039 | 55.858 | 38.0 | 0.25584 | 43.874 |
| 3 | 65.4 | 0.50039 | 55.858 | 64.6 | 0.25584 | 43.874 |
| 4 | 80.0 | 0.47914 | 58.335 | 80.0 | 0.23459 | 47.849 |
| 5 | 50.6 | 0.47914 | 58.335 | 50.6 | 0.23459 | 47.849 |
| 6 | 50.6 | 0.47914 | 58.335 | 50.6 | 0.23459 | 47.849 |
| 7 | 80.0 | 0.02125 | 0 | 80.0 | 0.02125 | 0 |
| 8 | 38.0 | 0.02125 | 0 | 38.0 | 0.02125 | 0 |
| 9 | 6.0 | 0.02125 | 0 | 6.0 | 0.02125 | 0 |
| 10 | 6.0 | 0.02125 | 0 | 6.0 | 0.02125 | 0 |
| 11 | 90.0 | 2.43054 | 0 | 90.0 | 2.34078 | 0 |
| 12 | 83.0 | 2.43054 | 0 | 83.0 | 2.34078 | 0 |
| 13 | 30.0 | 3.29257 | 0 | 30.0 | 3.17298 | 0 |
| 14 | 35.0 | 3.29257 | 0 | 35.0 | 3.17298 | 0 |
| 15 | 30.0 | 2.53054 | 0 | 30.0 | 2.53054 | 0 |
| 16 | 35.0 | 2.53054 | 0 | 35.0 | 2.53054 | 0 |
| 17 | 13.0 | 2.39232 | 0 | 13.0 | 2.39232 | 0 |
| 18 | 8.0 | 2.39232 | 0 | 8.0 | 2.39232 | 0 |
| Items | LiBr-H2O | LiCl-H2O |
|---|---|---|
| Heat transfer rate of component (kW) | ||
| Generator (QG) | 71.12 | 68.49 |
| Absorber (QA) | 68.81 | 66.32 |
| Condenser (QC) | 52.89 | 52.89 |
| Evaporator (QE) | 50 | 50 |
| Solution heat exchanger (QSHE) | 27.29 | 18.45 |
| COP | 0.703 | 0.730 |
| Heat transfer characteristics (kW·°C−1) | ||
| Generator (UAG) | 5.287 | 4.973 |
| Absorber (UAA) | 6.049 | 5.829 |
| Condenser (UAC) | 10.387 | 10.387 |
| Evaporator (UAE) | 12.566 | 12.566 |
| Solution heat exchanger (UAS) | 2.009 | 1.323 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Qian, Z.; Yao, Z.; Gan, N.; Zhang, Y. Thermodynamic Evaluation of LiCl-H2O and LiBr-H2O Absorption Refrigeration Systems Based on a Novel Model and Algorithm. Energies 2019, 12, 3037. https://doi.org/10.3390/en12153037
Ren J, Qian Z, Yao Z, Gan N, Zhang Y. Thermodynamic Evaluation of LiCl-H2O and LiBr-H2O Absorption Refrigeration Systems Based on a Novel Model and Algorithm. Energies. 2019; 12(15):3037. https://doi.org/10.3390/en12153037
Chicago/Turabian StyleRen, Jie, Zuoqin Qian, Zhimin Yao, Nianzhong Gan, and Yujia Zhang. 2019. "Thermodynamic Evaluation of LiCl-H2O and LiBr-H2O Absorption Refrigeration Systems Based on a Novel Model and Algorithm" Energies 12, no. 15: 3037. https://doi.org/10.3390/en12153037
APA StyleRen, J., Qian, Z., Yao, Z., Gan, N., & Zhang, Y. (2019). Thermodynamic Evaluation of LiCl-H2O and LiBr-H2O Absorption Refrigeration Systems Based on a Novel Model and Algorithm. Energies, 12(15), 3037. https://doi.org/10.3390/en12153037





