Research on Double-Layer Optimal Scheduling Model of Integrated Energy Park Based on Non-Cooperative Game
Abstract
1. Introduction
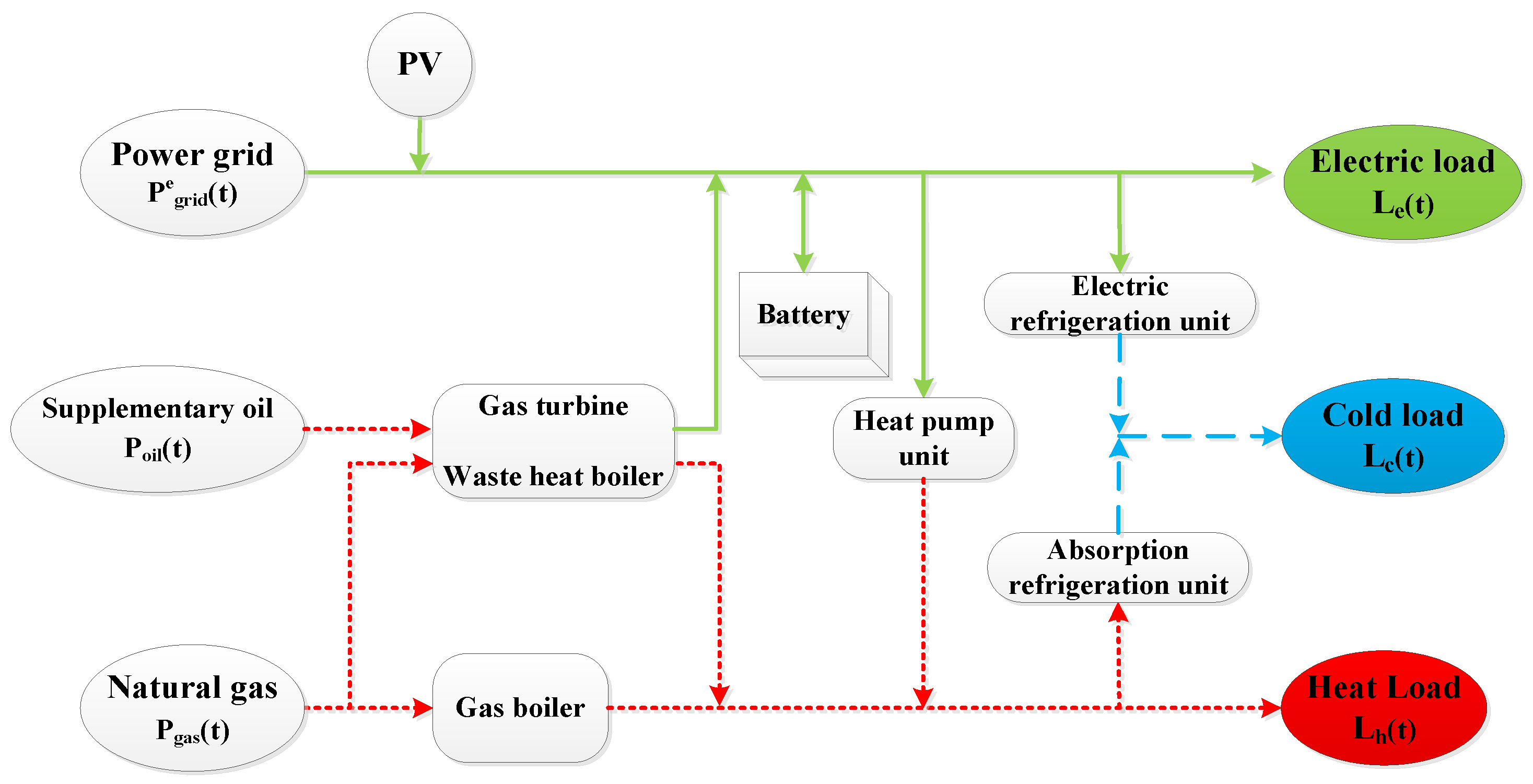
2. Operation Analysis of Integrated Energy Park
2.1. Typical Integrated Energy Park
2.2. Equipment Output Model of Integrated Energy Park
2.3. Daily Cost Model of Park
2.3.1. Daily Operating Cost of the Park
2.3.2. Daily Environmental Value Cost of the Park
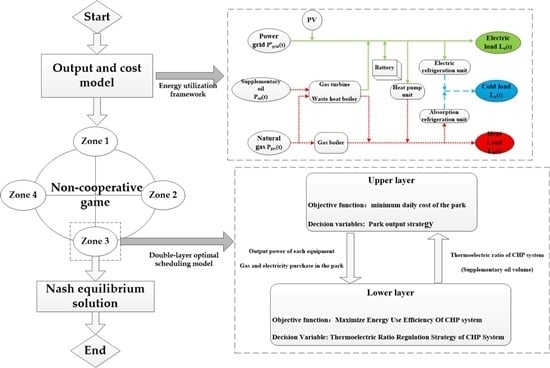
3. Double-Layer Optimal Scheduling Model Based on Non-Cooperative Game
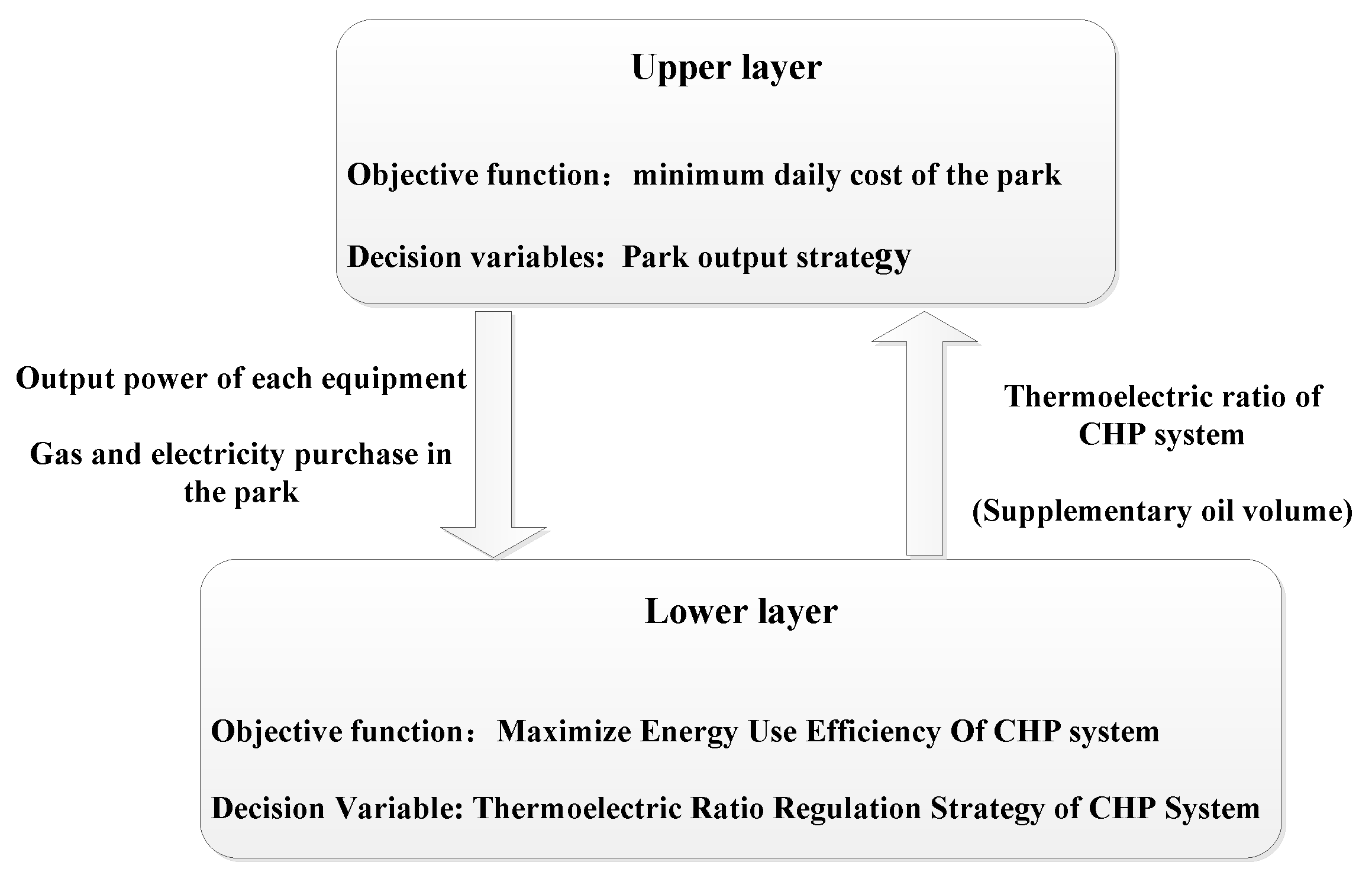
3.1. Upper Layer Model
3.1.1. Objective Function
3.1.2. Constraint Condition
3.2. Lower Layer Model
3.2.1. Objective Function
3.2.2. Constraint Condition
3.3. Non-Cooperative Game
4. Solution of the Model
- Set the initial value of the operation strategies of N zones (sn(t)) and set the precision (ε).
- For the nth zone, the operation strategies of the remaining N − 1 zones (S−n(t)) are regarded as fixed values, the optimal solution of output strategy (bn(t)) and daily cost of the zone (cn) are obtained by calculating formula (20).
- The optimal solution of the output strategy is input to the lower layer, the optimal solution of the thermoelectric ratio regulation strategy () is obtained by calculating formula (28).
- The upper objective function is recalculated according to , and the new optimal solution of the output strategy (bn*(t)) and the daily cost of the zone (cn*) are obtained.
- When , the currently operation strategy is the optimal strategy for the zone, otherwise repeat step 3.
- Repeat steps 2–5 to find the optimal operation strategies of the remaining N − 1 zones.
- Repeat steps 2–6 until the optimal operation strategies of N zones do not change, and then the operation strategy of each zone under Nash equilibrium solution is obtained.
5. Analysis of Examples
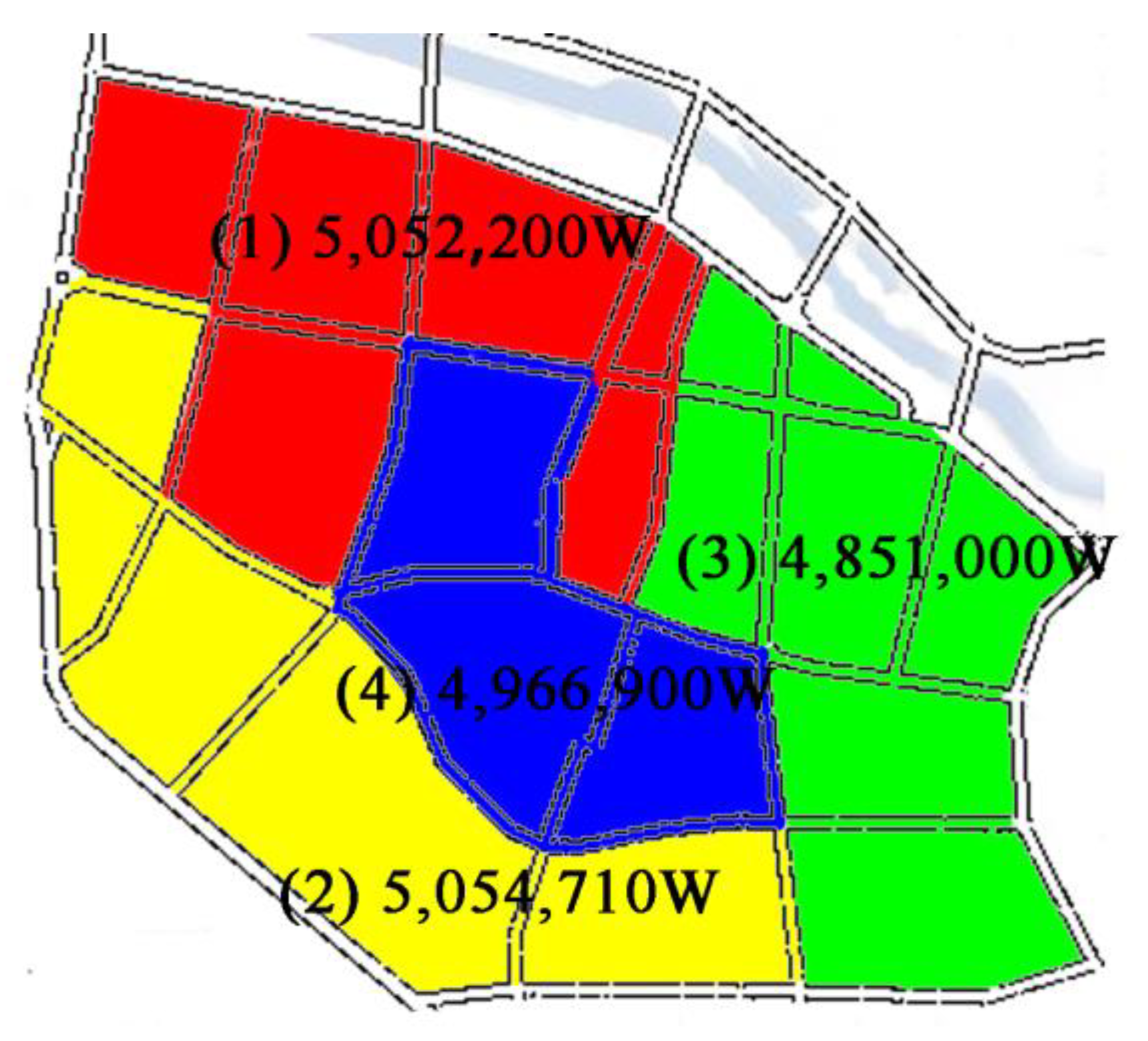
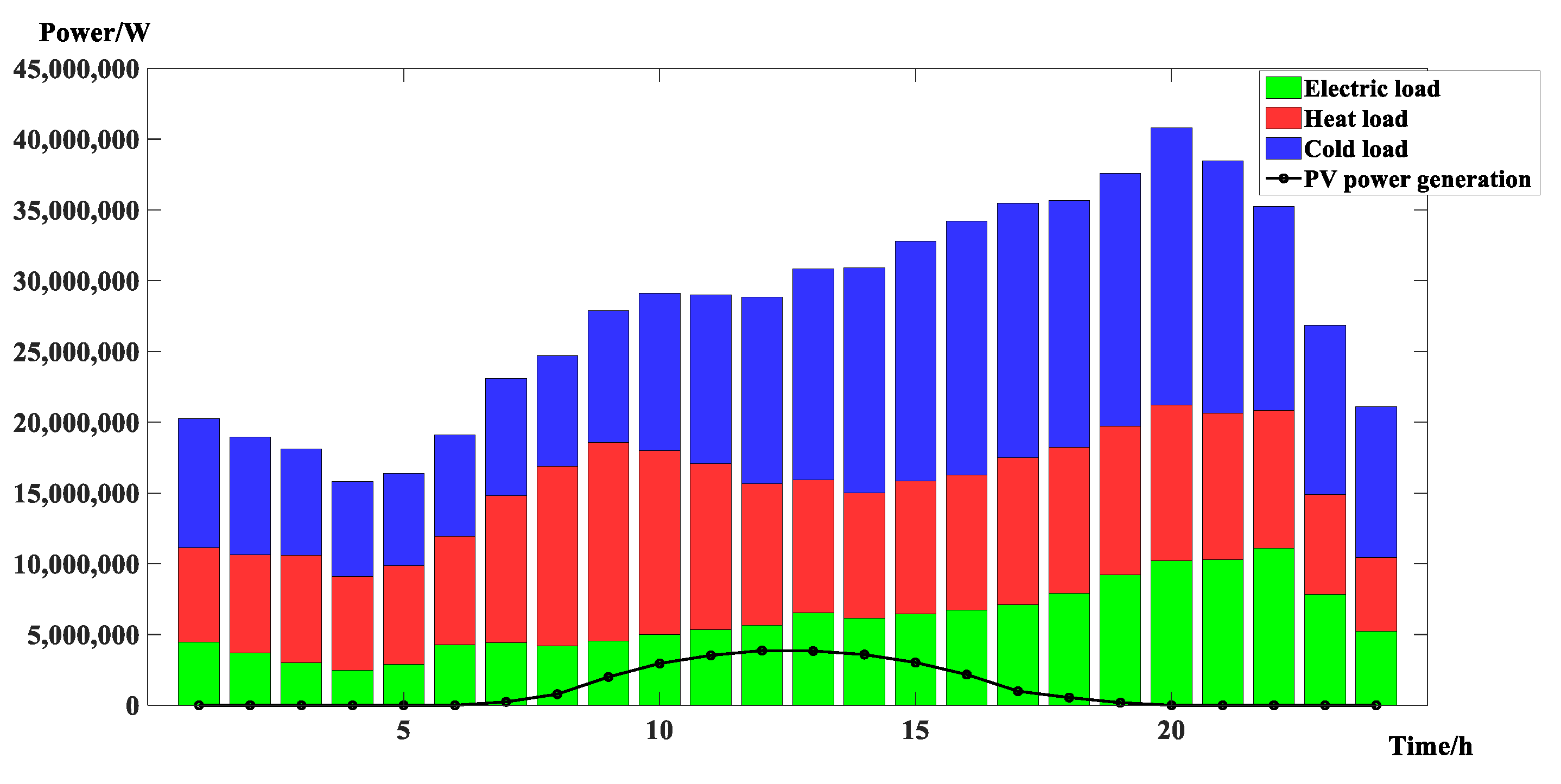
5.1. Basic Data and Assumptions
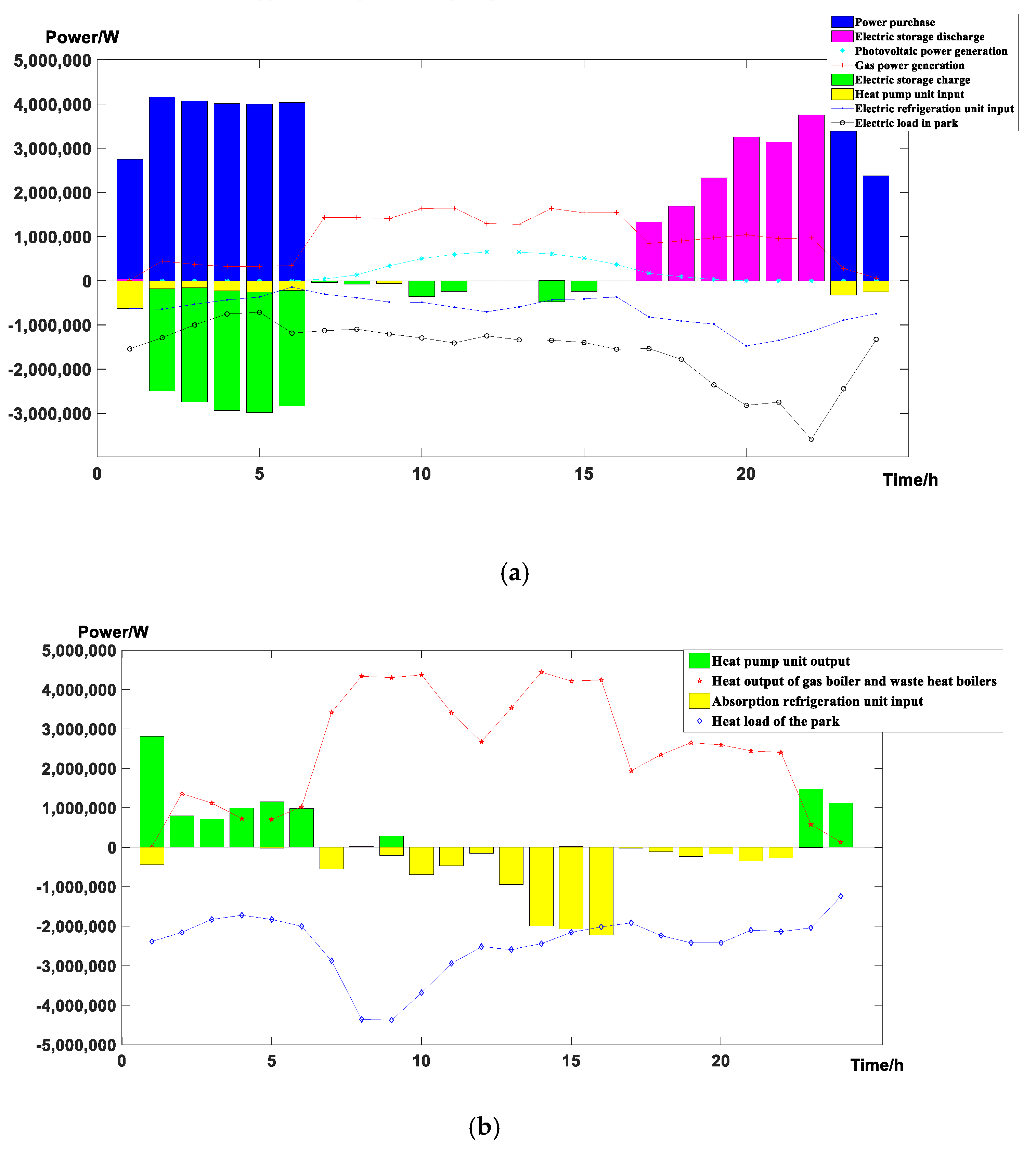
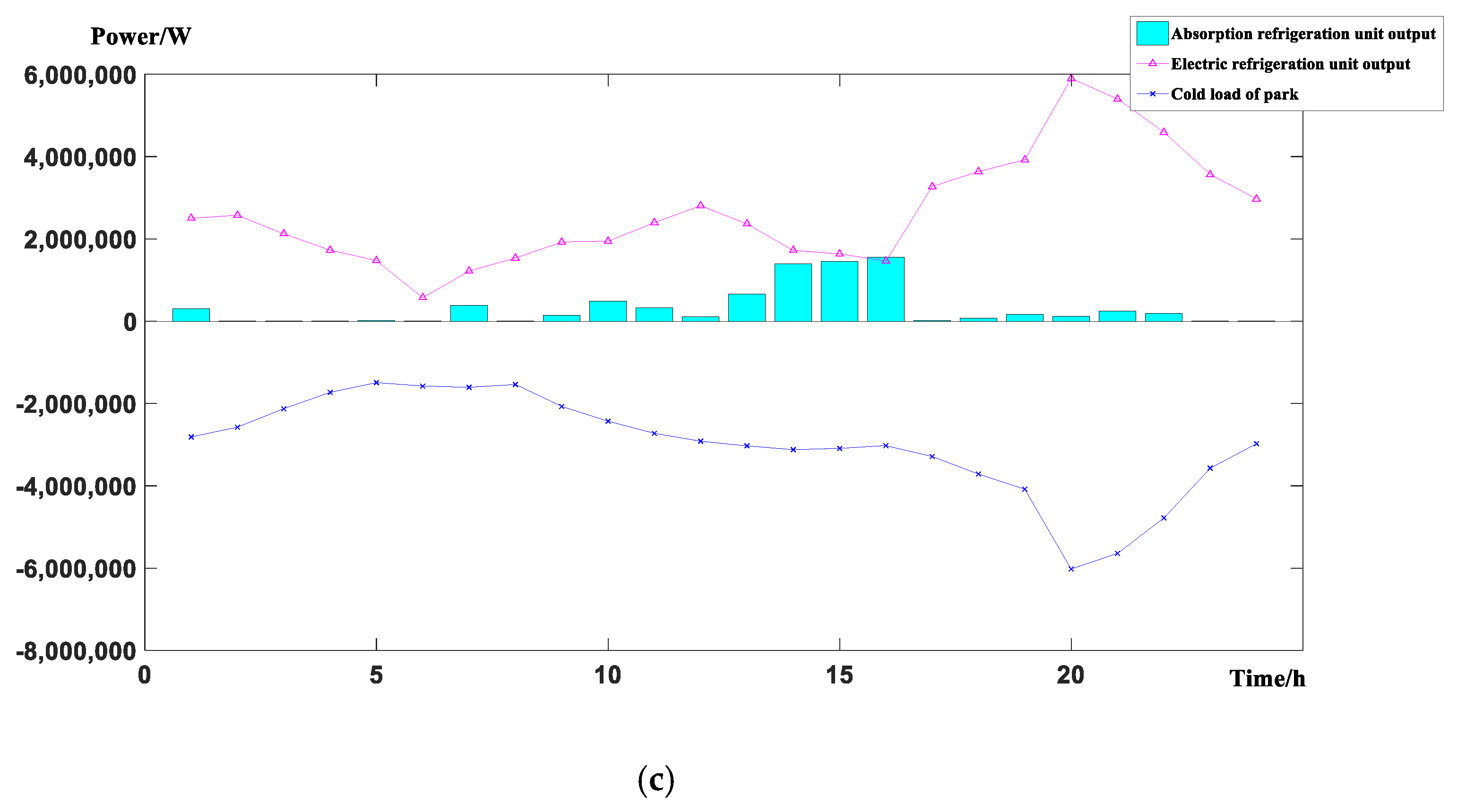
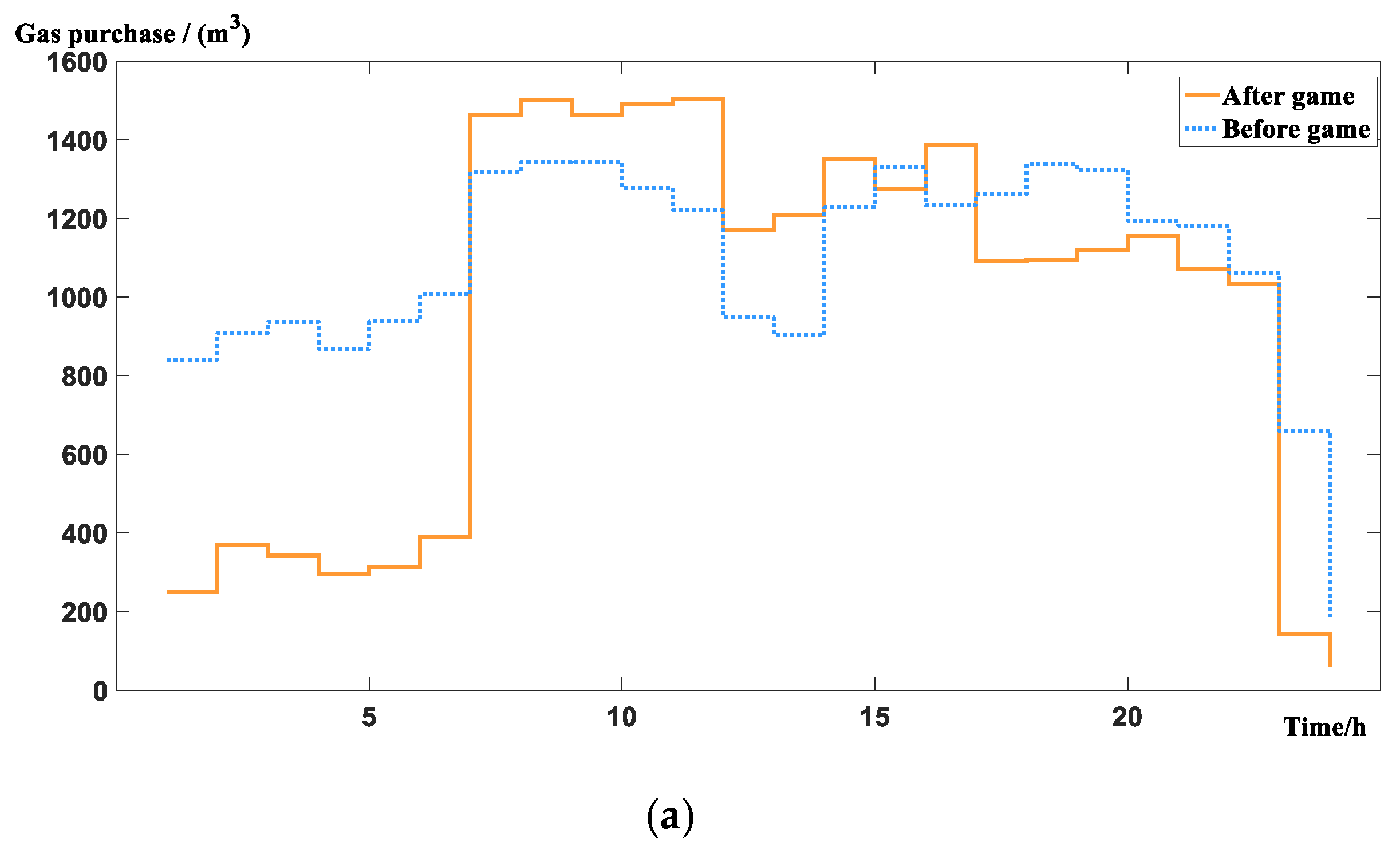
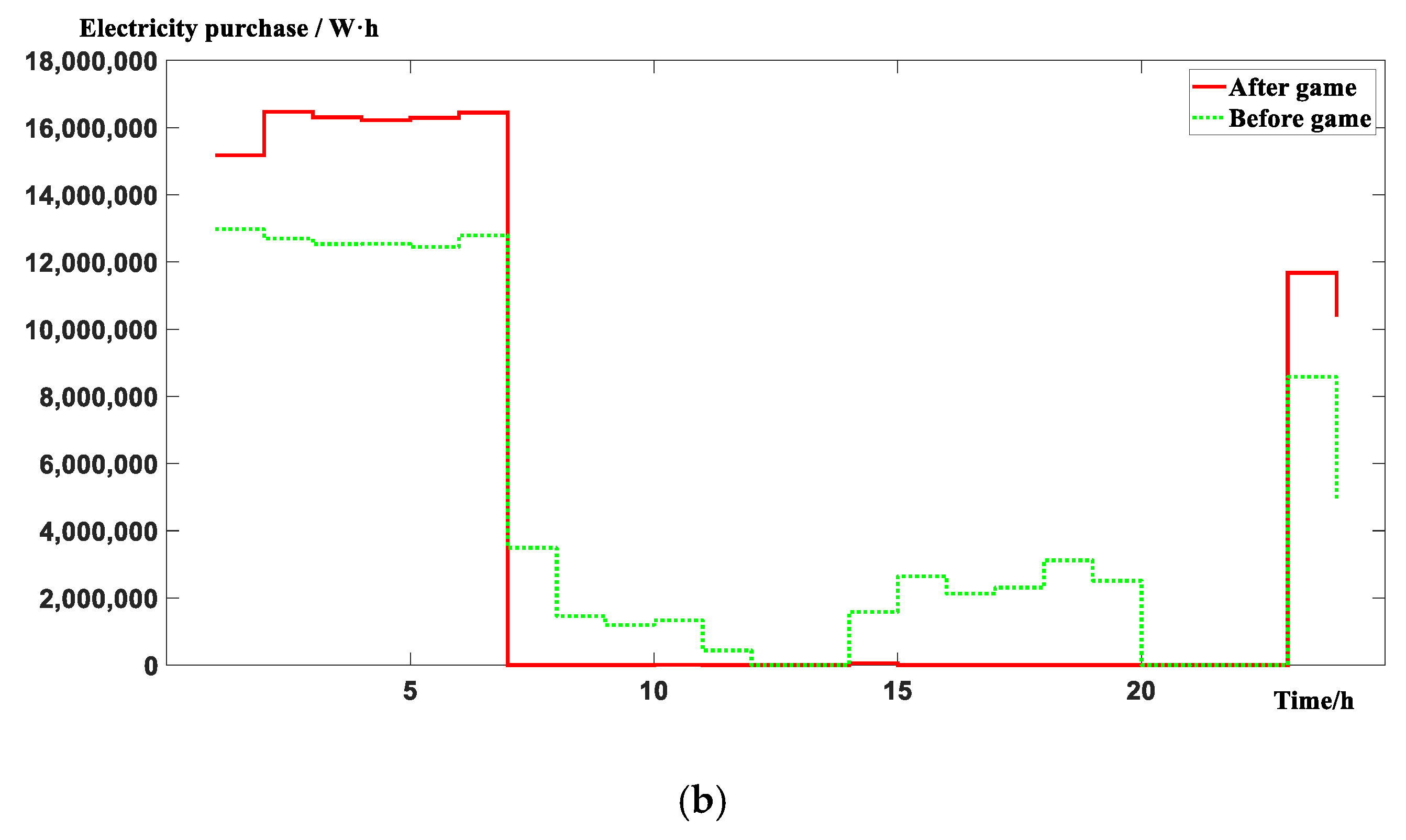
5.2. Results and Analysis of Examples
6. Conclusions
- (1)
- The model proposed in this paper can make the zones adjust their operation strategies more reasonably. After the game, the total cost of all the zones is less than the cost of the whole energy park before the game, and the average energy efficiency of CHP system is improved.
- (2)
- After the game, the amount of natural gas used by each zone has been reduced, which meets the needs of energy saving and emission reduction in the current age. At the same time, the purchase of electricity from the power grid is concentrated in the electricity valley, which has a certain role in peak shaving and valley filling.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IES | integrated energy system |
| P2G | power to gas |
| CCHP | combined cool, heat and power |
| CHP | combined heat and power |
References
- Qureshi, M.I.; Rasli, A.M.; Zaman, K. Energy crisis, greenhouse gas emissions and sectoral growth reforms: Repairing the fabricated mosaic. J. Clean. Prod. 2016, 112, 3657–3666. [Google Scholar] [CrossRef]
- Xiang, L. Energy network dispatch optimization under emergency of local energy shortage with web tool for automatic large group decision-making. Energy 2017, 120, 740–750. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, S.; Liao, Q. Non-cooperative Trading Method for Three Market Entities in Integrated Community Energy System. Autom. Electr. Power Syst. 2018, 42, 32–39. [Google Scholar]
- Voropai, N.; Stennikov, V.; Senderov, S.; Barakhtenko, E.; Voitov, O.; Ustinov, A. Modeling of Integrated Energy Supply Systems: Main Principles, Model, and Applications. J. Energy Eng. 2017, 143, 04017011. [Google Scholar] [CrossRef]
- Tang, B.; Gao, G.; Xia, X.; Yang, X.; Bo, T.; Gangfeng, G.; Xiangwu, X.; Xiu, Y. Integrated Energy System Configuration Optimization for Multi-Zone Heat-Supply Network Interaction. Energies 2018, 11, 3052. [Google Scholar]
- Zeng, M. Key Support Technologies for the Future Development of Distributed Energy under the Background of Energy Internet. Electr. Age 2018, 1, 36–37. [Google Scholar]
- Chen, F.; Gao, Y.; Liang, H.; Duan, J. Energy Consumption Characteristic Evaluation Model and Energy Supply Partition Method of Integrated Energy Park Based on Geographical Partition. Electr. Power Constr. 2019, 6, 23–32. [Google Scholar]
- Patwal, R.S.; Narang, N. Optimal Economic Emission Scheduling of Integrated Energy Systems Using Heuristic Optimization Technique. In Proceedings of the 2018 2nd International Conference on Power, Energy and Environment: Towards Smart Technology (ICEPE), Shillong, India, 1–2 June 2018. [Google Scholar]
- Brożyna, J.; Mentel, G.; Szetela, B.; Strielkowski, W. Multi-Seasonality in the TBATS Model Using Demand for Electric Energy as a Case Study. Econ. Comput. Econ. Cybern. Stud. Res. 2018, 52, 229–246. [Google Scholar] [CrossRef]
- Yang, D.; Xi, Y.; Cai, G. Day-Ahead Dispatch Model of Electro-Thermal Integrated Energy System with Power to Gas Function. Appl. Sci. 2017, 7, 1326. [Google Scholar] [CrossRef]
- Ghasemi, A.; Banejad, M.; Rahimiyan, M. Integrated energy scheduling under uncertainty in a micro energy grid. IET Gener. Transm. Distrib. 2018, 12, 2887–2896. [Google Scholar] [CrossRef]
- Khani, H.; Farag, H.E.Z.; Farag, H.E.Z. Optimal Day-Ahead Scheduling of Power-to-Gas Energy Storage and Gas Load Management in Wholesale Electricity and Gas Markets. IEEE Trans. Sustain. Energy 2018, 9, 940–951. [Google Scholar] [CrossRef]
- Zhang, L. Analysis and Forecast of Market Clearing Price Law; North China Electric Power University: Beijing, China, 2007. [Google Scholar]
- Cao, J. Current Electricity Market and Generator Bidding; Xiamen University: Xiamen, China, 2001. [Google Scholar]
- Liu, Y. Improving the natural gas pricing mechanism for residential consumers in China. Nat. Gas Ind. 2018, 38, 130–141. [Google Scholar]
- Zhao, S.; Ying, G. On Natural Gas price mechanism given present context of China’s natural gas industry. In Proceedings of the 2008 International Conference on Management Science and Engineering 15th Annual Conference Proceedings, Long Beach, CA, USA, 10–12 September 2008; pp. 1873–1879. [Google Scholar]
- Yu, C.; Wang, J.; He, N. A Study of the Supplementary-firing Burner Unit for a Heat Recovery Steam Generator. J. Eng. Therm. Energy Power 2004, 19, 534–536. [Google Scholar]
- Li, P.; Zang, X.; Liu, Y.; Liu, L. Rational determination to heat and power ratio for distributed CHP Plant. Gas Turbine Technol. 2005, 4, 43–46. [Google Scholar]
- Colson, B.; Marcotte, P.; Savard, G. An overview of bilevel optimization. Ann. Oper. Res. 2007, 153, 235–256. [Google Scholar] [CrossRef]
- Shi, J.; Xu, J.; Zeng, B.; Zhang, J. A Bi-Level Optimal Operation for Energy Hub Based on Regulating Heat-to-Electric Ratio Mode. Power Syst. Technol. 2016, 40, 2959–2966. [Google Scholar]
- Fu, S.; Su, Z. Dynamic Power Strategy Space for Non-Cooperative Power Game with Pricing. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–6. [Google Scholar]
- Wu, F.; Liu, X.; Sun, Y.; Chen, N.; Yuan, T.; Gao, B. Multi-Park Game Optimizing Strategy Based on CCHP. Autom. Electr. Power Syst. 2018, 42, 68–75. [Google Scholar]
- Yang, Z.; Zhang, F.; Liang, X.; Han, X.; Xu, Z. Economic Operation of Microgrid with Heat Pump and Energy Storage. Power Syst. Technol. 2018, 42, 1735–1743. [Google Scholar]
- Wang, H. Study on Optimum Configuration of Natural Gas Cogeneration System Based on Gas Turbine; Hunan University: Changsha, China, 2015. [Google Scholar]
- Mao, M.; Jin, P.; Zhang, L.; Ding, Y.; Xu, H. Optimization of Operation Strategies and Economic Analysis of PV Microgrid for Industries. Trans. China Electrotech. Soc. 2014, 29, 35–45. [Google Scholar]
- Bao, N.; Zhu, R.; Ni, W. Cost of electricity analysis of the hybrid power system combining wind farm with gas turbine. Gas Turbine Technol. 2006, 4, 1–5. [Google Scholar]

| Efficiency | Numerical Value(%) | Operation Cost | Numerical Value (USD/J) |
|---|---|---|---|
| ηeCHP | 35 | CHP system c1 | 1.37 × 10−9 |
| ηGB | 90 | Gas boiler c2 | 8.7 × 10−11 |
| ηec | 400 | Electric refrigeration unit c3 | 3.91 × 10−10 |
| ηeh | 450 | Heat pump unit c4 | 1.05 × 10−9 |
| ηhc | 70 | Absorption refrigeration unit c5 | 3.22 × 10−10 |
| ηsto | 95 | Energy storage csto | 7.25 × 10−11 |
| Pollutant Species | SO2 | NOx | CO | CO2 | TSP |
|---|---|---|---|---|---|
| Gas turbine (kg/J) | 6.4 × 10−13 | 3.4 × 10−10 | 0 | 1.1 × 10−7 | 1.3 × 10−11 |
| Waste heat boiler (kg/J) | 2.4 × 10−9 | 1.1 × 10−9 | 3.4 × 10−11 | 2.3 × 10−7 | 5.3 × 10−11 |
| Gas boiler (kg/J) | 2.6 × 10−13 | 1.6 × 10−10 | 0 | 4.6 × 10−8 | 6.0 × 10−12 |
| Environmental cost (USD/kg) | 0.87 | 1.16 | 0.145 | 0.0033 | 0.319 |
| Parameter | Total Cost Csum (USD) | Efficiency (%) | |
|---|---|---|---|
| Object | |||
| Zone 1 | 4795.4 | 74.14 | |
| Zone 2 | 4281.8 | 67.49 | |
| Zone 3 | 4210.8 | 70.79 | |
| Zone 4 | 4648.8 | 64.94 | |
| Summary of zones | 17,936.8 | 69.34 | |
| The whole park before game | 19,678.82 | 67.33 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Liang, H.; Gao, Y.; Yang, Y.; Chen, Y. Research on Double-Layer Optimal Scheduling Model of Integrated Energy Park Based on Non-Cooperative Game. Energies 2019, 12, 3164. https://doi.org/10.3390/en12163164
Chen F, Liang H, Gao Y, Yang Y, Chen Y. Research on Double-Layer Optimal Scheduling Model of Integrated Energy Park Based on Non-Cooperative Game. Energies. 2019; 12(16):3164. https://doi.org/10.3390/en12163164
Chicago/Turabian StyleChen, Feifan, Haifeng Liang, Yajing Gao, Yongchun Yang, and Yuxuan Chen. 2019. "Research on Double-Layer Optimal Scheduling Model of Integrated Energy Park Based on Non-Cooperative Game" Energies 12, no. 16: 3164. https://doi.org/10.3390/en12163164
APA StyleChen, F., Liang, H., Gao, Y., Yang, Y., & Chen, Y. (2019). Research on Double-Layer Optimal Scheduling Model of Integrated Energy Park Based on Non-Cooperative Game. Energies, 12(16), 3164. https://doi.org/10.3390/en12163164