Flexibility from Electric Boiler and Thermal Storage for Multi Energy System Interaction

Abstract

Active use of heat accumulators in the thermal system has the potential for achieving flexibility in district heating with the power to heat (P2H) units, such as electric boilers (EB) and heat pumps. Thermal storage tanks can decouple demand and generation, enhancing accommodation of sustainable energy sources such as solar and wind. The overview of flexibility, using EB and storage, supported by investigating the nature of thermal demand in a Danish residential area, is presented in this paper. Based on the analysis, curve-fitting tools, such as neural net and similar day method, are trained to estimate the residential thermal demand. Utilizing the estimated demand and hourly market spot price of electricity, the operation of the EB is scheduled for storing and fulfilling demand and minimizing energy cost simultaneously. This demonstrates flexibility and controlling the EB integrated into a multi-energy system framework. Results show that the curve fitting tool is effectively suitable to acknowledge thermal demands of residential area based on the environmental factor as well as user behaviour. The thermal storage has the capability of operating as a flexible load to support P2H system as well as minimize the effect of estimation error in fulfilling actual thermal demand simultaneously.

1. Introduction

District heating (DH) supplied hot water to 63% of the private Danish houses in 2015 [1]. The concept of 4th generation district heating/cooling system, supported by renewable, is presented in [2]. With the goal to become carbon neutral in the heating sector by 2030, renewables need to contribute all the heating demands. Thus, there is a possibility to integrate the thermal and electric networks to support grid ancillary services by the flexible electrical loads, such as electric boilers (EBs) and heat pumps (HPs), supporting the thermal system [2,3]. The electricity and heating network are coupled together as power-to-heat (P2H) to utilize renewable electricity for district heating. Integrated heat storage decouples demand and generation, to enhance flexibility for a better adaptation of energy requirements. The concept of P2H in the multi-energy system requires minor expansion of grid and storage [4].

The objective of this paper is to acknowledge flexible operation of the thermal unit consisting of an electric boiler (EB) and a storage tank modelled with stratified layers, as a part of P2H system. This is primarily realized through analysis of metered thermal consumption data from the residential area and estimating thermal demand using curve fitting, followed by an optimal schedule of the EB based on the spot price. The multilayer stratified thermal storage tank model is suitably identified for electric grid integration and flexible operation to compensate the error in estimation of thermal demand. The method could as well be applied for a heat-pump system. However, the application of EB is quite significant nowadays in providing energy flexiblity as well as system frequency services [5]. As an example, an EB of 50 kW is used as a flexible load in LIVØ island, Denmark to increase the self-consumption from wind and PV units installed in the island [6].

Advantages of centralized thermal storage in terms of operational flexibility of CHP (combined heat and Power) for district heating is well-explored in [7]. The flexibility of a district heating network for automatic frequency restoration reserve market is studied in [8]. The balancing markets provide an opportunity for introducing more EBs into DH and increase its contribution to flexibility [9]. A crucial aspect here is how system deployment can be realized effectively. Ref. [7] addresses the flexible operation of heat pumps using predictive control strategy, neglecting consumption of hot water for its highly randomized and hardly predictable nature. The predictive control of the heat pump by estimating only outdoor temperature has been studied in [10]. Thus, there is a necessity to investigate simple and effective methods to determine the influencing parameters for thermal demand prediction to manage the flexible operation of the thermal units in P2H technology.

The perspective of heat electrification in a wind dominated market using resistive heating and storage is the most carbon-intensive method [11] with lower investment cost compared to HP [9,12]. Further, large HPs take a long time from a cold start until they reach their optimal efficiency. Thus, they are not very active at balancing markets between hours, due to short start–stop intervals. Rather, they are mainly used as base load [9]. Hence, the flexibility in easy start–stop in balancing services is the main driver for introducing more EBs into the system. EBs in district heating have the potential for negative secondary control power by increasing consumption and supporting grid balance [13]. Reference [14] realized the benefit of demand-side management and the ability of demand response to improve power system efficiency with integrated wind power and electric heating devices considering constant heat load through the day. Higher potential of HPs in DH systems in the future is realized in [15]. Integration of EB with storage in low voltage residential grid as flexible consumer load has been presented in [16]. Hence, there is the potential of good harmony and flexibility between electrical and thermal energy sector supporting each other in multi-energy systems.

The investigation of space heating and domestic hot water needs is presented in [17] based on curve fitting and distribution functions. In [18] peak load ratio index of buildings are used for determining the diversity in thermal loads to generate the thermal profile for residential buildings. Reference [19] calculates the probability of domestic hot water drawn at a time(t) which depends upon probability during the day, weekday, season and holiday as a function of time(t). Higher probability step functions for weekends in comparison to weekdays are used to indicate higher consumption of domestic hot water on weekends. The thermal demand for space heating in a typical winter day is explored in [20]. However, the pattern of usage for the combined effect of space heating (SH) and domestic hot water ($DHW$) still remains unrealized. Proper knowledge of demand pattern for space heating and domestic use, as presented in this paper, is the key factor for developing a good and applicable estimating tool for thermal demand. This is italic in the main text and equations. For the consistence in the paper, please carefully check and change them to italic.

The possibility of estimating heat demand for space heating just a few hours in advance using neural network based on heat consumption in Polish buildings is matched against weather conditions over a 10-year period in [21]. In [21], the forecasting method is based on time series neural network with temperature and thermal consumption at a particular hour, day and previous history are taken into consideration. One month data from a DH network in Riga has been analysed for forecasting in [22] with the comparison between methods using an artificial neural network, polynomial regression model and the combination of both. With these methods, forecasts are performed by updating the statistics of actual load and temperature of the previous measurement. DH from Czechia has been analysed in [23] in a forecast model based on time series of outdoor temperature and time-dependent social components, which may vary for different weekdays and seasons. The Box–Jenkins method is used to realize the forecast of the social component. Reference [24] addresses issues on the selection of appropriate input variables from building energy management systems sensors. Ambient temperature and relative humidity along with solar radiation are the predominant factors for the predictive model [24,25]. In [26], forecasting based on similar day method is well presented for day-ahead power output for small scale solar PV system. However, none of the literature discussed regarding district heating in both summer and winter, as well as thermal demand prediction based on a combined effect of the time factor and environment variables (such as outdoor temperature, humidity, and wind velocity) together. These aspects are significant to be studied in an integrated framework to clearly understand the effective potential of thermal units like EBs. In this way, it is possible for such flexible units to render energy flexibility necessary to support integration of renewable energy in future energy systems.

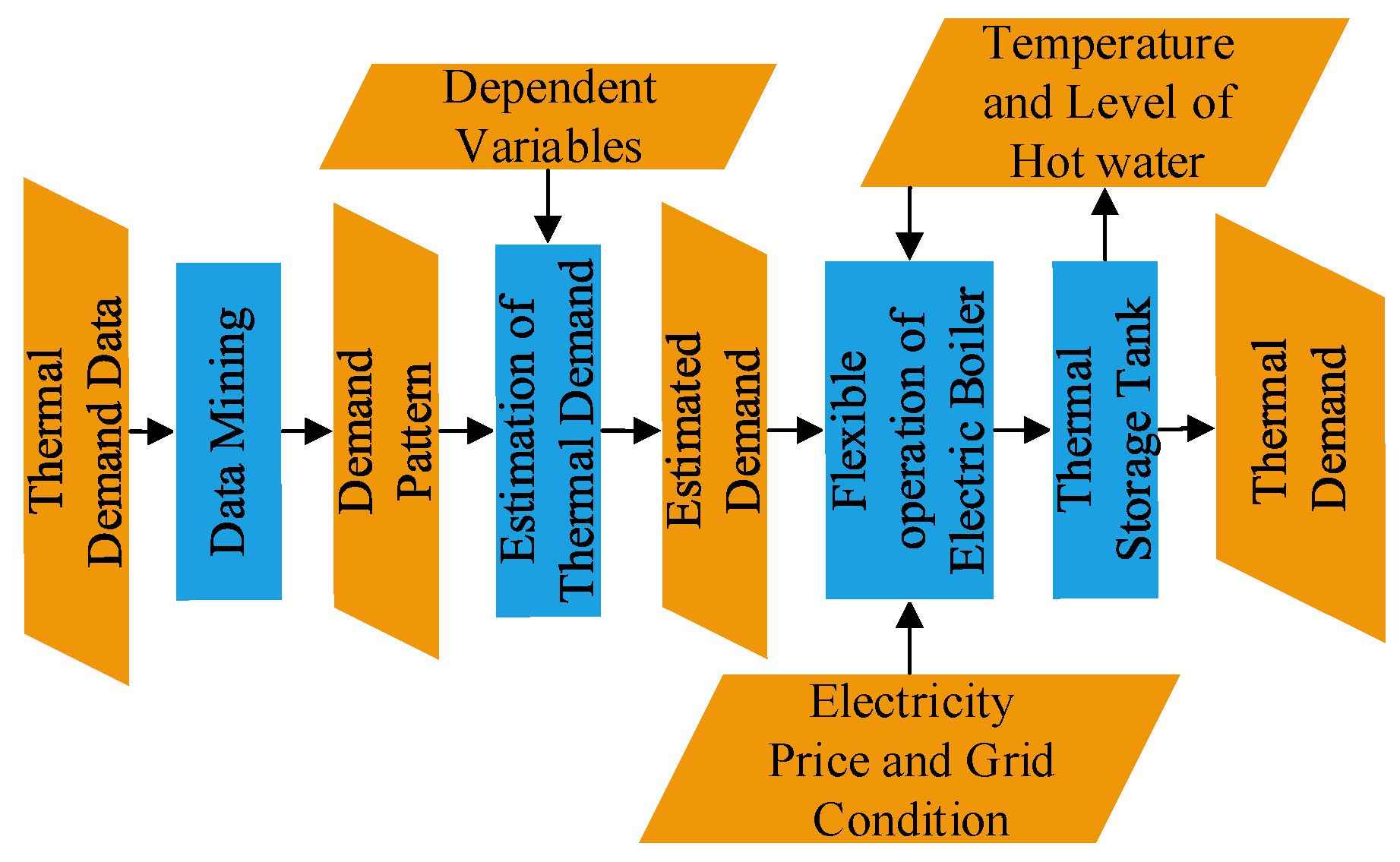
In this paper, the proposed methodology to obtain flexibility with EB in P2H is summarised in the block diagram as shown in Figure 1. The significant contributions in this paper are the identification of thermal demand pattern, estimation of thermal demand using curve fitting tool, and use of stratified storage tank to verify flexible operation of EB. Actual thermal data from DH operator are analysed to unleash the specific consumption pattern of residential areas associated with usage based on different time factors such as hourly, weekdays, weekends, and seasonal. This information is useful while training the curve fitting tool to estimate thermal demand. With reference to [21,22,23], thermal demand estimation is based on the past and its current state for winter. A simple, yet effective curve fitting technique for estimating the thermal demand in the residential area, based on dependent parameters such as time factor (based on consumption profile) and environment variables (apparent temperature), has been investigated and compared with actual data as well as results from existing literature. The analysis is performed for thermal demand estimation during winter as well as summer. The curve fitting is simple and overcomes the problem encountered with the update of measured data (due to the failure of measuring equipment) as in time series estimation. The estimated demand is used to determine the optimal schedule of the EB operation in P2H, for the planning of capacities to store and fulfil thermal energy demand simultaneously, based on the spot price of electricity. The use of stratified storage tank in combination with EB emulates the real operating condition where the temperature of hot water being delivered is more realistic compared to ones from an average model of the storage tank, where hot water temperature decreases gradually. The outcome is verified with actual thermal demand to illustrate how the thermal storage copes up with the error in forecasting and contribute as an example of a flexible load in the P2H concept.

The paper is structured as follows. Analysis of thermal load consumption based on actual measurements at one particular residential site in Denmark supplied with five feeders is analysed to unleash the specific usage pattern and is identified in Section 2. Selection of parameters for effective estimation of thermal demand using various tools such as neural net fitting, and similar day method are discussed in Section 3. Overview of the modelling approach of the stratified hot water storage tank and EB is presented in Section 4 along with validation of the model. In Section 5, the methodology for optimized operation schedule of EB is presented along with EB ON/OFF control strategy. Results of the estimated demand are discussed in Section 6, followed with its application in flexible scheduling of the EB for demand response. Finally, the paper is concluded with the outcome of the research work in Section 7.

2. Analysis of Thermal Data

Thermal data measured at the terminal of five thermal distribution feeders ($F_1-F_5$) supplying a number of residential buildings, in one particular residential area of Aalborg, Denmark, are used for analysis. Available measured data of hourly thermal consumption, from the period of 21 December 2015 to 4 December 2016 are analysed. Figure 2 shows the total annual consumption of thermal demand ($Q_{DHW}$) for residences in feeders ($F_1-F_5$) supplying residential buildings. The annual consumption varies from 723.7 MWh as lowest consumption for $F_1$ to 1278.5 MWh as the highest consumption in $F_4$. This variation is due to the different number of residents in the area and their level of comfort. The total annual consumption was 5195.7 MWh. Figure 3a,b shows the plot of hourly consumption of $Q_{DHW}$ for feeders ($F_1-F_5$) and their total consumptions respectively, throughout the year. Figure 3a,b clearly shows that there is seasonal variation.

Figure 3b shows that there is a sudden transition in thermal consumption at certain time period such as towards the end of January, mid of March, and beginning of May. However, there is a significant difference in thermal consumption between mid-May to September end which is less than 35% of the peak winter consumption. Thus, to simplify the further analysis, the trend of thermal consumption is roughly divided into two seasons, winter and summer, irrespective of autumn and spring. Hence, October to April is considered as winter season and May to September is considered as summer season. The transition period at the beginning of May and October is not considered in this analysis. It seems that there is slightly more thermal demand in May than in September, due to transition from winter to summer and is around 30 ± 5% of the peak winter consumption. It is interesting to see the analysis of data from seasonal perspectives: winter and summer consumption. In the rest of the paper, analysis is done taking the combined effect of all feeders. As a result, the maximum heat demand is likely to be less than the sum of the individual feeder’s peak load. This also reduces the intermittent variation in demand for individual feeders.

The average consumption per hour of $Q_{DHW}$ for all the feeders, considering yearly consumption, is 618.5 kWh. During winter, it is 881.8 kWh, which is 205.8% more than summer consumption of 288.4 kWh.

Figure 4a,c shows the graph of hourly average thermal consumption pattern of different days of the week during winter and summer respectively. It is clearly seen that there exist a unique pattern of average thermal consumption with peaks. The pattern is different on weekends (Saturday and Sunday) in comparison to weekdays (Monday–Friday). To simplify the graphs shown in Figure 4a,c, graphs with an average consumption of thermal energy during the week, weekdays and weekend has been plotted in Figure 4b,d for winter and summer respectively. It is observed that there are some definite patterns of hourly usage of an average $Q_{DHW}$. There are two peaks and two valleys. It is clear that the amount of variation in thermal consumption with respect to minimum consumption is higher for weekends than for weekdays indicating higher consumption of domestic hot water as mentioned in [19].

Figure 5 shows the consumption pattern for the week, weekdays and weekends for the period of Dec 2016 to Aug 2017 for winter and summer respectively.

Unlike in Figure 4b,d the total consumption at weekends are lower than weekdays. Thus, the amount of thermal consumption based on weekend and weekdays are not much relevant. However, the hourly pattern of consumption for weekdays and weekends are comparable with similar peaks and valley at particular hours seen in Figure 4b,d. Hence, knowledge of these patterns of thermal consumption during weekdays and weekend is much helpful to train the estimation tool to compensate for the error due to temperature independent factors such as user behaviour. The lowest consumption is during the period 03:00–04:59 h which rises gradually until 07:00–07:59 h during normal weekdays when people get ready for their job (Figure 4b,d). On the weekend there is a shift in this peak which is around 10:00–12:59 h. The shift in peak could be because people prefer to wake up late on the weekend. After the morning peak, there is decrement of thermal consumption until 2:00–3:59 h when people are at work during weekdays. Throughout the week, the evening peak is around 18:00–20:59 which gradually decreases to 4:59 h in the early morning. However, in summer there is a shift in evening peak compared to that in winter. This analysis shows the relevance of time, day and season to determine the usage pattern of thermal consumption and that it is significant for forecasting as seen in [21] for thermal load similar to the forecasting of electrical load [27].

3. Thermal Demand Estimation

It is difficult to estimate thermal demand for the residential area, as it is not only largely depending on the environmental variables (weather), but also on the user behaviour and building geometry. In reality, analysis for occupancy and user level comfort is difficult and leads to challenges incorporated with privacy issues of the individuals. This leads to a significant effort to compromise between errors in estimated variable and dependent parameters. Analysis of thermal data from residential areas gives remarkable information on the pattern of thermal demand, without compromising the privacy issue of individuals. These informations are helpful in selecting effective variables for the estimation of thermal demand from the perspective of user behaviour, which defines the pattern of demand. Time of day and days of the week (weekdays or weekends) are the two major parameters associated with the pattern of thermal consumption based on user level comfort.

The estimated parameters are subjected to identify the flexible operation of the thermal system based on demand, supply, capacity, and energy prices. In this paper, for the estimation of thermal consumption in the residential area, thermal data associated with Figure 5 are used.

3.1. Dependent Variables for Thermal Demand Estimation

Thermal demand is highly influenced by the environmental variable such as air temperature. Figure 6a shows the hourly value of thermal demand and corresponding average external temperature of the environment. It shows that decrease in temperature increases thermal demand. Beside air temperature, cold air with high relative humidity increases the conduction of heat from the body in comparison to dry air with the same temperature. In order to incorporate the combined effect of relative humidity, wind and air temperature together, responsible for heat loss from a body, apparent temperature is considered. The apparent temperature is calculated using (1) and (2) [28]. Figure 6b shows the hourly value of thermal demand and corresponding apparent temperature. The correlation coefficient of thermal demand with respect to external ambient temperature and apparent temperature, is −0.88 and −0.89 respectively.

$$AT=T_a+0.33e-0.7v-4.00$$

(1)

$$e=\frac{RH}{100}6.105\exp \left(\frac{17.27T_a}{237.7+T_a}\right)$$

(2)

where, $AT$ = Apparent Temperature [$°$C]. $T_a$ = Dry bulb temperature of external environment [$°$C]. e = water vapour pressure [hpa]. v = wind speed [m/s]. $RH$ = Relative humidity [%].

Figure 7a shows the graph of apparent temperature vs. thermal demand throughout the period of December 2016 to August 2017. Figure 7b shows the distribution of thermal demand with respect to apparent temperature during summer and winter only. It is clear from Figure 7b that thermal demand during winter is inversely proportional to the apparent temperature. Whereas, during summer, proportional relationship between each other is very small. This could be due to the reason that apart from external temperature, thermal consumption is mostly for domestic purposes such as bathing, washing, space heating for toilet/bathroom, and transmission losses. Thus, it is logical to conclude that seasonal effect needs to be considered as input variable in the model for estimation.

The parameters for estimation of thermal loads in residential areas are based on factors such as user behaviour (hour, weekdays, and weekends), and environmental condition (apparent temperature and season).

3.2. Estimation Technique of Thermal Demand

Different approaches to estimating thermal demand based on curve fitting technique such as the neural net fitting, and similar day method are considered as they are widely used. MATLAB inbuilt tools and functions are used for developing the estimation model using the neural net tool. Different scenarios based on the seasonal variations (summer and winter) are analysed.

For the neural net fitting tool, 50% of the seasonal data set are used for training, 25% for validating, and 25% for testing to develop the model. The datasets are divided randomly for training, testing, and validation of the model. After developing the model, 50% of the remaining seasonal data set are used in estimation.

For the similar day approach, the hourly data of a day is arranged according to season (summer and winter) and weekdays and weekends as shown in Figure 8.

50% of each dataset (weekdays and weekends for summer and winter) are used as the historical data to build a Euclidean distance (ED) for measure of similarity. In similar day method, it is assumed that the thermal demand is associated with apparent temperature ($AT$) for similar day (weekdays and weekends for summer or winter), and will result into similar thermal demand. EDs value based on recorded normalised $AT$ ($\widetilde{AT}$) values at particular hour(h) of the day (d) are calculated for each and every historical similar days ($d^i$) using (3) [26]

$$ED(\widetilde{AT},d,d^i)=\sum _{h=1}^{24}{({\widetilde{AT}}_h^{\left(d\right)}-{\widetilde{AT}}_h^{\left(d^i\right)})}^2$$

(3)

where, $ED(\widetilde{AT},d,d^i)$ is the ED between day d and historical days $d^i$ with respect to the value of $\widetilde{AT}$. Days with similar pattern of $AT$ will have very small values of ED, hence corresponding value of thermal demand is selected as the estimated value.The parameters for AT can be achieved from the forecasted meteorology data.

4. Electric Boiler and Stratified Storage Tank

Modelling of the hot water storage tank for the electric boiler (EB) is equally important to be able to analyze the flexibility in power to heat conversion with effective thermal demand and supply. The EB and a storage tank with stratified layers as shown in Figure 9, has been well-defined and theoretically verified in [29] based on the principle of conservation of energy in a control volume and surface. The detailed derivation of EB and storage tank presented here is suitably adapted to utilize flexibility in its synergy operation with the electricity network. Also, the single general equation is derived which is suitable for charging and discharging of the storage tank, with and without discharge of hot water from the tank.

In Figure 9, $T_s$ = temperature of supply hot water in the tank [K], $T_r$ = temperature of return water in the tank [K], $T_a$ = temperature of ambient environment [K], $T_i$ = temperature of ith stratified layers, $(i=1,2,...n)$ [K], ${\dot{m}}_e$= effective mass flow between the stratified layer [kg/s], ${\dot{m}}_s$ and ${\dot{m}}_d$ are the inlet and demand mass flow [kg/s] of water from the heating source, and out of storage tank respectively.

4.1. Modelling of EB and Storage Tank

The EB is considered to be a constant impedance load [30] and is operated with constant power ($P_{r,b}$ = rated power of boiler [W]) as shown in (4). Here, $V_{r,b}$ and $V_{poc}$ are rated voltage of boiler [V] and voltage at point of coupling of boiler into the grid [V] respectively. $\eta$ is the efficiency of boiler [%] and ${\dot{Q}}_{heat}$ is the heat flow rate of heating element [J/s]. $C_w$ is the specific heat capacity of water [J/kg·K]. As per the manufacturer, the recommended flow of ${\dot{m}}_s$ is produced at a $\Delta T=10 °$C ($\Delta T=T_s-T_n$) with the EB on full power. However, the allowable maximum flow of ${\dot{m}}_s$ is produced at $\Delta T=5 °$C.

$${\dot{Q}}_{heat}=\frac{\eta }{100}{\left(\frac{V_{poc}}{V_{r,b}}\right)}^2{P}_{r,b}={\dot{m}}_s{C}_w(T_s-T_n)\left[\mathrm{W}\right]$$

(4)

The energy flow in different layers of stratification is shown in Figure 10. The amount of heat exchanged by the layer i of thickness z with the surrounding layers ($i-1$) and ($i+1$) of same thickness (z) and area ($A_q$) due to thermal conduction (${\dot{Q}}_{exc}$) in vertical direction of the storage tank is calculated using (5) [29].

$$\begin{array}{cc}\hfill {\dot{Q}}_{exc,i}& ={\dot{Q}}_{exc,i-1\to i}-{\dot{Q}}_{exc,i\to i+1}\hfill \\ \hfill & =\frac{A_q{\lambda }_w}{z}(T_{i-1}-T_i)-\frac{A_q{\lambda }_w}{z}(T_i-T_{i+1})\hfill \\ \hfill & =\frac{A_q{\lambda }_w}{z}(T_{i-1}+T_{i+1}-2T_i)\hfill \end{array}$$

(5)

where, ${\lambda }_w$ = effective vertical heat conductivity of water (1–1.5 W/mK) [29]. ${\dot{Q}}_{exc}$ is heat exchange due to natural convection and thermal conduction [W]. The effective mass flow of water between the stratified layer (${\dot{m}}_e$) is given by (6).

$${\dot{m}}_e={\dot{m}}_s-{\dot{m}}_d\left[\mathrm{kg}/\mathrm{s}\right]$$

(6)

Let, ${\delta }^{+}$ (7) and ${\delta }^{-}$ (8) indicate an effective flow of water inside the storage tank from top to bottom or bottom to top respectively. ${\delta }^{+}=1$ represents that the heat transfer inside the storage tank due to the water mixing is from top to bottom (downwards). Similarly, ${\delta }^{-}=1$ indicates that the heat transfer inside the storage tank due to the mixing of water is from bottom to top (upward).

$$\begin{array}{cc}\hfill {\delta }^{+}& =1\mathrm{if}{\dot{m}}_e>0\hfill \\ \hfill & =0\mathrm{if}{\dot{m}}_e\le 0\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\delta }^{-}& =1\mathrm{if}{\dot{m}}_e<0\hfill \\ \hfill & =0\mathrm{if}{\dot{m}}_e\ge 0\hfill \end{array}$$

(8)

Let, ${\delta }_{\left(X\right)}$ be the conditional operator as defined in (9). ${\delta }_{\left(X\right)}=1$ when conditions defined by X is true, else, ${\delta }_{\left(X\right)}=0$

$$\begin{array}{cc}\hfill {\delta }_{\left(X\right)}& =1\mathrm{if}X=\mathrm{True}\hfill \\ \hfill & =0\mathrm{if}X=\mathrm{False}\hfill \end{array}$$

(9)

A general equation for n stratified layers, considering $i=1$ as the top layer and $i=n$ as the bottom layer, is derived and given by (10).

$$\begin{array}{cc}\hfill m{C}_w\frac{d{T}_i}{dt}=& {\dot{m}}_s{C}_w(T_s-T_1){\delta }_{(i=1)}+{\dot{m}}_d{C}_w(T_r-T_n){\delta }_{(i=n)}\hfill \\ \hfill & +{\dot{m}}_e{C}_w(T_{i-1}-T_i){\delta }^{+}{\delta }_{(i\ne 1)}+{\dot{m}}_e{C}_w(T_i-T_{i+1}){\delta }^{-}{\delta }_{(i\ne n)}\hfill \\ \hfill & -U{A}_s(T_i-T_a)+\frac{A_q{\lambda }_w}{z}[(T_{i-1}-T_i){\delta }_{(i\ne 1)}-(T_i-T_{i+1}){\delta }_{(i\ne n)}]\hfill \end{array}$$

(10)

Here, U = overall heat transfer coefficient [W/m${}^2·$K].

4.2. Model Verification

The dynamic EB storage was verified based on three different scenarios as classified in

Table 1. Electric boiler (EB) storage model verification scenarios.

Scenario	Situation	${\dot{\mathit{m}}}_{\mathit{d}}$	${\mathit{T}}_{\mathit{s}}$	${\mathit{T}}_{\mathit{r}}$
Scenario 1	Discharging	10-L/s	−	$40 °$C
Scenario 2	Charging	0-L/s	$80 °$C	-
Scenario 2	Charging and Discharging	10-L/s	$80 °$C	$40 °$C

. These values were taken just to verify the model.

The technical parameters of EB and storage is presented in

Table 2. Technical parameters of EB and storage.

Parameters	Definition	Value	Units
V	storage volume	200	[m${}^3$]
n	number of stratified layers in storage tank	10	-
${\lambda }_w$	effective heat conductivity of water	0.644	[W/mK]
U	heat transfer coeff. of the storage walls	0.12	[W/m${}^2$K]
x	diameter to height ratio of storage	2.24	-
$T_a$	ambient Temperature	10	[$°$C]
x $T_s$	supply Temperature	80	[$°$C]
$T_r$	return Temperature	40	[$°$C]
$P_b$	Rated Power of EB	2.4	[MW]
$C_w$	specific heat capacity of water	4190	[J/kg·K]

. The temperature distribution for a 200-m${}^3$ hot water storage tank with 10 stratified layers are shown in Figure 11a for all three scenarios mentioned in Table 1. Figure 11b represents the EB status (ON/OFF) and discharge of hot water from the storage tank (L/s) corresponding to Figure 11a.

Scenario 1 represents the temperature dynamic in the storage tank subjected to discharge of hot water at a constant rate of 10-L/s and the constant return temperature of cold water ($T_r=40 °$C). Initially, the storage tank is fully charged and is filled with hot water with an initial temperature of all layers ($T_i(ini$)) equal to $80 °$C. The temperature gradient of each layer is different and falls gradually until it reaches $40 °$C and this situation is considered as a fully discharged storage tank. The temperature of the bottom layer drops rapidly compared to the adjacent top layer.

Scenario 2 represents the temperature dynamic in the storage tank subjected to charging with hot water from EB of power rating 2.4 MW based on Equation (4). The temperature of supply hot water is maintained constant at $T_s=80 °$C. The discharge from the storage tank during this period is 0-L/s. The temperature of each layer in the storage tank gradually increases until $T_{10}=75 °$C, so that the allowable maximum flow from EB is not exceeded as discussed in Section 4.1. The temperature of the top layer increases quickly compared to the adjacent bottom layer.

Scenario 3 represents the temperature dynamic in the storage tank subjected to both charging and discharging process to resemble an actual scenario. Initially, the storage is fully charged. It is then discharged at the rate of 10-L/s with the heater turned off until the temperature of 7th layer is below $50 °$C. Now, the heater is turned ON with discharge remaining 10-L/s from the storage tank. During this period, the temperature of water in different layers rises at a slower rate compared to charging without any discharge. The temperature of the bottom layer increases at a much slower rate compared to its adjacent top layer. Hence, the mode of EB storage tank defined by (10) is verified using these different scenarios.

5. Operation Schedule of EB for Flexibility

In order to schedule the time of operation of the EB to charge the hot water storage tank, the optimization procedure given by (11) and (12) are followed. The objective function is to minimize the cost of electricity for production of hot water to meet the demand and storage needs. The constraints calculate the energy stored in storage tank and does not allow the storage tank to charge more than its allowable maximum and minimum limit. The energy extracted from the grid is either 0 (when EB is turned OFF) or is equal to the rated power of EB heater ($P_b$, when EB is turned ON). The energy extracted from the grid must be able to charge the storage as well as fulfil the demand. Although there are possibilities to control the EB power in several stages, the problem here is simplified with just ON and OFF in order to demonstrate the flexibility in operation of EBs under dynamic tariff conditions, with the help of estimated demand. Also, the operation of EB during peak hours in evening are restricted to minimise problems related to grid congestion and under voltage in Danish low voltage residential grid, due to integration and operation of electric boilers (EBs) [6]. The thermal energy stored in the tank at the end of the day is maximized to illustrate that storage tank is not only providing flexibility by supplying the thermal demand at the time of high electricity price and peak electricity demand, but also stores energy during the period of low electricity price during the 24 hour period of spot price in the electricity market.

$$\begin{array}{cc}\hfill \mathrm{Minimize}& \sum _{t=1}^{24}{C}_t{P}_{g,t}\hfill \end{array}$$

(11)

$$\begin{array}{c}\hfill \mathrm{Constraints}\\ \hfill & S_{t+1}=S_t-Q_{DHW,t}+P_{g,t}\hfill \\ \hfill & S_{\min }\le S_t\le S_{\max }\hfill \\ \hfill & P_{g,t}\in [0,P_b\Delta t]\hfill \\ \hfill & P_{g,t}=0for17\le t\le 20\hfill \\ \hfill & (S_{\max }-P_b\Delta t)\le S_t\le S_{\max }fort=24\hfill \end{array}$$

(12)

Here, C = energy price[EUR/MWh]. $P_g$= energy extracted from the grid [MWh]. S = energy that can be extracted from storage [MWh]. $Q_{DHW}$ = thermal demand [MWh]. $P_b$ = rated power of EB [2.4 MW]. Subscripts: t = time [h], min = minimum, max = maximum, ini = initial value. The maximum energy that can be stored in hot water storage tank is given by (13)

$$S_{\max }=M_b{C}_w(T_s-T_r)/(3600\times {10}^6)\left[\mathrm{MWh}\right]$$

(13)

$$S_{\min }=0.4\times S_{\max }\left[\mathrm{MWh}\right]$$

(14)

Here, $M_b$ = Mass of water in storage [$2\times {10}^5$kg]. $T_s$ = temperature of supply hot water in the tank [$80 °$C]. $T_r$ = temperature of return water in the tank [$40 °$C]. $C_w$ = specific heat capacity of water [4190 J/kg·K].

The optimization problem was solved by minimizing the cost function using brute force optimization in MATLAB. All possible candidates for the solutions are generated and then checked against the satisfaction of problem statement as given in (11) and (12). For more than one solutions, the solution with less ON/OFF operation of EB is selected. The solutions were verified using “PuLP”, linear programming modeller written in python.

Control of EB

The optimized schedule for operation of the EB is determined based on the estimated thermal demand. On the other hand, the actual thermal demand would vary to some extent compared to the estimated value. This leads to an estimation error. In case the error is large, it can lead storage tank temperature to be away from the specified limit ($T_{10}\le 75 °$C when storage is charged and $T_7\ge 46 °$C to limit storage discharge up to 70% of its capacity). Thus, in order to compensate for the large error in estimated demand with respect to the actual value, the optimized schedule for operation of EB is reinforced with limit controllers based on hysteresis control, realized with RS flipflop, to turn ON/OFF EB as shown in Figure 12. This ensures that the temperature of hot water in the storage tank is within the specified limit.

Figure 12a shows that, when the temperature of bottom layer $T_{10}\ge 75 °$C the EB needs to be turned OFF as discussed in Section 4.1. It is turned OFF only for a short period until the temperature of the seventh layer ($T_7$) is less than $78 °$C, so that it can further follow the schedule. Figure 12b ensures that if $T_7<46 °$C (storage is discharged more than 70% of its capacity), EB is turned ON until it is fully charged (i.e., $T_{10}\ge 75 °$C). Apart from these two conditions, the EB is operated as per the determined schedule. The overall control strategy is shown in

Table 3. Truth table for control of EB based on outputs of Figure 12.

${\mathit{T}}_{\mathbf{OFF}}$	${\mathit{T}}_{\mathbf{ON}}$	${\mathit{C}}_{\mathit{a}}$
1	x	0
x	1	1
0	0	$C_{a1}$

, where $C_a$ is the Control signal for turning ON and OFF of EB and $C_{a1}$ is the signal from scheduled ON/OFF of EB.

6. Result and Discussion

6.1. Thermal Demand Estimation

Figure 13a,b shows the estimated vs. actual demand and associated %error in estimation using the neural net fitting tool are presented respectively. The range of %error associated with the neural net tool is lower than for the similar day method. Figure 13c presents the histogram of %error normalized with the frequency of occurrence as well as the probability density function. The normal distribution of %error is well-defined with the mean and standard deviation of error as well as its deviation from the mean. Finally, the average value of estimated data and actual data are compared with respect to time of day, weekdays and weekend in Figure 13d. The estimated data closely follow the trend and pattern associated with thermal demand.

Similar analysis has been conducted for a similar day method and is presented in Figure 14. The range of percentage error between estimated and actual value (Figure 14b1,b2) is higher than with the neural net fitting tool. However, with less number of the dataset, similar day approach is equally reliable as a neural net fitting tool.

Table 4. Errors from thermal demand estimations.

	Neural Network		Similar Day
	Summer	Winter	Summer	Winter
MAPE	5.459	7.30	9.57	9.72
RMSE	0.016	0.08	0.028	0.103
Mean ($\mu$) %error	1.73	2.16	2.68	3.14
Std.Dev ($\sigma$)	6.73	9.31	11.56	11.77

summarises the results of different methods of estimation. Root mean square error (RMSE) is used to measure the difference between the estimated value by a model and the actual values observed. Mean absolute percentage error (MAPE) estimates how close estimated values are to actual values in percentage.

Results in Figure 13 and Figure 14 shows that the knowledge of apparent temperature, (which includes the effect of wind, relative humidity, water vapour pressure, and ambient temperature) along with the user pattern behaviour was good enough for the estimation of thermal demand, for both summer and winter season, without considering user behaviour and geometry of the building. The consumption pattern of thermal demand with peaks and valleys were well preserved with estimated demand as seen in Figure 13d1,d2 and Figure 14d1,d2. This pattern is due to training of estimation tool based on parameters such as time, day and season as well. However, the error in the magnitude of estimated demand was expected from the thermal components that were not much dependent on the external temperature, e.g., domestic hot water usage. Using a thermal storage tank, error in estimated demand wes well compensated.

Results of thermal demand estimation using a curve fitting technique based on neural net fitting were compared with the results from time series estimation, in existing literature, based on estimation errors. Errors in the estimated value using the neural net fitting tool for winter season ranged between −23 and 31 whereas, in [22] it ranged from −33 to 15 (with 10% less range) with use of time series ANN. Further, the MAPE for 24 h ahead forecast according to [23] was 7.28% for winter which is similar to 7.3% during winter using neural net fitting as discussed here. Also, in [25] the MAPE errors for different machine learning technique and for different area varies between 5–27%. Hence, the curve fitting techniques discussed here is a well effective and simple estimation tool for thermal demand estimation using AT and hourly pattern with respect to weekdays and seasons.

6.2. Flexible Operation of Electric Boiler

One of the important applications of deploying thermal demand estimation is to prepare an algorithm for energy management, to support the future smart grid system. An example of scheduling thermal storage under dynamic tariff condition is introduced in [31] with an average model of the storage tank. Here, a time series based concept for thermal demand forecast and the schedule is proposed for heat pumps without considering ON/OFF delay for thermal production. It usually takes around 10–15 min to achieve a steady state condition [32]. In [6] the models of EB and HP with a storage tank having only two stratified layers, are briefly discussed in relation to the actual control and flexibility based on grid condition and status of storage tank temperature or position of the stratified layer.

The EB with an n-stratified layered storage tank as modelled in Section 4 is used to acknowledge its operational flexibility. The optimal schedule of the EB is based on estimated thermal demand using the curve fitting technique. The temperature of hot water inside the storage tank at different layers (1, 7, and 10 as in Figure 9) gives the indication of flexibility performance of the storage tank to be able to supply the demand. The operational flexibility in terms of ON and OFF of the EB under dynamic tariff conditions based on estimated thermal demand is presented in this section. The storage is never scheduled to discharge more than up to 40% of its maximum capacity in order to accommodate substantial error in the estimation of thermal demand. Figure 15 shows the complete system methodology implemented for flexible operation of the EB. Thermal demand estimation and optimized schedule for operation of EB are determined using Matlab. Then the flexibility in the operation of the EB is verified using DigSILENT power factory simulation tool.

Figure 16a shows the day-ahead hourly spot price of Denmark’s northern region for case 1: 6 January 2017 [33]. On this particular day, the price seems to be decreasing gradually according to the time of the day. Sometimes the prices even go to negative as on case 2: 24 December 2016 [33]. This is because of the high electricity generation from renewable sources such as wind or solar. With an optimization problem to reduce energy cost, it is obviously beneficial to turn ON the boiler during low electricity price to store thermal energy.

Figure 16b shows the estimated thermal demand based on the neural network on 6 January 2017 and is compared with actual demand on the same day. Here, the MAPE error is significantly less compared to other days estimation. Based on the estimated thermal demand, the optimal schedule of EB, as well as thermal energy storage status, is determined (0 = fully discharged, 1 = fully charged) to avoid higher price and time of peak electrical demand as shown in Figure 16c for case 1. Using this schedule for operation of the EB with actual demand, the storage temperature is monitored in Figure 16d. It is observed from Figure 16c that the controller ($C_a$) follows the estimated schedule ($C_{a1}$). The actual EB storage status ($A{S}_{status}$) is also closer to estimated value ($P{S}_{status}$). A similar observation is made for case 2 as well. The storage temperature of the top layer confirms that demand has been fulfilled taking care of grid flexibility and end-user satisfaction. The storage tanks are charged when the electricity price is lower as seen from case 1 and case 2, where spot pricing is different whereas demand remains the same for both cases.

Similarly, Figure 17a shows the electricity price of 23 March 2017. Here, the estimated value of thermal demand has the maximum forecasting error as seen in Figure 17b. Estimated EB schedule ($C_{a1}$) along with the controller action ($C_a$) is shown in Figure 17c. The controller turns OFF the EB twice during, 6th and 24th hour as the storage tank is fully charged as seen in Figure 17d. This is due to the over estimation of thermal demand. The temperature of the hot water as seen from Figure 17d indicates that storage has been fully charged and heating element needs to be shut down.

The knowledge of apparent temperature, and hourly pattern of thermal consumption during weekdays or weekends has helped the estimation tool to estimate the thermal demand effectively. The estimation of thermal demand has supported immensely in the decision-making process to schedule flexible operation of the EB in the multi-energy system, where energy prices are lower during high generation from renewable sources such as solar and wind. Despite a substantial error in estimation, the thermal storage has the capability of operating as a flexible load by decoupling demand and generation, and enhancing accommodation of renewable energy. The energy in the storage tank tries to attain at its best status to fulfil evening thermal peak demand, as well as avoid EB operation to support peak shaping during high electricity demand in the evening. The temperature of the top bottom and middle layer of stratified hot water storage tank indicates that the thermal demand is fulfilled by maintaining operational flexibility. The use of stratified layered storage tank has the advantage over average temperature model of storage tank, as an average model is not able to illustrate the actual condition of supply temperature which regulates the flow of hot water from the EB to storage tank while charging process and monitor the status of storage tank as realized in practice.

7. Conclusions

This paper shows insight on the daily usage pattern of the thermal energy, during summer and winter, in a residential area along with the factors influencing the estimation of thermal demand such as user behaviour parameters and external environment parameters. Based on these factors, the neural network model and the similar day method for estimation has been implemented. Using this model, estimation of thermal usage for the same area can be achieved, but not for other areas. So, an already available model is unlikely to be used for new subjects. However, the findings of this paper on the use of input parameters for determining the thermal demand of a particular area and its influence on the pattern of usage has been justified.

The findings of the data analysis of thermal consumption ($Q_{DHW}$) yields some important conclusions on the pattern of energy demand based on time and day of usage reflecting user behaviour without compromising the privacy issue of individuals. This valuable information is useful for determining the generation of thermal demand and need for storage. When large CHP units are replaced by small heat pumps or electric boilers and integrated to the electric grid network, it will increase the electricity demand with the profile discussed in Figure 4. Thus, during off-peak hours, when electricity demand is low, the thermal storage unit can be used to store the surplus electricity generated by wind turbines and other renewable generation. This storage of thermal power can be utilized during its peak hours reducing greenhouse emission on the production of hot water. Further, the estimated value of thermal demand helps in determining the range of requirement of thermal storage to meet the consumer demand as well as demand response to utilizing thermal storage unit as flexible consumer load in the multi-energy system.