Approximating the Temperature–Entropy Saturation Curve of ORC Working Fluids From the Ideal Gas Isobaric Heat Capacity
Abstract
:1. Introduction
2. A Semiempirical Method for the - Saturation Curve
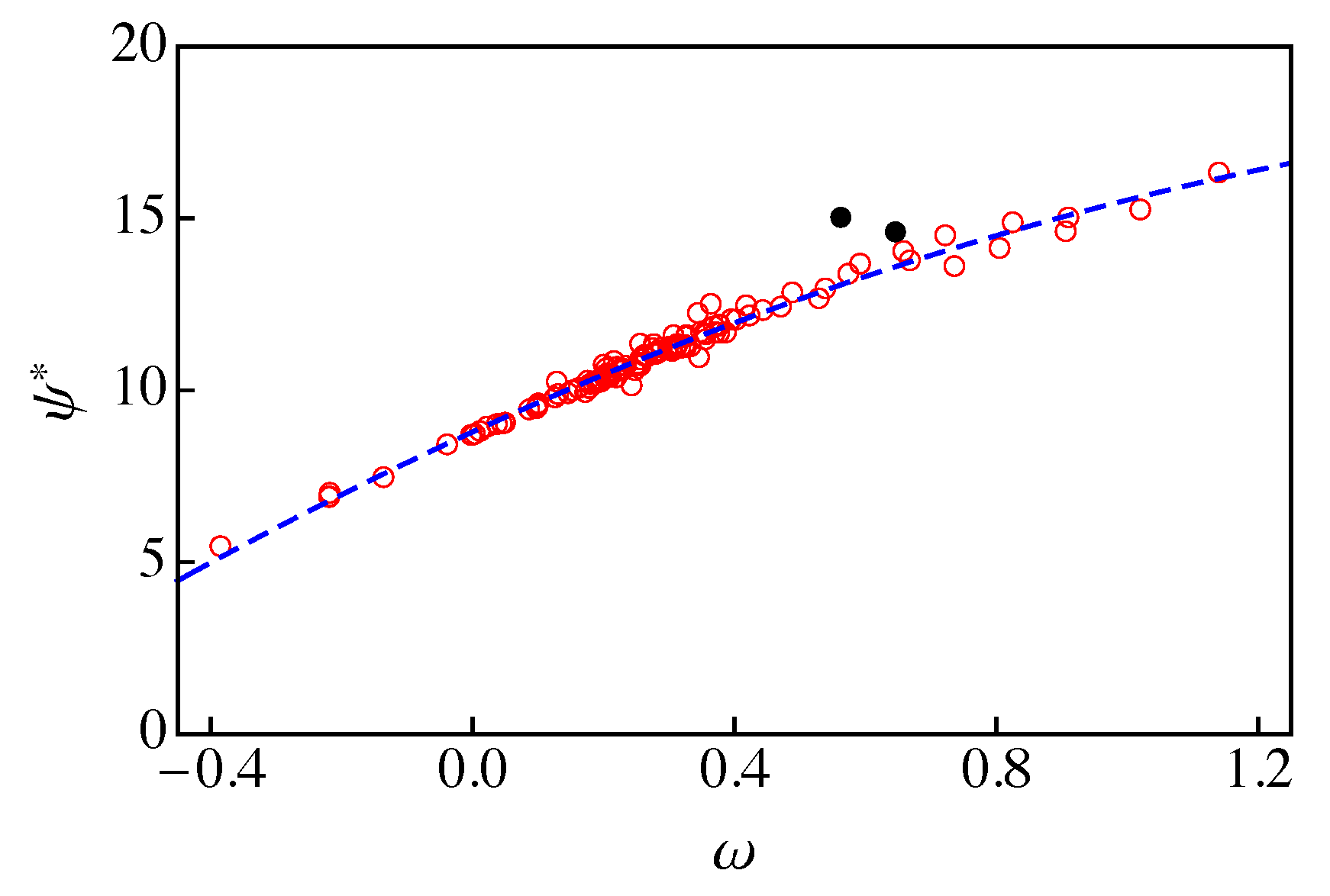
3. The Ideal Gas Contribution to the Entropy
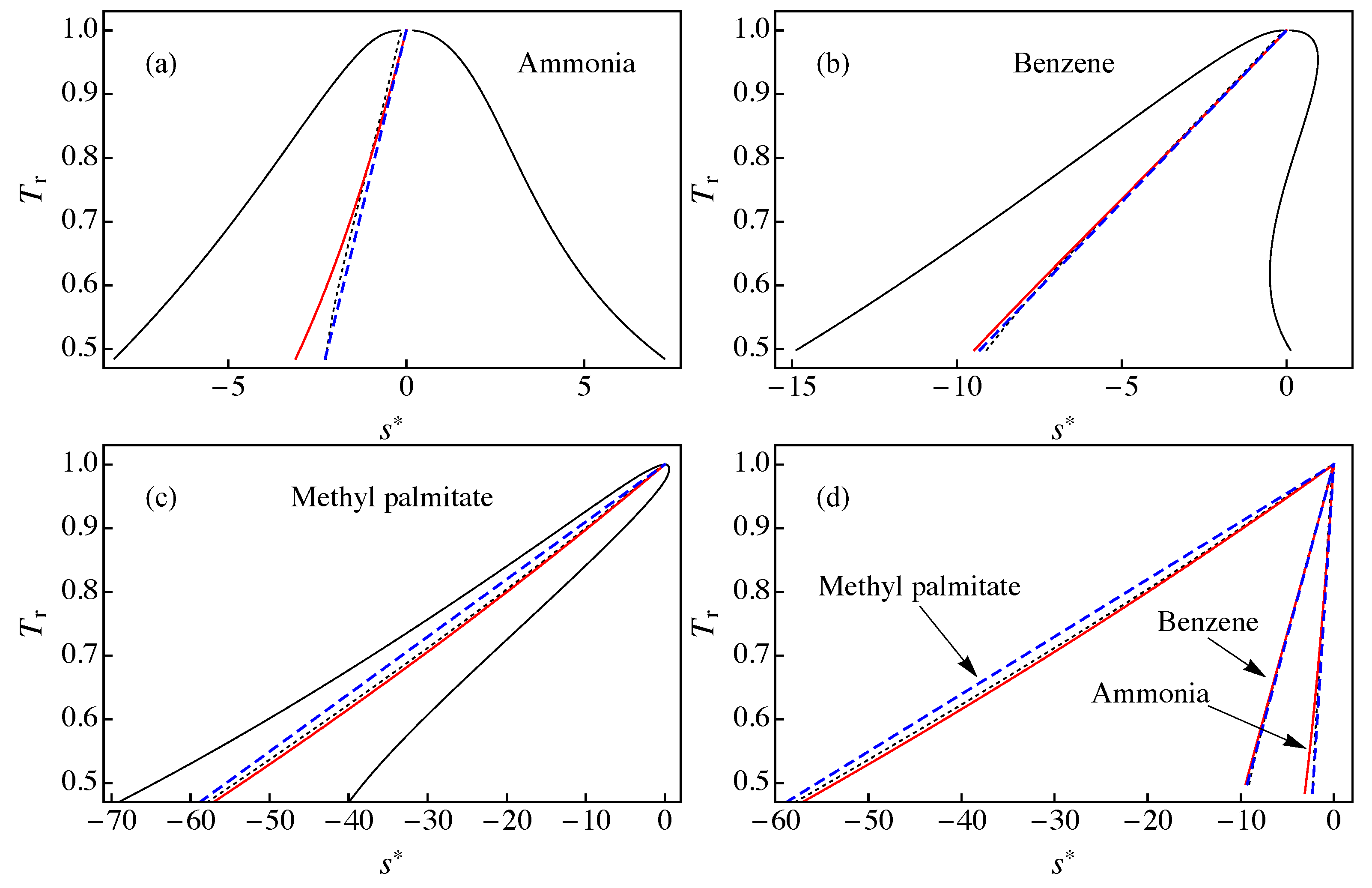
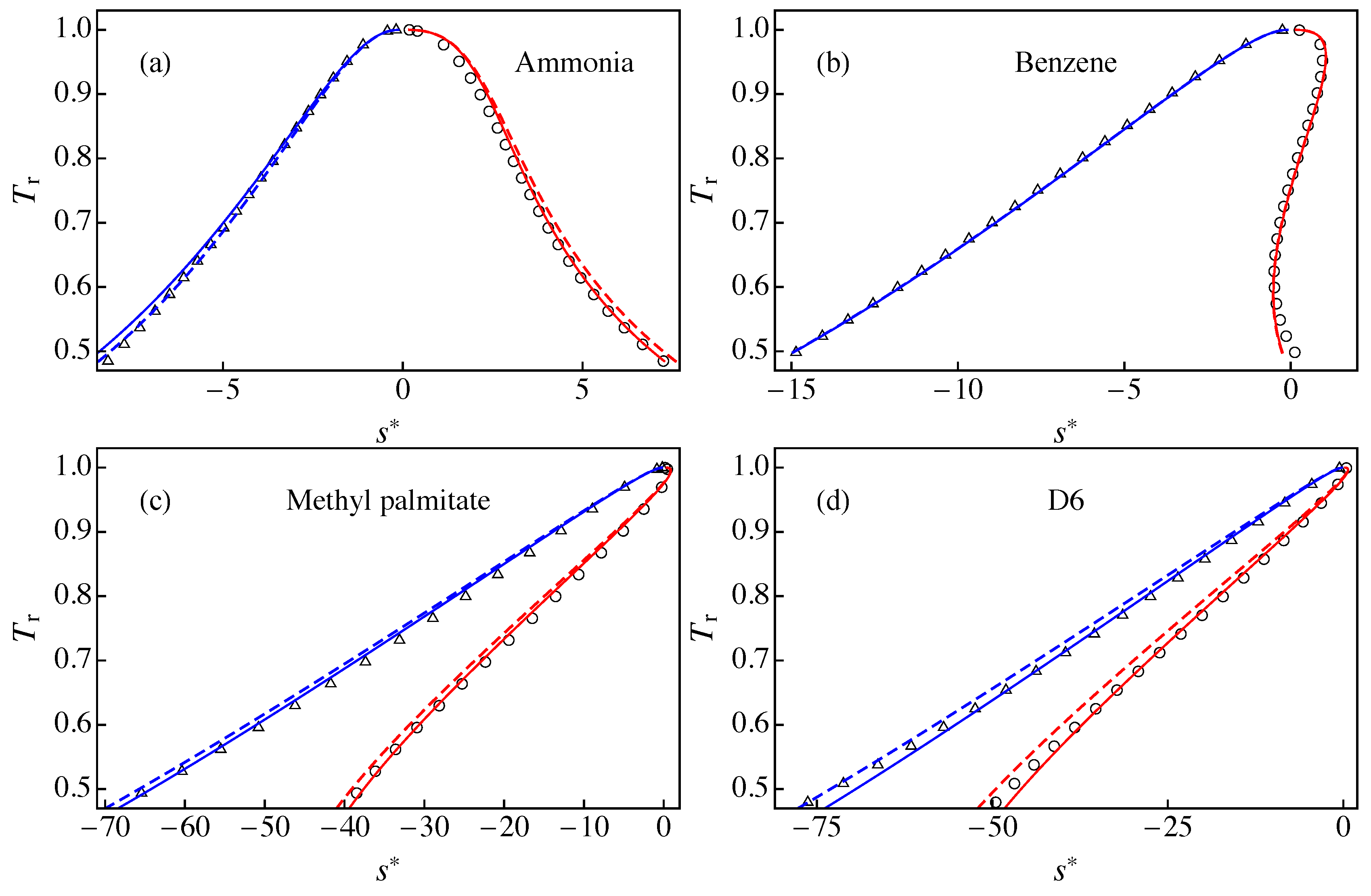
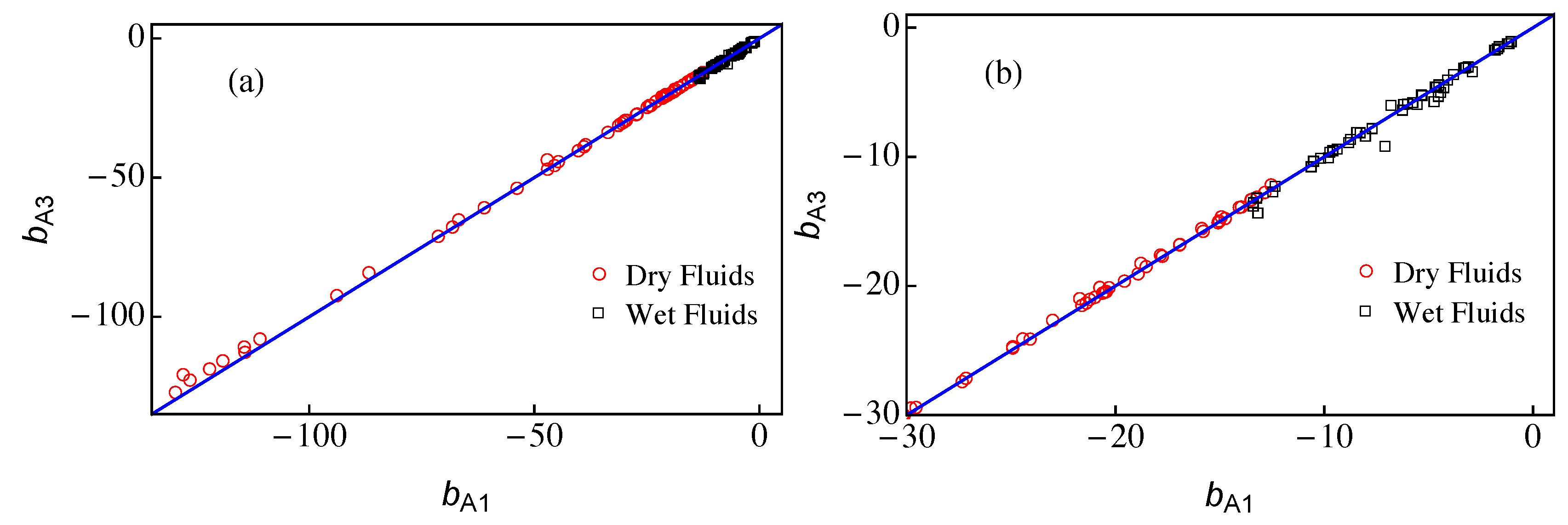
4. A New Approximation for the - Saturation Curve
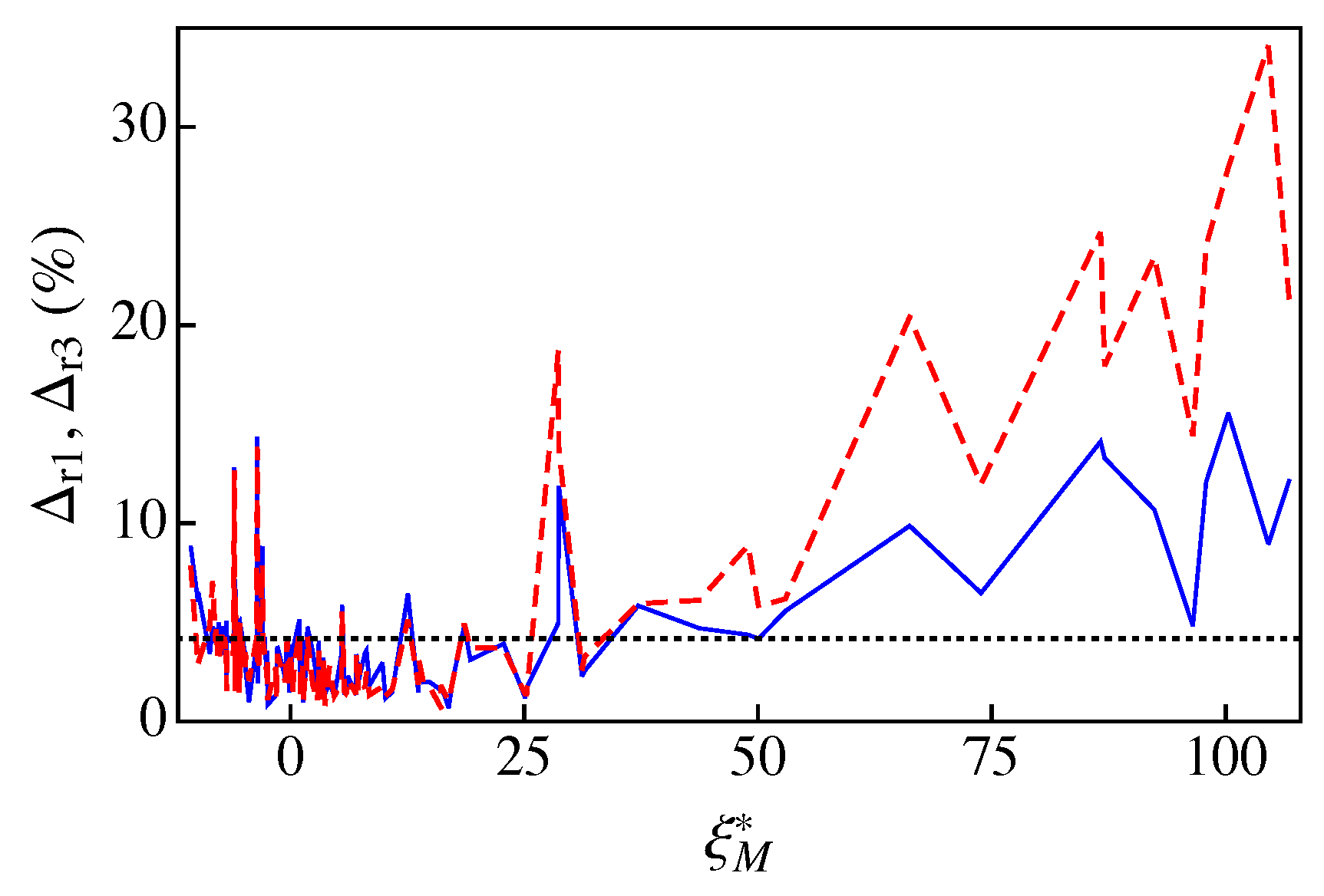
5. Results
6. Summary
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Slope of the modified rectilinear diameter | |
| Percent relative deviation | |
| Molar enthalpy of vaporization, J/mol | |
| Molar volume, m/kmol | |
| Isobaric molar heat capacity, J/(mol K) | |
| p | Pressure, MPa |
| q | Quality |
| R | Gas constant, 8.314472 J/(molK) |
| s | Molar entropy, J/(molK) |
| T | Temperature, K |
| Greek letters | |
| Acentric factor | |
| Inverse of the slope of the saturated vapor curve, J/(molK) | |
| Superscripts | |
| ∗ | Dimensionless |
| ex | Excess |
| ig | Ideal gas |
| r | Residual |
| Subscripts | |
| A1, A2, A3 | Approximations used in this work |
| c | Critical |
| con | Condensation |
| ev | Evaporation |
| g | Saturated vapor |
| l | Saturated liquid |
| M | Point for which presents a maximum |
| r | Reduced |
| Acronyms | |
| ORC | Organic Rankine cycle |
Appendix A
| Fluid | (K) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| methanol | 513.38 | 0.5625 | −10.6364 | 0.7874 | 6.3594 | −7.0892 | −9.1848 | 7.74 | 8.78 |
| heavy water | 643.85 | 0.364 | −9.877 | 0.8071 | 4.5129 | −4.7427 | −5.7266 | 2.86 | 6.06 |
| water | 647.1 | 0.3443 | −9.846 | 0.8018 | 4.2676 | −4.534 | −5.3207 | 2.96 | 6.51 |
| ammonia | 405.4 | 0.256 | −8.6109 | 0.8162 | 4.3795 | −4.4225 | −5.0275 | 4.82 | 3.42 |
| hydrogen chloride | 324.55 | 0.1288 | −8.3196 | 0.8228 | 3.5036 | −2.9154 | −3.4131 | 7.06 | 4.78 |
| R41 | 317.28 | 0.2004 | −7.9926 | 0.8146 | 4.2702 | −4.2672 | −4.6467 | 4.02 | 4.02 |
| carbon dioxide | 304.13 | 0.2239 | −7.9381 | 0.8219 | 4.1683 | −4.6244 | −4.6224 | 4.71 | 4.72 |
| R32 | 351.26 | 0.2769 | −7.7684 | 0.8198 | 5.0411 | −5.5457 | −5.9418 | 3.34 | 3.34 |
| xenon | 289.73 | 0.0036 | −7.6918 | 0.8142 | 2.5 | −1.8437 | −1.7513 | 3.95 | 4.69 |
| krypton | 209.48 | −0.0009 | −7.6578 | 0.8124 | 2.5 | −1.8225 | −1.738 | 4.31 | 4.99 |
| argon | 150.69 | −0.0022 | −7.6561 | 0.8117 | 2.5 | −1.8092 | −1.7342 | 2.99 | 3.6 |
| neon | 44.49 | −0.0387 | −7.3103 | 0.8012 | 2.5 | −1.7047 | −1.6313 | 4.27 | 4.81 |
| sulfur dioxide | 430.64 | 0.2557 | −7.2518 | 0.8202 | 5.0139 | −5.7622 | −5.8093 | 3.64 | 3.36 |
| nitrous oxide | 309.52 | 0.162 | −7.0185 | 0.8224 | 4.3649 | −4.6784 | −4.6055 | 4.23 | 4.71 |
| R23 | 299.29 | 0.263 | −6.8638 | 0.8205 | 5.4574 | −6.2521 | −6.3906 | 3.13 | 2.54 |
| carbon monoxide | 132.86 | 0.0497 | −6.8622 | 0.8091 | 3.5003 | −3.328 | −3.1301 | 3.61 | 5.08 |
| fluorine | 144.41 | 0.0449 | −6.8234 | 0.8118 | 3.5034 | −3.2888 | −3.1183 | 1.54 | 1.93 |
| nitrogen | 126.19 | 0.0372 | −6.8113 | 0.806 | 3.5004 | −3.2219 | −3.0899 | 2.61 | 3.62 |
| hydrogen sulfide | 373.1 | 0.1005 | −6.8028 | 0.8072 | 4.1079 | −4.1004 | −4.0548 | 3.59 | 3.91 |
| oxygen | 154.58 | 0.0222 | −6.72 | 0.8054 | 3.5014 | −3.1095 | −3.044 | 3.77 | 4.28 |
| ethylene | 282.35 | 0.0866 | −6.1541 | 0.8156 | 4.4571 | −4.518 | −4.4365 | 3.39 | 3.97 |
| deuterium | 38.34 | −0.136 | −6.0597 | 0.7992 | 2.5576 | −1.638 | −1.4702 | 3.7 | 4.24 |
| R40 | 416.3 | 0.243 | −6.0057 | 0.8311 | 5.2349 | −6.8109 | −6.0242 | 12.65 | 12.83 |
| methane | 190.56 | 0.0114 | −5.9212 | 0.7978 | 4.0063 | −3.8044 | −3.6343 | 1.57 | 2.11 |
| nitrogen trifluoride | 234.0 | 0.126 | −5.8855 | 0.8261 | 5.0065 | −5.3046 | −5.2579 | 6.46 | 6.78 |
| R14 | 227.51 | 0.1785 | −5.7507 | 0.8153 | 5.4035 | −6.1996 | −5.9544 | 2.73 | 4.29 |
| orthohydrogen | 33.22 | −0.218 | −5.5374 | 0.7814 | 2.5 | −1.1452 | −1.2508 | 4.27 | 4.75 |
| carbonyl sulfide | 378.77 | 0.0978 | −5.4797 | 0.8131 | 5.0426 | −5.3573 | −5.1989 | 1.53 | 2.64 |
| ethanol | 514.71 | 0.646 | −5.4382 | 0.8407 | 10.0811 | −13.1771 | −14.3512 | 1.56 | 4.68 |
| parahydrogen | 32.94 | −0.219 | −5.4225 | 0.7856 | 2.5 | −1.2215 | −1.2493 | 4.84 | 5.02 |
| hydrogen | 33.15 | −0.219 | −5.3996 | 0.7873 | 2.5 | −1.2346 | −1.2493 | 4.94 | 5.04 |
| ethane | 305.32 | 0.0995 | −4.838 | 0.8145 | 5.6208 | −6.0169 | −5.919 | 2.68 | 3.37 |
| R22 | 369.3 | 0.2208 | −4.8229 | 0.819 | 6.768 | −7.7051 | −7.8182 | 3.47 | 2.77 |
| R161 | 375.25 | 0.216 | −4.4255 | 0.8205 | 7.2552 | −8.0304 | −8.3988 | 2.05 | 0.98 |
| propyne | 402.38 | 0.204 | −3.5995 | 0.7971 | 7.7056 | −8.824 | −8.9033 | 4.22 | 3.92 |
| helium | 5.2 | −0.385 | −3.5483 | 0.7489 | 2.5 | −1.0479 | −1.0829 | 13.86 | 14.38 |
| R152a | 386.41 | 0.2752 | −3.4813 | 0.8223 | 8.3897 | −9.8009 | −10.0678 | 2.6 | 1.94 |
| R13 | 302.0 | 0.1723 | −3.3923 | 0.8226 | 7.1846 | −8.4474 | −8.1281 | 2.73 | 4.78 |
| cyclopropane | 398.3 | 0.1305 | −2.9929 | 0.8469 | 7.3234 | −8.2874 | −8.1353 | 7.88 | 8.84 |
| R21 | 451.48 | 0.2061 | −2.9492 | 0.818 | 8.1052 | −9.3764 | −9.4055 | 4.12 | 3.94 |
| propylene | 364.21 | 0.146 | −2.7352 | 0.8214 | 7.6869 | −8.7418 | −8.6436 | 3.39 | 4.04 |
| R143a | 345.86 | 0.2615 | −2.4733 | 0.8183 | 9.0101 | −10.6289 | −10.7696 | 2.09 | 1.83 |
| DME | 400.38 | 0.196 | −2.4475 | 0.8198 | 8.3359 | −9.7307 | −9.6474 | 3.03 | 3.56 |
| trifluoroiodomethane | 396.44 | 0.176 | −2.4241 | 0.7992 | 8.3047 | −9.5876 | −9.526 | 1.1 | 0.85 |
| R134a | 374.21 | 0.3268 | −1.5632 | 0.8172 | 10.3353 | −12.4667 | −12.7222 | 2.73 | 1.32 |
| R12 | 385.12 | 0.1795 | −1.508 | 0.8043 | 8.9565 | −10.516 | −10.345 | 1.23 | 2.2 |
| propane | 369.89 | 0.1521 | −1.3906 | 0.8214 | 8.8547 | −10.1711 | −10.1092 | 3.39 | 3.8 |
| R125 | 339.17 | 0.3052 | −0.5398 | 0.8089 | 10.8094 | −13.2288 | −13.1997 | 2.0 | 2.16 |
| acetone | 508.1 | 0.3071 | −0.3538 | 0.8173 | 11.3098 | −13.3968 | −13.8269 | 4.12 | 4.14 |
| RE143a | 377.92 | 0.289 | −0.1089 | 0.818 | 11.1559 | −13.3826 | −13.5488 | 1.71 | 1.47 |
| sulfur hexafluoride | 318.72 | 0.21 | −0.0175 | 0.8201 | 10.4336 | −12.3555 | −12.2969 | 3.52 | 3.85 |
| R142b | 410.26 | 0.2321 | 0.1386 | 0.8155 | 10.7276 | −12.8389 | −12.7565 | 2.49 | 2.99 |
| R11 | 471.11 | 0.1888 | 0.234 | 0.7864 | 10.4086 | −12.5436 | −12.1762 | 1.53 | 3.64 |
| R116 | 293.03 | 0.2566 | 0.4458 | 0.8128 | 11.087 | −13.5038 | −13.3111 | 2.89 | 4.02 |
| cis-butene | 435.75 | 0.202 | 0.9697 | 0.8248 | 11.1318 | −13.219 | −13.1247 | 4.54 | 5.13 |
| R1234ze | 382.51 | 0.313 | 1.0989 | 0.8034 | 12.2336 | −15.0186 | −14.9966 | 1.25 | 1.38 |
| 1-butene | 419.29 | 0.192 | 1.3717 | 0.823 | 11.331 | −13.4852 | −13.3283 | 3.11 | 4.1 |
| R1234yf | 367.85 | 0.276 | 1.3815 | 0.8076 | 12.1995 | −14.7444 | −14.7751 | 1.1 | 0.97 |
| R124 | 395.42 | 0.2881 | 1.5614 | 0.8091 | 12.4188 | −15.086 | −15.1036 | 2.17 | 2.07 |
| trans-butene | 428.61 | 0.21 | 1.6935 | 0.8185 | 11.7485 | −14.0718 | −13.9202 | 2.07 | 2.9 |
| isobutene | 418.09 | 0.193 | 1.8248 | 0.8193 | 11.7778 | −13.9628 | −13.8841 | 4.27 | 4.77 |
| R141b | 477.5 | 0.2195 | 2.3839 | 0.8112 | 12.3076 | −14.9281 | −14.6517 | 1.87 | 3.55 |
| R115 | 353.1 | 0.248 | 2.9004 | 0.8079 | 12.9368 | −15.8656 | −15.5554 | 1.01 | 1.9 |
| isobutane | 407.81 | 0.184 | 3.044 | 0.8223 | 12.6842 | −15.0477 | −14.9656 | 3.54 | 4.07 |
| R1233zd | 438.75 | 0.305 | 3.0552 | 0.7975 | 13.715 | −16.9118 | −16.786 | 1.27 | 1.43 |
| R123 | 456.83 | 0.2819 | 3.4213 | 0.7994 | 13.8353 | −16.9311 | −16.8226 | 1.04 | 1.31 |
| butane | 425.12 | 0.201 | 3.5432 | 0.8181 | 13.2787 | −15.7971 | −15.7709 | 3.05 | 3.21 |
| R1216 | 358.9 | 0.333 | 3.6838 | 0.8095 | 14.2629 | −17.844 | −17.6026 | 0.8 | 1.36 |
| R245fa | 427.16 | 0.3776 | 4.1683 | 0.8193 | 15.2535 | −18.9125 | −19.0593 | 2.73 | 1.96 |
| R236fa | 398.07 | 0.377 | 4.6989 | 0.7995 | 15.7142 | −19.5696 | −19.6248 | 1.28 | 1.28 |
| R114 | 418.83 | 0.2523 | 5.4626 | 0.7781 | 15.1045 | −18.7798 | −18.2512 | 1.94 | 3.41 |
| cyclopentane | 511.72 | 0.201 | 5.524 | 0.8268 | 14.8424 | −17.7562 | −17.7013 | 5.52 | 5.87 |
| R236ea | 412.44 | 0.369 | 5.7807 | 0.7922 | 16.5039 | −20.6118 | −20.5568 | 1.51 | 1.44 |
| R245ca | 447.57 | 0.355 | 5.9462 | 0.8074 | 16.4625 | −20.4352 | −20.4318 | 1.41 | 1.41 |
| R227ea | 374.9 | 0.357 | 6.0234 | 0.8071 | 16.5119 | −20.5427 | −20.5033 | 1.48 | 1.68 |
| benzene | 562.02 | 0.211 | 6.1558 | 0.8252 | 15.4544 | −18.5302 | −18.4997 | 2.11 | 2.28 |
| RE245cb2 | 406.81 | 0.354 | 7.0324 | 0.796 | 17.3379 | −21.6067 | −21.5073 | 1.39 | 1.36 |
| DEE | 466.7 | 0.281 | 7.039 | 0.8045 | 16.8075 | −20.4947 | −20.4877 | 3.34 | 3.38 |
| R218 | 345.02 | 0.3172 | 7.2705 | 0.8054 | 17.1169 | −21.2347 | −21.0463 | 1.59 | 2.63 |
| DMC | 557.0 | 0.346 | 7.3867 | 0.8129 | 16.9462 | −21.7114 | −20.982 | 2.91 | 2.14 |
| R113 | 487.21 | 0.2525 | 7.4017 | 0.7761 | 16.6127 | −20.7474 | −20.1141 | 2.43 | 2.28 |
| RE245fa2 | 444.88 | 0.387 | 7.9754 | 0.7977 | 18.1268 | −23.0079 | −22.6575 | 1.67 | 3.46 |
| neopentane | 433.74 | 0.1961 | 8.1324 | 0.8216 | 16.828 | −20.3068 | −20.1319 | 2.49 | 3.58 |
| isopentane | 460.35 | 0.2274 | 8.3612 | 0.8179 | 17.3273 | −20.9858 | −20.8834 | 1.81 | 2.43 |
| pentane | 469.7 | 0.251 | 8.4366 | 0.816 | 17.5954 | −21.4005 | −21.3204 | 1.33 | 1.81 |
| RC318 | 388.38 | 0.3553 | 9.8443 | 0.7961 | 19.431 | −24.4359 | −24.0982 | 1.76 | 2.96 |
| R365mfc | 460.0 | 0.377 | 10.1649 | 0.8151 | 19.9073 | −24.9196 | −24.8015 | 1.28 | 1.17 |
| toluene | 591.75 | 0.2657 | 10.8934 | 0.8121 | 19.8028 | −24.0839 | −24.1134 | 1.61 | 1.49 |
| cyclohexane | 553.6 | 0.2096 | 12.5657 | 0.8378 | 20.4864 | −24.9198 | −24.706 | 5.14 | 6.45 |
| hexane | 507.82 | 0.299 | 13.6814 | 0.8127 | 22.3454 | −27.3396 | −27.4114 | 1.87 | 1.46 |
| isohexane | 497.7 | 0.2797 | 13.7711 | 0.8125 | 22.2099 | −27.1569 | −27.1511 | 3.02 | 3.05 |
| RE347mcc | 437.7 | 0.403 | 14.2038 | 0.7903 | 23.5211 | −29.5492 | −29.405 | 2.02 | 1.97 |
| perfluorobutane | 386.33 | 0.371 | 14.8856 | 0.7876 | 23.6981 | −29.8004 | −29.4493 | 1.76 | 2.0 |
| m-xylene | 616.89 | 0.326 | 16.0966 | 0.8077 | 24.2987 | −30.1694 | −29.9569 | 0.7 | 1.58 |
| p-xylene | 616.17 | 0.324 | 16.0973 | 0.8127 | 24.3608 | −30.11 | −30.0235 | 1.82 | 1.82 |
| ethylbenzene | 617.12 | 0.305 | 16.926 | 0.8164 | 24.8511 | −30.6508 | −30.5343 | 1.03 | 0.68 |
| o-xylene | 630.26 | 0.312 | 17.4037 | 0.8105 | 25.3699 | −31.2593 | −31.2093 | 2.15 | 2.2 |
| methylcyclohexane | 572.2 | 0.234 | 18.5937 | 0.8222 | 25.7539 | −31.2969 | −31.316 | 4.93 | 4.82 |
| heptane | 540.13 | 0.349 | 19.2387 | 0.8059 | 27.2864 | −33.6527 | −33.7634 | 3.71 | 3.11 |
| perfluoropentane | 420.56 | 0.423 | 22.8082 | 0.7793 | 30.5375 | −38.5956 | −38.1795 | 3.7 | 3.92 |
| octane | 569.32 | 0.395 | 25.1117 | 0.8011 | 32.3926 | −40.2261 | −40.3133 | 1.37 | 1.19 |
| isooctane | 544.0 | 0.303 | 25.2627 | 0.8145 | 31.6407 | −38.968 | −38.9066 | 1.38 | 1.72 |
| novec649 | 441.81 | 0.471 | 28.6415 | 0.7003 | 34.7076 | −47.1405 | −43.6078 | 18.68 | 4.96 |
| MM | 518.7 | 0.418 | 28.6999 | 0.7645 | 35.4931 | −44.6629 | −44.2692 | 13.84 | 11.87 |
| nonane | 594.55 | 0.4433 | 31.1834 | 0.7963 | 37.5659 | −47.0458 | −46.9732 | 2.59 | 2.29 |
| propylcyclohhexane | 630.8 | 0.326 | 31.4514 | 0.8077 | 37.0298 | −45.5243 | −45.6744 | 3.26 | 2.55 |
| decane | 617.7 | 0.4884 | 37.192 | 0.7864 | 42.8909 | −53.8373 | −53.8158 | 5.94 | 5.84 |
| undecane | 638.8 | 0.539 | 43.7309 | 0.7863 | 48.299 | −61.1241 | −60.8093 | 6.12 | 4.7 |
| MDM | 564.09 | 0.529 | 48.9411 | 0.7539 | 51.8895 | −66.8028 | −65.1781 | 8.89 | 4.38 |
| dodecane | 658.1 | 0.574 | 50.0562 | 0.7743 | 53.7356 | −68.1724 | −67.75 | 5.8 | 4.17 |
| D4 | 586.49 | 0.592 | 52.9243 | 0.7727 | 56.3406 | −71.3409 | −71.0868 | 6.19 | 5.58 |
| MD2M | 599.4 | 0.668 | 66.2116 | 0.7353 | 66.5042 | −86.7477 | −84.1675 | 20.4 | 9.87 |
| D5 | 619.23 | 0.658 | 73.8466 | 0.7473 | 73.2238 | −93.8744 | −92.391 | 11.98 | 6.48 |
| methyl palmitate | 755.0 | 0.91 | 86.6279 | 0.7388 | 84.2017 | −110.949 | −107.9614 | 24.68 | 14.12 |
| methyl linolenate | 772.0 | 1.14 | 87.0511 | 0.7625 | 86.3193 | −114.2828 | −112.7746 | 17.94 | 13.3 |
| MD3M | 628.36 | 0.722 | 92.3726 | 0.7165 | 87.7973 | −114.4347 | −110.8565 | 23.44 | 10.69 |
| methyl linoleate | 799.0 | 0.805 | 96.4907 | 0.7361 | 91.2891 | −119.2024 | −115.8209 | 14.41 | 4.83 |
| methyl oleate | 782.0 | 0.906 | 97.9157 | 0.7395 | 92.9609 | −122.1459 | −118.7401 | 24.02 | 12.09 |
| methyl stearate | 775.0 | 1.02 | 100.2849 | 0.7366 | 95.3592 | −126.492 | −122.7452 | 27.94 | 15.56 |
| D6 | 645.78 | 0.736 | 104.5704 | 0.6897 | 95.7557 | −128.0031 | −120.7889 | 34.1 | 8.95 |
| MD4M | 653.2 | 0.825 | 106.7797 | 0.7384 | 100.342 | −129.7364 | −127.1614 | 21.34 | 12.13 |
References
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Tchanche, B.F.; Lemort, V. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles. Appl. Therm. Eng. 2011, 31, 2885–2893. [Google Scholar] [CrossRef] [Green Version]
- Wang, E.; Zhang, H.; Fan, B.; Ouyang, M.; Zhao, Y.; Mu, Q. Study of working fluid selection of organic Rankine cycle (ORC) for engine waste heat recovery. Energy 2011, 36, 3406–3418. [Google Scholar] [CrossRef]
- SprouseIII, C.; Depcik, C. Review of organic Rankine cycles for internal combustion engine exhaust waste heat recovery. Appl. Therm. Eng. 2013, 51, 711–722. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sust. Energ. Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Hærvig, J.; Sørensen, K.; Condra, T. Guidelines for optimal selection of working fluid for an organic Rankine cycle in relation to waste heat recovery. Energy 2016, 96, 592–602. [Google Scholar] [CrossRef]
- Liu, B.T.; Chien, K.H.; Wang, C.C. Effect of working fluids on organic Rankine cycle for waste heat recovery. Energy 2004, 29, 1207–1217. [Google Scholar] [CrossRef]
- Györke, G.; Deiters, U.K.; Groniewsky, A.; Lassu, I.; Imre, A.R. Novel classification of pure working fluids for Organic Rankine Cycle. Energy 2018, 145, 288–300. [Google Scholar] [CrossRef]
- Györke, G.; Groniewsky, A.; Imre, A.R. A Simple Method of Finding New Dry and Isentropic Working Fluids for Organic Rankine Cycle. Energies 2019, 12, 480. [Google Scholar] [CrossRef]
- Imre, A.R.; Kustán, R.; Groniewsky, A. Thermodynamic Selection of the Optimal Working Fluid for Organic Rankine Cycles. Energies 2019, 12, 2028. [Google Scholar] [CrossRef]
- Morrison, G. The shape of the temperature-entropy saturation boundary. Int. J. Refrig 1994, 17, 494–504. [Google Scholar] [CrossRef]
- Garrido, J.M.; Quinteros-Lama, H.; Mejía, A.; Wisniak, J.; Segura, H. A rigorous approach for predicting the slope and curvature of the temperature-entropy saturation boundary of pure fluids. Energy 2012, 45, 888–899. [Google Scholar] [CrossRef]
- Albornoz, J.; Mejía, A.; Quinteros-Lama, H.; Garrido, J.M. A rigorous and accurate approach for predicting the wet-to-dry transition for working mixtures in organic Rankine cycles. Energy 2018, 156, 509–519. [Google Scholar] [CrossRef]
- Groniewsky, A.; Györke, G.; Imre, A.R. Description of wet-to-dry transition in model ORC working fluids. Appl. Therm. Eng. 2017, 125, 963–971. [Google Scholar] [CrossRef]
- Groniewsky, A.; Imre, A.R. Prediction of the ORC Working Fluid’s Temperature-Entropy Saturation Boundary Using Redlich-Kwong Equation of State. Entropy 2018, 20, 93. [Google Scholar] [CrossRef]
- White, J.A.; Velasco, S. A Simple Semiempirical Method for Predicting the Temperature-Entropy Saturation Curve of Pure Fluids. Ind. Eng. Chem. Res. 2019, 58, 1038–1043. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.1. Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013.
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [Green Version]
- Mulero, A.; Cachadina, I.; Parra, M.I. Comparison of corresponding-states-based correlations for the prediction of the vaporization enthalpy of fluids. Ind. Eng. Chem. Res. 2008, 47, 7903–7916. [Google Scholar] [CrossRef]
- Velasco, S.; Santos, M.J.; White, J.A. Extended corresponding states expressions for the changes in enthalpy, compressibility factor and constant-volume heat capacity at vaporization. J. Chem. Thermodyn. 2015, 85, 68–76. [Google Scholar] [CrossRef]
- Watson, K. Prediction of critical temperatures and heats of vaporization. Ind. Eng. Chem. 1931, 23, 360–364. [Google Scholar] [CrossRef]
- Cailletet, L.; Mathias, E. Recherches sur les densités des gaz liquéfiés et de leurs vapeurs saturées. J. Phys. Theor. Appl. 1886, 5, 549–564. [Google Scholar] [CrossRef]
- White, J.; Velasco, S. Characterizing wet and dry fluids in temperature-entropy diagrams. Energy 2018, 154, 269–276. [Google Scholar] [CrossRef] [Green Version]
- Aly, F.A.; Lee, L.L. Self-consistent equations for calculating the ideal gas heat capacity, enthalpy, and entropy. Fluid Phase Equilib. 1981, 6, 169–179. [Google Scholar] [CrossRef]
- Rowley, R.; Wilding, W.; Oscarson, J.; Yang, Y.; Zundel, N.; Daubert, T.; Danner, R. DIPPR data compilation of pure chemical properties. In DIPPR Data Compilation of Pure Chemical Properties; Design Institute for Physical Properties: New York, NY, USA, 2006. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
White, J.A.; Velasco, S. Approximating the Temperature–Entropy Saturation Curve of ORC Working Fluids From the Ideal Gas Isobaric Heat Capacity. Energies 2019, 12, 3266. https://doi.org/10.3390/en12173266
White JA, Velasco S. Approximating the Temperature–Entropy Saturation Curve of ORC Working Fluids From the Ideal Gas Isobaric Heat Capacity. Energies. 2019; 12(17):3266. https://doi.org/10.3390/en12173266
Chicago/Turabian StyleWhite, Juan A., and Santiago Velasco. 2019. "Approximating the Temperature–Entropy Saturation Curve of ORC Working Fluids From the Ideal Gas Isobaric Heat Capacity" Energies 12, no. 17: 3266. https://doi.org/10.3390/en12173266
APA StyleWhite, J. A., & Velasco, S. (2019). Approximating the Temperature–Entropy Saturation Curve of ORC Working Fluids From the Ideal Gas Isobaric Heat Capacity. Energies, 12(17), 3266. https://doi.org/10.3390/en12173266





