Pure and Hydrocarbon Binary Mixtures as Possible Alternatives Working Fluids to the Usual Organic Rankine Cycles Biomass Conversion Systems
Abstract
1. Introduction
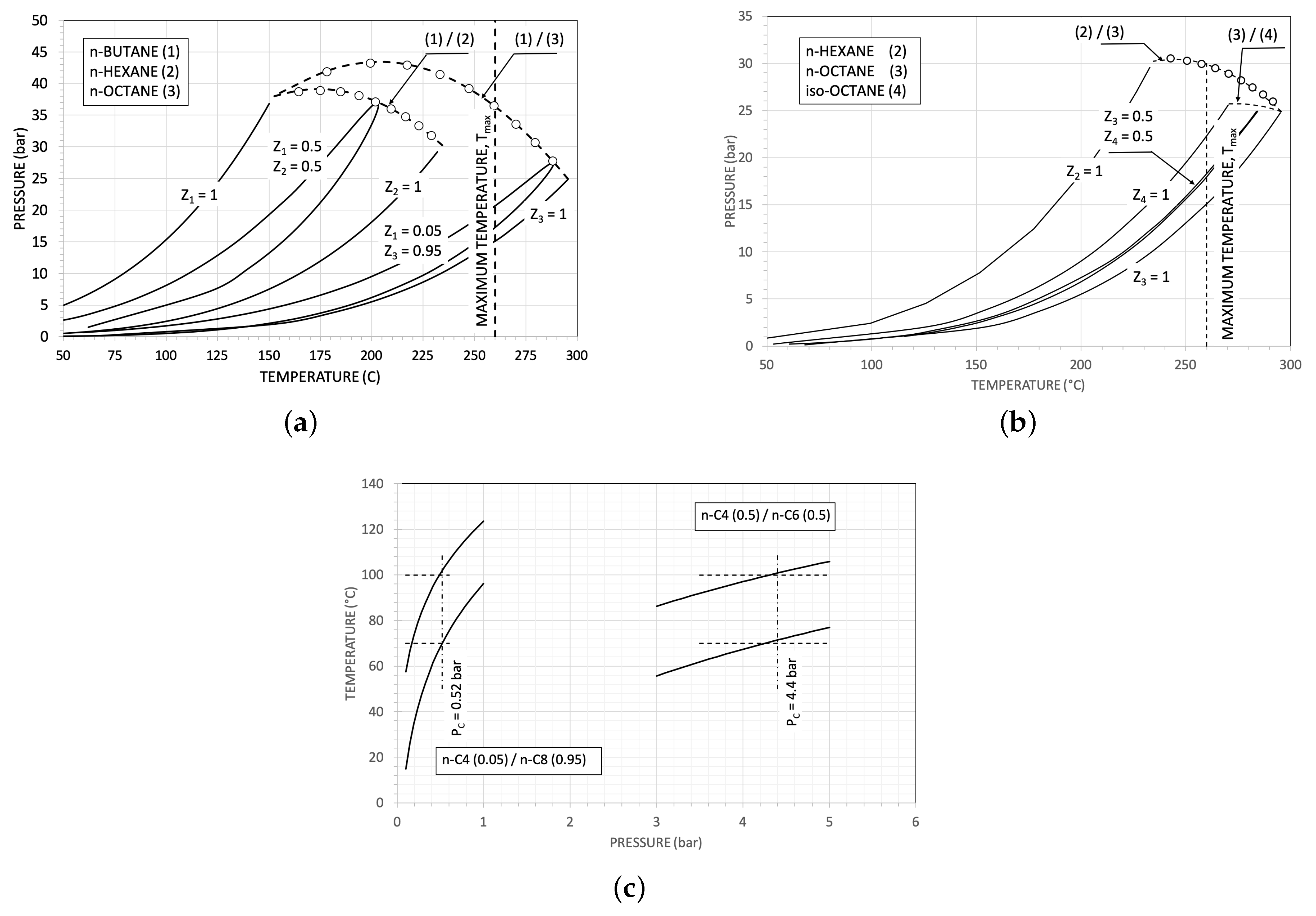
2. The Selection of The Working Fluids
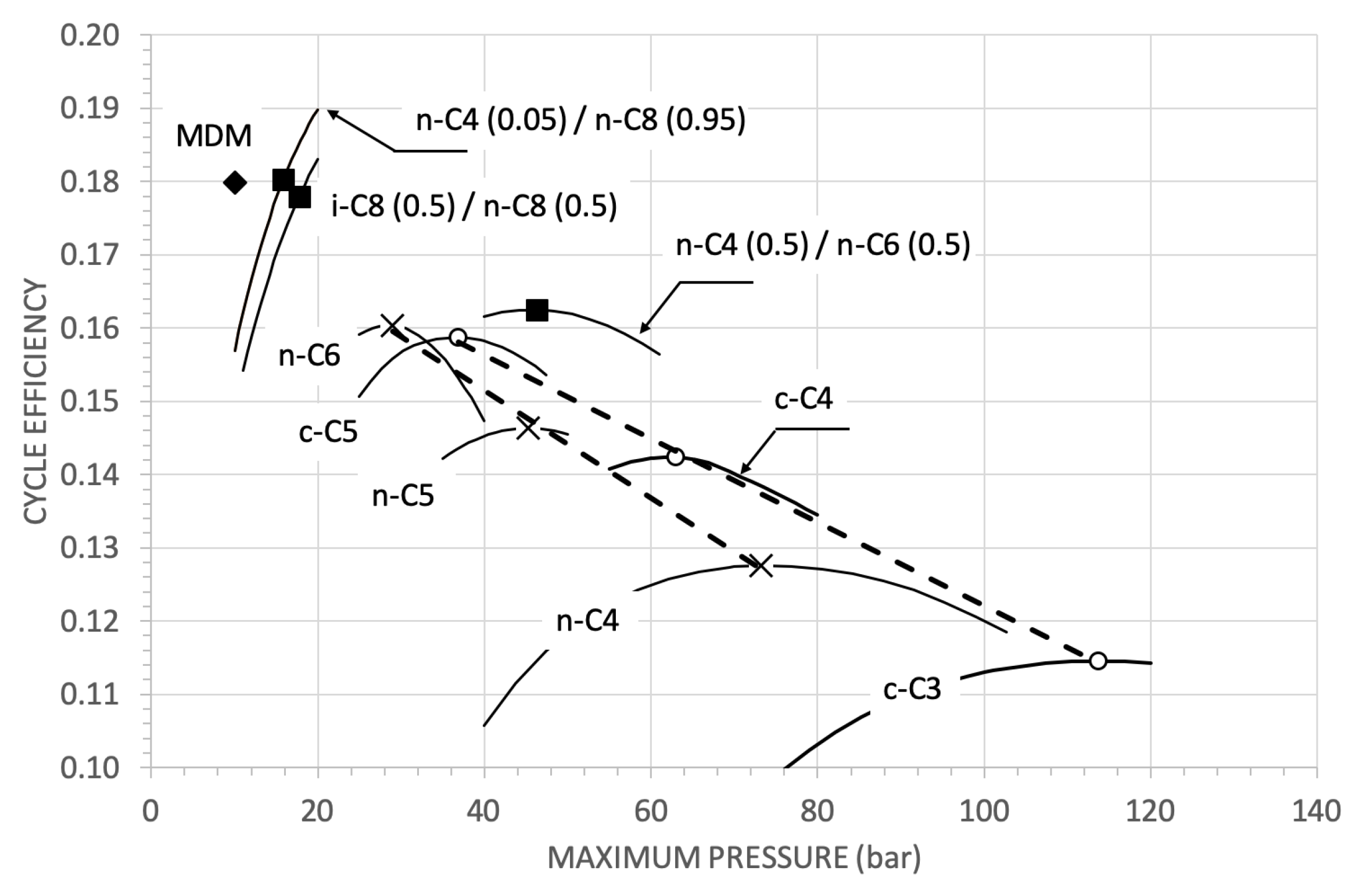
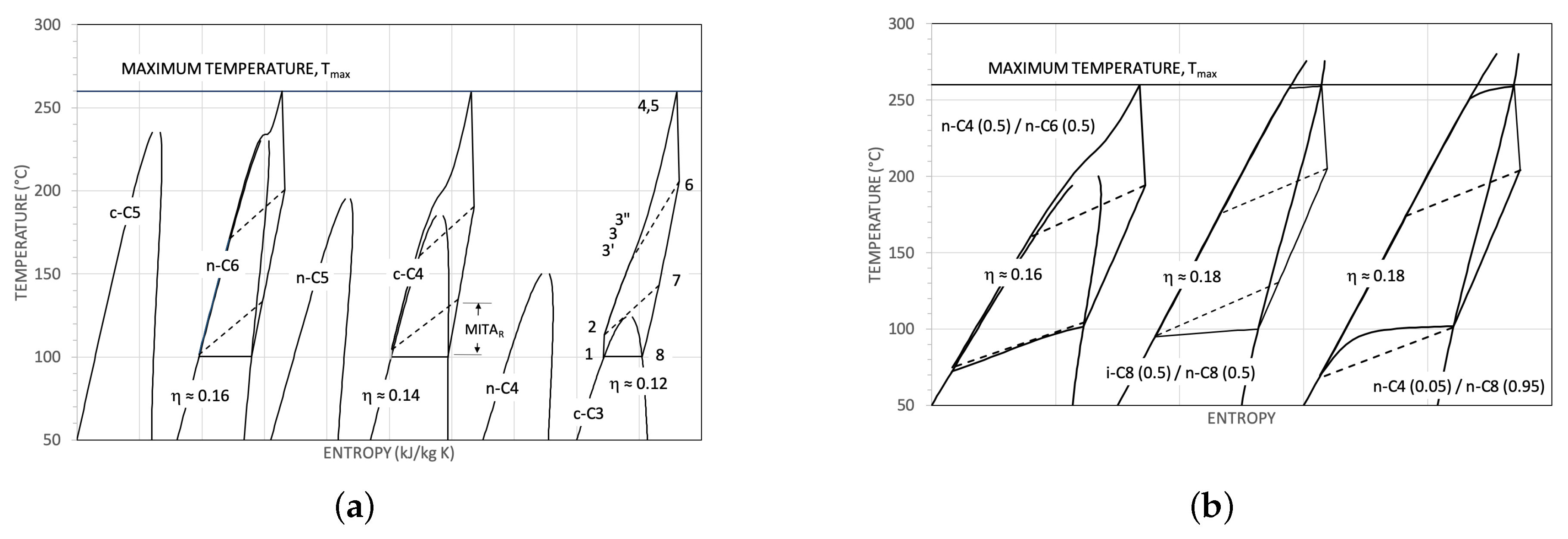
3. The Thermodynamic Results
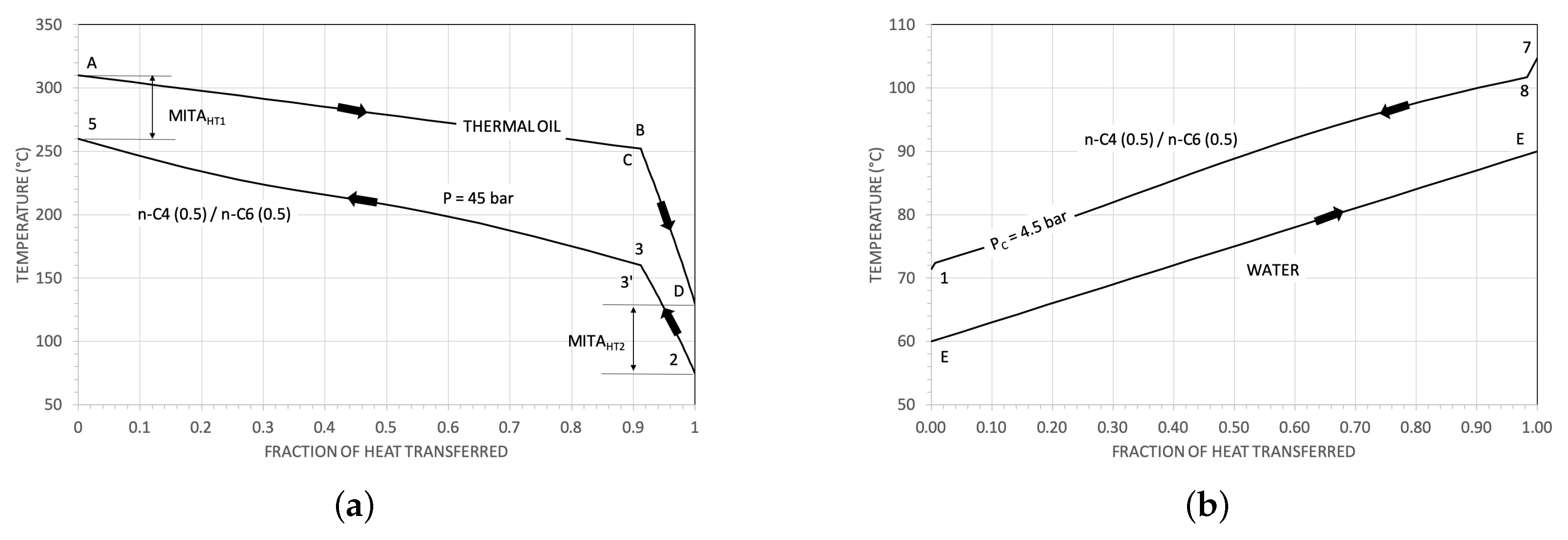
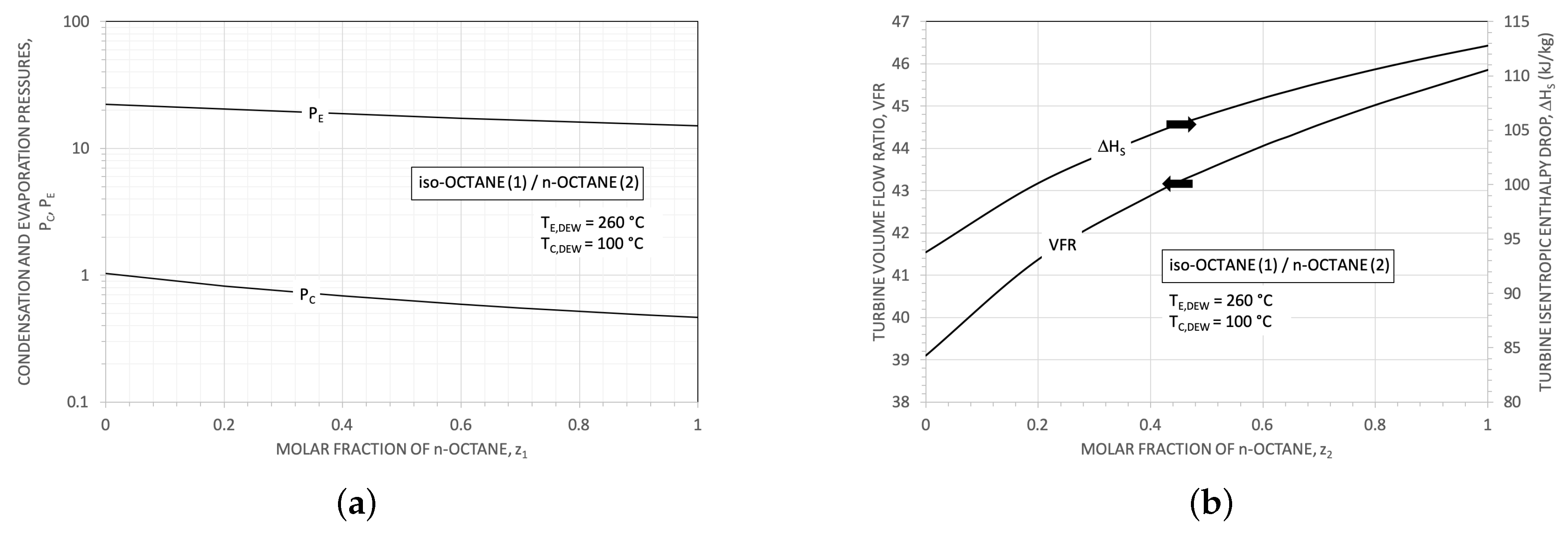
3.1. Some Results for the Heat Exchangers
3.2. Turbomachinery Considerations
4. Conclusions
- the super-critical cycles, mainly owing to their high pumping power relative to the expansion useful power, have basically lower thermodynamic efficiencies than the reference cycle. In the better cases, for example, 0.16 against 0.18. The use of mixtures, allowing in principle an optimisation of the diagram in condensation, performs a bit better than the pure fluids. But, at least in the considered cases, always worse of about 1.5 points percent than the reference thermodynamic efficiency;
- the considered saturated cycles have thermodynamic efficiencies completely comparable with the reference value.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A | total heat transfer area, (m2) |
| CHP | Combined and Heat Power |
| specific diameter | |
| D | mean turbine diameter (m) |
| Minimum Internal Temperature Approach in the recuperator (°C) | |
| Minimum Internal Temperature Approach in the HT heat exchanger (°C) | |
| MDM | Octamethyltrisiloxane |
| specific speed | |
| N | speed revolution (rpm) |
| condensation pressure (bar) | |
| critical pressure (bar) | |
| maximum cycle pressure (bar) | |
| PR EoS | Peng-Robinson Equation of State |
| inlet thermal power (kW) | |
| recovered thermal power (kW) | |
| R | gas constant (kJ kg−1 K−1) |
| S | entropy (kJ kg−1 K−1) |
| size parameter for a stage of axial turbine (m) | |
| T | temperature (°C or K) |
| maximum temperature of the heat source (thermal oil) (°C or K) | |
| critical temperature (°C or K) | |
| reduced temperature | |
| U | overall heat transfer coefficient (W m−2 K−1) |
| volumetric flow rate (m3 s−1) | |
| isentropic flow ratio | |
| mechanical or electrical power (kW) | |
| isentropic power (kW) | |
| z | molar fraction |
| isentropic turbine work (kJ kg−1) | |
| temperature difference (°C) | |
| turbine efficiency | |
| pump efficiency | |
| density (kg m−3) | |
| parameter of molecular complexity | |
| subscripts | |
| C | condensation |
| dew conditions | |
| E | evaporation |
| inlet | |
| maximum | |
| outlet | |
| P | pump |
| S | isentropic conditions |
| sv | saturated vapour |
| T | turbine |
References
- Anonymous. State of Play o the Sustainability of Solid and Gaseous Biomass Used for Electricity, Heating and Cooling in the EU. Commission Staff Working Document. Available online: https://ec.europa.eu/energy/en/topics/renewable-energy/biomass (accessed on 8 August 2019).
- Bogaert, S.; Pelkmans, L.; van den Heuvel, E.; Devriendt, N.; De Regel, S.; Hoefnahels, R.; Junginger, M.; Resch, G.; Liebmann, L.; Mantau, U.; et al. Sustainable and Optimal Use of Biomass for Energy in the EU beyond 2020—Final Report. May 2017. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/biosustain_report_final.pdf (accessed on 8 August 2019).
- Angelino, G.; Invernizzi, C. Cyclic Methylsiloxanes as Working Fluids for Space Power Cycles. Trans. ASME J. Sol. Energy Eng. 1993, 115, 130–137. [Google Scholar] [CrossRef]
- Obernberger, I.; Biedermann, F. Combustion and Gasification of Solid Biomass for Heat and Power Production in Europe – State-of-the-Art and Relevant Future Development. In Proceedings of the 8th European Conference on Industrial Furnaces and Boilers, Vilamoura, Portugal, 25–28 March 2008; Keynote Lecture. CENERTEC: Vilamoura, Portugal, 2008; pp. 1–24. [Google Scholar]
- Weith, T.; Heberle, F.; Preißinger, M.; Brüggermann, D. Performance of Siloxane Mixtures in a High-Temperature Organic Rankine Cycle Considering the Heat Transfer Characteristics during Evaporation. Energies 2014, 7, 5548–5565. [Google Scholar] [CrossRef]
- Preißinger, M.; Brüggermann, D. Thermal Stability of Hexamethyldisiloxane (MM) for High-Temperature Organic Rankine Cycle (ORC). Energies 2016, 9, 183. [Google Scholar] [CrossRef]
- Keulen, L.; Landolina, C.; Spinelli, A.; Iora, P.; Invernizzi, C.; Lietti, L.; Guardone, A. Thermal stability of hexamethyldisiloxane and octamethyltrisiloxane. Energy Part B 2018, 165, 868–876. [Google Scholar] [CrossRef]
- Dai, X.; Shi, L.; Qian, W. Thermal stability of hexamethyldisiloxane (MM) as a working fluid for organic Rankine cycles. Int. J. Energy Res. 2019, 43, 896–904. [Google Scholar] [CrossRef]
- Erhart, T.G.; Gölz, J.; Eicker, U.; van der Broek, M. Working Fluid Stability in Large-Scale Organic Rankine Cycle-Units Using Siloxanes—Long-Term Experiences and Fluid Recycling. Energies 2016, 9, 422. [Google Scholar] [CrossRef]
- Invernizzi, C.M.; Bonalumi, D. Thermal stability of organic fluids for Organic Rankine Cycle systems. In Organic Rankine Cycle (ORC) Power Systems. Technologies and Applications; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Duxford, UK, 2017; pp. 123–151. [Google Scholar]
- Rajabloo, T.; Bonalumi, D.; Iora, P. Effect of a partial decomposition of the working fluid on the performances of ORC power plants. Energy 2017, 133, 1013–1026. [Google Scholar] [CrossRef]
- Dai, X.; Shi, L.; An, Q.; Qian, W. Influence of alkane working fluid decomposition on supercritical organic Rankine cycle systems. Energy 2018, 153, 422–430. [Google Scholar] [CrossRef]
- Angelino, G.; Colonna di Paliano, P. Multicomponent Working Fluids For Organic Rankine Cycles (ORCs). Energy 1998, 23, 449–463. [Google Scholar] [CrossRef]
- Drescher, U.; Brüggermann, D. Fluid selection for the Organic Rankine Cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar] [CrossRef]
- Invernizzi, C.M.; Iora, P.; Bonalumi, D.; Macchi, E.; Roberto, R.; Caldera, M. Titanium tetrachloride as novel working fluid for high temperature Rankine Cycles: Thermodynamic analysis and experimental assessment of the thermal stability. Appl. Therm. Eng. 2016, 107, 21–27. [Google Scholar] [CrossRef]
- Invernizzi, C.; Binotti, M.; Bombarda, P.; Di Marcoberardino, G.; Iora, P.; Manzolini, G. Water Mixtures as Working Fluids in Organic Rankine Cycles. Energies 2019, 12, 2629. [Google Scholar] [CrossRef]
- Salogni, A.; Alberti, D.; Metelli, M.; Bertanzi, R. Operation and maintenance of a biomass fired—Organic Rankine Cycle—CHP plant: the experience of Cremona. Energy Procedia 2017, 129, 668–675. [Google Scholar] [CrossRef]
- Invernizzi, C.M.; van der Stelt, T. Supercritical and real gas Brayton cycles operating with mixtures of carbon dioxide and hydrocarbons. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 682–693. [Google Scholar] [CrossRef]
- Manente, G.; Lazzaretto, A. Innovative biomass to power conversion systems based on cascaded supercritical CO2 Brayton cycles. Biomass Bioenergy 2014, 69, 155–168. [Google Scholar] [CrossRef]
- Astolfi, M.; Lasala, S.; Macchi, E. Selection Maps For ORC And CO2 Systems For Low-Medium Temperature Heat Sources. Energy Procedia 2017, 129, 971–978. [Google Scholar] [CrossRef]
- Invernizzi, C.M. Prospects of Mixtures as Working Fluids in Real-Gas Brayton Cycles. Energies 2017, 10, 1649. [Google Scholar] [CrossRef]
- Invernizzi, C.M.; Iora, P.; Preißinger, M.; Manzolini, G. HFOs as substitute for R-134a as working fluids in ORC power plants: A thermodynamic assessment and thermal stability analysis. Appl. Therm. Eng. 2016, 103, 790–797. [Google Scholar] [CrossRef]
- Huo, E.; Liu, C.; Xin, L.; Li, X.; Xu, X.; Li, Q.; Wang, S.; Dang, C. Thermal stability and decomposition mechanism of HFO-1336mzz(Z) as an environmental friendly working fluid: Experimental and theoretical study. Int. J. Energy Res. 2019, 1–14. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P. On the systematic design and selection of optimal working fluids for Organic Rankine Cycles. Appl. Therm. Eng. 2010, 30, 760–769. [Google Scholar] [CrossRef]
- Toffolo, A.; Lazzaretto, A.; Manente, G.; Paci, M. A multi-criteria approach for the optimal selection of working fluid and design parameters in Organic Rankine Cycle systems. Appl. Energy 2014, 121, 219–232. [Google Scholar] [CrossRef]
- Vivian, J.; Manente, G.; Lazzaretto, A. A general framework to select working fluid and configuration of ORCs for low-to-medium temperature heat sources. Appl. Energy 2015, 156, 727–746. [Google Scholar] [CrossRef]
- Braimakis, K.; Preißinger, M.; Brüggermann, D.; Karellas, S.; Panopoulos, K. Low grade waste heat recovery with subcritical and supercritical Organic Rankine Cycle based on natural refrigerants and their binary mixtures. Energy 2015, 88, 80–92. [Google Scholar] [CrossRef]
- Astolfi, M.; Martelli, E.; Pierobon, L. Thermodynamic and technoeconomic optimization of Organic Rankine Cycle systems. In Organic Rankine Cycle (ORC) Power Systems. Technologies and Applications; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Duxford, UK, 2017; pp. 173–249. [Google Scholar]
- Scaccabarozzi, R.; Tavano, M.; Invernizzi, C.M.; Martelli, E. Comparison of working fluids and cycle optimization for heat recovery ORCs from large internal combustion engines. Energy 2018, 158, 396–416. [Google Scholar] [CrossRef]
- Miao, Z.; Zhang, K.; Wang, M.; Xu, J. Thermodynamic selection criteria of zeotropic mixtures for subcritical organic Rankine cycle. Energy 2019, 167, 484–497. [Google Scholar] [CrossRef]
- Yaǧli, H.; Koç, Y.; Koç, A.; Görgülü, A.; Tandiroǧlu, A. Parametric optimization and exergetic analysis comparison of subcritical and supercritical organic Rankine cycke (ORC) for biogas fuelled combined heat and power (CHP) engine exhaust gas waste heat. Energy 2016, 111, 923–932. [Google Scholar] [CrossRef]
- Imran, M.; Haglind, F.; Lemort, V.; Meroni, A. Optimization of organic Rankine cycle power systems for waste heat recovery on heavy-duty vehicles considering the performance, cost, mass and volume of the system. Energy 2019, 180, 229–241. [Google Scholar] [CrossRef]
- Bonafin, J.; Di Schio, C.R.; Duvia, A. Turboden, a Presentation of Recent Worldwide Developments and Large-Scale Geothermal ORC Power-Plants. Trans. Geotherm. Resour. Counc. 2015, 39, 827–831. [Google Scholar]
- Invernizzi, C.M. Closed Power Cycles—Thermodynamic Fundamentals and Applications; Springer: London, UK, 2013. [Google Scholar]
- Hicks, C.P.; Young, C.L. The Gas-Liquid Critical Properties of Binary Mixtures. Chem. Rev. 1975, 75, 119–175. [Google Scholar] [CrossRef]
- Rump, S.M. INTLAB—INTTerval LABoratory. In Developments in Reliable Computing; Csendes, T., Ed.; Springer Science+Business Media: Dordrecht, The Netherlands, 1999; pp. 77–104. [Google Scholar]
- Heidemann, R.A.; Khalil, A.M. The calculation of critical points. AIChE J. 1980, 26, 769–779. [Google Scholar] [CrossRef]
- Michelsen, M.L.; Heidemann, A.M. Calculation of critical points from cubic two-constant equation of state. AIChE J. 1981, 27, 521–523. [Google Scholar] [CrossRef]
- Pasetti, M.; Invernizzi, C.M.; Iora, P. Thermal stability of working fluids for organic Rankine cycles: An improved survey method and experimental results for cyclopentane, isopentane and n-butane. Appl. Therm. Eng. 2014, 73, 764–774. [Google Scholar] [CrossRef]
- Invernizzi, C.M.; Iora, P.; Manzolini, G.; Lasala, S. Thermal stability of n-pentane, cyclo-pentane and toluene as working fluids in organic Rankine engines. Appl. Therm. Eng. 2017, 121, 172–179. [Google Scholar] [CrossRef]
- Dai, X.; Shi, L.; An, Q.; Qian, W. Chemical kinetics method for evaluating the thermal stability of Organic Rankine Cycle working fluids. Appl. Therm. Eng. 2016, 100, 708–713. [Google Scholar] [CrossRef]
- Dai, X.; Shi, L.; An, Q.; Qian, W. Screening of hydrocarbons as supercritical ORCs working fluids by thermal stability. Energy Convers. Manag. 2016, 126, 632–637. [Google Scholar] [CrossRef]
- Invernizzi, C.; Bombarda, P. Thermodynamic performance of selected HCFCS for geothermal applications. Energy 1997, 22, 887–895. [Google Scholar] [CrossRef]
- Bromiley, E.C.; Quiggle, D. Vapor-Liquid Equilibria of Hydrocarbon Mixtures. Ind. Eng. Chem. 1933, 25, 1136–1138. [Google Scholar] [CrossRef]
- Macchi, E.; Astolfi, M. Axial flow turbines for Organic Rankine Cycle applications. In Organic Rankine Cycle (ORC) Power Systems. Technologies and Applications; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Duxford, UK, 2017; pp. 299–319. [Google Scholar]
- Bombarda, P.; Invernizzi, C. Binary liquid metal-organic Rankine cycle for small power distributed high efficiency systems. Proc. IMechE Part A J. Power Energy 2015, 229, 192–209. [Google Scholar] [CrossRef]
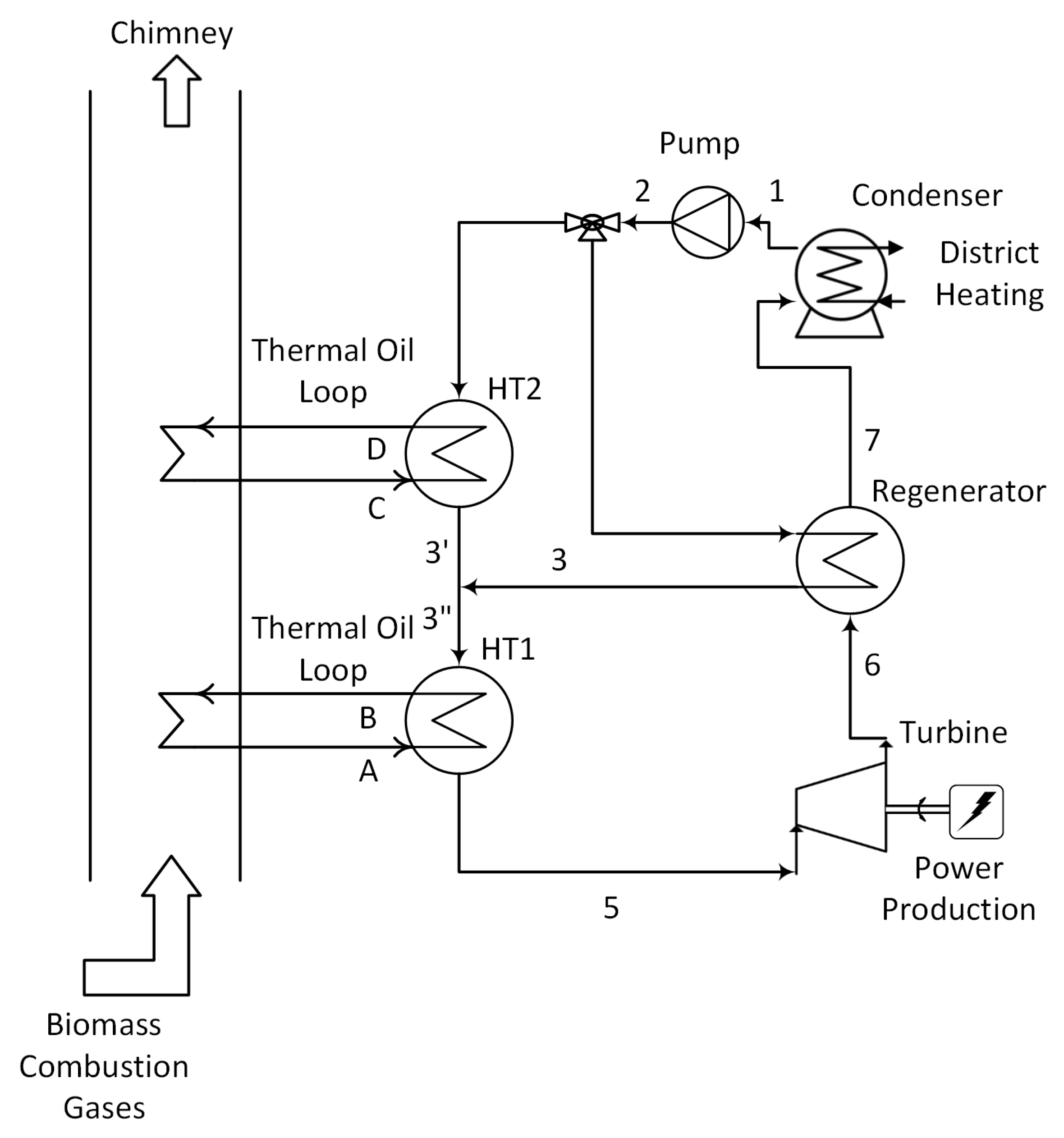
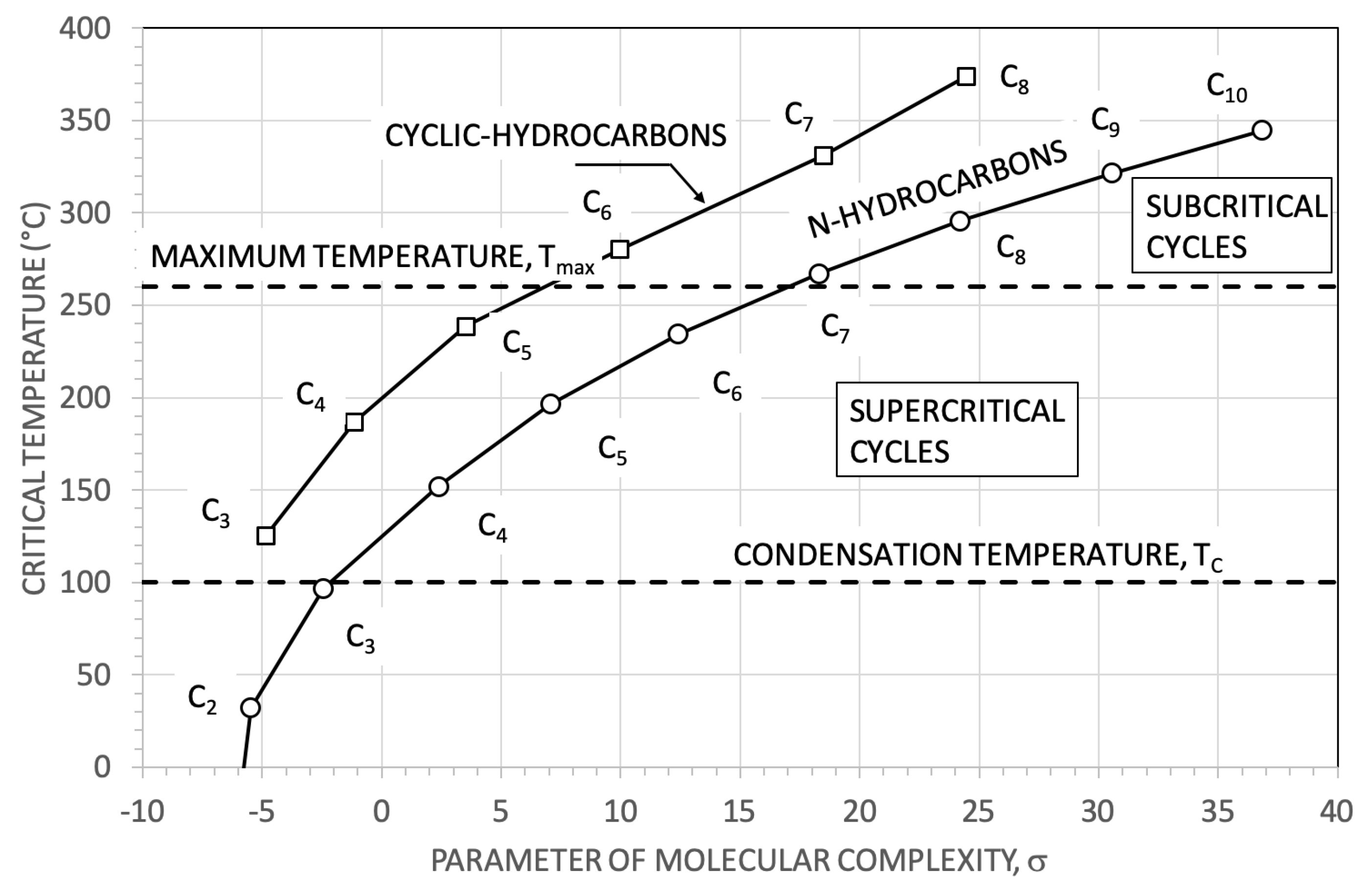
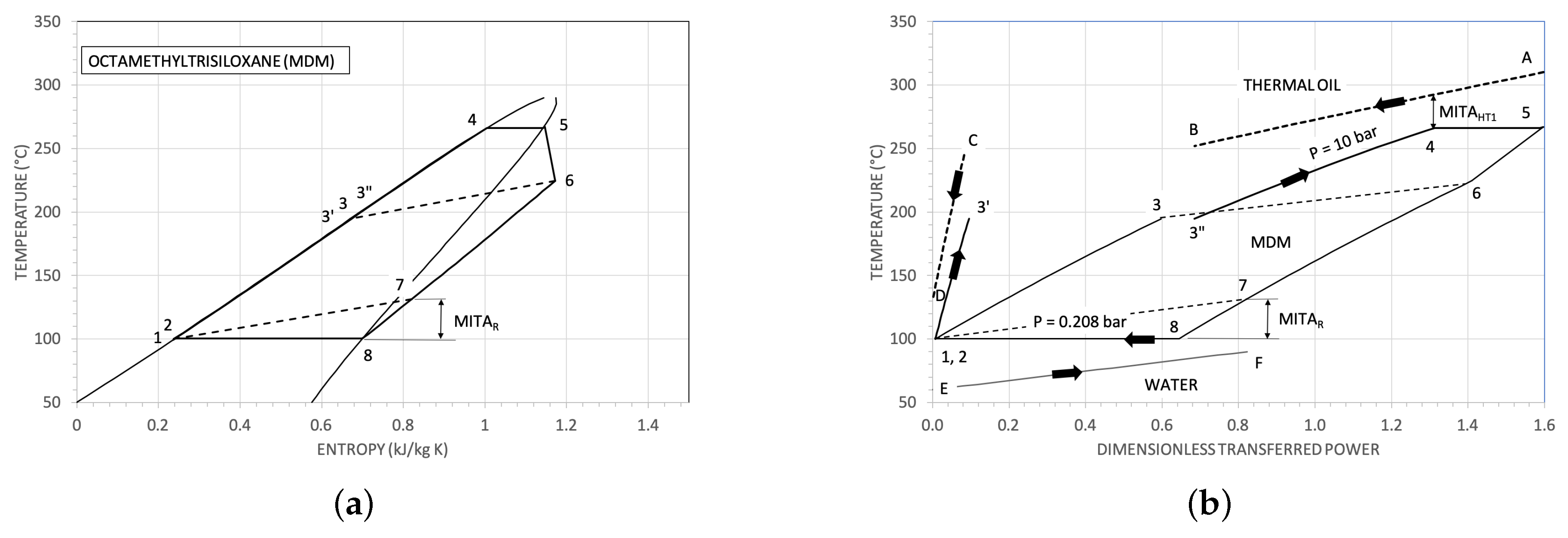
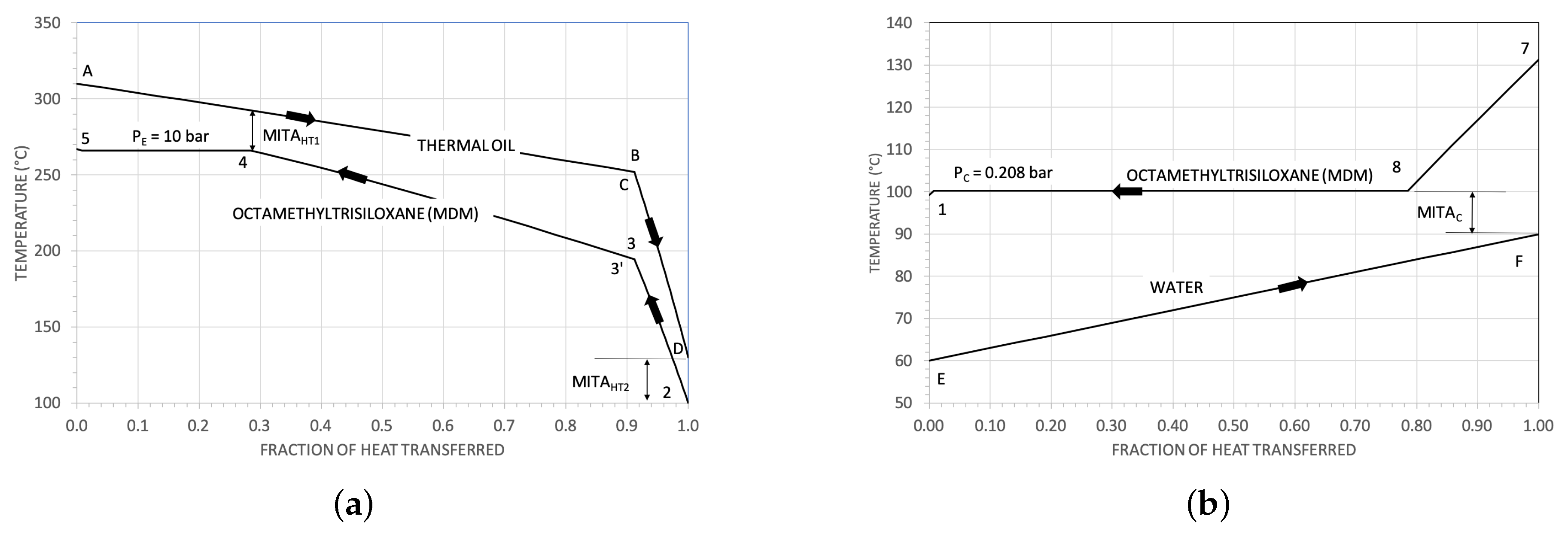
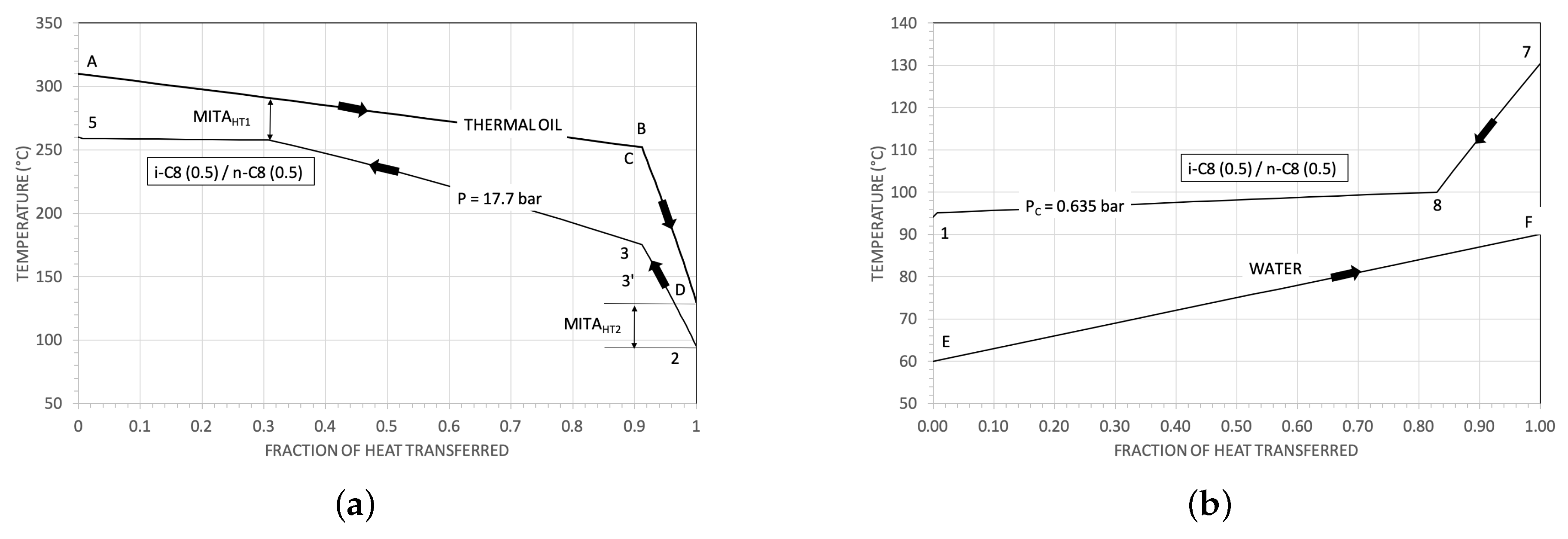
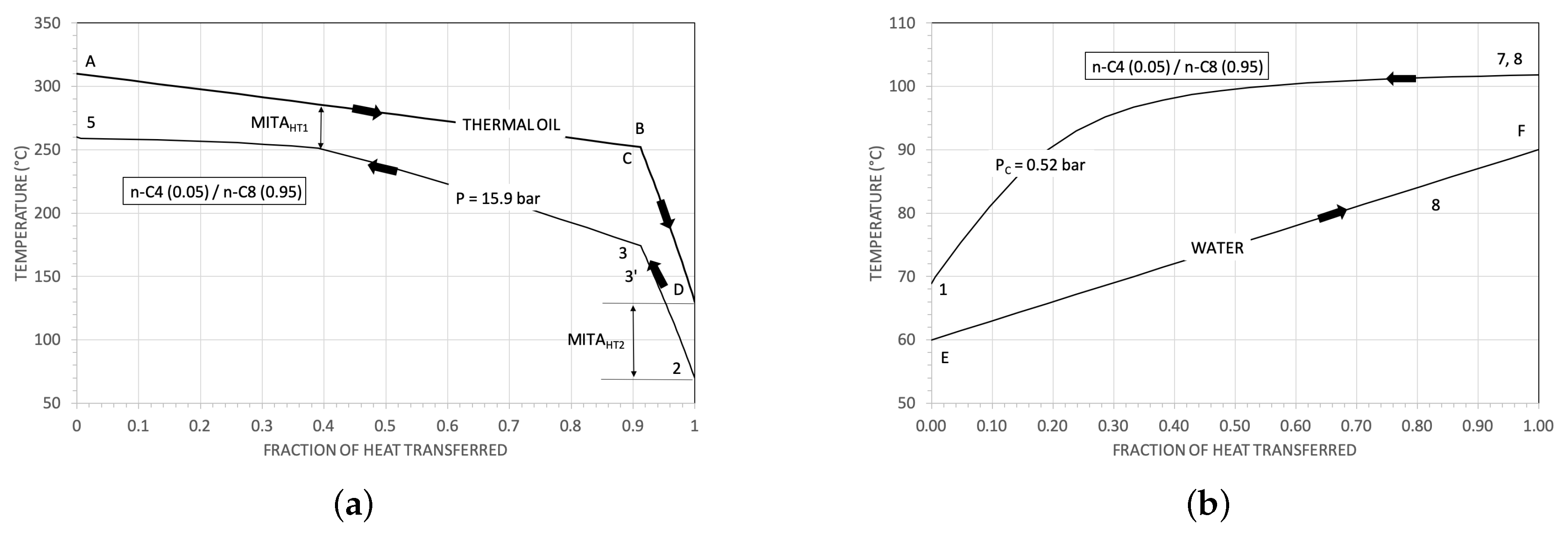
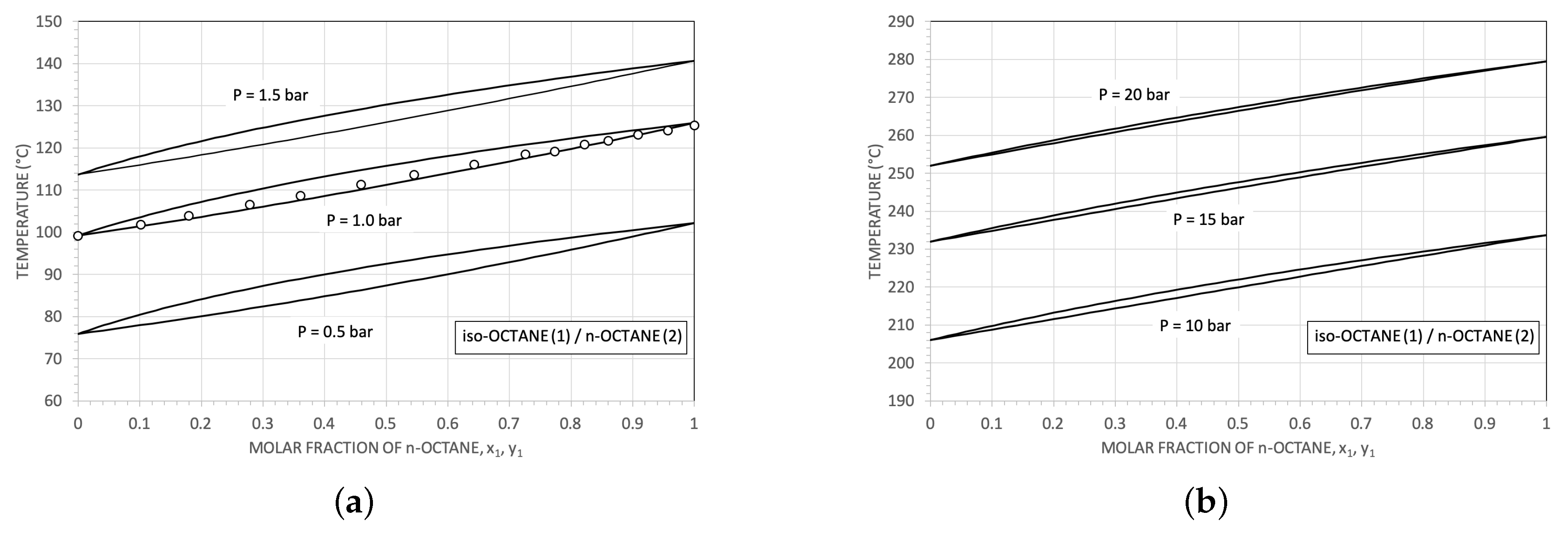
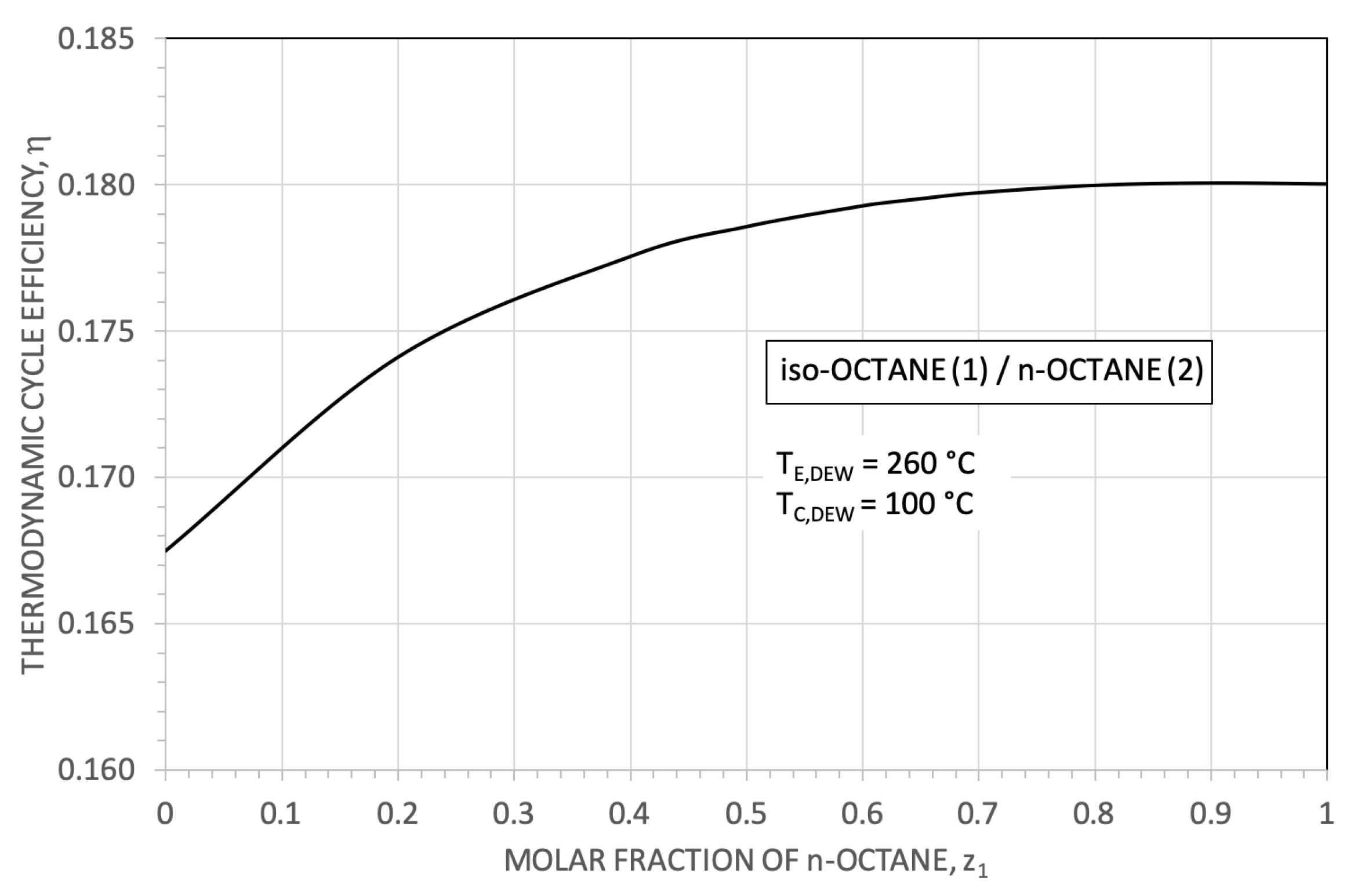
| Parameter | Reference Value |
|---|---|
| Thermal oil power- loop (kW) | 5503 |
| Thermal oil temperature- loop (inlet, /outlet, ) (°C) | 310/252 |
| Thermal oil power- loop (split loop) (kW) | 531 |
| Thermal oil temperature- loop (inlet, /outlet, ) (°C) | 252/130 |
| Overall thermal power to ORC (kW) | 6034 |
| Cooling water temperature (inlet/outlet) (°C) | 65/105 |
| Generator power (kW) | 999 |
| Gross efficiency (%) | 16.6 |
| Parameter | Assumed Value |
|---|---|
| pressure losses | none |
| minimum internal temperature approach in the recuperator, (°C) | 30 |
| turbine efficiency (a) | 0.8 |
| pump efficiency (a) | 0.75 |
| evaporation pressure for MDM (bar) | 10 |
| condensation temperature (°C) | 100 |
| cooling water temperature (inlet/outlet) (°C) | 60/90 |
| approach temperature difference in oil heat exchanger (b) (°C) | 50 |
| Fluid (Pure Fluid or Mixture) | Critical Temperature (°C) | Critical Pressure (bar) | Vapour Pressure at 100 °C (bar) | Binary Interaction Parameter, |
|---|---|---|---|---|
| n-butane, n-C4 | 151.97 | 37.96 | 15.33 | |
| n-pentane, n-C5 | 196.55 | 33.7 | 5.91 | |
| n-hexane, n-C6 | 234.45 | 30.25 | 2.45 | |
| cyclo-propane, c-C3 | 125.1 | 55.75 | 36.68 | |
| cyclo-butane, c-C4 | 186.85 | 49.8 | 11.27 | |
| cyclo-pentane, c-C5 | 238.45 | 45.08 | 4.15 | |
| n-C4 (0.5)/n-C6 (0.5) (a) | 203.6 | 37.06 | 4.4 (b) | −0.0056 |
| n-octane, n-C8 | 295.54 | 24.9 | 0.466 | |
| iso-octane, i-C8 | 270.65 | 25.7 | 1.04 | |
| i-C8 (0.5)/n-C8 (0.5) (a) | 284.91 | 25.51 | 0.635 (b) | −0.00570 |
| n-C4 (0.05)/n-C8 (0.95) (c) | 292.02 | 26.2 | 0.505 (b) | 0.00660 |
| n-C6 (0.5)/n-C8 (0.5) | 272.34 (a) | 28.74 (a) | 0.775 (b) | −0.01675 |
| MDM (d) | 291.25 | 14.6 | 0.2061 |
| Working Fluid | Maximum Pressure, (bar) | Condensation Pressure, (bar) | Thermodynamic Cycle Efficiency, | Turbine Isentropic Enthalpy Drop, (kJ kg−1) | Turbine Volume Flow Ratio, | |
|---|---|---|---|---|---|---|
| Super-Critical Cycles | n-C4 | 70 | 15.6 | 0.128 | 84.77 | 5.12 |
| n-C5 | 40 | 5.99 | 0.145 | 90.59 | 8.28 | |
| n-C6 | 30 | 2.49 | 0.160 | 99.83 | 16.94 | |
| c-C3 | 110 | 36.8 | 0.115 | 84.56 | 3.01 | |
| c-C4 | 60 | 11.35 | 0.142 | 98.42 | 6.04 | |
| c-C5 | 40 | 4.16 | 0.158 | 87.13 | 12.262 | |
| n-C4 (0.5)/n-C6 (0.5) | 45 | 4.4 | 0.164 | 108.62 | 13.36 | |
| Sub-Critical Cycles | n-C8 | 15 | 0.47 | 0.180 | 112.2 | 46.00 |
| i-C8 (0.5)/n-C8 (0.5) | 18 | 0.63 | 0.178 | 105.88 | 42.50 | |
| n-C4 (0.05)/n-C8 (0.95) | 16 | 0.52 | 0.180 | 112.99 | 43.01 | |
| MDM | 10 | 0.208 | 0.180 | 62.73 | 74.80 |
| First Stage | Second Stage | ||
|---|---|---|---|
| MDM | Number of revolutions (rpm) | 3000 | 3000 |
| Volume expansion ratio | 12.0 | 6.23 | |
| Isentropic work (kJ kg−1) | 31.3 | 31.3 | |
| Isentropic power per stage (kW) | 667 | 667 | |
| Rotor tip diameter (cm) | 0.455 | 0.487 | |
| Rotor mean diameter (cm) | 0.445 | 0.445 | |
| (a) | 0.023 | 0.093 | |
| 0.121 | 0.300 | ||
| n-Octane | Number of revolutions (rpm) | 3000 | 3000 |
| Volume expansion ratio | 8.83 | 5.21 | |
| Isentropic work (kJ kg−1) | 56.1 | 56.1 | |
| Isentropic power per stage (kW) | 2800 | 2800 | |
| Rotor tip diameter (cm) | 0.611 | 0.648 | |
| Rotor mean diameter (cm) | 0.596 | 0.596 | |
| (a) | 0.025 | 0.087 | |
| 0.170 | 0.385 | ||
| iso-Octane | Number of revolutions (rpm) | 3000 | 3000 |
| Volume expansion ratio | 9.15 | 4.20 | |
| Isentropic work (kJ kg−1) | 46.8 | 46.8 | |
| Isentropic power per stage (kW) | 3750 | 3750 | |
| Rotor tip diameter (cm) | 0.561 | 0.590 | |
| Rotor mean diameter (cm) | 0.545 | 0.545 | |
| (a) | 0.029 | 0.083 | |
| 0.167 | 0.340 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Invernizzi, C.M.; Ayub, A.; Di Marcoberardino, G.; Iora, P. Pure and Hydrocarbon Binary Mixtures as Possible Alternatives Working Fluids to the Usual Organic Rankine Cycles Biomass Conversion Systems. Energies 2019, 12, 4140. https://doi.org/10.3390/en12214140
Invernizzi CM, Ayub A, Di Marcoberardino G, Iora P. Pure and Hydrocarbon Binary Mixtures as Possible Alternatives Working Fluids to the Usual Organic Rankine Cycles Biomass Conversion Systems. Energies. 2019; 12(21):4140. https://doi.org/10.3390/en12214140
Chicago/Turabian StyleInvernizzi, Costante M., Abubakr Ayub, Gioele Di Marcoberardino, and Paolo Iora. 2019. "Pure and Hydrocarbon Binary Mixtures as Possible Alternatives Working Fluids to the Usual Organic Rankine Cycles Biomass Conversion Systems" Energies 12, no. 21: 4140. https://doi.org/10.3390/en12214140
APA StyleInvernizzi, C. M., Ayub, A., Di Marcoberardino, G., & Iora, P. (2019). Pure and Hydrocarbon Binary Mixtures as Possible Alternatives Working Fluids to the Usual Organic Rankine Cycles Biomass Conversion Systems. Energies, 12(21), 4140. https://doi.org/10.3390/en12214140






