Abstract
Computational Fluid Dynamics (CFD) has numerous applications in the field of energy research, in modelling the basic physics of combustion, multiphase flow and heat transfer; and in the simulation of mechanical devices such as turbines, wind wave and tidal devices, and other devices for energy generation. With the constant increase in available computing power, the fidelity and accuracy of CFD simulations have constantly improved, and the technique is now an integral part of research and development. In the past few years, the development of multiscale methods has emerged as a topic of intensive research. The variable scales may be associated with scales of turbulence, or other physical processes which operate across a range of different scales, and often lead to spatial and temporal scales crossing the boundaries of continuum and molecular mechanics. In this paper, we present a short review of multiscale CFD frameworks with potential applications to energy problems.
1. Introduction
Almost all engineered objects are immersed in either air or water (or both), or make use of some working fluid in their operation. This is particularly true of machines for energy generation and conversion, such as engines, turbines, and renewable energy devices such as wind turbines or wave-energy converters. The ability to model such devices is therefore a key enabling technology, and Computational Fluid Dynamics (CFD) is thus a key element of Digital Engineering. However, the situation is highly complex. As we show below, the basic equations are non-linear, which presents serious challenges; only the most straightforward cases are capable of algebraic solution, hence the development of computational methods. Although CFD could loosely be used to denote any computational solution of fluid flow problems, the subject is commonly understood to refer to the solution of the Euler or the Navier–Stokes equations, or equations derived from these, in two or three spatial dimensions. Moreover, other physical effects are often included, either out of interest or necessity. Turbulence is a state of fluid motion characterised by complex, transient, pseudo-random motion, and is almost ubiquitous in energy engineering; its modelling presents severe challenges in CFD. Other physical effects are often also included, such as chemical reaction and combustion, multiphase flow, free surface flow, etc. The challenges are both numerical and physical, and there are a number of reviews keyed towards specific industrial applications or areas of physics [1,2,3,4,5]. One of the key challenges though is the simulation of physical processes across a range of scales from the macro scales, which are well described by the Navier–Stokes equations of fluid flow, and thus accessible to conventional CFD simulation, right down to micro scales at which the continuum approximation no longer holds and for which kinetic equations for the system need to be solved. Many systems therefore require a holistic approach integrating different simulation approaches across a range of scales, i.e., a multiscale approach. The purpose of this review is to provide an introduction to multiscale methods, particularly as regards areas of CFD applicable to energy engineering, and of course biased to cover areas of interest to the authors, and to speculate about some future trends in the subject. Given the breadth and depth of the subject, inevitably this is a very brief and general overview of the subject, but it may also serve as a link to the other papers in the Special Issue.
The first part of the review, Section 2, covers macroscale fluid mechanical modelling based on the computational solution of the Navier–Stokes Equations. These are now well established techniques with numerous applications in energy (and other) research. The second half of the review paper, Section 3, describes Molecular Dynamics (MD), particle-based methods such as Lattice Boltzmann, and hybrid methods, which provide explicit models for the smallest length scales in flow problems; and describes how these can be integrated together to provide a complete simulation across all relevant scales. Finally, we present some conclusions from the review (Section 4).
2. Macroscale Simulation
2.1. Review of Equations and Challenges
In the most general case, Fluid Dynamics in the continuum limit is governed by the Navier–Stokes equations (NSE), representing conservation of mass, momentum and (where it is necessary to consider this) energy for the system. These equations may be derived as a specific limit of the Boltzmann transport equation for a system of particles (limiting behaviour as the system becomes continuous), but more conventionally and transparently they can be derived by considering conservation of mass, momentum and energy for an infinitesimal volume of space. The exact formulation depends on several factors, including notation; the equations can look startlingly different when written in component form, full tensor notation, or using vector calculus. The different flow regimes are also significant, particularly incompressible and compressible regimes. Additional equations are required to model the non-equilibrium gas dynamics in extreme regimes such as hypersonic flows.
In a compressible (variable density) form, the NSE can be written in vector notation as
where is the fluid density, the velocity, p the pressure and the dynamic viscosity, together with an energy equation whose form is discussed below. An appropriate Equation of State (EoS) also has to be provided, which is an algebraic equation connecting the state variables of pressure, volume and temperature, which closes the equation set. Equations (1) and (2) are a formulation of the equations in differential form; they may also be expressed in integral form integrated over a finite (maybe small) control volume . In this form, the equations are valid for a broad range of Mach numbers . For lower (), the change of density can be ignored, and the equations of conservation of mass (continuity) and momentum become
with as the kinematic viscosity. In both incompressible and compressible flows, we are faced with the solution of a set of partial differential equations which are non-linear (due to the term) and strongly inter-linked. Equations (1) and (2) represent four separate equations for five unknown variables; the EoS provides a closure for the system. For the incompressible case, Equation (4) represents three equations for four unknowns, with Equation (3) as a constraint on the velocity. In neither case is it possible to simplify these equations to remove their interdependency, although the mathematical rearrangement of Equations (3) and (4) to provide a Poisson equation for the pressure is a valuable first step in solution, and is the basis for a family of numerical algorithms (Pressure-Implicit with Splitting Operators (PISO) [6], and Semi-Implicit Method for Pressure Linked Equation (SIMPLE)) for their solution. For reasons of memory efficiency, solution is typically done through sequential solution, together with iteration to deal with linked dependence and the nonlinear term; however, block solution, where all equations are solved in one step, does provide considerable improvements in convergence [7].
The other significant equation to solve in CFD is the transport equation:
This represents the movement of an extensive or intensive quantity q by the flow , including diffusive effects (mediated by the coefficient ) and sources . One immediate observation is that this is very similar in form to Equations (2) and (4), which can indeed be regarded as transport equations for which (it also can be used to model other transport quantities), where q is some form of energy (internal, total or a variable related to energy such as temperature) then this can represent the conservation of energy in the system. Concentration parameters, reaction rates and progress variables, indicator functions, and turbulent parameters such as turbulent kinetic energy can also all be modelled in this way, and in fact the modelling process in CFD is very often influenced by the desire to represent the process being modelled by a transport equation of some form.
2.2. Basic Methodologies
As discussed in the preceding section, the basic equations of fluid dynamics are partial differential equations representing continuum mechanics problems, not intrinsically susceptible to analytic solution. Computational solution requires the reformulation of these equations to a form that can be processed by a computer, i.e., formulation in some kind of arithmetic form. In the case of CFD, this typically involves a process of discretisation where the dependent continuous variables are represented by values at a set of discrete points in space which make up a grid or mesh. The pre-eminent approach in most areas of Computational Continuum Mechanics is the Finite Element (FE) method; the discrete points are connected by lines (edges) to form a grid, and solution of the continuum equations is re-expressed as an integral minimisation process. In CFD specifically, the more dominant methodology is the Finite Volume (FV) methodology, where the fundamental unit of discretisation is the cell, and solution proceeds via the evaluation of fluxes across boundary faces of the cell. In fact, the two methodologies are closely linked; looked at as a numerical problem, either can be used to solve any set of continuum mechanics problems, and the (slight) preference for FV over FE in CFD is probably a combination of historical and philosophical; in the context of fluid flow, evaluating the flux of fluid into and out of a cell is a physically natural approach to the problem. These methods are implemented in a number of general purpose commercial and open source CFD codes [8], but higher order methodologies such as Discontinuous Galerkin are starting to be used for more complex industrial cases [9]. Some alternative methodologies are also used, but much less commonly. Two alternatives are particle-based methods such as Smoothed Particle Hydrodynamics, and kinetic approaches based on solving the Boltzmann transport equation directly, such as Lattice Boltzmann, which is covered in Section 3.3.1. Both have specific benefits; particle based codes are often used for free surface calculations where complex surfaces (e.g., wave-overtopping) are involved, whilst Lattice Boltzmann codes may run more efficiently on specific hardware such as GPUs.
2.3. Turbulence Modelling
Turbulence is a state of fluid motion characterised by the occurrence of random fluctuations of differing scales (spatial and temporal) within the flow. It is often described as pseudo-random; it can be characterised in terms of individual coherent eddies of different sizes, from the largest (Large Eddy scale) which drive the turbulence, down to the Kolmogorov length scale which is determined by the viscosity. Eddies at all scales interact, transferring energy from larger to smaller scales, and the overall effect is to transfer energy from the Large Eddy scales through this turbulent cascade and eventually dissipate it at the Kolmogorov length scale. It is a very common effect in Engineering fluid dynamics, and has consequences both desirable, e.g., enhanced mixing, and undesirable, e.g., increased energy dissipation. Since it is a fluid mechanical effect, it is describable by the NSE and one approach is to solve these equations for all length scales—Direct Numerical Simulation (DNS). However, this is a costly procedure (computational cost scales as [10]) which, whilst valuable as a fundamental research tool, is too costly for common engineering application.
The challenge of modelling turbulence consists of representing the random fluctuations in some cheaper form, making use of statistical rather than explicit representations. We can split the flow into a mean (average) and fluctuating component, so
where is some averaging operation. Applying this averaging operation to the NSE, we find
The term is challenging, but we can write
with denoting fluctuating and cross-terms, and so
is an averaged form of the NSE. Similar manipulations are possible for the density weighted form of the NSE.
There are now two questions to answer: What is our mathematical averaging operation? How do we determine so as to close these equations? To answer the first question, two main averages are possible. In ensemble or Reynolds averaging, the average is across an ensemble of equivalent representations of the flow
and this produces the Reynolds Averaged Navier–Stokes (RANS) equations, leading to a complete family of turbulence models, the RANS models [11]. The alternative approach is a scale separation, classically interpreted as a low-pass filter
Since this separates large from small scales, where the large scales will be explicitly simulated, this is the basis for an alternative set of models, the Large Eddy Simulation (LES) models.
Turning now to the second question, the tensor represents the effect of our modelled component of the flow on the simulated component. For RANS, is described as the Reynolds Stress and represents the effect of the statistical, turbulent fluctuations on the mean flow. A common assumption is that turbulence is isotropic and dissipative, and so this term can be modelled using the Boussinesq approximation
with the turbulent effects being reduced to a turbulent viscosity , which in turn can be related to turbulent properties such as the turbulent kinetic energy k and turbulent dissipation . This provides a family of models known as eddy viscosity models of which the standard model is the best known [12], although others such as the are becoming increasingly important [13,14]. Alternatively here, if the Boussinesq approximation is not appropriate, the individual terms of can be solved either algebraically, or as transport equations, resulting in various Reynolds Stress models [15,16].
Implicit in all RANS models is that there is a clear separation between the mean flow which is steady or at most, slowly varying, and the stochastically varying turbulent component of the flow which can validly be represented statistically. These assumptions frequently break down in practice; for many flows, turbulent and deterministic transient behaviours overlap in frequency space, and in many cases (combustion, aeroacoustic noise, and vortex-induced vibration), we are interested in the large scale fluctuating components of the flow regardless of whether these are strictly turbulent or deterministic. In these cases, LES, based purely on a separation of scales, is commonly used. In LES, the scale separation is implicitly set by the mesh resolution, and the flow divides into Grid-Scale (GS) components (grid scale velocity), which are explicitly solved for, and Sub-Grid Scale (SGS) components (such as SGS kinetic energy), which can be represented by a SGS model or ignored completely (Implicit LES or iLES [17]). As a rule of thumb, for accurate LES, of the turbulent kinetic energy in the flow needs to be resolved in the GS; although this can be relaxed (Very Large Eddy Simulation, or VLES); conversely, and in distinction to the case for RANS, if the mesh is refined sufficiently, then the equations reduce back to DNS, and we can distinguish quasi-DNS or qDNS simulations in this limit. LES has been shown to perform very well for several turbulent flow scenarios but there are still numerous challenges with near wall flows [18]. In these cases, a blending of RANS (near wall) and LES (free stream simulation) has been applied—Detached Eddy Simulation (DES) [19,20].
Implicit Large-Eddy Simulation (ILES) has its origins in the observations made in [21] that the numerical dissipation of particular numerical methods can substitute for the explicit sub-grid scale (SGS) models in classical LES. Modified Equation Analysis (MEA) [22] can be used to investigate the mathematical behaviour of the truncation errors in a discretised differential equation. Such analysis can be performed for the truncation error of numerical schemes commonly used in LES (e.g., [23,24,25,26,27,28,29]) and demonstrate that this sub-grid scale dissipation implicitly provides the correct mathematical behaviour as well as numerically stabilising the calculation. In ILES, the NSE are discretised using high-resolution/high-order non-oscillatory methods without the low-pass filtering operation, which gives rise to sub-grid scale (SGS) terms that require additional modelling. Instead, the (implicit) de facto filtering introduced through the finite volume integration of the NSE over the grid cells is utilised together with specific non-linear numerical schemes that satisfy particular principles (see [30], and reviews [28,29,31,32]). It has been shown [23] that ILES methods need to be carefully designed, optimised, and validated for the particular differential equation to be solved. MEA of high-resolution schemes for the Navier–Stokes equations is extremely difficult in practice, and so much of our understanding of the numerical properties of these methods still relies on performing computational experiments, see for example [17,29,33,34].
2.4. Sub-Grid Multiphysics Modelling
As discussed above, the core of CFD modelling is the solution of the Navier–Stokes equations governing continuum mechanics flow. Frequently, however, the behaviour of the macroscale flow is affected by microscale physical processes for which separate modelling is needed. Considered fully, this leads to the full multiscale modelling considered in Section 3, but before we get to this point it is worth mentioning other ways in which microscale physics have been introduced into CFD simulation. As shown above, LES is a good example where the effects of unresolved turbulent length scales is accounted for either explicitly or implicitly, but there are other areas where this is important, with combustion and dispersed multiphase flow being prominent and important topics for energies research. The purpose here is not to provide a full review of either topic (each would justify its own separate review article or book, of which there are many [35,36,37,38,39]) but to briefly summarise how these models are incorporated into the general CFD process.
In the case of combustion, typically the physical modelling is incorporated into the CFD solution through transport equations for physical quantities such as species concentration or reaction progress, frequently with multiple equations solved simultaneously (combustion processes may involve hundreds of individual chemical species not just fuel and oxidant and products, but other constituents of air such as and intermediate species such as radicals). The basic transport equation (Equation (5)) must be modified with complex additional models to represent the source (and sink) terms for these quantities. Examples include the Eddy Break Up (EBU) [40], Eddy Dissipation Model (EDM) [41] and Eddy Dissipation Concept [42] models. In other models, reaction progress variables such as mixture fraction Z can be modelled as single transport equations [43]. Details of which model to use depend on the physical regime (premixed/non-premixed, reaction speed, combustion versus turbulent length scales) and computational cost and accuracy.
In dispersed multiphase flow, two or more immiscible components are present in the flow. One of these comprises the continuous phase which is connected throughout the domain, whilst the other(s) are present as discrete particles (solid particles, liquid droplets or gas bubbles) whose dynamics affect and are affected by the dynamics of the continuous phase and, frequently, by particle-particle interaction if the phase fraction is high enough. There are a wide range of modelling methodologies, depending partly on the physical regime being investigated and partly on necessary or desired modelling complexity. At low phase fraction (low particle number), kinetic approaches can be used where the forces on the individual particles (primarily from the continuous phase) can be evaluated and Newton’s second law evaluated; this is often achieved by connecting CFD and Discrete Element Method (DEM) codes [44]. At higher phase fraction, the dispersed phase(s) can be treated as interpenetrating continua and phase averaging used to establish separate sets of Navier–Stokes equations for each phase [45], with the most complex models incorporating the effects of particle/particle kinetics at the sub-grid scale [46,47,48].
3. Multiscale Modelling
3.1. Motivation: Micro- and Nanotechnologies
As the precision and accuracy of manufacturing techniques improves, micro- and nanotechnologies are becoming widespread, providing engineering solutions to problems across different sectors. An important branch of nanotechnologies is micro- and nanofluidics, the study of fluid dynamics under severe confinement. Micro- and nanofluidics are becoming relevant in energy applications. From extraction and transportation methods of current energy sources, to harnessing renewable ones, they allow us to delineate the underlying physics and provide optimised solutions. From a passive point of view, understanding the fluid dynamics of oil and gas through the porous rocks in which they reside, can shed light on efficient means of extraction [49,50]. This is usually a non-trivial task, requiring resolution of multiphase flows through complex geometries [51].
Microfluidic devices can also be used to harness solar energy. For example, photobioreactors employ bacteria and algae to convert solar energy and some low energy carbon source, into a more useful form, such as hydrocarbons. These delicate photosynthetic organisms, require an appropriate level of lighting, as well as other conditions in order to thrive [52,53,54,55]. Microfluidics can be used to more efficiently provide such conditions. Photocatalysis, i.e., the use of solar energy to facilitate chemical reactions, is also related to solar energy. The use of microchannels can improve the transport properties of the reactants, leading to greater reaction rates compared to bulk reactions [52,53,54,55]. Liquid lenses [56], whose properties can be adjusted through the use of microfluidics, can also be used to concentrate solar energy (solar collectors). There is also the issue of carbon capture, storage and sequestration, a topical endeavour with major environmental implications. Several studies have investigated the possibility of using Carbon Nanotubes (CNTs) to collect CO [57,58,59,60]. Microfluidics have also studied sequestration, i.e., pumping the collected CO underground [61,62].
Due to the very large surface-to-volume ratio found in microfluidic, and especially in nanofluidic systems, interfacial effects can influence and even dominate the flow physics. CFD often fails to accurately capture such effects. Instead, atomistic-based methods, such as as Molecular Dynamics (MD) and Monte Carlo (MC) molecular models, are excellent tools and can provide insight into such surface phenomena. A good example is the velocity of a liquid at a boundary. Most CFD simulations considering viscous flows assume that the relative velocity between the solid and liquid is zero, the famous no-slip boundary condition. Alternatively, simple empirical models can be used that prescribe a boundary velocity. MD simulations, however, have demonstrated that the fluid slip is a complex function of the wetting properties of the solid and liquid, as well as the nano- and micro-scale roughness of the solid surface [63]. Another example in which molecular models identified physical phenomena not captured by traditional CFD, is in the thermodynamic properties of the liquid, such as thermal conductivity [64,65,66,67] and viscosity [68]. While these are generally considered constant, investigations have shown that they depend on the characteristic length of confinement, as well as the affinity of the liquid to the solid surface.
MD is one of the most commonly used molecular methods. It is deterministic and uses Newton’s second law to update the positions and momenta of all the atoms [69]. The force acting on each atom is calculated by first prescribing a potential function, , that describes the potential energy of the system as a function of the inter-atomic distances. Given such a function, the force acting on a particle labeled i is given by:
For physical systems in which quantum mechanical effects are negligible, MD provides a resolution high enough to delineate most physical phenomena of engineering interest. In theory, MD can be used to simulate and make accurate predictions for complex multiphase, multi-component, turbulent flows. In practice, however, the computational cost of MD is highly restrictive, and the method is usually limited to investigations on the fundamental physics revolving materials, and nanofluidic systems.
Considering simple, pair-wise interactions between particles, the computational complexity of molecular models scales as , where N is the number of particles in the system (Practically, we usually only consider interactions between neighbouring particles by selecting a cut-off distance, , beyond which all interactions are ignored. Taking this into account, the computational complexity of molecular dynamics becomes , where is the number of atoms within the cut-off distance from each particle). The computational expense prohibits the simulation of systems with more than a few hundred thousand atoms.
In addition to a restriction in number of atoms, MD simulations are also severely restricted by the timestep used to advance the solution. This restriction is due to the nature of the potential , which asymptotically tends to infinity as the interatomic distances tends to zero. The aim of this behaviour is to prevent atoms from overlapping, in honour of the Pauli exclusion principle of quantum mechanics. A good example is the Lennard–Jones potential, which is used, in some form or another, in the vast majority of MD simulations. The slope of the potential function increases drastically as the interatomic distance decreases. In turn, Equation (11) dictates that a large repulsive force will be exerted between the particles. A large timestep will usually result in significant overlapping, which in turn results large forces, temperature fluctuations, and divergence of the solution.
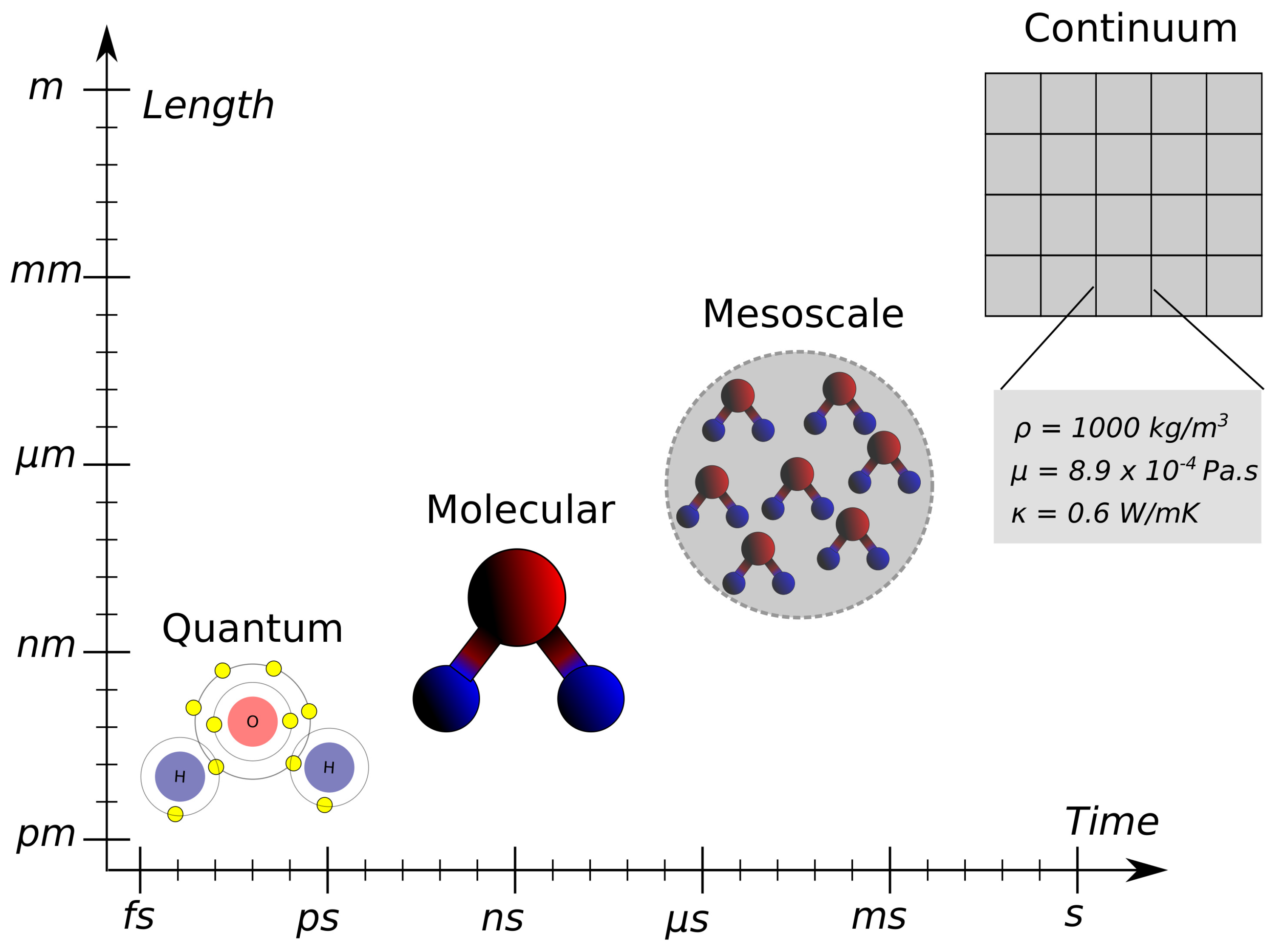
Thus, while MD is extremely capable of resolving the physics of most fluid dynamics problems, its high resolution is accompanied by prohibitive requirements for computational resources. Although CFD is significantly less computationally demanding, it often fails to resolve certain physical phenomena found in micro- and nanofluidic systems (see Figure 1). This necessitates the development of new computational models that bridge the gap between the large-scale continuum techniques, and smaller-scale molecular techniques. We refer to such models as multiscale modelling, and it is an active topic of academic and industrial interest.
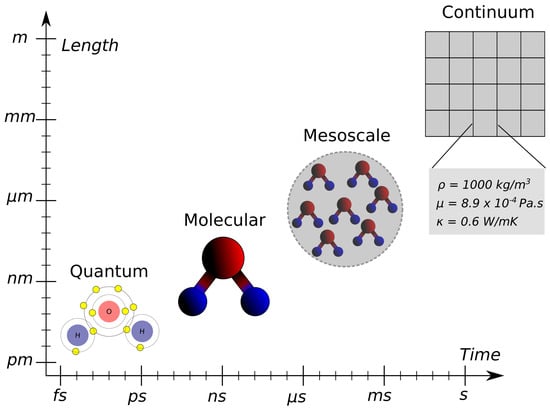
Figure 1.
Schematic representation of different scales at which a fluid (specifically here HO) can be modelled.
Multiscale modelling is a broad and complex discipline, with many different methods, variants and extensions. The purpose of this review is not to provide a detailed description of every simulation method, but to highlight the main models, and describe how these can be used to advance energy-related applications. For more information, refer to one of a number of review papers on the topic [70,71,72].
3.2. Hybrid Molecular–Continuum Methods
Hybrid Molecular–Continuum Methods (HMCM) refer to a class of multiscale models, in which both molecular (usually MD or MC) and continuum (usually CFD or FEM) solvers are used. The objective is to solve the problem by primarily using the more computationally efficient continuum solver, and use the molecular solver sparingly, only when required, in order to obtain the desired resolution. It is therefore of paramount importance to limit the use of the molecular solver to a fraction of the overall system. The decoupling of length-scales between the continuum and molecular solvers, i.e., the separation of the problem so that the two scales can be treated independently, is the primary goal of every HMCM. The decoupling of the timescales is achieved by having the molecular and continuum region running asynchronously. The molecular simulation runs for a short period of time, passes information to the continuous solver and then stops. The continuous solver uses the information to tailor the simulation, and then runs for some period of time using a relatively large timestep. After this period, determined by the physical problem solved, the molecular solver is called again, and the process repeats. Not all HMCMs allow decoupling of time.
There are a number of ways in which scales can be decoupled. Geometric Decomposition (GD) refers to a hybrid approach in which each region is treated exclusively by either a molecular or continuum solver. The molecular and continuum regions usually overlap and the two solvers share information through this overlapping region. One way of sharing this information is by exchanging state variables (i.e., temperature, density, velocity) [73,74,75]. Passing information from the molecular to the continuum solver is relatively straight forward. A statistical treatment of the atomic trajectories provides macroscopic properties, that are passed onto the continuum solver as boundary conditions. Conversely, to pass information from the continuum to the molecular region, material properties must be translated into atomic positions and momenta. This task is significantly more complex compared to the statistical averaging, as macroscopic properties can correspond to a very large number of microstates, corresponding to some volume in phase space. Another method in which the molecular and continuum solver can share information is or by monitoring the flux of mass, momentum and energy across the molecular/continuum boundary [76,77,78,79]. Matching fluxes, however, does not allow the decoupling of time, as fluxes must be continuously monitored by both the molecular and continuum solver [80,81]. A different approach for HMCM is called Pointwise Coupling (PC). In this approach, the continuum solver resolves the entire domain. The molecular solver runs sparsely in both space and time; calculates properties, constituents, etc.; and uses them simply to tweak the continuum solver. This can be used to resolve the flow field close to the boundary, or calculate constituent equations explicitly.
One of the complexities of HMCMs is the definition of the molecular domains. If we consider a Poiseuille flow through a microchannel, the molecular domain will be a region “close” to the wall, the word “close” being open to interpretation, depending on the specific physical case. In a colloidal system containing complex particles that can diffuse, aggregate, and form complex networks, the definition of the domains, in terms of position, length- and time-scales, becomes significantly more complex.
3.3. Mesoscale
HMCMs resolve parts of the system using pure, molecular simulations, and other parts using pure continuum simulations. Instead, mesoscale models resolve the entire system at some intermediate length and time scale. The general concept revolves around pseudo particles that correspond to a cluster of physical atoms and molecules. The interactions between these particles depend on the specific model, but the aim is to ensure that the average behaviour reconstructs the hydrodynamic equations, i.e., the Navier–Stokes equations.
The purpose of this section is not to describe every available mesoscale method, but to outline the potential of such methods in energy applications. For this task, we have chosen two of the most commonly used mesoscale approaches, the Lattice-Boltzmann method and the Dissipative Particle Dynamics method, as examples of what such models are capable of and how can they be used. Furthermore, these two computational techniques form a good basis for other mesoscale methods, as most of them will usually share similar features with one of the approaches introduced here.
3.3.1. Lattice-Boltzmann Method
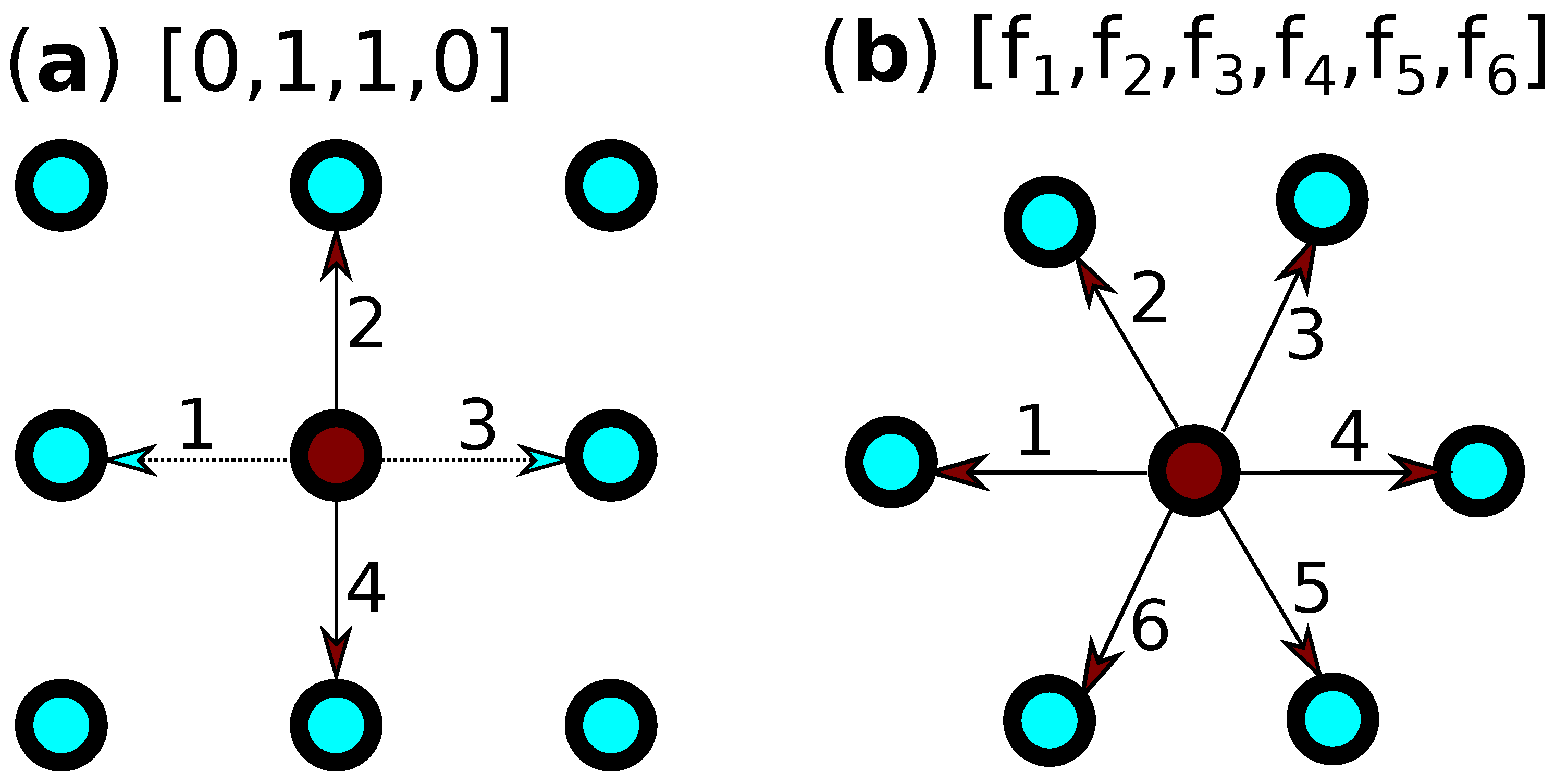
A prominent mesoscale method is the Lattice-Boltzmann Method (LBM), which approaches the problem by attempting to solve the Boltzmann Transport equation. The predecessor of LBM is the simpler Lattice Gas Automaton (LGA) [82,83]. In both methods, the domain is covered by a lattice. Particles can only be located at the lattice sites. Furthermore, each particle can only travel to a neighbouring vertex. Thus the velocities are restricted to the lattice directions and are represented as vectors , where d is the number of lattice vectors (see Figure 2a). The binary representation of the velocities implies that only one particle can move along a certain lattice link at each timestep.
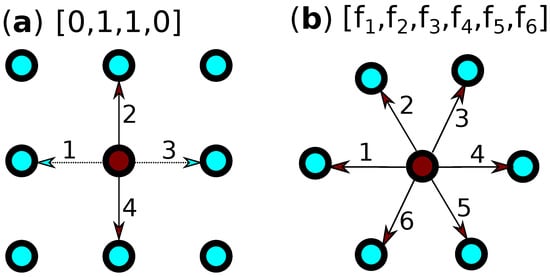
Figure 2.
Two example lattices that can be used in LGA and LBM. The arrows show the lattice vectors, along which particles can move from the red point to its neighbours (blue). The vector for the red lattice point is shown on top of each graph: (a) example of the velocity vector for LGA; and (b) example of the velocity vector for LBM.
At each timestep, two steps take place. The first is the propagation step, in which each particle moves to a neighbouring vertex, depending on its velocity. The second is the collision step, in which particles that are arriving to the same vertex (from different lattice sites), “collide”, and their velocities are re-distributed based on a collision operator. Averaging over a large number of vertices, the LBA can potentially reproduce the Navier–Stokes equations. This, however, requires a lattice with a sufficient amount of symmetry. The lattice in Figure 2a, for example, is not sufficient to reproduce the hydrodynamic equations, while that in Figure 2b is.
Despite the attractive simplicity of the method, it also has some obvious problems. Not only does the simplistic nature of the model introduces numerical noise, but the discrete nature of the velocities break Galilean invariance, i.e., the flow physics depend on the inertial frame of reference. The LBM resolved this problem by introducing a real vector-valued density function (Figure 2b), , such that
where is the lattice point; i is one of the possible lattice directions; is the portion of the density on the node x, travelling in the ith direction; and is the i-lattice vector.
As with LBA, an LBM timestep also includes a propagation and collision step. In the absence of collisions, the propagating particles retain the same velocity (both direction and magnitude), of the previous lattice node. In the presence of collisions, however, the propagation step is given by:
A frequently used operator is the Bhatnagar–Gross–Krook (BGK) operator [84], given by
where is the density distribution in equilibrium [85], as described by the Maxwell–Boltzmann distribution; and is the liquid relaxation time, i.e., the time in which the liquid atoms can retain their structure, and is related to the viscosity.
The collision operator can be modified at the boundaries, to produce desired boundary conditions. For Poisseuille flow, the collision function at the interface is adjusted so that particles incident on the wall have their velocities inverted. Similar treatment is used for shear-driven flows, with the addition that the boundary’s velocity is superposed into the incident particle [86]. This method models the boundaries at the midpoints between lattice vertices. While this treatment renders the method unsuitable for all but the most basic geometries, a number of studies provide extensions that allow more complex geometries. A number of adjustments can also be considered to model inlet and outlet boundary conditions [86,87,88]. Various modifications can also lead to more complex physics, including multiphase, multicomponent and particle-based flows. This often requires the addition of a body force in the propagation step, or adjustments in the velocity or equilibrium density distribution function. For example, by considering an external force acting on , Hyväluoma and Harting [89] simulated gas bubbles to study their effect on the boundary velocity at a rough solid surface.
LBM has been used successfully to study microfluidic systems, such as flows through porous rock [51,90,91,92], as well as other microfluidic applications [93]. Variants of LBM have also been used to investigate the efficiency of photovoltaic systems.
3.3.2. Dissipative Particle Dynamics
Dissipative Particle Dynamics (DPD) is a gridless mesoscale method [94]. Similar to MD, DPD applies Newton’s second law to update the position and momentum of every particle. In DPD, however, each particle corresponds to a (potentially large) number of atoms. As with MD, the force is calculated as the negative gradient of a the energy potential, which is a function of inter-particle positions. The main different lies in the nature of this potential function. In MD, usual candidates, such as the Lennard–Jones potential, are termed as “hard” potentials, referring to the large gradient, as the interatomic distance tends to zero. This gradient results in very large forces that prevent particles from overlapping.
For convenience, the mass of each particle is set to 1, so that the force acting on the particle simply equals its acceleration. The equation of motion is
where the labels and stand for body forces (e.g., gravity, electromagnetism) and internal forces (pressure, viscous, etc.). The internal forces are given by
where represents the conservative (non-dissipative) force, is the dissipative, viscous force, and is a random force that simulates the stochastic, thermal fluctuations.
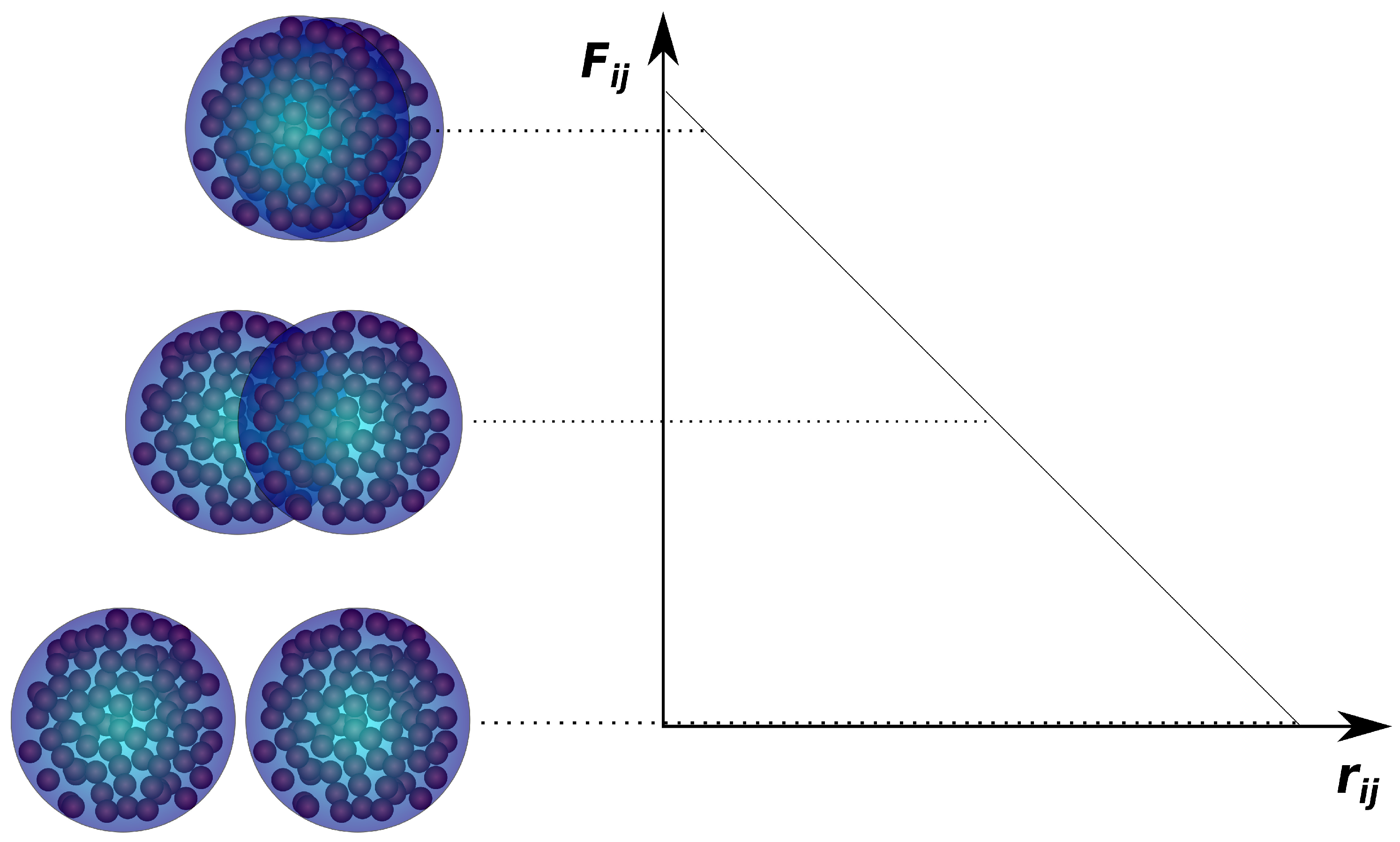
In the most basic form of DPD, the conservative forces are purely repulsive. Furthermore, they are “soft”, meaning that they, in contrast to the infinite repulsive forces exerted between overlapping atoms in MD, experience a finite repulsive force between them (Figure 3). This enables DPD to use much greater timesteps than in MD, since overlapping DPD particles do not result in massive velocities. The functional form of the conservative force in DPD is:
where is a unit vector in the direction from particle i to j. The weighting function scales the force, depending on the interatomic distance . The parameter determines the maximum strength of the repulsive force, in the case where the two particles are overlapping (i.e., ). Different types of particles will generally have different values of a. For example, the force between two water molecules might be determined by while the force between two solid molecules might be determined by . The interaction between water and solid will be determined by a yet different parameter . The relationship between the three coefficients determines, for example, the wetting properties of the solid. For example, if the ratio is close to zero, the solid will be hydrophobic, while, if it is close to one, it will be hydrophilic.
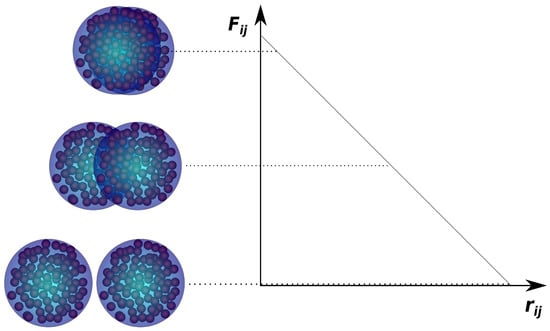
Figure 3.
Schematic of the conservative force acting between two DPD particles, as a function of the inter-particle distance. Since a DPD particle can be a manifestation of a cluster of particles, two particles can overlap with a finite repulsive force acting between them.
Note that, in the original formulation of DPD, the force is only repulsive. For condensed matter, this seems to be okay. As mentioned above, the “attractive” forces between different liquid–solid or liquid–liquid particles can be emulated by considering different values of a. For free-surfaces, liquid–gas interfaces (e.g., bubbly flows), variations of DPD can be used. One such popular method is the Many-Body DPD (MDPD) which includes an attractive component in its conservative force [95]. Furthermore, extensions and variations of the base model can allow for heat transfer across the system [96,97], something not possible with the initial formulation.
The obvious advantage of DPD compared to MD is that, now, each particle corresponds to a group of atoms and molecules, thus reducing computational expense. Of course, there is a trade-off between the coarse-graining factor, i.e., the number of physical particles encapsulated within a DPD particle, and accuracy. As expected, increasing the coarse-graining parameter lowers the accuracy. A good example of this is when simulating water where very large coarse-graining parameters can lead to significantly lower viscosity [98]. DPD can also use timesteps far greater than those considered in MD simulations. The disparity in time-lengths is due to the softer potential used in DPD, in which overlapping particles result in a much smaller force. In general, this force becomes weaker as the coarse-graining factor increases. Nevertheless, an appropriate timestep is required for accurate predictions. The rule of thumb is to have a timestep that is as large as possible, while still keeping the system in thermal equilibrium [99].
The mesoscale method is already being used in energy applications, such as studying the dynamics and properties of oil–water emulsions in the presence of polymers [100] and surfactants [101,102]. DPD has also been used to study the morphology of solar cells [103], as well as to investigate energy storage in phase change materials [104].
4. Conclusions
Multiscale modelling and simulation is a broad term that encompasses methods in the frameworks of continuum and molecular mechanics, as well as across boundaries. This article did not aim to cover the numerical and physics modelling challenges associated with the above topics, but to provide a short introduction to methodologies and outline some of the issues that future research should address. The main take-home points are summarised below:
- We have good reason to believe that continuum fluid mechanics and the Navier–Stokes equations represent a good description of many systems of interest, particularly to those studying branches of engineering related to the topics covered in the journal Energies. With modern computational resources, CFD based on these principles can give accurate answers and represents a valuable tool in modern engineering practice.
- One of the main challenges to CFD though is how to deal with different physical processes operating across a range of scales. This can include scales which we are unable to adequately resolve for reasons of computational cost, such as turbulence, and also where the fundamental physics has changed nature, such as small scales where the continuum approximation is no longer valid.
- Turbulence is a key aspect of many if not most engineering flows and its modelling is still an important area of research in CFD. No universal turbulence model has been developed and it is unlikely to be found; instead, the choice of turbulence model used depends on the type of flow being studied, the cost and level of accuracy needed and so forth. RANS methods are largely mature and are valuable for a wide range of cases of engineering importance.
- Particularly for cases where the fluctuating component of the flow (irrespective of whether this is turbulent or deterministic) is important, LES and related methods are frequently used. Implicit Large Eddy Simulation has been established as promising approach to modelling and simulating turbulent flows, particularly compressible flows. There is significant progress in subgrid scale modelling in the framework of classical LES and in some applications, e.g., multispecies turbulent flows a combination of classical LES and iLES may offer an alternative path of future research.
- There are still challenges to be solved in LES (both classical and iLES), particularly in terms of the treatment of boundary conditions, where wall modelling and hybrid approaches such as DES are of interest.
- Microscale physical modelling can be included into CFD in the form of continuum mechanics models where appropriate, allowing us to model not only turbulence but also processes such as combustion and dispersed multiphase flow. The development of such models and their validation is a challenge and the resulting models often represent a tradeoff between cost and accuracy. Where the microscale physics is no longer a continuum mechanics process, alternative (usually kinetic-based) modelling must be integrated into the CFD.
- Coupling of continuum and molecular fluid dynamics methods remains a challenging problem due to the large variations of spatial and time scales. There is currently no accurate theoretical framework that can be used for exchanging information across scales, e.g., at the molecular–continuum interface.
- The multiscale modelling can provide significant predictive capability in energy problems, e.g., in problems involving particles, and at the fluid–material interfaces where heat transfer issues become important.
Author Contributions
All authors contributed equally to the writing of this paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spalart, P.R.; Venkatakrishnan, V. On the role and challenges of CFD in the aerospace industry. Aeronaut. J. 2016, 120, 209–232. [Google Scholar] [CrossRef]
- Rider, W.; Kamm, J.; Weirs, V. Verification, validation, and uncertainty quantification for coarse grained simulation. Coarse Grained Simul. Turbul. Mix. 2016, 168–189. [Google Scholar]
- Drikakis, D.; Kwak, D.; Kiris, C. Computational Aerodynamics: Advances and Challenges. Aeronaut. J. 2016, 120, 13–36. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W. Computational fluid dynamics (CFD)—An effective and efficient design and analysis tool for the food industry: A review. Trends Food Sci. Technol. 2006, 17, 600–620. [Google Scholar] [CrossRef]
- Kobayashi, T.; Tsubokura, M. CFD Application in Automotive Industry. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Berlin/Heidelberg, Germany, 2009; Volume 100. [Google Scholar]
- Issa, R.I. Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Splitting. J. Comp. Phys. 1985, 62, 40–65. [Google Scholar] [CrossRef]
- Uroic, T.; Jasak, H. Block-selective algebraic multigrid for implicitly coupled pressure-velocity system. Comput. Fluids 2018, 167, 100–110. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A Tensorial Approach to Computational Continuum Mechanics using Object Orientated Techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Cantwell, C.; Moxey, D.; Comerford, A.; Bolis, A.; Rocco, G.; Mengaldo, G.; De Grazia, A.; Yakovlev, S.; Lombard, J.E.; Ekelschot, D.; et al. Nektar++: An open-source spectral/hp element framework. Comput. Phys. Commun. 2015, 192, 205–219. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Durbin, P.A. Some Recent Developments in Turbulence Closure Modeling. Annu. Rev. Fluid Mech. 2018, 50, 77–103. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Jiang, L.; Tabor, G.; Gao, G. A new turbulence model for separated flows. Int. J. Comp. Fluid Dyn. 2011, 25, 427–438. [Google Scholar] [CrossRef]
- Speziale, C.G. Analytical Methods for the Development of Reynolds-Stress Closures in Turbulence. Ann. Rev. Fluid Mech. 1991, 23, 107–157. [Google Scholar] [CrossRef]
- Wilcox, D.C. Simulating transition with a two-equation turbulence model. AIAA J. 1994, 32, 247–255. [Google Scholar] [CrossRef]
- Drikakis, D.; Hahn, M.; Mosedale, A.; Thornber, B. Large eddy simulation using high-resolution and high-order methods. Philos. Trans. R. Soc. A 2009, 367, 2985–2998. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.T.; Park, G.I. Wall-Modeled Large-Eddy Simulation for Complex Turbulent Flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef]
- Spalart, P.; Jou, W.; Strelets, M.; Allmaras, S. Comments of feasibility of LES for wings, and on a hybrid RANS/LES approach. In Proceedings of the International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Spalart, P.R. Detached Eddy Simulation. Ann. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Boris, J.; Grinstein, F.; Oran, E.; Kolbe, R. New insights into large eddy simulation. Fluid Dyn. Res. 1992, 10, 199–228. [Google Scholar] [CrossRef]
- Hirt, C. Heuristic stability theory for finite-difference equations. J. Comput. Phys. 1968, 2, 339–355. [Google Scholar] [CrossRef]
- Domaradzki, J.A.; Radhakrishnan, S. Effective eddy viscosities in implicit modeling of decaying high Reynolds number turbulence with and without rotation. Fluid Dyn. Res. 2005, 36, 385–406. [Google Scholar] [CrossRef]
- Margolin, L.G.; Rider, W.J. A rationale for implicit turbulence modelling. Int. J. Numer. Methods Fluids 2002, 39, 821–841. [Google Scholar] [CrossRef]
- Rider, W.; Margolin, L. From numerical analysis to implicit subgrid turbulence modeling. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003. [Google Scholar] [CrossRef]
- Margolin, L.G.; Rider, W.J. The design and construction of implicit LES models. Int. J. Numer. Methods Fluids 2005, 47, 1173–1179. [Google Scholar] [CrossRef]
- Margolin, L.G.; Rider, W.J.; Grinstein, F.F. Modeling turbulent flow with implicit LES. J. Turbul. 2006, 7, 27. [Google Scholar] [CrossRef]
- Drikakis, D.; Rider, J. High-Resolution Methods for Incompressible and Low-Speed Flows; Springer: Berlin, Germany, 2004; Volume 1. [Google Scholar]
- Grinstein, F.F.; Margolin, L.G.; Rider, W.J. Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics; Cambridge University Press: Cambridg, UK, 2007. [Google Scholar]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer: Berlin, Germany, 1999. [Google Scholar]
- Drikakis, D. Advances in turbulent flow computations using high-resolution methods. Prog. Aerosp. Sci. 2003, 39, 405–424. [Google Scholar] [CrossRef]
- Mosedale, A.; Drikakis, D. Assessment of very high-order of accuracy in LES models. J. Fluids Eng. 2007, 129, 1497–1503. [Google Scholar] [CrossRef]
- Hahn, M.; Drikakis, D. Assessment of large-eddy simulation of internal separated flow. J. Fluids Eng. Trans. ASME 2009, 131, 0712011–07120115. [Google Scholar] [CrossRef]
- Balachandar, S.; Eaton, J.K. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Fox, R.O. Large-Eddy-Simulation Tools for Multiphase Flows. Annu. Rev. Fluid Mech. 2012, 44, 47–76. [Google Scholar] [CrossRef]
- Yeoh, G.H.; Tu, J. Computational Techniques for Multiphase Flows, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Roekaerts, D.; Vervisch, L. (Eds.) Best Practice Guidelines for Computational Fluid Dynamics of Turbulent Combustion; BPG, ERCOFTAC: Brussels, Belgium, 2016. [Google Scholar]
- Sommerfeld, M.; van Wachem, B.; Oliemans, R. (Eds.) Best Practice Guidelines for Computational Fluid Dynamics of Dispersed Multi-Phase Flows; BPG, ERCOFTAC: Brussels, Belgium, 2008. [Google Scholar]
- Spalding, D.B. Mixing and Chemical Reaction in Steady Confined Turbulent Flames. In Proceedings of the Thirteenth Symposium (International) on Combustion, Salt Lake City, UT, USA, 23–29 August 1970; p. 649. [Google Scholar]
- Magnussen, B.F. On the Structure of Turbulence and a Generalized Eddy Dissipation Concept for Chemical Reaction in Turbulent Flow. In Proceedings of the 19th Aerospace Sciences Meeting, St. Louis, MO, USA, 12–15 January 1981; p. 42. [Google Scholar]
- Ertesvag, I.S.; Magnussen, B.F. The Eddy Dissipation Turbulence Energy Cascade Model. Combust. Sci. Technol. 2000, 159, 213–235. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 2nd ed.; R.T. Edwards, Inc.: Philadelphia, PA, USA, 2005. [Google Scholar]
- Peters, B.; Baniasadi, M.; Baniasadi, M.; Besseron, X.; Donoso, A.E.; Mohseni, M.; Pozzetti, G. XDEM multi-physics and multi-scale simulation technology: Review of DEM–CFD coupling, methodology and engineering applications. Particuology 2019, 44, 176–193. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical Modelling of Two-Phase Flow. Ann. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Fox, R.O. On multiphase turbulence models for collisional fluid–particle flows. J. Fluid Mech. 2014, 742, 368–424. [Google Scholar] [CrossRef]
- Riella, M.; Kahraman, R.; Tabor, G. Reynolds-Averaged Two-Fluid Model prediction of moderately dilute fluid-particle flow over a backward-facing step. Int. J. Multiph. Flow 2018, 106, 95–108. [Google Scholar] [CrossRef]
- Riella, M.; Kahraman, R.; Tabor, G. Inhomogeneity and anisotropy in Eulerian–Eulerian near-wall modelling. Int. J. Multiph. Flow 2019, 114, 9–18. [Google Scholar] [CrossRef]
- Wu, L.; Ho, M.T.; Germanou, L.; Gu, X.J.; Liu, C.; Xu, K.; Zhang, Y. On the apparent permeability of porous media in rarefied gas flows. J. Fluid Mech. 2017, 822, 398–417. [Google Scholar] [CrossRef]
- Germanou, L.; Ho, M.T.; Zhang, Y.; Wu, L. Intrinsic and apparent gas permeability of heterogeneous and anisotropic ultra-tight porous media. J. Nat. Gas Sci. Eng. 2018, 60, 271–283. [Google Scholar] [CrossRef]
- Boek, E.S.; Venturoli, M. Lattice-Boltzmann studies of fluid flow in porous media with realistic rock geometries. Comput. Math. Appl. 2010, 59, 2305–2314. [Google Scholar] [CrossRef]
- Lei, L.; Wang, N.; Zhang, X.; Tai, Q.; Tsai, D.P.; Chan, H.L. Optofluidic planar reactors for photocatalytic water treatment using solar energy. Biomicrofluidics 2010, 4, 043004. [Google Scholar] [CrossRef]
- Adleman, J.R.; Boyd, D.A.; Goodwin, D.G.; Psaltis, D. Heterogenous catalysis mediated by plasmon heating. Nano Lett. 2009, 9, 4417–4423. [Google Scholar] [CrossRef]
- Lee, M.T.; Werhahn, M.; Hwang, D.J.; Hotz, N.; Greif, R.; Poulikakos, D.; Grigoropoulos, C.P. Hydrogen production with a solar steam–Methanol reformer and colloid nanocatalyst. Int. J. Hydrog. Energy 2010, 35, 118–126. [Google Scholar] [CrossRef]
- Zimmerman, R.; Morrison, G.; Rosengarten, G. A microsolar collector for hydrogen production by methanol reforming. J. Sol. Energy Eng. 2010, 132, 011005. [Google Scholar] [CrossRef]
- Hendriks, B.; Kuiper, S.; As, M.V.; Renders, C.; Tukker, T. Electrowetting-based variable-focus lens for miniature systems. Opt. Rev. 2005, 12, 255–259. [Google Scholar] [CrossRef]
- Mantzalis, D.; Asproulis, N.; Drikakis, D. Filtering carbon dioxide through carbon nanotubes. Chem. Phys. Lett. 2011, 506, 81–85. [Google Scholar] [CrossRef]
- Mantzalis, D.; Asproulis, N.; Drikakis, D. Enhanced carbon dioxide adsorption through carbon nanoscrolls. Phys. Rev. E 2011, 84, 066304. [Google Scholar] [CrossRef]
- Drikakis, D.; Asproulis, N.; Mantzalis, D. Carbon Dioxide Capture Using Multi-Walled Carbon Nanotubes. J. Comput. Theor. Nanosci. 2015, 12, 3981–3993. [Google Scholar] [CrossRef]
- Mantzalis, D.; Asproulis, N.; Drikakis, D. Carbon Dioxide Transport in Carbon Nanopores; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2012; Volume 362, p. 012018. [Google Scholar]
- Kim, M.; Sell, A.; Sinton, D. Aquifer-on-a-Chip: Understanding pore-scale salt precipitation dynamics during CO2 sequestration. Lab Chip 2013, 13, 2508–2518. [Google Scholar] [CrossRef]
- Song, W.; Fadaei, H.; Sinton, D. Determination of dew point conditions for CO2 with impurities using microfluidics. Environ. Sci. Technol. 2014, 48, 3567–3574. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Frank, M.; Drikakis, D. Nanoflow over a fractal surface. Phys. Fluids 2016, 28, 082001. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.; Liakopoulos, A. Transport properties of liquid argon in krypton nanochannels: anisotropy and non-homogeneity introduced by the solid walls. Int. J. Heat Mass Transf. 2009, 52, 735–743. [Google Scholar] [CrossRef]
- Giannakopoulos, A.; Sofos, F.; Karakasidis, T.; Liakopoulos, A. Unified description of size effects of transport properties of liquids flowing in nanochannels. Int. J. Heat Mass Transf. 2012, 55, 5087–5092. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D. Solid-like heat transfer in confined liquids. Microfluid. Nanofluidics 2017, 21, 148. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D. Thermodynamics at Solid–Liquid Interfaces. Entropy 2018, 20, 362. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Frank, M.; Drikakis, D. Effects of surface roughness on shear viscosity. Phys. Rev. E 2017, 95, 033108. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Kalweit, M.; Drikakis, D. Multiscale methods for micro/nano flows and materials. J. Comput. Theor. Nanosci. 2008, 5, 1923–1938. [Google Scholar] [CrossRef]
- Kalweit, M.; Drikakis, D. Multiscale simulation strategies and mesoscale modelling of gas and liquid flows. IMA J. Appl. Math. 2011, 76, 661–671. [Google Scholar] [CrossRef]
- Drikakis, D.; Frank, M. Advances and challenges in computational research of micro-and nanoflows. Microfluid. Nanofluidics 2015, 19, 1019–1033. [Google Scholar] [CrossRef][Green Version]
- Hadjiconstantinou, N.G.; Patera, A.T. Heterogeneous atomistic-continuum representations for dense fluid systems. Int. J. Mod. Phys. C 1997, 8, 967–976. [Google Scholar] [CrossRef]
- Hadjiconstantinou, N.G. Hybrid atomistic—Continuum formulations and the moving contact-line problem. J. Comput. Phys. 1999, 154, 245–265. [Google Scholar] [CrossRef]
- Werder, T.; Walther, J.H.; Koumoutsakos, P. Hybrid atomistic—Continuum method for the simulation of dense fluid flows. J. Comput. Phys. 2005, 205, 373–390. [Google Scholar] [CrossRef]
- Delgado-Buscalioni, R.; Coveney, P. Continuum-particle hybrid coupling for mass, momentum, and energy transfers in unsteady fluid flow. Phys. Rev. E 2003, 67, 046704. [Google Scholar] [CrossRef]
- Barsky, S.; Delgado-Buscalioni, R.; Coveney, P.V. Comparison of molecular dynamics with hybrid continuum—Molecular dynamics for a single tethered polymer in a solvent. J. Chem. Phys. 2004, 121, 2403–2411. [Google Scholar] [CrossRef]
- De Fabritiis, G.; Serrano, M.; Delgado-Buscalioni, R.; Coveney, P. Fluctuating hydrodynamic modeling of fluids at the nanoscale. Phys. Rev. E 2007, 75, 026307. [Google Scholar] [CrossRef]
- Delgado-Buscalioni, R.; Flekkøy, E.; Coveney, P. Fluctuations and continuity in particle-continuum hybrid simulations of unsteady flows based on flux-exchange. Europhys. Lett. 2005, 69, 959. [Google Scholar] [CrossRef][Green Version]
- Wijesinghe, H.S.; Hadjiconstantinou, N.G. Discussion of hybrid atomistic-continuum methods for multiscale hydrodynamics. Int. J. Multiscale Comput. Eng. 2004, 2, 189–202. [Google Scholar] [CrossRef]
- Koumoutsakos, P. Multiscale flow simulations using particles. Annu. Rev. Fluid Mech. 2005, 37, 457–487. [Google Scholar] [CrossRef]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier-Stokes equation. Phys. Rev. Lett. 1986, 56, 1505. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular automaton fluids 1: Basic theory. J. Stat. Phys. 1986, 45, 471–526. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Ladd, A.J. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Izquierdo, S.; Martínez-Lera, P.; Fueyo, N. Analysis of open boundary effects in unsteady lattice Boltzmann simulations. Comput. Math. Appl. 2009, 58, 914–921. [Google Scholar] [CrossRef]
- Hyväluoma, J.; Harting, J. Slip flow over structured surfaces with entrapped microbubbles. Phys. Rev. Lett. 2008, 100, 246001. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T. Lattice Boltzmann model for incompressible flows through porous media. Phys. Rev. E 2002, 66, 036304. [Google Scholar] [CrossRef]
- Pan, C.; Hilpert, M.; Miller, C. Lattice-Boltzmann simulation of two-phase flow in porous media. Water Resour. Res. 2004, 40, 160. [Google Scholar] [CrossRef]
- Pan, C.; Luo, L.S.; Miller, C.T. An evaluation of lattice Boltzmann schemes for porous medium flow simulation. Comput. Fluids 2006, 35, 898–909. [Google Scholar] [CrossRef]
- Zhang, J. Lattice Boltzmann method for microfluidics: Models and applications. Microfluid. Nanofluidics 2011, 10, 1–28. [Google Scholar]
- Hoogerbrugge, P.; Koelman, J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155. [Google Scholar] [CrossRef]
- Li, Z.; Hu, G.H.; Wang, Z.L.; Ma, Y.B.; Zhou, Z.W. Three dimensional flow structures in a moving droplet on substrate: A dissipative particle dynamics study. Phys. Fluids 2013, 25, 072103. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Y.H.; Lei, H.; Caswell, B.; Karniadakis, G.E. Energy-conserving dissipative particle dynamics with temperature-dependent properties. J. Comput. Phys. 2014, 265, 113–127. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Y.H.; Li, X.; Karniadakis, G.E. Mesoscale modeling of phase transition dynamics of thermoresponsive polymers. Chem. Commun. 2015, 51, 11038–11040. [Google Scholar] [CrossRef] [PubMed]
- Pivkin, I.V.; Karniadakis, G.E. Coarse-graining limits in open and wall-bounded dissipative particle dynamics systems. J. Chem. Phys. 2006, 124, 184101. [Google Scholar] [CrossRef] [PubMed]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Alvarez, F.; Flores, E.; Castro, L.; Hernández, J.; López, A.; Vazquez, F. Dissipative particle dynamics (DPD) study of crude oil- water emulsions in the presence of a functionalized co-polymer. Energy Fuels 2010, 25, 562–567. [Google Scholar] [CrossRef]
- Deguillard, E.; Pannacci, N.; Creton, B.; Rousseau, B. Interfacial tension in oil–water–surfactant systems: On the role of intra-molecular forces on interfacial tension values using DPD simulations. J. Chem. Phys. 2013, 138, 144102. [Google Scholar] [CrossRef]
- Rezaei, H.; Amjad-Iranagh, S.; Modarress, H. Self-Accumulation of Uncharged Polyaromatic Surfactants at Crude Oil–Water Interface: A Mesoscopic DPD Study. Energy Fuels 2016, 30, 6626–6639. [Google Scholar] [CrossRef]
- Du, C.; Ji, Y.; Xue, J.; Hou, T.; Tang, J.; Lee, S.T.; Li, Y. Morphology and performance of polymer solar cell characterized by DPD simulation and graph theory. Sci. Rep. 2015, 5, 16854. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S.; Peng, F.; Zhang, W.; Zhang, Y. Dissipative particle dynamics investigation of microencapsulated thermal energy storage phase change materials. Energy 2012, 44, 805–812. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).