Power Quality Services Provided by Virtually Synchronous FACTS
Abstract
:1. Introduction
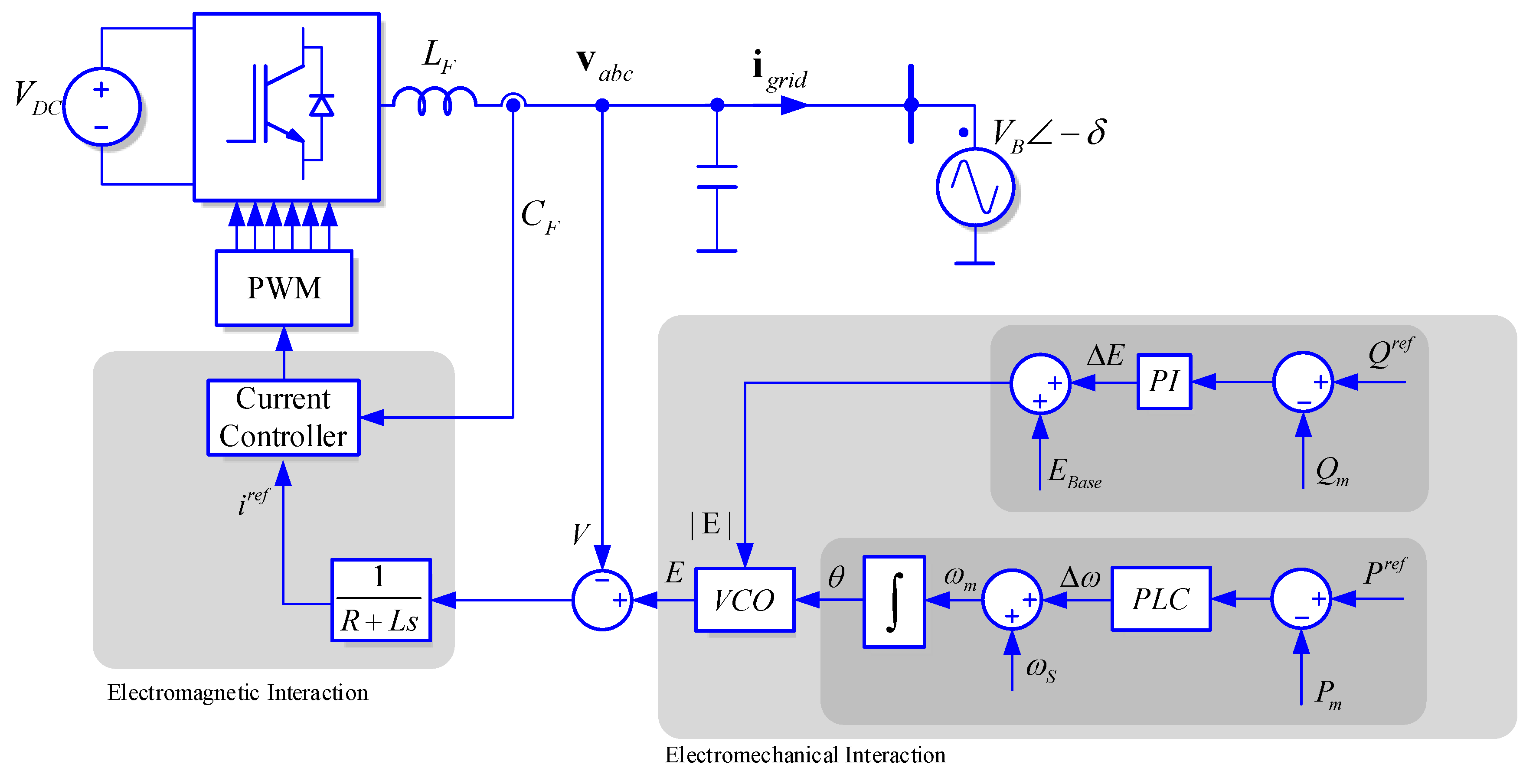
2. FACTS Based on Virtually Synchronous Power Converters
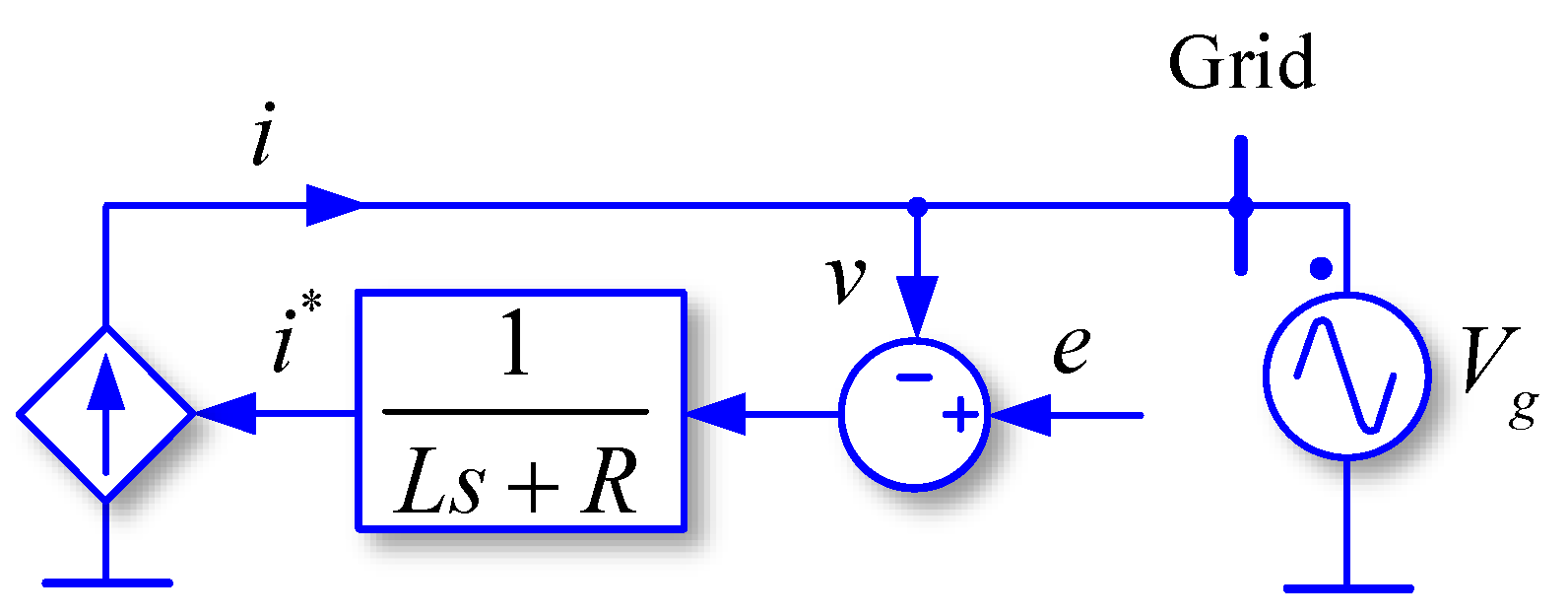
3. Synchronous Power Controller
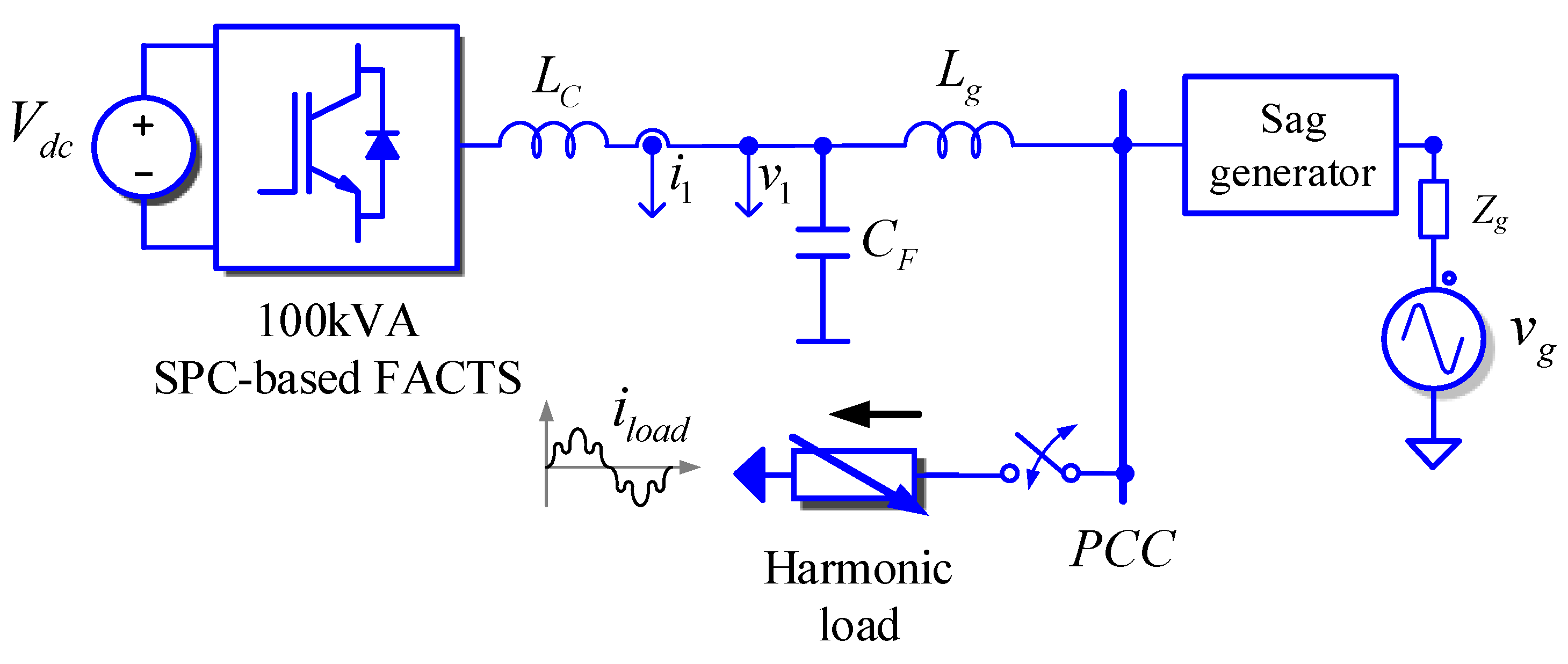
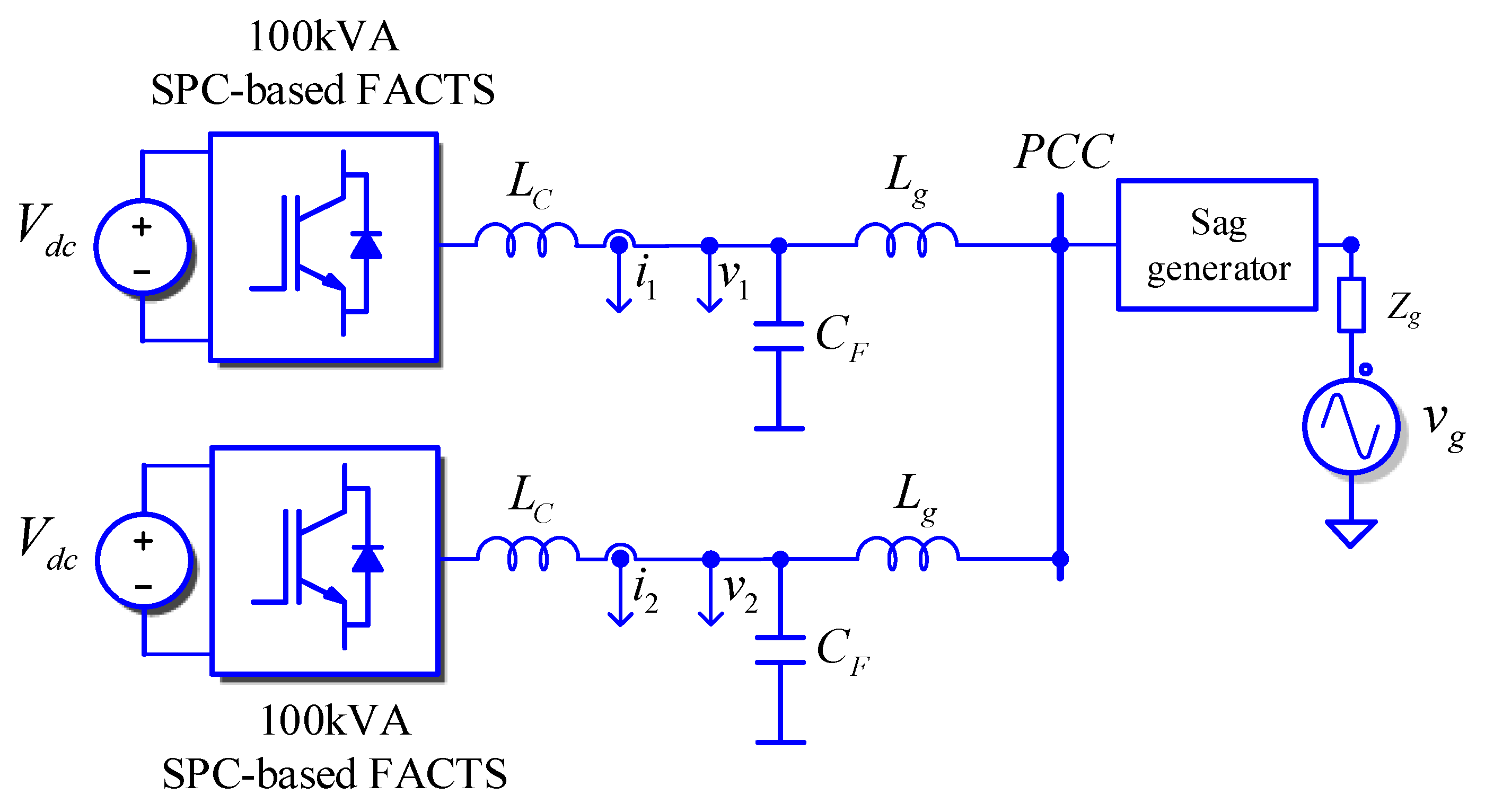
4. Simulation Results
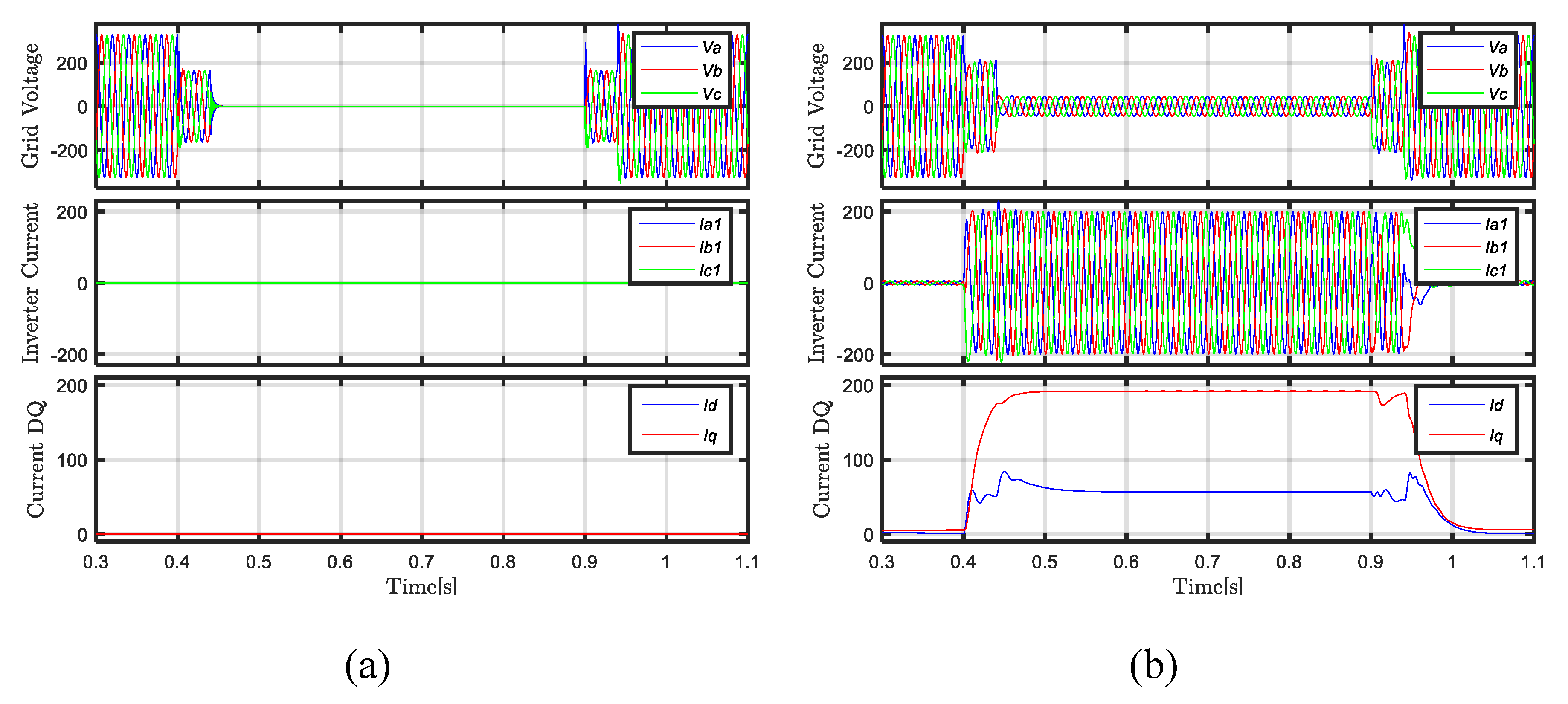
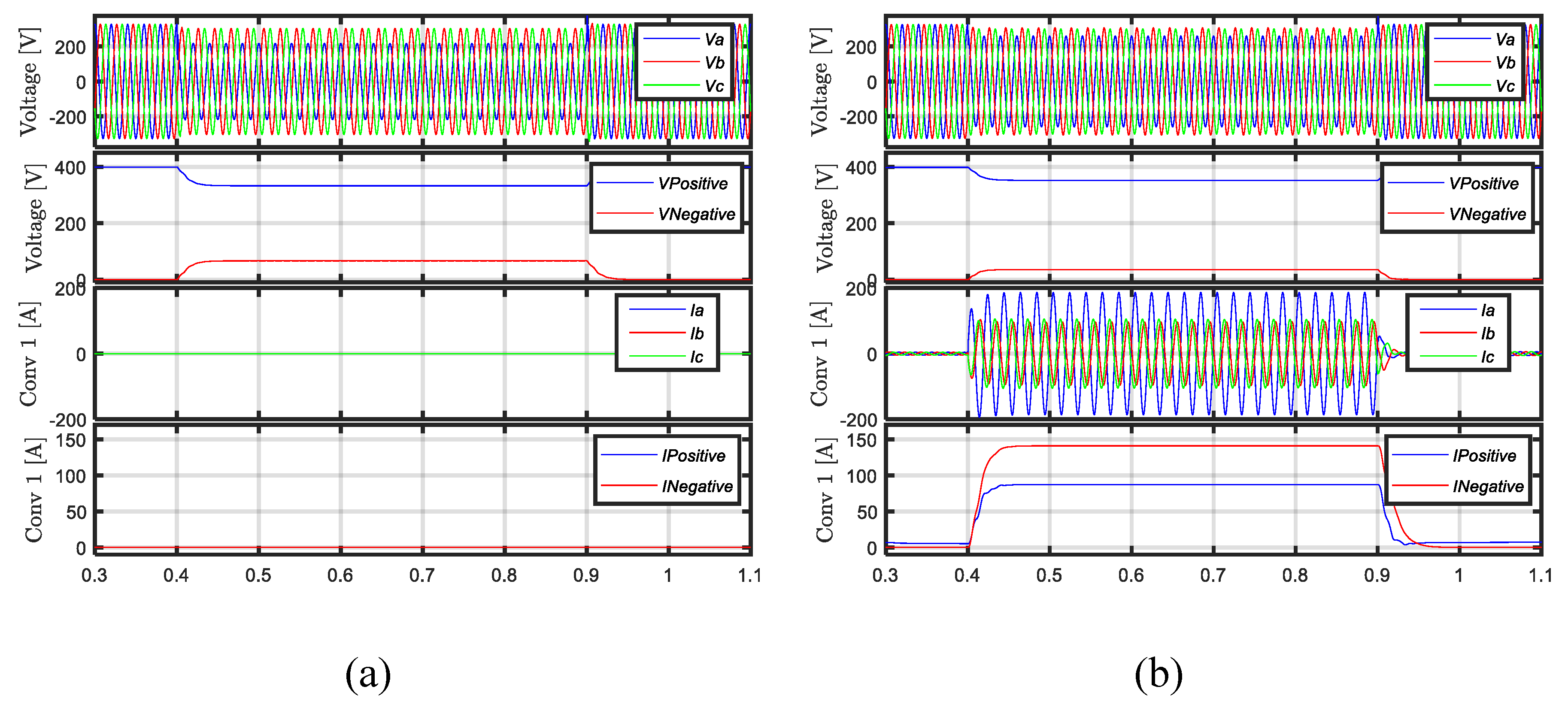
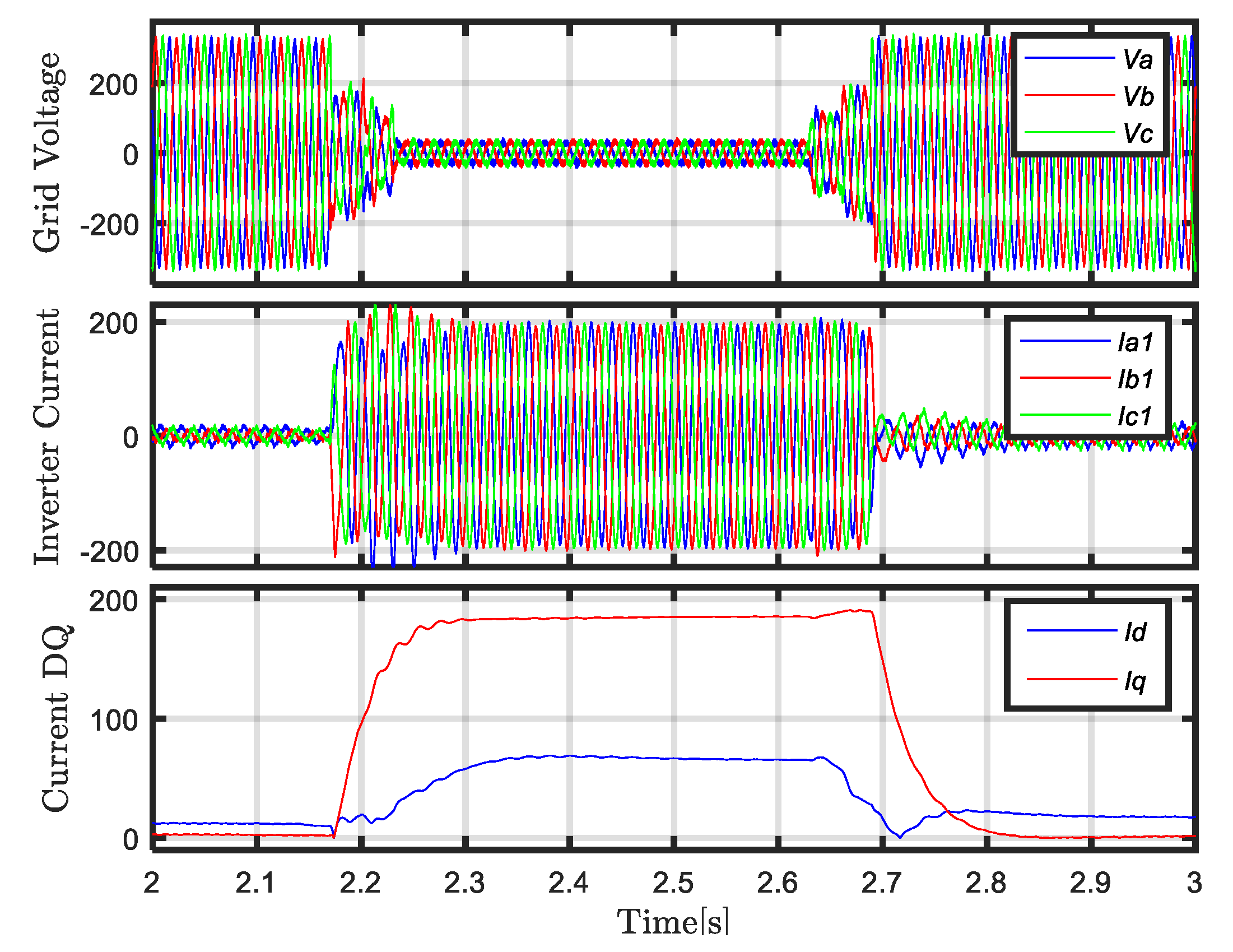
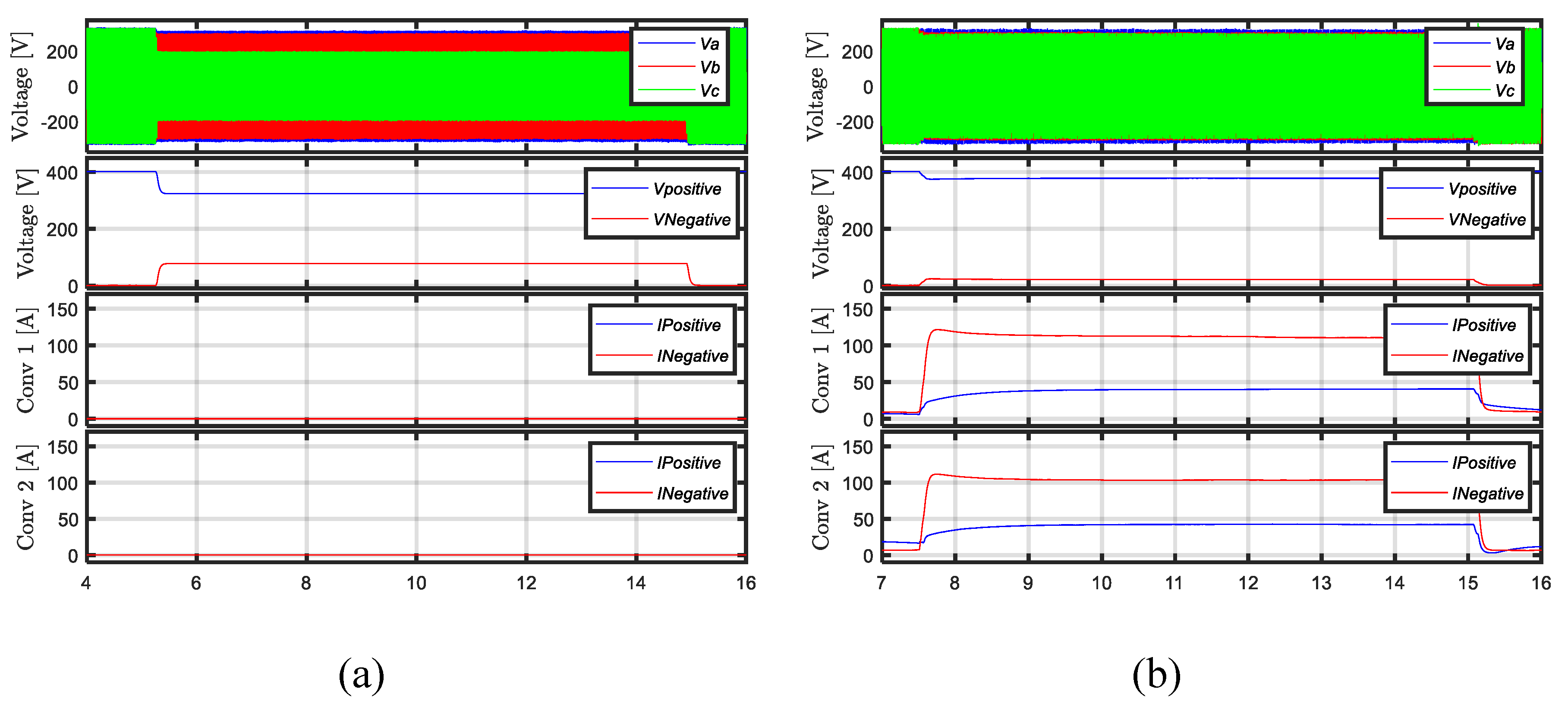
4.1. Balanced LVRT
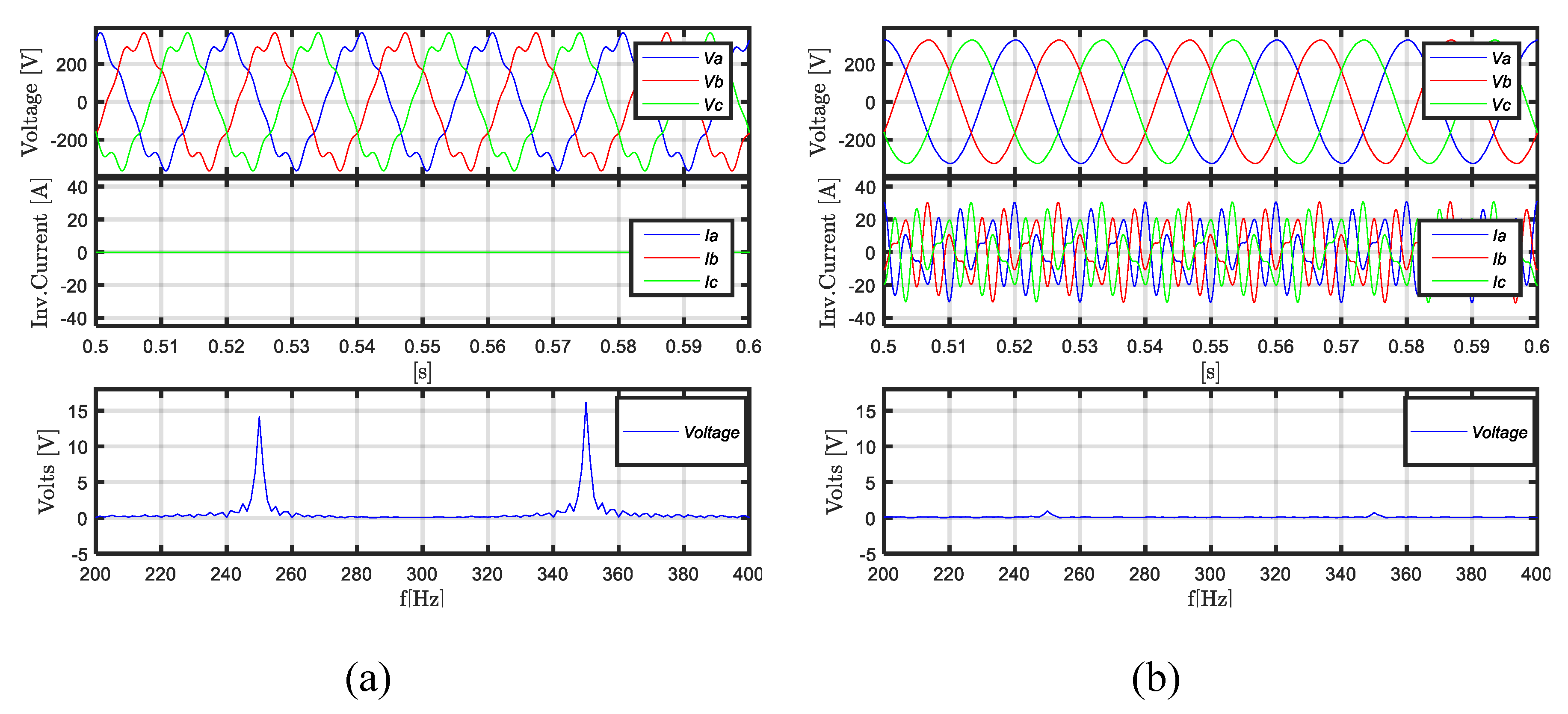
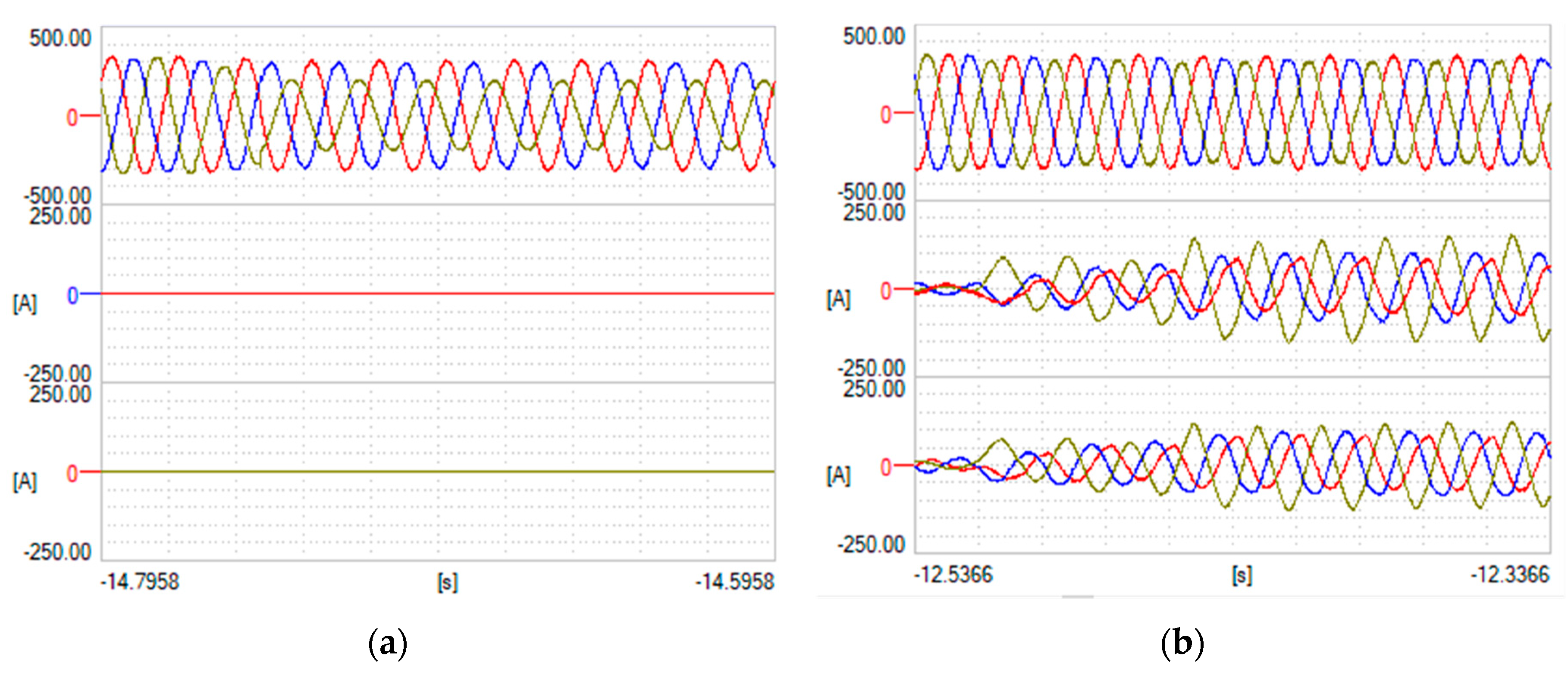
4.2. Unbalanced LVRT
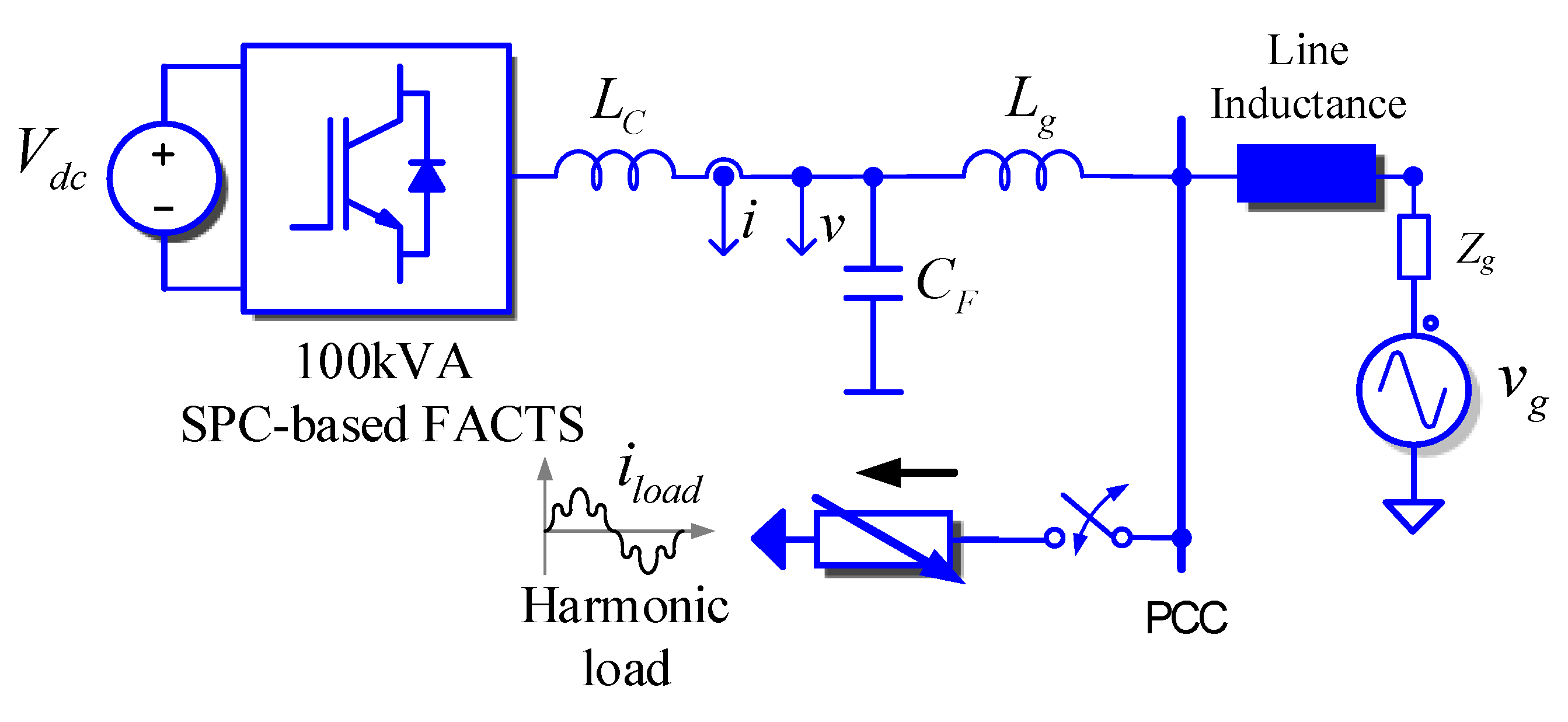
4.3. Harmonic Compensation
5. Experimental Results
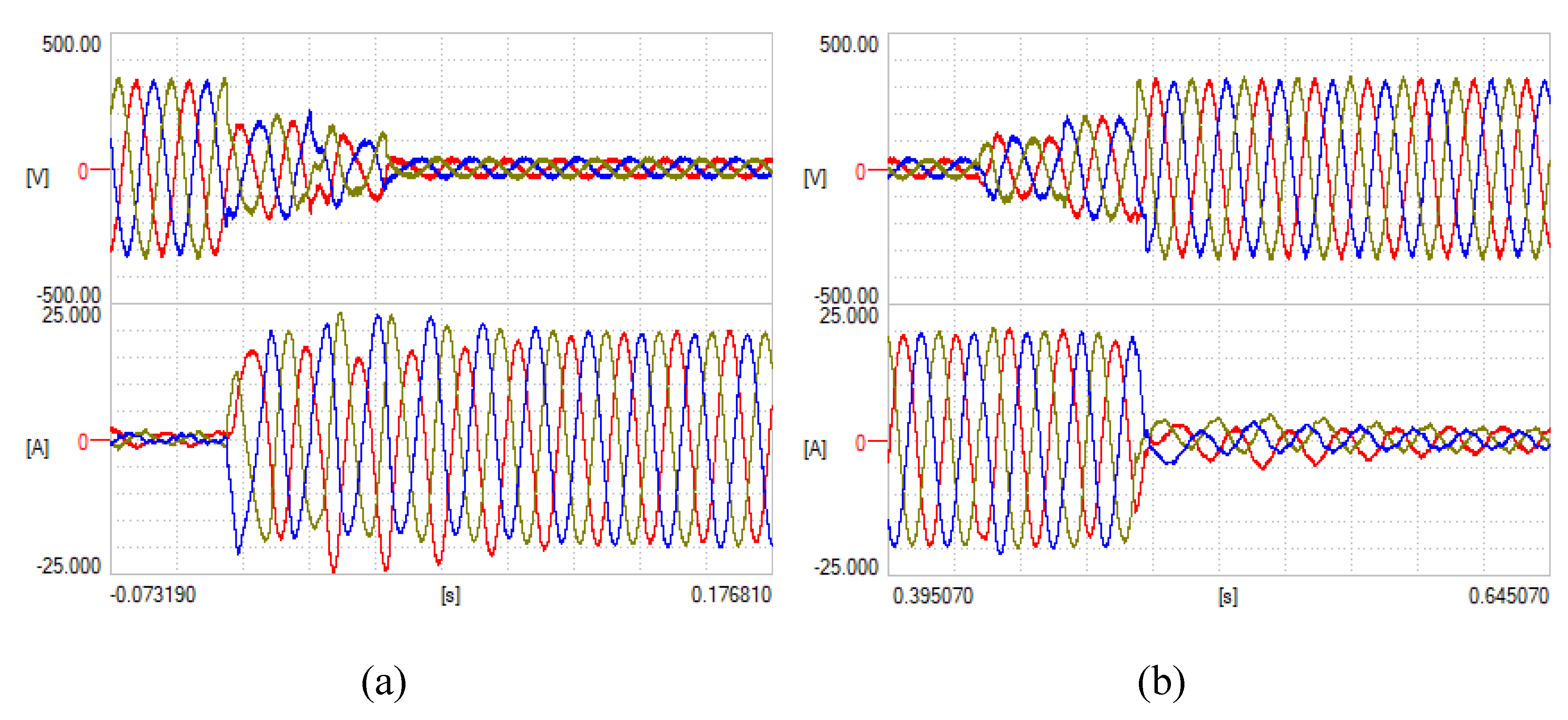
5.1. Balance LVRT
5.2. Unbalanced LVRT
5.3. Harmonic Compensation
6. Conclusions
7. Patents
- WO 2012/117131 A1. “Synchronous controller for a generating system based on static power converters”, Priority date: 18/02/2011 Licensed by: Abengoa Solar NT, S.A.
- WO 2012/117132 A1 “Controller of the electro-mechanical characteristic of a static power converter”, Priority date: 18/02/2011 Licensed by: Abengoa Solar NT, S.A.
- WO 2012/117133 A1 “Virtual admittance controller for a static power converter”, Priority date: 18/02/2011 Licensed by: Abengoa Solar NT, S.A.
Author Contributions
Funding
Conflicts of Interest
References
- Machowski, J.; Bialek, J.; Bumby, J. Power System Dynamics: Stability and Control, 2nd ed.; Wiley: Hoboken, NJ, USA, October 2008. [Google Scholar]
- Morjaria, M.; Anichkov, D.; Chadliev, V.; Soni, S. A Grid-Friendly Plant: The Role of Utility-Scale Photovoltaic Plants in Grid Stability and Reliability. IEEE Power Energy Mag. 2014, 12, 87–95. [Google Scholar] [CrossRef]
- Bae, Y.; Vu, T.; Kim, R. Implemental Control Strategy for Grid Stabilization of Grid-Connected PV System Based on German Grid Code in Symmetrical Low-to-Medium Voltage Network. IEEE Trans. Energy Convers. 2013, 28, 619–631. [Google Scholar] [CrossRef]
- Hingorani, N.G. High Power Electronics and flexible AC Transmission System. IEEE Power Eng. Rev. 1988, 8, 3–4. [Google Scholar] [CrossRef]
- Van Wyk, J.D.; Lee, F.C. On a Future for Power Electronics. IEEE Trans. Emerg. Sel. Top. Power Electron. 2013, 1, 59–72. [Google Scholar] [CrossRef]
- Edris, A.A. Proposed terms and definitions for flexible AC transmission system (FACTS). IEEE Trans. Power Deliv. 1997, 12, 1848–1853. [Google Scholar]
- Gandoman, F.; Ahmadi, A.; Sharaf, A.; Siano, P.; Pou, J.; Hredzak, B.; Agelidis, V. Review of FACTS technologies and applications for power quality in smart grids with renewable energy systems. Renew. Sustain. Energy Rev. 2018, 82, 502–514. [Google Scholar] [CrossRef]
- Padiyar, K.R.; Kulkarni, A.M. Modeling and Analysis of FACTS and HVDC Controllers. Dynamics and Control of Electric Transmission and Microgrids; Wiley-IEEE Press: Hoboken, NJ, USA, 2019; pp. 145–194. [Google Scholar]
- Bruno, S.; de Carne, G.; la Scala, M. Transmission Grid Control Through TCSC Dynamic Series Compensation. IEEE Trans. Power Syst. 2016, 31, 3202–3211. [Google Scholar] [CrossRef]
- Farahani, M. Damping of subsynchronous oscillations in power system using static synchronous series compensator. IET Gener. Transm. Distrib. 2012, 6, 539–544. [Google Scholar] [CrossRef]
- Jiang, F.; Tu, C.; Guo, Q.; Shuai, Z.; He, X.; He, J. Dual-Functional Dynamic Voltage Restorer to Limit Fault Current. IEEE Trans. Ind. Electron. 2019, 66, 5300–5309. [Google Scholar] [CrossRef]
- Kim, H.; Yu, S.-D.; Kim, H.; Kim, W.-S.; Yang, S.-G.; Lee, J.-Y. Demonstration of a Superconducting Fault Current Limiter in a Real Grid. IEEE Trans. Appl. Supercond. 2013, 23, 5603604. [Google Scholar]
- Singh, B.; Saha, R.; Chandra, A.; Al-Haddad, K. Static synchronous compensators (STATCOM): A review. IET Power Electron. 2009, 2, 297–324. [Google Scholar] [CrossRef]
- Teleke, S.; Abdulahovic, T.; Thiringer, T.; Svensson, J. Dynamic Performance Comparison of Synchronous Condenser and SVC. IEEE Trans. Power Deliv. 2018, 23, 1606–1612. [Google Scholar] [CrossRef]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K.; Dessaint, L.A. A Combination of Shunt Hybrid Power Filter and Thyristor-Controlled Reactor for Power Quality. IEEE Trans. Ind. Electron. 2014, 61, 2152–2164. [Google Scholar] [CrossRef]
- Ghosh, S.; Ali, M.H. Power quality enhancement by coordinated operation of thyristor switched capacitor and optimal reclosing of circuit breakers. IET Gener. Transm. Distrib. 2015, 9, 1301–1307. [Google Scholar] [CrossRef] [Green Version]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Shunt Active Filters. Instantaneous Power Theory and Applications to Power Conditioning; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Gyugyi, L.; Schauder, C.D.; Williams, S.L.; Rietman, T.R.; Torgerson, D.R.; Edris, A. The unified power flow controller: A new approach to power transmission control. IEEE Trans. Power Deliv. 1995, 10, 1085–1097. [Google Scholar] [CrossRef]
- Arabi, S.; Hamadanizadeh, H.; Fardanesh, B.B. Convertible static compensator performance studies on the NY state transmission system. IEEE Trans. Power Syst. 2002, 17, 701–706. [Google Scholar] [CrossRef]
- Fujita, H.; Akagi, H. The unified power quality conditioner: the integration of series- and shunt-active filters. IEEE Trans. Power Electron. 1998, 13, 315–322. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, G.-C.; Hung, J.C. Phase-locked loop techniques. A survey. IEEE Trans. Ind. Electron. 1996, 43, 609–615. [Google Scholar] [CrossRef]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. Decoupled Double Synchronous Reference Frame PLL for Power Converters Control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Beck, H.; Hesse, R. Virtual synchronous machine. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Rodriguez, P.; Candela, I.; Luna, A. Control of PV generation systems using the synchronous power controller. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 993–998. [Google Scholar]
- Zhang, W.; Rouzbehi, K.; Luna, A.; Gharehpetian, G.B.; Rodriguez, P. Multi-terminal HVDC grids with inertia mimicry capability. IET Renew. Power Gener. 2016, 7, 752–760. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Cantarellas, A.M.; Garcia, J.M.; Rodriguez, P. Virtual Synchronous Power Strategy for Multiple HVDC Interconnections of Multi-Area AGC Power Systems. IEEE Trans. Power Syst. 2017, 32, 1665–1677. [Google Scholar] [CrossRef]
- Li, C.; Burgos, R.; Cvetkovic, I.; Boroyevich, D.; Mili, L.; Rodriguez, P. Evaluation and control design of virtual-synchronous-machine-based STATCOM for grids with high penetration of renewable energy. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 5652–5658. [Google Scholar]
- Khoshooei, A.; Moghani, J.S.; Candela, I.; Rodriguez, P. Control of D-STATCOM During Unbalanced Grid Faults Based on DC Voltage Oscillations and Peak Current Limitations. IEEE Trans. Ind. Appl. 2018, 54, 1680–1690. [Google Scholar] [CrossRef]
- Rodriguez, P.; Candela, J.I.; Rocabert, J.; Teodorescu, R. Synchronous Power Controller for a Generating System Based on Static Power Converters. U.S. Patent 9,166,508, 20 October 2015. [Google Scholar]
- Tarrasó, A.; Candela, J.I.; Rocabert, J.; Rodriguez, P. Grid voltage harmonic damping method for SPC based power converters with multiple virtual admittance control. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Remon, D.; Cantarellas, A.M.; Mauricio, J.M.; Rodriguez, P. Power system stability analysis under increasing penetration of photovoltaic power plants with synchronous power controllers. IET Renew. Power Gener. 2017, 11, 733–741. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous power controller with flexible droop characteristics for renewable power generation systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]





| Inverter Parameters | |
|---|---|
| Total output power | 100 kVA |
| Filter Parameters | |
| Converter Inductor | 777 μH |
| Grid Inductor | 294 μH |
| Damping resistor | 0.5 ohm |
| Capacitor | 66 μF |
| Voltage sag Gen. Inductance | 400 μH |
| Grid Parameters | |
| Grid Inductor | 400 Uh |
| Grid Resistor | 0.152 ohm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarraso, A.; Lai, N.-B.; Baltas, G.N.; Rodriguez, P. Power Quality Services Provided by Virtually Synchronous FACTS. Energies 2019, 12, 3292. https://doi.org/10.3390/en12173292
Tarraso A, Lai N-B, Baltas GN, Rodriguez P. Power Quality Services Provided by Virtually Synchronous FACTS. Energies. 2019; 12(17):3292. https://doi.org/10.3390/en12173292
Chicago/Turabian StyleTarraso, Andres, Ngoc-Bao Lai, Gregory N. Baltas, and Pedro Rodriguez. 2019. "Power Quality Services Provided by Virtually Synchronous FACTS" Energies 12, no. 17: 3292. https://doi.org/10.3390/en12173292
APA StyleTarraso, A., Lai, N.-B., Baltas, G. N., & Rodriguez, P. (2019). Power Quality Services Provided by Virtually Synchronous FACTS. Energies, 12(17), 3292. https://doi.org/10.3390/en12173292






