Modeling and Control of a Novel Hybrid Power Quality Compensation System for 25-kV Electrified Railway
Abstract
:1. Introduction
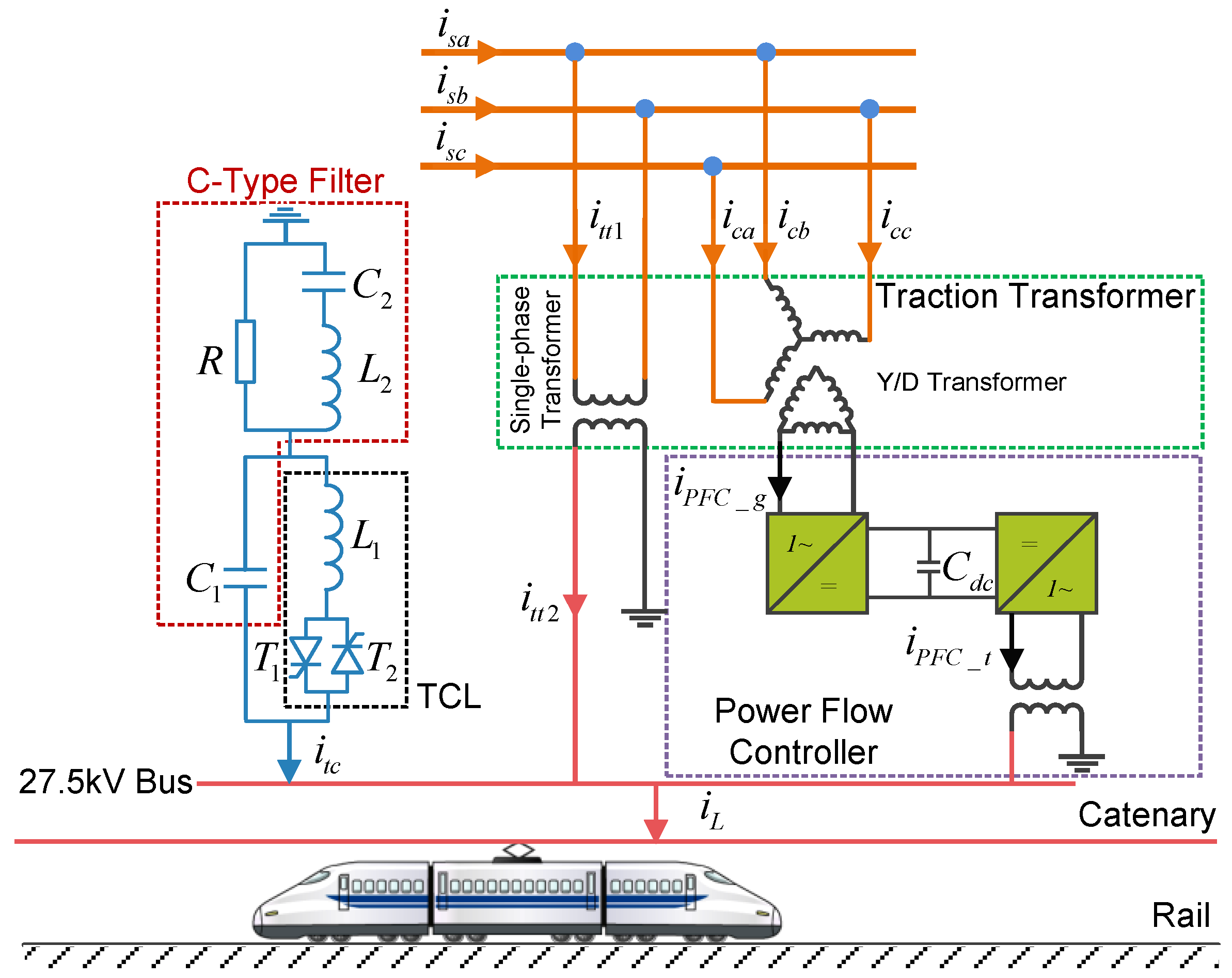
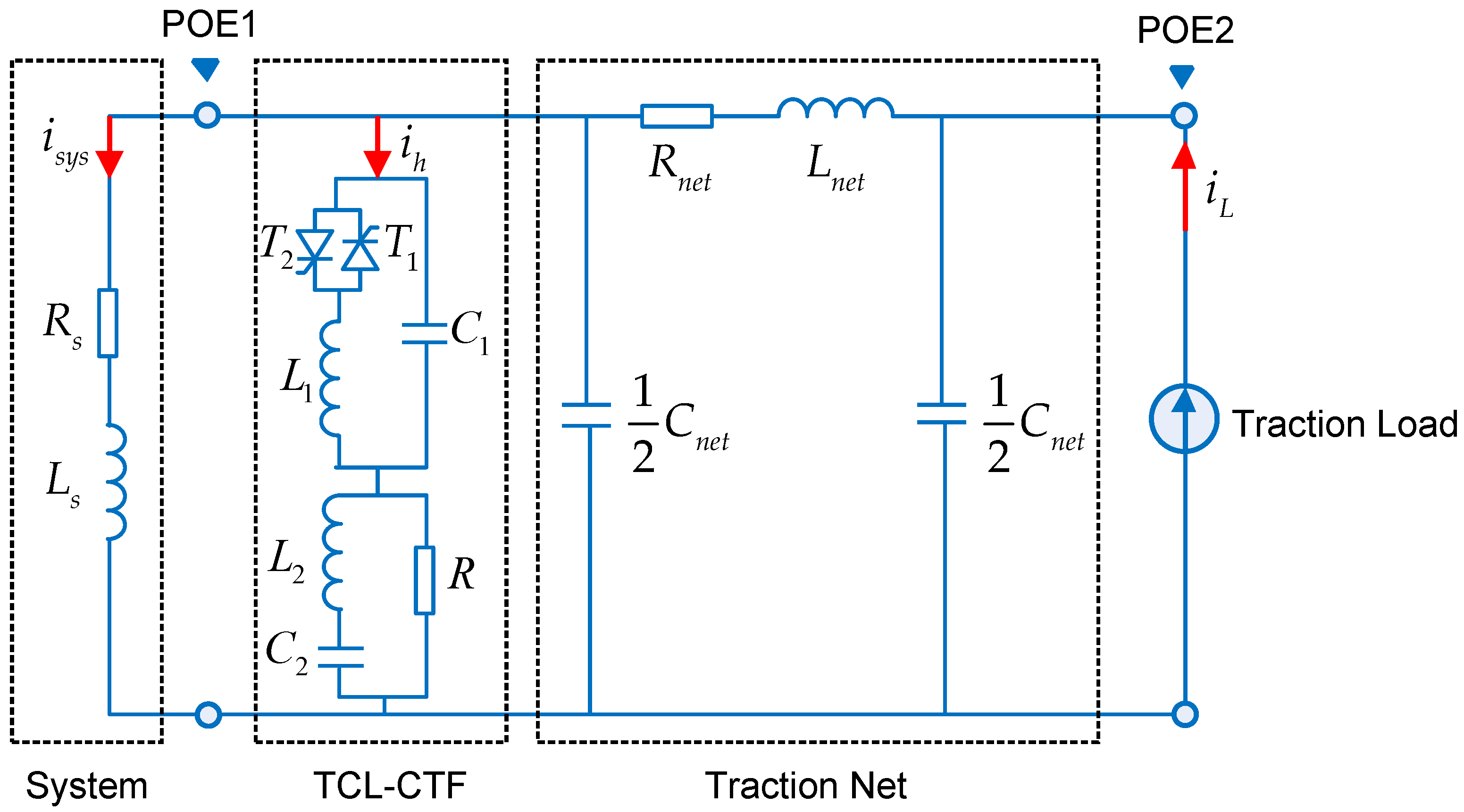
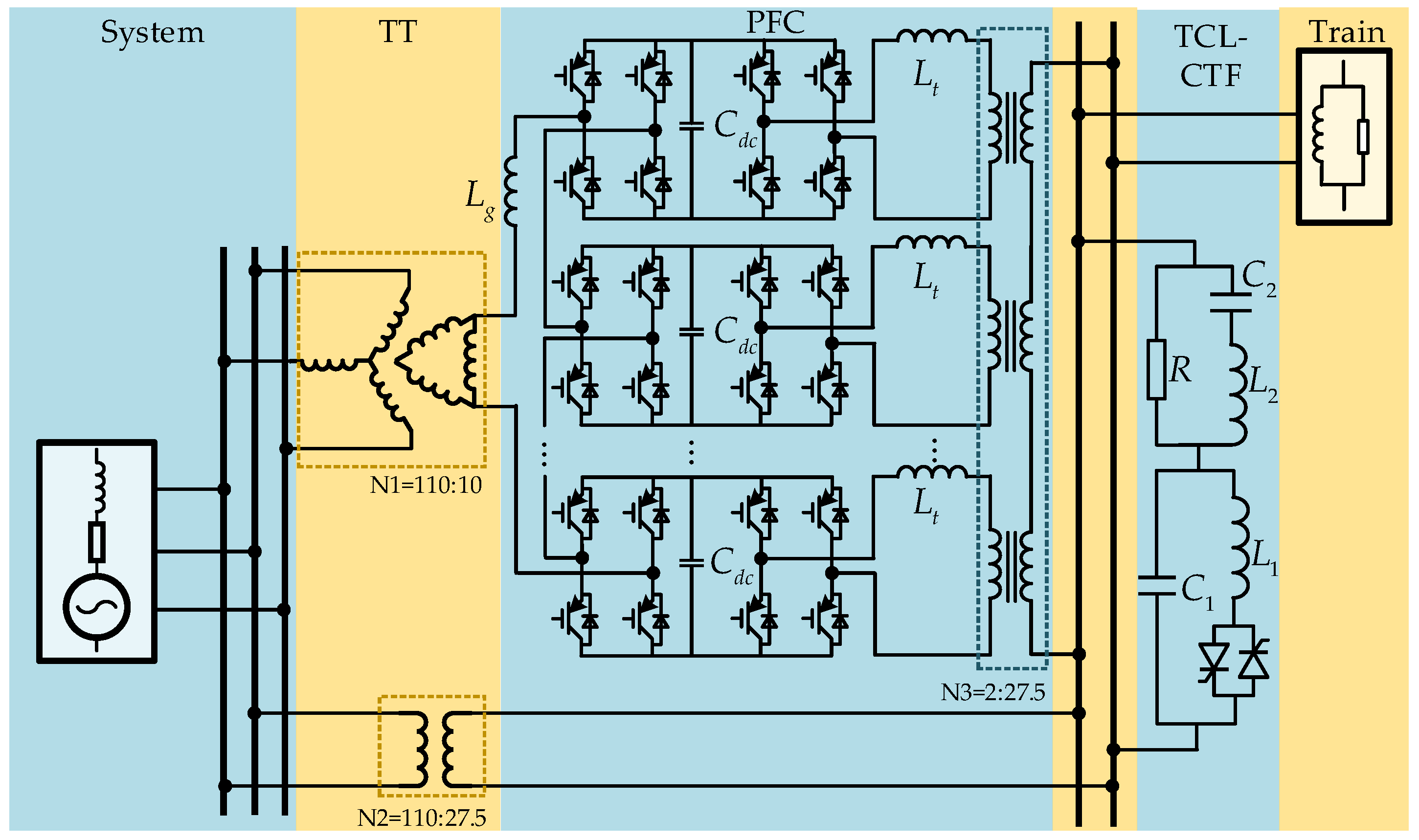
2. Circuit Configuration of the Proposed Hybrid Compensation System
3. Power Analysis of the Proposed Hybrid Compensation System
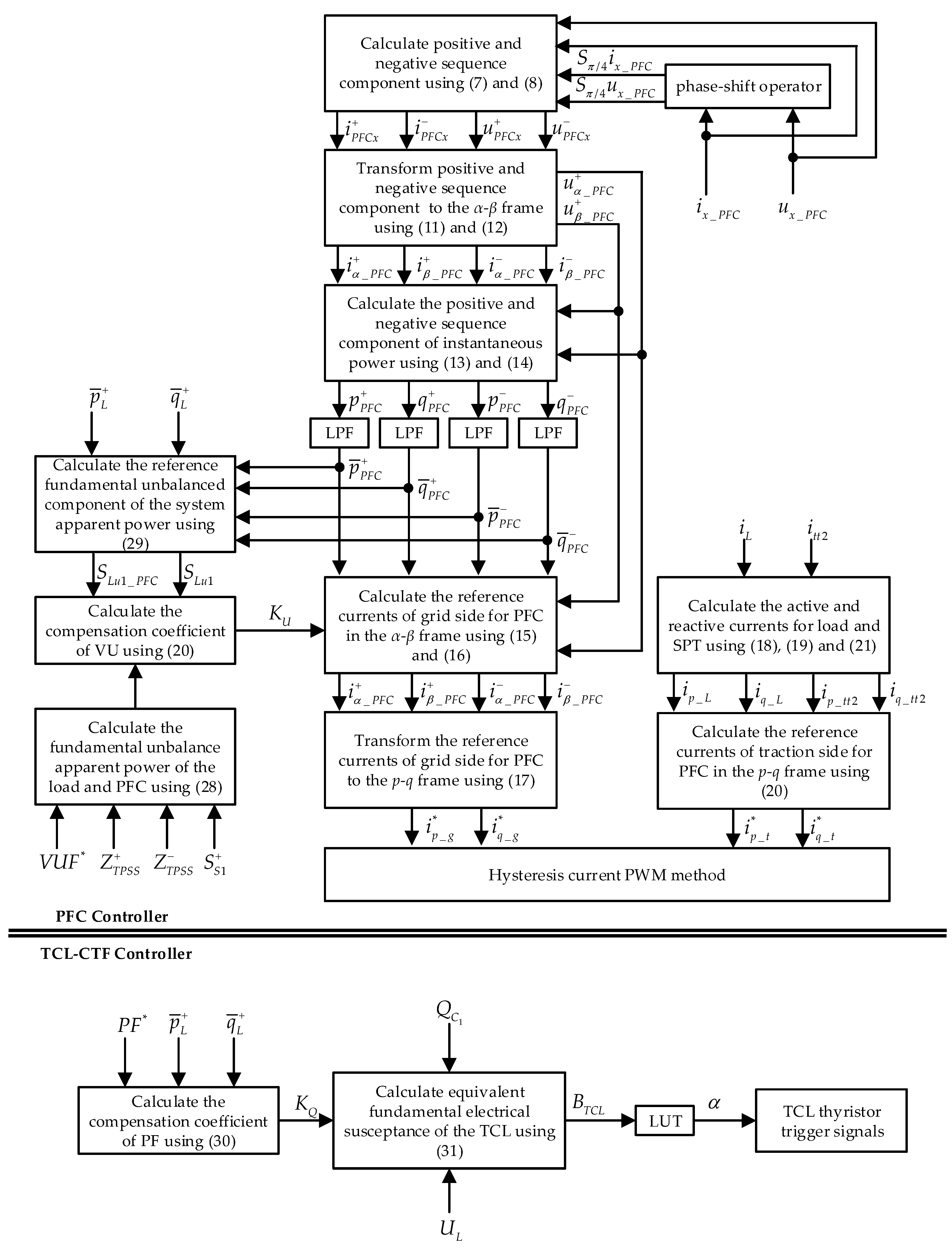
4. Control Strategy of the Proposed Hybrid Compensation System
4.1. PFC Part Control
4.2. TCL-CTF Part Control
4.3. Compensation Parameters Calculation between and
4.3.1. Compensation Coefficient of VU
4.3.2. Compensation Coefficient of PF
4.4. Control Block of the Proposed System
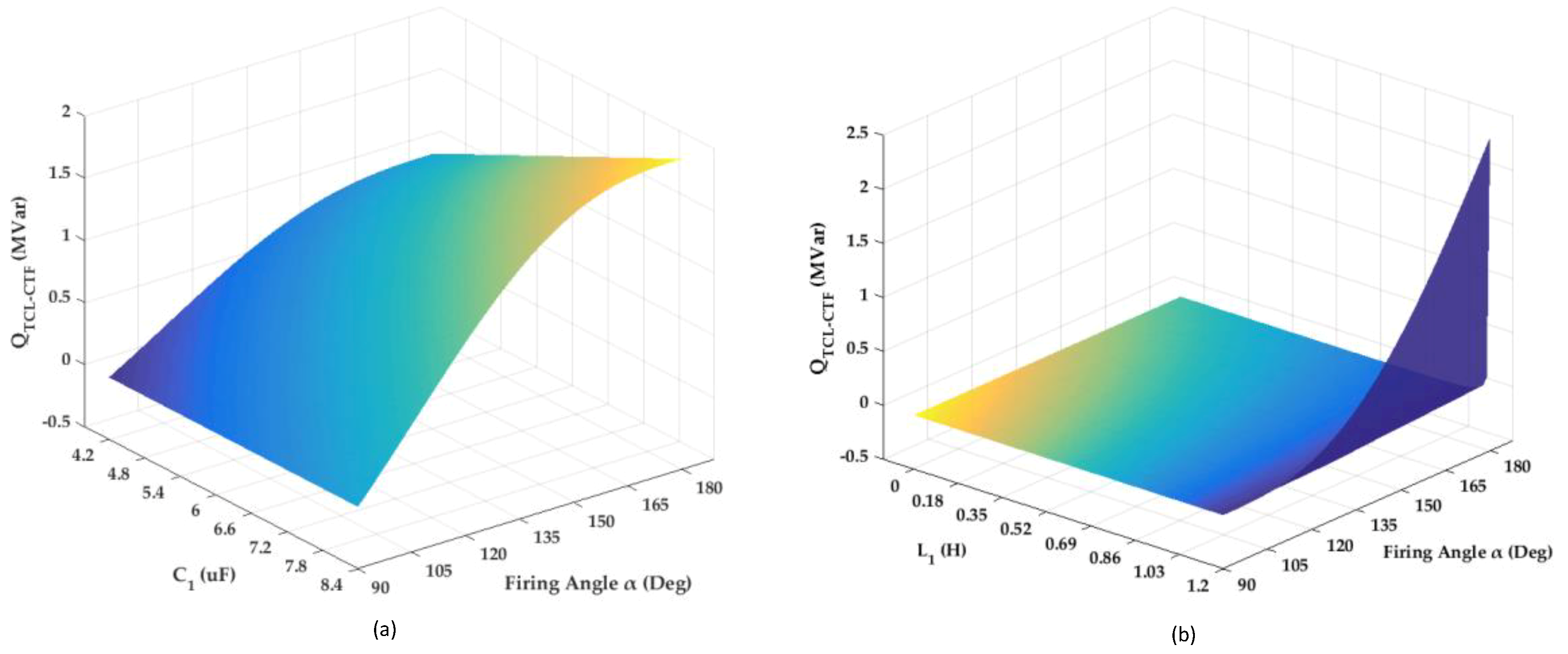
5. Designing Parameters of the TCL-CTF
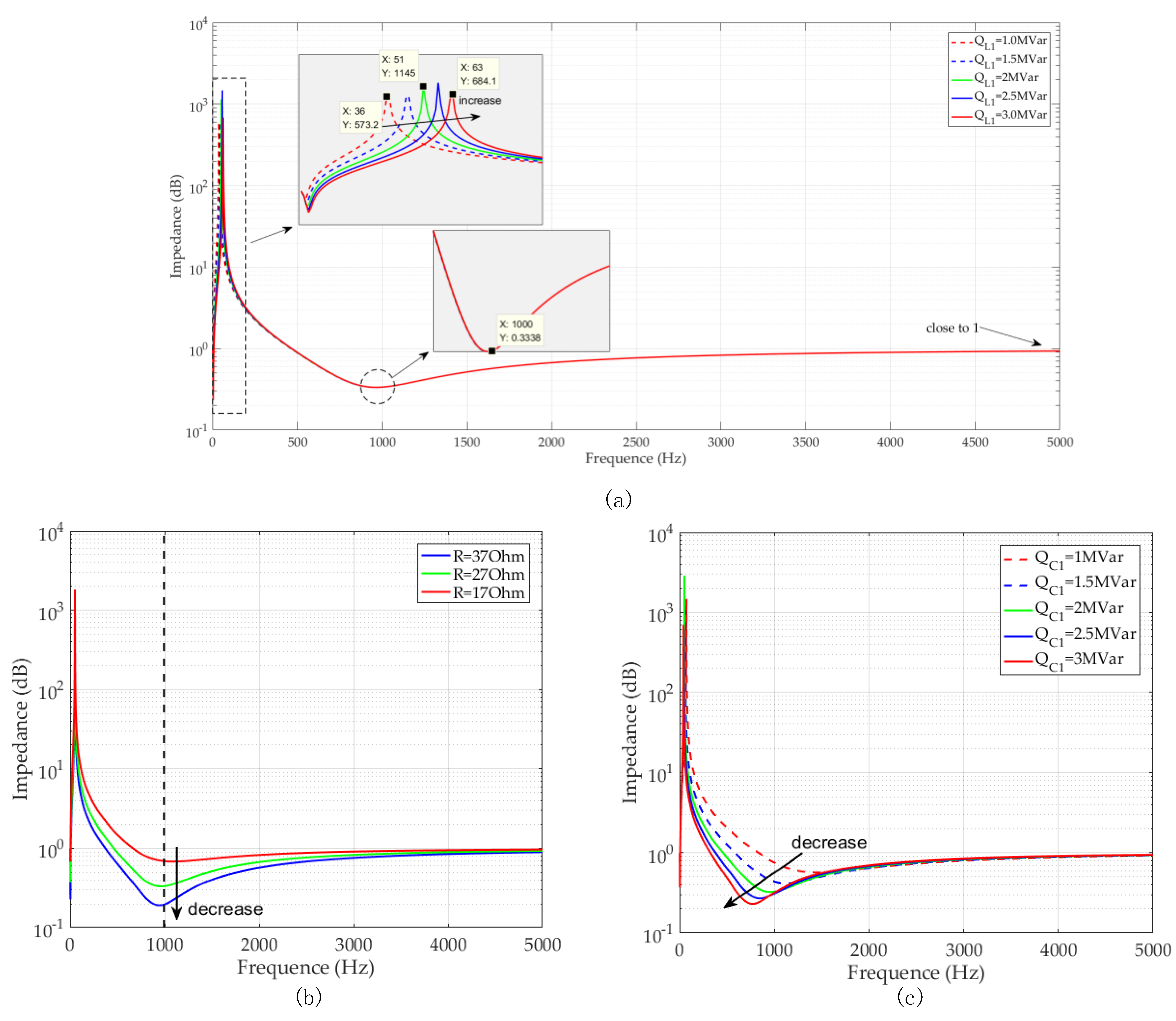
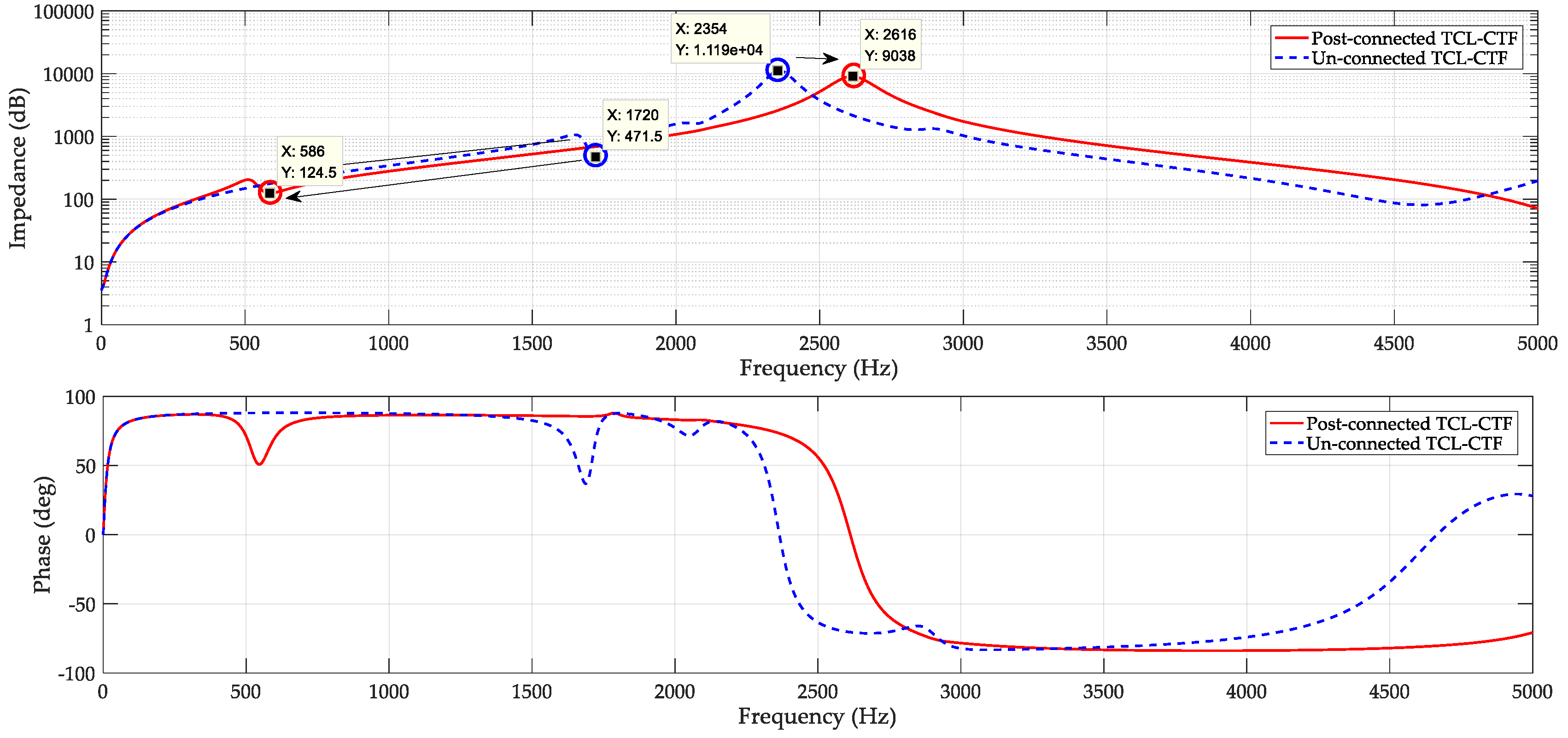
5.1. Resonance Damping Analysis
5.2. Designing Parameters of CTF
6. Simulation and Experimental Validation
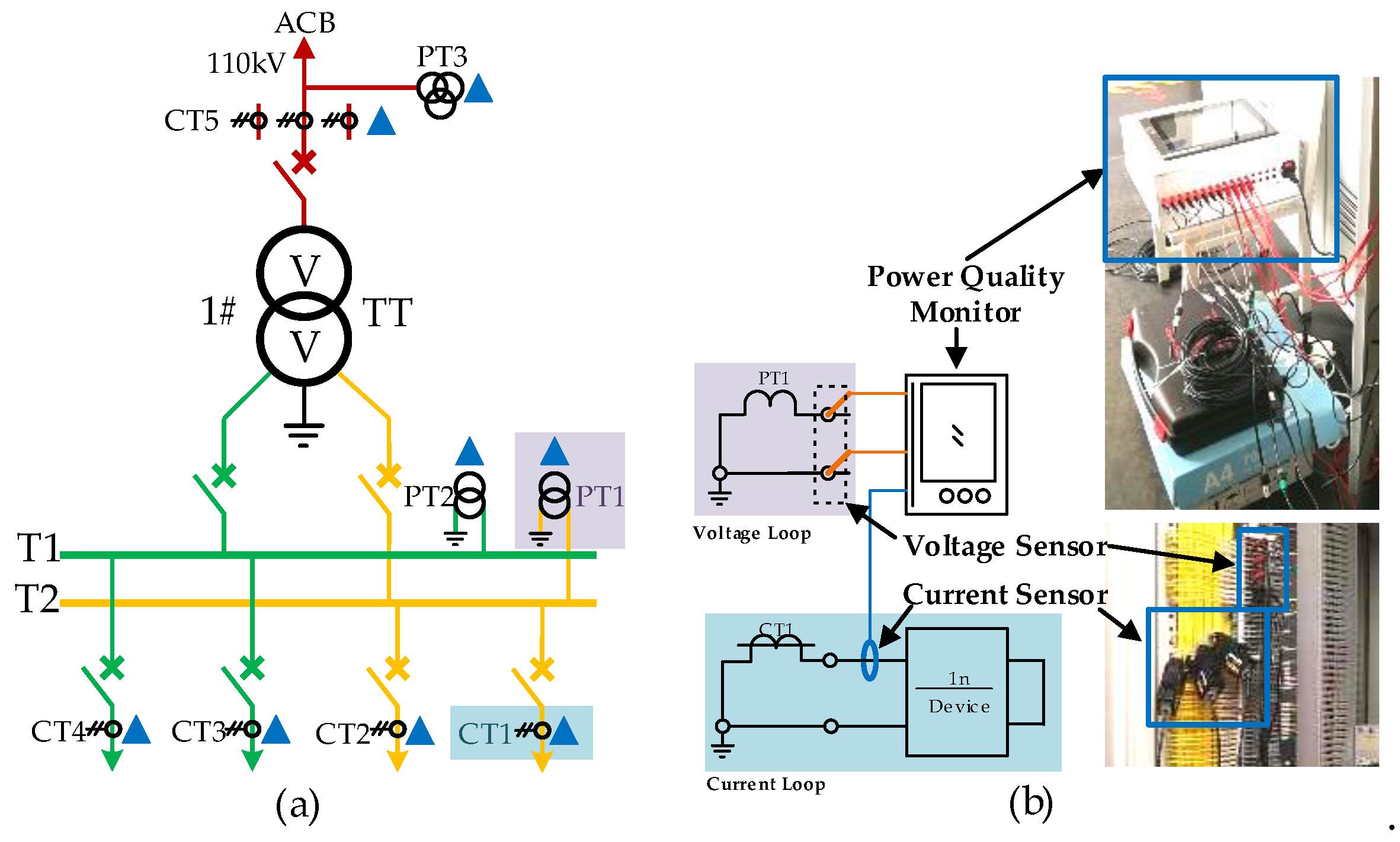
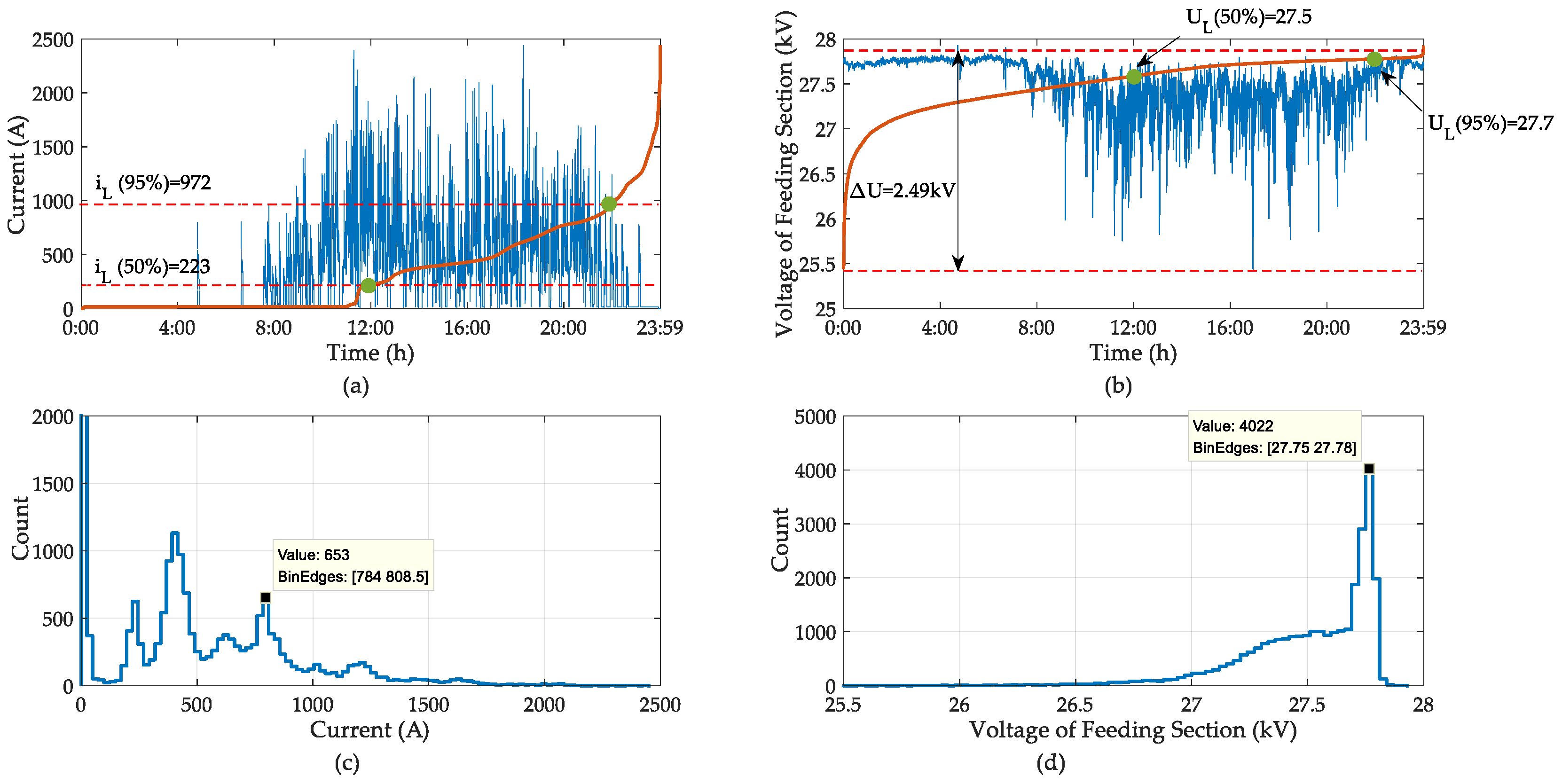
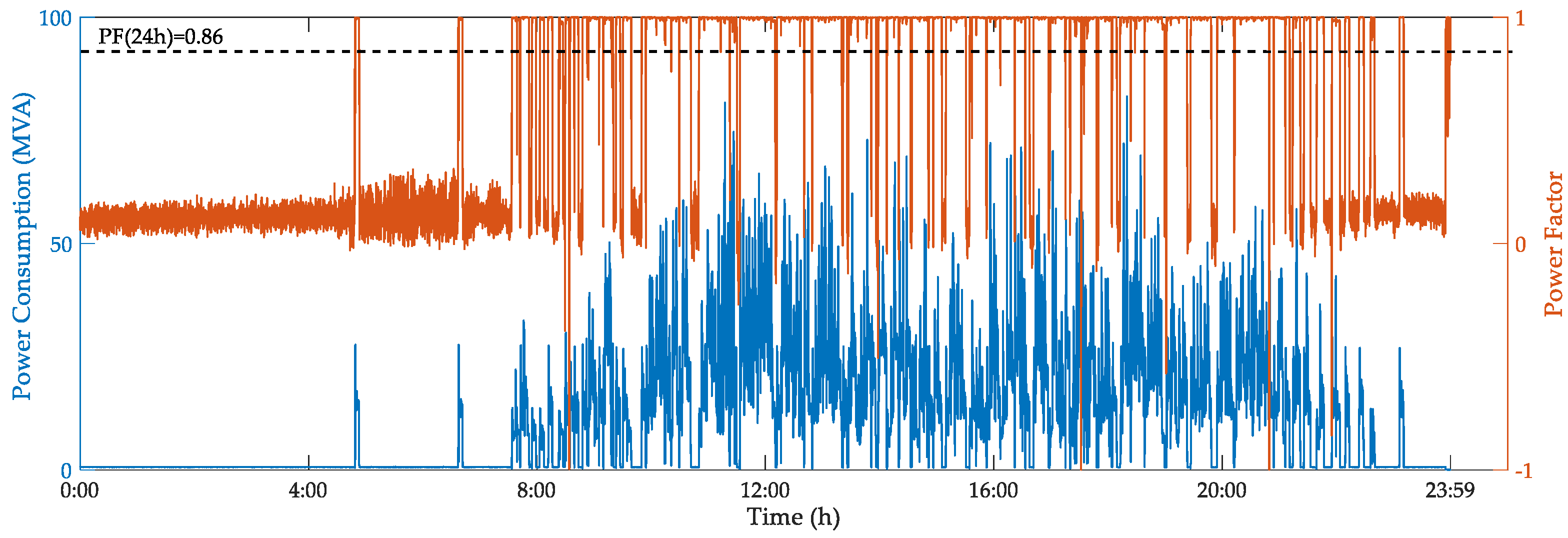
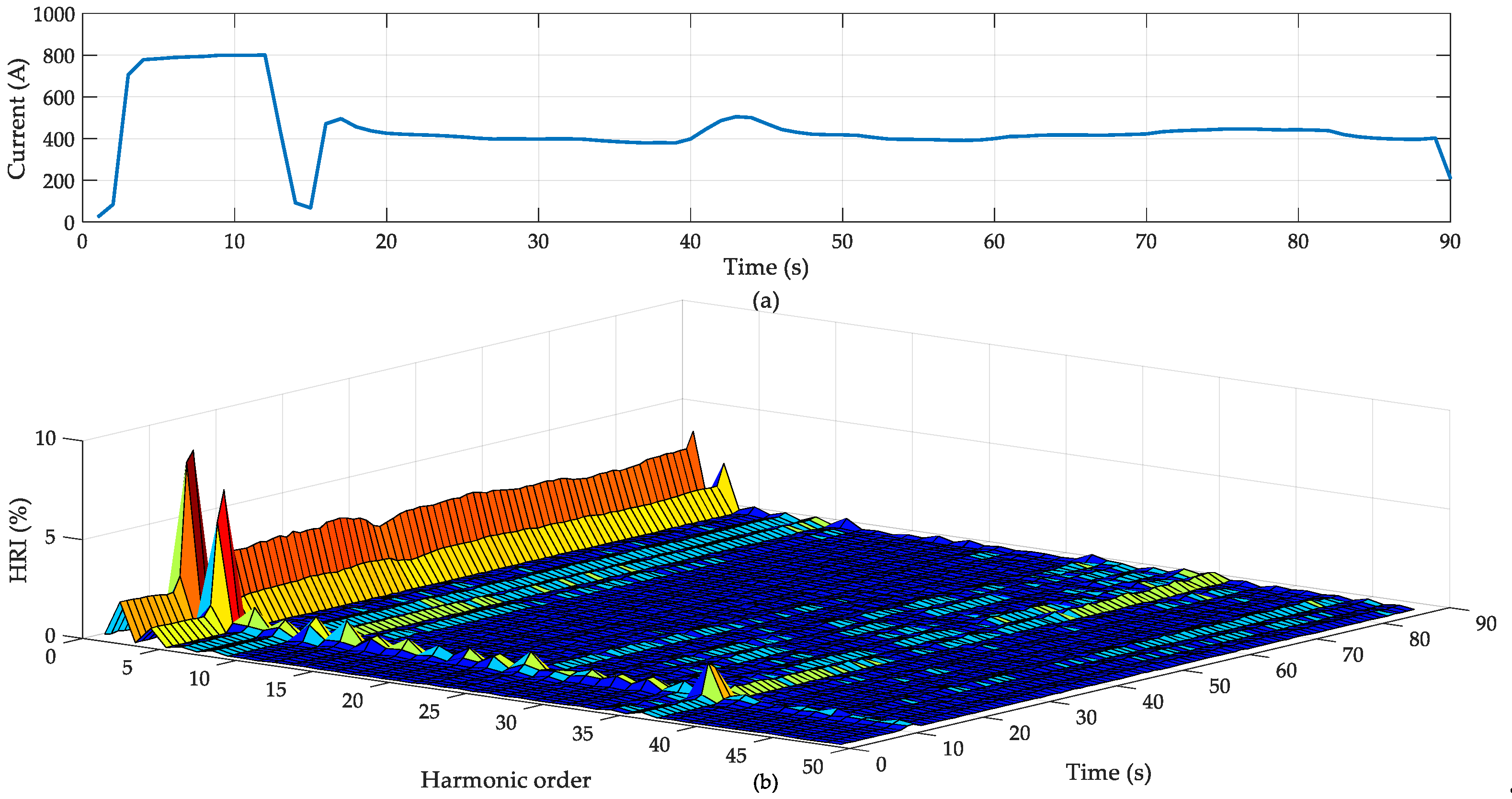
6.1. Field Testing and Designing Parameter of TCL-CTF
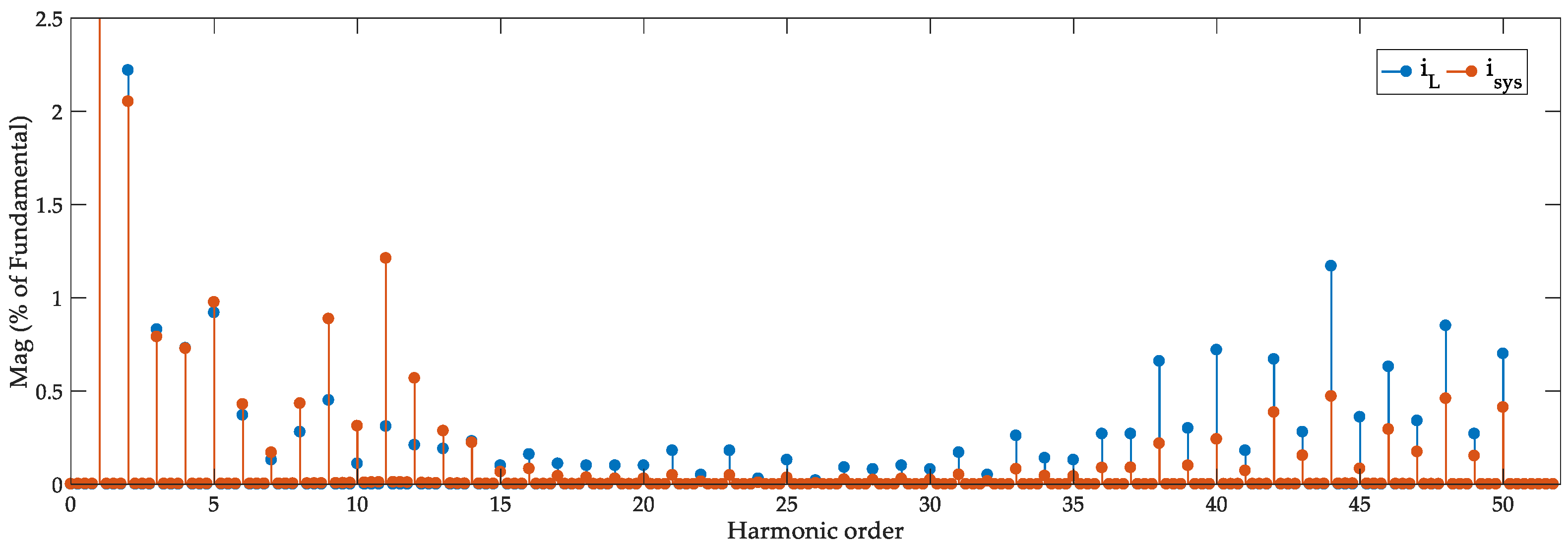
6.2. Vaildation of Filtering Performance
6.2.1. Simulation Results
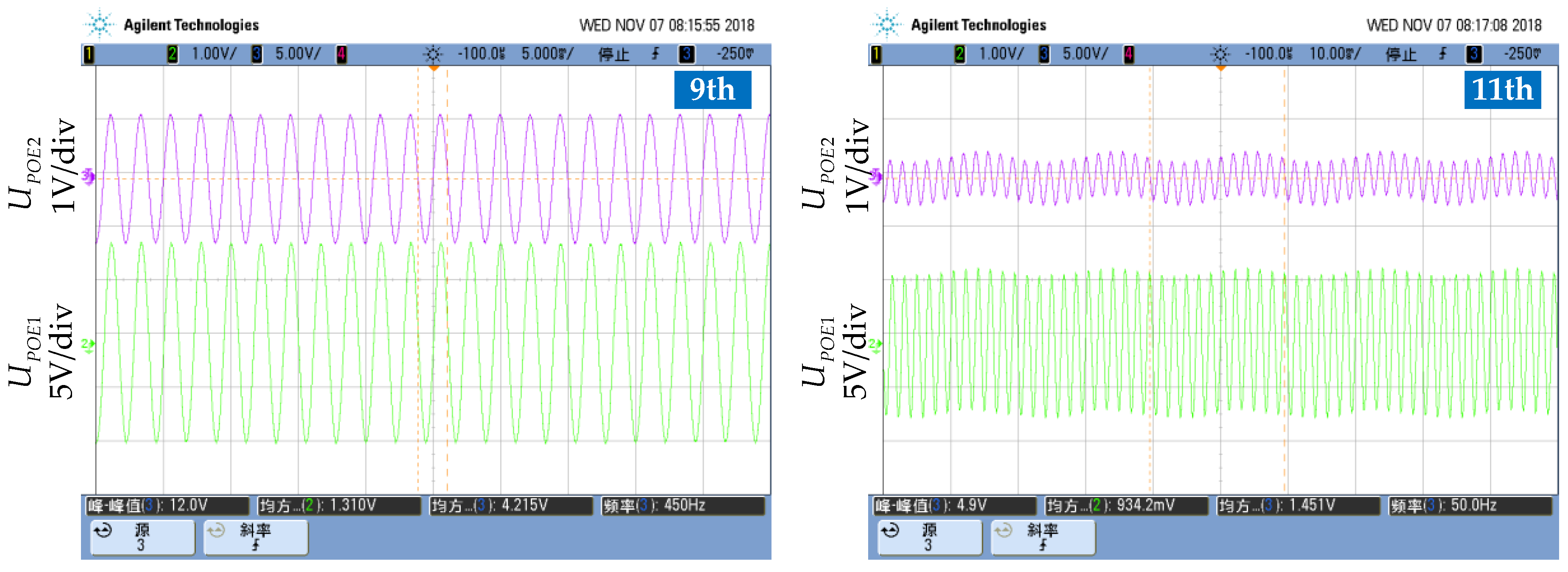
6.2.2. Experimental Results
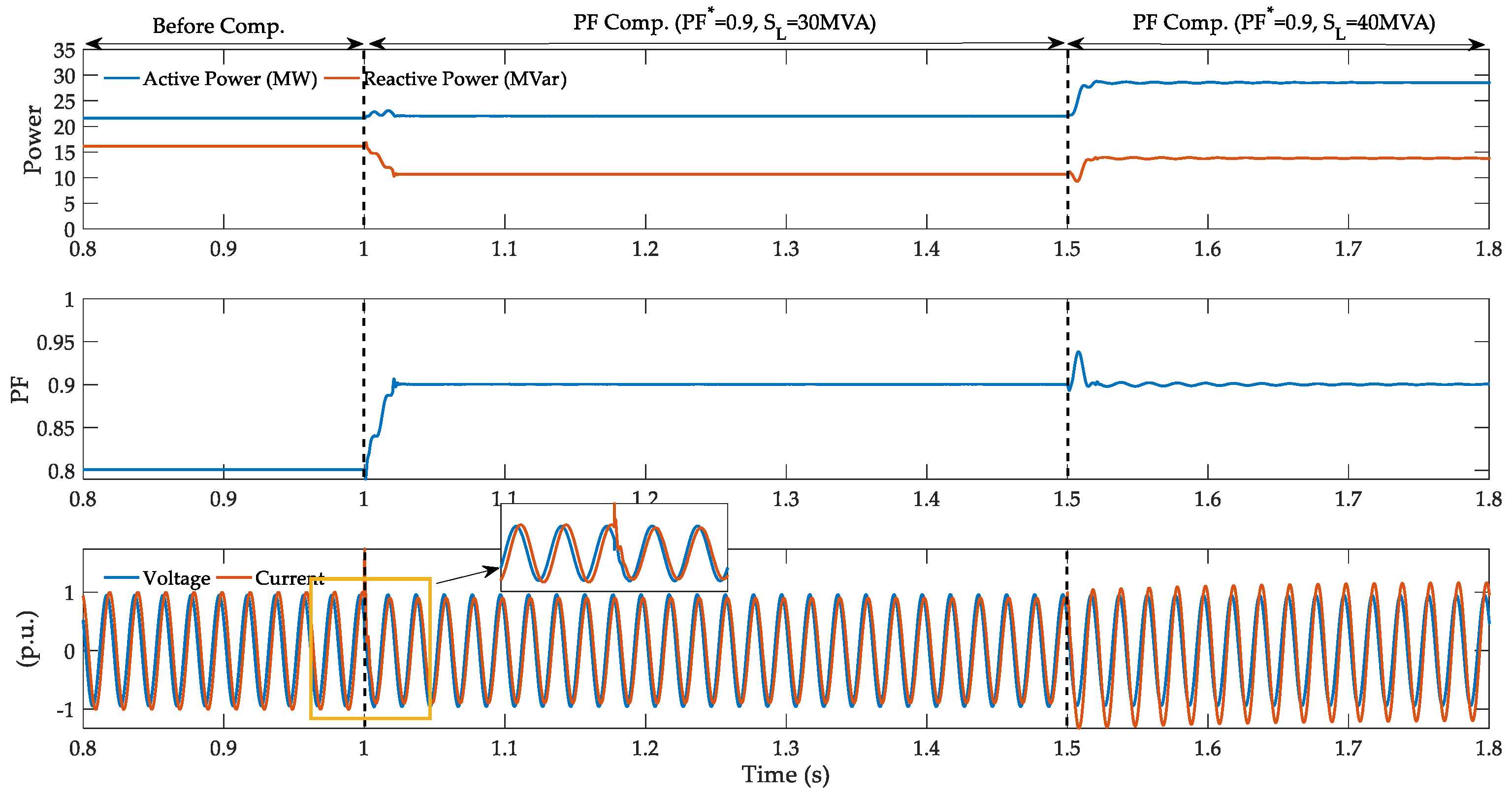
6.3. Vaildation of Compensation Performance
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| APF | Active power filter |
| DC | Direct current |
| EMU | Electric multiple unit |
| IGBT | Insulated gate bipolar transistor |
| LUT | Look-up table |
| MMC | Modular multilevel converter |
| MOSFET | Metal-oxide-semiconductor field-effect transistor |
| NSC | Negative-sequence current |
| PF | Power factor |
| PFC | Power flow converter |
| POE | Point of evaluation |
| PPF | Passive power filter |
| RPC | Railway static power conditioner |
| SPT | Single-phase transformer |
| SVC | Static var compensator |
| TCLC | Thyristor-controlled LC-coupling |
| TCL-CTF | Thyristor-controlled L and C-type filter |
| TPSS | Traction power supply system |
| TT | Traction transformer |
| VU | Voltage unbalance |
| VUF | Voltage unbalance factor |
References
- Chen, Z.; Haynes, K.E. Impact of high-speed rail on regional economic disparity in China. J. Trans. Geog. 2017, 65, 80–91. [Google Scholar] [CrossRef]
- Diao, M. Does growth follow the rail? The potential impact of high-speed rail on the economic geography of China. Trans. Res. Part A Policy Pract. 2018, 113, 279–290. [Google Scholar] [CrossRef]
- Development Plan of Modern Integrated Transport System in the 13th Five-Year Plan. Available online: http://www.ndrc.gov.cn/gzdt/201703/t20170302_840225 (accessed on 3 February 2017).
- Gazafrudi, S.M.M.; Langerudy, A.T.; Fuchs, E.F.; Al-Haddad, K. Power Quality Issues in Railway Electrification: A Comprehensive Perspective. IEEE Trans. Ind. Electron. 2015, 62, 3081–3090. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M.; Tian, Z.; Liu, L.; Hillmansen, S. VU limit pre-assessment for high-speed railway considering a grid connection scheme. IET Gener. Transm. Distrib. 2019, 13, 1121–1131. [Google Scholar] [CrossRef]
- Kotsampopoulos, P.; Georgilakis, P.; Lagos, D.T.; Kleftakis, V.; Hatziargyriou, N. FACTS Providing Grid Services: Applications and Testing. Energies 2019, 12, 2554. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Ahmadi, A.; Sharaf, A.M.; Siano, P.; Pou, J.; Hredzak, B.; Agelidis, V.G. Review of FACTS technologies and applications for power quality in smart grids with renewable energy systems. Renew. Sustain. Energy Rev. 2018, 82, 502–514. [Google Scholar] [CrossRef]
- Serrano-Jiménez, D.; Abrahamsson, L.; Castaño-Solís, S.; Sanz-Feito, J. Electrical railway power supply systems: Current situation and future trends. Int. J. Electr Power Energy Syst. 2017, 92, 181–192. [Google Scholar] [CrossRef]
- Morimoto, H.; Ando, M.; Mochinaga, Y.; Kato, T.; Yoshizawa, J.; Gomi, T.; Oozeki, S. Development of railway static power conditioner used at substation for Shinkansen. In Proceedings of the Power Conversion Conference, Osaka, Japan, 2–5 April 2002; pp. 1108–1111. [Google Scholar]
- Roudsari, M.H.; Jalilian, A.; Jamali, S. Flexible Fractional Compensating Mode for Railway Static Power Conditioner in a v/v Traction Power Supply System. IEEE Trans. Ind. Electron. 2018, 65, 7963–7974. [Google Scholar] [CrossRef]
- Cui, G.; Luo, L.; Li, Y.; Liang, C.; Hu, S.; Xie, B.; Wang, T. YN/VD connected balance transformer-based hybrid power quality compensator for harmonic suppression and reactive power compensation of electrical railway power systems. Int. J. Electr. Power Energy Syst. 2019, 113, 481–491. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, B.; Hu, S.; Li, Y.; Luo, L.; Rehtanz, C.; Krause, O. Reactive Power Compensation and Negative-Sequence Current Suppression System for Electrical Railways with YNvd-Connected Balance Transformer—Part I: Theoretical Analysis. IEEE Trans. Power Electron. 2018, 33, 272–282. [Google Scholar] [CrossRef]
- Li, Q. New Generation Traction Power Supply System and its Key Technologies for Electrified Railways. J. Mod. Transp. 2015, 23, 1–11. [Google Scholar] [CrossRef]
- Shu, Z.; Xie, S.; Lu, K.; Zhao, Y.; Nan, X.; Qiu, D.; Zhou, F.; Gao, S.; Li, Q. Digital Detection, Control, and Distribution System for Co-Phase Traction Power Supply Application. IEEE Trans. Ind. Electron. 2013, 60, 1831–1839. [Google Scholar] [CrossRef]
- He, X.; Ren, H.; Lin, J.; Han, P.; Wang, Y.; Peng, X.; Shu, Z. Power Flow Analysis of the Advanced Co-Phase Traction Power Supply System. Energies 2019, 12, 754. [Google Scholar] [CrossRef]
- Dai, N.Y.; Lao, K.; Lam, C. Hybrid Railway Power Conditioner with Partial Compensation for Converter Rating Reduction. IEEE Trans. Ind. Appl. 2015, 51, 4130–4138. [Google Scholar] [CrossRef]
- Chen, M.; Li, Q.; Roberts, C.; Hillmansen, S.; Tricoli, P.; Zhao, N.; Krastev, I. Modelling and performance analysis of advanced combined co-phase traction power supply system in electrified railway. IET Gener. Transm. Distrib. 2016, 10, 906–916. [Google Scholar] [CrossRef]
- Chen, M.; Roberts, C.; Weston, P.; Hillmansen, S.; Zhao, N.; Han, X. Harmonic modelling and prediction of high-speed electric train based on non-parametric confidence interval estimation method. Int. J. Electr. Power Energy Syst. 2017, 87, 176–186. [Google Scholar] [CrossRef]
- Zhang, R.; Lin, F.; Yang, Z.; Cao, H.; Liu, Y. A harmonic resonance suppression strategy for a high-speed railway traction power supply system with a SHE-PWM four-quadrant converter based on active-set secondary optimization. Energies 2017, 10, 1567. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Kalair, A.R.; Saleem, Z.; Khan, N. Review of harmonic analysis, modeling and mitigation techniques. Renew. Sustain. Energy Rev. 2017, 78, 1152–1187. [Google Scholar] [CrossRef]
- Lamlom, A.; Ibrahim, A.; Balci, M.E.; Karadeniz, A.; Aleem, S.H.A. Optimal design and analysis of anti-resonance C-type high-pass filters. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Iwamuro, N.; Laska, T. IGBT History, State-of-the-Art, and Future Prospects. IEEE Trans. Electron. Devices 2017, 64, 741–752. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.; Wong, M. Design of a Thyristor Controlled LC Compensator for Dynamic Reactive Power Compensation in Smart Grid. IEEE Trans. Smart Grid 2017, 8, 409–417. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.; Wong, M. Selective Compensation of Distortion, Unbalanced and Reactive Power of a Thyristor-Controlled LC -Coupling Hybrid Active Power Filter (TCLC-HAPF). IEEE Trans. Power Electron. 2017, 32, 9065–9077. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.; Wong, M. Hybrid Structure of Static Var Compensator and Hybrid Active Power Filter (SVC//HAPF) for Medium-Voltage Heavy Loads Compensation. IEEE Trans. Ind. Electron. 2018, 65, 4432–4442. [Google Scholar] [CrossRef]
- Leon, J.; Vazquez, S.; Franquelo, L. Multilevel Converters: Control and Modulation Techniques for Their Operation and Industrial Applications. Proc. IEEE 2017, 105, 2066–2081. [Google Scholar] [CrossRef]
- Chen, M.; Liu, R.; Xie, S.; Zhang, X.; Zhou, Y. Modeling and Simulation of Novel Railway Power Supply System Based on Power Conversion Technology. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 2547–2551. [Google Scholar]
- Kukačka, L.; Kraus, J.; Kolář, M.; Dupuis, P.; Zissis, G. Review of AC power theories under stationary and non-stationary, clean and distorted conditions. IET Gener. Transm. Distrib. 2016, 10, 221–231. [Google Scholar] [CrossRef]
- Emanuel, E.A. Summary of IEEE standard 1459: Definitions for the measurement of electric power quantities under sinusoidal, nonsinusoidal, balanced, or unbalanced conditions. IEEE Trans. Ind. Appl. 2004, 40, 869–876. [Google Scholar] [CrossRef]
- Yazdani, D.; Mojiri, M.; Bakhshai, A.; JoÓs, G. A Fast and Accurate Synchronization Technique for Extraction of Symmetrical Components. IEEE Trans. Power Electron. 2009, 24, 674–684. [Google Scholar] [CrossRef]
- Yao, W.; Teng, Z.; Tang, Q.; Gao, Y. Measurement of power system harmonic based on adaptive Kaiser self-convolution window. IET Gener. Transm. Distrib. 2016, 10, 390–398. [Google Scholar] [CrossRef]
- Cai, G.; Wang, L.; Yang, D.; Sun, Z.; Wang, B. Harmonic detection for power grids using adaptive variational mode decomposition. Energies 2019, 12, 232. [Google Scholar] [CrossRef]






| EN 50160 | EDF Emeraude Contract A.2 | Grid Code | GB/T 15543-2008 | |
|---|---|---|---|---|
| Country/Organizations | EU | France | Britain | China |
| VU limit in low-voltage, medium-voltage power system | 2% | 2% | 2% (<150 kV) | 2% |
| VU limit in high-voltage, extra-high-voltage power system | / | 2% | 1.5% | 2% |
| Parameters | Values | Parameters | Values | ||
|---|---|---|---|---|---|
| Current Transformer | Rated current of primary side (A) | 1500 | Current Sensor | Nominal current range (A) | 5 A |
| Rated current of second side (A) | 5 | Basic Accuracy | 1% | ||
| Useable frequency (Hz) | 40~5 K |
| Input Parameters | Values | Output Parameters | Values |
|---|---|---|---|
| 0.90 | (μF) | 10 | |
| 0.86 | (H) | 1.2 | |
| (MW) | 22 | (mF) | 3.5 |
| (kV) | 27.7 | (mH) | 2.9 |
| (MVar) | 2.45 | R (Ω) | 27.12 |
| ht | 20 |
| Parameters | Values |
|---|---|
| 0.122 Ω | |
| 6.27 mH | |
| 3.5 Ω | |
| 39.01 mH |
| Parameters | Values |
|---|---|
| 20 mH | |
| 4000 μF | |
| 3 kV | |
| 3 mH | |
| Number of H-bridges | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Chen, Y.; Wei, M. Modeling and Control of a Novel Hybrid Power Quality Compensation System for 25-kV Electrified Railway. Energies 2019, 12, 3303. https://doi.org/10.3390/en12173303
Chen M, Chen Y, Wei M. Modeling and Control of a Novel Hybrid Power Quality Compensation System for 25-kV Electrified Railway. Energies. 2019; 12(17):3303. https://doi.org/10.3390/en12173303
Chicago/Turabian StyleChen, Minwu, Yinyu Chen, and Mingchi Wei. 2019. "Modeling and Control of a Novel Hybrid Power Quality Compensation System for 25-kV Electrified Railway" Energies 12, no. 17: 3303. https://doi.org/10.3390/en12173303
APA StyleChen, M., Chen, Y., & Wei, M. (2019). Modeling and Control of a Novel Hybrid Power Quality Compensation System for 25-kV Electrified Railway. Energies, 12(17), 3303. https://doi.org/10.3390/en12173303





