Game-Based Hierarchical Cooperative Control for Electric Vehicle Lateral Stability via Active Four-Wheel Steering and Direct Yaw-Moment Control
Abstract
1. Introduction
2. Control Structure and Control-Oriented Model
2.1. Overall Control Strategy
2.2. Control-Oriented Model
3. Upper-Level Controller
3.1. Division of Control Modes
3.2. Stackelberg Game-Based Coordinated Control Strategy
3.2.1. Construction of Cost Function
3.2.2. Stackelberg Game-Based Controller
3.3. LQR-Based Control Strategy
4. Lower-Level Controller
| Algorithm 1: Iteration process of SQP Algorithm |
| 1: Initializing Fxn and Hessian matrix Hn. |
| 2: Defining ρ > 0, υ > 0, n = 0. |
| 3: Solving dn in the QP sub-problem in (43). If |dn| ≤ ρ, then break; If |dn | > ρ, continue; |
| 4: Calculating the step length parameter ζn that can make a decrease of merit function l(Fxn) [38,41].
|
| 5: Calculating the next step value of Fx(n+1):
|
| 6: Updating the Hessian matrix Hn+1 by using the BFGS [39] method:
|
| 7: Setting n = n + 1; then return to step 3 and continue. |
5. Simulation Results
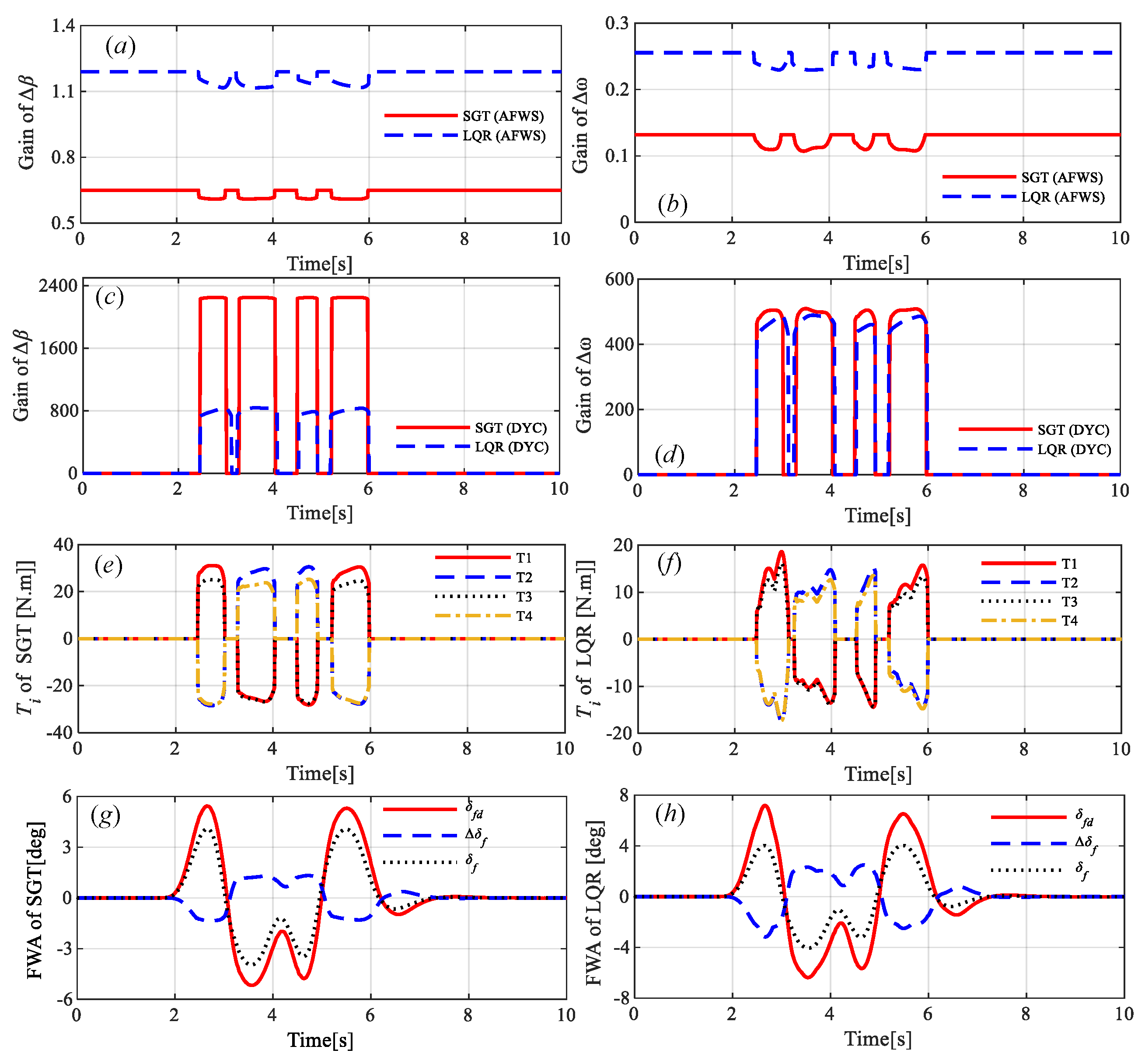
5.1. Open-Loop Sinusoidal Input Test
5.2. Closed-Loop Double-Lane-Change Test
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, C.; Wang, R.; Yan, F. Integral Sliding Mode-Based Composite Nonlinear Feedback Control for Path Following of Four-Wheel Independently Actuated Autonomous Vehicles. IEEE Trans. Transp. Electr. 2016, 2, 221–230. [Google Scholar] [CrossRef]
- Cao, W.; Liu, H.; Lin, C.; Chang, Y.; Liu, Z.; Szumanowski, A. Co-Design Based Lateral Motion Control of All-Wheel-Independent-Drive Electric Vehicles with Network Congestion. Energies 2017, 10, 1641. [Google Scholar] [CrossRef]
- Hori, Y. Future vehicle driven by electricity and Control-research on four-wheel-motored “UOT electric march II”. IEEE Trans. Ind. Electron. 2004, 51, 954–962. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, S.; Liu, B.; Liu, C.; Sciubba, E. A Human-Machine-Cooperative-Driving Controller Based on AFS and DYC for Vehicle Dynamic Stability. Energies 2017, 10, 1737. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Zhang, L.; Wang, Y. Automotive ABS/DYC Coordinated Control under Complex Driving Conditions. IEEE Access 2018, 6, 32769–32779. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, Y.; Zhao, J. Integrated chassis control of active front steering and yaw stability control based on improved inverse nyquist array method. Sci. World J. 2014, 2014, 919847. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Yu, Z.; Yin, G.; Wang, J. Improving Vehicle Handling Stability Based on Combined AFS and DYC System via Robust Takagi-Sugeno Fuzzy Control. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2696–2707. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Feng, N. Simulation Research on an Electric Vehicle Chassis System Based on a Collaborative Control System. Energies 2013, 6, 312–328. [Google Scholar] [CrossRef]
- Mokhiamar, O.; Abe, M. Simultaneous optimal distribution of lateral and longitudinal tire forces for the model following control. J. Dyn. Syst. Meas. Control 2004, 126, 753–763. [Google Scholar] [CrossRef]
- Tamaddoni, S.H.; Taheri, S.; Ahmadian, M. Optimal preview game theory approach to vehicle stability controller design. Veh. Syst. Dyn. 2011, 49, 1967–1979. [Google Scholar] [CrossRef]
- Cruz, J., Jr. Survey of nash and stackelberg equilibrium strategies in dynamic games. In Annals of Economic and Social Measurement; Berg, S.V., Ed.; NBER: Cambridge, MA, USA, 1975; Volume 4, pp. 339–344. [Google Scholar]
- Başar, T.; Olsder, G.J. Dynamic Noncooperative Game Theory, 2nd ed.; Academic Press: New York, NY, USA, 1995; pp. 365–421. [Google Scholar]
- Na, X.; Cole, D.J. Modelling Driver-AFS Interactive Steering Control Using the Principle of Open-Loop Stackelberg Equilibrium; CUED/TR. 101; Department of Engineering, University of Cambridge: Cambridge, UK, 2013. [Google Scholar]
- Na, X.; Cole, D.J. Game-Theoretic Modeling of the Steering Interaction between a Human Driver and a Vehicle Collision Avoidance Controller. IEEE Trans. Hum. Mach. Syst. 2015, 45, 25–38. [Google Scholar] [CrossRef]
- Myerson, R.B. Game Theory: Analysis of Conflict; Harvard University Press: Cambridge, MA, USA, 1991; pp. 1–33. [Google Scholar]
- Tamaddoni, S.H.; Taheri, S.; Ahmadian, M. Optimal VSC design based on Nash strategy for differential 2-player games. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009. [Google Scholar]
- Tamaddoni, S.H.; Taheri, S.; Ahmadian, M. Optimal Direct Yaw Controller Design for Vehicle Systems with Human Driver. SAE Int. J. Commer. Veh. 2011, 4, 13–21. [Google Scholar] [CrossRef]
- Na, X.; Cole, D.J. Linear quadratic game and non-cooperative predictive methods for potential application to modelling driver-AFS interactive steering control. Veh. Syst. Dyn. 2012, 51, 165–198. [Google Scholar] [CrossRef]
- Ji, X.; Liu, Y.; Na, X.; Liu, Y. Research on interactive steering control strategy between driver and AFS in different game equilibrium strategies and information patterns. Veh. Syst. Dyn. 2018, 56, 1344–1374. [Google Scholar] [CrossRef]
- Jie, Z.; Zhang, Y. Fractional-order PIλDμ control and optimization for vehicle active steering. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25 June 2008. [Google Scholar]
- Na, X.; Cole, D.J. Application of Open-Loop Stackelberg Equilibrium to Modeling a Driver’s Interaction with Vehicle Active Steering Control in Obstacle Avoidance. IEEE Trans. Hum. Mach. Syst. 2017, 47, 673–685. [Google Scholar] [CrossRef]
- Nagai, M.; Hirano, Y.; Yamanaka, S. Integrated Robust Control of Active Rear Wheel Steering and Direct Yaw Moment Control. Veh. Syst. Dyn. 2007, 29, 416–421. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science Business: New York, NY, USA, 2006; pp. 221–255. [Google Scholar]
- Sano, S. Four wheel steering system with rear wheel steer angle controlled as a function of steering wheel angle. SAE Trans. 1986, 95, 880–893. [Google Scholar]
- Yang, X.; Wang, Z.; Peng, W. Coordinated control of AFS and DYC for vehicle handling and stability based on optimal guaranteed cost theory. Veh. Syst. Dyn. 2008, 47, 57–79. [Google Scholar] [CrossRef]
- Nagai, M.; Shino, M.; Gao, F. Study on integrated control of active front steer angle and direct yaw moment. JSAE Rev. 2002, 23, 309–315. [Google Scholar] [CrossRef]
- Beal, C.E.; Bobier, C.G.; Gerdes, J.C. Controlling vehicle instability through stable handling envelopes. In Proceedings of the ASME 2011 Dynamic Systems and Control Conference and Bath/ASME Symposium on Fluid Power and Motion Control, Arlington, VA, USA, 1 January 2011. [Google Scholar]
- Cheng, S.; Li, L.; Mei, M.M.; Nie, Y.L.; Zhao, L. Multiple-Objective Adaptive Cruise Control System Integrated with DYC. IEEE Trans. Veh. Technol. 2019, 68, 4550–4559. [Google Scholar] [CrossRef]
- Manning, W.; Selby, M.; Crolla, D.; Brown, M. IVMC: Intelligent Vehicle Motion Control. In Proceedings of the SAE International, SAE Technical Paper 2002-01-0821. Detroit, MI, USA, 4–7 March 2002. [Google Scholar]
- Wang, J.; Longoria, R.G. Coordinated and Reconfigurable Vehicle Dynamics Control. IEEE Trans. Control Syst. Technol. 2009, 17, 723–732. [Google Scholar] [CrossRef]
- Li, M.; Cruz, J.; Simaan, M.A. An approach to discrete-time incentive feedback Stackelberg games. IEEE Trans. Syst. Man. Cybern. A Syst. Hum. 2002, 32, 472–481. [Google Scholar]
- Lewis, F.L.; Vrabie, D.L.; Syrmos, V.L. Optimal Control, 3rd ed.; John Wiley& Sons: Hoboken, NJ, USA, 2015; pp. 19–102. [Google Scholar]
- Hungerländer, P.; Neck, R. An Algorithmic Equilibrium Solution for N-Person Dynamic Stackelberg Difference Games with Open-Loop Information Pattern. In Computational Methods in Economic Dynamics; Springer: Berlin, Germany, 2011; pp. 197–214. [Google Scholar]
- Wang, J.; Longoria, R.G. Coordinated vehicle dynamics control with control distribution. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Lu, S.; Cen, S.; Zhang, Y. Driver Model-Based Fault-Tolerant Control of Independent Driving Electric Vehicle Suffering Steering Failure. Autom. Innov. 2018, 1, 85–94. [Google Scholar] [CrossRef]
- Hsiao, T.; Lan, J.; Yang, H. Integrated estimation of vehicle states, tire forces, and tire-road friction coefficients. In Proceedings of the 14th International Conference on Control, Automation and Systems (ICCAS), Seoul, Korea, 22–25 October 2014. [Google Scholar]
- Ding, N.; Taheri, S. An adaptive integrated algorithm for active front steering and direct yaw moment control based on direct Lyapunov method. Veh. Syst. Dyn. 2010, 48, 1193–1213. [Google Scholar] [CrossRef]
- Yi, L.; Jinwu, X. Optimization of range and endurance of a propeller UAV based on SQP algorithm. In Proceedings of the IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 27–29 October 2017. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Science Business: New York, NY, USA, 2006; pp. 529–561. [Google Scholar]
- Padilla, G.P.; Weiland, S.; Donkers, M.C.F. A Global Optimal Solution to the Eco-Driving Problem. IEEE Control Syst. Lett. 2018, 2, 599–604. [Google Scholar] [CrossRef]
- Morshed, M.J.; Asgharpour, A. Hybrid imperialist competitive-sequential quadratic programming (HIC-SQP) algorithm for solving economic load dispatch with incorporating stochastic wind power: A comparative study on heuristic optimization techniques. Energy Convers. Manag. 2014, 84, 30–40. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J. Fault-Tolerant Control with Active Fault Diagnosis for Four-Wheel Independently Driven Electric Ground Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 4276–4287. [Google Scholar] [CrossRef]
- Jin, L.; Gao, L.; Jiang, Y.; Chen, M.; Zheng, Y.; Li, K. Research on the control and coordination of four-wheel independent driving/steering electric vehicle. Adv. Mech. Eng. 2017, 9, 1–13. [Google Scholar] [CrossRef]









| Variable | Parameter Name | Units | Value |
|---|---|---|---|
| m | Vehicle mass | kg | 1140 |
| kf | Cornering stiffness of front tires | N/rad | 82,000 |
| kr | Cornering stiffness of front tires | N/rad | 130,000 |
| a | Distance from CG to front axle | m | 1.165 |
| b | Distance from CG to rear axle | m | 1.165 |
| r | Radius of wheel | m | 0.31 |
| Rst | Steering gear ratio | / | 14.5 |
| Iz | Yaw moment of inertia | kg/m2 | 996 |
| t | Track distance | m | 1.481 |
| h | Height of CG | m | 0.375 |
| Tmax | Peak torque of motor | N.m | 500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Lu, S.; Zhang, B. Game-Based Hierarchical Cooperative Control for Electric Vehicle Lateral Stability via Active Four-Wheel Steering and Direct Yaw-Moment Control. Energies 2019, 12, 3339. https://doi.org/10.3390/en12173339
Zhao L, Lu S, Zhang B. Game-Based Hierarchical Cooperative Control for Electric Vehicle Lateral Stability via Active Four-Wheel Steering and Direct Yaw-Moment Control. Energies. 2019; 12(17):3339. https://doi.org/10.3390/en12173339
Chicago/Turabian StyleZhao, Lin, Shaobo Lu, and Bohan Zhang. 2019. "Game-Based Hierarchical Cooperative Control for Electric Vehicle Lateral Stability via Active Four-Wheel Steering and Direct Yaw-Moment Control" Energies 12, no. 17: 3339. https://doi.org/10.3390/en12173339
APA StyleZhao, L., Lu, S., & Zhang, B. (2019). Game-Based Hierarchical Cooperative Control for Electric Vehicle Lateral Stability via Active Four-Wheel Steering and Direct Yaw-Moment Control. Energies, 12(17), 3339. https://doi.org/10.3390/en12173339





