A Comprehensive Evaluation Model for Curtain Grouting Efficiency Assessment Based on Prospect Theory and Interval-Valued Intuitionistic Fuzzy Sets Extended by Improved D Numbers
Abstract
:1. Introduction
- The existing evaluation methods for grouting efficiency do not consider the hesitation and bounded rationality of experts, and it is difficult to handle the problem of incomplete decision-making information when using them. Due to the redundancy of information, incompleteness of expert knowledge, and effect of the decision-making environment, the experts will hesitate [28], have bounded rationality [29] in the decision-making process, and may even forfeit the evaluation. Existing grouting-efficiency evaluation methods have difficulty in considering such hesitation and bounded rationality and have difficulty in handling the incomplete information generated by the experts after they have forfeited the evaluation, which causes a lack of rationality and objectivity in the evaluation results. Therefore, it is very important to use scientific methods to evaluate the grouting efficiency and to obtain reasonable and objective evaluation results.
- The diversity of the evaluation indicators can be further improved. The main aim of curtain grouting is to prevent leakage and to improve the strength of the ground under the dam foundation [30]. The construction efficiency of curtain grouting is closely related to the groutability (whether the grouting material can continue to be injected) [27]. The existing research mostly describes the groutability of a rock mass using permeability. However, they cannot be completely equivalent. The main reason for this is that there are usually many microfractures in the rock of the dam foundation, so there will be a situation where “the water permeability is very large and the cement intake is very small”. In addition, although a few studies have considered indicators such as the FFR and RQD, the diversity of the evaluation indicators can be further improved. Therefore, it is necessary to establish an evaluation indicator system that can comprehensively reflect the groutability of the rock considered.
2. Related Work
2.1. Comprehensive Evaluation Methods under Interval-Valued Intuitionistic Fuzzy Environment
2.2. Comprehensive Evaluation Methods under D Numbers
2.3. Comprehensive Evaluation Methods under Prospect Theory
2.4. Prospect Theory and Interval-Valued Intuitionistic Fuzzy Sets Extended by Improved D-Number Methods for Comprehensive Evaluation
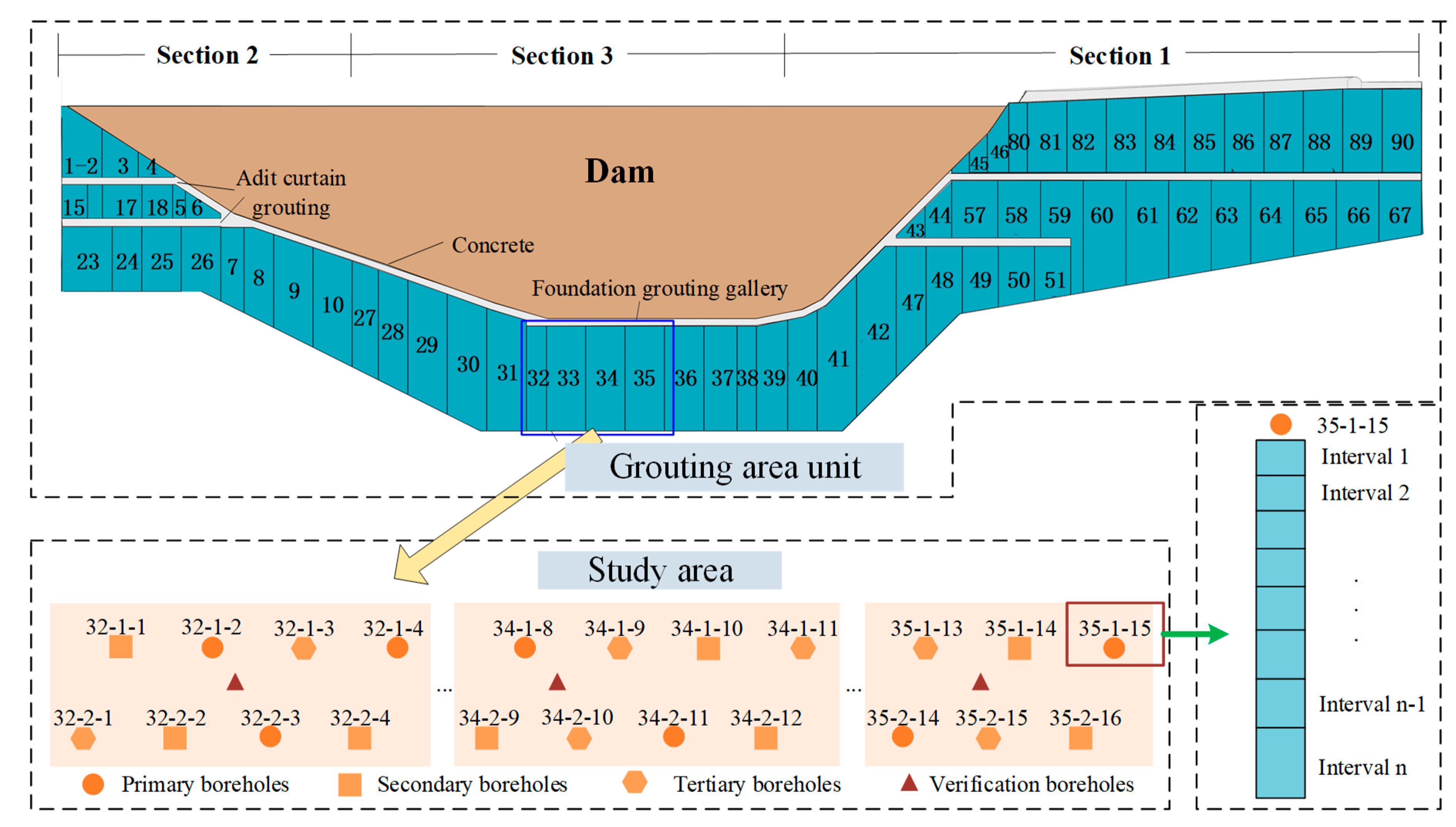
3. Grouting-Efficiency Evaluation Indicators System
3.1. Indicator System for Curtain-Grouting Evaluation
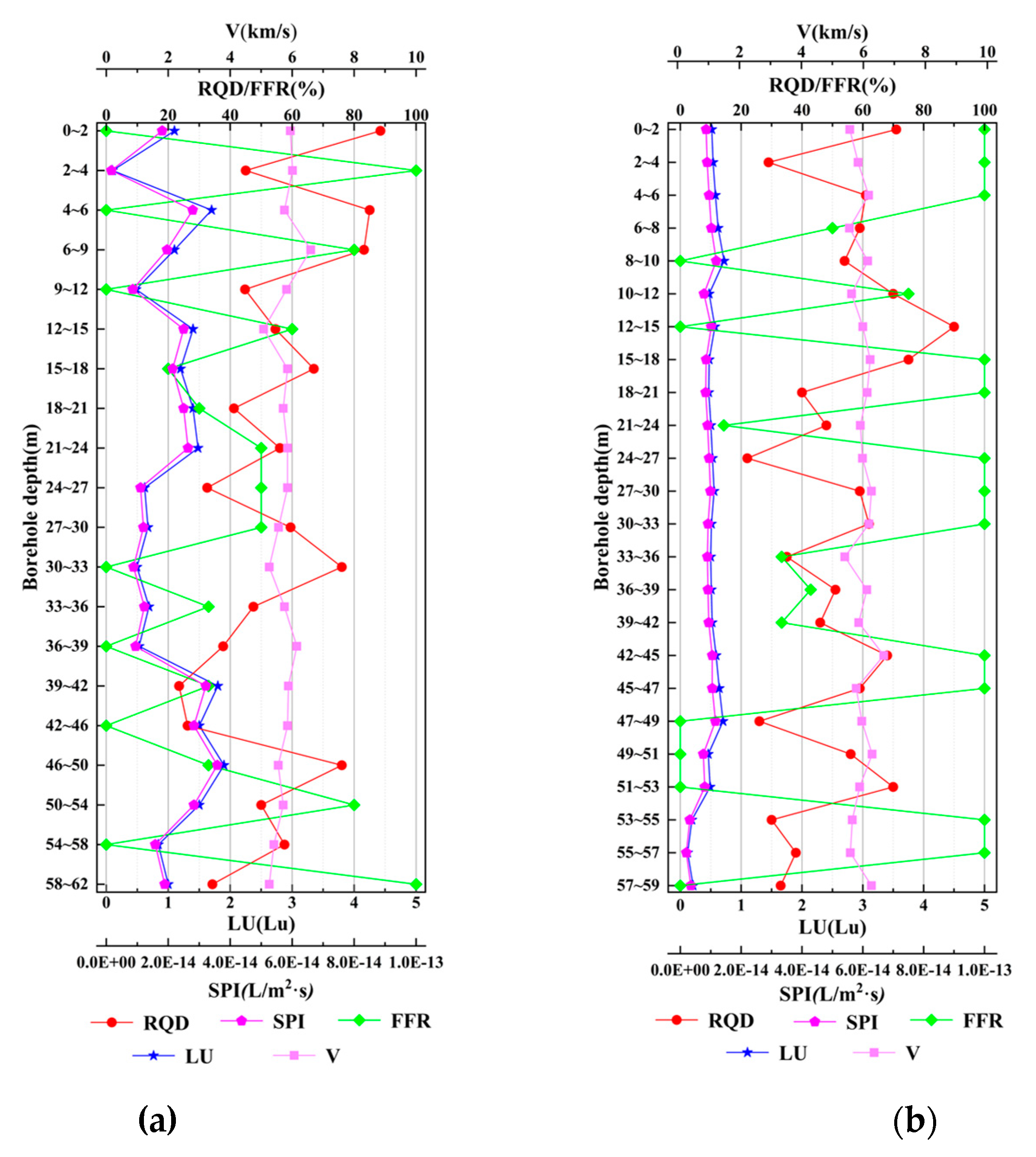
3.2. Calculation of the Evaluation Indicators
3.2.1. Secondary Permeability Index (SPI)
3.2.2. Permeability (LU)
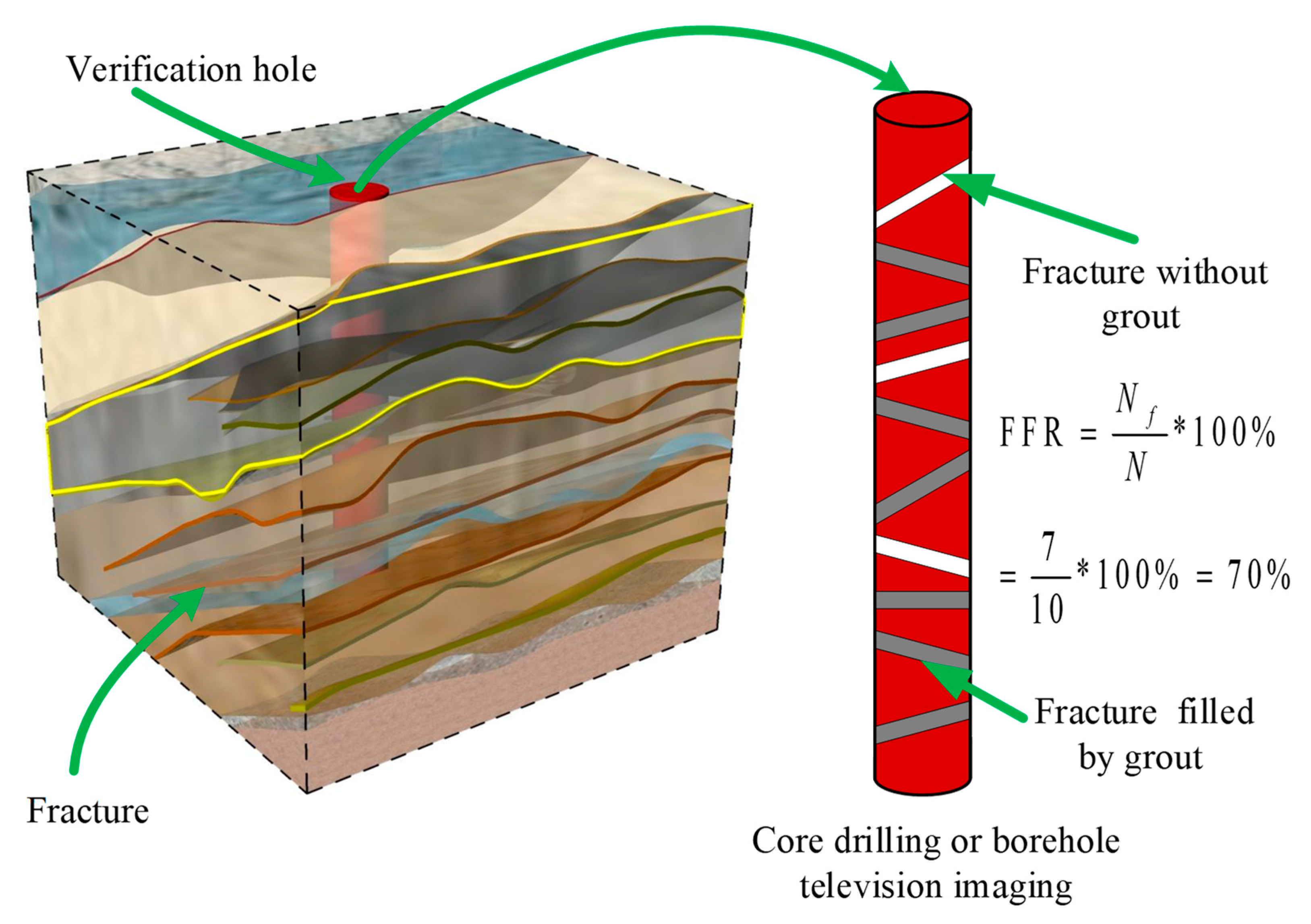
3.2.3. Fracture-Filled Rate (FFR)
3.2.4. Rock-Quality Designation (RQD)
3.2.5. Acoustic Velocity (V)
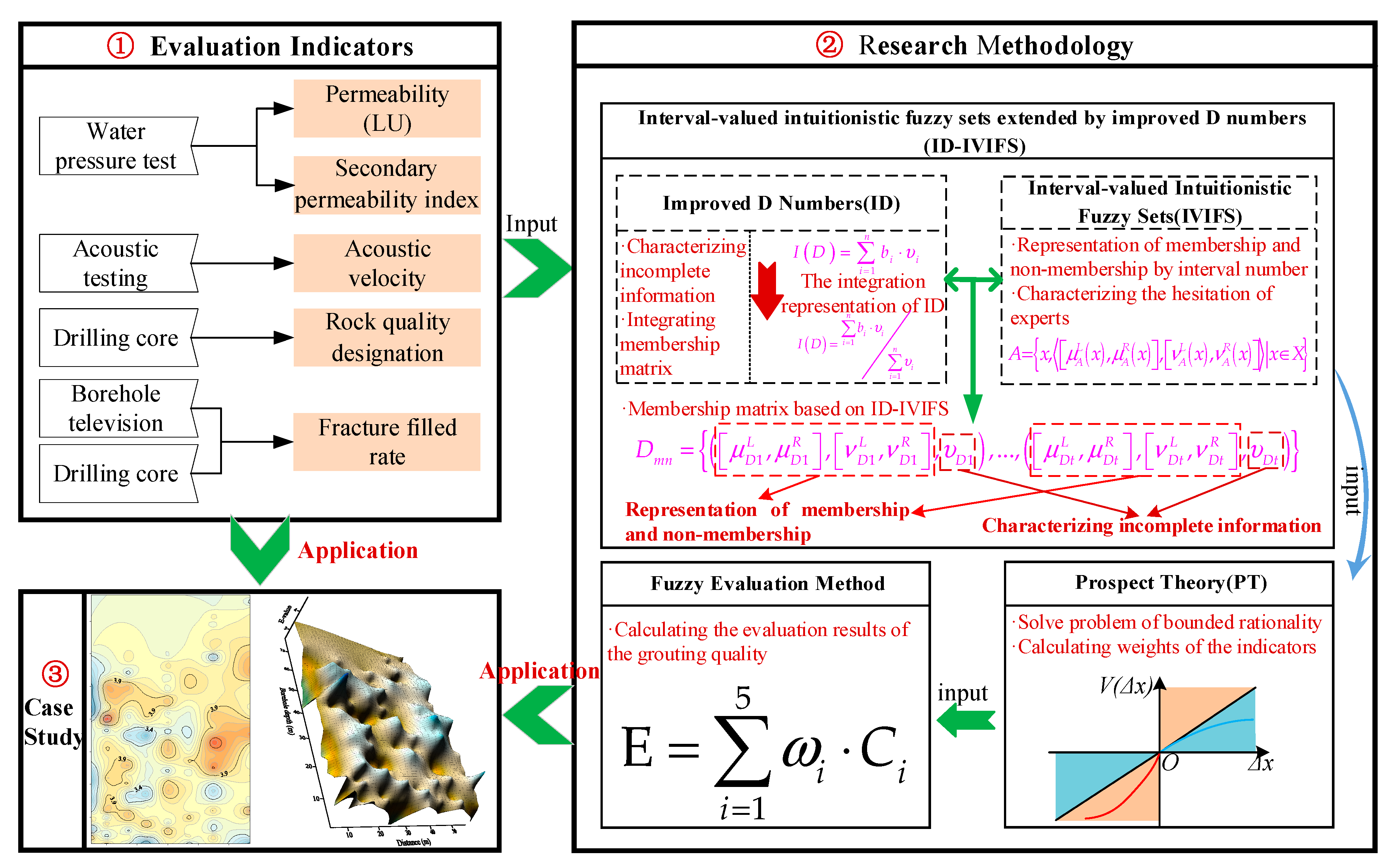
4. Methodology
4.1. Mathematical Model of the Evaluation Method
4.2. Preliminaries
4.2.1. D Numbers
4.2.2. Interval-Valued Intuitionistic Fuzzy Sets (IVIFS)
- 1
- If S(A) > S(B), then A > B;
- 2
- If S(A) = S(B) and H(A) > H(B), then A > B; and
- 3
- If S(A) = S(B) and H(A) = H(B), then A = B.
4.2.3. Prospect Theory (PT)
4.3. ID-IVIFS Method
4.3.1. Improved D Numbers
4.3.2. ID-IVIFS Method
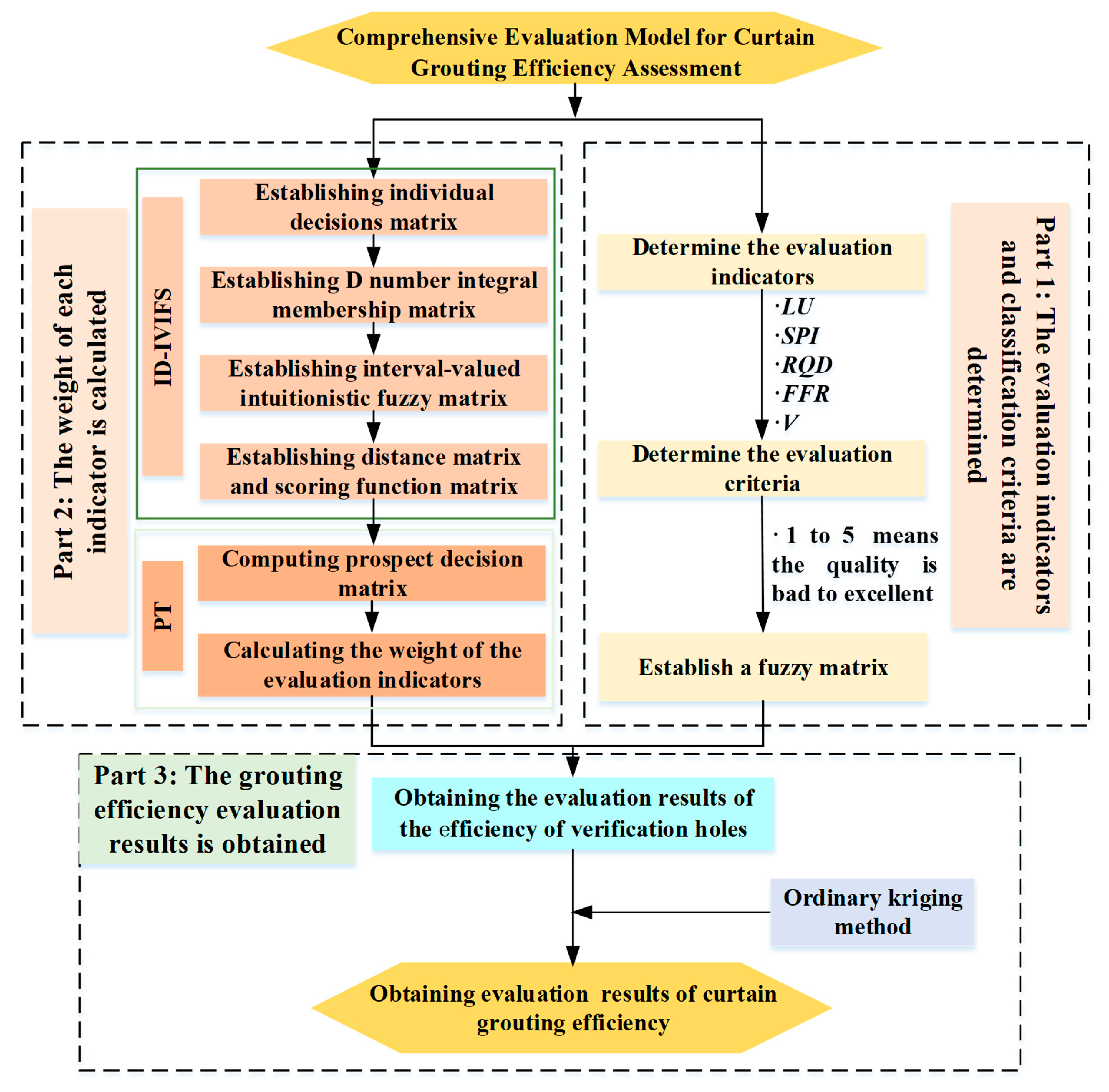
4.4. Procedures for Comprehensive Evaluation
5. Case Study
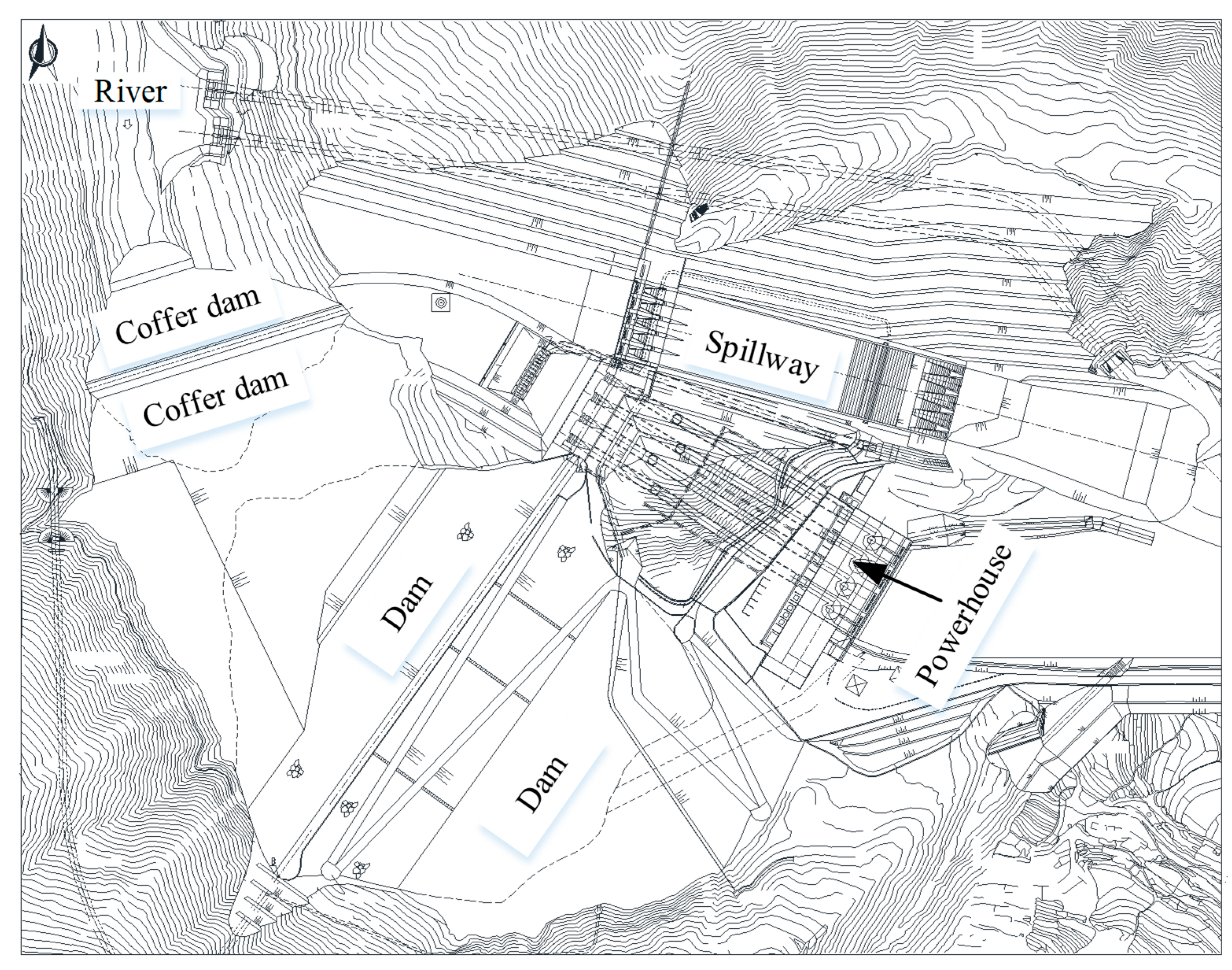
5.1. Project Overview
5.2. Determining Evaluation Indicators and Criteria
5.3. Data Collection
5.4. Calculating the Weights of the Indicators
- 1
- Firstly, considering that all the grouting-efficiency evaluation indicators are quantitative attributes, 10 experts from the industry were invited to consult and provide interval-valued (non-) membership of each evaluation indicator relative to each unit and an individual evaluation decision matrix is established. During the consultation process, the experts agreed that the average result of the evaluations of 10 experts was to be used as a reference point. The evaluation membership matrix was converted into a D number integral form evaluation matrix based on the improved D numbers, as shown in Table 5, where indicates that all experts agreed that the FFR relative to the unit 2 evaluation interval-valued (non-) membership was .
- 2
- Secondly, the collective interval-valued intuitionistic fuzzy evaluation membership matrix was established. Using the overall integration representation solution method (Equation (25)) proposed in this study, the D number integral form evaluation matrix in step (1) was transformed into the collective interval-valued intuitionistic fuzzy evaluation membership matrix, as tabulated in Table 6. The reference points O of LU, SPI, FFR, RQD, and V were ([0.817, 0.903], [0.036, 0.075]), ([0.764, 0.841], [0.092, 0.145]), ([0.514, 0.778], [0.054, 0.167]), ([0.446, 0.776], [0.097, 0.167]), and ([0.663, 0.767], [0.071, 0.141]).
- 3
- Thirdly, based on the score and accuracy of the interval-valued intuitionistic fuzzy sets (Equations (17) and (18)), the scoring function matrix was established. The results are shown in Table 7.
- 4
- Finally, the weights of each indicator were solved based on the principle of prospect value maximization. Primarily, based on the interval-valued intuitionistic fuzzy sets judgment criterion, the size of the interval-valued intuitionistic fuzzy sets, reference point O of each evaluation indicator, and the solution method of the value function were determined. Then, the distance between each indicator and reference point O was found using Equation (16) in order to establish the distance matrix. Finally, the value function was solved, the prospect decision matrix was established, and the weights of each indicator were solved. The prospect decision matrix is shown in Table 8. The weights of LU, SPI, FFR, RQD, and V based on Equation (26) were .
5.5. Evaluation Results
6. Discussion
6.1. Rationality of Evaluation Method
- 1
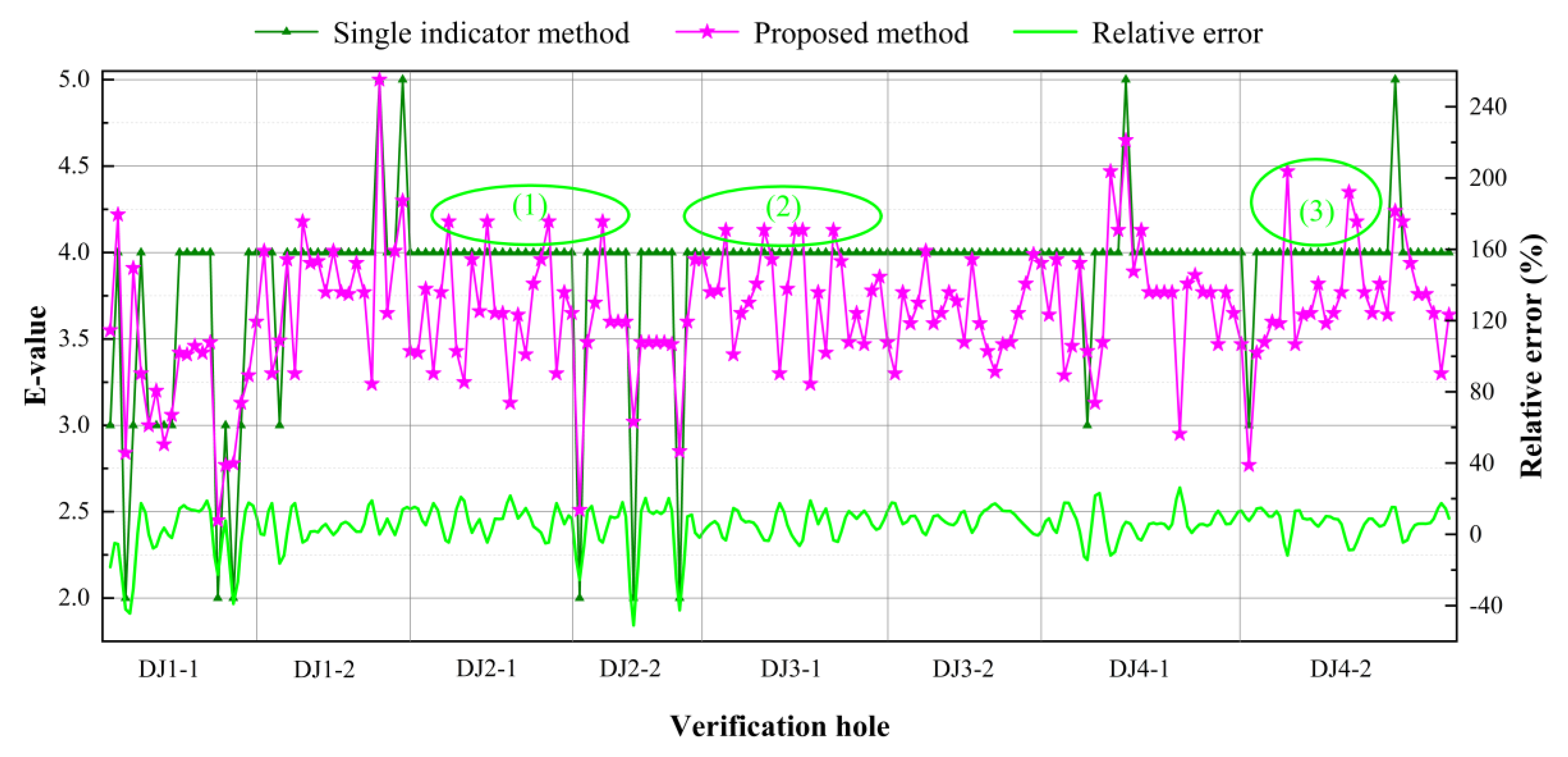
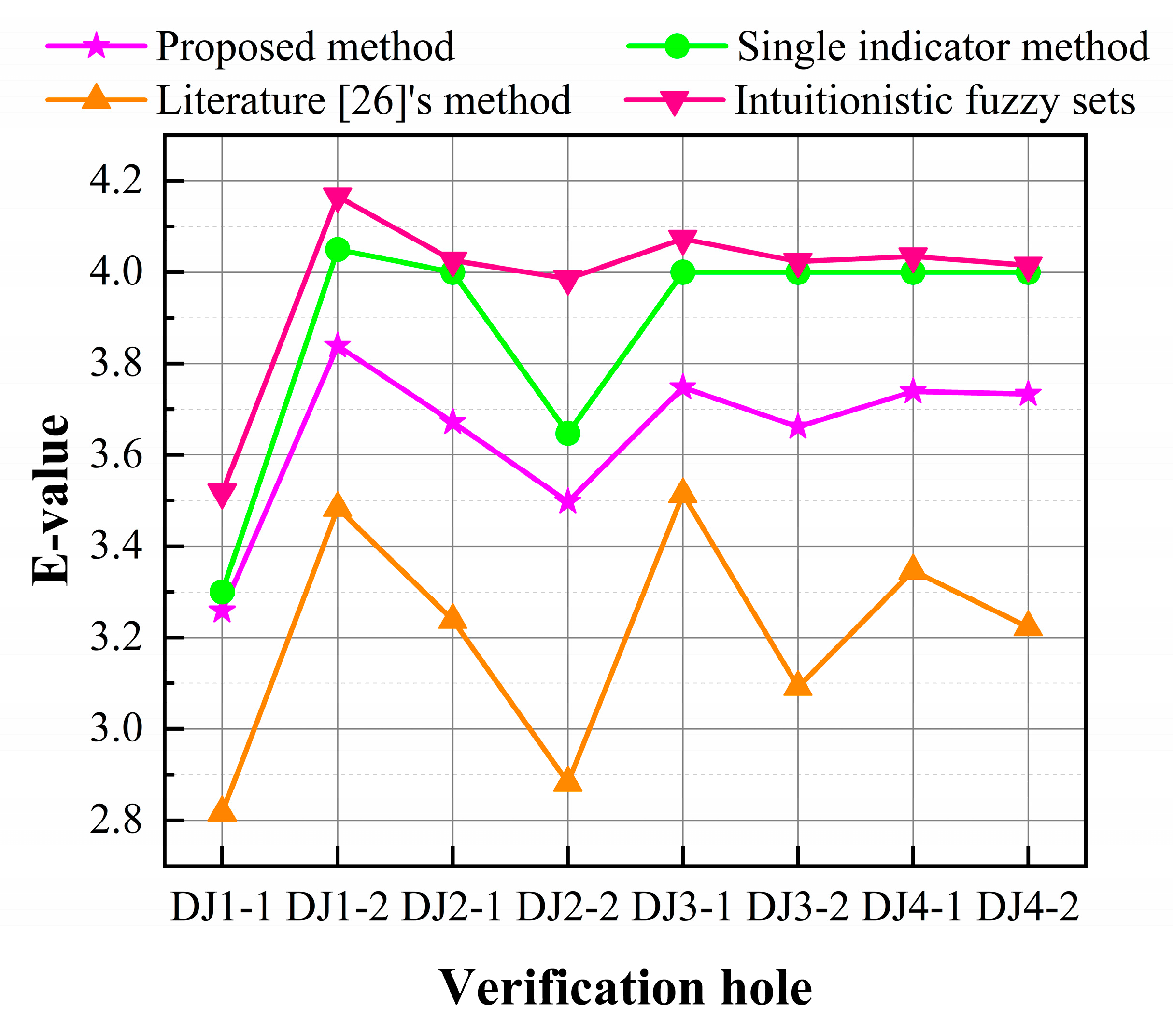
- Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show that the three methods had consistent evaluation results. First, the mean values of the evaluation results were almost identical: The average value of the proposed method was 3.64, the average value based on the single-indicator evaluation was 3.87, and the average value based on the method of Reference [26] was 3.20. According to the evaluation-level classification criteria, the evaluation results of the three methods show that the grouting efficiency of the study area was generally good. Second, from the details, the results of all three methods at A were 5, which consistently indicated that the grouting efficiency was excellent, and all evaluation results at B were 2–3, which consistently showed that the grouting efficiency was ordinary. Finally, the average relative error between the evaluation results of the proposed method and that of the single-indicator evaluation was only 5% and the average relative error between the evaluation results of the proposed method and that of the evaluation results of the method in Reference [26] was -16%; therefore, the results of the three methods tended to be consistent. Therefore, the proposed method has consistent evaluation results with the original method.
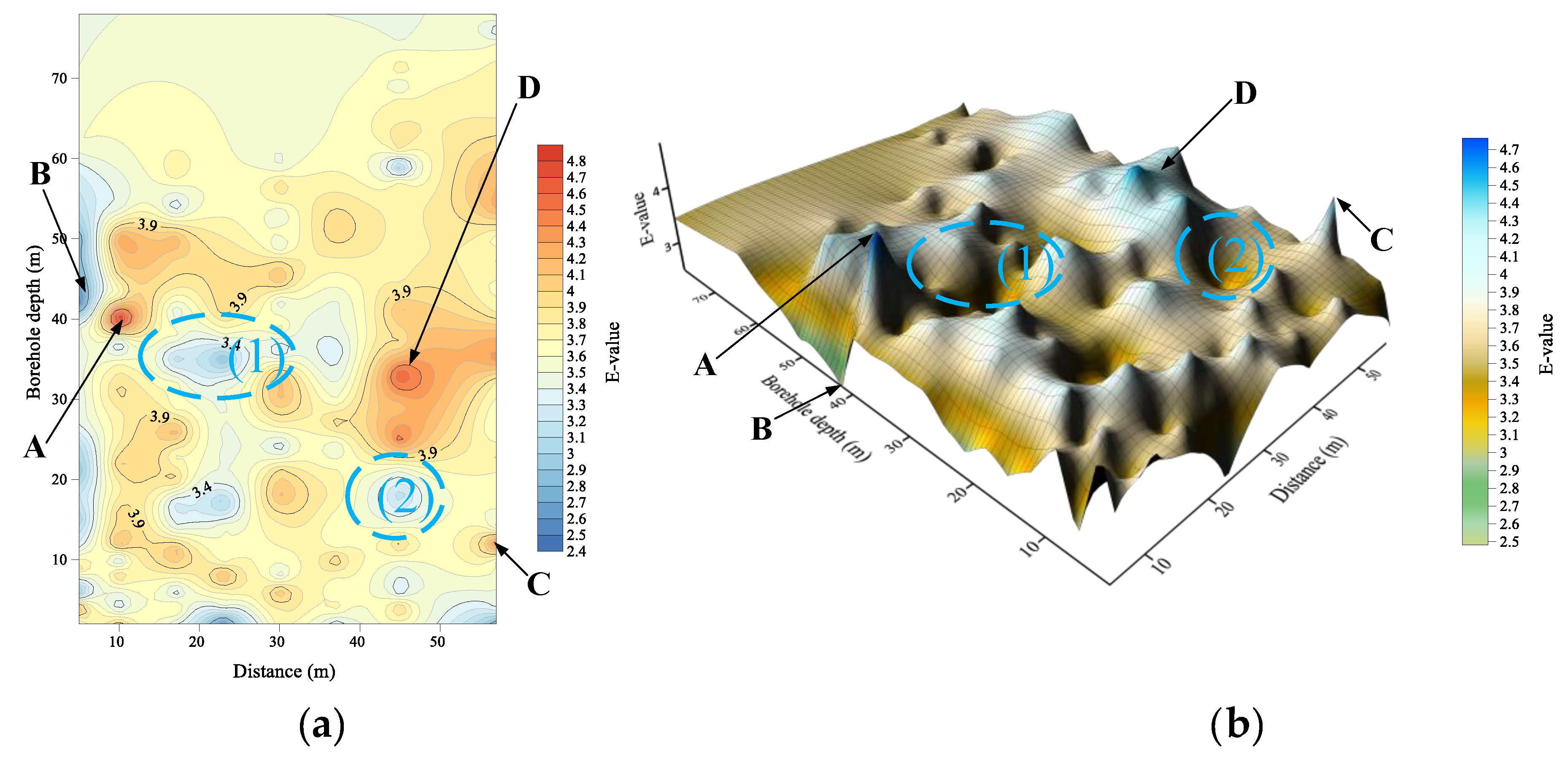
- 2
- The evaluation results of the proposed method were representative. From the results of the consistency analysis, the results of the proposed method were between the results of the single-indicator evaluation and the method in Reference [26]. In other words, the proposed method led to a lower evaluation level than the single-indicator evaluation. This conclusion can be verified in some areas, but the opposite was shown at C and D. At C and D, the results of the single-indicator evaluation were less than 4, which were at the good level, and the results of the proposed method were greater than 4.4, which were at the excellent level; so, the evaluation levels increased. Based on the evaluation results of the method of Reference [26], the rationality of the evaluation results of the proposed method at C and D can be verified. Second, Figure 14 shows that the proposed method had better results than the single-indicator evaluation results in the green areas (1)–(3). Finally, the proposed method had larger evaluation results than the single-indicator evaluation, which accounted for 21.14% of the total 175 intervals. The results of the two methods tended to be identical (the relative errors differing by ±10%) for 108 intervals, which accounted for 61.71% of the total. From the consistency analysis results, compared with the mean value of the method of Reference [26], the evaluation results of the proposed method increased the evaluation level; however, this conclusion could only be verified in some areas. In Figure 15, the evaluation result of the proposed method was less than that of the method of Reference [26] for 35 intervals, which accounted for 20% of the total. The results of the two methods tended to be consistent for 38 intervals, which accounted for 33.14% of the total. Therefore, the proposed method in this paper neither reduces nor improves the evaluation level. It considers the effects of multiple factors on the grouting efficiency; enriches the information in the evaluation result E; enhances the refinement evaluation ability of the grouting efficiency; and makes the grouting-efficiency evaluation results more scientific, reasonable, and representative.
- 3
- The evaluation results based on the proposed method were superior. First, the original single-indicator evaluation method only relies on the permeability (Lugeon, LU) to evaluate grouting efficiency. There is only one indicator, and it is difficult to achieve a refined evaluation of the grouting efficiency. As the LU of each interval of DJ2-1, DJ3-1, and DJ3-2 was between 0.1–1, as shown in Figure 14, the single-indicator evaluation method considered that each interval E was 4. However, the grouting efficiency is related to LU along with other indicators, such as SPI, V, RQD, and FFR. Therefore, it is difficult to achieve a refined evaluation of grouting using only single-indicator evaluation. Second, compared with the evaluation method proposed in Reference [26], the proposed method can consider the hesitation and bounded rationality of the experts and conforms to the actual decision-making process of the experts, such that the evaluation results are more reasonable.
6.2. Rationality of Interval-Valued Intuitionistic Fuzzy Sets
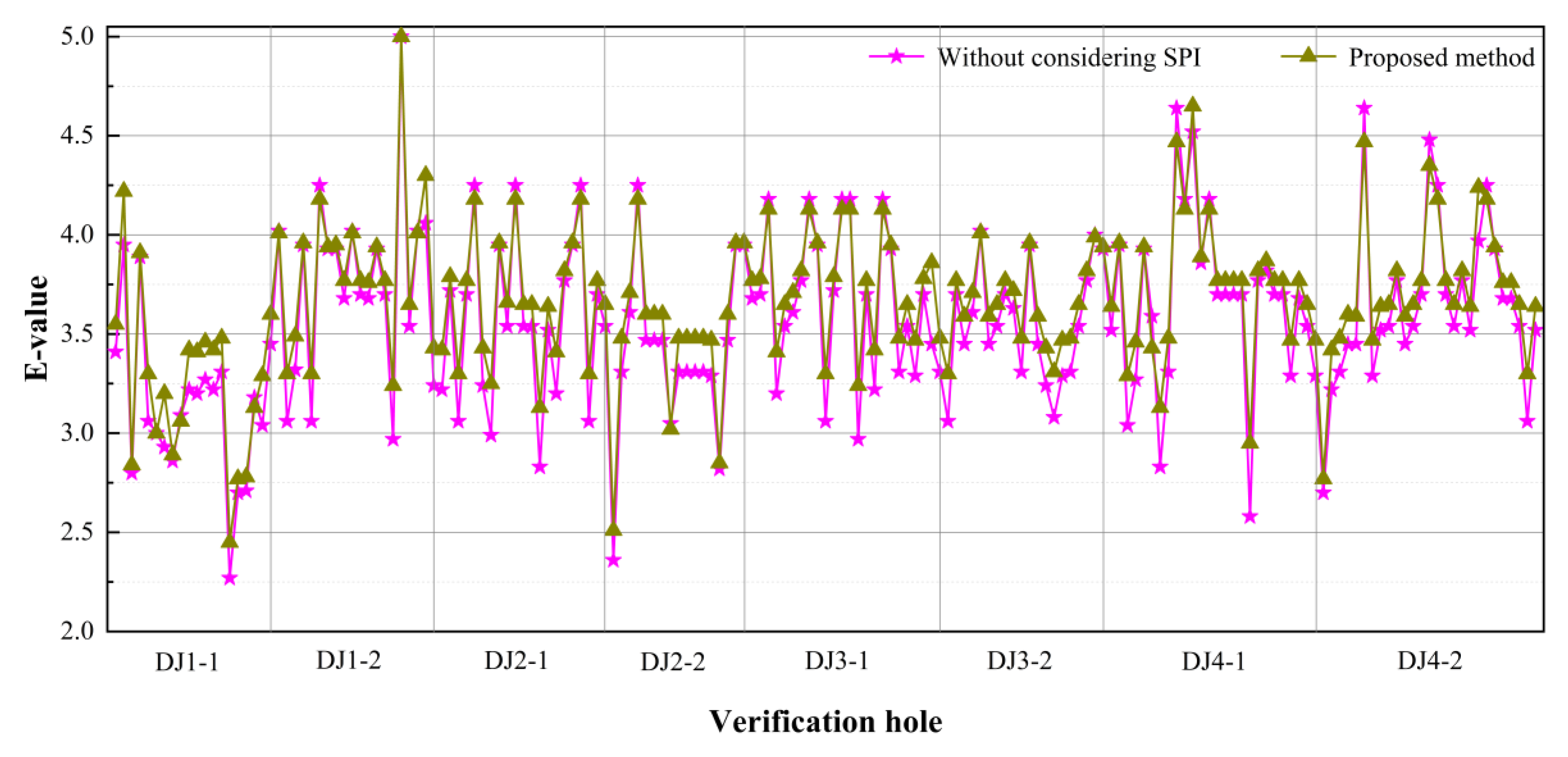
6.3. Necessity of the Secondary Permeability Index
7. Conclusions
- 1
- The comprehensive evaluation model proposed in this paper, which combines the strength of interval-valued intuitionistic fuzzy sets in defining the expert’s hesitation, the advantage of prospect theory in considering the bounded rationality of experts, and the superiority of improved D numbers in effectively handling incomplete decision-making information in the evaluation process, makes the evaluation results more objective and reasonable.
- 2
- Considering the effect of the secondary permeability index, the proposed evaluation indicators system consists of LU, SPI, FFR, RQD, and V; integrates several types of grouting-efficiency evaluation technologies, and ensures a more comprehensive evaluation result. In addition, based on the ordinary Kriging method, the evaluation results of the verification holes are mapped to the grouting construction area, which realizes the comprehensive evaluation of grouting efficiency.
- 3
- Compared with the original evaluation methods, the proposed method has the advantages of consistency, representativeness, and superiority, which can increase the reliability of the grouting-efficiency evaluation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Li, X.; Zhong, D.; Ren, B.; Fan, G.; Cui, B. Prediction of curtain grouting efficiency based on ANFIS. Bull. Eng. Geol. Environ. 2019, 78, 281–309. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, X.; Deng, S.; Chen, W.; Shi, Z.; Xue, L.; Lv, M. Grouting Process Simulation Based on 3D Fracture Network Considering Fluid–Structure Interaction. Appl. Sci. 2019, 9, 667. [Google Scholar] [CrossRef]
- Dreese, T.L.; Wilson, D.B.; Heenan, D.M.; Cockburn, J. State of the Art in Computer Monitoring and Analysis of Grouting. In Proceedings of the Third International Conference on Grouting and Ground Treatment, New Orleans, Louisiana, 10–12 February 2003; pp. 1440–1453. [Google Scholar]
- Kvartsberg, S.; Fransson, Å. Hydrogeological characterisation and stochastic modelling of a hydraulically conductive fracture system affected by grouting: A case study of horizontal circular drifts. Tunn. Undergr. Sp. Technol. 2013, 38, 38–49. [Google Scholar] [CrossRef]
- Alberti, L.; Angelotti, A.; Antelmi, M.; La Licata, I. A numerical study on the impact of grouting material on borehole heat exchangers performance in aquifers. Energies 2017, 10, 703. [Google Scholar] [CrossRef]
- Tinoco, J.; Gomes Correia, A.; Cortez, P. Application of data mining techniques in the estimation of the uniaxial compressive strength of jet grouting columns over time. Constr. Build. Mater. 2011, 25, 1257–1262. [Google Scholar] [CrossRef] [Green Version]
- Spross, J.; Johansson, F.; Uotinen, L.K.T.; Rafi, J.Y. Using Observational Method to Manage Safety Aspects of Remedial Grouting of Concrete Dam Foundations. Geotech. Geol. Eng. 2016, 34, 1613–1630. [Google Scholar] [CrossRef] [Green Version]
- Lisa, H.; Christian, B.; Åsa, F.; Gunnar, G.; Johan, F. A hard rock tunnel case study: Characterization of the water-bearing fracture system for tunnel grouting. Tunn. Undergr. Sp. Technol. 2012, 30, 132–144. [Google Scholar] [CrossRef]
- Kim, Y.U.; Park, J.; Chun, Y.W.; Zhang, G.M. Evaluation and prediction of physical properties of pressure grouting using laboratory testing and elastic wave velocity. KSCE J. Civ. Eng. 2013, 17, 364–367. [Google Scholar] [CrossRef]
- Le, H.; Sun, S.; Wei, J. Influence of Types of Grouting Materials on Compressive Strength and Crack Behavior of Rocklike Specimens with Single Grout-Infilled Flaw under Axial Loads. J. Mater. Civ. Eng. 2018, 31, 06018022. [Google Scholar] [CrossRef]
- Barrages et Geologic Methods de Recherché Terrasement et un Permeabilisation. Available online: https://link.springer.com/article/10.1007/s12205-019-0519-y (accessed on 28 August 2019).
- Roman, W.M.; Hockenberry, A.N.; Berezniak, J.N.; Wilson, D.B.; Knight, M.A. Evaluation of grouting for hydraulic barriers in rock. Environ. Eng. Geosci. 2013, 19, 363–375. [Google Scholar] [CrossRef]
- Saeidi, H.; Ghafoori, M.; Lashkaripour, G.R.; Ghafoori, M. Evaluation of grout curtain performance and seepage behavior in Doosti Dam, Iran. Indian J. Nat. Sci. 2015, 6, 8539–8551. [Google Scholar]
- Lisa, H.; Gunnar, G.; Åsa, F.; Tommy, N. A statistical grouting decision method based on water pressure tests for the tunnel construction stage-A case study. Tunn. Undergr. Sp. Technol. 2013, 33, 54–62. [Google Scholar] [CrossRef]
- Sadeghiyeh, S.M.; Hashemi, M.; Ajalloeian, R. Comparison of permeability and groutability of ostur dam site rock mass for grout curtain design. Rock Mech. Rock Eng. 2013, 46, 341–357. [Google Scholar] [CrossRef]
- Butrón, C.; Gustafson, G.; Fransson, Å.; Funehag, J. Drip sealing of tunnels in hard rock: A new concept for the design and evaluation of permeation grouting. Tunn. Undergr. Sp. Technol. 2010, 25, 114–121. [Google Scholar] [CrossRef]
- Deng, S.; Wang, X.; Zhu, Y.; Lv, F.; Wang, J. Hybrid Grey Wolf Optimization Algorithm–Based Support Vector Machine for Groutability Prediction of Fractured Rock Mass. J. Comput. Civ. Eng. 2018, 33, 1–9. [Google Scholar] [CrossRef]
- Öge, İ.F. Prediction of cementitious grout take for a mine shaft permeation by adaptive neuro-fuzzy inference system and multiple regression. Eng. Geol. 2017, 228, 238–248. [Google Scholar] [CrossRef]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock-New design criteria tested in the field, Part II. Tunn. Undergr. Sp. Technol. 2008, 23, 9–17. [Google Scholar] [CrossRef]
- Hernqvist, L.; Fransson, Å.; Gustafson, G.; Emmelin, A.; Eriksson, M.; Stille, H. Analyses of the grouting results for a section of the APSE tunnel at Äspö Hard Rock Laboratory. Int. J. Rock Mech. Min. Sci. 2009, 46, 439–449. [Google Scholar] [CrossRef]
- Chen, M.; Lu, W.; Zhang, W.; Yan, P.; Zhou, C. An Analysis of Consolidation Grouting Effect of Bedrock Based on its Acoustic Velocity Increase. Rock Mech. Rock Eng. 2015, 48, 1259–1274. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, P.; Zhao, W.; Tian, H. Application of a combined supporting technology with U-shaped steel support and anchor-grouting to surrounding soft rock reinforcement in roadway. J. Cent. South Univ. 2018, 25, 1240–1250. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Sohrabi Bidar, A.; Maleki Javan, M.R.; Haftani, M.; Mehinrad, A. Evaluation of rock mass improvement due to cement grouting by Q-system at Bakhtiary dam site. Int. J. Rock Mech. Min. Sci. 2015, 74, 38–44. [Google Scholar] [CrossRef]
- Bryson, L.S.; Ortiz, R.; Leandre, J. Effects of a grout curtain on hydraulic and electrical conductivity in a laboratory-scale seepage model. In Proceedings of the Geo-Congress 2014: Geo-characterization and Modeling for Sustainability, Atlanta, GA, USA, 23–26 February 2014; pp. 3233–3242. [Google Scholar]
- Wang, X.; Qin, Q.; Fan, C. Research on comprehensive evaluation for grouting effect of broken and soft floor. Arab. J. Geosci. 2017, 10, 1–7. [Google Scholar] [CrossRef]
- Fan, G.; Zhong, D.; Yan, F.; Yue, P. A hybrid fuzzy evaluation method for curtain grouting efficiency assessment based on an AHP method extended by D numbers. Expert Syst. Appl. 2016, 44, 289–303. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, X.; Deng, S.; Zhao, M.; Ao, X. Evaluation of Curtain Grouting Efficiency by Cloud Model–Based Fuzzy Comprehensive Evaluation Method. KSCE J. Civ. Eng. 2019. [Google Scholar] [CrossRef]
- Xu, W.; Shang, X.; Wang, J.; Li, W. A Novel Approach to Multi-Attribute Group Decision-Making based on Interval-Valued Intuitionistic Fuzzy Power Muirhead Mean. Symmetry 2019, 11, 441. [Google Scholar] [CrossRef]
- Phochanikorn, P.; Tan, C. An Integrated Multi-Criteria Decision-Making Model Based on Prospect Theory for Green Supplier Selection under Uncertain Environment: A Case Study of the Thailand Palm Oil Products Industry. Sustainability 2019, 11, 1872. [Google Scholar] [CrossRef]
- Saeidi, O.; Azadmehr, A.; Torabi, S.R. Development of a Rock Groutability Index Based on the Rock Engineering Systems (RES): A Case Study. Indian Geotech. J. 2014, 44, 49–58. [Google Scholar] [CrossRef]
- Roy, J.; Das, S.; Kar, S.; Pamučar, D. An Extension of the CODAS Approach Using Interval-Valued Intuitionistic Fuzzy Set for Sustainable Material Selection in Construction Projects with Incomplete Weight Information. Symmetry 2019, 11, 393. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Supplier selection using AHP methodology extended by D numbers. Expert Syst. Appl. 2014, 41, 156–167. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Algorithms for interval-valued fuzzy soft sets in stochastic multi-criteria decision making based on regret theory and prospect theory with combined weight. Appl. Soft Comput. 2017, 54, 415–430. [Google Scholar] [CrossRef]
- Wang, N.; Liu, F.; Wei, D. A Modified Combination Rule for D Numbers Theory. Math. Probl. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Zhong, D.H.; Yan, F.G.; Li, M.C.; Huang, C.X.; Fan, K.; Tang, J.F. A Real-Time Analysis and Feedback System for Quality Control of Dam Foundation Grouting Engineering. Rock Mech. Rock Eng. 2015, 48, 1947–1968. [Google Scholar] [CrossRef]
- Foyo, A.; Sánchez, M.A.; Tomillo, C. A proposal for a Secondary Permeability Index obtained from water pressure tests in dam foundations. Eng. Geol. 2005, 77, 69–82. [Google Scholar] [CrossRef]
- Azimian, A.; Ajalloeian, R. Permeability and groutability appraisal of the Nargesi dam site in Iran based on the secondary permeability index, joint hydraulic aperture and Lugeon tests. Bull. Eng. Geol. Environ. 2015, 74, 845–859. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, S.; Liu, X.; Qiu, L.; Yi, G. A Least Squares Ensemble Model Based on Regularization and Augmentation Strategy. Appl. Sci. 2019, 9, 1845. [Google Scholar] [CrossRef]
- Atanassov, K.T. Interval-valued Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, J. Approach to Group Decision Making Based on Interval-Valued. Syst. Eng. Theory Pract. 2007, 27, 1–5. [Google Scholar] [CrossRef]
- Zhao, X. TOPSIS method for interval-valued intuitionistic fuzzy multiple attribute decision making and its application to teaching quality evaluation. J. Intell. Fuzzy Syst. 2014, 26, 3049–3055. [Google Scholar]
- Gu, S.; Hua, J.; Lv, T. Evaluation of customer satisfaction of “door-to-Door” whole-process logistic service with interval-valued intuitionistic fuzzy information. J. Intell. Fuzzy Syst. 2016, 30, 2487–2495. [Google Scholar] [CrossRef]
- Liu, P. Some geometric aggregation operators based on interval intuitionistic uncertain linguistic variables and their application to group decision making. Appl. Math. Model. 2013, 37, 2430–2444. [Google Scholar] [CrossRef]
- Wang, C.; Cai, X.; Li, B. Fuzzy comprehensive evaluation based on multi-attribute group decision making for business intelligence system. J. Intell. Fuzzy Syst. 2016, 31, 2203–2212. [Google Scholar]
- Oztaysi, B.; Onar, S.C.; Goztepe, K.; Kahraman, C. Evaluation of research proposals for grant funding using interval-valued intuitionistic fuzzy sets. Soft Comput. 2017, 21, 1203–1218. [Google Scholar] [CrossRef]
- Liu, S.; Yu, F.; Wang, P.S.P. Granularity Approach for Multi-Criteria Decision Making About Hybrid Evaluation Information. Int. J. Pattern Recognit. Artif. Intell. 2018, 32, 1859020. [Google Scholar] [CrossRef]
- Liu, H.-C.; Quan, M.-Y.; Li, Z.; Wang, Z.-L. A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment. Inf. Sci. 2019, 486, 254–270. [Google Scholar] [CrossRef]
- Deng, Y. D Numbers: Theory and Applications Background Knowledge. J. Inf. Comput. Sci. 2012, 9, 2421–2428. [Google Scholar]
- Duan, Y.; Cai, Y.; Wang, Z.; Deng, X. A Novel Network Security Risk Assessment Approach by Combining Subjective and Objective Weights under Uncertainty. Appl. Sci. 2018, 8, 428. [Google Scholar] [CrossRef]
- Chen, L.; Deng, X. A Modified Method for Evaluating Sustainable Transport Solutions Based on AHP and Dempster–Shafer Evidence Theory. Appl. Sci. 2018, 8, 563. [Google Scholar] [CrossRef]
- Ye, H. Assessment of E-learning system in higher education based on hesitant fuzzy information with incomplete attribute weights. Int. J. Emerg. Technol. Learn. 2015, 10, 34–37. [Google Scholar] [CrossRef]
- Lin, S.; Li, C.; Xu, F.; Liu, D.; Liu, J. Risk identification and analysis for new energy power system in China based on D numbers and decision-making trial and evaluation laboratory (DEMATEL). J. Clean. Prod. 2018, 180, 81–96. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. Fuzzy risk evaluation in failure mode and effects analysis using a D numbers based multi-sensor information fusion method. Sensors 2017, 17, 2086. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Guo, S.; Zhao, H. Selecting the Optimal Micro-Grid Planning Program Using a Novel Multi-Criteria Decision Making Model Based on Grey Cumulative Prospect Theory. Energies 2018, 11, 1840. [Google Scholar] [CrossRef]
- Bao, T.; Xie, X.; Long, P.; Wei, Z. MADM method based on prospect theory and evidential reasoning approach with unknown attribute weights under intuitionistic fuzzy environment. Expert Syst. Appl. 2017, 88, 305–317. [Google Scholar] [CrossRef]
- Luca, S.-D.; Pace, R.-D. Evaluation of Risk Perception in Route Choice Experiments: An Application of the Cumulative Prospect Theory. IEEE Conf. Intell. Transp. Syst. Proc. ITSC 2015, 10, 309–315. [Google Scholar]
- Wu, Y.; Xu, C.; Zhang, T. Evaluation of renewable power sources using a fuzzy MCDM based on cumulative prospect theory: A case in China. Energy 2018, 147, 1227–1239. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Qin, Y.; Fu, Y. A risk evaluation and prioritization method for FMEA with prospect theory and Choquet integral. Saf. Sci. 2018, 110, 152–163. [Google Scholar] [CrossRef]
- Król, A.; Ksiȩzak, J.; Kubińska, E.; Rozakis, S. Evaluation of sustainability of maize cultivation in Poland. A prospect theory-PROMETHEE approach. Sustainability 2018, 10, 4263. [Google Scholar] [CrossRef]
- Liu, H.H.; Song, Y.Y.; Yang, G.L. Cross-efficiency evaluation in data envelopment analysis based on prospect theory. Eur. J. Oper. Res. 2019, 273, 364–375. [Google Scholar] [CrossRef]
- Metzger, L.P.; Rieger, M.O. Non-cooperative games with prospect theory players and dominated strategies. Games Econ. Behav. 2019, 115, 396–409. [Google Scholar] [CrossRef]
- Gonzalez-Ramirez, J.; Arora, P.; Podesta, G. Using insights from prospect theory to enhance sustainable decision making by agribusinesses in Argentina. Sustainability 2018, 10, 2693. [Google Scholar] [CrossRef]
- Oztaysi, B.; Cevik Onar, S.; Kahraman, C.; Yavuz, M. Multi-criteria alternative-fuel technology selection using interval-valued intuitionistic fuzzy sets. Transp. Res. Part D Transp. Environ. 2017, 53, 128–148. [Google Scholar] [CrossRef]
- Onar, S.C.; Oztaysi, B.; Otay, I.; Kahraman, C. Multi-expert wind energy technology selection using interval-valued intuitionistic fuzzy sets. Energy 2015, 90, 274–285. [Google Scholar] [CrossRef]
- Deere, D.U. Technical description of rock cores for engineering purpose. Rock Mech. Eng. Geol. 1964, 1, 17–22. [Google Scholar]
- Wan, S.; Li, D. Atanassov’s intuitionistic fuzzy programming method for heterogeneous multiattribute group decision making with Atanassov’s intuitionistic fuzzy truth degrees. IEEE Trans. Fuzzy Syst. 2013, 22, 300–312. [Google Scholar] [CrossRef]
- Wan, S.; Xu, G.; Wang, F.; Dong, J. A new method for Atanassov’s interval-valued intuitionistic fuzzy MAGDM with incomplete attribute weight information. Inf. Sci. 2015, 316, 329–347. [Google Scholar] [CrossRef]
- Xu, Z. Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis. 2007, 2, 19. [Google Scholar]
- Chiclana, F.; Herrera, F.; Herrera-Viedma, E. Integrating three representation models in fuzzy multipurpose decision making based on fuzzy preference relations. Fuzzy Sets Syst. 1998, 97, 33–48. [Google Scholar] [CrossRef]
- Hashemi, H.; Bazargan, J.; Mousavi, S.M.; Vahdani, B. An extended compromise ratio model with an application to reservoir flood control operation under an interval-valued intuitionistic fuzzy environment. Appl. Math. Model. 2014, 38, 3495–3511. [Google Scholar] [CrossRef]
- Gao, J.; Liu, H.; Gu, Y. Interval-valued intuitionistic fuzzy multi-criteria decision-makingmethod based on prospect theory. Syst. Eng. Theory Pract. 2014, 34, 3175–3181. (In Chinese) [Google Scholar]






| Level | LU (Lu) | SPI (×10−15 L/m2·s) | RQD (%) | FFR (%) | V (km/s) | Score |
|---|---|---|---|---|---|---|
| excellent | <0.1 | <2.16 | 90–100 | 90–100 | >5.90 | 5 |
| good | 0.1–1.0 | 2.16–21.60 | 75–90 | 75–90 | 5.58–5.90 | 4 |
| ordinary | 1.0–1.5 | 21.60–172 | 50–75 | 50–75 | 4.93–5.58 | 3 |
| poor | 1.5–2.0 | 172–1720 | 25–50 | 25–50 | 4.60–4.93 | 2 |
| bad | >2.0 | >1720 | <25 | <25 | <4.60 | 1 |
| Verification Hole | Interval | C | L (m) | r (m) | V (L) | t (s) | H (m) | SPI (L/m2·s) |
|---|---|---|---|---|---|---|---|---|
| DJ1-1 | 1 | 1.49 × 10−10 | 2 | 0.04 | 9.02 | 471 | 58 | 1.80582 × 10−14 |
| DJ1-1 | 2 | 1.49 × 10−10 | 2 | 0.04 | 1.26 | 425 | 99 | 1.64165 × 10−15 |
| DJ1-1 | 3 | 1.49 × 10−10 | 2 | 0.04 | 37.35 | 535 | 137 | 2.79081 × 10−14 |
| DJ1-1 | 4 | 1.49 × 10−10 | 3 | 0.04 | 27.18 | 458 | 120 | 1.96317 × 10−14 |
| DJ1-1 | 5 | 1.49 × 10−10 | 3 | 0.04 | 4.98 | 231 | 100 | 8.56658 × 10−15 |
| DJ1-1 | 6 | 1.49 × 10−10 | 3 | 0.04 | 35.99 | 555 | 103 | 2.49858 × 10−14 |
| DJ1-1 | 7 | 1.49 × 10−10 | 3 | 0.04 | 8.49 | 154 | 102 | 2.14164 × 10−14 |
| DJ1-1 | 8 | 1.49 × 10−10 | 3 | 0.04 | 24.11 | 379 | 101 | 2.49858 × 10−14 |
| DJ1-1 | 9 | 1.49 × 10−10 | 3 | 0.04 | 38.02 | 577 | 99 | 2.64136 × 10−14 |
| DJ1-1 | 10 | 1.49 × 10−10 | 3 | 0.04 | 8.66 | 471 | 100 | 1.10668 × 10−14 |
| Interval | Q (L/min) | L (m) | P (MPa) | LU (Lu) | Interval | Q (L/min) | L (m) | P (MPa) | LU (Lu) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.28 | 2 | 0.58 | 1.10 | 11 | 2.42 | 3 | 1.20 | 0.67 |
| 2 | 0.20 | 2 | 0.99 | 0.10 | 12 | 1.34 | 3 | 0.90 | 0.49 |
| 3 | 4.66 | 2 | 1.37 | 1.70 | 13 | 2.17 | 3 | 1.05 | 0.69 |
| 4 | 3.96 | 3 | 1.20 | 1.10 | 14 | 1.93 | 3 | 1.21 | 0.53 |
| 5 | 1.44 | 3 | 1.00 | 0.48 | 15 | 5.51 | 3 | 1.02 | 1.80 |
| 6 | 4.33 | 3 | 1.03 | 1.40 | 16 | 6.00 | 4 | 1.00 | 1.50 |
| 7 | 3.67 | 3 | 1.02 | 1.20 | 17 | 7.52 | 4 | 0.99 | 1.90 |
| 8 | 4.24 | 3 | 1.01 | 1.40 | 18 | 6.06 | 4 | 1.01 | 1.50 |
| 9 | 4.40 | 3 | 0.99 | 1.48 | 19 | 3.36 | 4 | 1.00 | 0.84 |
| 10 | 1.86 | 3 | 1.00 | 0.62 | 20 | 4.08 | 4 | 1.02 | 1.00 |
| Level | Indicator | Unit | Number | Ratio (%) | Min | Max | Mean | Std |
|---|---|---|---|---|---|---|---|---|
| bad | LU | Lu | 0 | 0.00 | - | - | - | - |
| SPI | L/m2·s | 0 | 0.00 | - | - | - | - | |
| FFR | % | 67 | 38.29 | 0 | 20 | 2 | 5.49 | |
| RQD | % | 12 | 6.86 | 0 | 24 | 17 | 7.85 | |
| V | km/s | 0 | 0.00 | - | - | - | - | |
| poor | LU | Lu | 6 | 3.43 | 1.52 | 1.9 | 1.69 | 0.14 |
| SPI | L/m2·s | 0 | 0.00 | - | - | - | - | |
| FFR | % | 52 | 29.71 | 25 | 50 | 39 | 10.25 | |
| RQD | % | 52 | 29.71 | 25 | 50 | 38 | 7.88 | |
| V | km/s | 0 | 0.00 | - | - | - | - | |
| ordinary | LU | Lu | 11 | 6.29 | 1.1 | 1.5 | 1.34 | 0.16 |
| SPI | L/m2·s | 13 | 7.43 | 2.33 × 10−14 | 3.58 × 10−14 | 2.77 × 10−14 | 3.33 × 10−15 | |
| FFR | % | 8 | 4.57 | 60 | 75 | 67 | 4.92 | |
| RQD | % | 70 | 40.00 | 51 | 75 | 63 | 6.98 | |
| V | km/s | 19 | 10.86 | 5.08 | 5.58 | 5.36 | 0.17 | |
| good | LU | Lu | 154 | 88.00 | 0.1 | 1 | 0.54 | 0.17 |
| SPI | L/m2·s | 156 | 89.14 | 2.68 × 10−15 | 2.14 × 10−14 | 9.75 × 10−15 | 3.32 × 10−15 | |
| FFR | % | 15 | 8.57 | 80 | 90 | 82 | 4.14 | |
| RQD | % | 35 | 20.00 | 75.5 | 90 | 82 | 4.49 | |
| V | km/s | 54 | 30.86 | 5.59 | 5.9 | 5.78 | 0.09 | |
| excellent | LU | Lu | 4 | 2.29 | 0 | 0.09 | 0.04 | 0.05 |
| SPI | L/m2·s | 6 | 3.43 | 0 | 1.97 × 10−15 | 1.10 × 10−15 | 8.80 × 10−16 | |
| FFR | % | 33 | 18.86 | 100 | 100 | 100 | 0 | |
| RQD | % | 6 | 3.43 | 91 | 100 | 96 | 4.1 | |
| V | km/s | 102 | 58.29 | 5.91 | 7 | 6.27 | 0.27 |
| Project | Unit 32 | Unit 33 | Unit 34 | Unit 35 |
|---|---|---|---|---|
| LU | ||||
| SPI | ||||
| FFR | ||||
| RQD | ||||
| V |
| Project | Unit 32 | Unit 33 | Unit 34 | Unit 35 |
|---|---|---|---|---|
| LU | ([0.87,0.94],[0.01,0.05]) | ([0.85,0.88],[0.05,0.09]) | ([0.80,0.89],[0.03,0.07]) | ([0.75,0.90],[0.06,0.08]) |
| SPI | ([0.71,0.81],[0.10,0.19]) | ([0.77,0.82],[0.13,0.18]) | ([0.78,0.82],[0.10,0.15]) | ([0.80,0.91],[0.04,0.06]) |
| FFR | ([0.56,0.78],[0.09,0.19]) | ([0.35,0.85],[0.03,0.05]) | ([0.40,0.65],[0.05,0.30]) | ([0.75,0.83],[0.05,0.13]) |
| RQD | ([0.35,0.70],[0.15,0.20]) | ([0.45,0.85],[0.05,0.15]) | ([0.40,0.73],[0.14,0.19]) | ([0.58,0.82],[0.05,0.13]) |
| V | ([0.60,0.75],[0.11,0.16]) | ([0.71,0.80],[0.08,0.13]) | ([0.70,0.82],[0.05,0.13]) | ([0.65,0.70],[0.05,0.15]) |
| Project | Unit 32 | Unit 33 | Unit 34 | Unit 35 | O |
|---|---|---|---|---|---|
| LU | [0.873, 0.937] | [0.795, 0.939] | [0.795, 0.894] | [0.753, 0.894] | [0.804, 0.930] |
| SPI | [0.617, 0.906] | [0.640, 0.950] | [0.675, 0.925] | [0.806, 0.903] | [0.684, 0.851] |
| FFR | [0.533, 0.803] | [0.560, 0.640] | [0.350, 0.700] | [0.700, 0.883] | [0.536, 0.738] |
| RQD | [0.350, 0.700] | [0.550, 0.750] | [0.404, 0.732] | [0.610, 0.790] | [0.479, 0.700] |
| V | [0.543, 0.803] | [0.649, 0.855] | [0.670, 0.850] | [0.575, 0.775] | [0.609, 0.815] |
| Project | Unit 32 | Unit 33 | Unit 34 | Unit 35 |
|---|---|---|---|---|
| LU | 0.059 | −0.109 | −0.072 | −0.142 |
| SPI | −0.145 | −0.122 | −0.073 | 0.091 |
| FFR | −0.151 | 0.182 | −0.357 | 0.209 |
| RQD | −0.230 | 0.081 | −0.131 | 0.118 |
| V | −0.140 | 0.057 | 0.060 | −0.159 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Song, W.; Cui, B.; Wang, X.; Yu, H. A Comprehensive Evaluation Model for Curtain Grouting Efficiency Assessment Based on Prospect Theory and Interval-Valued Intuitionistic Fuzzy Sets Extended by Improved D Numbers. Energies 2019, 12, 3674. https://doi.org/10.3390/en12193674
Liu Z, Song W, Cui B, Wang X, Yu H. A Comprehensive Evaluation Model for Curtain Grouting Efficiency Assessment Based on Prospect Theory and Interval-Valued Intuitionistic Fuzzy Sets Extended by Improved D Numbers. Energies. 2019; 12(19):3674. https://doi.org/10.3390/en12193674
Chicago/Turabian StyleLiu, Zongxian, Wenshuai Song, Bo Cui, Xiaoling Wang, and Hongling Yu. 2019. "A Comprehensive Evaluation Model for Curtain Grouting Efficiency Assessment Based on Prospect Theory and Interval-Valued Intuitionistic Fuzzy Sets Extended by Improved D Numbers" Energies 12, no. 19: 3674. https://doi.org/10.3390/en12193674
APA StyleLiu, Z., Song, W., Cui, B., Wang, X., & Yu, H. (2019). A Comprehensive Evaluation Model for Curtain Grouting Efficiency Assessment Based on Prospect Theory and Interval-Valued Intuitionistic Fuzzy Sets Extended by Improved D Numbers. Energies, 12(19), 3674. https://doi.org/10.3390/en12193674





