Research on Windage Yaw Flashovers of Transmission Lines under Wind and Rain Conditions

Abstract

Windage yaw flashovers under strong wind and rain conditions leave a negative impact on the safe operation of transmission lines. However, the mechanism behind this is not well known yet. Therefore, this paper proposes a systematic method, including three basic parts described as simulation of wind and rain loads, calculation of windage yaw, and flashover analysis, to analyze windage yaw flashovers of transmission lines. The YanMeng-particle swarm optimization (YanMeng-PSO) algorithm is proposed to enhance the simulation accuracy. Unlike the conventional approach, the windage yaw status of conductors and insulator strings is dynamically described with key nodes and the breakdown voltage of their clearances rather than windage yaw angle. Furthermore, in the second part, a new method named key-node method (KNM) is proposed to calculate the conductors’ windage yaw. Moreover, the rain effect is also considered in this paper. This paper then presents a case study on a 110 kV double-circuit transmission line section that suffered severe collapse when the typhoon Rammasun landed in Hainan island. Particular focus was placed on the windage yaw flashover before the structural failure of the transmission line. The results validated the significant rain effect and found that conductors/ground suffer more severe windage yaw flashover than insulator strings. Finally, constructive solutions such as interphase spacers, reasonable conductor arrangement in the design phase, and regular measurements and adjustments of conductor sag in the maintenance phase are proposed to improve the design of transmission lines to enhance their capacity against windage yaw flashovers.

1. Introduction

Windage yaw flashovers due to extreme wind and rain conditions under typhoon weather greatly threaten the stability of transmission lines, especially for the coastal area with an average of nine typhoons landing [1]. According to the accident analysis report provided by the Hainan power grid, there were totally 117 trippings that happened in transmission lines with a voltage level of 35 kV and above in Hainan when the super typhoon Rammasun landed. About 29.42% of trippings were ascertained to be caused by towers collapses and strand fractures, while 59 trippings accounted for approximately 50.43% of the total due to unknown reasons, which were likely to be windage yaw flashovers. Therefore, to reduce the losses caused by strong wind and rain conditions under typhoon and ensure the stability of transmission lines, it is of great significance to study the mechanisms of windage yaw flashovers. Figure 1 shows the windage yaw phenomenon during transmission line operation under wind conditions.

Numerous studies across the world have made their contributions to this area. Deng and Yang tried to study the response of a tower-line system under wind conditions through numerical simulation [2,3]. An’s research based on numerical simulation considered both wind and rain effect [4,5]. However, their study mainly focused on structural failure of towers. Liu Xiaohui tried to study windage yaw of transmission lines under loads through numerical simulation [6], however, without rain effect taken into account. Numerous studies care about the insulation performance of air clearance under certain conditions, which can provide some contributions to the design and maintenance of transmission lines to reduce the risk of flashover. In 2002, Yamagata carried out the full-scale experiment on insulation with different gap lengths in dry and wet conditions using shielding rings [7]. Hu [8] studied the influence of rain and wind on power frequency breakdown characteristic of conductor-to-tower clearance in 2008. These literatures offered convincing data about the breakdown characteristics of air clearance based on experiments. At the same time, some researchers tried to analyze windage yaw of insulator strings and wires due to wind and rain loads. Yan et al. [9] introduced a numerical model of transmission line section to calculate the dynamic swing of the suspension insulator. Chao Zhou [10] proposed a model with derived stability criterion to analyze the large swing of the overhead conductor under wind and rain conditions. These two studies have made valuable work in this area, however, they just studied the motion of windage yaw, without considering the flashover characteristics of clearance under windage yaw situation. Moreover, windage yaw of insulator strings and conductors/ground wires are both critical for transmission lines, requiring comprehensive consideration in the study.

Therefore, a systematic analysis method consisting of three basic parts is proposed to analyze the windage yaw flashovers of transmission lines in this paper. The wind and rain loads are simulated using a corresponding numerical model according to the data established by the Chinese meteorological station. Furthermore, the YanMeng-particle swarm optimization (PSO) algorithm is proposed to enhance the simulation accuracy of average wind speed. Then windage yaw is calculated with a tower-line system model built up using the finite element method. A new approach named key-note method (KNM) is put forward to calculate the conductors/ground wires’ windage yaw. The safety factor, R, is introduced to conduct the flashover analysis. Finally some constructive improvements about transmission line design can be put forward according to the analysis results.

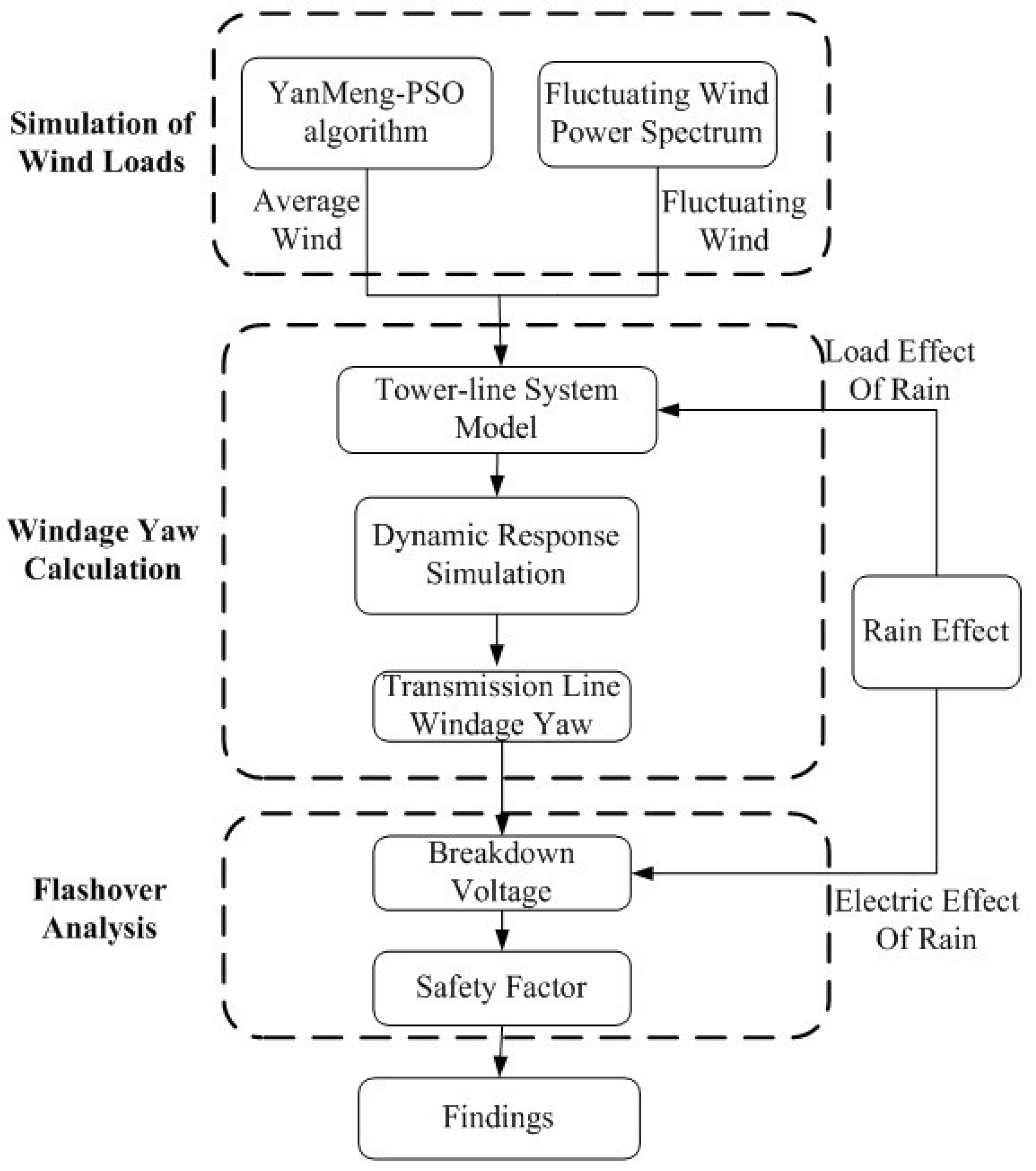
2. Windage Yaw Flashover Analysis Method

2.1. The Proposed Method

As shown in Figure 2, a systematic procedure was introduced to conduct analysis of the transmission line windage yaw flashovers. There were three basic parts in the procedure: simulation of wind loads, windage yaw calculation, and flashover analysis. In the first part, the 10 min average wind speed at 10 m height was simulated using the YanMeng typhoon model that was dynamically optimized by a PSO algorithm, which is called YanMeng-PSO in this paper. Meanwhile, the fluctuating wind speed was simulated using a power spectrum. The dynamic response simulation of the tower-line system model was then conducted using the finite element method with wind and rain loads applied. Moreover, the transmission line windage yaw was calculated in the second part. After that, the safety factor, R, was used to evaluate the flashover danger that a transmission line may encounter under strong wind and rain conditions. Finally, findings about the transmission line windage yaw flashovers were obtained through the analysis.

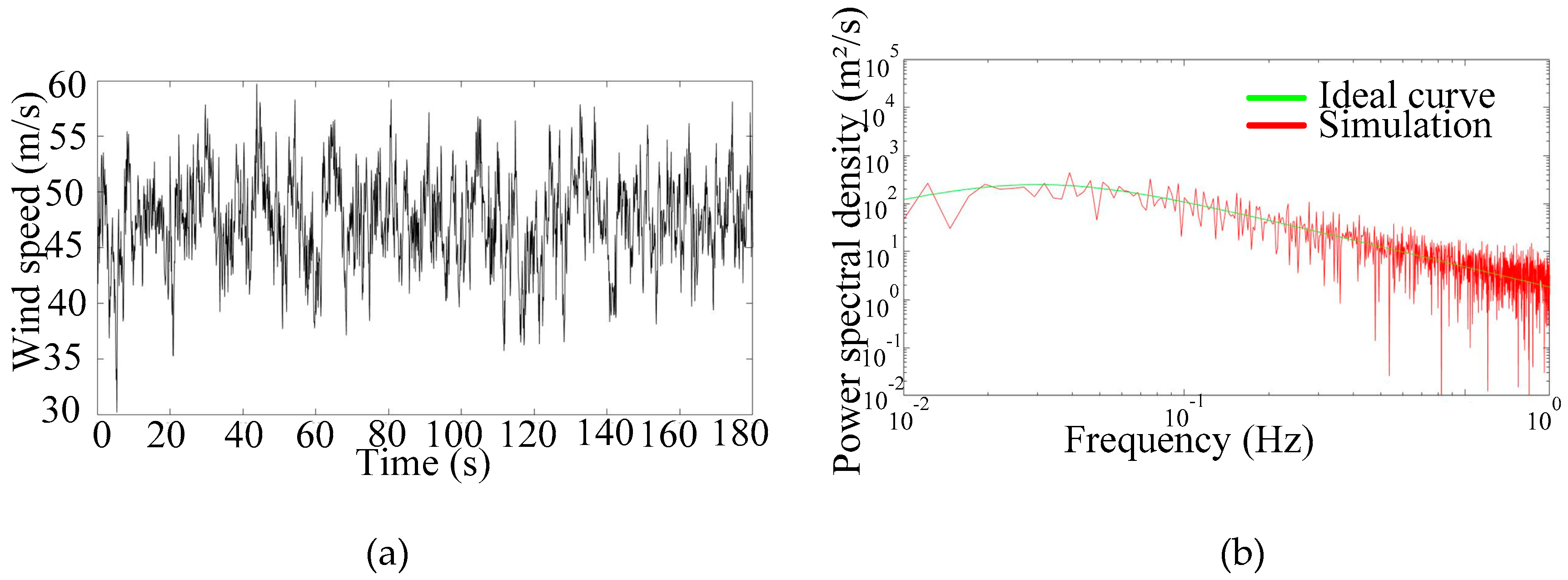
2.2. Simulation of Wind Loads

The wind loads under typhoon weather generally consist of two parts, average wind loads and fluctuating wind loads. The average wind speed at 10 m height during the typhoon Rammasun can be simulated with the YanMeng typhoon wind field considering the friction effect in the boundary layer [11,12]. Its equilibrium equation is written as:

$$\frac{\partial v_t}{\partial t}+v_t\cdot \nabla v_t=-\frac{1}{{\rho }_a}\nabla p_a-f_{c}k\times v_t+F_t,$$

(1)

where v_t is the typhoon wind speed, ρ_a is the air density, f_c is the Coriolis force parameter, and F_t is the boundary layer friction force, k is a unit vector.

The simulation accuracy greatly depends on two critical parameters in the YanMeng wind field, the equivalent roughness length, z₀, and the Holland pressure profile parameter, B. z₀ describes the friction impact on v_t due to topography, while B directly decides the pressure distribution in the wind field, as shown in Equation (2) [13]:

$$P(r)=P_0+\Delta P\cdot \exp [-{(R_m/r)}^B],$$

(2)

where P₀ is the typhoon center pressure; R_m is the maximum wind speed radius; B is the Holland pressure profile parameter; $\Delta P=P_{\infty }-P_0$ with P_∞ taken as 1010 hPa.

They are both highly related to the simulation accuracy of typhoon average wind speed. Therefore, to enhance to simulation accuracy, the two parameters were dynamically determined by an algorithm named YanMeng-PSO, instead of by the conventional way, data fitting, in this paper.

The YanMeng-PSO algorithm creatively connects a typical PSO algorithm [14] and the YanMeng wind field together. The basic idea of a typical PSO comes from the predation behavior of a bird swarm in nature. To find out the best place with the most food, each bird in the swarm keeps improving its search strategy according to its own experiences and predation information provided by other birds. In the YanMeng-PSO algorithm, what a particle does is similar to what a bird does. Each particle carries a z₀ and B and keeps searching for better parameters according to its own search experience, which is also called individual experience. All particles share their search experience with each other to find out the best value of the two parameters. So a particle can obtain search experience form other particles. This is called social experience. Then, a particle changes its z₀ and B considering both individual experience and social experience.

The brief procedure of YanMeng-PSO is shown in Figure 3.

1. Parameter initiation

As the first step of the whole YanMeng-PSO procedure, a few critical parameters are required to be determined in this part before the algorithm functions. The swarm size represents the total amount of particles in the swarm. Greater swarm size can speed up the convergence, however, this brings heavy calculation workload for computers. It was taken as 500 in this paper. Number of iteration represents how many times the swarm conducts the search. Less iterations may cause instability of solution while more iterations can slow down the calculation speed. It was determined as 100 through numerous tests.

2. Objective function calculation

The second step is particle objective function calculation. Every time the swarm conducts the search, an objective function is used to evaluate the performance of each particle with the contrast between the simulated wind speed/direction and real-time measured wind speed/direction. The objective function used is expressed by the Equation (3):

$$F=1/\sqrt{{(v_t-v_r)}^2+{({\psi }_t-{\theta }_r)}^2},$$

(3)

where F is the objective function value for a particle, v_t is the simulated average wind speed, v_r is the real-time measured average wind speed, Ψ_t is the simulated average wind direction, θ_r is the real-time measured wind direction.

3. Experience update

Then it will be evaluated whether the best objective function value for the whole swarm is great enough, in other words, whether the simulated average wind speed meets the accuracy conditions. If not, it will go to the next part, experience update. Each particle needs to update the optimization experience in iteration, including individual experience and social experience.

4. Parameter adjustment

In the most cases, individual experience is different from the social experience. Therefore, a particle needs to make a decision about parameter adjustment considering both of them. For any particle, i, the adjustment of parameter B during the YanMeng-PSO procedure is conducted according to the following Equations (4) and (5):

$$\Delta B_i=c_{ita}\Delta B_i{}^{\prime }+c_{ind}{r}_{ind}(B_{ind}-B_i{}^{\prime })+c_{swm}{r}_{swm}(B_{swm}-B_i{}^{\prime }),$$

(4)

$$B_i=B_i{}^{\prime }+\Delta B_i,$$

(5)

where ΔB_i is the adjustment of parameter B for particle i in the current iteration, ΔB_i′ is the adjustment of parameter B for particle i in the last iteration, c_ita is the inertia constant, c_ind is the constant of individual experience, r_ind is a random value for individual experience, B_ind is the best value of B ever found in history for particle i, B_i is the value of B for the particle i in the current iteration, B_i′ is the value of B for the particle i in the last iteration, c_swm is the constant of swarm experience, r_swm is a random value for swarm experience, B_swm is the best value of B ever found in history for the whole swarm. The adjustment of parameter B is illustrated in Figure 4.

The adjustment of the parameter z₀ is the same as that of B, expressed as:

$$\Delta z_{\mathit{0}}{}_i=c_{ita}•\Delta z_{\mathit{0}}{{}_i}^{\prime }+c_{ind}•r_{ind}•(z_{\mathit{0}}{}_{ind}-z_{\mathit{0}}{{}_i}^{\prime })+c_{swm}•r_{swm}•(z_{\mathit{0}}{}_{swm}-z_{\mathit{0}}{{}_i}^{\prime }),$$

(6)

$$z_{\mathit{0}}{}_i=z_{\mathit{0}}{{}_i}^{\prime }+\Delta z_{\mathit{0}}{}_i,$$

(7)

where Δz_0i is the adjustment of parameter z₀ for particle i in the current iteration, Δz_0i′ is the adjustment of parameter z₀ for particle i in the last iteration, z_0ind is the best value of z₀ ever found in history for particle i, z_0i is the value of z₀ for the particle i in the current iteration, z_0i′ is the value of z₀ for the particle i in the last iteration, z_0swm is the best value of z₀ ever found in history for the whole swarm.

After the parameter adjustment, the YanMeng-PSO algorithm will carry on to the next iteration. The circle will keep functioning until the average wind speed meets the accuracy conditions.

2.3. Calculation of Rain Loads

During the rainfall accompanying the typhoon, the speed of the raindrops reduces sharply to become 0 when they collide with transmission line towers or wires. This process follows Newton’s second law. The mass of the raindrop, m_r, is expressed as [15,16]:

m_r = ρ_rπd_r³/6,

(8)

where d_r is the diameter of the raindrop, ρ_r is the density of rainfall.

The action time is τ = d_r/(2V_rs), according to the momentum theorem:

$${\displaystyle {\int }_0^{\tau }f(t)dt+{\displaystyle {\int }_{V_{r\mathrm{s}}}^0{m}_r}dv=0},$$

(9)

where, V_rs is the raindrop’s velocity before the collision. The mean impinging force, F(τ), of a droplet during time τ is:

$$F(\tau )=\frac{1}{\tau }{\displaystyle {\int }_0^{\tau }f(t)dt=\frac{m_r{V}_{rs}}{\tau }}.$$

(10)

The action area on of each raindrop is A_r = πd_r²/4, and the action force of raindrop can be converted into a uniform load using Equation (11):

$$F=F(\tau )/{\mathrm{A}}_r\cdot b_r\cdot {\alpha }_r.$$

(11)

The rain load (N/m) calculation can be simplified to be Equation (12).

$$F=\frac{4}{3}{\alpha }_r{\rho }_r{V}_{rs}{}^2{b}_r,$$

(12)

where α_r is the percentage of raindrops per unit volume of air at a certain rainfall intensity; b_r is the effective width of the object impacted. It is taken as the diameter for the conductor and ground wire and as the equivalent width of each panel for the tower body. The equation for calculating α_r is:

$${\alpha }_r=\frac{1}{6}\pi d_r{}^{3}N(D),$$

(13)

$$N(D)={\displaystyle {\int }_0^{D}n(r)dr},$$

(14)

where N(D) is the number of the raindrops with diameter D of per unit volume of air in 1/mm³. In order to establish a more accurate rain load model, the distribution of corresponding raindrops and raindrops during rainfall should be addressed. The Marshall–Palmer exponential distribution [17] is used to describe how the number of raindrops distributed with the size of the raindrops, as shown in Equation (15):

$$n(D)=n_{\mathit{0}}\exp (-\Lambda D),$$

(15)

where n₀ = 8 × 10³ in 1/(m³·mm), the gradient factor Λ = k_ΛR_h^−0.21 in 1/mm, constant k_Λ = 4.1(h/mm)^−0.21, R_h is the horizontal rain intensity in mm/h.

2.4. Calculation of Windage Yaw

In the Chinese code of transmission line design [18], the most emphasis will be put on insulator string windage yaw for it is taken as the main reason for the flashover. With the wind and rain loads applying on insulator strings and conductors, the conductor suspension points get close to the tower body and the cross-arm, which may lead to flashover phenomenon if the spacing is reduced to below the permissible value for the certain voltage level. What is more, the windage yaw of conductors/ground wires is also considered and studied through the numerical simulation in this paper to find out the root cause of transmission line trippings under strong wind conditions.

With wind and rain loads applied, the finite element model of tower-line system needs to be built up according to the detailed information of transmission line, such as the structure of towers, the span of line, etc. The dynamic response of the finite element model with a certain duration is simulated to calculate windage yaw.

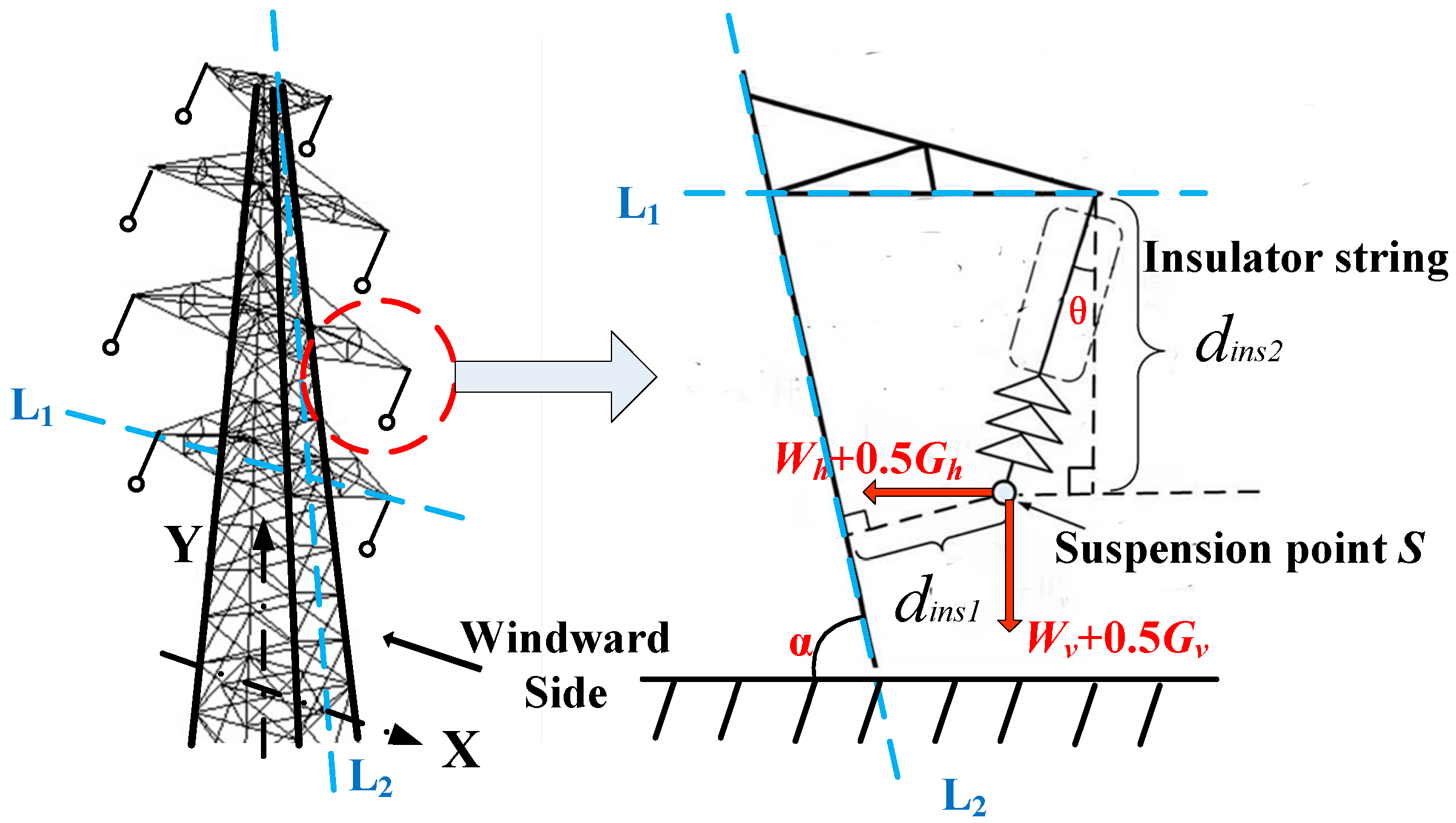
2.4.1. Calculation of Insulator String Windage Yaw

So far, in the design procedure of overhead transmission line, two kinds of static methods, polygon method and rigid straight bar method, are mainly used for calculation of windage yaw [19,20]. In the transmission line design, the insulator string is usually regarded as a rigid body with a straight rod shape, not considering its relatively tiny bending effect. Figure 5 shows all the loads acting on an insulator string. Then the action point of all loads is moved to the conductor suspension point according to the moment invariance principle. Furthermore, the clearance of the conductor suspension point to the tower, d_ins1 and d_ins2 can be derived as the Expressions (17) and (18) using mechanics and geometry.

In Figure 5, G_v is the vertical load of fittings and insulator string; G_h is the horizontal load of fittings and insulator string; W_v is the vertical load of conductor; W_h is the horizontal load of conductor.

$${\theta }_{}=\arctan \frac{W_v+0.5G_v}{W_h+0.5G_h},$$

(16)

$$d_{ins\mathit{1}}=l\cos \theta ,$$

(17)

$$d_{ins\mathit{2}}=(L-lsin\theta -\frac{l{\cos }^2\theta }{\sin \theta })sin\alpha ,$$

(18)

where d_ins1 is the clearance of the conductor suspension point to the cross-arm; d_ins2 is the clearance of the conductor suspension point to the tower body; L is the length of the cross arm; l is the length of the insulator string; θ is the angle between the insulator string and the vertical direction; α is the angle between the tower outline and the ground; L₁ is the central axis in the bottom plane of the cross-arm; L₂ is the central axis in the windward side of the tower body.

Though the static methods are convenient to implement as demonstrated above, the bad accuracy cannot be ignored. Therefore, the transmission line windage yaw was calculated through dynamical simulation based on the finite element method in this paper. The three-dimensional tower-line system model was built up according to transmission line characteristics. In the tower-line system model, the spatial position of suspension point, S (x,y,z), and the analytical equation of L₁ and L₂ can be obtained in the dynamic response simulation. Moreover, the clearance, d_ins1, is equal to the distance between S and L₁, and d_ins2 is equal to the distance between S and L₂.

The shorter clearance, d_ins, is regarded as the most dangerous clearance in the insulator string windage yaw situation, as expressed in Equation (19):

d_ins = min{d_ins1, d_ins2}.

(19)

2.4.2. Calculation of Conductor/Ground Wire Windage Yaw

Unlike the windage yaw of the insulator string, the windage yaw of conductors/ground wires is much more complicated as wires swing asynchronously during the wind loads impact. This paper creatively proposes a new approach named key-node method (KNM) to solve this problem. In this approach, movements of conductor key nodes in the tower-line system model are used to study the mechanisms of conductor windage yaw.

The basic idea of KNM is to estimate the clearance of different conductors/ground wires through investigating the clearance of certain key nodes during the dynamic response simulation of tower-line system model. Before the wind loads were applied on the tower-line system model, conductor/ground wires were in a static state with no windage yaw. Those key nodes approximately in the same X–Y plane are classified to the same group, as shown in Figure 6. The group is called the key-node group (KNG) and the X–Y plane is called key-node-group plane (KNG plane).

Figure 7 shows the basic flow chart of the KNM. The first step in KNM is to choose KNG within the span. Equal and proper spatial distances between two adjacent KNG plane need to be guaranteed. Additionally, each KNG plane represents the windage yaw situation of a different part of the span.

Then clearances of conductor-to-conductor and conductor-to-ground wire are calculated respectively using the Equations (20) and (21):

D_p-p = {d_pi,pj}(i ≠ j, i,j = 1,2,3,…,m),

(20)

D_p-g = {d_pi,gj}(i =1,2,3,…,m, j = 1,2,3,…,n),

(21)

where D_p-p is the set of the clearance for phase conductor key node to phase conductor key node, pi (i = 1,2,…,m) represents any phase conductor key node, m is the number of the phase conductor key nodes in a KNG plane, D_p-g is the set of the clearance for phase conductor key node to ground wire key node, g_i (i = 1,2,…,n) represents any ground wire conductor key node, n is the number of the ground wire key nodes in a KNG plane. d_A,B represents the clearance of key node A and key node B. The spatial coordinates of the key nodes A and B can be expressed as (x_A, y_A, z_A) and (x_B, y_B, z_B), and the d_A,B is given by Equation (22):

$$d_{A,B}={\sqrt{{(x_A-x_B)}^2 + (y_A-y_B{)}^2 + (z_A-z_B{)}^2}}^{}.$$

(22)

The minimum clearance of two phase conductor key nodes for a KNG is expressed as

d_min,p-p = min(D_p-p).

(23)

Additionally, the minimum clearance of the phase conductor key node to the ground wire key node for a KNG is expressed as

d_min,p-g = min(D_p-g).

(24)

d_min,p-p and d_min,p-g stand for the most dangerous clearance, after these two minimum clearances are found, information about their KNG number and their key node number will be recorded for further flashover analysis.

2.5. Flashover Analysis

The windage yaw status of transmission lines is dynamically described with key nodes and the breakdown voltage of their clearances in this paper, different from the conventional static method. The safety factor, R, is proposed to conduct the flashover analysis of the transmission line under strong wind and rain load conditions, as shown in Equation (25):

R = U_f/U_max,

(25)

where U_f is the breakdown voltage of the most dangerous clearances d_min,p-p and d_min,p-g calculated in the Section 2.4 previously. With rain effect correction, U_max is the maximum working voltage of the transmission line during operation under power frequency condition. A smaller R value represents higher danger level, with greater probability of windage yaw flashover. It is reasonable to estimate that flashover can happen when the R is below 1.0—the safety criterion taken in this paper.

U_f is calculated using Equation (26):

U_f = k_rU_50%,

(26)

where U_50% is voltage with a breakdown probability of 50%, which is broadly used to describe the characteristics of clearance in electrical engineering. Chinese standard GB 50545-2010 [15] provides the flashover characteristics curve of clearance under a few kinds of situations, as shown in Figure 7. Curve No. 1 in the figure represents the clearance of conductor–conductor and rod–rod, while curve No. 2 stands for the clearance of conductor–tower. U_50% of clearance is given according to Figure 8 [18]. It is worth noting that other convincing data based on experiments about flashover characteristics in addition to the Chinese standard GB 50545-2010 are also available in the systematic method.

k_r is the rain effect coefficient. Geng Cui-ying et al. [21] studied clearance breakdown characteristics in rainy weather under power frequency through an artificial simulation test. In this paper, the coefficient of rain effect, k_r, was determined by fitting the test data, as expressed by Equation (27):

$$k_r=a_{\mathit{1}}{d}^2+a_{\mathit{2}}d+a_{\mathit{3}},$$

(27)

where d represents clearance; coefficients a₁, a₂, and a₃ were fitted according to experimental data using quadratic polynomial fitting.

Table 1. Fitting coefficients.

Rainwater Density ρr (mm/h)	a1	a2	a3	SSE	RMSE
144	−0.7166	1.399	0.2337	1.647 × 10−7	4.058 × 10−4
288	−0.6966	1.381	0.2077	5.309 × 10−8	2.304 × 10−4
576	−0.6994	1.405	0.1656	1.207 × 10−5	3.474 × 10−3
864	−0.6865	1.391	0.1555	5.505 × 10−6	2.346 × 10−3

Note: SSE represents sum of squares for error, RMSE represents root mean square error.

shows the fitting results.

3. Case Study

This paper presents a case study on a section of 110 kV double-circuit transmission line named Baoyi II in Hainan island. It suffered severe collapse when the super typhoon Rammasun swept across Hainan in 2014. The particular focus is placed on the windage yaw situation of transmission line before its structural failure due to the strong wind and rainfall.

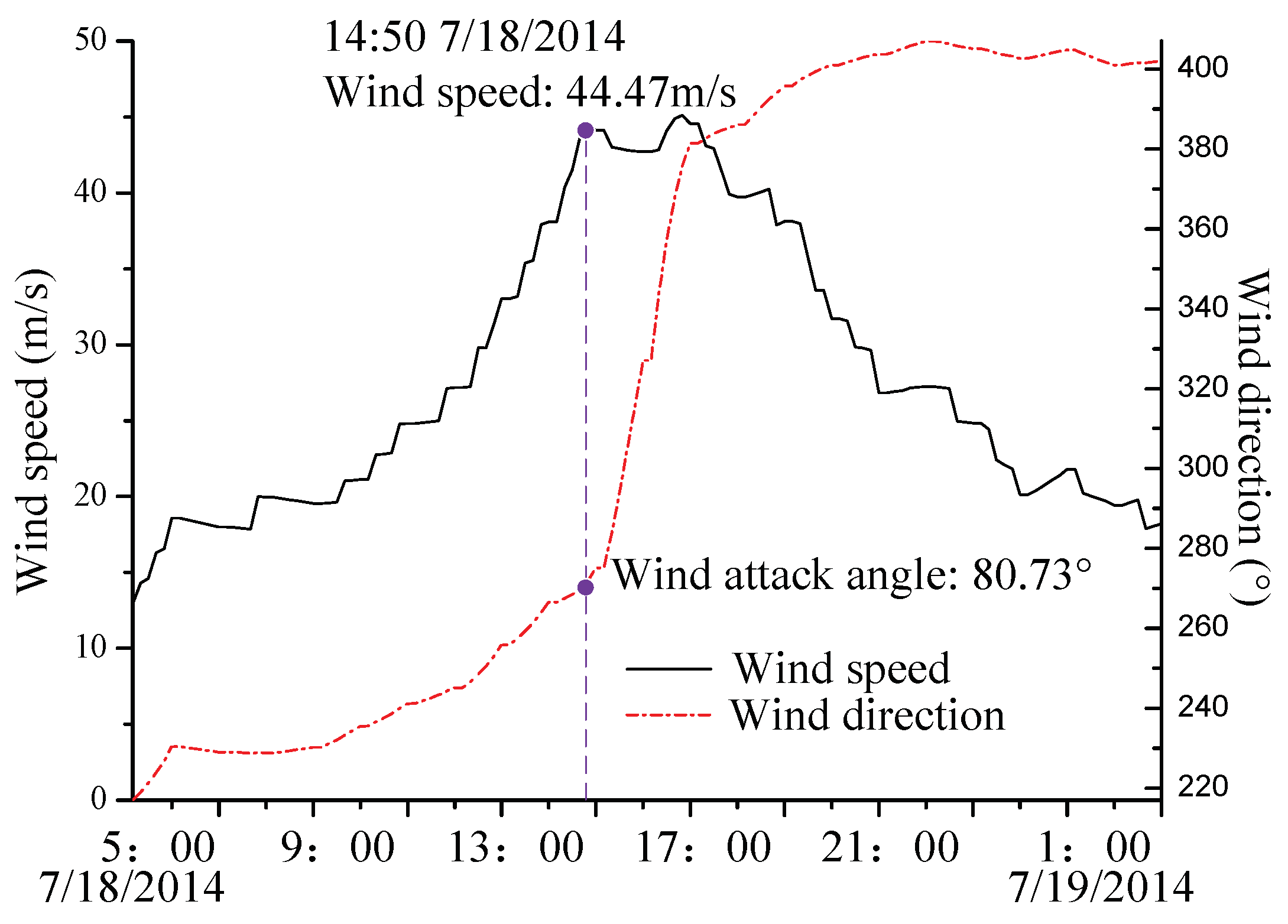
3.1. Wind and Rain Load of the Rammasun

Rammasun caused catastrophic damage to the power grid in Hainan province, including 117 tower trippings and 27 tower collapses in several transmission lines of 35 kV, 110 kV, and above. Figure 9 shows the 10 min average wind speed and direction at 10 m height of the Rammasun. It strengthened sharply from 5:00 on July 18 and landed in Wenchang City, Hainan at 15:30 [22].

It is speculated that the collapse of this transmission line section likely occurred at about 15:00 on 18 July because the average wind speed exceeded the design wind speed and the wind attack angle was approximately 90 degrees [23]. Therefore, this study conducted dynamic response simulation at 14:50 on 18 July, slightly before the potential failure moment. The 10 min average wind speed and the wind attack angle were simulated to be 44.47 m/s and 80.73 degrees. The fluctuating wind was then simulated using the Shiyuan wind power spectrum [24] based on the average wind. The following Equation (28) describes the relation between the power of the fluctuating wind and its frequency.

$$S_v(n)=\frac{5.64k{V}_{10}^2{x}^{2.4}}{n{(1+1.5x^2)}^{1.4}},$$

(28)

where x = 1200 n/V₁₀; S_v (m²/s) is the fluctuating wind power spectrum; V₁₀ (m/s) is the average wind speed at 10 m height; k is the surface frictional drag coefficient and taken as 0.003; n (Hz) is the fluctuating wind frequency.

Figure 10 shows the fluctuating wind at 10 m height and the power spectral density curve.

It was reported by the Chinese meteorological station that the super typhoon Rammasun brought severe rainfall to Hainan Province. Haikou city, where the transmission line was located, suffered a severe rainfall intensity of more than 100 mm/h. The corresponding load effect and electric effect of rainfall were then simulated in the study.

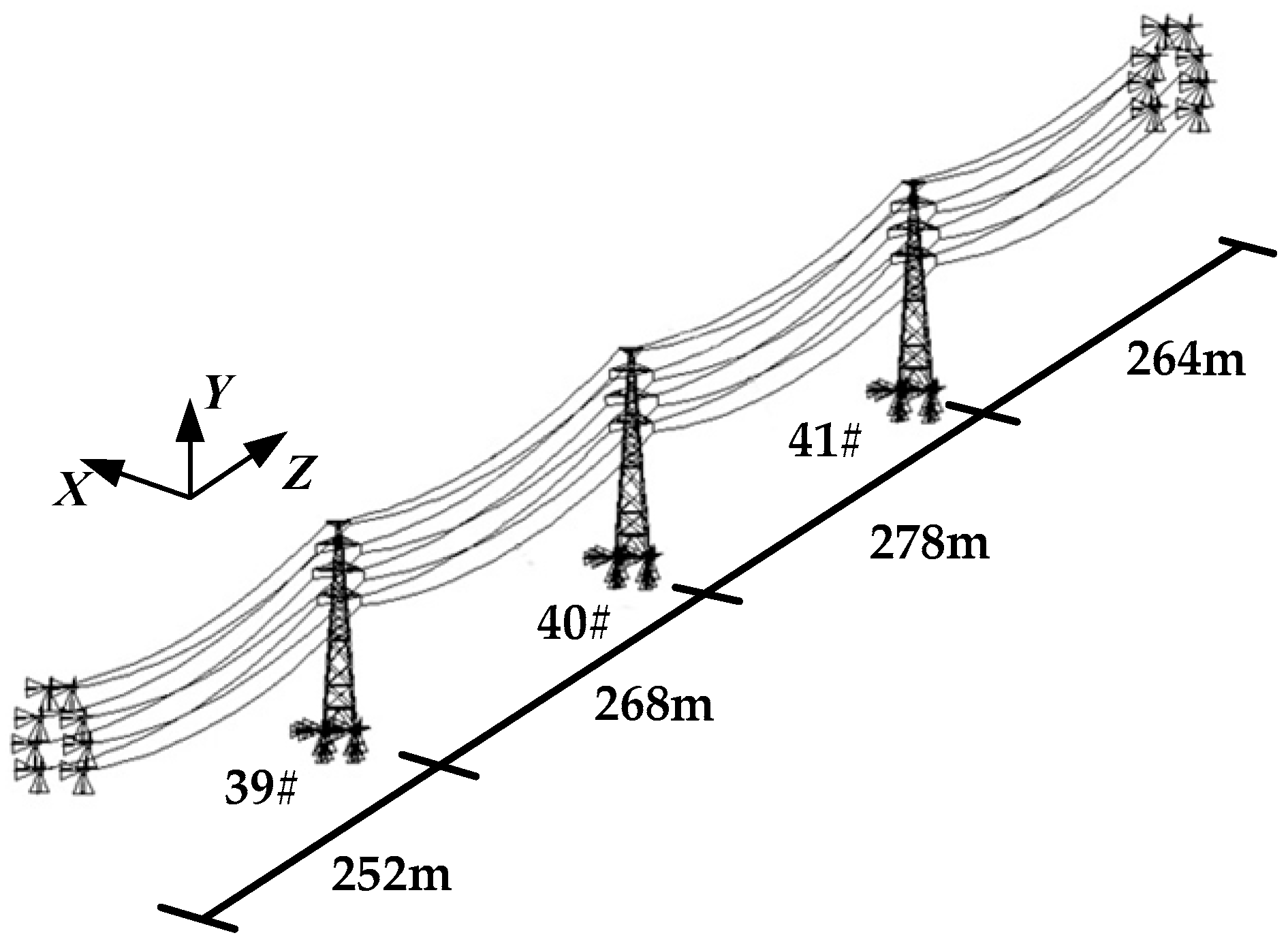
3.2. Modeling of the Tower-Line System

The tower-line system model with three towers and four spans was built according to the characteristics of the transmission line section, as shown in Figure 11. The insulator string model installed in suspension tangent towers in this transmission line was rod suspension composite insulator FXBW4-110/100, whose technical parameters are shown in

Table 2. Technical parameters of rod suspension composite insulator FXBW4-110/100.

Composite Insulator Type	FXBW4-110/100
Rated voltage (kV)	110
Rated mechanical tensile load (kN)	100
Structural height (mm)	1240 ± 15
Minimum arc distance (mm)	1015
Minimum nominal creepage distance (mm)	3150
Lightning full-wave withstand voltage (kV)	550
Power frequency withstand voltage (kV)	230

.

Table 3. Characteristics of conductors and ground wires.

Type	JL/LB1A-240/40	JLB23-50
Area (mm2)	277.74	49.86
Diameter (mm)	21.66	9.00
Mass per unit length (kg/km)	916.9	315.1
Rated tensile strength (N)	85,851	54,900
Elastic modulus (N/mm2)	69,990	141,300
Linear expansion coefficient (1/°C)	19.76 × 10−6	12.9 × 10−6
Maximum working strength (N)	30,207	16,486

shows the detailed characteristics of conductors and ground wires.

The finite element model of tower-line system was built up with the commercial software ANSYS (15.0, Pittsburgh, PA, USA) according to the characteristics of the transmission line section focused on. In the finite element model, the tower legs and bracing members are modeled with element “beam188”, a 3D two-node beam element in ANSYS with six degrees of freedom per node. Considering that relative rotation and friction effect tend to be very minor, an insulator string and an auxiliary member can be regarded as an equivalent rigid body, modeled with a uniaxial tension–compression (truss) element named “link8” with translational degrees of freedom in the nodal X, Y, and Z directions. Conductors and ground wires were modeled according to catenary equation with numerous “link10” elements, uniaxial tension-only two-node truss elements in ANSYS, considering the slack of conductors and ground wires. At the same time, fixed constraints were applied on the bottom of each tower.

1998 “beam188” elements were used for modeling tower legs and bracing members, 1216 “link8” elements for insulator strings and auxiliary members, and 892 “link10” elements for conductors and ground wires.

3.3. Windage Yaw Flashover Analysis

The wind and rain loads simulated previously were applied on the tower-line system and the dynamic response simulation with a duration of 180 s was conducted using the finite element method. Then, the transmission line windage yaw was calculated through the method mentioned before in Section 2. After that, the safety factor, R, was used to evaluate the flashover danger that the line section might encountered before its structural failure. Figure 12a shows the safety factor, R, of the conductor span between tower No. 39 and No. 40 in time domain. Figure 12b shows the safety factor, R, for three conductor insulator strings of windward side of tower No. 39.

In Figure 12, the bold black line stands for the minimum R value during the dynamic response simulation of 180 s. Every peak below 1.0, the safety criterion, represents a possible windage flashover. There are 34 peaks of the conductors/ground wires and 29 peaks of the insulator string. Detailed information about conductors/ground wires is illustrated in Figure 13.

It can be inferred from Figure 13 that the spatial distance of two wires is the most crucial factor that decides the probability of windage yaw flashover occurring between them. The least value of safety factor, R, occurred between vertically adjacent wires, such as upper conductor and middle conductor, middle conductor and lower conductor, mainly because there were close to each other. The number of peaks for upper conductor and middle conductor reached 13, the largest among all situations, while that for combinations with relatively greater vertical distance such as ground wire and lower conductor, was 0, i.e., much lesser. Another interesting phenomenon is that the combination of the same type of wires rarely encountered flashover, such as upper conductor and upper conductor, middle conductor and middle conductor. It was probably because they were impacted by similar wind loads at the same height.

As mentioned previously, the windage yaw flashover analysis considers the rain effect, including load effect and electric effect. Figure 14 shows the results.

Figure 14 shows the comparison between R value with rain effect and that without rain effect. Conclusions can be drawn as follows: Accompanying heavy rain during the super typhoon Rammasun significantly reduced the safety factor, R, with root mean square (RMS) obviously dropped down. For conductors/ground wires, RMS dropped down from 2.4751 to 1.6531 while that of insulator strings dropped down from 2.5721 to 1.9735. Moreover, the RMS of insulator strings was much less than 3.3642, which was calculated with static method presented in the previous section. Therefore, the rain effect cannot be ignored when studying the windage yaw flashover. On the other hand, it can be seen in Figure 14 that the RMS of the minimum R value of insulator string windage yaw is 1.9735, while the R of conductors/ground wires windage yaw is 1.6531, pointing out that conductors/ground may suffer more severe windage yaw flashover that insulator strings.

4. Conclusions and Future Study

This paper proposes a systematic method to conduct the analysis of transmission line windage yaw flashover. A case study was done on a section of 110 kV double-circuit transmission line named Baoyi II in Hainan island that suffered severe collapse when the typhoon Rammasun landed Hainan island. The conclusions in this study are drawn as follows:

• The analysis of transmission lines windage yaw flashovers was conducted using a creative systematic method proposed in the paper. The first step was to simulate the average wind, fluctuating wind, and accompanying rain loads. Then windage yaw was calculated using the finite element method with tower-line system model built up. Finally, windage flashovers danger was evaluated according to the safety factor, R, which compares the breakdown voltage of the minimum clearance, U_f, and the maximum working voltage, U_max.
• The YanMeng-PSO algorithm was creatively used to improve the simulation accuracy of average wind speed. Additionally, a new approach named KNM was proposed to calculate clearance of conductors/ground wires under strong wind and rain conditions.
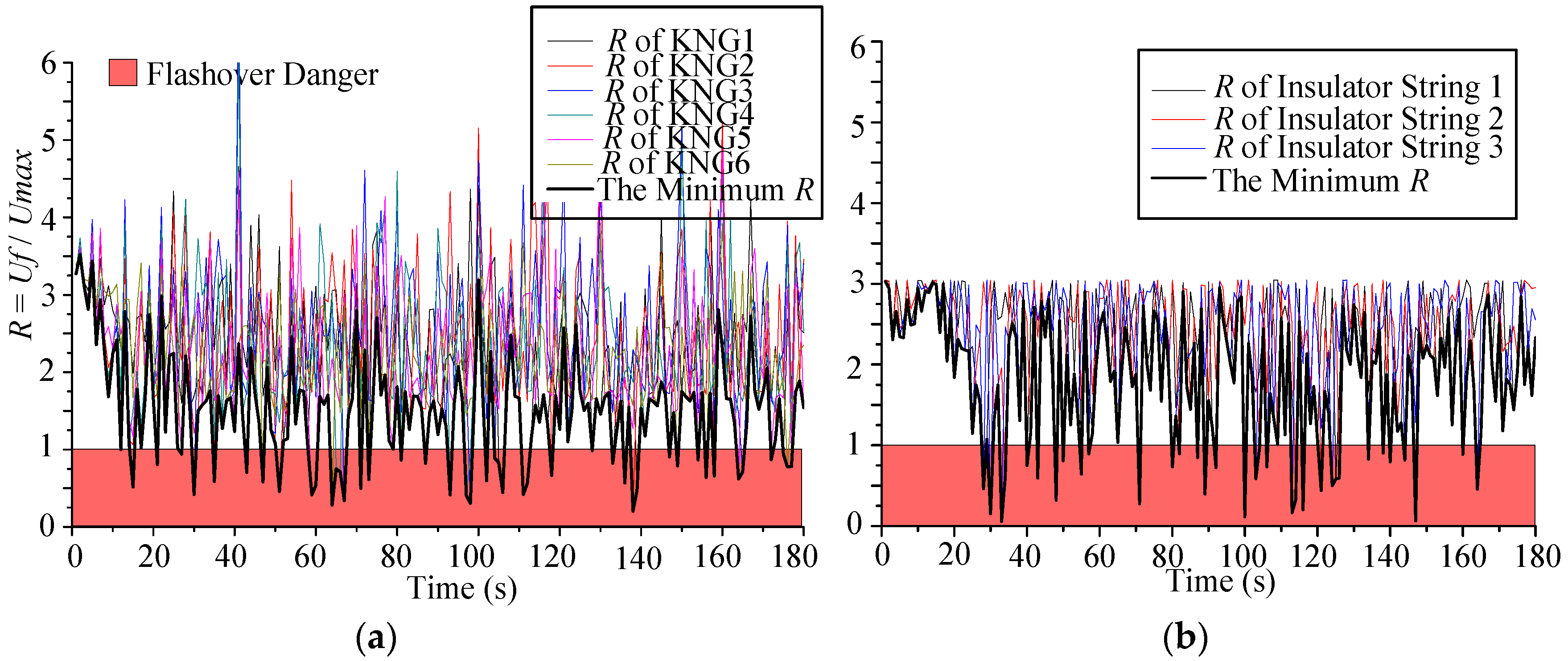
• According to the analysis results of the case study, safety factor, R, significantly reduced with rain effect. It dropped down to 1.6531 from 2.4751 for conductors/ground wires while that of insulator strings dropped down to 1.9735 from 2.5721. Therefore, it can be concluded that the heavy rain along with the strong wind has significant impact on transmission line windage yaw in two aspects. One is that raindrops increase the load acting on tower-line system, the other is that raindrops reduce the breakdown voltage of clearance by changing the ambient electric field distribution. The rain effect requires more consideration when it comes to transmission line design. However, it is quite insufficient in the present design code. The design clearance (including interphase clearance and clearance between insulator string to tower) requires appropriate increment to enhance the capacity of lines against windage yaw under wind and rain conditions.
• In the case study results, the RMS of the minimum R value of insulator string was 1.9735, greater than the R of conductors/ground wires, 1.6531. Moreover, the amount of R peaks below the safety criterion for conductors/ground wires was 34, more than that for insulator string, 29. The conclusion is thus drawn that conductors/ground wires suffer more severe windage yaw flashover than insulator strings. There are several ways to reduce the conductors/ground wires windage yaw flashovers. On the one hand, an anti-galloping device such as an interphase spacer is an effective solution reducing the swing of wires. Moreover, reasonable conductor arrangement in design phase and regular measurements and adjustments of conductor sag in maintenance phase are required to ensure that the interphase clearance is within safe arrangement.

As the mechanisms of windage yaw flashover in transmission line are not well known so far, some further study is necessary for the safety and stability of electric power system in coastal areas, maybe including: dynamic calculation of windage yaw for transmission line, windage yaw flashover analysis of bundled conductors, relation between transmission line span and windage yaw flashover.