A New Conceptual Design and Dynamic Analysis of a Spar-Type Offshore Wind Turbine Combined with a Moonpool
Abstract
:1. Introduction
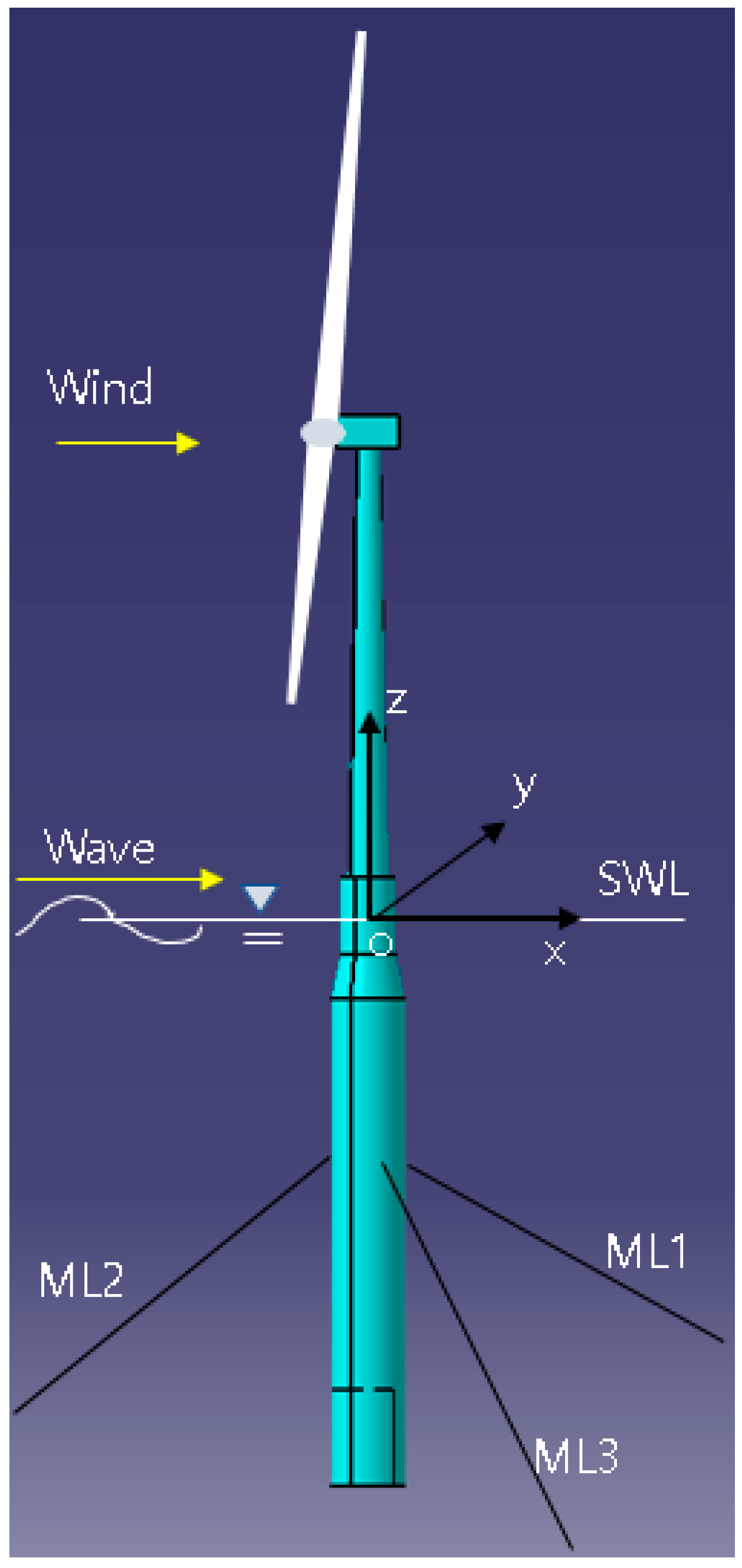
2. Model Descriptions
3. Design Process
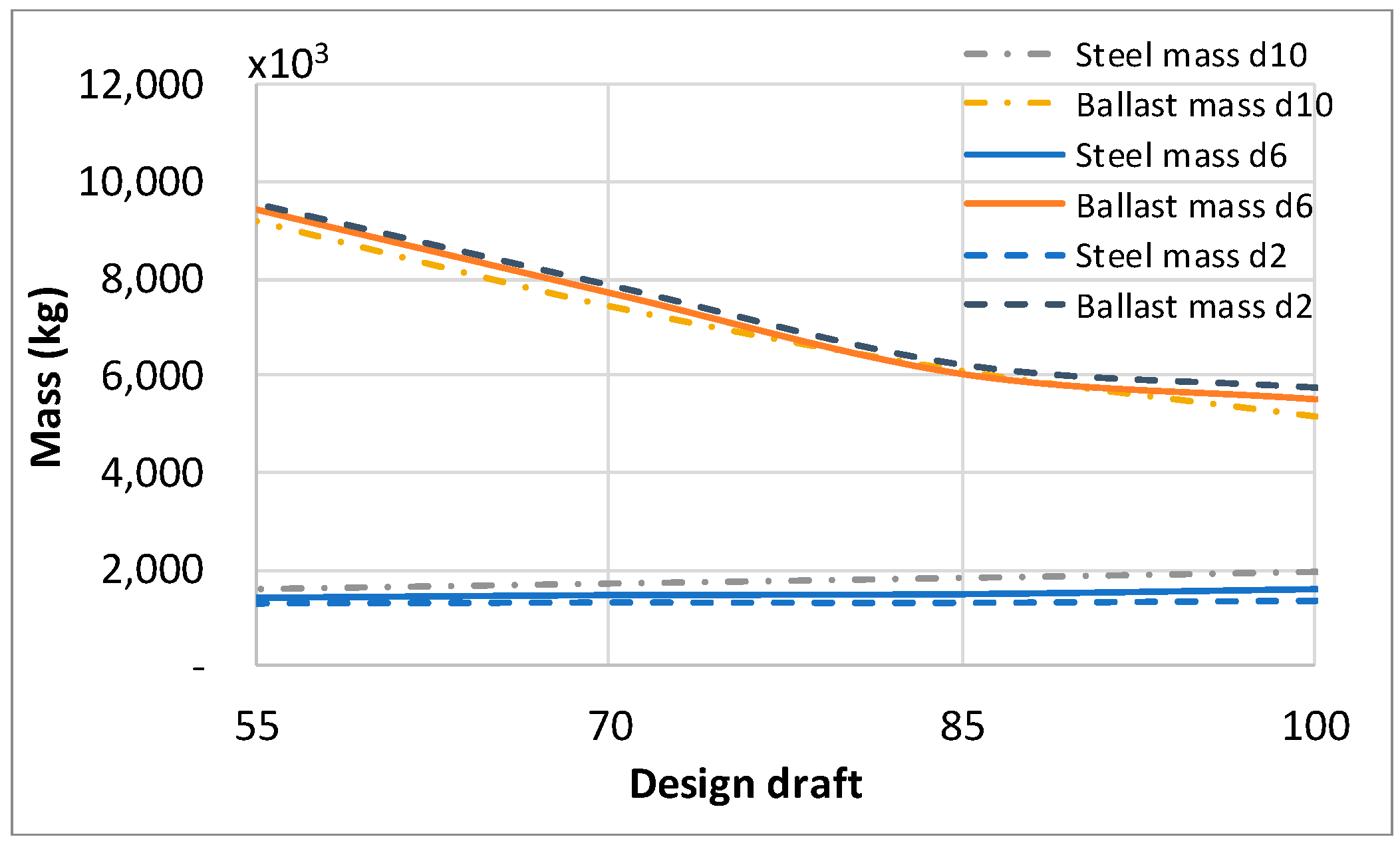
3.1. Hydrostatic Optimization
3.2. Hydrodynamic Optimization
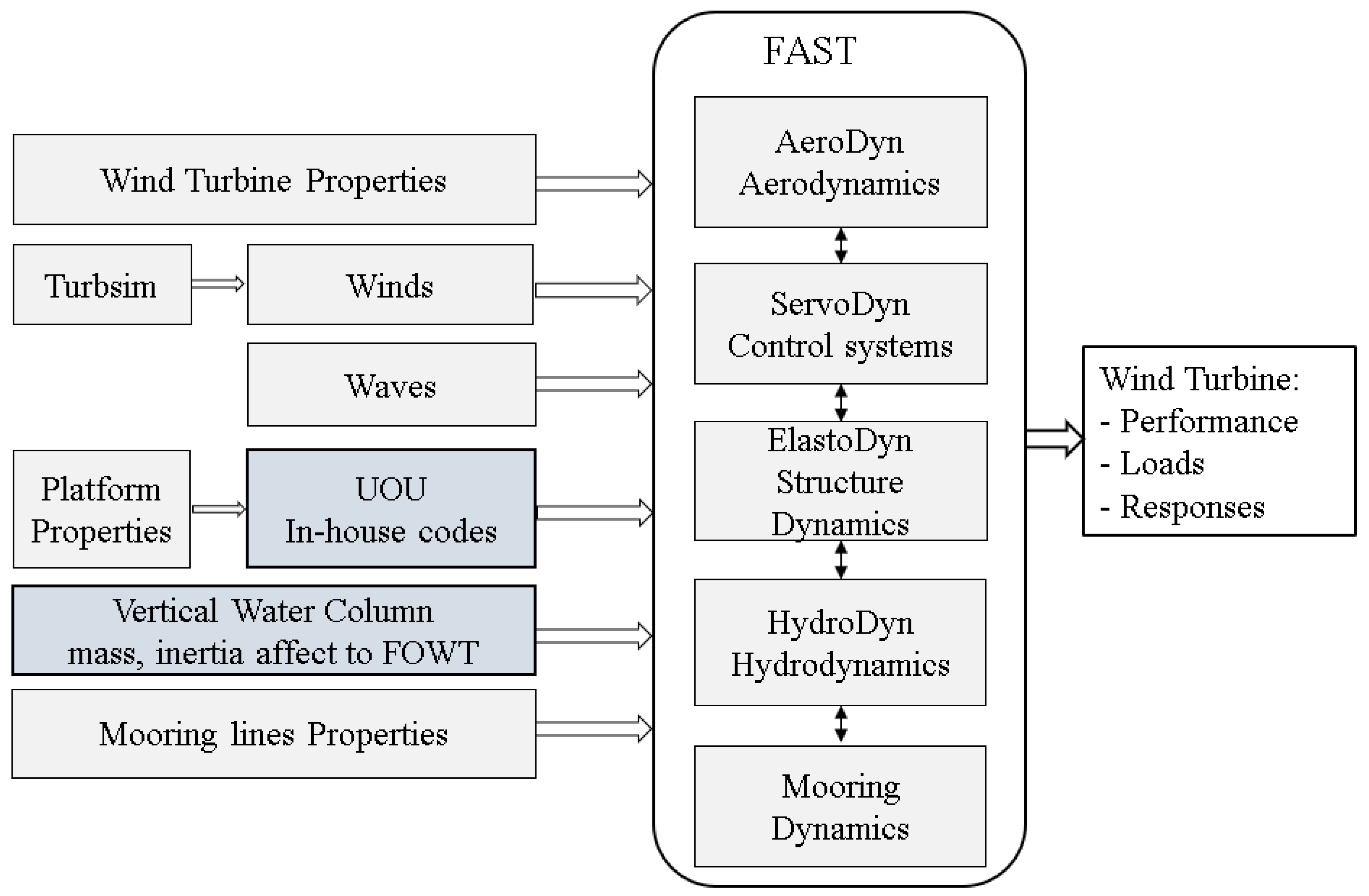
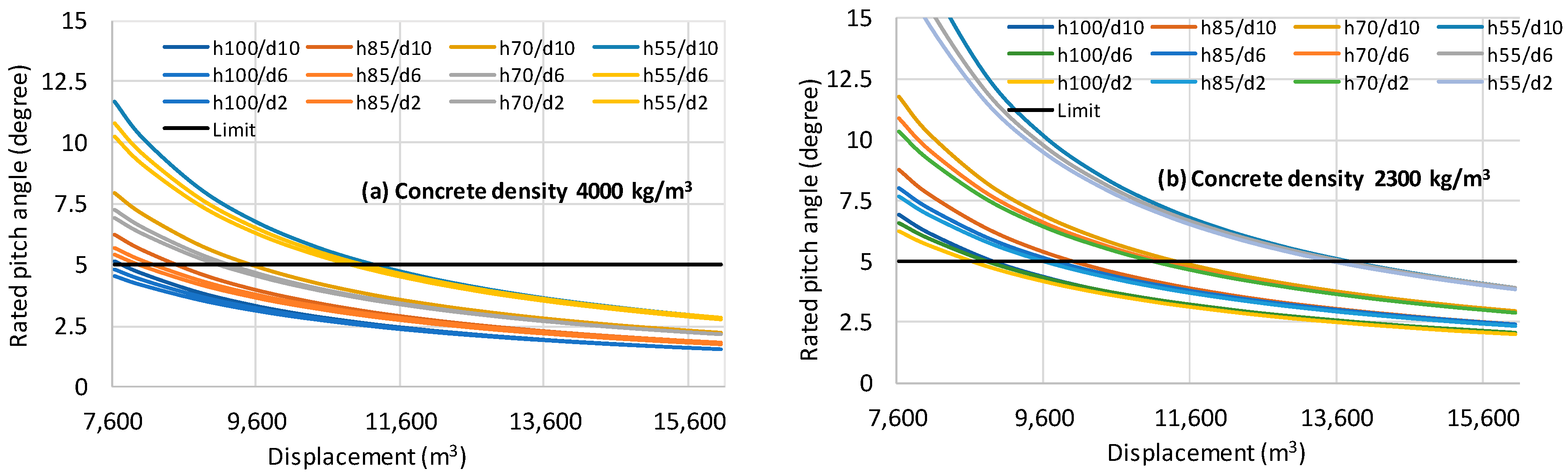
3.3. Fully Coupled Hydro-Aero-Servo-Elastic Dynamic Optimization
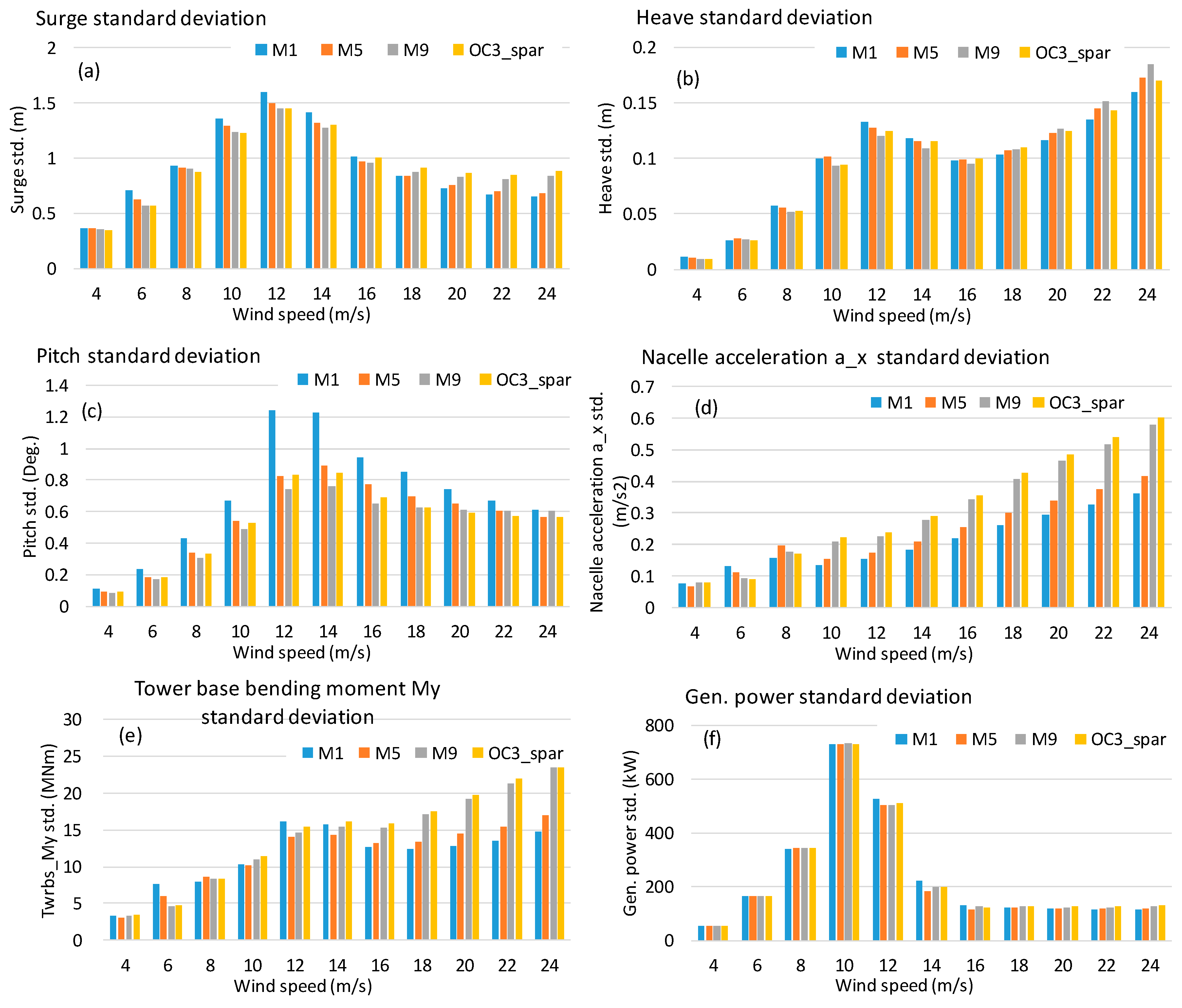
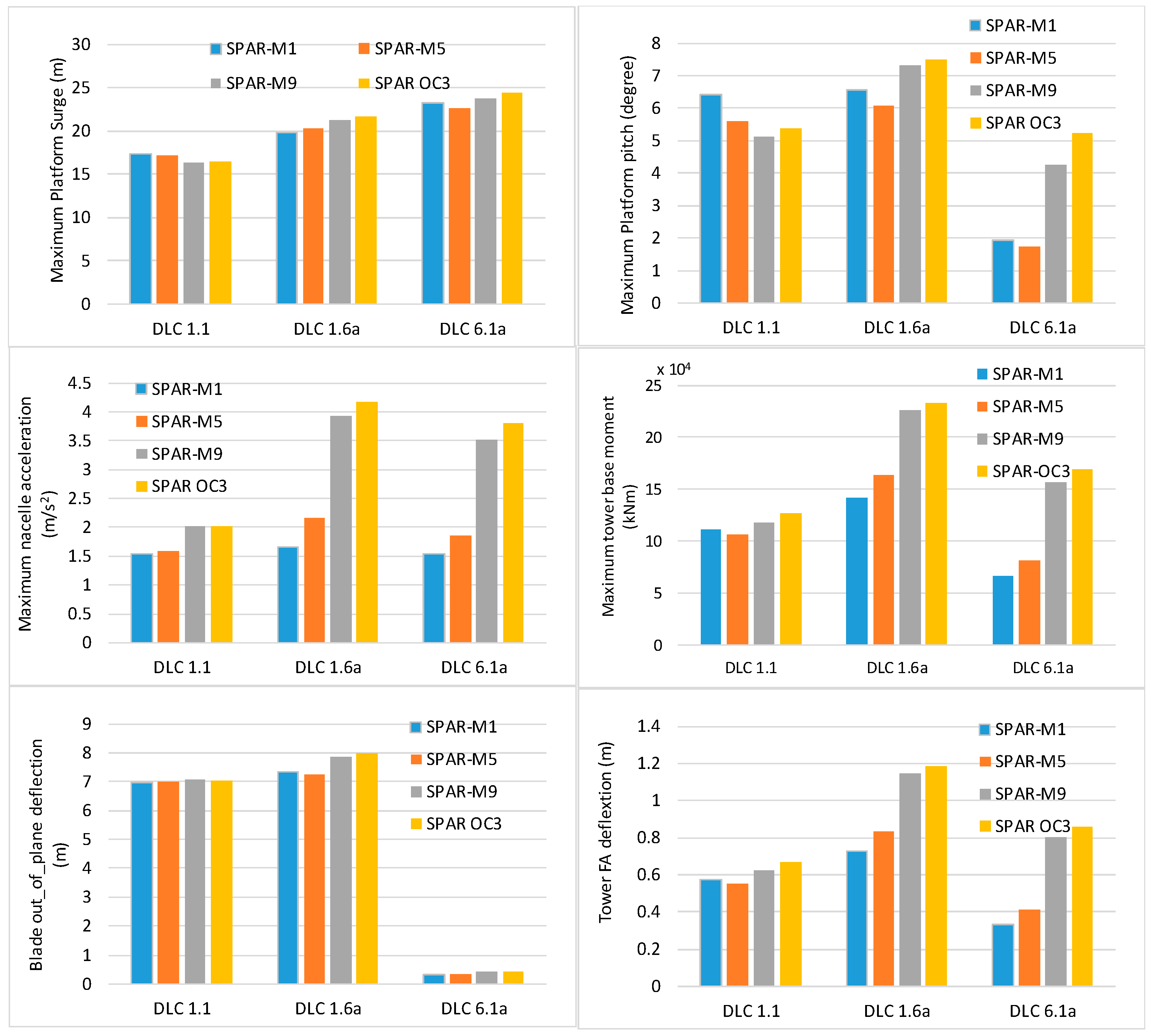
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 33104. [Google Scholar] [CrossRef]
- Fukushima Forward Fukushima Floating Offshore Wind Farm Demonstration Project; Fukushima offshore Wind Consortium: Tokyo, Japan, 2014.
- Viselli, A.M.; Goupee, A.J.; Dagher, H.J. Model Test of a 1:8-Scale Floating Wind Turbine Offshore in the Gulf of Maine1. J. Offshore Mech. Arct. Eng. 2015, 137, 041901. [Google Scholar] [CrossRef] [Green Version]
- Robertson, A.; Jonkman, J.; Masciola, M. Definition of the Semisubmersible Floating System for Phase II of OC4; Technical Report NREL/TP-5000-60601; National Renewable Energy Laboratory-NREL: Golden, CO, USA, 2014. [Google Scholar]
- Kvittem, M.I.; Berthelsen, P.A.; Eliassen, L.; Thys, M. Calibration of Hydrodynamic Coefficients for a Semi-Submersible 10 MW Wind Turbine. ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers Digital Collection: 2018; V010T09A080. Available online: https://asmedigitalcollection.asme.org/OMAE/proceedings-abstract/OMAE2018/51319/V010T09A080/278216 (accessed on 1 September 2019).
- Berthelsen, P.A.; Bachynski, E.E.; Karimirad, M.; Thys, M. Real-Time Hybrid Model Tests of a Braceless Semi-Submersible Wind Turbine: Part III—Calibration of a Numerical Model. ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers Digital Collection: 2016; V006T09A047. Available online: https://asmedigitalcollection.asme.org/OMAE/proceedings-abstract/OMAE2016/49972/V006T09A047/281295 (accessed on 1 September 2019).
- Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in semi-submersible floating foundations supporting wind turbines: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 60, 433–449. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Moan, T. Design considerations for tension leg platform wind turbines. Mar. Struct. 2012, 29, 89–114. [Google Scholar] [CrossRef]
- Oguz, E.; Clelland, D.; Day, A.H.; Incecik, A.; López, J.A.; Sánchez, G.; Almeria, G.G. Experimental and numerical analysis of a TLP floating offshore wind turbine. Ocean Eng. 2018, 147, 591–605. [Google Scholar] [CrossRef] [Green Version]
- Kausche, M.; Adam, F.; Dahlhaus, F.; Großmann, J. Floating offshore wind—Economic and ecological challenges of a TLP solution. Renew. Energy 2018, 126, 270–280. [Google Scholar] [CrossRef]
- Jonkman, J. Definition of the Floating System for Phase IV of OC3; Technical Report NREL/TP-500-47535; National Renewable Energy Laboratory-NREL: Golden, CO, USA, 2010. [Google Scholar]
- Bredmose, H.; Lemmer, F.; Borg, M.; Pegalajar-Jurado, A.; Mikkelsen, R.F.; Larsen, T.S.; Fjelstrup, T.; Yu, W.; Lomholt, A.K.; Boehm, L.; et al. The Triple Spar campaign: Model tests of a 10MW floating wind turbine with waves, wind and pitch control. Energy Procedia 2017, 137, 58–76. [Google Scholar] [CrossRef] [Green Version]
- Utsunomiya, T.; Matsukuma, H.; Minoura, S.; Ko, K.; Hamamura, H.; Kobayashi, O.; Sato, I.; Nomoto, Y.; Yasui, K. On Sea Experiment of a Hybrid SPAR for Floating Offshore Wind Turbine Using 1/10 Scale Model. J. Offshore Mech. Arct. Eng. 2013, 135, 034503. [Google Scholar] [CrossRef]
- Shin, H.; Dam, P.T.; Jung, K.J.; Song, J.; Rim, C.; Chung, T. Model test of new floating offshore wind turbine platforms. Int. J. Nav. Archit. Ocean Eng. 2013, 5, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Shin, H.; Lee, W.; Jung, K.; Kim, J. Model test and simulation of modified spar type floating offshore wind turbine with three catenary mooring lines. J. Renew. Sustain. Energy 2014, 6, 042009. [Google Scholar] [CrossRef]
- Skaare, B. Development of the Hywind Concept. In 2017 36th International Conference on Ocean, Offshore and Arctic Engineering; American Society of Mechanical Engineers Digital Collection: 2017; V009T12A050; Available online: https://asmedigitalcollection.asme.org/OMAE/proceedings-abstract/OMAE2017/57779/V009T12A050/279375 (accessed on 1 September 2019).
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory-NREL: Golden, CO, USA, 2009. [Google Scholar]
- Matha, D. Model Development and Loads Analysis of an Offshore Wind Turbine on a Tension Leg Platform with a Comparison to Other Floating Turbine Concepts; National Renewable Energy Laboratory-NREL: Golden, CO, USA, 2009. [Google Scholar]
- Jonkman, J.M.; Matha, D. Dynamics of offshore floating wind turbines—Analysis of three concepts. Wind Energy 2011, 14, 557–569. [Google Scholar] [CrossRef]
- Goupee, A.J.; Koo, B.J.; Kimball, R.W.; Lambrakos, K.F.; Dagher, H.J. Experimental Comparison of Three Floating Wind Turbine Concepts. J. Offshore Mech. Arct. Eng. 2014, 136, 020906. [Google Scholar] [CrossRef]
- DNV.GL. DNVGL-OS-E302 Offshore Mooring Chain; DNV-GL: Oslo, Norway, 2015. [Google Scholar]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1994; ISBN 0521372852. [Google Scholar]
- Jonkman, B.; Jonkman, J. FAST v8. 2018. Available online: https://nwtc.nrel.gov/FAST8 (accessed on 27 July 2016).
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; National Renewable Energy Laboratory-NREL: Golden, CO, USA, 2005. [Google Scholar]
- International Electrotechnical Commission. IEC 61400-3-2, Wind Energy Generation System—Part 3-2: Design Requirements for Floating Offshore Wind Turbines; Technical Specification; IEC: Geneva, Switzerland, 2019; ISBN 978-2-8322-5986-3. [Google Scholar]
- Jonkman, B.J. TurbSim User’s Guide v2. 00.00; National Renewable Energy Laboratory-NREL: Golden, CO, USA, 2014. [Google Scholar]







| Parameter | Unit | Value |
|---|---|---|
| Design Water Depth | m | 150 |
| Wind Turbine Rated Power | MW | 5 |
| Hub Height | m | 90 |
| Cut-In, Rated, and Cut-Out Wind Speeds | m/s | 3, 11.4, 25 |
| Rotor Mass | kg | 110,000 |
| Nacelle Mass | kg | 240,000 |
| Tower Mass (for offshore) | kg | 249,718 |
| Vertical Center of Mass (CM) of Wind Turbine (Rotor, Nacelle, and Tower) | m | 70.34 |
| Parameter | Unit | Value |
|---|---|---|
| Number of Mooring Lines | - | 3 |
| Angle Between Adjacent Lines | Degree | 120 |
| Depth to Anchors Below Sea Water Level (SWL) (Water Depth) | m | 150 |
| Depth to Fairleads Below SWL | m | 41 |
| Distance from Fairlead to Anchor | m | 939 |
| Unstretched Mooring Line Length | m | 970 |
| Mooring Chain Common Link Diameter | mm | 90 |
| Mooring Line Mass Density in Air | kg/m | 178 |
| Mooring Line Weight in Water (μ) | N/m | 1518.8 |
| Mooring Line Extensional Stiffness | MN | 729.0 |
| Minimum Breaking Load (MBL) | MN | 6.65 |
| Total Weight Effect of Three Mooring Lines in Static Condition | kgf | 120,946 |
| Item | DLC 1.1 | DLC 1.6a | DLC 6.1a |
|---|---|---|---|
| Wind | NTM | NTM | EWM |
| Waves | NSS | SSS | ESS |
| Wind and wave directionality | 0°, COD | 0°, COD | 0°, COD, Yaw ±8°, 0° |
| Current | NCM | NCM | ECM |
| Wind turbine status | Operation | Operation | Parked, blades:90° |
| Sea State | Mean Wind Speed at Hub (m/s) | Irregular Wave | Current Speed (m/s) | |
|---|---|---|---|---|
| Hs (m) | Tp (s) | |||
| 1 | 4 | 0.78 | 6.20 | 0.37 |
| 2 | 6 | 0.78 | 6.20 | 0.37 |
| 3 | 8 | 0.80 | 6.22 | 0.37 |
| 4 | 10 | 0.94 | 6.32 | 0.37 |
| 5 | 12 | 1.60 | 6.83 | 0.37 |
| 6 | 14 | 2.26 | 7.34 | 0.37 |
| 7 | 16 | 2.92 | 7.85 | 0.37 |
| 8 | 18 | 3.58 | 8.36 | 0.37 |
| 9 | 20 | 4.25 | 8.87 | 0.37 |
| 10 | 22 | 4.91 | 9.38 | 0.37 |
| 11 | 24 | 5.57 | 9.89 | 0.37 |
| 12 | 39.5 | 11.57 | 14.52 | 1.63 |
| Model/Parameter | Displacement | h | d1 | d2 | d | Platform Mass | Platform CM |
|---|---|---|---|---|---|---|---|
| (m3) | (m) | (m) | (m) | (m) | (Ton) | (m) | |
| M1 | 7627.55 | 100.00 | 11.93 | 14.22 | 10.00 | 7097.33 | −79.63 |
| M2 | 8430.45 | 85.00 | 11.93 | 15.34 | 10.00 | 7920.31 | −69.22 |
| M3 | 9634.80 | 70.00 | 11.93 | 17.12 | 10.00 | 9154.77 | −58.26 |
| M4 | 11,240.60 | 55.00 | 11.93 | 19.98 | 10.00 | 10,800.71 | −46.74 |
| M5 | 7627.55 | 100.00 | 8.85 | 11.75 | 6.00 | 7097.33 | −81.56 |
| M6 | 8430.45 | 85.00 | 8.85 | 13.09 | 6.00 | 7920.31 | −70.45 |
| M7 | 9634.80 | 70.00 | 8.85 | 15.14 | 6.00 | 9154.77 | −58.99 |
| M8 | 11,240.60 | 55.00 | 8.85 | 18.33 | 6.00 | 10,800.71 | −47.15 |
| M9 | 7627.55 | 100.00 | 6.80 | 10.30 | 2.00 | 7097.33 | −82.71 |
| M10 | 8430.45 | 85.00 | 6.80 | 11.81 | 2.00 | 7920.31 | −71.18 |
| M11 | 9634.80 | 70.00 | 6.80 | 14.06 | 2.00 | 9154.77 | −59.43 |
| M12 | 11,240.60 | 55.00 | 6.80 | 17.46 | 2.00 | 10,800.71 | −47.40 |
| Natural Frequencies | Unit | M1 | M5 | M9 | OC3-Hywind | ||||
|---|---|---|---|---|---|---|---|---|---|
| Cal. | Sim. | Cal. | Sim. | Cal. | Sim. | Cal. | Sim. | ||
| Surge | Hz | - | 0.006 | - | 0.007 | - | 0.008 | - | 0.0085 |
| Heave | Hz | 0.032 | 0.032 | 0.032 | 0.032 | 0.033 | 0.033 | 0.032 | 0.033 |
| Pitch | Hz | 0.023 | 0.021 | 0.029 | 0.027 | 0.033 | 0.035 | 0.033 | 0.032 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.D.; Shin, H. A New Conceptual Design and Dynamic Analysis of a Spar-Type Offshore Wind Turbine Combined with a Moonpool. Energies 2019, 12, 3737. https://doi.org/10.3390/en12193737
Pham TD, Shin H. A New Conceptual Design and Dynamic Analysis of a Spar-Type Offshore Wind Turbine Combined with a Moonpool. Energies. 2019; 12(19):3737. https://doi.org/10.3390/en12193737
Chicago/Turabian StylePham, Thanh Dam, and Hyunkyoung Shin. 2019. "A New Conceptual Design and Dynamic Analysis of a Spar-Type Offshore Wind Turbine Combined with a Moonpool" Energies 12, no. 19: 3737. https://doi.org/10.3390/en12193737
APA StylePham, T. D., & Shin, H. (2019). A New Conceptual Design and Dynamic Analysis of a Spar-Type Offshore Wind Turbine Combined with a Moonpool. Energies, 12(19), 3737. https://doi.org/10.3390/en12193737






