The Band Structures of Zn1?xMgxO(In) and the Simulation of CdTe Solar Cells with a Zn1?xMgxO(In) Window Layer by SCAPS
Abstract
:1. Introduction
2. Theoretical Model and Computational Methods
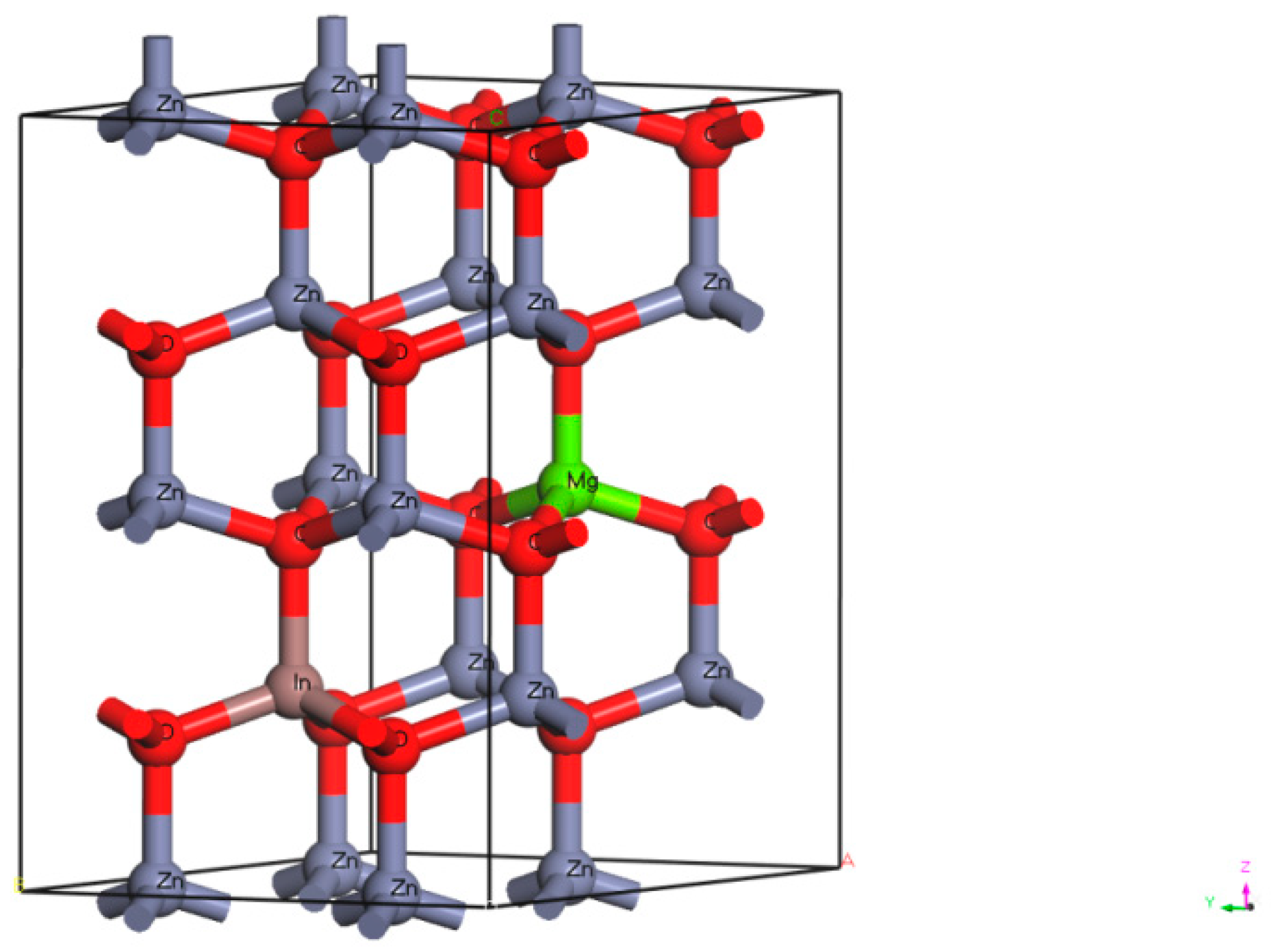
2.1. ZMO:In Model and Computational Method
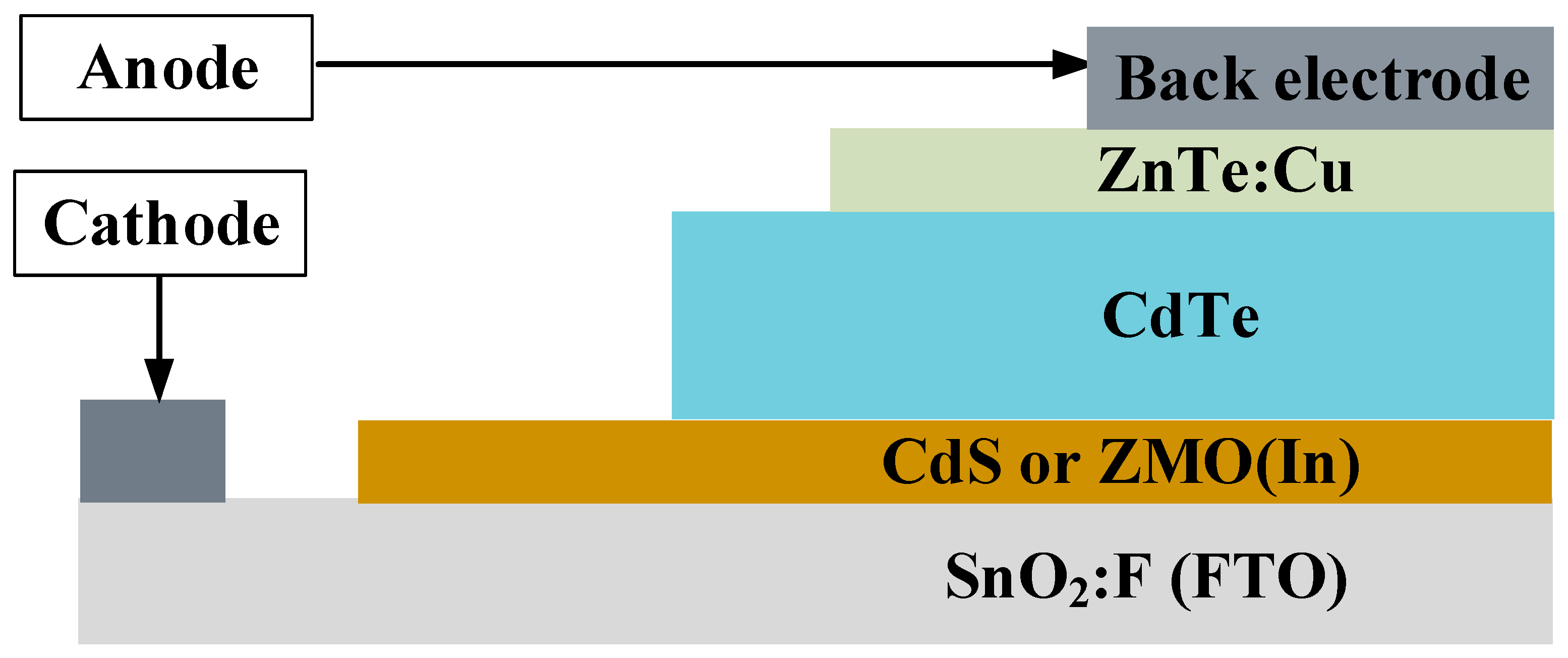
2.2. CdTe Solar Cell Model and Simulation
3. Results and discussion
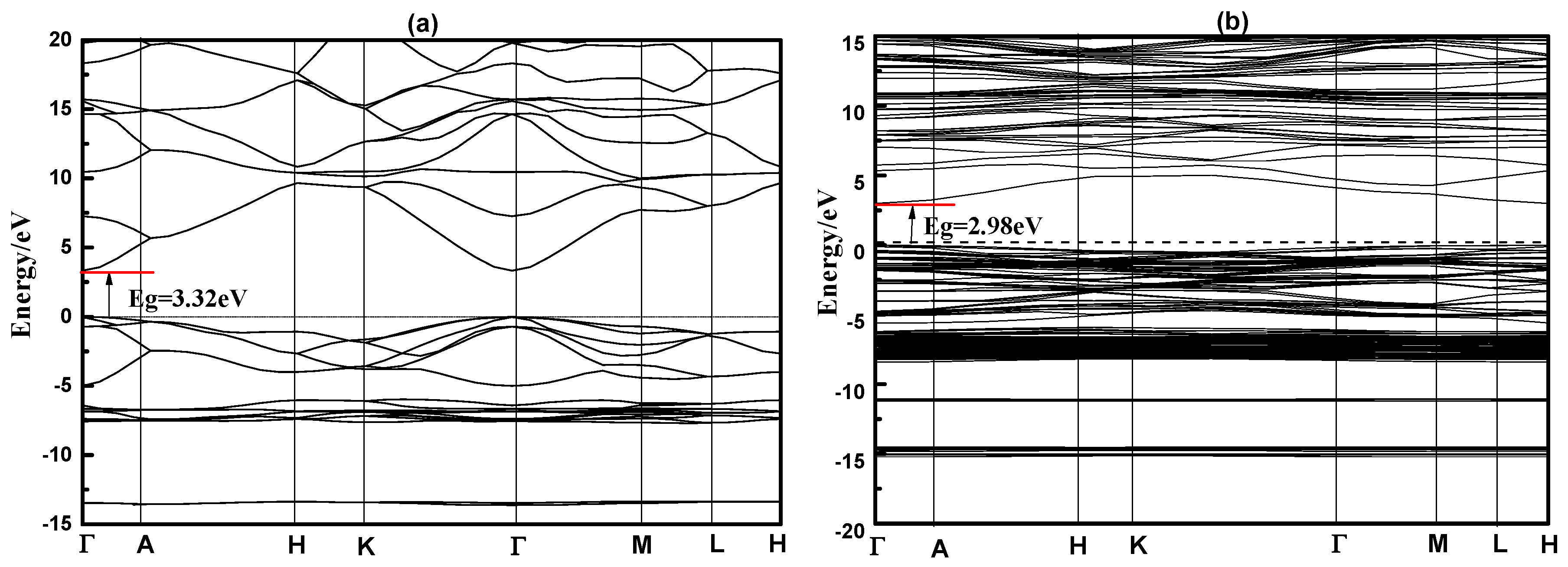
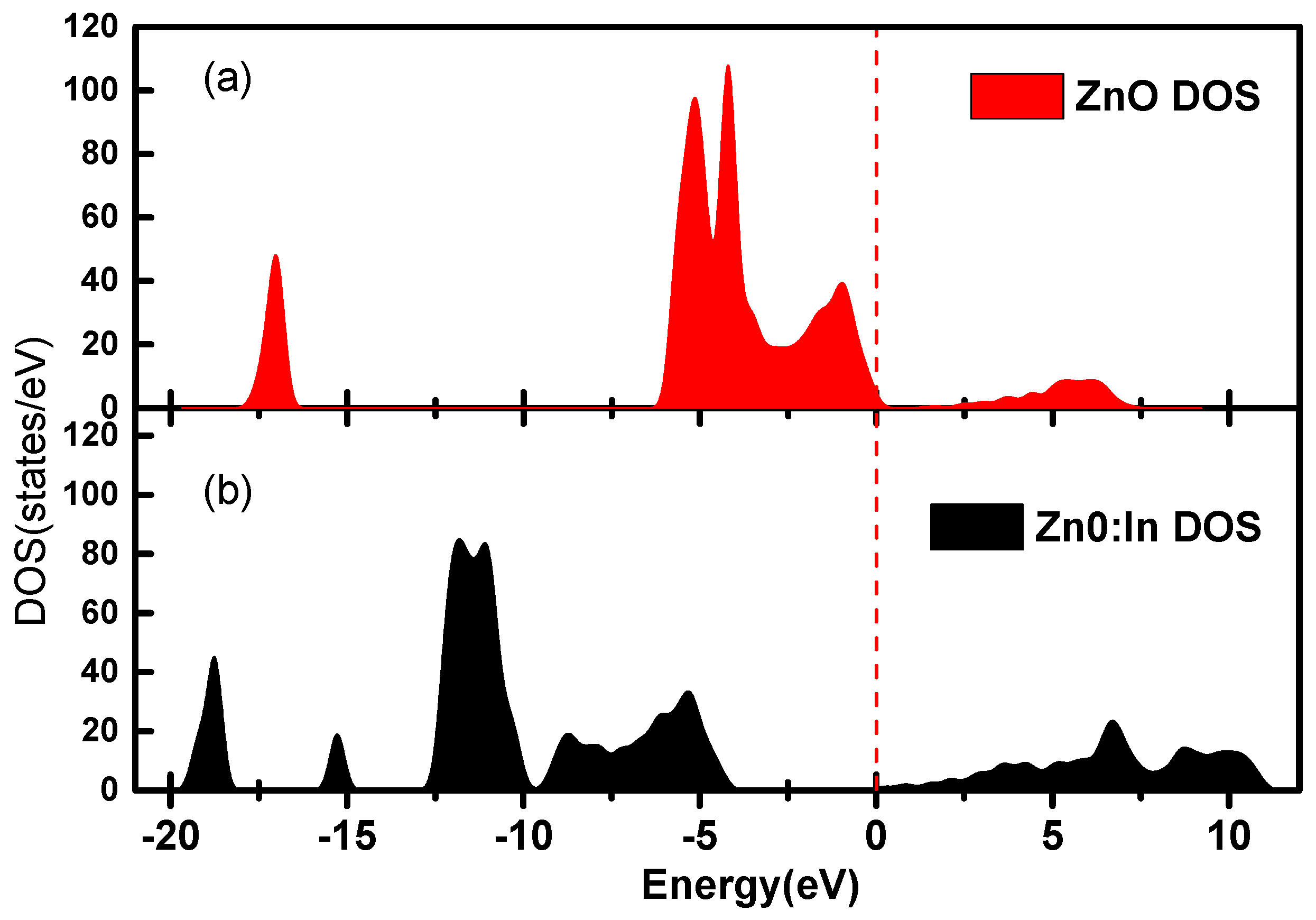
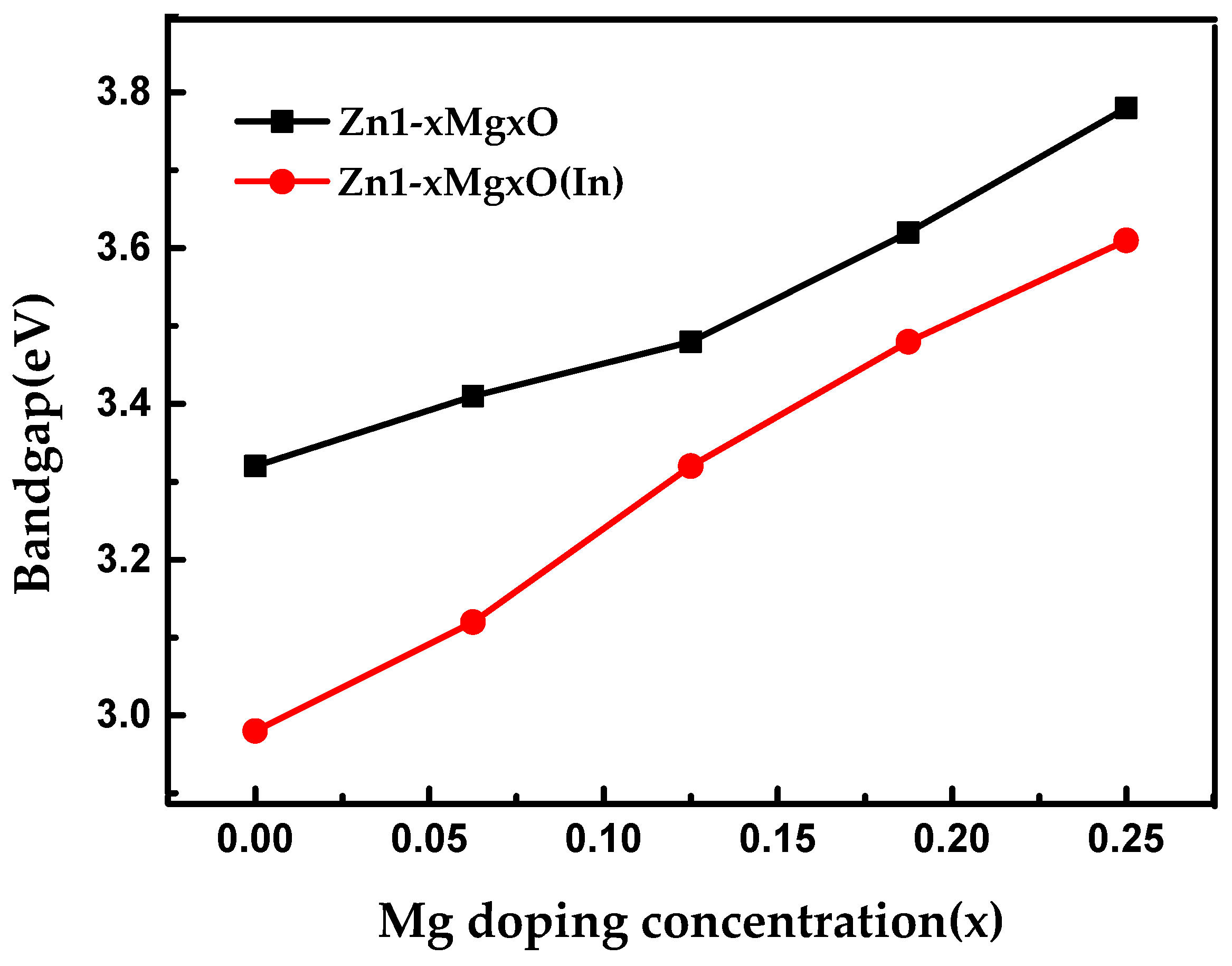
3.1. The Band Structure of ZMO:In
3.2. The Photovoltaic Applications of ZMO:In
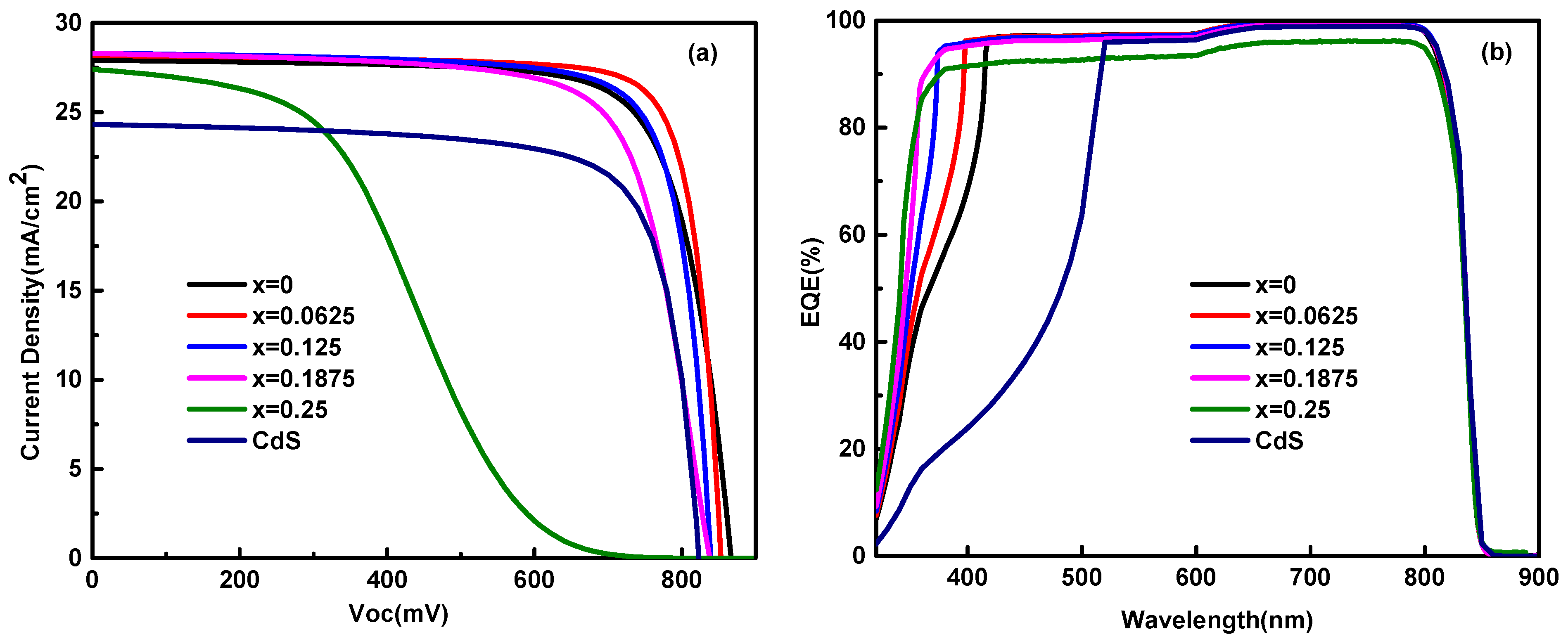
3.2.1. The Performance of CdTe Solar Cells with ZMO:In Window Layers
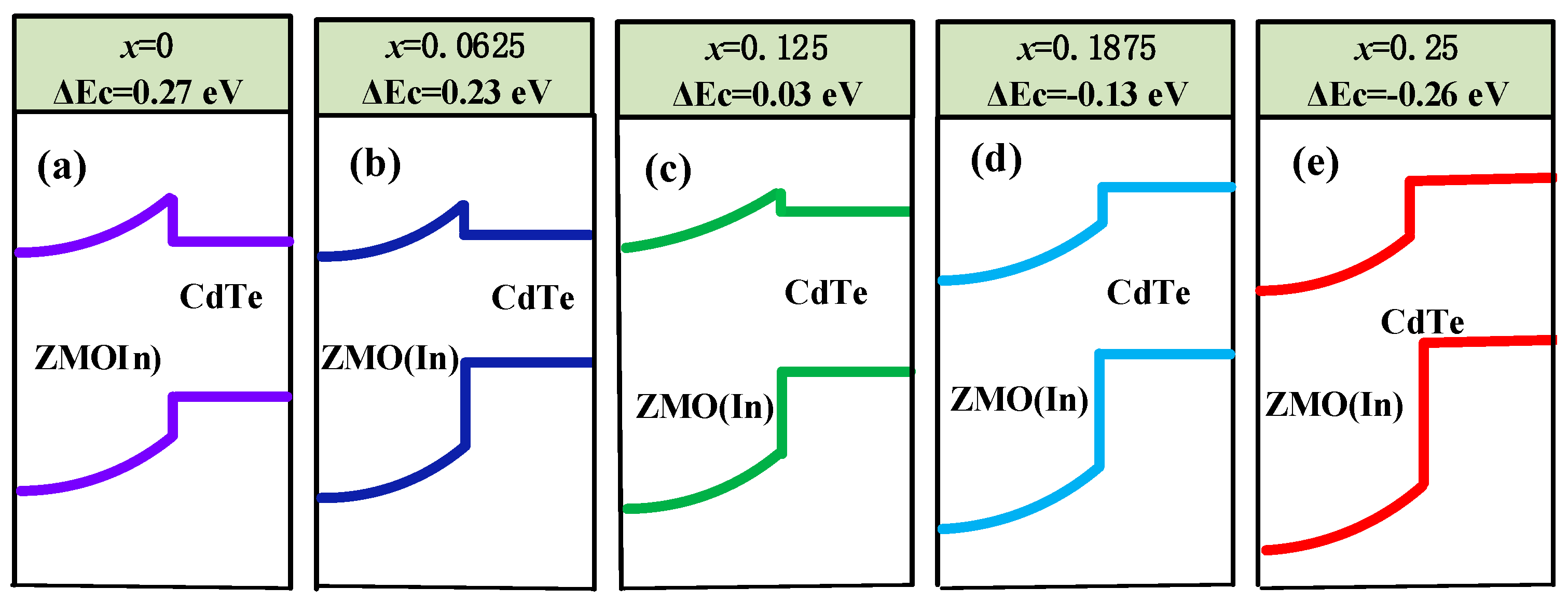
3.2.2. The Energy Band Alignment of the ZMO:In/CdTe Interface
3.2.3. Effect of ZMO:In (x = 0.0625) Thickness on CdTe Solar Cells Performances
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cruz, L.R.; Pinheiro, W.A.; Medeiro, R.A.; Ferreira, C.L.; Dhere, R.G.; Duenow, J.N. Influence of heat treatment and back contact processing on the performance of CdS/CdTe thin film solar cells produced in a CSS in-line system. Vacuum 2013, 87, 45–49. [Google Scholar] [CrossRef]
- Kephart, J.M.; Geisthardt, R.M.; Sampath, W.S. Optimization of CdTe thin-film solar cell efficiency using a sputtered, oxygenated CdS window layer. Prog. Photovolt. Res. Appl. 2015, 23, 1484–1492. [Google Scholar] [CrossRef]
- Marjani, S.; Khosroabadi, S.; Sabaghi, M.A. High Efficiency Ultrathin CdTe Solar Cell for Nano-Area Applications. Opt. Photonics J. 2016, 6, 15–23. [Google Scholar] [CrossRef]
- Paudel, N.R.; Yan, Y. Enhancing the photo-currents of CdTe thin-film solar cells in both short and long wavelength regions. Appl. Phys. Lett. 2014, 105, 606–3911. [Google Scholar] [CrossRef]
- Green, M.A.; Hishikawa, Y.; Dunlop, E.D.; Levi, D.H.; Hohl-Ebinger, J.; Yoshita, M.; Ho-Baillie, A.W. Solar cell efficiency tables (Version 53). Prog. Photovolt. Res. Appl. 2018, 27, 3–12. [Google Scholar] [CrossRef]
- Korevaar, B.A.; Cournoyer, J.R.; Sulima, O.; Yakimov, A.; Johnson, J.N. Role of oxygen during CdTe growth for CdTe photovoltaic devices. Prog. Photovolt. Res. Appl. 2015, 22, 1040–1049. [Google Scholar] [CrossRef]
- Colegrove, E.; Blissett, C.; Buurma, C.; Ellsworth, J.; Morley, M. High-Efficiency Polycrystalline CdS/CdTe Solar Cells on Buffered Commercial TCO-Coated Glass. J. Electron. Mater. 2012, 41, 2833–2837. [Google Scholar] [CrossRef]
- Martin, A.; Emery, K. Solar cell efficiency tables (version 42). Prog. Photovolt. Res. Appl. 2013, 21, 827–837. [Google Scholar] [Green Version]
- Peelaers, H.; Kioupakis, E.; Van de Walle, C.G. Fundamental limits on optical transparency of transparent conducting oxides: Free-carrier absorption in SnO2. Appl. Phys. Lett. 2012, 100, 011914. [Google Scholar] [CrossRef]
- Yi, K.; Lany, S.; Berry, J.J.; Perkins, J.D.; Parilla, P.A. Enhanced Electron Mobility Due to Dopant-Defect Pairing in Conductive ZnMgO. Adv. Funct. Mater. 2014, 24, 2875–2882. [Google Scholar]
- Kephart, J.M.; McCamy, J.W.; Ma, Z.; Ganjoo, A.; Alamgir, F.M.; Sampath, W.S. Band alignment of front contact layers for high-efficiency CdTe solar cells. Sol. Energy Mater. Sol. Cells 2016, 157, 266–275. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Song, Y.H.; Wu, L.L.; Li, C.X.; Zhang, J.Q.; Feng, L.H. Simulation of high-efficiency CdTe solar cells with Zn1−xMgxO window layer by SCAPS software. Mater. Res. Express 2018, 5, 065907. [Google Scholar] [CrossRef]
- Minemoto, T.; Hashimoto, Y.; Satoh, T.; Negami, T.; Takakura, H.; Hamakawa, Y. Cu(In,Ga)Se2 solar cells with controlled conduction band offset of window/Cu(In,Ga)Se2 layers. J. Appl. Phys. 2001, 89, 8327–8330. [Google Scholar] [CrossRef]
- Pettersson, J.; Platzer, B.; Rkman, C.; Zimmermann, U. Baseline model of graded-absorber Cu(In,Ga)Se2 solar cells applied to cells with Zn1−xMgxO buffer layers. Thin Solid Films 2011, 519, 7476–7480. [Google Scholar] [CrossRef]
- Minemoto, T.; Matsui, T.; Takakura, H.; Hamakawa, Y.; Negami, T.; Hashimoto, Y.; Uenoyama, T.; Kitagawa, M. Theoretical analysis of the effect of conduction band offset of window/CIS layers on performance of CIS solar cells using device simulation. Sol. Energy Mater. Sol. Cells 2001, 67, 83–88. [Google Scholar] [CrossRef]
- Patel, M.; Ray, A. Enhancement of output performance of Cu2ZnSnS4 thin film solar cells—A numerical simulation approach and comparison to experiments. Phys. B Condens. Matter 2012, 407, 4391–4397. [Google Scholar] [CrossRef]
- Olopade, M.A.; Oyebola, O.O.; Adeleke, B.S. Investigation of some materials as buffer layer in copper zinc tin sulphide (Cu2ZnSnS4) solar cells by SCAPS-1D. Adv. Appl. Sci. Res. 2012, 3, 3396–3400. [Google Scholar]
- Clayton, A.J.; Carlo, V.D.; Irvine, S.J.C. Investigation into ultrathin CdTe solar cell Voc using SCAPS modelling. Mater. Res. Innov. 2014, 18, 505–508. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.H.; Chuang, W.J. Dependence of performance parameters of CdTe solar cells on semiconductor properties studied by using SCAPS-1D. Vacuum 2015, 118, 32–37. [Google Scholar] [CrossRef]
- He, X.; Ren, S.Q.; Li, C.X.; Wu, L.L.; Zhang, J.Q.; Du, Z. Zn1−xMgxO: Band Structure and Simulation as Window Layer for CdTe Solar Cell by SCAPS Software. J. Inorg. Mater. 2018, 33, 635–640. [Google Scholar]
- Wang, T.; Ren, S.; Li, C.; Li, W.; Liu, C.; Zhang, J.; Wu, L.; Li, B.; Zeng, G. Exploring window buffer layer technology to enhance CdTe solar cell performance. Sol. Energy 2018, 164, 180–186. [Google Scholar] [CrossRef]
- Ke, Y.; Berry, J.; Parilla, P.; Zakutayev, A.; O’Hayre, R.; Ginley, D. The origin of electrical property deterioration with increasing Mg concentration in ZnMgO:Ga. Thin Solid Films 2012, 520, 3697–3702. [Google Scholar] [CrossRef]
- Matsubara, K.; Tampo, H.; Shibata, H.; Yamada, A.; Fons, P.; Iwata, K.; Niki, S. Band-gap modified Al-doped Zn1−xMgxO transparent conducting films deposited by pulsed laser deposition. Appl. Phys. Lett. 2004, 85, 1374–1376. [Google Scholar] [CrossRef]
- Senthil, T.S.; Muthukumarasamy, N.; Kang, M. Improved performance of ZnO thin film solar cells by doping magnesium ions. J. Mater. Sci. Mater. Electron. 2013, 24, 3963–3969. [Google Scholar] [CrossRef]
- Zhu, Y.Z.; Chen, G.D.; Ye, H. Electronic Structure and Phase Stability of MgO, ZnO, CdO, and Related Ternary Alloys. Phys. Rev. B 2008, 77, 245209. [Google Scholar] [CrossRef]
- Tampo, H.; Yamada, A.; Fons, P. Degenerate layers in epitaxial ZnO films grown on sapphire substrates. Appl. Phys. Lett. 2004, 84, 4412–4414. [Google Scholar] [CrossRef]
- Si, X.; Liu, Y.; Lei, W. First-principles investigation on the optoelectronic performance of Mg doped and Mg–Al co-doped ZnO. Mater. Des. 2016, 93, 128–132. [Google Scholar] [CrossRef]
- Sheetz, R.M.; Ponomareva, I.; Richter, E.; Andriotis, A.N.; Menon, M. Defect-induced optical absorption in the visible range in ZnO nanowires. Phys. Rev. B Condens. Matter 2009, 80, 195314. [Google Scholar] [CrossRef]
- Zhang, J.Q. Study on CdTe and Related Compound Polycrystalline Thin Films as well as CdTe Solar Cell. Ph.D. Thesis, Sichuan University, Chengdu, China, 2002. [Google Scholar]
- Paul, B.; Singh, B.; Ghosh, S.; Roy, A. A comparative study on electrical and optical properties of group III (Al, Ga, In) doped ZnO. Thin Solid Film 2016, 603, 21–28. [Google Scholar] [CrossRef]
- Han, J.F.; Spanheimer, C.; Haindl, G.; Fu, G.H.; Krishnakumar, V. Optimized chemical bath deposited CdS layers for the improvement of CdTe solar cells. Sol. Energy Mater. Sol. Cells 2011, 95, 816–820. [Google Scholar] [CrossRef]
- Ichikawa, M.; Suto, E.; Jeon, H.G. Sensitization of organic photovoltaic cells based on interlayer excitation energy transfer. Org. Electron. 2010, 11, 700–704. [Google Scholar] [CrossRef] [Green Version]
- Niles, D.W.; Hartmut, H. Band offsets and interfacial properties of cubic CdS grown by molecular-beam epitaxy on CdTe(110). Phys. Rev. B Condens. Matter 1990, 41, 12710–12719. [Google Scholar] [CrossRef] [PubMed]

| Layer Parameters | FTO [19] | CdS [14,19,29] | Zn1−xMgxO(In) [20,29] | CdTe [29] | ZnTe:Cu [29] | ||||
|---|---|---|---|---|---|---|---|---|---|
| x = 0 | x = 0.0625 | x = 0.125 | x = 0.1875 | x = 0.25 | |||||
| Eg/eV | 3.6 | 2.4 | 2.98 | 3.12 | 3.32 | 3.48 | 3.61 | 1.45 | 2.26 |
| ε/ε0 | 8.9 | 9 | 10 | 10 | 10 | 10 | 10 | 10 | 10.1 |
| Nc/cm−3 | 5.2 × 1018 | 2.2 × 1018 | 5 × 1018 | 9 × 1017 | 1 × 1017 | 9 × 1016 | 1 × 1016 | 9.2 × 1017 | 1.5 × 1018 |
| Nv/cm−3 | 1.0 × 1019 | 1.8 × 1019 | 9 × 1018 | 9 × 1018 | 1 × 1018 | 9 × 1017 | 1 × 1017 | 5.2 × 1018 | 1.16 × 1019 |
| Ve/cm.s−1 | 1.0 × 107 | 3.1 × 107 | 2.4 × 107 | 2 × 107 | 2 × 107 | 2 × 107 | 2 × 107 | 1 × 107 | 1 × 107 |
| Vp/cm.s−1 | 1.0 × 107 | 1.6 × 107 | 1.3 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| μn/cm2.v−1.s−1 | 100 | 340 | 100 | 100 | 100 | 100 | 100 | 400 | 400 |
| μp/cm2.v−1.s−1 | 25 | 50 | 50 | 50 | 50 | 50 | 50 | 60 | 50 |
| Carrier density/cm−3 | n = 1 × 1020 | n = 1 × 1017 | n = 5 × 1017 | n = 9 × 1016 | n = 1 × 1016 | n = 9 × 1015 | n = 1 × 1015 | p = 1.5 × 1014 | p = 1.5 × 1020 |
| Thickness/nm | 350 | 70 | 70 | 70 | 70 | 70 | 70 | 5000 | 70 |
| Parameters | CdS | Zn1−xMgxO:In (x Represents Mg Concentration) | ||||
|---|---|---|---|---|---|---|
| x = 0 | x = 0.0625 | x = 0.125 | x = 0.1875 | x = 0.25 | ||
| Voc (mV) | 821 | 866 | 853 | 839 | 837 | 858 |
| Jsc (mA·cm−2) | 24.34 | 27.89 | 28.16 | 28.29 | 28.27 | 27.39 |
| FF (%) | 75.18 | 76.22 | 81.70 | 78.84 | 73.17 | 32.81 |
| H (%) | 15.06 | 18.43 | 19.63 | 18.72 | 17.33 | 7.72 |
| Rs (Ω·cm2) | 4.6 | 5.2 | 6.8 | 7.9 | 9.6 | 25.8 |
| Rsh (Ω·cm2) | 812 | 1019 | 1253 | 1156 | 971 | 236 |
| x | 0 | 0.0625 | 0.125 | 0.1875 | 0.25 |
|---|---|---|---|---|---|
| Eg (eV) | 2.98 | 3.12 | 3.32 | 3.48 | 3.61 |
| Ef (eV) | 2.48 | 2.51 | 2.76 | 2.89 | 2.97 |
| χ (eV) | 4.77 | 4.73 | 4.53 | 4.37 | 4.24 |
| Φ (eV) | 5.37 | 5.34 | 5.09 | 4.96 | 4.88 |
| Thickness (nm) | 70 | 100 | 120 | 150 | 200 |
| Voc (mV) | 853 | 853 | 853 | 852 | 852 |
| Jsc (mA·cm−2) | 28.16 | 28.03 | 27.96 | 27.88 | 27.78 |
| FF (%) | 81.71 | 81.71 | 81.71 | 81.71 | 81.70 |
| η (%) | 19.63 | 19.54 | 19.49 | 19.43 | 19.35 |
| Rs (Ω·cm2) | 6.8 | 6.9 | 6.9 | 7.1 | 7.3 |
| Rsh (Ω·cm2) | 1253 | 1208 | 1179 | 1093 | 1025 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Wu, L.; Hao, X.; Zhang, J.; Li, C.; Wang, W.; Feng, L.; Du, Z. The Band Structures of Zn1?xMgxO(In) and the Simulation of CdTe Solar Cells with a Zn1?xMgxO(In) Window Layer by SCAPS. Energies 2019, 12, 291. https://doi.org/10.3390/en12020291
He X, Wu L, Hao X, Zhang J, Li C, Wang W, Feng L, Du Z. The Band Structures of Zn1?xMgxO(In) and the Simulation of CdTe Solar Cells with a Zn1?xMgxO(In) Window Layer by SCAPS. Energies. 2019; 12(2):291. https://doi.org/10.3390/en12020291
Chicago/Turabian StyleHe, Xu, Lili Wu, Xia Hao, Jingquan Zhang, Chunxiu Li, Wenwu Wang, Lianghuan Feng, and Zheng Du. 2019. "The Band Structures of Zn1?xMgxO(In) and the Simulation of CdTe Solar Cells with a Zn1?xMgxO(In) Window Layer by SCAPS" Energies 12, no. 2: 291. https://doi.org/10.3390/en12020291
APA StyleHe, X., Wu, L., Hao, X., Zhang, J., Li, C., Wang, W., Feng, L., & Du, Z. (2019). The Band Structures of Zn1?xMgxO(In) and the Simulation of CdTe Solar Cells with a Zn1?xMgxO(In) Window Layer by SCAPS. Energies, 12(2), 291. https://doi.org/10.3390/en12020291




