Building Energy Performance Analysis: An Experimental Validation of an In-House Dynamic Simulation Tool through a Real Test Room

Abstract

This paper focuses on the experimental validation of a building energy performance simulation tool by means of a comparative analysis between numerical results and measurements obtained on a real test room. The empirical tests were carried out for several months under variable weather conditions and in free-floating indoor temperature regime (switched off HVAC system). Measurements were exploited for validating an in-house simulation tool, implemented in MatLab and called DETECt, developed for dynamically assessing the energy performance of buildings. Results show that simulated indoor air and surface room temperatures resulted in very good agreement with the corresponding experimental data; the detected differences were often lower than 0.5 °C and almost always lower than 1 °C. Very low mean absolute and percentage errors were always achieved. In order to show the capabilities of the developed simulation tool, a suitable case study focused on innovative solar radiation high-reflective coatings, and infrared low-emissivity materials is also presented. The performance of these coatings and materials was investigated through a comparative analysis conducted to evaluate their heating and cooling energy saving potentials. Simulation results, obtained for the real test cell considered as equipped with such innovative coatings and material, show that for the weather zone of Naples a 5% saving is obtained both in summer and in winter by simultaneously adopting a high-reflectance coating and a low- emissivity plaster for roof/external walls and interior walls, respectively.

1. Introduction

The use of Building Energy Performance Simulation (BEPS) tools is more and more crucial for the assessment of the environmental and energy-related impacts of buildings, which are responsible for about 37% of the worldwide total final energy use [1]. In order to reduce the energy demand of the building sector, an impressive effort has been made by the research community and governments, who have been working on setting out energy policies to promote the efficient design of buildings and the integration of renewable energy technologies, considered as crucial to achieve the Nearly Zero Energy Building (NZEB) goal [2].

1.1. Literature Review

The sustainable energy transition of the building sector is driven by the proper implementation of energy efficiency actions. In this regard, the use of BEPS tools is essential for predicting all the possible benefits achievable through innovative solutions and techniques conceived for energy saving purposes [3,4]. Given the growing concern about the energy efficiency in buildings, several tools have been developed with the aim of assessing the energy performance of single buildings as well as of providing global and city-scale planning and setting guidance for the use of policy-makers and stakeholders [5]. Concerning the individual building analysis, the available tools have been mostly developed and used with the following aims:

• to support an energy efficient building design or redesign, construction or refurbishment, and operation [6,7,8];
• to deal with all the most important phenomena occurring in the building [9,10,11];
• to address the effectiveness of applied energy efficiency techniques or renewable energy sources [12,13] while promoting their implementation for the building energy diagnosis [14,15].

Building simulation models mostly differ in temporal and spatial resolution and modelling approaches. An overview of theory and assumptions is presented in reference [16]. Here, authors compare the capabilities of the major building energy simulation tools [17], whereas selection criteria, based on energy’s user needs, are discussed in reference [18]. Reviews of BEPS tools are proposed by several authors, concerning the analysis of the integration of renewable energy [19,20], the simulation of district-level energy systems [21,22], and the performance of low-energy buildings [18,23].

Although BEPS tools have been in use throughout the building energy community for decades, their adoption has been boosted by the recent advances in computational methods and computer calculation power [24], which provide opportunities for the enhancement of simulation tools and for the development of new ones, especially developed for simulating innovative building energy efficient technologies [25]. In fact, despite the availability of commercial BEPS codes (often characterized by high level of flexibility and complete user interfaces/data libraries), the development of up to date tools and novel in-house simulation models has become more and more common for research aims and, more in general, for aiding the implementation of new unreleased energy efficiency measures (e.g., [26,27,28,29,30]). In this regard, the use of BEPS codes in the building design process is highly recommended especially for the design of the next generation of buildings requiring different innovative features/materials and energy efficient measures (e.g., phase change materials, thermally activated systems, passive strategies, integrated renewable technologies, etc.). In case of new and/or not commercialized technologies and materials, for which no experimental data are available yet [31], the development of suitable simulation models is often required and recommended. This is particularly true for the design of the next generation of buildings (as NZEBs) to be carried out through suitable computer-based energy analyses [12,32,33,34]. New BEPS tools are also developed with the purpose to evaluate the occupants’ comfort, and to stimulate models’ robustness and fidelity also toward the implementation of innovative control strategies [16,31].

Despite such progress and effort, building energy simulation is still nowadays a complicated process that requires and involves modelling and analytical skills [35]. The use and development of BEPS tools and the analysis of the obtained results can be considered as a challenge for building designers and practitioners, sometimes undecided about the choice of the BEPS tool to be adopted as well as by the reliability of the related calculation results [31]. In this regard, since these tools are developed to predict the thermal performance of new buildings or to recommend energy retrofit packages for refurbishment, validation procedures (sometimes improperly substituted by calibration ones) are necessary to reduce simulation uncertainties [36,37]. In fact, the validation of a novel in-house developed BEPS tool is mandatory to ensure unfailing and accurate energy analyses and to prevent untrustworthy results.

To ensure the reliability of a BEPS code, standard validation processes are frequently used [31] to validate new models, examples are reported in references [33,38,39,40]. The use of validation procedures has been recently emphasized by the Energy Performance Building Directive (EPBD) issued by the European Union, which also underlines the need of new certified tools for decision-makers and practitioners to be developed with the aim to support integrated building design applications while ensuring the compliance with higher energy efficiency standards.

The available literature includes several general criteria and standard procedures for the validation of novel BEPS tools [41,42]. These procedures consist of comprehensive and integrated suites of building energy analysis tool tests, involving empirical, analytical, and comparative approaches [37,43,44]. Here, the differences depend on the method in which the calculated outputs (i.e., by a subroutine, algorithm, software, etc.) are compared to the data considered as reference ones [41,45]. Specifically, simulation results relative to a building tool or component to be validated can be compared to (i) measured data, obtained by a real building, a test cell, or laboratory experiments, in case of the empirical validation, (ii) results from accepted numerical methods or standard analytical solutions (i.e., simulation of the heat transfer mechanisms under certain boundary conditions), in case of the analytical verification procedure, (iii) results obtained by the current state-of-the-art codes (considered as reference tools and more reliable than the code under examination), in case of the comparative test procedure [43]. More details regarding the advantages and disadvantages of such procedures are reported in references [37,44].

Despite of the progresses in validation methods for building energy simulation tools, the validation process is still time consuming and rather difficult to be accomplished [46]. Although empirical validation procedures, based on real metering and auditing data, are considered as very reliable procedures [47], they are often used for the validation of tools and mathematical models developed for simulating specific phenomena. In this regard, the literature shows several examples of such a procedure applied to the validation of models relative to thermally activated building systems [48,49,50], daylighting or HVAC interactions with respect to window or solar gain [51,52], double skin facades or ventilated cavity [53,54,55,56], activities of occupants and their interaction with the building loads [57], etc. It is worth noting that though experimental validations of single mathematical models for the simulation of the energy performance of a specific new building’s technology, component or material, can be often easily carried out, the experimental validation of whole BEPS tools is mostly unfeasible. This is the case of dynamic building simulation tools including innovative and integrated energy and building envelope solutions which would require extensive testing procedures, costly and time consuming [12,58]. For this reason, very often new and validated subroutines (developed for simulating specific innovative technologies) are added to commercial BEPS tools [31] for conducting whole building energy simulation analyses. Nevertheless, the correct experimental validation of whole BEPS tools integrating novel technologies would require the construction of full-scale buildings, rather expensive and often impracticable. For these reasons, experimental validation procedures through suitable test cells or scale building models are becoming more and more frequent [59]. For novel thermal models few empirical validation-works are available in the literature, as reported in references [48,60,61]. Here, suitable test cells are often used for analyzing the accuracy of the related results, whereas idealized test cells are built for suitably taking into account the effects of specific building features to be studied [37]. In case of unavailability or unfeasibility of a suitable experimental set-up, the comparative approach (also known as code- to- code validation) is considered. Here, the results obtained by the simulation model under examination are compared to those obtained by different comparative tests cases, necessary to evaluate the reliability of the building simulation model under different operating conditions. From this point of view, the International Energy Agency, IEA, commissioned a number of projects for developing proper validation methodologies for building energy models [37,62,63,64]. Among these, the Building Energy Simulation Test (BESTEST) [43,44,65] and the ANSI/ASHRAE Standard 140 [66] suites aim to increase confidence in the use of BEPS tools, by producing standardized test procedures for validating, diagnosing, and improving the current generation of software.

1.2. Aim of the Work and Content of the Paper

This paper aims to respond to the twofold need of the research focused on BEPS tools, i.e., to develop the following:

• a reliable dynamic simulation tool for the building energy performance analysis capable of reliably predicting the related energy demands and the indoor environmental conditions [67,68,69];
• a flexible tool to be used for the implementation of new add-on models able to suitably assess the energy performance of future building research challenges (e.g., innovative envelope integrated technologies and strategies, new energy efficiency construction materials, real users’ interaction with the building indoor environmental control systems, innovative building plants, etc.) [48,70,71].

In this framework, this paper presents the results of an empirical validation of an in-house developed building simulation model, implemented in a computer tool written in MatLab and called DETECt [72]. The presented simulation model has been used by researchers of different backgrounds in order to investigate the energy performance of novel building envelope measures and energy saving technologies, as well as innovative strategies for the hygrothermal indoor conditions control [73,74,75,76,77,78]. The tool was previously and successfully verified through the results obtained by other similar models as well as the above mentioned BESTEST standard procedure, showing low or very low deviations between the obtained simulation results and those provided by test suites [72,79]. The validation procedure is now completed by following the experimental approach. Specifically, in this paper the DETECt simulation results are compared to measurements obtained through a real test-room located in Naples (South-Italy). The overall validation procedure here presented resulted in being more costly (in terms of required time and effort) than the comparative ones detailed in references [72,79]. From this point of view this paper and the included results can be considered as the continuation and conclusion of the starting research work reported in reference [72].

The empirical validation test of DETECt was also conceived in order to assess the influence of building thermal properties and weather parameters on the tool reliability. The paper includes many details and results of the experimental validation process, also describing the experimental setup design, the measured boundary conditions and the applied metrics for the empirical validation. Note that, DETECt can be coupled to additional simulation tools purposely developed for dynamically analyzing traditional and innovative building systems and plants (e.g., different renewable energy technologies, HVAC systems, adaptive indoor air conditions controls, etc.). Therefore, by such complete tool, energy and economic performance, analyses of whole building-plant systems can be carried out.

One of the novelties of this research consists of the development and use of a new dynamic simulation tool for assessing the energy performance of new building technologies that are not implemented yet or cannot be precisely modelled in the available simulation codes. The use of simulation tools is always required to investigate in advance the energy performance of forthcoming themes and applications, as well as future building materials and/or innovative techniques. From this point of view, in recent years DETECt was uninterruptedly refined and updated by the authors with new functions and subroutines, and the related experimental validation has to be considered as a crucial step of the carried-out research work on developing this tool.

• Finally, as DETECt successfully surpassed the validation process, which intrinsically suggests the consistency of the developed models in properly predicting the indoor space thermal behavior, a novel case study analysis developed through DETECt is presented here. Specifically, the use of solar radiation reflective coatings and low-emissivity plasters for building opaque elements is investigated. It is worth noting that such innovative passive envelope solutions [80,81,82] are gaining much more interest as they can be easily implemented in new or existing buildings in order to reduce their energy consumption [83]. Nevertheless, the available literature on these materials (e.g., references [84,85,86,87,88,89]) highlights that much research work is needed, because of the following:
• In case of high-reflective paints, the majority of papers regard applications for horizontal or tilted external surfaces (i.e., cool roofs [86]), whereas only few works are focused on vertical ones [88,89];
• For internal surfaces finishing, the low emissivity effects for longwave infrared radiation are rarely investigated [85,87], and few building energy simulation tools allow the selection of low-emissivity features for the internal surfaces [87];
• Commercial software often does not allow variable optical properties of the envelope surfaces (e.g., solar reflectance) to be setup, or to take into account the effective spectral distribution of the incident solar radiation (e.g., [90]).

In DETECt all the above-mentioned limitations and lacks are exceeded. Therefore, a suitable case study was developed with the aim of assessing the energy performance of such innovative building surface coatings. The potential energy savings and the benefits on the building thermal behavior, obtained through cool paints on external surfaces and through low-emissivity coatings on internal ones, were assessed for the weather conditions of Naples. In the case study different combinations of such materials were considered and the best energy performance was achieved by simultaneously applying cool paint and low-e plaster on the room exterior and interior surfaces, respectively. An energy saving of about 5% was achieved on both heating and cooling season for indoor air setpoint temperatures of 20 and 26 °C, respectively.

2. Model Description

2.1. Description of the Framework and General Consideration

The selection of a BEPS tool depends highly on the trade-off between the accuracy of the implemented models and the computing time, whereas the reliability of simulation results depends on the mathematical models and assumptions made to describe the occurring building physical phenomena [64]. Simulation models based on steady state methods neglect the transient effect of variables (e.g., thermal inertia) and other sensible assumptions; thus, they are not suitable for the optimal design of the building and its HVAC systems. Conversely, dynamic simulation models are capable of tracking peak loads and are useful to capture thermal effects, providing accurate details on how to reduce the energy demand and to improve the thermal comfort of occupants. Computational time is largely dependent on the numerical treatment of the considered structural components. In this regard, among physics-based models dealing with the spatial dependency of the thermal behavior of buildings, different modelling approaches can be used, such as, i) zonal method, ii) thermal network, iii) nodal method, iv) Computational Fluid Dynamics (CFD).

By the zonal approach, a building is split into different thermal zones [91], where thermal and mass balances are used to determine the occurring temperature distribution.

Thermal network models are, instead, frequently used because of the related simple and efficient approach, wherein the spatial dependency is accounted for by distributing resistors and capacitors in different spatial directions. Thus, as the method aims to capture the dominant building physics behaviors while ignoring nonlinearities (also necessary for the development of building control strategies [92,93]), there is no need to solve partial differential equations, simplifying the mathematical model formulation. For example, in some building simulation tools the conduction heat transfer is solved by lumping all the building thermal masses in a single node of the considered thermal network, avoiding the adoption and the resolution of many partial differential equations [94]. Nevertheless, despite their simplicity, lumped model approaches do not allow one to obtain details about the building surfaces temperatures, necessary for simulating the frequent rapid variation of the thermal conditions occurring in buildings as well as for indoor comfort analyses [95]. If the flow field and the spatial domain to be discretized are a priori known, thermal network-based models could be preferable than more computationally expensive and complex building thermal ones [96]. For this reason, suitable detailed mathematical algorithms/models based on the thermal network approach have become more and more developed and are used to predict the whole building thermodynamic behavior and for analyzing the energy performance of building-plant systems [28,97,98,99]. Typically, in order to develop straightforward tools through such an approach, only few system phenomena are modelled and only the most significant physical aspects occurring in the dynamic building thermal behavior are considered. In order to simulate the building dynamic interactions within a reasonable computing time, one-dimensional modelling approaches of heat transfer phenomena within the building envelope are often employed [48,100]. A summary about assumptions, features, and limitations of such models is reported in references [16,101,102].

The nodal method, derived from the thermal network one, considers each building zone element (i.e., indoor air, wall, etc.) as a homogeneous volume. Here, uniform state variables and appropriate heat transfer equations are applied to each node and solved by using transfer functions or finite difference methods [103]. Nodal approaches are employed by numerous BEPS tools, widely used in the research community. EnergyPlus [10] and TRNSYS [3] are two popular examples.

Tools based on the CFD approach are characterized by the highest accuracy and by long computing time, rather unsuitable to perform yearly simulations at a whole building level [25].

The thermal model implemented in DETECt is based on a nodal description of the building elements with a one-dimensional modelling of the thermal conduction phenomena (the transverse heat transfer is disregarded [104]). With the aim to analyze the effect of the spatial distribution of the heat capacity on the heat flux through the building envelope elements, the developed thermal network includes a high number of thermal capacitances, following a distributed parameters approach [105]. Specifically, in DETECt a transient distributed parameters heat transfer model is implemented to allow accurate simulations of dynamic effects driven by the thermal mass. Such a method allows one to dynamically calculate the temperature of indoor air and building surfaces, necessary for indoor comfort analyses and for simulating the temperature and flux fields of a mono-zone, multi-zone and multi-story building.

The developed simulation model is implemented in MatLab environment [106], which includes built in solvers for differential equations systems and mathematical functions. DETECt is subdivided into several sub-models, dedicated to the calculation of different phenomena. All sub-models are grouped in a single calculation tool, described inreference [79], whose simulator scheme is shown in Figure 1. A description of the thermal model is provided hereafter with the aim of showing the mathematical approach and algorithms included in DETECt, as well as the model assumptions that primarily influence the fidelity and accuracy of the simulation results.

2.2. Heat Flow Calculation Procedure

The transient heat transfer through building elements is simulated by taking into account the finite difference method based on the thermal Resistance Capacitance (RC) network approach. Each thermal zone of the simulated building is modelled by lumping the indoor air mass in a single uniform temperature node, whereas each envelope elements (wall, roof, ceiling, floor, interior wall, window) is split into uniform multi-layers, where thermal masses are lumped. For homogeneous layers of different thicknesses, isotropic and time-invariant thermo-physical properties (density, specific heat and conductivity) are assumed. By following such assumptions, each n-th sub-layer (1 ≤ n ≤ N) of each m-th building element (1 ≤ m ≤ M) is modelled by a single uniform temperature node including two conductive resistances and a single lumped capacitance, as shown in Figure 2. Each m-th building element includes two additional surface non-capacitive thermal nodes (n = 0 and n = N + 1), considered as boundary nodes linked to the outdoor and indoor air temperatures (not shown in Figure 2).

Building internal and external solicitations are taken into account to assess the dynamics of the whole set of nodal temperatures of the RC network, described by a number of algebraic and differential equations (according to the discretization level, automatically selected to obtain an acceptable simulation results accuracy as well as a sufficiently short computational time [105]). A built-in ODE solver, provided by MatLab and based on variable step size Runge–Kutta and trapezoidal rule integration methods, is considered to solve the system equations [106].

The differential equation describing the heat transfer of each capacitive n-th node of the m-th building element is calculated in each t-th time step as:

$$C_{m,n}\frac{d{T}_{m,n}}{dt}={\displaystyle \sum _{j=n-1}^{n+1}\frac{T_{m,j}-T_{m,n}}{R_{m,n}^{cond}}}+\gamma \cdot {\dot{Q}}_{m,n}^{rad}$$

(1)

where T and C are the temperature and thermal capacitance, R^cond is the conductive thermal resistance between two nodes, ${\dot{Q}}^{rad}$ is the radiative forcing function acting on non-capacitive nodes (γ ≠ 0 if n = 0 or n = N + 1, being γ = 0 elsewhere). Note that, ${\dot{Q}}^{rad}$ depends on the typology and geometry of the considered building element (assumed as either separating two indoor zones or an indoor zone from the outdoor environment). On external opaque and glazed surfaces (n = 0), ${\dot{Q}}_{m,0}^{rad}$ includes both the solar and long wave radiations, while on inner opaque and glazed surfaces (n = N + 1), ${\dot{Q}}_{m,N+1}^{rad}$ accounts for the incident solar radiation entering through windows and the net long wave radiation load exchanged with the remaining internal surfaces of the considered thermal zone. Such terms, for each m-th building element of the heat exchange surface area, A_m, are calculated as:

$$\begin{array}{l}{\dot{Q}}_{m,0}^{rad}=\left[{\epsilon }_m^{ext}\cdot \sigma \cdot f\cdot (T_{sky}^4-T_{m,1}^4)+{\alpha }_m^{ext}\cdot I_m^{ext}\right]\cdot A_m\\ {\dot{Q}}_{m,N+1}^{rad}=\left[{\epsilon }_m^{int}\cdot \sigma \cdot {\displaystyle \sum _{i=1}^M{G}_{bm}\cdot (T_{i,N}^4-T_{m,N}^4)}+{\alpha }_m^{int}\cdot I_m^{\mathrm{int}}\right]\cdot A_m\end{array}$$

(2)

where f is the external surface view factor, T_sky is the sky temperature, Ɛ is the emissivity of the surface, ɑ is the average spectral absorption factor (calculated through spectral reflectance curves integrated across the whole solar range), G_bm accounts for the long-wave radiation exchange on the internal surface of the considered thermal zone, I is the total solar radiation flux (depending on geometrical relationships implemented in a specific subroutine [107]). Note that further details about the solar radiation subroutine, not reported for the sake of brevity, are available in reference [108].

The calculation of the solar radiation entering through transparent elements and distributed within the internal space is carried out by means of the selected absorption, reflection, and view factors. In particular, the total solar radiation flux striking an internal m-th surface, $I_m^{\mathrm{int}}$, includes the solar irradiance reflected by other interior surfaces and it is calculated as:

$$\left(\begin{array}{c}{I}_1^{int}\\ I_2^{int}\\ \dots \\ I_M^{int}\end{array}\right)={\left(\begin{array}{cccc}\left(1-F_{11}{\rho }_1^S\right)& -F_{12}{\rho }_2^S& -\dots & -F_{1M}{\rho }_M^S\\ -F_{21}{\rho }_1^S& \left(1-F_{22}{\rho }_2^S\right)& -\dots & -F_{2M}{\rho }_M^S\\ \dots & \dots & \dots & \dots \\ -F_{M1}{\rho }_1^S& -F_{M2}{\rho }_2^S& -\dots & \left(1-F_{MM}{\rho }_M^S\right)\end{array}\right)}^{-1}\cdot \left(\begin{array}{c}{I}_1^0\\ I_2^0\\ \dots \\ I_M^0\end{array}\right)$$

(3)

where ${\rho }^S$ are the internal surfaces solar reflectivity coefficients, F are the internal surfaces view factors, automatically calculated for parallelepipedal structures [109], $I_{}^0$ is the vector of the solar radiation directly received by the interior surfaces. It is worth noting that the coefficients of the $\left(\overline{I}-F\cdot P_S\right)$ matrix shown in Equation (3) are calculated at the beginning of the simulation, remaining constant at each simulation time-step. The long-wave radiation exchange on the internal surfaces of the considered thermal zone is assessed through the Gebhart’s absorption method [110,111], and the G_mb generic coefficient of the Gebhart’s matrix (namely G and consisting of several vectors) is calculated as:

$$\left(\begin{array}{c}{G}_{1m}\\ G_{2m}\\ \dots \\ G_{Mm}\end{array}\right)={\left(\begin{array}{cccc}\left(1-F_{11}{\rho }_1^{LW}\right)& -F_{12}{\rho }_2^{LW}& -\dots & -F_{1M}{\rho }_M^{LW}\\ -F_{21}{\rho }_1^{LW}& \left(1-F_{22}{\rho }_2^{LW}\right)& -\dots & -F_{2M}{\rho }_M^{LW}\\ \dots & \dots & \dots & \dots \\ -F_{M1}{\rho }_1^{LW}& -F_{M2}{\rho }_2^{LW}& -\dots & \left(1-F_{MM}{\rho }_M^{LW}\right)\end{array}\right)}^{-1}\cdot \left(\begin{array}{c}{F}_{1m}{\epsilon }_m^{LW}\\ F_{2m}{\epsilon }_m^{LW}\\ \dots \\ F_{Mm}{\epsilon }_m^{LW}\end{array}\right)$$

(4)

where each G_mb is the fraction of the radiation emitted from the interior surface and absorbed by the remaining ones, ρ^LW and ε^LW are long-wave reflectivity and emissivity coefficients. Note that, G is calculated at the beginning of the simulation, remaining constant at each time-step, as it depends on surface geometry and constant material thermal properties.

Note that, in case of outer (n = 0) and inner (n = N + 1) surface non-capacitive nodes, the algebraic equation describing the heat transfer is obtained by Equation (1) setting the thermal capacitance, C_m,n, to zero. In this case, convective resistances can be either set as constant (based on the surface type) or calculated as a function of the surface unitary convection heat transfer coefficients (calculated by empirical relationships [72,74]). Note that, convection heat transfer coefficients can be assumed as time variant when the wind velocity is available as input data (from measurements or weather data files); otherwise, constant coefficients are considered, by assuming a wind velocity equal to 5 m/s.

Finally, the equation describing the heat transfer of the indoor air node is calculated as:

$$C_{in}\frac{d{T}_{in}}{dt}={\displaystyle \sum _{m=1}^M\frac{T_{m,N}-T_{in}}{R_{m,\mathrm{int}}^{conv}}}+{\dot{Q}}_{gain}+{\dot{Q}}_{vent}\pm {\dot{Q}}_{HVAC}$$

(5)

where C_in is the thermal capacitance of the zone indoor air, and R^conv is the internal convective resistance, assessed as a function of the surfaces inclination and flow condition, ${\dot{Q}}_{gain}$, ${\dot{Q}}_{vent}$ and ${\dot{Q}}_{HVAC}$ are sensible heat gains, considered as purely convective and, respectively, due to, (i) occupants, lights and equipment, (ii) infiltration and ventilation, and (iii) sensible heat to be supplied to or to be removed from the building space (by an ideal heating and cooling system). ${\dot{Q}}_{HVAC}$ is required to maintain the indoor air at the considered set point temperatures and it is calculated according to a Proportional Integral (PI) controller, whose gains vary as a function of the operating conditions [112].

Further details of the developed mathematical model and concerning the related capabilities are available in references [72,108].

3. Model Validation

In the following, the results of a suitable empirical validation procedure conducted for assessing the DETECt reliability are discussed in detail.

It is worth noting that DETECt successfully surpassed a previous comparative validation process performed by means of the BESTEST standard procedure [43,44,65]. This approach includes several test cases, organized in diagnostic and qualification (mandatory) series, which allow one to analyze the influence of different physical phenomena on the numerical results provided by BEPS tools and building energy models under examination. Such test cases cover a high number of physical occurrences and model features (i.e., thermal mass, solar and internal heat gains, window-shading devices, infiltration, setback thermostat control, etc.). The BESTEST procedure has been widely adopted for assessing the accuracy of a number of building simulation tools capable of performing energy analyses [37,62,63,64]. Such iterative diagnostic procedure allows codes to be examined over a broad range of parametric interactions that cannot be easily considered through experimental analyses [65].

For both the winter and summer reference days considered in the BESTEST procedure, dynamic results achieved by DETECt for the free-floating indoor air temperature and the corresponding heating and cooling requirements are always included within the BESTEST confidence intervals, confirming an initial reliability of the developed code. More details about the code-to-code validation of DETECt are reported in reference [108].

Furthermore, an additional comparison with two commercial tools (TRNSYS and Energy-Plus) was also conducted in order to check the code reliability with respect to different building geometries and uses, HVAC activation scheduling, and weather conditions. The deviation detected between the results obtained with DETECt and with these standard tools was almost always lower than 10% [72].

3.1. Empirical Validation Procedure

In this section, details about the design of the experimental setup and the developed analyses are reported. Then, a discussion of the results obtained through the carried out empirical validation process of DETECt is provided.

3.1.1. Experimental Set-Up

The testing facility employed for the validation process of DETECt consists of a real test room located in the main building of the cluster hosting the School of Polytechnic and Basic Sciences of the University of Naples Federico II, situated in the neighborhood of Fuorigrotta, Naples (South-Italy, 40.83999°N, 14.25176°E). Note that, a temperate climate is observed in this location, featured by rather long winters and rather hot and humid summers. The building cluster was built in multiple phases between 1955 and 1980, and it consists of lower bodies and a main block of twelve floors (60 m height). The real test room is located on the twelfth floor of the main high-rise building, and it corresponds to a typical test cell, because of its shape and features.

It is worth noting that a test-box typically consists of a single room, well insulated from its surroundings on all the related walls except one exposed to the outdoor climate conditions to allow the investigation of solar gain and temperature effects on its energy behavior (also through the use of different windows and materials on the exposed walls) [113]. Sensors are placed throughout the room and outside to allow the data collection of temperatures, humidity, and solar radiation. The considered room is operated under free-floating temperature conditions; thus heating, cooling, and lighting system schedules are not considered.

The test room used for the presented analysis has a parallelepipedal shape (2.60 m height, 3.39 m length and 2.26 m width) and only two external walls, the South-West one including one window, and the North-West one, as shown in Figure 3. The window (0.87 m length and 1.18 m height) is made of two single (8 mm thickness) glass panels (0.30 m length and 1.18 m height, for 0.6 m² area and SHGC = 0.78), and the frame (for 0.43 m² area) is made of a traditional aluminum profile; the average U-value = 5.2 W/m²K.

The South-East wall, including a wood door (2.10 m height, 0.99 m width, 0.04 m thick), is an interior wall, adjacent to a corridor of the above mentioned twelfth floor, whereas the North-East one separates the test room from another indoor space in which several machineries are continuously switched on (thus a rather high indoor temperature is observed all over the year). A 1.2 m depth horizontal overhang is located on the South-West wall. The ceiling is made for 3/5 of its surface of concrete and for the remaining part of thermally insulated aluminum sheet, and a similar thermal transmittance of such two roofs is observed.

In order to verify the layer layout of walls, ceiling and floor layers, an investigation of the available technical documentation as well as suitable low-invasive endoscopic analyses were carried out. For achieving the endoscopic investigation, several 1.5 cm diameter holes were made through the walls and the ceiling, as shown in Figure 4. Here, a picture of the adopted endoscope probe (Figure 4a), the autoclaved concrete layer of the South-West and North-West walls (Figure 4b), the thermal insulation material surrounded by steel sheets of the South-West and North-West walls (Figure 4c), and the air-gap between the two semi-hollow brick layers of the South-West wall (Figure 4d), are reported. As a result of this analysis, a complete assessment of the test room envelope layout was carried out. Specifically, details about the related layers and thermophysical properties were detected.

The thermophysical properties and thicknesses of the considered test-room walls are reported in

Table 1. Walls layers thickness and thermophysical properties (from outdoor to indoor).

South-West, North-West and North-East Walls	Layer Material	Thickness	Thermal Conductivity	Density	Specific Heat
Wall thickness 0.19 m, U-value = 0.54 W/m2K		(m)	(W/mK)	(kg/m3)	(J/kg K)
	Bitumen	0.004	0.2	1075	1000
	Steel	0.0025	36	7700	500
	Thermal insulation	0.05	0.065	44	1458
	Steel	0.0025	36	7700	500
	Thermal insulation	0.05	0.065	44	1458
	Autoclaved cellular concrete	0.05	0.25	800	1000
	Plaster	0.015	0.2	1075	1000
South-East Wall	Material Layer	Thickness	Thermal Conductivity	Density	Specific Heat
Wall thickness 0.47 m, U-value = 0.57 W/m2K		(m)	(W/mK)	(kg/m3)	(J/kg K)
	Plaster	0.015	0.35	750	1000
	Semi-hollow brick	0.20	0.32	1200	840
	Air	0.04	0.27	1.3	1008
	Semi-hollow brick	0.20	0.32	1200	840
	Plaster	0.015	0.35	750	1000

, whereas for the ceiling and floor they are shown in

Table 2. Ceiling and floor layers thickness and thermophysical properties (from outdoor to indoor).

Floor	Material Layer	Thickness	Thermal Conductivity	Density	Specific Heat
Wall thickness 0.48 m, U-value = 1.40 W/m2K		(m)	(W/mK)	(kg/m3)	(J/kg K)
	Plaster	0.015	0.35	750	1000
	Hollow block	0.18	0.6	1400	840
	Concrete slab	0.20	1.6	2200	1000
	Mortar bed	0.05	0.9	1800	1000
	Marble	0.03	1.3	2300	840
Ceiling	Material Layer	Thickness	Thermal Conductivity	Density	Specific Heat
Average U-value = 0.16 W/m2K		(m)	(W/mK)	(kg/m3)	(J/kg K)
Horizontal attic side	Bitumen	0.02	0.20	1075	1000
	Mortar bed	0.05	0.9	1800	1000
	Concrete slab	0.20	1.6	2200	1000
	Hollow block	0.18	0.6	1400	840
Tilted aluminum sheet side	Aluminum	0.002	190	2700	900
	Polyurethane foam	0.05	0.028	44	1458
	Aluminum	0.002	190	2700	900
	Air	0.1–0.3	0.27	1.3	1008
	Bitumen	0.004	0.20	1075	1000
	Steel	0.0025	36	7700	500
	Thermal insulation	0.06	0.028	44	1458
	Steel	0.0025	36	7700	500
	Thermal insulation	0.06	0.028	44	1458
	Air	0.04	0.27	1.3	1008
	Plasterboard	0.015	0.21	900	840

. The long-wave emissivity and reflectivity (ε^LW and ρ^LW) of the interior surfaces are set to 0.9 and 0.1, respectively. The solar absorptance coefficients of the interior surfaces (α_int) are set to 0.25, whereas for the exterior ones (α_est) are set to 0.3 (walls) and 0.6 (roof).

Sensors and instrumentations applied into the test room are:

• Six thermocouples for measuring the internal surfaces temperature of the North-West, North-East, South-East, South-West walls, ceiling and floor (K-type, model TC Direct 402–805. Measuring range: from −250 to 150 °C. Accuracy: ± 1.0 °C or ±0.75%). See Figure 5a. Note that, the temperature homogeneity on the surfaces of such test room elements was repeatedly verified by means of an infrared thermo-camera (FLIR, model T335. Measuring range: from –20 to 650 °C; in 3 ranges: −20 to 120 °C or 0 to 350 °C or 200 to 650 °C. Accuracy: ±2 °C or 2%. Thermal sensitivity/NETD 50 mK at 30 °C. IR resolution: 320 × 240 pixels).
• Three thermoresistances for measuring the temperature of internal surfaces of the door and of window glass and frame (PT 100, model TC Direct 515–680. Measuring range: from −50 to 150 °C. Accuracy: ± 0.3 °C at 0 °C). See Figure 5b.
• One hygro-thermometer for measuring the indoor air temperature and humidity (HD 9008 TRR. Platinum resistance thermometer, 100 Ω. 4–20 mA output, and 10–30 VDC power supply. Temperature measuring range: −40 to 80 °C. Accuracy: ± 0.15 °C or ± 0.1%. Hygroscopic polymer humidity sensor. 4–20 mA output. Relative humidity measuring range: from 0 to 100%. Accuracy: ± 1.5% in the range 0%–90% and ± 2.0% elsewhere. See Figure 5c, right.
• One globe-thermometer for measuring the mean radiant temperature of the test room indoor surfaces, with an inside thermocouple (K-type, model TC Direct 402–805. Measuring range: from −250 to 150 °C. Accuracy: ± 1.0 °C or ± 0.75%). See Figure 5c, left.

Note that, to avoid the window solar radiation effect on all such sensors, suitable shields were used during the experimental analysis (not shown on the reported pictures for the sake of clarity).

Sensors and instrumentations, applied to the measurements of boundary conditions, are as follows:

• One hygro-thermometer for measuring the outdoor air temperature and humidity (HD 9008 TRR, above described), protected by a multi-plate radiation shield. See Figure 6a.
• One pyranometer for measuring the horizontal global incident solar radiation (Delta Ohm, LP Pyra 02 AC. First Class pyranometer based on a thermopile sensor. 4–20 mA output. Measuring range: 0–2000 W/m². Operating temperature range: −40–80 °C. Sensitivity: 10 µV/W/m². Impedance: 33–45 Ω. Device protected by two concentric domes. See Figure 6b,c;
• One pyranometer for measuring the vertical South-West global incident solar radiation (Delta Ohm, LP Pyra 08 BL. Second Class pyranometer. 4–20 mA output. Measuring range: 0–2000 W/m². Operating temperature range: −40 to 80 °C. Sensitivity: 15 mV/kW/m². Impedance: 5 Ω. Device protected by two concentric domes. Figure 6b,c.
• Two hygro-thermometers for measuring the temperature and humidity boundary conditions external to the test cell. One placed in the corridor of the twelfth floor (linked to the South-West tests room wall), and the other one at the eleventh floor of the building, in the floor adjacent space to the test room (Testo 174H. 2-channel temperature and humidity mini data logger for continuous building climate monitoring. Temperature measuring range: from −20 to +70 °C. Accuracy: ± 0.5 °C. Resolution: 0.1 °C. Relative humidity measuring range: from 2% to 98%. Accuracy ± 3%. Resolution: 0.1%).

All the above described sensors (except Testo 174H devices) were connected to a Compact Rio NI 9146 data logger (Figure 7), linked through an Ethernet cable to a suitable dedicated PC. Note that the Testo 174 H data loggers were synchronized to the Compact Rio in order to obtain simultaneous measurement data acquisition. In order to process and convert the logged signals a suitable LabView tool was purposely developed. Such a computer code was also used for real-time monitoring of all the measurements of solar radiation, temperature and humidity in and out the test room. In Figure 8 the front panel of such a LabView tool is depicted.

The empirical analysis, conducted through the described experimental setup, was run from February to October 2018 in order to collect data in all the possible weather conditions (winter, spring, summer, and autumn climates). Several logged parameters were used as input data to the DETECt simulation model, whereas other measurements were compared for validating purposes to the obtained simulation results. In the following, procedure details are provided. In addition, simulations were conducted by setting indoor gains equal at about 50 W (sensible constant value due to measuring equipment), the air exchange rate at 0.2 ACH.

3.1.2. Experimental Analysis

With the aim of considering dynamic weather conditions (featured by high meteorological variabilities), continuous experimental measurements were conducted between February and October 2018. For the sake of brevity, several significant days, well representing the winter and summer climates of the considered weather zone on Naples (South-Italy), are considered in the succeeding discussion. Note that cold and temperature sunny winter days and hot sunny summer days are selected with the aim to test the code capability in simulating the solar radiation effect on the thermal behavior of the test cell. Specifically, they refer to the following sample weeks:

• from March 23rd at 12:00 am to March 29th at 11:59 pm (winter climate time);
• from July 1st at 12:00 am to July 7th at 11:59 pm (summer climate time);

During the carried-out measurements the HVAC system was switched off (free floating temperature regime). The experimental data logging time step was set at 360 s (i.e., records were collected each 6 min).

Figure 9 shows, for both the selected winter and summer reference weeks, the time histories of the measured indoor and outdoor air temperatures (T_IN,exp and T_OUT,exp, respectively) and the solar radiation on the outdoor vertical South-West façade and on the outdoor horizontal roof surface (I_TOTver and I_TOThor, respectively). In Figure 9, it is possible to observe that the dynamic profile of outdoor air temperature (T_OUT,exp) coherently varies (throughout the days) according to the solar radiation trends. Note also that, the measured indoor air temperature (T_IN,exp) peaks are time shifted with respect to the outdoor ones (T_OUT,exp). This is due to the thermal inertia phenomena of the whole test room envelope, as well as to the occurring solar radiation effect through the window, located on the room vertical South-West wall (Figure 9, green line). The thermal capacitance effect of the test room envelope also softens the T_IN,exp fluctuation in both the winter and summer weeks.

Note that, the occurring indoor conditions dynamically vary according to the climate of the considered weather zone. Such a result is also visible in Figure 10 which shows, for the same sample weeks, the measured time histories of the indoor and outdoor relative humidity (ϕ_IN,exp and ϕ_OUT,exp, respectively), together with those of T_IN,exp and T_OUT,exp. It is noteworthy to observe that the trend of ϕ_OUT,exp highlights the presence of significant rainfall occurrences during the considered winter week (Figure 10, top) and high outdoor humidity hours in summer (Figure 10, bottom), as expected in a Mediterranean temperate climate.

Figure 11 shows the time histories of the internal surface temperatures of the test room walls, measured during the selected sample winter and summer weeks (Figure 11, top and bottom, respectively). Since the North-East (NE) wall is adjacent to a control room in which high continuous internal thermal loads are implemented, the related surface temperature, T_NE,exp, is always the highest one during the winter time (Figure 11, top) and on average the highest one along the summer period (with respect to the other measured surface temperatures). This result is clearly visible especially during night times. An exception is observed during some sunny days where T_NE,exp is surpassed by the South-West (SW) wall temperature, T_SW,exp (Figure 11, bottom). Note that, in the carried out validation procedure, the dynamically measured T_NE,exp temperatures are inputted in the DETECt simulation code as boundary conditions. It is of note that the measured surface temperatures of the South-West (SW) and North-West (NW) walls (T_NW,exp and T_SW,exp, respectively) are remarkably variable during the daily hours (Figure 11), accordingly to the relevant variations of the outdoor thermal solicitations and the low thermal capacitance of such walls. Conversely, the measured surface temperatures of the South-East (SE) wall (T_SE,exp) are weakly variable, accordingly to the related high thermal mass of such a wall with respect to the other ones. Note that, the twelfth-floor corridor is confined on the SW and NE sides by a large glazed surface (Figure 3). Therefore, the T_SE,exp time profile is influenced by the correspondent solar radiation (especially during the afternoon), in both winter and summer seasons. Specifically, although T_SE,exp shows slight fluctuations, a recurring growth is observed in afternoon times, especially in the case of serene sky conditions. Note that, in the performed validation procedure, also the dynamically measured T_SE,exp temperatures are inputted into the simulation code as boundary conditions.

In Figure 12, a rather different behavior is observed for the temperature of wooden door, T_door,exp, included in the SE wall (Figure 3). Because of its lower thermal capacitance with respect to the correspondent wall and due to highly variable thermal solicitations of the adjacent corridor, for such a door a significant temperature fluctuation is observed in all the days of the summer sample week (Figure 12, bottom) and in the third, fifth, and sixth day of the winter one (Figure 12, top). For both weeks, Figure 12 also shows the measured temperatures of the floor and ceiling surfaces (T_floor,exp and T_ceiling,exp, respectively) together with the occurring incident solar radiations.

It is worth noting that higher (lower) floor temperatures are always detected with respect to the ceiling ones in winter (summer). Such an outcome is due to the adjacency of the room floor and ceiling to an indoor space of the building and to the outdoor environment (ceiling–roof), respectively. Note that, due to the high thermal mass of the floor and to the lower one of the ceiling, the fluctuation of T_floor,exp is always weak whilst the swing of T_ceiling,exp is significant. This result is mostly evident in summer-time, when the solar radiation is the highest temperature variation driving force, Figure 12.

3.2. Experimental vs. Simulated Results

In order to validate DETECt by means of measurement data, the free-floating temperature regime of walls, floor, ceiling, and indoor air obtained by means of dynamic simulations was compared to the empirical ones achieved through the described experimental setup. To this aim,the test room was suitably modelled in DETECt by implementing within the code all the related geometrical features and thermophysical properties. In addition, several measured indoor and outdoor environmental variables were assumed as dynamic input data and boundary conditions, such as the following:

• global radiation on the outdoor horizontal roof surface, I_TOThor, and vertical South-West façade, I_TOTver. Note that, the global radiation on the vertical North-West façade is calculated starting from the measured global radiation on the outdoor horizontal surface;
• outdoor air temperature, T_OUT,exp;
• indoor air temperature of the corridor at the twelfth building floor limiting the SE wall (Figure 3). Such a temperature was implemented as boundary condition of the room SE wall;
• indoor air temperature of the building space at the eleventh floor. Such a temperature was implemented as boundary condition of the floor partition;
• internal surface temperature of the North-East wall, T_NE,exp.

By dynamically logging such parameters a suitable data file to be inputted to DETECt, concerning all the thermal solicitations received by the test room, was obtained. As mentioned above, the test room was monitored for a long period with the aim of collecting a high number of measurements (considering the different occurring meteorological conditions). The simulation time step was set, according to measurements, at 360 s. The initial conditions relative to all the modelled temperature were set at the starting measured temperatures collected on February 2nd.

The comparison between measured data and DETECt simulation outcomes are reported by several graphs depicted from Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19. Here, for both the considered sample winter and summer weeks (March 23rd–29th and July 1st–7th) the time histories of the simulated indoor air and internal surfaces temperatures (red lines) are compared to the corresponding measured data (black lines). To this aim, additional lines (red dash and dot ones) are reported in these figures. They are obtained by adding and subtracting ±1.0 °C (i.e., the instrument error of the considered thermocouples) to the experimental data. Furthermore, a narrower temperature interval given by ±0.5 °C is also included (grey band) with the aim of enhancing the evaluation of each simulated variable under examination.

Results for the indoor air temperature (T_IN,sim) are reported in Figure 13 whereas those related to all the internal surface temperatures of the room walls, i.e., South-West (T_SW,sim), North-West (T_NW,sim), South-East (T_SE,sim), ceiling (T_ceiling,sim), and floor (T_floor,sim), are reported in Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, respectively. The comparison between the simulated and empirical mean radiant temperatures is also carried out, the obtained results are depicted in Figure 19.

For both the selected winter and summer periods, simulated and measured temperatures resulted in being very close (for the indoor air and all the considered surfaces temperatures). It is noteworthy to observe that the simulated temperatures are almost always included between the band-range of ±0.5 °C. It is noteworthy to highlight that for each investigated temperature, with respect to the accuracy required by the previously mentioned code-to-code validation procedure (i.e., BESTEST), a much higher accuracy of the simulated results is now obtained. In fact, the BESTEST validation process takes into account a ±5 °C range of variation for the obtained simulation results with respect to the reference one. Conversely, in the conducted experimental validation procedure, a definitely lower range of variation is observed, highlighting a very high accuracy of the results achieved through the DETECt dynamic simulation model.

With such figures it can be detected that the highest differences between simulation and experimental results are obtained for the temperatures of the ceiling (T_ceiling) and of the South-East internal surface (T_SE), which shows the highest differences, especially during winter. On the other hand, very low variances are found out for the remaining internal surface temperatures. The lowest ones are observed for the indoor air temperature, T_IN, and for the mean radiant temperature, T_MR.

Referring to the winter season, from Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 it can be observed that the minimum temperatures are rather high with respect to the expected ones. As an example, the indoor air temperature never falls under 16.8 °C (Figure 13). This result is due to the North-East (NE) wall that, as mentioned above, is adjacent to another room in which machineries are continuously switched on (T_NE,exp is never lower than 18.5 °C, even during winter time, see Figure 11, top). Therefore, the behavior of such an element could be considered as a continuous indoor thermal load acting in the test room.

The simulated and experimental indoor air and surfaces temperatures are further compared with the aim to better assess the reliability of DETECt. Specifically, for all the investigated parameters the comparison analysis is carried out for the whole period in which the investigation was conducted (from February to November 2018). From this point of view, all the obtained simulation results are plotted against the corresponding measured ones. For the indoor air temperature (T_IN), the result of this analysis is reported in Figure 20, whereas those of all the considered internal surface temperatures (i.e., T_SW, T_NW, T_SE, T_ceiling, and T_floor) and of the Mean Radiant one (T_MR) are shown in Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26, respectively. Such figures allow one to easily detect the overall distance between simulation results (i.e., plotted points) and the bisector (corresponding measured temperatures): the lower the detected deviations, the higher the simulation reliability. Also in this case, all these figures include the confidence instrument interval, i.e., the error band range (internal to the red dash and dot lines), obtained by shifting the bisector toward ±1.0 °C. A narrower interval given by ±0.5 °C is included too (grey band) with the aim to enhance the reliability evaluation of simulation results.

By such analysis it can be observed that, for almost all the simulated indoor air and surfaces temperatures, good agreements between numerical and experimental results are achieved. Almost all the simulation results are included into the band range of ±1.0 °C. Note that similar results were obtained by comparing the simulated and experimental temperatures of the window glass and frame and of the door of the considered test room (not reported for sake of brevity).

By observing Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26 it can be noticed that during winter hours, temperatures are always higher than 16 °C (despite the measured much lower outdoor air temperatures). These rather high room temperatures are a consequence of the continuous (above mentioned) room thermal load due to the North-East wall. The lowest measured winter temperatures are detected on the ceiling (Figure 24). During summer hours all the examined temperatures never exceed 35 °C. For the South-East wall and floor, a lower number of temperature points seemingly appear in the reported plots with respect to those of the remaining building elements. In reality, the plotted points are throughout the same but those of such two elements often overlap because of the related slight time variations of temperature. This effect is due to the higher thermal inertia of the South-East wall and floor versus that of the other room elements.

Error Analysis

In order to better assess the reliability of the obtained simulation results with respect to the measured ones, the related Mean Error (ME) and Mean Percentage Error (MPE), calculated on the total number of measurements (Z = 38764), are considered:

$$\mathrm{ME}=\frac{1}{\mathrm{Z}}\cdot {\displaystyle \sum _z\left|{\mathrm{T}}_{\mathrm{sim},\mathrm{z}}{-\mathrm{T}}_{\exp ,\mathrm{z}}\right|}$$

(6)

$$\mathrm{MPE}=\frac{1}{Z}\cdot {\displaystyle \sum _z\frac{\left|T_{sim,z}-T_{\exp ,z}\right|}{T_{\exp ,z}}\cdot 100}$$

(7)

By computing ME and MPE for all the investigated parameters from February to October 2018, very low errors are detected. Specifically, the following MEs and MPEs are obtained:

• Indoor air temperature (T_IN): 0.39 °C and 1.47%;
• South-West wall temperature (T_SW): 0.45 °C and 1.79%;
• North-West wall temperature (T_NW): 0.36 °C and 1.40%;
• South-East wall temperature (T_SE): 0.42 °C and 1.57%;
• Ceiling temperature (T_ceiling): 0.48 °C and 1.92%;
• Floor temperature (T_floor): 0.61 °C and 2.30%;
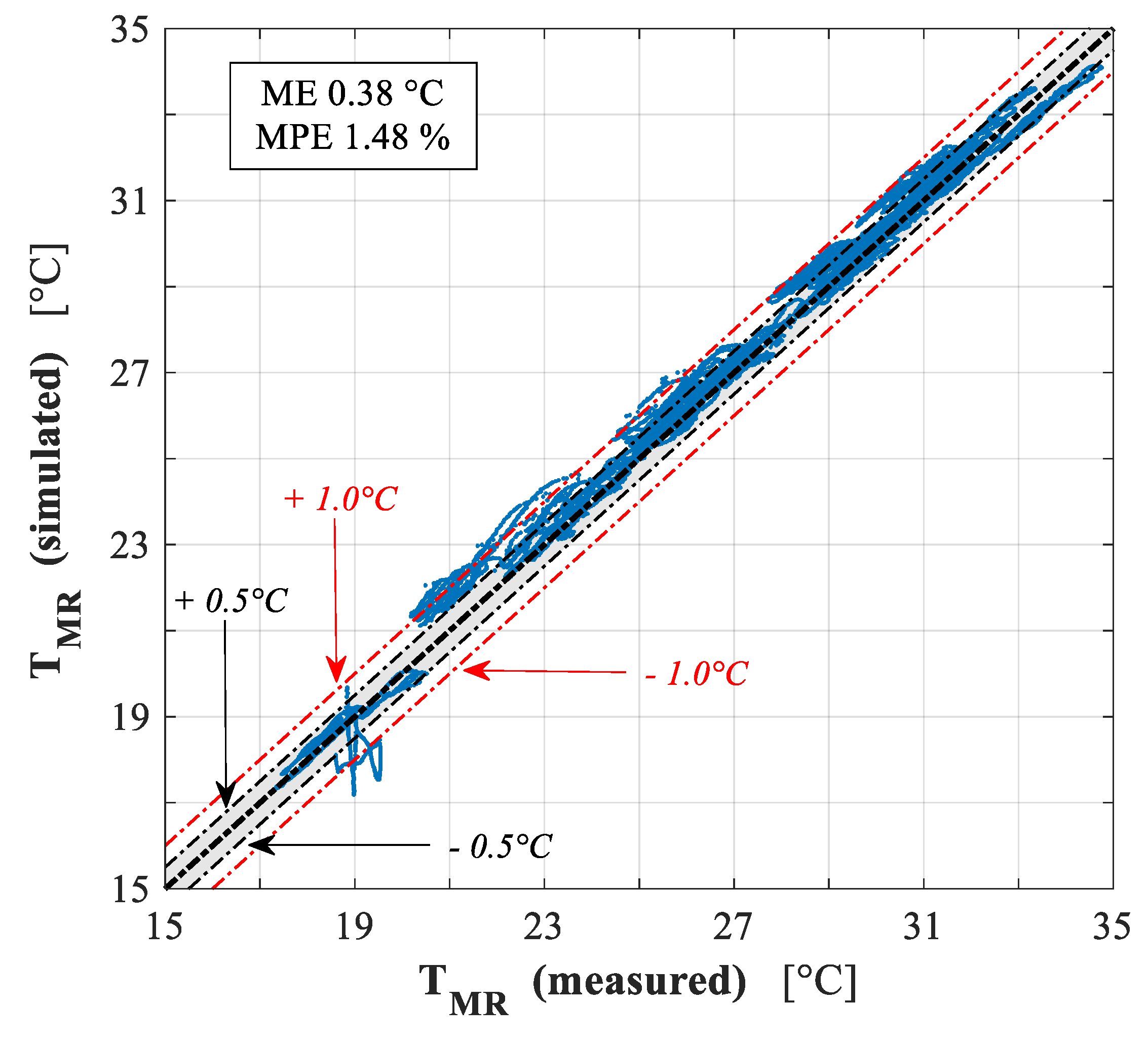
• Mean radiant temperature (T_MR): 0.38 °C and 1.48%.

It is noteworthy to observe that MEs and MPEs are always lower than 0.5 °C and 2%, respectively. An exception is obtained for T_floor for which the slightly higher ME and MPE values (0.61% and 2.3%) are probably due to uncertainty about the floor slab materials thermophysical properties.

4. Case Study

In order to show the potentiality of the developed and validated simulation tool, a novel case study is presented. Here, DETECt was used to assess the energy performance of the following:

• high solar reflective materials for reducing the outdoor surface temperature of buildings, and thus the related cooling peak and demand. Such materials (e.g., heat-reflective coatings, cool roof paints, etc.) are typically adopted for decreasing the summer overheating effect of building roofs due to the solar radiation;
• low-emittance materials to decrease the indoor surface temperature of buildings, and thus the related heating peak and demand. Such materials (low-e plasters, etc.) are typically adopted for reducing the winter heat dissipation effect due to the longwave infrared radiation energy absorbed by building perimeter walls.

High reflectance materials are used to decrease the required cooling energy and to increase the thermal comfort of buildings during the summer season, as this occurs through other passive strategies (e.g., natural ventilation, solar shading, high thermal mass, etc.). In fact, such materials allow the envelope to reflect a high amount of the incident solar radiation (as it is required in hot climate areas where buildings should be featured by white or light colored envelopes), mitigating the urban island effect, UHI [86]. For such materials a high reflectance over the solar spectrum is required and a high durability in preserving the original color and resistance to ageing [86].

In order to model through DETECt high reflectance coatings for opaque materials, suitable absorption factors are taken into account through spectral reflectance curves, by integrating such values across the whole solar range (300–2500 nm). Thus, the assessment of average absorptance, α_ext, in the above reported Equation (2), is numerically handled by dividing the solar energy spectrum into some wavelength intervals, automatically selected as a function of the shape of the spectral reflectance curves (to be inputted by the user). The average α_ext is calculated as:

$${\alpha }_{ext,m}^{}\approx {\displaystyle \sum _{i=\text{}1}^{N_{\lambda }}{\overline{\alpha }}_i(\lambda ){\left(dE\right)}_i}/{\displaystyle \sum _{i=\text{}1}^{N_{\lambda }}{\left(dE\right)}_i}$$

(8)

where $dE=J_s\left(\lambda \right)d\lambda$ is the incremental solar energy within each wavelength interval. Figure 27 shows the solar reflectance curve of a cool roof material (selected according to reference [114], i.e., light beige roof tiles, namely “H American”), and the extra-terrestrial Spectral Irradiance Distribution (SID), assessed on different size wavelength intervals shaped on the solar reflectance curve. A future enhancement will regard the calculation of the SID at the earth level assessed as a function of the air mass (given the hourly transmittance of direct-beam solar radiation under cloudless skies at a specific wavelength [115]).

Low-emittance building plasters can reduce the winter heat dissipation by increasing the building energy efficiency. They interfere with the radiation exchanges occurring among the indoor space interior surfaces (depending on the related infrared thermal emissivities). The emittances of the traditional plasters (and in general of all the construction materials) are typically high, usually ranging between 0.85 and 0.9. The corresponding absorptances are high too, contributing to a temperature increase of the building envelope where such materials are applied. Consequently, relevant conduction thermal losses potentially occur. If low-emittance internal perimeter surfaces are adopted, an effective reflection of the incident longwave radiation emitted by the indoor environment is obtained. In this case reduced thermal losses of the building are achieved (especially in cold climates) [85].

Note that the energy benefit obtained by each of such materials in the heating season may be a disadvantage in the cooling one, and vice versa. As an example, the avoided overheating obtained through roof cool paints in summer becomes an avoided free heating in winter whereas the reduction of thermal losses obtained by internal low-e plasters in winter decrease the heat dissipation in summer. In some cases, just one of such two materials can be effectively useful, the related undesired effect being negligible. Hot climate areas benefit only from external cool paints, the related avoided free heating being negligible; whereas in cold climates only internal low-e plasters are useful, the related avoided summer heat dissipation being slight.

On the other hand, in the case of temperate climate zones (e.g., Mediterranean ones) the simultaneous adoption of both such materials can be potentially convenient both the heating and cooling energy demands, being relevant. By the following analysis such occurrence is investigated through a suitable comparison study. Specifically, in the presented case study a suitable low-emittance plaster applied to the vertical internal surfaces of the above discussed test room and a cool paint finishing for related external walls and roof are considered. The system modelling and the simulation analysis is performed through DETECt. The same boundary conditions of the previously described experimental analysis (i.e., solar radiations, external temperatures, etc.) are taken into account in the simulations. The considered climate and the obtained results are referred to by the weather zone of Naples (Mediterranean zone) and to the same previously considered sample weeks (winter: March 23rd–29th; summer: July 1st–7th).

A comparison was carried out between the results obtained for the original traditional building envelope and those related to the innovative ones. Specifically, in order to assess the impact of such innovative building materials on the thermal behavior of the considered test room, the following different cases were modelled (

Table 3. Case study: radiative parameters.

Case	αext (-)		αint (-)		LW (-)	LW (-)
	Roof	Wall	Ceiling/Floor	Wall	Interior Surfaces
Reference (RC)	0.6	0.3	0.25/0.5	0.25	0.1	0.9
Low-Emissivity (LEC)				0.15	0.9	0.1
Cool Coating (CCC)	0.33–0.6 (calculated by Equation (8))	0.15–0.3 (calculated by Equation (8))		0.25	0.1	0.9
Low-Emissivity and Cool Coating (LEC&CCC)				0.15	0.9	0.1

):

• Reference Case (RC): α_ext is set to 0.3 for the exterior vertical surfaces and to 0.6 for the roof external surface, whereas ^LW of the interior surfaces is assumed to be 0.9.
• Low-Emissivity plaster Case (LEC): α_ext is set to 0.3 for the exterior vertical surfaces and to 0.6 for the roof (as for the reference case, RC), whereas ^LW of the interior surfaces is assumed to be 0.1 [87].
• Cool Coating Case (CCC): α_ext is calculated according to Equation (8), as a function of the solar reflectance data provided by reference [114] for the roof (as shown in Figure 27, varying from 0.33 to averagely 0.6), and by reference [116] for vertical surfaces coatings (varying from 0.15 to 0.3), whereas ^LW of the interior surfaces is assumed to be 0.9 (as for the reference case, RC);

Low-Emissivity plaster Case and Cool Coating Case (LEC&CCC): α_ext is calculated according to reference [114] for the roof, being on average 0.33, and by reference [116] for vertical surfaces coatings, being on average 0.15 (as for CCC), whereas ^LW of the interior surfaces is assumed to be 0.1 (as for LEC).

Results and Discussion of the Case Study

The effect due to the adoption of the considered cool coating and low-emissivity plaster on the test room is shown in Figure 28, where the time histories of indoor air and South-West internal wall surface temperatures (T_IN and T_SW, respectively) are reported in the case of the free floating temperature regime. Note that, for the sake of brevity in the following graphs only two such temperatures are considered.

In Figure 28, the results of the carried-out simulations are referred to as RC, LEC and CCC. By this figure, it is possible to note that the calculated T_IN for LEC is always higher than those of RC and CCC. Such result is a benefit in winter, when lower heating demands are needed for energy saving purposes, whereas it is undesired in summer. Here, higher cooling demands are observed (because of the overheating effect mostly detected during night times vs. RC). Regarding the cool coating materials, simulation results show lower T_IN levels with respect to those observed for RC (as expected). This result is clearly visible mostly in summer times and especially during the sunny hours. Of course, this result is a benefit of CCC for the summer season where lower cooling energies are required and a drawback for the winter one where a higher heating energy is necessary with respect to RC.

In Figure 28 (bottom), the effects of the considered low-emissivity plaster and cool coating finishing on T_SW are reported. As expected, in both the winter and summer weeks the calculated results show a decrease of T_SW profiles in both LEC and CCC with respect to RC.

In Figure 29 the time histories of T_IN and T_SW are compared for LEC&CCC and RC. Here, it is possible to observe that the calculated winter T_IN for LEC&CCC is almost always higher than for RC (mostly during the colder daily hours). In winter, this is due to the weak solar radiation heat gain effect compared to the avoided heat dissipation one linked to the occurring indoor longwave radiation. For the summer week, T_IN for LEC&CCC is always lower than for RC. In both winter and summer season HVAC system energy savings are obtained potentially.

Figure 29 (bottom) shows that with the simultaneous adoption of low-e plasters for interior walls and external cool coatings finishing, lower T_SW are achieved. Such an effect is obviously obtained for longer hourly periods in summer than in winter.

An energy performance analysis was carried out by considering the activation of a suitable space heating system. Here, a set point temperature of 20 °C for the indoor air and a time scheduling for the system activation from 09:00 to 19:00 were taken into account. The results of this analysis are reported in Figure 30 (left), where the weekly heating demands are shown for all the considered cases (RC, CCC, LEC, and LEC&CCC). In particular, an increase of the heating demand (3.23%) is obtained by CCC versus RC (i.e., cool paints for exterior building surfaces are not beneficial during winter). Conversely, satisfactory heating demand decreases of LEC and LEC&CCC with respect to RC are observed (7.79% and 4.96%, respectively).

The same analysis was carried out for the summer sample week. Here, a set point temperature for the indoor air of 26 °C and a time scheduling for the cooling system activation from 09:00 to 19:00 were taken into account. The results of this analysis are reported in Figure 30 (right) where the weekly cooling demands are shown for all the examined cases. Specifically, an increase of the cooling demand (1.53%) is obtained by LEC versus RC (i.e., low-e plasters for interior walls are not beneficial during summer). Conversely, significant cooling demand reductions of CCC and LEC&CCC with respect to RC, are observed (7.58% and 5.26%, respectively).

Future analyses will be conducted with the aim to further investigate the impact of CCC and LEC on the building energy performance. For a complete investigation, different case studies relative to building geometries, HVAC scheduling, air ventilation rates, indoor air gains, and weather conditions will be simulated and compared with the aim of providing design criteria useful for stakeholders.

5. Conclusions

This paper regards the experimental validation of an in-house developed dynamic simulation model for the building energy performance analysis. This model, implemented in a MatLab tool called DETECt, is conceived for research purposes with the aim to assess the energy performance of innovative building technologies. DETECt has been uninterruptedly refined and updated by authors with new functions and subroutines, and the presented experimental validation has to be considered as one step of the conducted research work in developing this tool. DETECt can be coupled to additional tools purposely developed for simulating innovative building plants (renewable energy systems, novel HVAC system, etc.).

The reliability of the presented model to simulate the building heat transfer and thermodynamic behavior was investigated through a suitable procedure performed by means of a purposely developed real test room located at the University of Naples Federico II, Naples, South Italy (the architectural and material features of such test room correspond to those of many Italian buildings). In the paper, details regarding the design of the developed experimental set-up, the carried out empirical analysis, and the results of the experimental validation process are discussed.

DETECt was successfully experimentally validated. Simulated indoor air and surface temperatures resulted in very good agreement with the corresponding experimental data (differences between simulated and measured temperatures were often lower than 0.5 °C and almost always lower than 1 °C). Furthermore, very low mean absolute and percentage errors were detected (e.g., for the indoor air temperature, 0.4 °C and 1.4% were achieved, respectively).

In order to show the capabilities and output features of the validated tool, a novel case study was presented. It concerns the energy performance analysis of innovative low-emissivity plasters for internal building walls and cool paints for external surfaces. The conducted investigation was also aimed at comparing different innovative passive envelope layouts adopting such materials. The analysis referred to both free floating temperature and switched on HVAC system regimes. Results included simulated time histories of indoor air and internal/external wall temperatures of the examined sample space as well as the potential heating and cooling savings.

Useful design criteria for designers and practitioners can be inferred by analyzing the reported outcomes. Specifically, for the temperate Mediterranean climate of Naples, results show that a minimum of 5% of energy saving can be obtained by simultaneously adopting low-emissivity plasters for internal walls and cool paints for external surfaces.