Brownian Motion and Thermophoretic Diffusion Effects on Micropolar Type Nanofluid Flow with Soret and Dufour Impacts over an Inclined Sheet: Keller-Box Simulations
Abstract
:1. Introduction
2. Problem Formulation
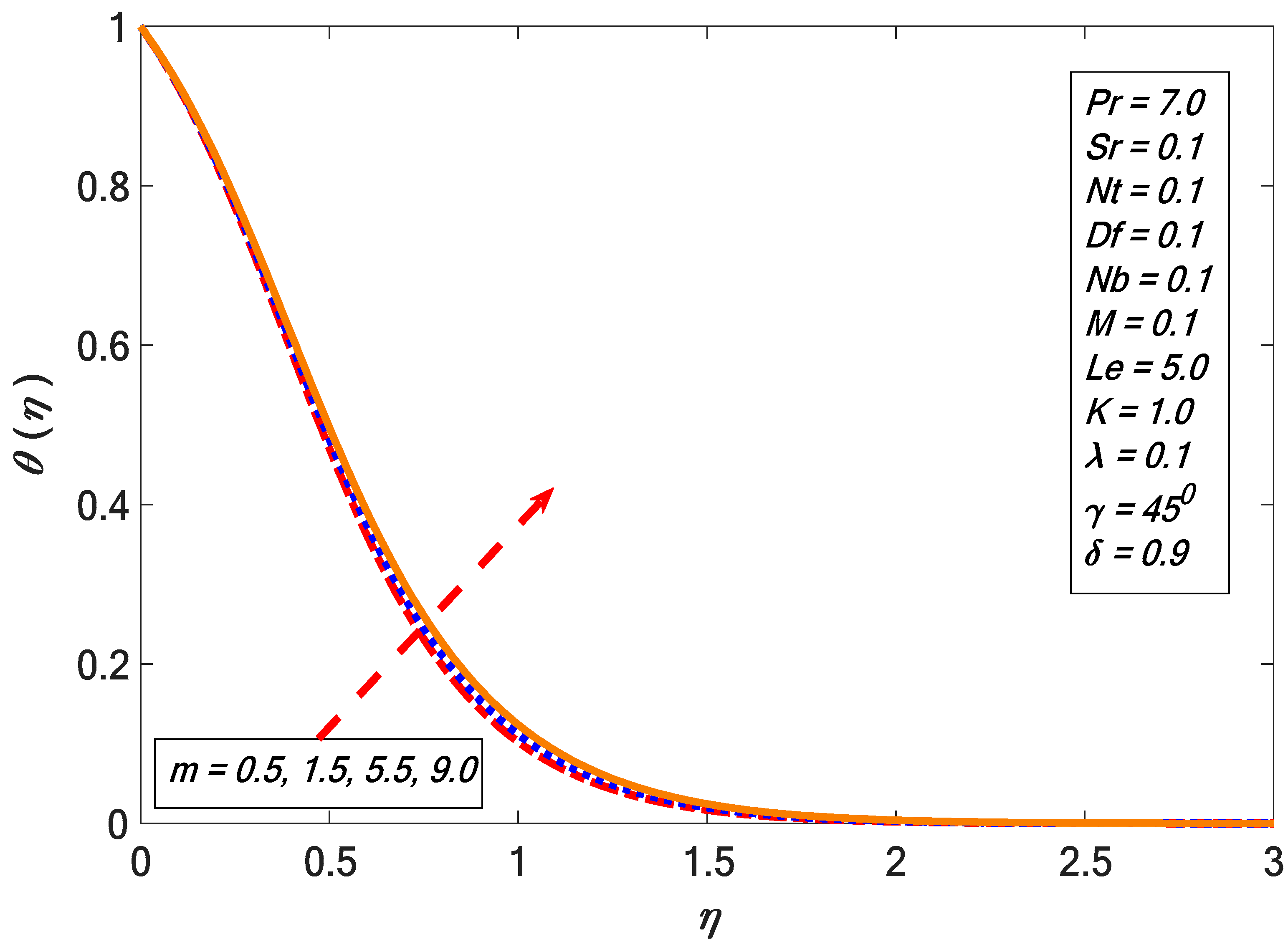
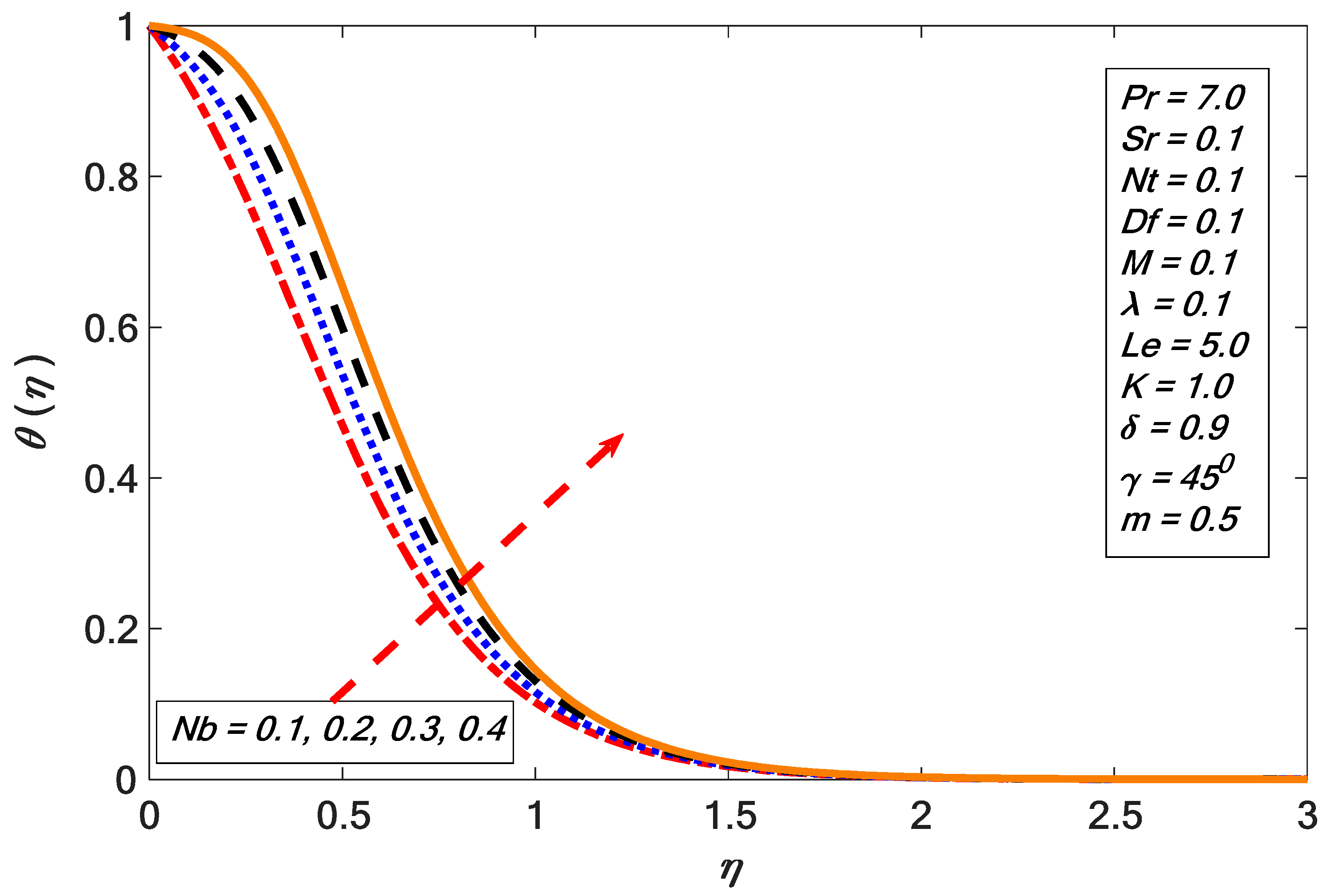
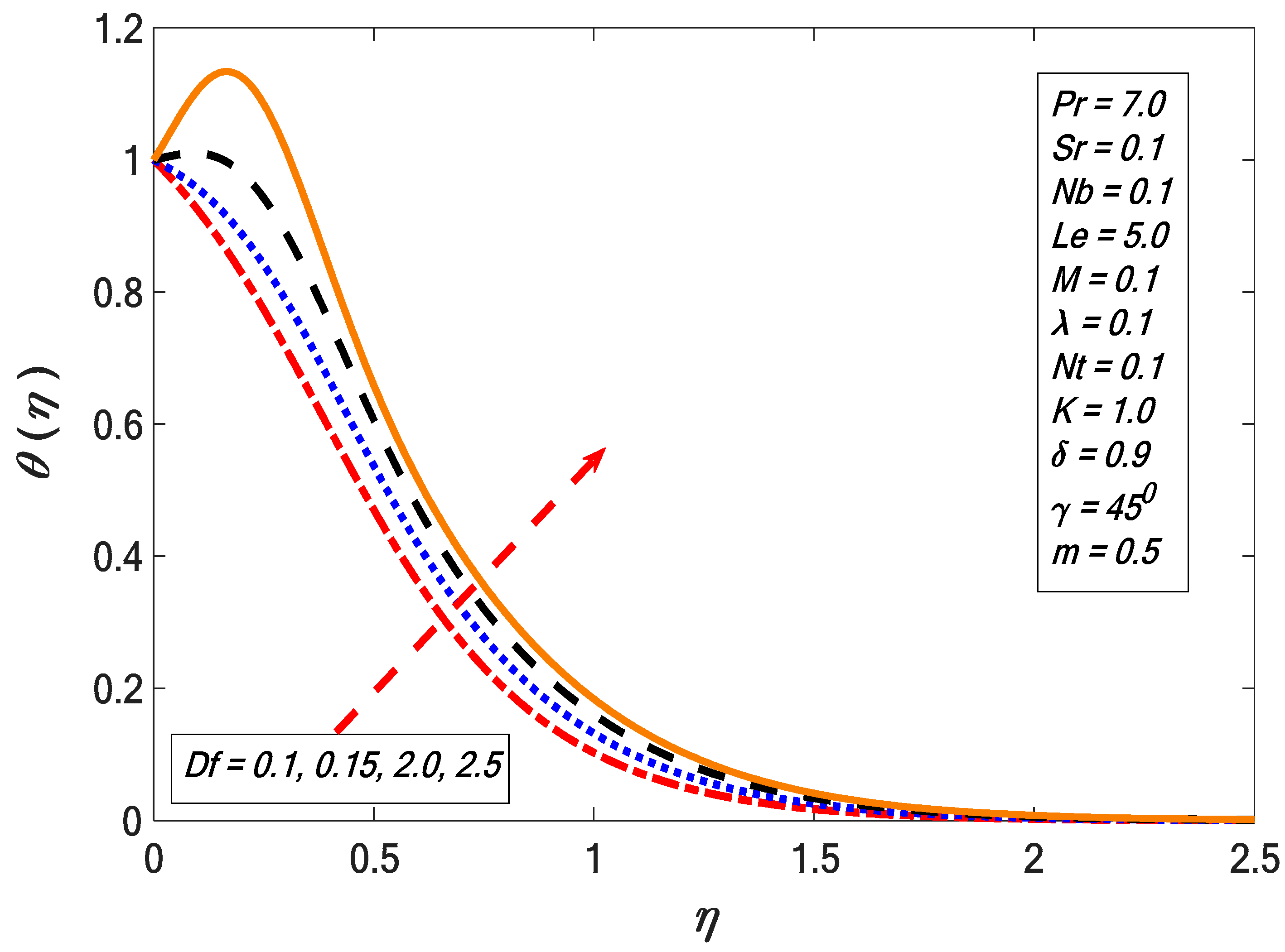
3. Results and Discussion
4. Conclusions
- ➢
- The skin friction was enhanced by enhancing the Dufour effects and decreased for large values of Soret effects.
- ➢
- The Sherwood number increased as we enhanced the Soret and Dufour effects.
- ➢
- The Nusselt number declined for increasing the Soret and Dufour effects.
- ➢
- The temperature profile was enhanced by increasing the Dufour effects.
- ➢
- The concentration profile decreased by enhancing the Soret effect.
- ➢
- The velocity profile decreased with the growth of the nonlinear stretching factor.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Fluid concentration | Soret effect parameter | Dufour effect parameter | |||
| Skin friction coefficient | Stretching rate | Reynolds number | |||
| Ambient nanoparticle volume fraction | Lewis number | Sherwood number | |||
| Surface volume fraction | Brownian motion parameter | Fluid temperature | |||
| Specific heat at constant pressure | Thermophoretic parameter | Wall temperature | |||
| Brownian diffusion coefficient | Nusselt number | Ambient temperature | |||
| Thermophoretic diffusion coefficient | Prandtl number | Wall velocity | |||
| Similarity function for velocity | Gravitational acceleration | Ambient velocity | |||
| Volume heat capacity | Kinematic viscosity | Dynamic viscosity | |||
| Dimensionless solid volume fraction | Condition at the wall | Ambient condition | |||
| Solutal buoyancy parameter | Thermal expansion coefficient | Concentration expansion coefficient | |||
| Electric conductivity | Spin gradient viscosity | Vertex viscosity | |||
| Micro inertia per unit mass | Inclination parameter | Differentiation with respect to | |||
| Velocity in direction | Velocity in direction | Cartesian coordinate | |||
| Dimensionless temperature | Non-linear stretching parameter | Thermal conductivity | |||
| Fluid density | Bouncy parameter | Uniform magnetic field strength | |||
| Material parameter | Similarity independent variable | Thermal diffusivity | |||
| Non-dimensional angular velocity |
References
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Gireesha, B.J.; Bagewadi, C.S. Heat transfer in MHD dusty boundary layer flow over an inclined stretching sheet with non-uniform heat source/sink. Adv. Math. Phys. 2012, 2012, 657805. [Google Scholar] [CrossRef]
- Singh, P.K. Heat and mass transfer in MHD boundary layer flow past an inclined plate with viscous dissipation in porous medium. Int. J. Sci. Eng. Res. 2012, 3, 1–11. [Google Scholar]
- Ali, M.; Alim, M.A.; Alam, M.S. Similarity Solution of Heat and Mass Transfer Flow over an Inclined Stretching Sheet with Viscous Dissipation and Constant Heat Flux in Presence of Magnetic Field. Procedia Eng. 2015, 105, 557–569. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, G.K.; Chamkha, A.J.; Gireesha, B.J. Boundary layer flow past an inclined stationary/moving flat plate with convective boundary condition. Afr. Mat. 2015. [Google Scholar] [CrossRef]
- Malik, M.Y.; Rehman, K.U. Effects of the chemical reaction on MHD free convection dissipative fluid flow past an inclined porous surface by way of heat generation: A Lie group analysis. Inf. Sci. Lett. 2016, 5, 35–45. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Asghar, S. Radiation effects on the mixed convection flow induced by an inclined stretching cylinder with non-uniform heat source/sink. PLoS ONE 2017, 12, e0175584. [Google Scholar] [CrossRef]
- Balla, C.S.; Kishan, N.; Gorla, R.S.R.; Gireesha, B.J. MHD boundary layer flow and heat transfer in an inclined porous square cavity filled with nanofluids. Ain Shams Eng. J. 2017, 8, 237–254. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticle. Mater. Sci. 1995, 231, 99–105. [Google Scholar]
- Nakhjavani, M.; Nikkhah, V.; Sarafraz, M.M.; Shoja, S.; Sarafraz, M. Green synthesis of silver nanoparticles using green tea leaves: Experimental study on the morphological, rheological and antibacterial behaviour. Heat Mass Transf. 2017, 53, 3201–3209. [Google Scholar] [CrossRef]
- Kamalgharibi, M.; Hormozi, F.; Zamzamian, S.A.H.; Sarafraz, M.M. Experimental studies on the stability of CuO nanoparticles dispersed in different base fluids: Influence of stirring, sonication and surface active agents. Heat Mass Transf. 2016, 52, 55–62. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid. Sci. Rep. 2014, 4, 4404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef]
- Sandeep, N.; Kumar, M.S. Heat and Mass Transfer in Nanofluid Flow over an Inclined Stretching Sheet with Volume Fraction of Dust and Nanoparticles. J. Appl. Fluid Mech. 2016, 9, 2205–2215. [Google Scholar] [CrossRef]
- Suriyakumar, P.; Devi, S.A. Effects of Suction and Internal Heat Generation on Hydromagnetic Mixed Convective Nanofluid Flow over an Inclined Stretching Plate. Eur. J. Adv. Eng. Technol. 2015, 2, 51–58. [Google Scholar]
- Ziaei-Rad, M.; Kasaeipoor, A.; Rashidi, M.M.; Lorenzini, G. A Similarity Solution for Mixed-Convection Boundary Layer Nanofluid Flow on an Inclined Permeable Surface. J. Therm. Sci. Eng. Appl. 2017. [Google Scholar] [CrossRef]
- Rashad, A. Unsteady nanofluid flow over an inclined stretching surface with convective boundary condition and anisotropic slip impact. Int. J. Heat Technol. 2017, 35, 82–90. [Google Scholar] [CrossRef]
- Mitra, A. Computational Modelling of Boundary-Layer Flow of a Nano fluid Over a Convective Heated Inclined Plate. J. Mech. Contin. Math. Sci. 2018, 13, 88–94. [Google Scholar] [CrossRef]
- Khan, M.; Shahid, A.; Malik, M.Y.; Salahuddin, T. Thermal and concentration diffusion in Jeffery nanofluid flow over an inclined stretching sheet: A generalized Fourier’s and Fick’s perspective. J. Mol. Liq. 2018, 251, 7–14. [Google Scholar] [CrossRef]
- Hatami, M.; Jing, D.; Yousif, M.A. Three-dimensional analysis of condensation nanofluid film on an inclined rotating disk by efficient analytical methods. Arab J. Basic Appl. Sci. 2018, 25, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Rafique, K.; Anwar, M.I.; Misiran, M. Keller-box study on casson nano fluid flow over a slanted permeable surface with chemical reaction. Asian Res. J. Math. 2019, 14, 1–17. [Google Scholar] [CrossRef]
- Eckert, E.R.G.; Drake, R.M., Jr. Analysis of Heat and Mass Transfer; Hemisphere Publishing: New York, NY, USA, 1987. [Google Scholar]
- Bég, O.A.; Bég, T.A.; Bakier, A.Y.; Prasad, V.R. Chemically-reacting mixed convective heat and mass transfer along inclined and vertical plates with Soret and Dufour effects: Numerical solutions. Int. J. Appl. Math. Mech. 2009, 5, 39–57. [Google Scholar]
- Pal, D.; Chatterjee, S. Soret and Dufour effects on MHD convective heat and mass transfer of a power-law fluid over an inclined plate with variable thermal conductivity in a porous medium. Appl. Math. Comput. 2013, 219, 7556–7574. [Google Scholar] [CrossRef]
- Balla, C.S.; Naikoti, K. Soret and Dufour effects on free convective heat and solute transfer in fluid saturated inclined porous cavity. Eng. Sci. Technol. Int. J. 2015, 18, 543–554. [Google Scholar] [CrossRef] [Green Version]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of thermomicrofluids. J. Math. Anal. Appl. 1972, 38, 480–496. [Google Scholar] [CrossRef] [Green Version]
- Ariman, T.M.A.N.D.; Turk, M.A.; Sylvester, N.D. Microcontinuum fluid mechanics—A review. Int. J. Eng. Sci. 1973, 11, 905–930. [Google Scholar] [CrossRef]
- Qukaszewicz, G. Micropolar Fluids: Theory and Application; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Eringen, A.C. Microcontinuum Field Theories, II; Fluent Media: New York, NY, USA, 2001. [Google Scholar]
- Rahman, M.M.; Aziz, A.; Al-Lawatia, M.A. Heat transfer in micropolar fluid along an inclined permeable plate with variable fluid properties. Int. J. Therm. Sci. 2010, 49, 993–1002. [Google Scholar] [CrossRef]
- Das, K. Slip effects on heat and mass transfer in MHD micropolar fluid flow over an inclined plate with thermal radiation and chemical reaction. Int. J. Numer. Methods Fluids 2012, 70, 96–113. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Mohammad, N.F.; Shafie, S. Unsteady MHD mixed convection flow of a micropolar fluid along an inclined stretching plate. Heat Transf. Asian Res. 2013, 42, 89–99. [Google Scholar]
- Srinivasacharya, D.; Bindu, K.H. Entropy generation in a micropolar fluid flow through an inclined channel. Alex. Eng. J. 2016, 55, 973–982. [Google Scholar] [CrossRef] [Green Version]
- Hazbavi, A.; Sharhani, S. Micropolar Fluid Flow Between Two Inclined Parallel Plates. In ASME 2017 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar] [Green Version]
- Shamshuddin, M.D.; Mishra, S.R.; Bég, O.A.; Kadir, A. Unsteady reactive magnetic radiative micropolar flow, heat and mass transfer from an inclined plate with joule heating: A model for magnetic polymer processing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 1246–1261. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; RamReddy, C.; Naveen, P. Double dispersion effect on nonlinear convective flow over an inclined plate in a micropolar fluid saturated non-Darcy porous medium. Eng. Sci. Technol. 2018, 21, 984–995. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Numerical Study on Micropolar Nanofluid Flow over an Inclined Surface by Means of Keller-Box. Asian J. Probab. Stat. 2019, 4, 1–21. [Google Scholar] [CrossRef]
- Mishra, S.R.; Baag, S.; Mohapatra, D.K. Engineering Science and Technology, an International Journal Chemical reaction and Soret effects on hydromagnetic micropolar fluid along a stretching sheet. Eng. Sci. Technol. 2016, 19, 1919–1928. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]





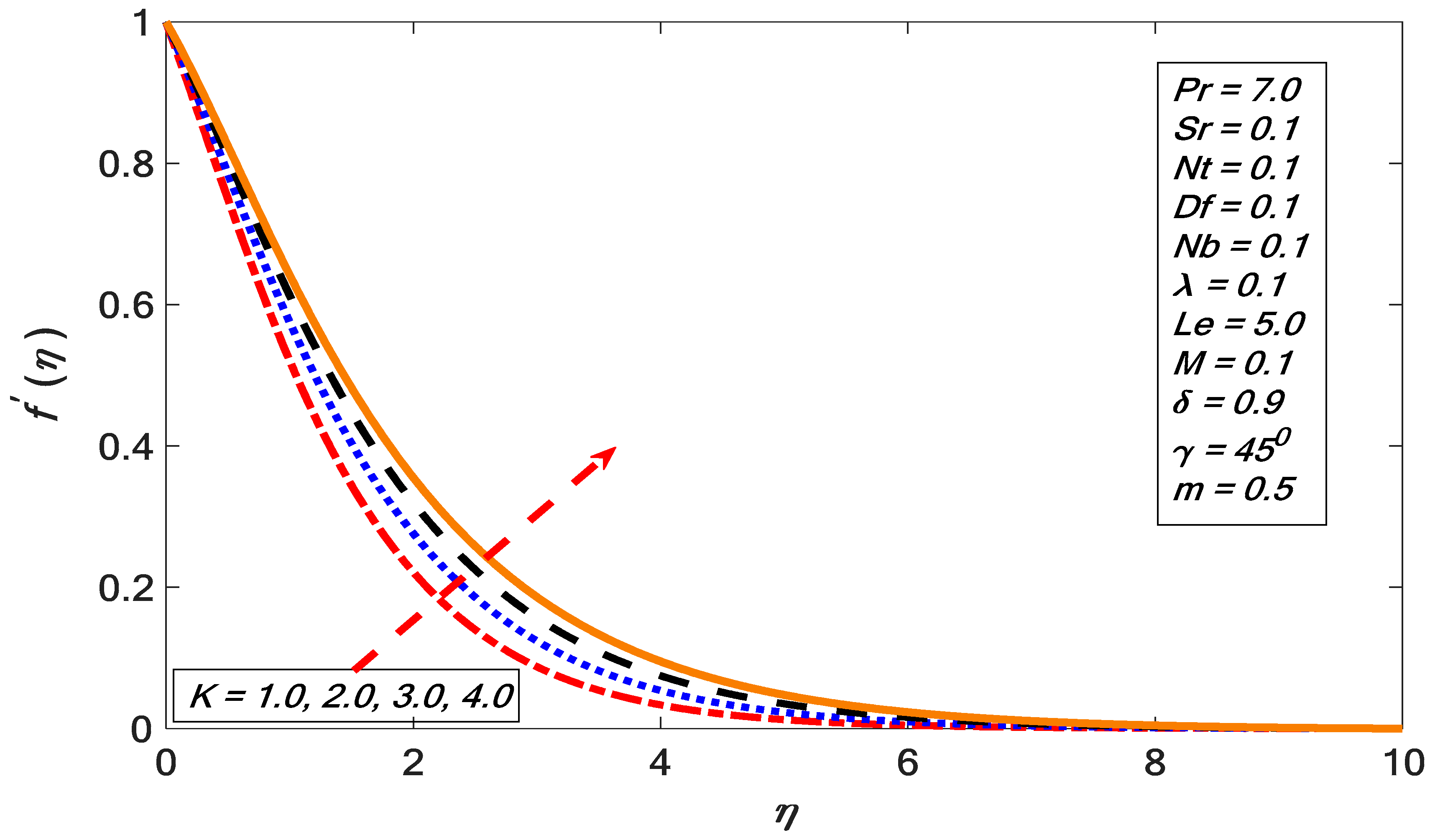



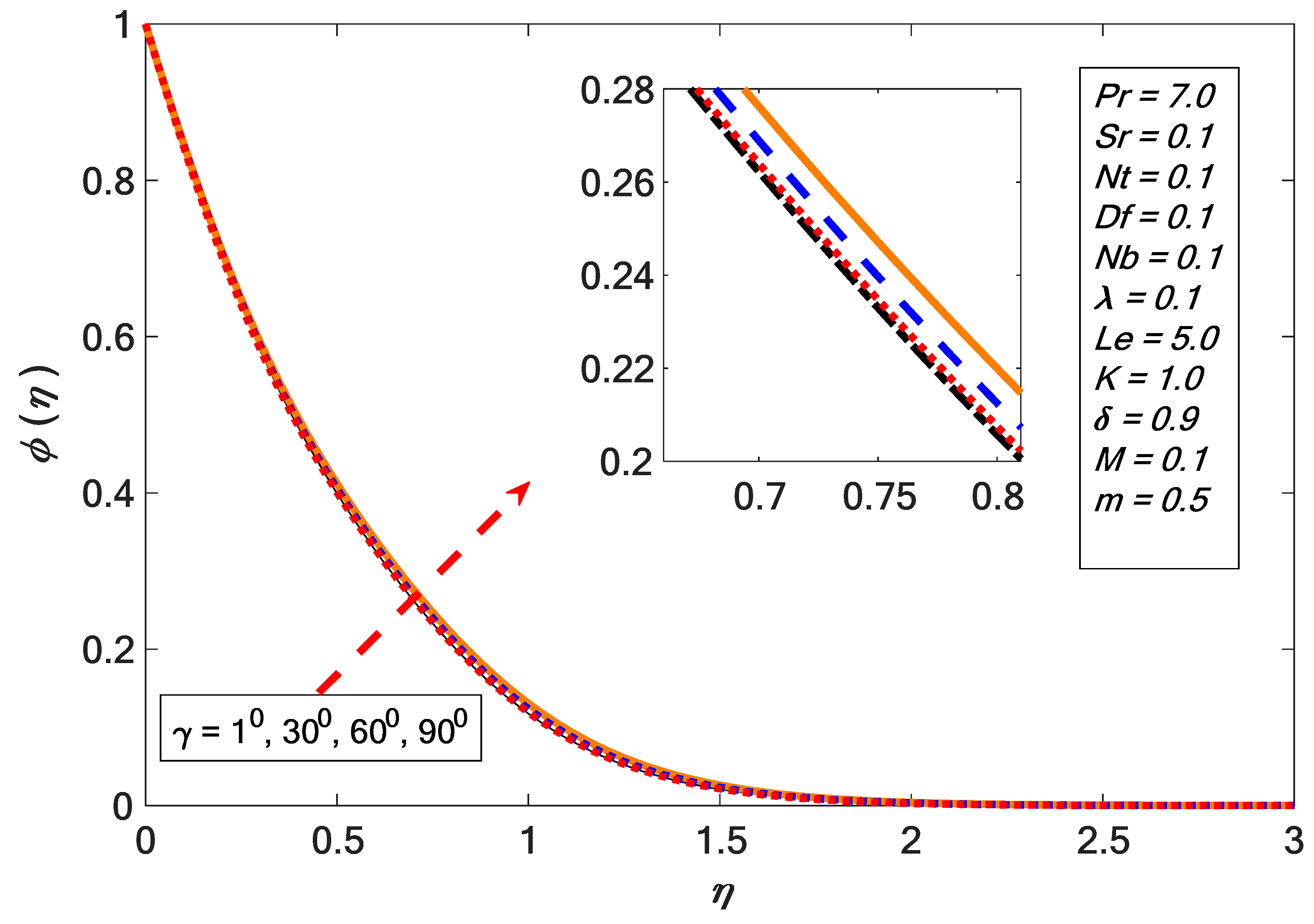




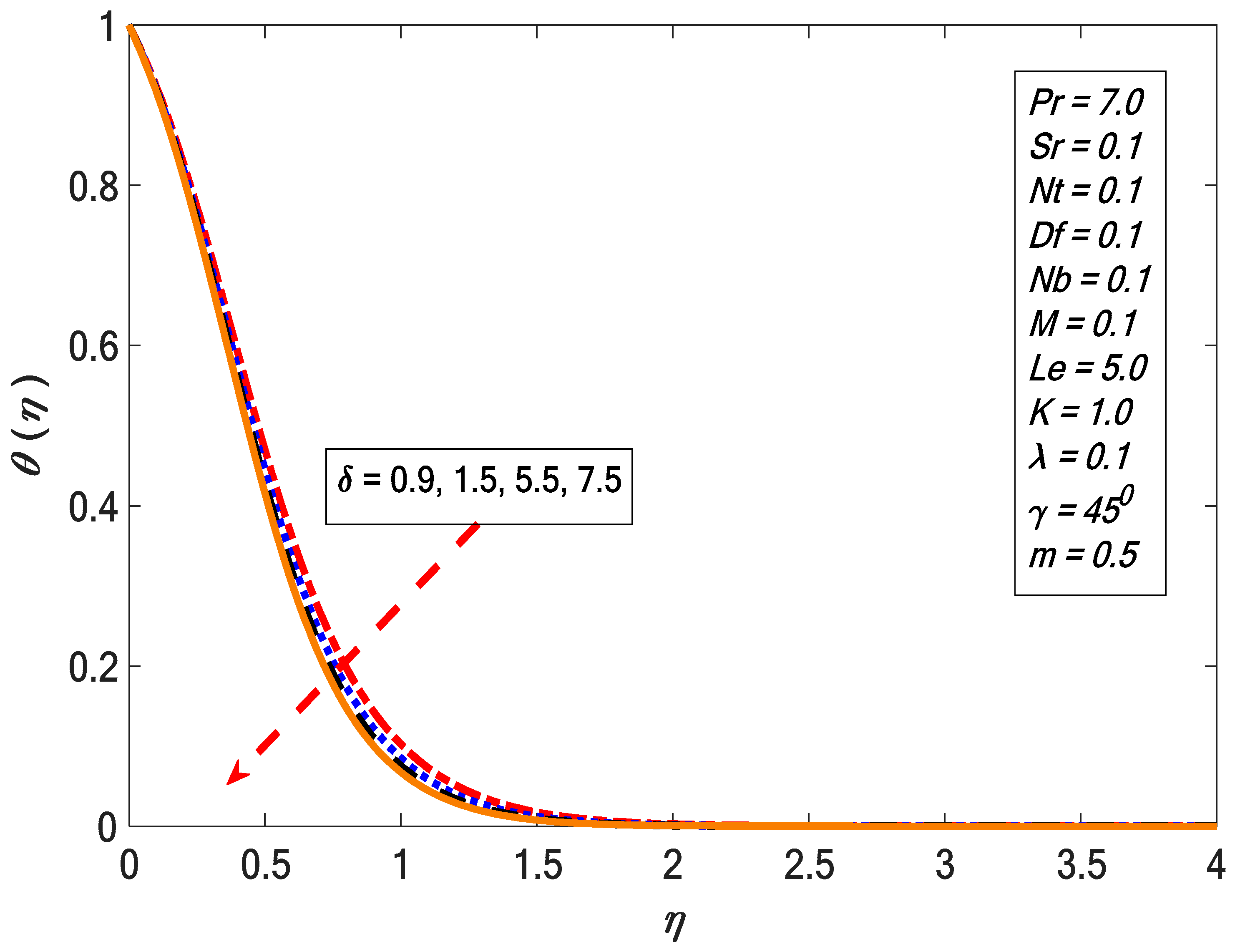

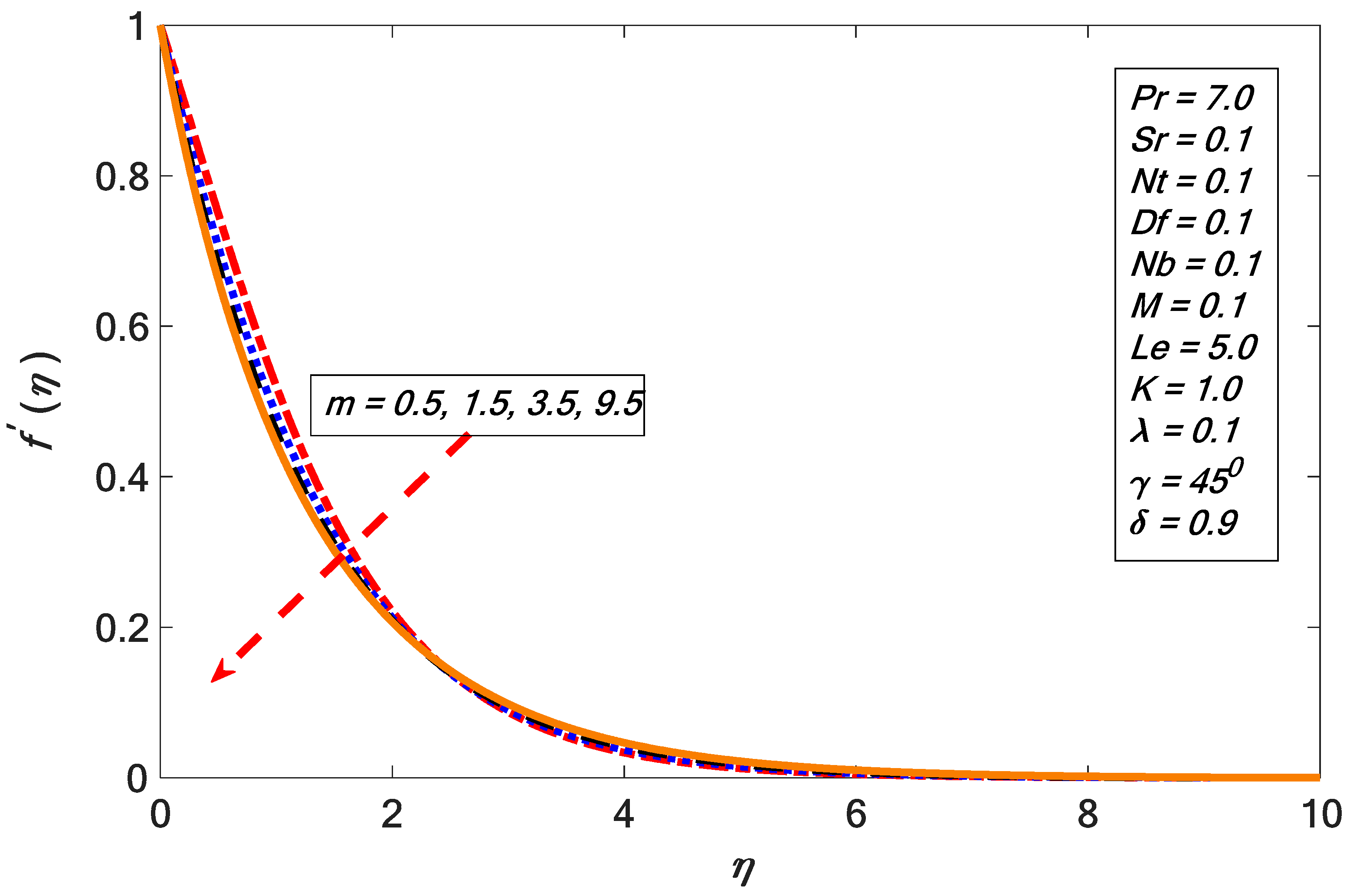







| Khan and Pop [42] | Present Results | ||||
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.9524 | 2.1294 | 0.9524 | 2.1294 |
| 0.2 | 0.2 | 0.3654 | 2.5152 | 0.3654 | 2.5152 |
| 0.3 | 0.3 | 0.1355 | 2.6088 | 0.1355 | 2.6088 |
| 0.4 | 0.4 | 0.0495 | 2.6038 | 0.0495 | 2.6038 |
| 0.5 | 0.5 | 0.0179 | 2.5731 | 0.0179 | 2.5731 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | 0.6675 | 1.6243 | 0.9558 |
| 0.3 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | 0.1634 | 1.8170 | 0.9590 |
| 0.1 | 0.3 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | 0.2360 | 1.7656 | 0.9589 |
| 0.1 | 0.1 | 10.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | 0.4982 | 1.7180 | 0.9567 |
| 0.1 | 0.1 | 7.0 | 10.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | −0.1126 | 3.0497 | 1.0268 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.5 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | 0.6555 | 1.5786 | 1.2956 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 5.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | 0.6830 | 1.6879 | 1.6675 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.5 | 0.9 | 0.1 | 0.1 | 0.5 | 450 | 0.6716 | 1.6369 | 0.8096 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 2.0 | 0.1 | 0.1 | 0.5 | 450 | 0.6774 | 1.6550 | 0.5960 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.2 | 0.1 | 0.5 | 450 | 0.5478 | 1.7375 | 0.9107 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.2 | 0.5 | 450 | −0.1503 | 1.9520 | 0.9602 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 1.0 | 450 | 0.6609 | 1.6037 | 1.1812 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 0.1 | 0.9 | 0.1 | 0.1 | 0.5 | 900 | 0.6574 | 1.5927 | 1.3004 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Nisar, K.S. Brownian Motion and Thermophoretic Diffusion Effects on Micropolar Type Nanofluid Flow with Soret and Dufour Impacts over an Inclined Sheet: Keller-Box Simulations. Energies 2019, 12, 4191. https://doi.org/10.3390/en12214191
Rafique K, Anwar MI, Misiran M, Khan I, Seikh AH, Sherif E-SM, Nisar KS. Brownian Motion and Thermophoretic Diffusion Effects on Micropolar Type Nanofluid Flow with Soret and Dufour Impacts over an Inclined Sheet: Keller-Box Simulations. Energies. 2019; 12(21):4191. https://doi.org/10.3390/en12214191
Chicago/Turabian StyleRafique, Khuram, Muhammad Imran Anwar, Masnita Misiran, Ilyas Khan, Asiful H. Seikh, El-Sayed M. Sherif, and Kottakkaran Sooppy Nisar. 2019. "Brownian Motion and Thermophoretic Diffusion Effects on Micropolar Type Nanofluid Flow with Soret and Dufour Impacts over an Inclined Sheet: Keller-Box Simulations" Energies 12, no. 21: 4191. https://doi.org/10.3390/en12214191







