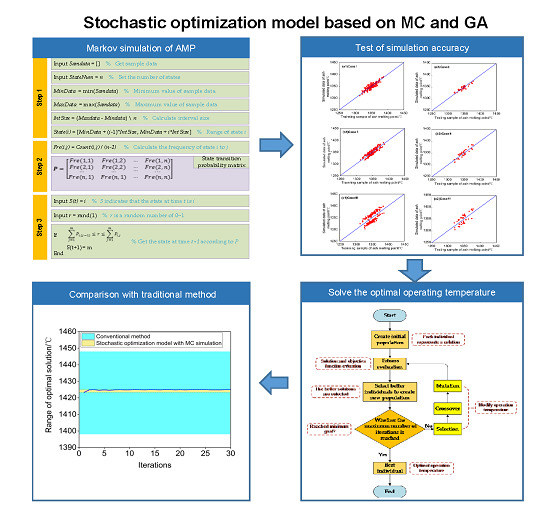
Markov Chain Simulation of Coal Ash Melting Point and Stochastic Optimization of Operation Temperature for Entrained Flow Coal Gasification
Abstract
:1. Introduction
2. Simulation Approach for AMP Series
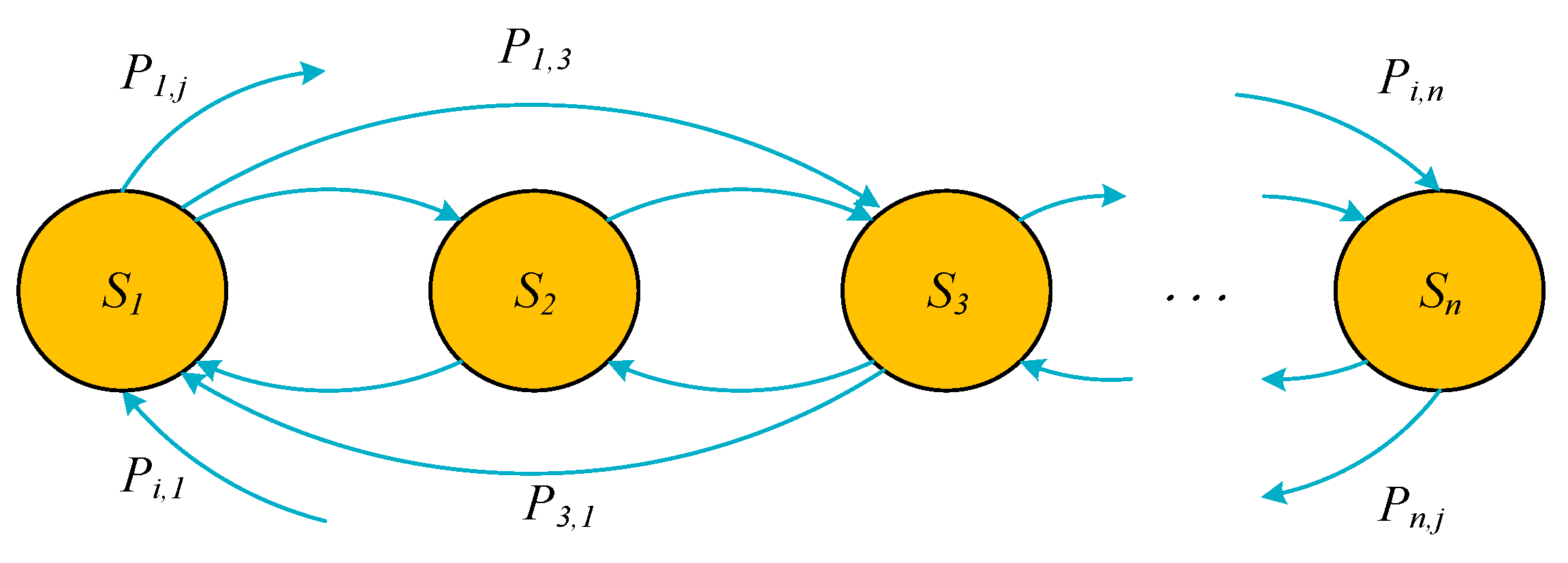
2.1. Marckov Chain
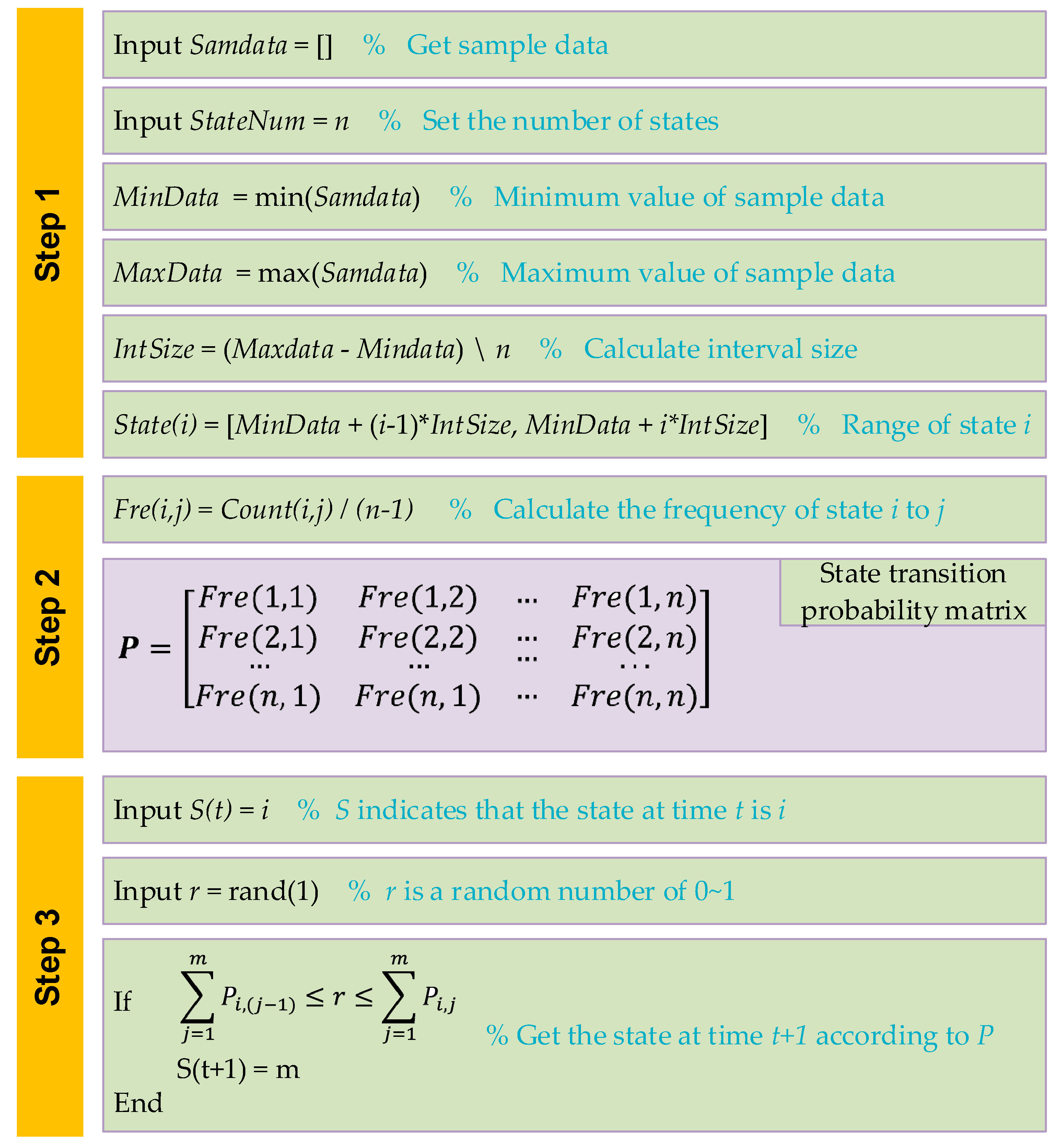
2.2. MC Simulation Procedure for AMP
- Step 1: Partitioning the state. In order to convert the AMP data into state variables for the Markov process, the data should be divided into several regions and each region could be regarded as states . The number of states depends on the capacity of the original AMP data. The interval length of each state depends on the upper and lower bounds of the original AMP data and the error range of the final simulation data.
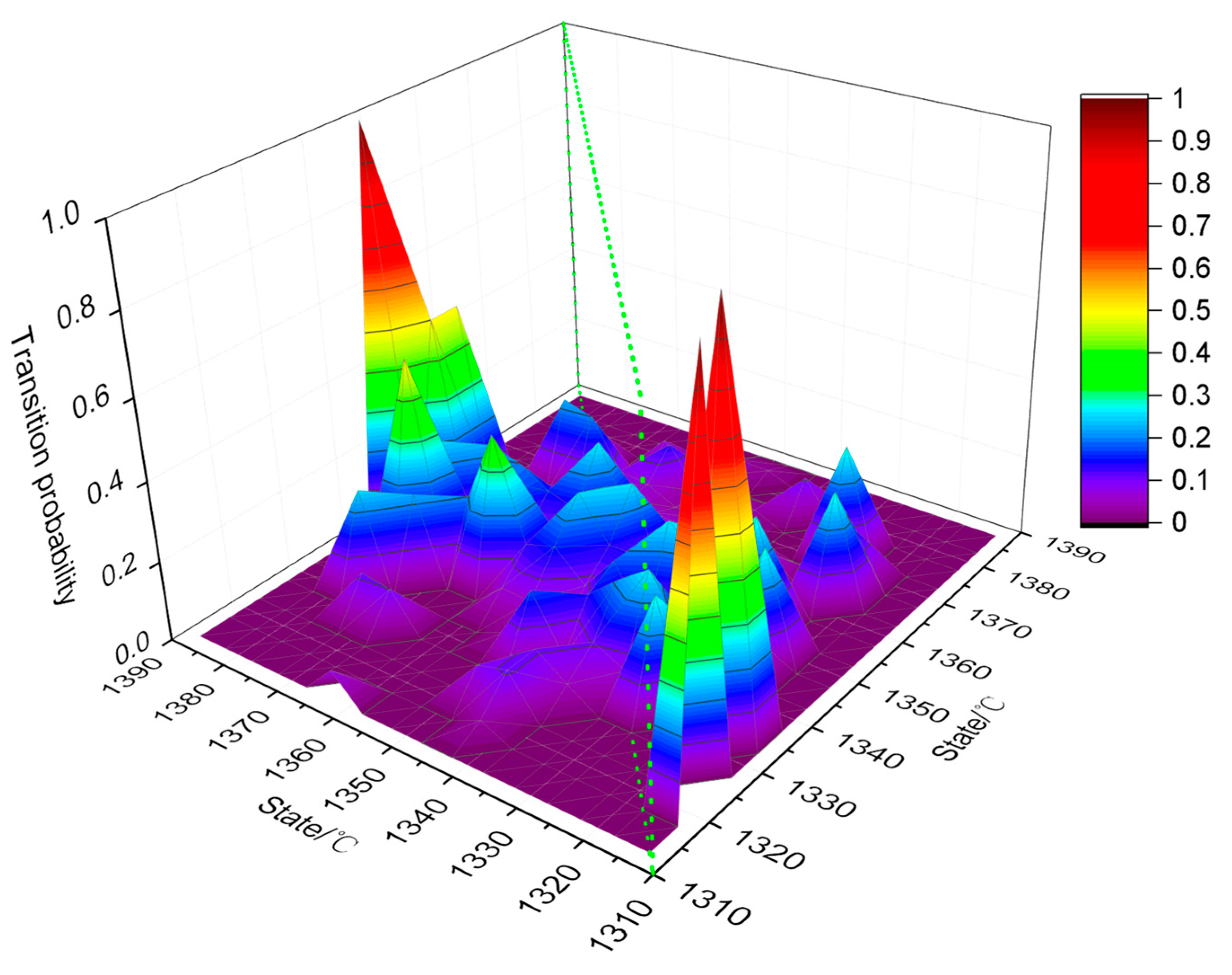
- Step 2: Constructing the probability matrix of state transition. The AMP sample data is regarded as time series, and the change of data in time series is regarded as state transition. By counting the frequency of each state transition, the probability matrix of state transition could be constructed.
- Step 3: Simulating the Markov sequences. It is assumed that the state transition probability vector of the initial state is and is a random number of . If is satisfied with:
3. Markov Chain Simulation for AMP Series
3.1. MC Simulation for AMP
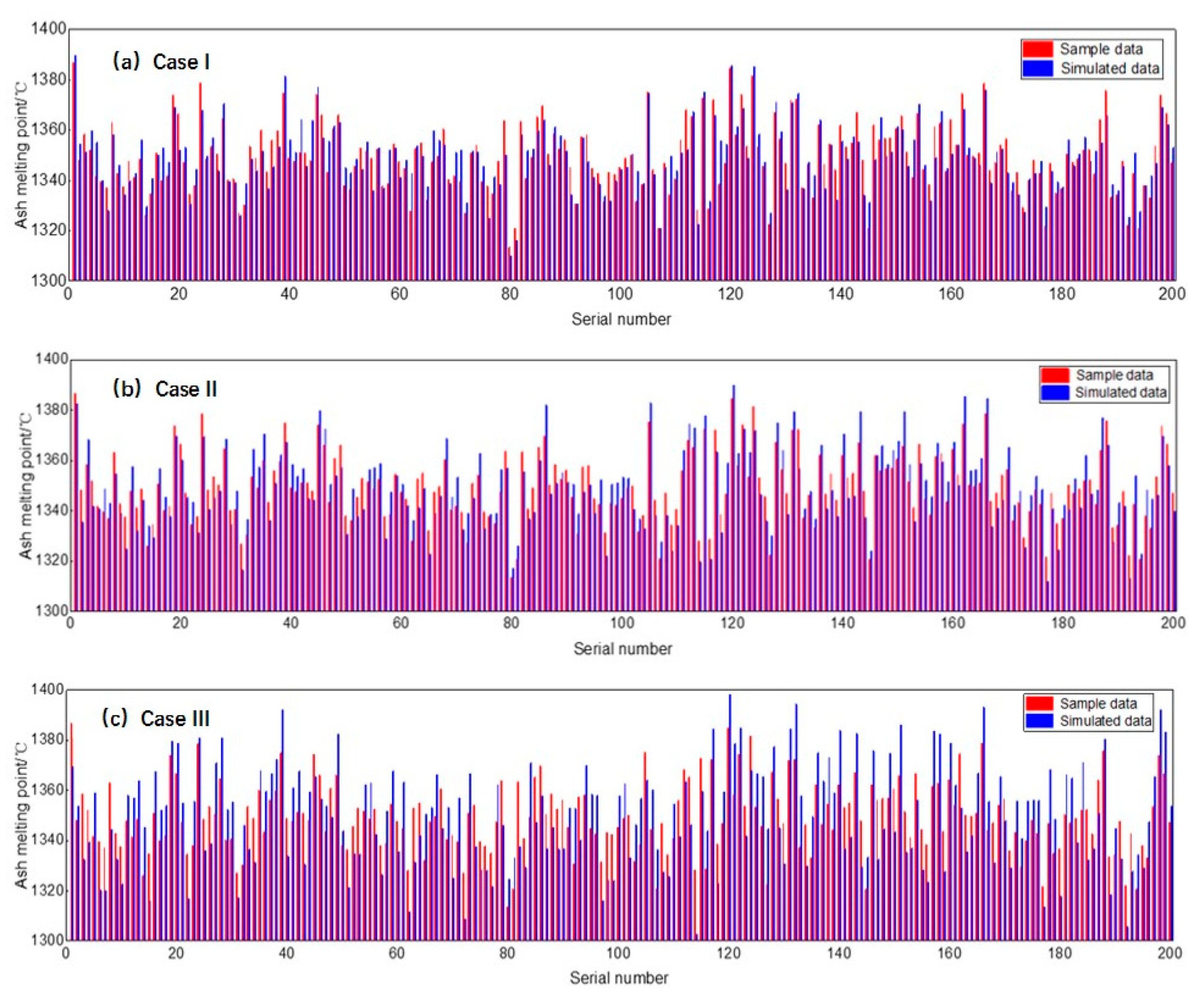
- Case I: dividing the original AMP data into 16 states.
- Case II: dividing the original AMP data into 8 states.
- Case III: dividing the original AMP data into 4 states.
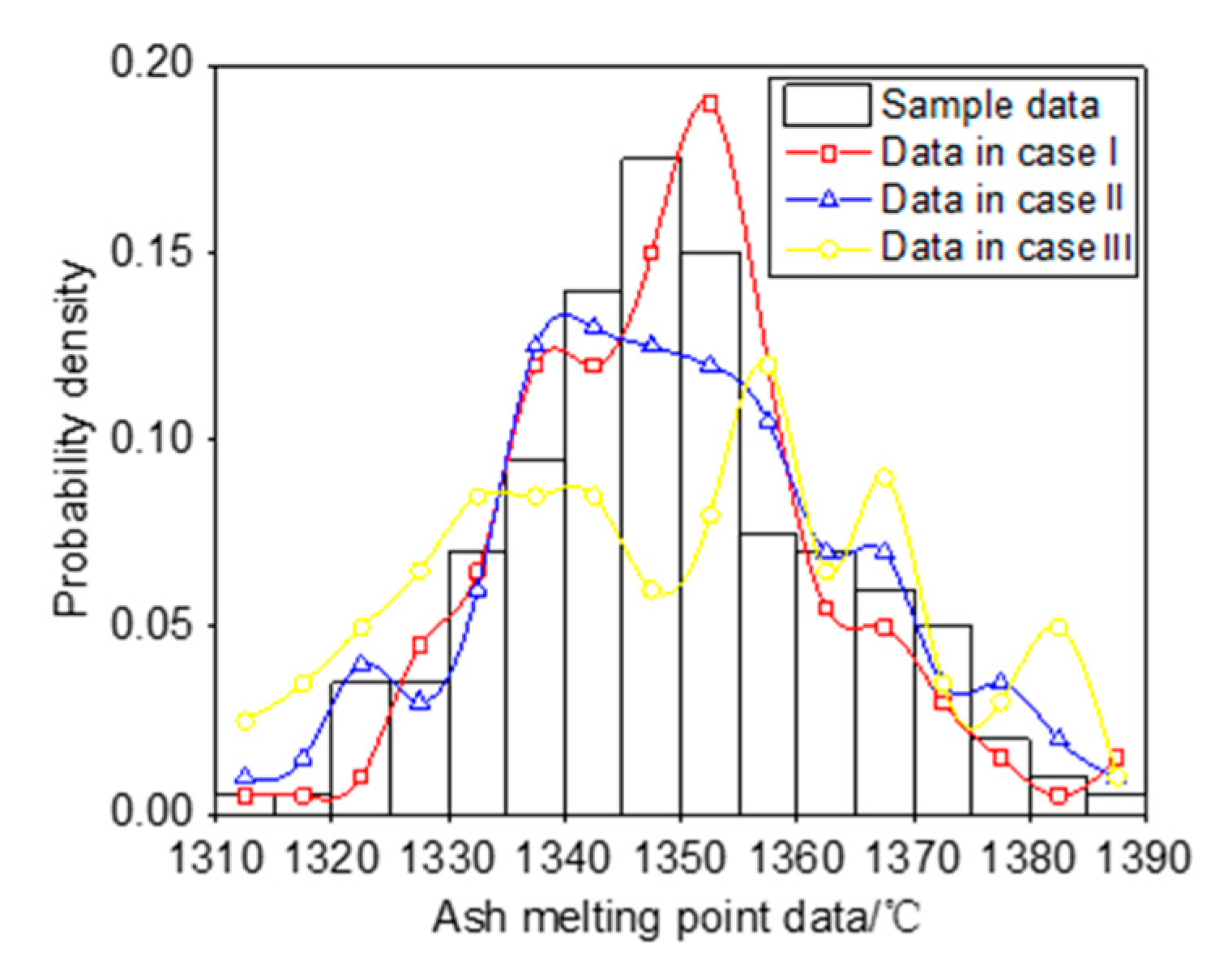
3.2. Accuracy Test
3.3. Further Discussion on the Selection of State Number
4. Stochastic Optimization of OT
4.1. Stochastic Programing Modelling Based on MC Simulation
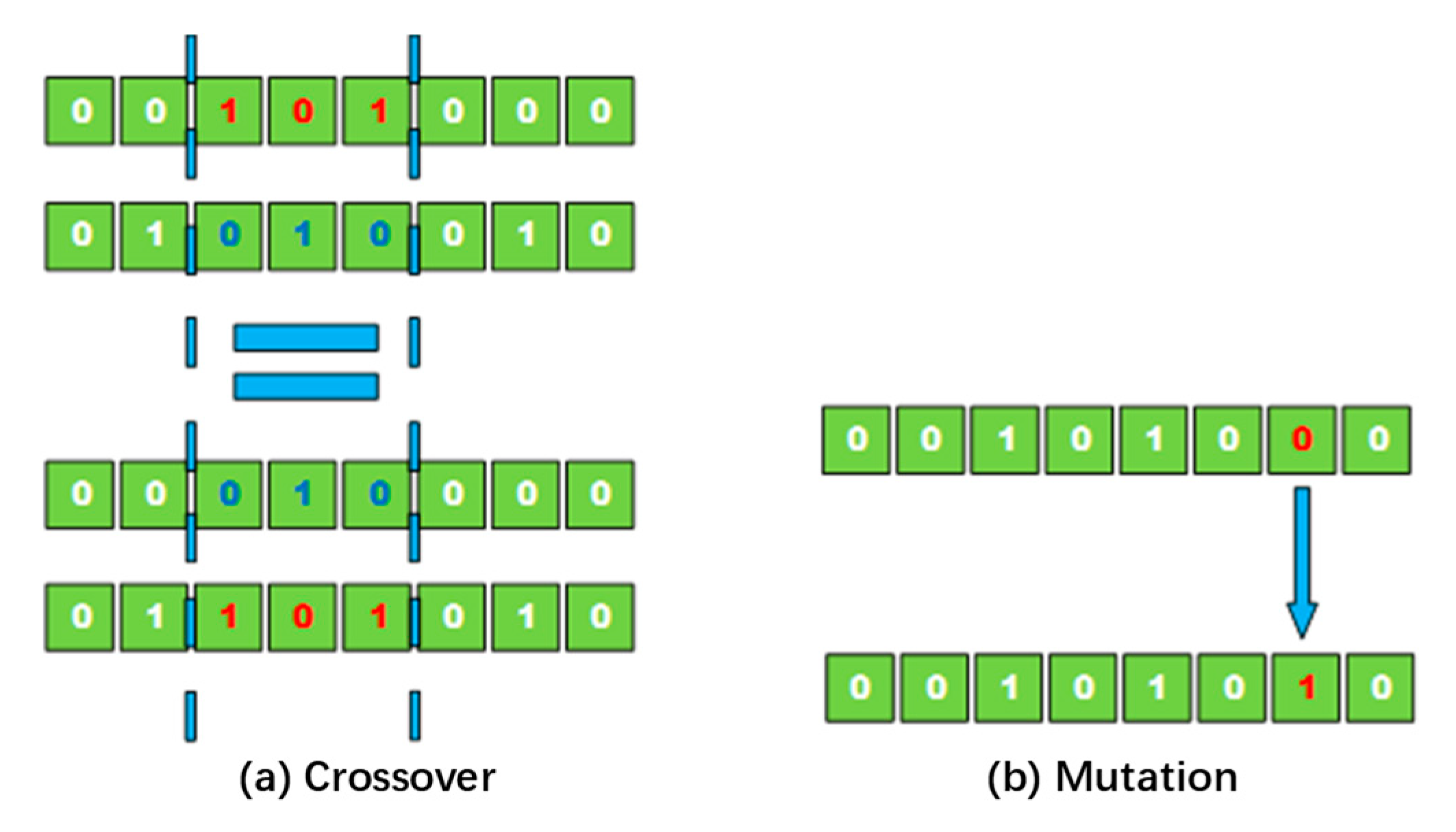
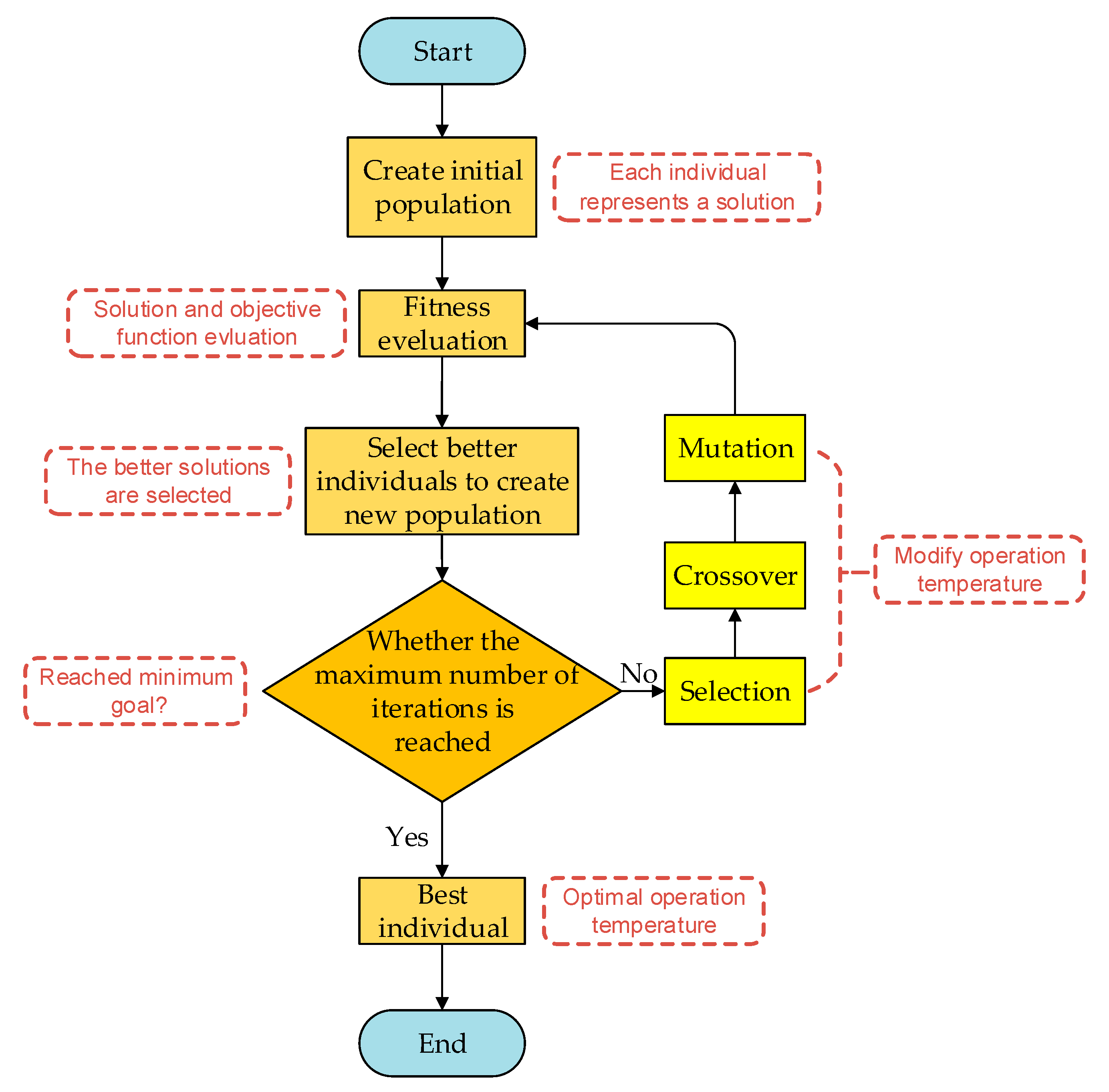
4.2. Parameter Optimization Using GA
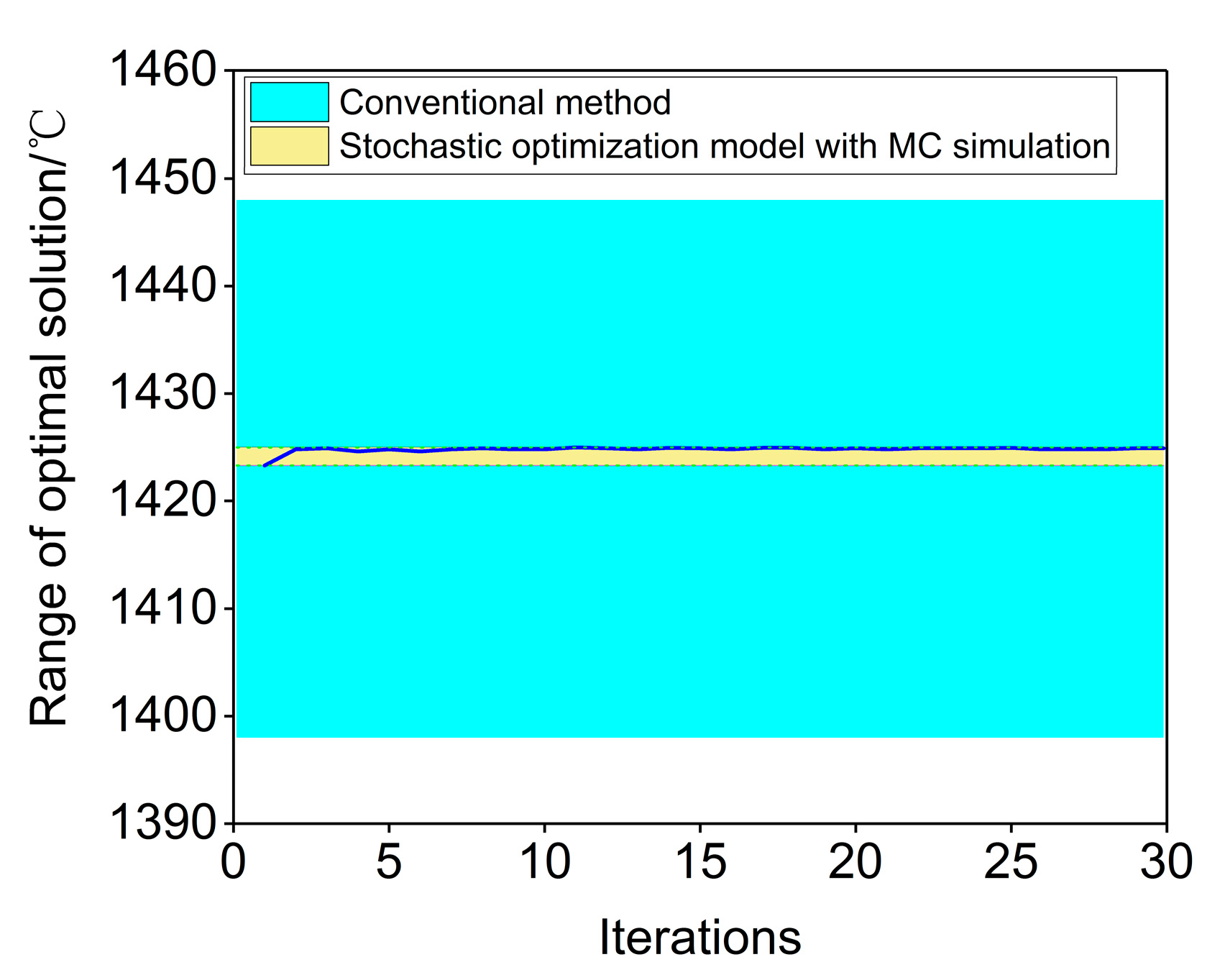
4.3. Optimization Results Comparison between Stochastic Model and Conventional Model
5. Conclusions
- (1)
- MC is an effective simulation method to describe the dynamic changes in the AMP series when considering the characteristic variations of the feed coal from batch to batch. The MC simulation method can be further used in OT optimization.
- (2)
- In the application of MC to simulate the collected original AMP data, the simulation result is best when the original AMP series is divided into 13 states. Under this partition scheme, the average relative deviation between the simulated and the original AMP is only 0.35%, which is very small. This indicates that founded MC simulation model under this scheme can accurately describe the dynamic change of AMP.
- (3)
- Compared to the conventional OT determination method that just according to the AMP mean of the feed coal over a period of time or several successive batches, the proposed stochastic programing model that integrating MC simulation for OT optimization has obvious advantages, because the dynamic changes in AMP series are taken into account. Moreover, the final optimal OT value is , which is more accurate than the result obtained with the conventional method.
- (4)
- The proposed stochastic programing model for OT optimization is a co-integration dynamic optimization problem, which can be optimized by some intelligent algorithms. The final optimal OT ascertained from the proposed stochastic programing model is more accurate than that obtained using the conventional method, which has been verified by comparing the results. Thesr show that the proposed OT optimization model based on MC simulation can provide more accurate and reliable references for actual production.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviation | Meaning |
| AMP | Ash melting point |
| OT | Operating temperature |
| MC | Markov chain |
| GA | Genetic algorithm |
| ANN | Artificial neural network |
| SVM | Support vector machine |
| RSM | Response surface methodology |
| CFD | Computational fluid dynamics |
| IADP | Iterative adaptive dynamic programming |
| MAD | Mean absolute deviation |
| RMSE | Root mean square error |
| AARE | Absolute average relative error |
| SAA | Simulated annealing algorithm |
| PSO | Particle swarm optimization |
| Symbols | |
| State at time t | |
| State set | |
| Transition probability from state i to state j | |
| State transition probability matrix | |
| Number of States | |
| n-step transition probability of state i | |
| Stationary distribution vector | |
| A random number of [0, 1] | |
| The i-th simulated data | |
| The i-th sample data | |
| T | Actual operating temperature |
| Ideal operating temperature at time t | |
| Ash melting point at time t | |
| The uniform distribution | |
| A random number of [0, 1] at time t | |
| State of ash melting point at time t | |
| N | Population size |
| Crossover probability | |
| Variation probability |
Appendix A
| SerialNumber | Sample Data/°C | Simulated Data/°C | Absolute Deviation/°C | Relative Deviation | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case I | Case II | Case III | Case I | Case II | Case III | Case I | Case II | Case III | ||
| Training set | ||||||||||
| 1 | 1386.73 | 1389.71 | 1382.70 | 1369.38 | 2.98 | 4.03 | 17.35 | 0.21% | 0.29% | 1.25% |
| 2 | 1348.07 | 1354.56 | 1335.43 | 1353.52 | 6.49 | 12.64 | 5.45 | 0.48% | 0.94% | 0.40% |
| 3 | 1358.40 | 1351.29 | 1368.33 | 1332.41 | 7.11 | 9.93 | 25.99 | 0.52% | 0.73% | 1.91% |
| 4 | 1351.90 | 1359.78 | 1341.63 | 1339.37 | 7.88 | 10.27 | 12.53 | 0.58% | 0.76% | 0.93% |
| 5 | 1341.64 | 1355.24 | 1340.72 | 1358.78 | 13.60 | 0.92 | 17.14 | 1.01% | 0.07% | 1.28% |
| 6 | 1339.47 | 1339.87 | 1348.71 | 1320.35 | 0.40 | 9.24 | 19.12 | 0.03% | 0.69% | 1.43% |
| 7 | 1337.02 | 1327.97 | 1343.08 | 1319.99 | 9.05 | 6.06 | 17.03 | 0.68% | 0.45% | 1.26% |
| 8 | 1363.06 | 1358.19 | 1354.76 | 1344.43 | 4.87 | 8.30 | 18.63 | 0.36% | 0.61% | 1.38% |
| 9 | 1342.80 | 1345.99 | 1338.90 | 1332.40 | 3.19 | 3.90 | 10.40 | 0.24% | 0.29% | 0.77% |
| 10 | 1337.50 | 1334.19 | 1324.86 | 1322.72 | 3.31 | 12.64 | 14.78 | 0.25% | 0.94% | 1.09% |
| 11 | 1347.74 | 1339.69 | 1357.57 | 1357.87 | 8.05 | 9.83 | 10.13 | 0.60% | 0.73% | 0.75% |
| 12 | 1341.27 | 1342.88 | 1331.90 | 1356.87 | 1.61 | 9.37 | 15.60 | 0.12% | 0.69% | 1.16% |
| 13 | 1348.54 | 1356.14 | 1344.16 | 1363.90 | 7.60 | 4.38 | 15.36 | 0.56% | 0.32% | 1.14% |
| 14 | 1325.90 | 1329.68 | 1333.87 | 1345.15 | 3.78 | 7.97 | 19.25 | 0.29% | 0.59% | 1.43% |
| 15 | 1334.57 | 1340.74 | 1329.23 | 1316.11 | 6.17 | 5.34 | 18.46 | 0.46% | 0.40% | 1.37% |
| 16 | 1350.79 | 1350.08 | 1356.87 | 1367.46 | 0.71 | 6.08 | 16.67 | 0.05% | 0.45% | 1.24% |
| 17 | 1340.03 | 1352.85 | 1345.33 | 1352.07 | 12.82 | 5.30 | 12.04 | 0.96% | 0.39% | 0.89% |
| 18 | 1341.68 | 1347.05 | 1337.75 | 1353.84 | 5.37 | 3.93 | 12.16 | 0.40% | 0.29% | 0.90% |
| 19 | 1373.85 | 1369.05 | 1369.57 | 1379.70 | 4.80 | 4.28 | 5.85 | 0.35% | 0.32% | 0.43% |
| 20 | 1366.54 | 1352.19 | 1360.16 | 1378.81 | 14.35 | 6.38 | 12.27 | 1.05% | 0.47% | 0.91% |
| 21 | 1347.12 | 1353.11 | 1345.21 | 1354.98 | 5.99 | 1.91 | 7.86 | 0.44% | 0.14% | 0.58% |
| 22 | 1334.47 | 1330.38 | 1343.30 | 1316.69 | 4.09 | 8.83 | 17.78 | 0.31% | 0.65% | 1.32% |
| 23 | 1337.85 | 1344.44 | 1331.19 | 1355.52 | 6.59 | 6.66 | 17.67 | 0.49% | 0.49% | 1.31% |
| 24 | 1378.56 | 1367.74 | 1369.45 | 1393.17 | 10.82 | 9.11 | 14.61 | 0.78% | 0.67% | 1.08% |
| 25 | 1348.31 | 1349.75 | 1340.49 | 1335.76 | 1.44 | 7.82 | 12.55 | 0.11% | 0.58% | 0.93% |
| 26 | 1353.46 | 1356.85 | 1344.97 | 1338.83 | 3.39 | 8.49 | 14.63 | 0.25% | 0.63% | 1.08% |
| 27 | 1350.38 | 1343.74 | 1347.82 | 1370.86 | 6.64 | 2.56 | 20.48 | 0.49% | 0.19% | 1.52% |
| 28 | 1364.58 | 1370.52 | 1368.53 | 1384.04 | 5.94 | 3.95 | 19.46 | 0.44% | 0.29% | 1.44% |
| 29 | 1340.07 | 1339.51 | 1334.40 | 1352.34 | 0.56 | 5.67 | 12.27 | 0.04% | 0.42% | 0.91% |
| 30 | 1340.46 | 1339.14 | 1347.80 | 1355.19 | 1.32 | 7.34 | 14.73 | 0.10% | 0.54% | 1.09% |
| 31 | 1326.93 | 1325.98 | 1316.53 | 1317.35 | 0.95 | 10.40 | 9.58 | 0.07% | 0.77% | 0.71% |
| 32 | 1330.30 | 1338.52 | 1336.44 | 1345.96 | 8.22 | 6.14 | 15.66 | 0.62% | 0.45% | 1.16% |
| 33 | 1353.48 | 1348.41 | 1364.27 | 1336.46 | 5.07 | 10.79 | 17.02 | 0.37% | 0.80% | 1.26% |
| 34 | 1348.87 | 1343.86 | 1357.31 | 1331.21 | 5.01 | 8.44 | 17.66 | 0.37% | 0.62% | 1.31% |
| 35 | 1359.93 | 1351.68 | 1370.46 | 1367.87 | 8.25 | 10.53 | 7.94 | 0.61% | 0.78% | 0.59% |
| 36 | 1343.38 | 1336.63 | 1335.99 | 1359.46 | 6.75 | 7.39 | 16.08 | 0.50% | 0.55% | 1.19% |
| 37 | 1355.89 | 1345.46 | 1350.85 | 1366.49 | 10.43 | 5.04 | 10.60 | 0.77% | 0.37% | 0.79% |
| 38 | 1359.67 | 1353.25 | 1362.24 | 1372.22 | 6.41 | 2.57 | 12.55 | 0.47% | 0.19% | 0.93% |
| 39 | 1374.85 | 1381.48 | 1367.37 | 1392.06 | 6.63 | 7.48 | 17.21 | 0.48% | 0.55% | 1.27% |
| 40 | 1348.89 | 1356.08 | 1358.36 | 1333.64 | 7.19 | 9.47 | 15.25 | 0.53% | 0.70% | 1.13% |
| 41 | 1347.63 | 1351.04 | 1353.76 | 1361.04 | 3.41 | 6.13 | 13.41 | 0.25% | 0.45% | 0.99% |
| 42 | 1351.14 | 1364.14 | 1356.53 | 1367.63 | 13.00 | 5.39 | 16.49 | 0.96% | 0.40% | 1.22% |
| 43 | 1350.96 | 1345.71 | 1344.88 | 1330.36 | 5.25 | 6.08 | 20.60 | 0.39% | 0.45% | 1.53% |
| 44 | 1347.80 | 1363.86 | 1344.08 | 1359.37 | 16.06 | 3.72 | 11.57 | 1.19% | 0.28% | 0.86% |
| 45 | 1374.19 | 1377.24 | 1379.72 | 1365.53 | 3.05 | 5.53 | 8.66 | 0.22% | 0.41% | 0.64% |
| 46 | 1365.98 | 1356.92 | 1372.45 | 1356.57 | 9.06 | 6.47 | 9.41 | 0.66% | 0.48% | 0.70% |
| 47 | 1343.31 | 1355.47 | 1350.46 | 1353.59 | 12.16 | 7.15 | 10.28 | 0.91% | 0.53% | 0.76% |
| 48 | 1360.68 | 1361.70 | 1353.86 | 1349.30 | 1.03 | 6.82 | 11.38 | 0.08% | 0.51% | 0.84% |
| 49 | 1366.05 | 1362.88 | 1357.21 | 1382.42 | 3.17 | 8.84 | 16.37 | 0.23% | 0.66% | 1.21% |
| 50 | 1337.96 | 1344.97 | 1330.62 | 1343.68 | 7.01 | 7.34 | 5.72 | 0.52% | 0.54% | 0.42% |
| 51 | 1336.16 | 1342.94 | 1348.61 | 1321.16 | 6.77 | 12.45 | 15.00 | 0.51% | 0.92% | 1.11% |
| 52 | 1345.54 | 1348.27 | 1337.59 | 1334.59 | 2.72 | 7.95 | 10.95 | 0.20% | 0.59% | 0.81% |
| 53 | 1352.97 | 1344.34 | 1340.55 | 1334.51 | 8.63 | 12.42 | 18.46 | 0.64% | 0.92% | 1.37% |
| 54 | 1351.54 | 1355.40 | 1356.38 | 1362.18 | 3.86 | 4.84 | 10.64 | 0.29% | 0.36% | 0.79% |
| 55 | 1348.66 | 1335.77 | 1357.25 | 1362.75 | 12.89 | 8.59 | 14.09 | 0.96% | 0.64% | 1.04% |
| 56 | 1352.53 | 1352.86 | 1358.76 | 1342.22 | 0.32 | 6.23 | 10.31 | 0.02% | 0.46% | 0.76% |
| 57 | 1337.70 | 1336.94 | 1328.89 | 1326.37 | 0.76 | 8.81 | 11.33 | 0.06% | 0.65% | 0.84% |
| 58 | 1338.66 | 1351.89 | 1347.45 | 1351.68 | 13.23 | 8.79 | 13.02 | 0.99% | 0.65% | 0.96% |
| 59 | 1354.47 | 1352.95 | 1354.02 | 1367.61 | 1.52 | 0.45 | 13.14 | 0.11% | 0.03% | 0.97% |
| 60 | 1347.44 | 1341.09 | 1350.47 | 1335.48 | 6.35 | 3.03 | 11.96 | 0.47% | 0.22% | 0.89% |
| 61 | 1344.64 | 1347.91 | 1341.95 | 1363.21 | 3.27 | 2.69 | 18.57 | 0.24% | 0.20% | 1.38% |
| 62 | 1327.90 | 1342.77 | 1336.12 | 1311.64 | 14.87 | 8.22 | 16.26 | 1.12% | 0.61% | 1.20% |
| 63 | 1352.71 | 1353.57 | 1341.29 | 1331.23 | 0.87 | 11.42 | 21.48 | 0.06% | 0.85% | 1.59% |
| 64 | 1354.91 | 1349.64 | 1348.88 | 1341.96 | 5.27 | 6.03 | 12.95 | 0.39% | 0.45% | 0.96% |
| 65 | 1332.03 | 1337.47 | 1322.58 | 1350.36 | 5.44 | 9.45 | 18.33 | 0.41% | 0.70% | 1.36% |
| 66 | 1347.41 | 1359.71 | 1338.76 | 1353.07 | 12.31 | 8.65 | 5.66 | 0.91% | 0.64% | 0.42% |
| 67 | 1349.66 | 1355.90 | 1345.80 | 1366.27 | 6.24 | 3.86 | 16.61 | 0.46% | 0.29% | 1.23% |
| 68 | 1360.46 | 1354.14 | 1368.66 | 1344.91 | 6.32 | 8.20 | 15.55 | 0.46% | 0.61% | 1.15% |
| 69 | 1340.45 | 1338.66 | 1345.20 | 1353.01 | 1.78 | 4.75 | 12.56 | 0.13% | 0.35% | 0.93% |
| 70 | 1341.74 | 1351.11 | 1353.30 | 1324.90 | 9.37 | 11.56 | 16.84 | 0.70% | 0.86% | 1.25% |
| 71 | 1339.48 | 1352.09 | 1332.57 | 1357.05 | 12.61 | 6.91 | 17.57 | 0.94% | 0.51% | 1.30% |
| 72 | 1327.03 | 1331.12 | 1338.95 | 1308.84 | 4.09 | 11.92 | 18.19 | 0.31% | 0.88% | 1.35% |
| 73 | 1350.83 | 1351.57 | 1345.10 | 1366.57 | 0.73 | 5.73 | 15.74 | 0.05% | 0.42% | 1.17% |
| 74 | 1354.03 | 1351.31 | 1362.81 | 1337.57 | 2.72 | 8.78 | 16.46 | 0.20% | 0.65% | 1.22% |
| 75 | 1339.63 | 1345.42 | 1332.81 | 1328.27 | 5.79 | 6.82 | 11.36 | 0.43% | 0.51% | 0.84% |
| 76 | 1337.69 | 1325.01 | 1338.63 | 1328.01 | 12.68 | 0.94 | 9.68 | 0.95% | 0.07% | 0.72% |
| 77 | 1334.78 | 1341.37 | 1338.84 | 1321.79 | 6.60 | 4.06 | 12.99 | 0.49% | 0.30% | 0.96% |
| 78 | 1347.45 | 1338.16 | 1356.30 | 1362.26 | 9.29 | 8.85 | 14.81 | 0.69% | 0.66% | 1.10% |
| 79 | 1363.75 | 1350.05 | 1356.90 | 1345.89 | 13.70 | 6.85 | 17.86 | 1.00% | 0.51% | 1.32% |
| 80 | 1313.52 | 1310.03 | 1317.17 | 1324.42 | 3.49 | 3.65 | 10.90 | 0.27% | 0.27% | 0.81% |
| 81 | 1320.76 | 1315.98 | 1325.89 | 1332.86 | 4.77 | 5.13 | 12.10 | 0.36% | 0.38% | 0.90% |
| 82 | 1363.40 | 1358.01 | 1355.64 | 1337.44 | 5.39 | 7.76 | 25.96 | 0.40% | 0.57% | 1.92% |
| 83 | 1340.73 | 1351.84 | 1336.70 | 1329.16 | 11.10 | 4.03 | 11.57 | 0.83% | 0.30% | 0.86% |
| 84 | 1349.17 | 1352.50 | 1339.24 | 1370.91 | 3.33 | 9.93 | 21.74 | 0.25% | 0.74% | 1.61% |
| 85 | 1365.20 | 1359.60 | 1360.11 | 1347.30 | 5.60 | 5.09 | 17.90 | 0.41% | 0.38% | 1.33% |
| 86 | 1369.65 | 1363.96 | 1382.09 | 1357.82 | 5.69 | 12.44 | 11.83 | 0.42% | 0.92% | 0.88% |
| 87 | 1350.39 | 1346.00 | 1346.62 | 1336.76 | 4.39 | 3.77 | 13.63 | 0.32% | 0.28% | 1.01% |
| 88 | 1358.48 | 1361.27 | 1350.87 | 1345.28 | 2.79 | 7.61 | 13.20 | 0.21% | 0.56% | 0.98% |
| 89 | 1352.43 | 1357.78 | 1354.88 | 1336.48 | 5.34 | 2.45 | 15.95 | 0.40% | 0.18% | 1.18% |
| 90 | 1356.11 | 1351.59 | 1351.27 | 1336.59 | 4.52 | 4.84 | 19.52 | 0.33% | 0.36% | 1.45% |
| 91 | 1345.23 | 1334.22 | 1350.46 | 1352.74 | 11.01 | 5.23 | 7.51 | 0.82% | 0.39% | 0.56% |
| 92 | 1330.57 | 1330.46 | 1338.78 | 1352.72 | 0.11 | 8.21 | 22.15 | 0.01% | 0.61% | 1.64% |
| 93 | 1357.34 | 1357.05 | 1347.50 | 1340.17 | 0.28 | 9.84 | 17.17 | 0.02% | 0.73% | 1.27% |
| 94 | 1358.07 | 1347.44 | 1350.16 | 1369.93 | 10.63 | 7.91 | 11.86 | 0.78% | 0.59% | 0.88% |
| 95 | 1344.80 | 1341.04 | 1338.91 | 1358.36 | 3.76 | 5.89 | 13.56 | 0.28% | 0.44% | 1.00% |
| 96 | 1342.66 | 1338.62 | 1352.12 | 1357.92 | 4.05 | 9.46 | 15.26 | 0.30% | 0.70% | 1.13% |
| 97 | 1331.24 | 1333.67 | 1321.83 | 1316.00 | 2.43 | 9.41 | 15.24 | 0.18% | 0.70% | 1.13% |
| 98 | 1343.07 | 1331.82 | 1350.44 | 1324.21 | 11.26 | 7.37 | 18.86 | 0.84% | 0.55% | 1.40% |
| 99 | 1342.28 | 1339.84 | 1351.00 | 1323.86 | 2.44 | 8.72 | 18.42 | 0.18% | 0.65% | 1.36% |
| 100 | 1345.14 | 1344.47 | 1353.39 | 1357.77 | 0.67 | 8.25 | 12.63 | 0.05% | 0.61% | 0.94% |
| 101 | 1348.86 | 1345.30 | 1352.91 | 1362.40 | 3.55 | 4.05 | 13.54 | 0.26% | 0.30% | 1.00% |
| 102 | 1349.97 | 1350.20 | 1340.68 | 1332.98 | 0.23 | 9.29 | 16.99 | 0.02% | 0.69% | 1.26% |
| 103 | 1331.63 | 1343.49 | 1336.67 | 1346.17 | 11.86 | 5.04 | 14.54 | 0.89% | 0.37% | 1.08% |
| 104 | 1338.13 | 1338.67 | 1332.93 | 1356.74 | 0.54 | 5.20 | 18.61 | 0.04% | 0.39% | 1.38% |
| 105 | 1375.26 | 1374.54 | 1382.80 | 1363.95 | 0.72 | 7.54 | 11.31 | 0.05% | 0.56% | 0.84% |
| 106 | 1344.16 | 1342.38 | 1338.07 | 1360.11 | 1.78 | 6.09 | 15.95 | 0.13% | 0.45% | 1.18% |
| 107 | 1321.02 | 1320.90 | 1327.63 | 1336.23 | 0.12 | 6.61 | 15.21 | 0.01% | 0.49% | 1.13% |
| 108 | 1346.84 | 1344.96 | 1338.04 | 1327.21 | 1.88 | 8.80 | 19.63 | 0.14% | 0.65% | 1.45% |
| 109 | 1334.22 | 1349.67 | 1324.07 | 1325.54 | 15.45 | 10.15 | 8.68 | 1.16% | 0.75% | 0.64% |
| 110 | 1340.50 | 1343.81 | 1334.08 | 1354.56 | 3.31 | 6.42 | 14.06 | 0.25% | 0.48% | 1.04% |
| 111 | 1355.88 | 1350.83 | 1363.87 | 1341.61 | 5.05 | 7.99 | 14.27 | 0.37% | 0.59% | 1.06% |
| 112 | 1368.10 | 1352.21 | 1374.40 | 1363.41 | 15.89 | 6.30 | 4.69 | 1.16% | 0.47% | 0.35% |
| 113 | 1365.28 | 1367.24 | 1372.98 | 1346.23 | 1.96 | 7.70 | 19.05 | 0.14% | 0.57% | 1.41% |
| 114 | 1328.10 | 1322.52 | 1319.77 | 1302.80 | 5.58 | 8.33 | 25.30 | 0.42% | 0.62% | 1.87% |
| 115 | 1372.65 | 1375.14 | 1377.81 | 1359.52 | 2.49 | 5.16 | 13.13 | 0.18% | 0.38% | 0.97% |
| 116 | 1328.56 | 1331.64 | 1320.73 | 1343.77 | 3.08 | 7.83 | 15.21 | 0.23% | 0.58% | 1.13% |
| 117 | 1372.20 | 1365.77 | 1363.39 | 1384.40 | 6.42 | 8.81 | 12.20 | 0.47% | 0.65% | 0.90% |
| 118 | 1338.50 | 1355.56 | 1331.21 | 1322.90 | 17.06 | 7.29 | 15.60 | 1.27% | 0.54% | 1.16% |
| 119 | 1346.74 | 1354.33 | 1358.94 | 1359.28 | 7.59 | 12.20 | 12.54 | 0.56% | 0.90% | 0.93% |
| 120 | 1384.66 | 1385.74 | 1389.84 | 1398.31 | 1.08 | 5.18 | 13.65 | 0.08% | 0.38% | 1.01% |
| 121 | 1358.05 | 1361.48 | 1362.85 | 1378.58 | 3.44 | 4.80 | 20.53 | 0.25% | 0.36% | 1.52% |
| 122 | 1374.22 | 1368.69 | 1372.46 | 1384.89 | 5.53 | 1.76 | 10.67 | 0.40% | 0.13% | 0.79% |
| 123 | 1353.48 | 1348.76 | 1363.22 | 1341.72 | 4.72 | 9.74 | 11.76 | 0.35% | 0.72% | 0.87% |
| 124 | 1381.55 | 1385.28 | 1371.94 | 1367.79 | 3.73 | 9.61 | 13.76 | 0.27% | 0.71% | 1.02% |
| 125 | 1353.16 | 1358.33 | 1346.39 | 1366.69 | 5.17 | 6.77 | 13.53 | 0.38% | 0.50% | 1.00% |
| 126 | 1345.60 | 1347.33 | 1335.89 | 1365.42 | 1.74 | 9.71 | 19.82 | 0.13% | 0.72% | 1.47% |
| 127 | 1322.46 | 1326.85 | 1330.02 | 1344.65 | 4.38 | 7.56 | 22.19 | 0.33% | 0.56% | 1.64% |
| 128 | 1367.18 | 1370.83 | 1375.06 | 1377.33 | 3.65 | 7.88 | 10.15 | 0.27% | 0.58% | 0.75% |
| 129 | 1356.45 | 1359.37 | 1363.80 | 1344.95 | 2.91 | 7.35 | 11.50 | 0.21% | 0.54% | 0.85% |
| 130 | 1346.80 | 1336.37 | 1338.47 | 1330.66 | 10.43 | 8.33 | 16.14 | 0.77% | 0.62% | 1.20% |
| 131 | 1371.95 | 1370.92 | 1379.26 | 1384.49 | 1.03 | 7.31 | 12.54 | 0.07% | 0.54% | 0.93% |
| 132 | 1372.25 | 1374.51 | 1356.88 | 1394.28 | 2.26 | 15.37 | 22.03 | 0.16% | 1.14% | 1.63% |
| 133 | 1337.22 | 1336.79 | 1340.73 | 1357.82 | 0.44 | 3.51 | 20.60 | 0.03% | 0.26% | 1.53% |
| 134 | 1346.18 | 1347.23 | 1347.63 | 1329.88 | 1.05 | 1.45 | 16.30 | 0.08% | 0.11% | 1.21% |
| 135 | 1333.10 | 1341.81 | 1336.69 | 1349.41 | 8.70 | 3.59 | 16.31 | 0.65% | 0.27% | 1.21% |
| 136 | 1362.21 | 1363.98 | 1365.94 | 1374.92 | 1.76 | 3.73 | 12.71 | 0.13% | 0.28% | 0.94% |
| 137 | 1346.47 | 1336.83 | 1340.76 | 1363.58 | 9.64 | 5.71 | 17.11 | 0.72% | 0.42% | 1.27% |
| 138 | 1354.52 | 1354.09 | 1348.02 | 1373.09 | 0.42 | 6.50 | 18.57 | 0.03% | 0.48% | 1.38% |
| 139 | 1344.18 | 1332.21 | 1337.83 | 1358.81 | 11.97 | 6.35 | 14.63 | 0.89% | 0.47% | 1.08% |
| 140 | 1362.00 | 1355.51 | 1370.63 | 1383.77 | 6.49 | 8.63 | 21.77 | 0.48% | 0.64% | 1.61% |
| 141 | 1353.16 | 1348.27 | 1344.98 | 1336.42 | 4.88 | 8.18 | 16.74 | 0.36% | 0.61% | 1.24% |
| 142 | 1354.90 | 1357.30 | 1345.64 | 1341.28 | 2.40 | 9.26 | 13.62 | 0.18% | 0.69% | 1.01% |
| 143 | 1367.08 | 1355.35 | 1379.42 | 1382.62 | 11.74 | 12.34 | 15.54 | 0.86% | 0.91% | 1.15% |
| 144 | 1347.93 | 1333.99 | 1337.25 | 1329.48 | 13.94 | 10.68 | 18.45 | 1.03% | 0.79% | 1.37% |
| 145 | 1320.76 | 1331.25 | 1323.92 | 1333.23 | 10.49 | 3.16 | 12.47 | 0.79% | 0.23% | 0.92% |
| 146 | 1362.00 | 1348.15 | 1362.02 | 1375.72 | 13.86 | 0.02 | 13.72 | 1.02% | 0.00% | 1.02% |
| 147 | 1356.05 | 1365.03 | 1365.77 | 1332.50 | 8.98 | 9.72 | 23.55 | 0.66% | 0.72% | 1.74% |
| 148 | 1356.70 | 1349.51 | 1358.20 | 1344.54 | 7.18 | 1.50 | 12.16 | 0.53% | 0.11% | 0.90% |
| 149 | 1356.92 | 1351.13 | 1364.13 | 1374.77 | 5.79 | 7.21 | 17.85 | 0.43% | 0.53% | 1.32% |
| 150 | 1360.67 | 1361.51 | 1367.79 | 1343.34 | 0.83 | 7.12 | 17.33 | 0.06% | 0.53% | 1.28% |
| 151 | 1365.73 | 1360.14 | 1379.42 | 1386.15 | 5.60 | 13.69 | 20.42 | 0.41% | 1.01% | 1.51% |
| 152 | 1351.39 | 1345.53 | 1358.19 | 1335.23 | 5.86 | 6.80 | 16.16 | 0.43% | 0.50% | 1.20% |
| 153 | 1341.11 | 1356.04 | 1335.62 | 1336.91 | 14.93 | 5.49 | 4.20 | 1.11% | 0.41% | 0.31% |
| 154 | 1366.60 | 1370.32 | 1358.88 | 1355.95 | 3.72 | 7.72 | 10.65 | 0.27% | 0.57% | 0.79% |
| 155 | 1344.35 | 1345.94 | 1352.10 | 1328.24 | 1.59 | 7.75 | 16.11 | 0.12% | 0.57% | 1.19% |
| 156 | 1338.34 | 1331.92 | 1345.56 | 1323.25 | 6.42 | 7.22 | 15.09 | 0.48% | 0.53% | 1.12% |
| 157 | 1361.52 | 1349.03 | 1366.70 | 1383.43 | 12.50 | 5.18 | 21.91 | 0.92% | 0.38% | 1.62% |
| 158 | 1362.76 | 1367.41 | 1359.42 | 1382.45 | 4.65 | 3.34 | 19.69 | 0.34% | 0.25% | 1.46% |
| 159 | 1343.63 | 1344.88 | 1351.59 | 1327.58 | 1.25 | 7.96 | 16.05 | 0.09% | 0.59% | 1.19% |
| 160 | 1364.30 | 1350.40 | 1367.28 | 1378.69 | 13.90 | 2.98 | 14.39 | 1.02% | 0.22% | 1.07% |
| Average | — | — | — | — | 5.93 | 7.00 | 14.94 | 0.44% | 0.52% | 1.11% |
| Testing set | ||||||||||
| 161 | 1354.05 | 1354.20 | 1350.14 | 1361.92 | 0.15 | 3.91 | 7.87 | 0.01% | 0.29% | 0.58% |
| 162 | 1374.49 | 1368.33 | 1385.49 | 1352.98 | 6.16 | 11.00 | 21.51 | 0.45% | 0.82% | 1.59% |
| 163 | 1350.13 | 1352.84 | 1355.88 | 1335.53 | 2.71 | 5.75 | 14.60 | 0.20% | 0.43% | 1.08% |
| 164 | 1349.69 | 1348.67 | 1356.28 | 1341.81 | 1.02 | 6.59 | 7.88 | 0.08% | 0.49% | 0.58% |
| 165 | 1350.97 | 1345.98 | 1360.68 | 1366.76 | 4.98 | 9.71 | 15.79 | 0.37% | 0.72% | 1.17% |
| 166 | 1378.59 | 1375.78 | 1384.70 | 1393.06 | 2.81 | 6.11 | 14.47 | 0.20% | 0.45% | 1.07% |
| 167 | 1343.81 | 1338.89 | 1333.71 | 1355.59 | 4.92 | 10.10 | 11.78 | 0.37% | 0.75% | 0.87% |
| 168 | 1346.99 | 1351.28 | 1341.02 | 1330.96 | 4.28 | 5.97 | 16.03 | 0.32% | 0.44% | 1.19% |
| 169 | 1354.18 | 1352.49 | 1344.13 | 1365.41 | 1.69 | 10.05 | 11.23 | 0.12% | 0.74% | 0.83% |
| 170 | 1356.40 | 1342.92 | 1365.30 | 1347.73 | 13.49 | 8.90 | 8.67 | 0.99% | 0.66% | 0.64% |
| 171 | 1335.90 | 1339.09 | 1342.27 | 1328.86 | 3.19 | 6.37 | 7.04 | 0.24% | 0.47% | 0.52% |
| 172 | 1343.18 | 1334.27 | 1347.59 | 1355.78 | 8.91 | 4.41 | 12.60 | 0.66% | 0.33% | 0.93% |
| 173 | 1329.18 | 1327.50 | 1325.30 | 1340.73 | 1.69 | 3.88 | 11.55 | 0.13% | 0.29% | 0.86% |
| 174 | 1339.83 | 1340.50 | 1346.03 | 1355.65 | 0.67 | 6.20 | 15.82 | 0.05% | 0.46% | 1.17% |
| 175 | 1348.02 | 1342.93 | 1353.72 | 1356.07 | 5.09 | 5.70 | 8.05 | 0.38% | 0.42% | 0.60% |
| 176 | 1342.70 | 1347.59 | 1348.48 | 1355.93 | 4.89 | 5.78 | 13.23 | 0.36% | 0.43% | 0.98% |
| 177 | 1321.68 | 1329.50 | 1311.72 | 1313.64 | 7.81 | 9.96 | 8.04 | 0.59% | 0.74% | 0.60% |
| 178 | 1346.92 | 1343.46 | 1340.80 | 1368.22 | 3.46 | 6.12 | 21.30 | 0.26% | 0.45% | 1.58% |
| 179 | 1334.86 | 1339.25 | 1324.42 | 1348.45 | 4.39 | 10.44 | 13.59 | 0.33% | 0.77% | 1.01% |
| 180 | 1336.79 | 1337.33 | 1342.21 | 1317.83 | 0.55 | 5.42 | 18.96 | 0.04% | 0.40% | 1.40% |
| 181 | 1350.31 | 1356.17 | 1340.38 | 1366.35 | 5.86 | 9.93 | 16.04 | 0.43% | 0.74% | 1.19% |
| 182 | 1347.10 | 1345.93 | 1352.54 | 1364.79 | 1.17 | 5.44 | 17.69 | 0.09% | 0.40% | 1.31% |
| 183 | 1348.67 | 1350.40 | 1341.13 | 1339.23 | 1.73 | 7.54 | 9.44 | 0.13% | 0.56% | 0.70% |
| 184 | 1352.02 | 1357.13 | 1361.94 | 1371.11 | 5.11 | 9.92 | 19.09 | 0.38% | 0.73% | 1.41% |
| 185 | 1352.23 | 1347.39 | 1346.46 | 1332.36 | 4.84 | 5.77 | 19.87 | 0.36% | 0.43% | 1.47% |
| 186 | 1342.50 | 1351.54 | 1348.20 | 1336.75 | 9.04 | 5.70 | 5.75 | 0.67% | 0.42% | 0.43% |
| 187 | 1364.00 | 1354.88 | 1377.02 | 1350.65 | 9.12 | 13.02 | 13.35 | 0.67% | 0.96% | 0.99% |
| 188 | 1375.80 | 1365.70 | 1365.94 | 1387.25 | 10.09 | 9.86 | 11.45 | 0.73% | 0.73% | 0.85% |
| 189 | 1333.28 | 1338.41 | 1327.57 | 1318.59 | 5.13 | 5.71 | 14.69 | 0.38% | 0.42% | 1.09% |
| 190 | 1334.23 | 1335.92 | 1343.19 | 1344.89 | 1.70 | 8.96 | 10.66 | 0.13% | 0.66% | 0.79% |
| 191 | 1347.61 | 1345.71 | 1341.68 | 1332.43 | 1.90 | 5.93 | 15.18 | 0.14% | 0.44% | 1.12% |
| 192 | 1322.17 | 1325.41 | 1313.04 | 1305.72 | 3.24 | 9.13 | 16.45 | 0.24% | 0.68% | 1.22% |
| 193 | 1342.65 | 1350.87 | 1353.91 | 1327.61 | 8.21 | 11.26 | 15.04 | 0.61% | 0.83% | 1.11% |
| 194 | 1320.65 | 1327.58 | 1322.85 | 1334.24 | 6.92 | 2.20 | 13.59 | 0.52% | 0.16% | 1.01% |
| 195 | 1337.95 | 1337.95 | 1348.05 | 1329.05 | 0.00 | 10.10 | 8.90 | 0.00% | 0.75% | 0.66% |
| 196 | 1333.07 | 1341.68 | 1344.45 | 1347.36 | 8.61 | 11.38 | 14.29 | 0.65% | 0.84% | 1.06% |
| 197 | 1353.43 | 1346.88 | 1346.28 | 1365.41 | 6.55 | 7.15 | 11.98 | 0.48% | 0.53% | 0.89% |
| 198 | 1373.85 | 1369.05 | 1369.84 | 1392.12 | 4.80 | 4.01 | 18.27 | 0.35% | 0.29% | 1.33% |
| 199 | 1366.54 | 1362.19 | 1358.02 | 1383.25 | 4.35 | 8.52 | 16.71 | 0.32% | 0.62% | 1.22% |
| 200 | 1347.12 | 1353.11 | 1339.85 | 1353.64 | 5.99 | 7.27 | 6.52 | 0.44% | 0.54% | 0.48% |
| Average | — | — | — | — | 4.68 | 7.53 | 13.37 | 0.35% | 0.56% | 0.99% |
Appendix B
- # Constructing State Transition Probability Matrix
- clear
- A = xlsread(‘200sample’, ‘A1:A200′);
- t = length(A);
- B = unique(A);
- tt = length(B);
- E = sort(B,’ascend’);
- T = zeros(16,16);
- TR = zeros(16,16);
- a = 0;
- b = 0;
- c = 0;
- d = 0;
- e = 0;
- f = 0;
- g = 0;
- h = 0;
- k = 0;
- l = 0;
- m = 0;
- n = 0;
- o = 0;
- p = 0;
- q = 0;
- r = 0;
- for j=1:1:tt
- Localization=find(A==E(j));
- for i=1:1:length(Localization)
- if Localization(i)+1>t
- break;
- elseif A(Localization(i)+1)==E(1)
- a = a+1;
- elseif A(Localization(i)+1)==E(2)
- b = b+1;
- elseif A(Localization(i)+1)==E(3)
- c = c+1;
- elseif A(Localization(i)+1)==E(4)
- d = d+1;
- elseif A(Localization(i)+1)==E(5)
- e = e+1;
- elseif A(Localization(i)+1)==E(6)
- f = f+1;
- elseif A(Localization(i)+1)==E(7)
- g = g+1;
- elseif A(Localization(i)+1)==E(8)
- h = h+1;
- elseif A(Localization(i)+1)==E(9)
- k = k+1;
- elseif A(Localization(i)+1)==E(10)
- l = l+1;
- elseif A(Localization(i)+1)==E(11)
- m = m+1;
- elseif A(Localization(i)+1)==E(12)
- n = n+1;
- elseif A(Localization(i)+1)==E(13)
- o = o+1;
- elseif A(Localization(i)+1)==E(14)
- p = p+1;
- elseif A(Localization(i)+1)==E(15)
- q = q+1;
- elseif A(Localization(i)+1)==E(16)
- r = r+1;
- end
- end
- T(j,1:tt) = [a,b,c,d,e,f,g,h,k,l,m,n,o,p,q,r];
- end
- TT = T;
- for u=2:1:tt
- TT(u,:)=T(u,:)-T(u-1,:);
- end
- TT;
- Y = sum(TT,2);
- for uu = 1:1:tt
- TR(uu,:) = TT(uu,:)./Y(uu,1);
- end
- TR
- # Simulating 100000 AMP data
- clear
- A = xlsread(‘200sample’, ‘W1:AL16′);#A is the state transition probability matrix TR
- B = zeros(1,100000);
- B(1) = 16;
- i = 16;
- s = zeros(1,16);
- n = 2;
- for n = 2:100000
- r = rand(1);
- i = B(n-1);
- s(1) = A(i,1);
- for j = 2:16
- s(j) = s(j-1)+A(i,j);
- if r >= 0&&r <= s(1)
- B(n) = 1;
- elseif r >= s(j-1)&&r <= s(j)
- B(n) = j;
- end
- end
- end
- B
- for i = 1:100000
- r = rand(1);
- B(i) = 1310+B(i)*5-5*r;
- end
- B’
References
- Bezdek, R.H.; Wendling, R.M. The return on investment of the clean coal technology program in the USA. Energy Policy 2013, 54, 104–112. [Google Scholar] [CrossRef]
- Chang, S.; Zhuo, J.; Meng, S.; Qin, S.; Yao, Q. Clean coal technologies in China: Current status and future perspectives. Engineering 2016, 2, 447–459. [Google Scholar] [CrossRef]
- Cui, L.; Li, Y.; Tang, Y.; Shi, Y.; Wang, Q.; Yuan, X.; Kellett, J. Integrated assessment of the environmental and economic effects of an ultra-clean flue gas treatment process in coal-fired power plant. J. Clean. Prod. 2018, 199, 359–368. [Google Scholar] [CrossRef]
- Tang, X.; Snowden, S.; McLellan, B.C.; Höök, M. Clean coal use in China: Challenges and policy implications. Energy Policy 2015, 87, 517–523. [Google Scholar] [CrossRef] [Green Version]
- Christopher, H.; Samuel, T. Advances in coal gasification, hydrogenation, and gas treating for the production of chemicals and fuels. Chem. Rev. 2014, 114, 1673–1708. [Google Scholar]
- di Carlo, A.; Borello, D.; Bocci, E. Process simulation of a hybrid SOFC/mGT and enriched air/steam fluidized bed gasifier power plant. Int. J. Hydrogen Energy 2013, 38, 5857–5874. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, J.; Yang, Y.; Qiang, Z.; Wu, L.; Li, F.; Ma, J. Numerical and statistical analyzing the effect of operating parameters on syngas yield fluctuation in entrained flow coal gasification using Split-plot design. Energy Fuels 2017, 31, 5870–5881. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, J. Robust optimization of the efficient syngas fractions in entrained flow coal gasification using Taguchi method and response surface methodology. Int. J. Hydrogen Energy 2017, 42, 4908–4921. [Google Scholar] [CrossRef]
- Nguyen, T.D.B.; Lim, Y.; Song, B.; Kim, S.; Joo, Y.; Ahn, D. Two-stage equilibrium model applicable to the wide range of operating conditions in entrained-flow coal gasifiers. Fuel 2010, 89, 3901–3910. [Google Scholar] [CrossRef]
- Sasi, T.; Mighani, M.; Örs, E.; Tawani, R.; Gräbner, M. Prediction of ash fusion behavior from coal ash composition for entrained-flow gasification. Fuel Process. Technol. 2018, 176, 64–75. [Google Scholar] [CrossRef]
- Patterson, J.H.; Hurst, H.J. Ash and slag qualities of Australian bituminous coals for use in slagging gasifiers. Fuel 2000, 79, 1671–1678. [Google Scholar] [CrossRef]
- Kong, L.; Bai, J.; Bai, Z.; Guo, Z.; Li, W. Improvement of ash flow properties of low-rank coal for entrained flow gasifier. Fuel 2014, 120, 122–129. [Google Scholar] [CrossRef]
- Hsieh, P.Y.; Kwong, K.; Bennett, J. Correlation between the critical viscosity and ash fusion temperatures of coal gasifier ashes. Fuel Process. Technol. 2016, 142, 13–26. [Google Scholar] [CrossRef]
- Chakravarty, S.; Mohanty, A.; Banerjee, A.; Tripathy, R.; Mandal, G.K.; Basariya, M.R.; Sharma, M. Composition, mineral matter characteristics and ash fusion behavior of some Indian coals. Fuel 2015, 150, 96–101. [Google Scholar] [CrossRef]
- Dai, X.; He, J.; Bai, J.; Huang, Q.; Du, S. Ash fusion properties from molecular dynamics simulation: Role of the ratio of silicon and aluminum. Energy Fuels 2016, 30, 2407–2413. [Google Scholar] [CrossRef]
- Weber, R.; Mancini, M.; Schaffel-Mancini, N.; Kupka, T. On predicting the ash behaviour using Computational Fluid Dynamics. Fuel Process. Technol. 2013, 105, 113–128. [Google Scholar] [CrossRef]
- Kim, J.; Kim, G.; Jeon, C. Prediction of correlation between ash fusion temperature of ASTM and Thermo-Mechanical Analysis. Appl. Therm. Eng. 2017, 125, 1291–1299. [Google Scholar] [CrossRef]
- Tambe, S.S.; Naniwadekar, M.; Tiwary, S.; Mukherjee, A.; Das, T.B. Prediction of coal ash fusion temperatures using computational intelligence based models. Int. J. Coal Sci. Technol. 2018, 5, 486–507. [Google Scholar] [CrossRef] [Green Version]
- Özbayoğlu, G.; Özbayoğlu, M.E. A new approach for the prediction of ash fusion temperatures: A case study using Turkish lignites. Fuel 2006, 85, 545–552. [Google Scholar] [CrossRef]
- Ding, W.; Wu, X.; Wei, H. Coal ash fusion temperature forecast based on Gaussian regularization RBF neural network. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; pp. 3006–3009. [Google Scholar]
- Yin, C.; Luo, Z.; Ni, M.; Cen, K. Predicting coal ash fusion temperature with a back-propagation neural network model. Fuel 1998, 77, 1777–1782. [Google Scholar] [CrossRef]
- Liu, Y.P.; Wu, M.G.; Qian, J.X. Predicting coal ash fusion temperature based on its chemical composition using ACO-BP neural network. Thermochim. Acta 2007, 454, 64–68. [Google Scholar] [CrossRef]
- Wang, C.L. The study of building model to predict ash fusion temperature. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 5217–5221. [Google Scholar]
- Gao, F.; Han, P.; Zhai, Y.J.; Chen, L.X. Application of support vector machine and ant colony algorithm in optimization of coal ash fusion temperature. In Proceedings of the 2011 International Conference on Machine Learning and Cybernetics, Guilin, China, 10–13 July 2011; Volume 2, pp. 666–672. [Google Scholar]
- Zhao, B.; Zhang, Z.; Wu, X. Prediction of coal ash fusion temperature by least-squares support vector machine model. Energy Fuels 2010, 24, 3066–3071. [Google Scholar] [CrossRef]
- Chen, W.H.; Chen, C.J.; Hung, C.I. Taguchi approach for co-gasification optimization of torrefied biomass and coal. Bioresour. Technol. 2013, 144, 615–622. [Google Scholar] [CrossRef] [PubMed]
- Vejahati, F.; Katalambula, H.; Gupta, R. Entrained-flow gasification of oil sand coke with coal: Assessment of operating variables and blending ratio via response surface methodology. Energy Fuels 2012, 26, 219–232. [Google Scholar] [CrossRef]
- Emun, F.; Gadalla, M.; Majozi, T.; Boer, D. Integrated gasification combined cycle (IGCC) process simulation and optimization. Comput. Chem. Eng. 2010, 34, 331–338. [Google Scholar] [CrossRef] [Green Version]
- Biagini, E.; Bardi, A.; Pannocchia, G.; Tognotti, L. Development of an entrained flow gasifier model for process optimization study. Ind. Eng. Chem. Res. 2009, 48, 9028–9033. [Google Scholar] [CrossRef]
- Chen, C.; Hung, C. Optimization of co-gasification Process in an entrained-flow gasifier using the Taguchi Method. J. Therm. Sci. Technol. 2013, 8, 190–208. [Google Scholar] [CrossRef]
- Shastri, Y.; Diwekar, U. Stochastic modeling for uncertainty analysis and multiobjective optimization of IGCC system with single-stage coal gasification. Ind. Eng. Chem. Res. 2011, 50, 4879–4892. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D. Adaptive dynamic programming for optimal tracking control of unknown nonlinear systems with application to coal gasification. IEEE Trans. Autom. Sci. Eng. 2013, 11, 1020–1036. [Google Scholar] [CrossRef]
- Milios, D.; Gilmore, S. Markov chain simulation with fewer random samples. Electron. Notes Theor. Comput. Sci. 2013, 296, 183–197. [Google Scholar] [CrossRef]
- Afzal, M.S.; Al-Dabbagh, A.W. Forecasting in industrial process control: A hidden Markov model approach. IFAC PapersOnLine 2017, 50, 14770–14775. [Google Scholar] [CrossRef]
- Cui, Z.; Kirkby, J.L.; Nguyen, D. A general framework for time-changed Markov processes and applications. Eur. J. Oper. Res. 2019, 273, 785–800. [Google Scholar] [CrossRef]
- Dimopoulou, S.; Oppermann, A.; Boggasch, E.; Rausch, A. A Markov Decision Process for managing a Hybrid Energy Storage System. J. Energy Storage 2018, 19, 160–169. [Google Scholar] [CrossRef]
- Duan, C.; Makis, V.; Deng, C. Optimal Bayesian early fault detection for CNC equipment using hidden semi-Markov process. Mech. Syst. Signal Process. 2019, 122, 290–306. [Google Scholar] [CrossRef]
- Fadıloğlu, M.M.; Bulut, Ö. An embedded Markov chain approach to stock rationing under batch orders. Oper. Res. Lett. 2019, 47, 92–98. [Google Scholar] [CrossRef]
- Munkhammar, J.; Widén, J. A Markov-chain probability distribution mixture approach to the clear-sky index. Sol. Energy 2018, 170, 174–183. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Q.; Wang, Z.; Chen, Z.; Cai, X. Markov chain-based approach of the driving cycle development for electric vehicle application. Energy Procedia 2018, 152, 502–507. [Google Scholar] [CrossRef]
- Yu, X.; Gao, S.; Hu, X.; Park, H. A Markov decision process approach to vacant taxi routing with e-hailing. Transp. Res. Part B Methodol. 2019, 121, 114–134. [Google Scholar] [CrossRef]
- Yu, G.; Zhou, Z.; Qiang, Q.; Yu, Z. Experimental studying and stochastic modeling of residence time distribution in jet-entrained gasifier. Chem. Eng. Process. Process Intensif. 2002, 41, 595–600. [Google Scholar]
- Guo, Q.; Liang, Q.; Ni, J.; Xu, S.; Yu, G.; Yu, Z. Markov chain model of residence time distribution in a new type entrained-flow gasifier. Chem. Eng. Process. Process Intensif. 2008, 47, 2061–2065. [Google Scholar] [CrossRef]
- Bonakdari, H.; Zaji, A.H.; Binns, A.D.; Gharabaghi, B. Integrated Markov chains and uncertainty analysis techniques to more accurately forecast floods using satellite signals. J. Hydrol. 2019, 572, 75–95. [Google Scholar] [CrossRef]
- Carapellucci, R.; Giordano, L. A new approach for synthetically generating wind speeds: A comparison with the Markov chains method. Energy 2013, 49, 298–305. [Google Scholar] [CrossRef]
- Alinovi, D.; Ferrari, G.; Pisani, F.; Raheli, R. Markov chain modeling and simulation of breathing patterns. Biomed. Signal Process. Control 2017, 33, 245–254. [Google Scholar] [CrossRef] [Green Version]
- Masseran, N. Markov chain model for the stochastic behaviors of wind-direction data. Energy Convers. Manag. 2015, 92, 266–274. [Google Scholar] [CrossRef]
- Wilinski, A. Time series modeling and forecasting based on a Markov chain with changing transition matrices. Expert Syst. Appl. 2019, 133, 163–172. [Google Scholar] [CrossRef]
- Li, F.; Ma, X.; Xu, M.; Fang, Y. Regulation of ash-fusion behaviors for high ash-fusion-temperature coal by coal blending. Fuel Process. Technol. 2017, 166, 131–139. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparison between genetic algorithms and particle swarm optimization: Evolutionary programming VII. In Proceedings of the International Conference on Evolutionary Programming, San Diego, CA, USA, 25–27 March 1998; pp. 611–616. [Google Scholar]
- Lee, C.K.H. A review of applications of genetic algorithms in operations management. Eng. Appl. Artif. Intell. 2018, 76, 1–12. [Google Scholar] [CrossRef]
- Shieh, H.; Kuo, C.; Chiang, C. Modified particle swarm optimization algorithm with simulated annealing behavior and its numerical verification. Appl. Math. Comput. 2011, 218, 4365–4383. [Google Scholar] [CrossRef]
- Qin, H.; Guo, Y.; Liu, Z.; Liu, Y.; Zhong, H. Shape optimization of automotive body frame using an improved genetic algorithm optimizer. Adv. Eng. Softw. 2018, 121, 235–249. [Google Scholar] [CrossRef]
- Bottura, F.B.; Bernardes, W.M.; Oleskovicz, M.; Asada, E.N. Setting directional overcurrent protection parameters using hybrid GA optimizer. Electr. Power Syst. Res. 2017, 143, 400–408. [Google Scholar] [CrossRef]
- Tao, Y.; Zhang, Y.; Wang, Q. Fuzzy c-mean clustering-based decomposition with GA optimizer for FSM synthesis targeting to low power. Eng. Appl. Artif. Intell. 2018, 68, 40–52. [Google Scholar] [CrossRef]
- Salman, S.; Alaswad, S. Alleviating road network congestion: Traffic pattern optimization using Markov chain traffic assignment. Comput. Oper. Res. 2018, 99, 191–205. [Google Scholar] [CrossRef]
- Mandol, S.; Bhattacharjee, D.; Dan, P.K. Structural optimisation of wind turbine gearbox deployed in non-conventional energy generation. In Proceedings of the International Conference on Research into Design, Guwahati, India, 9–11 January 2017; pp. 835–848. [Google Scholar]
- Sreenivasan, K.S.; Kumar, S.S.; Katiravan, J. Genetic algorithm based optimization of friction welding process parameters on AA7075-SiC composite. Eng. Sci. Technol. Int. J. 2019, 41, 269–273. [Google Scholar] [CrossRef]




| Statistical Indexes | Case I | Case II | Case III |
|---|---|---|---|
| MAD | 5.67 | 7.01 | 14.06 |
| RMSE | 6.98 | 7.63 | 15.21 |
| AARE | 0.42% | 0.52% | 1.04% |
| State Number | Evaluation Index of Simulation Results | ||
|---|---|---|---|
| MAD | RMSE | AARE | |
| 4 | 14.06 | 15.21 | 1.04% |
| 5 | 11.53 | 12.49 | 0.86% |
| 6 | 9.78 | 10.31 | 0.72% |
| 7 | 8.23 | 8.58 | 0.59% |
| 8 | 7.01 | 7.63 | 0.52% |
| 9 | 6.24 | 6.42 | 0.45% |
| 10 | 5.68 | 6.13 | 0.41% |
| 11 | 5.10 | 5.89 | 0.38% |
| 12 | 4.69 | 4.77 | 0.36% |
| 13 | 4.38 | 4.52 | 0.35% |
| 14 | 4.79 | 5.01 | 0.36% |
| 15 | 5.46 | 5.98 | 0.38% |
| 16 | 5.67 | 6.98 | 0.42% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Guan, S.; Hou, J.; Zhang, Z.; Li, Z.; Meng, X.; Wang, C. Markov Chain Simulation of Coal Ash Melting Point and Stochastic Optimization of Operation Temperature for Entrained Flow Coal Gasification. Energies 2019, 12, 4245. https://doi.org/10.3390/en12224245
Zhang J, Guan S, Hou J, Zhang Z, Li Z, Meng X, Wang C. Markov Chain Simulation of Coal Ash Melting Point and Stochastic Optimization of Operation Temperature for Entrained Flow Coal Gasification. Energies. 2019; 12(22):4245. https://doi.org/10.3390/en12224245
Chicago/Turabian StyleZhang, Jinchun, Shiheng Guan, Jinxiu Hou, Zichuan Zhang, Zhaoqian Li, Xiangzhong Meng, and Chao Wang. 2019. "Markov Chain Simulation of Coal Ash Melting Point and Stochastic Optimization of Operation Temperature for Entrained Flow Coal Gasification" Energies 12, no. 22: 4245. https://doi.org/10.3390/en12224245
APA StyleZhang, J., Guan, S., Hou, J., Zhang, Z., Li, Z., Meng, X., & Wang, C. (2019). Markov Chain Simulation of Coal Ash Melting Point and Stochastic Optimization of Operation Temperature for Entrained Flow Coal Gasification. Energies, 12(22), 4245. https://doi.org/10.3390/en12224245