Research on the Interrelation between Temperature Distribution and Dry Band on Wet Contaminated Insulators

Abstract

In this paper, the interrelation between temperature distribution and dry band on wet contaminated insulators is studied by theoretical analysis, numerical simulation, and a high-voltage artificial contamination experiment. The influences of the composition of the contaminant and the relative humidity of the environment on the moisture absorption of the contamination layer are studied. It is indicated that the critical relative humidity (CRH) of the soluble mixture in the contamination layer decreases with the increase of the variety of soluble substances. This can be considered as a previously neglected reason for the inconsistency between the result of an artificial contamination test and that of a natural contamination test. Furthermore, the influences of the maximum temperature, wind speed, altitude, relative humidity, and the composition of the contamination on the water evaporation rate of the contaminated layer are also studied. The formation of dry band is predicted by studying the law of water transport in the contamination layer. The influence of the location, width, drying degree, and quantity of dry bands on the insulator surface temperature are studied by numerical simulation. An infrared thermal imager and ultraviolet camera are adopted to measure the temperature distribution and the discharge phenomenon on the insulator surface separately, which verifies the above numerical simulation. The study results deepen the research on the moisture absorption characteristics, the law of temperature distribution, the formation of dry bands, and the influence of dry bands on the temperature distribution of wet contaminated insulators.

1. Introduction

With the expansion of the power-grid scale and environmental pollution, insulator flashover accidents caused by contamination pose a serious threat to the safety and stability of power systems. Taking China’s electric power system as an example, large-scale contamination flashovers have occurred in six major domestic power grids, resulting in huge economic losses. From the 1980s to the beginning of the 21st century, there have been about 60 regional and large-scale blackouts in China, 29 blackouts caused by line contamination flashovers, and three blackouts caused by contamination flashovers in the substation and booster station of power plants. The number of blackouts caused by contamination flashovers constitutes half of the total number of blackouts. For instance, in 2001, 238 transmission lines with 66–500 kV voltage and 34 substations in the North China Power Grid suffered contamination flashover successively, resulting in large-scale blackouts. In 2011, serious contamination flashovers occurred in eight 110-kV substations and one 220-kV substation of the Xinjiang Power Grid, resulting in the split between the southern Xinjiang power grid and the main power grid. Due to the seriousness of the contamination flashover problem, relevant research has drawn a lot of attention from researchers [1,2,3,4].

In operation, a wetted and polluted insulator generates and dissipates heat under the influence of voltage. The shape of a disc insulator is complicated, and its heating power varies. Therefore, an area with high heating power has a high temperature. Heat conducts from high- to low-temperature areas and transfers to the outside environment through radiation and convection. An infrared camera can be used to measure the distribution of the temperature field on the surface of an insulator when thermal equilibrium is reached. Since the structure and shape of an insulator are complicated, the distribution of heating power across its surface varies significantly. So far, the research on the heat generation mechanism of wetted and polluted insulators, the distribution of temperature fields, and the conditions for the formation of dry bands or dry band arcs is still imperfect. In [5], it was assumed that the convection of the pollution layer and the air is the main mode of heat dissipation, and a thermodynamic model for insulators was established to numerically calculate the heat distribution on the surface of porcelain insulators. In [6], the critical value of currents generated by the discharges of the dry bands on wetted and polluted insulators was studied. In [7], operating voltage was applied to the wet contaminated porcelain insulator string to record the heat generation on the insulator surface. It was shown that compared with other parts of the insulator, the maximum temperature rise and discharges occurred in the annular area of the disc surface around a steel ball pin. In [8,9,10,11,12,13], the mechanism and characteristics of polluted flashovers of insulators were studied.

In this paper, an infrared thermal imager and ultraviolet camera are applied to a high-voltage artificial contamination experiment to study the temperature distribution on an insulator surface and discharge characteristics. Based on the study of hygroscopic characteristics of soluble substances in a contamination mixture, an explanation for the inconsistency between an artificial contamination test and natural contamination test is proposed. A formula for the formation conditions of dry bands is derived. Based on this formula, the distribution rule of the insulator surface temperature and the influence of distribution voltage, wind speed, and altitude on the formation of dry bands are studied. The influence of the location, width, and quantity of dry bands on the insulator surface temperature and the influence of the drying degree of dry bands on the maximum temperature are studied by the numerical simulation method. Based on the results obtained, the hygroscopicity and water evaporation rate of the pollution layer on different areas of insulators are further investigated, and the conditions for dry band formation are obtained.

2. Surface Temperature Distribution of Wet Contaminated Insulators in High Voltage Operation

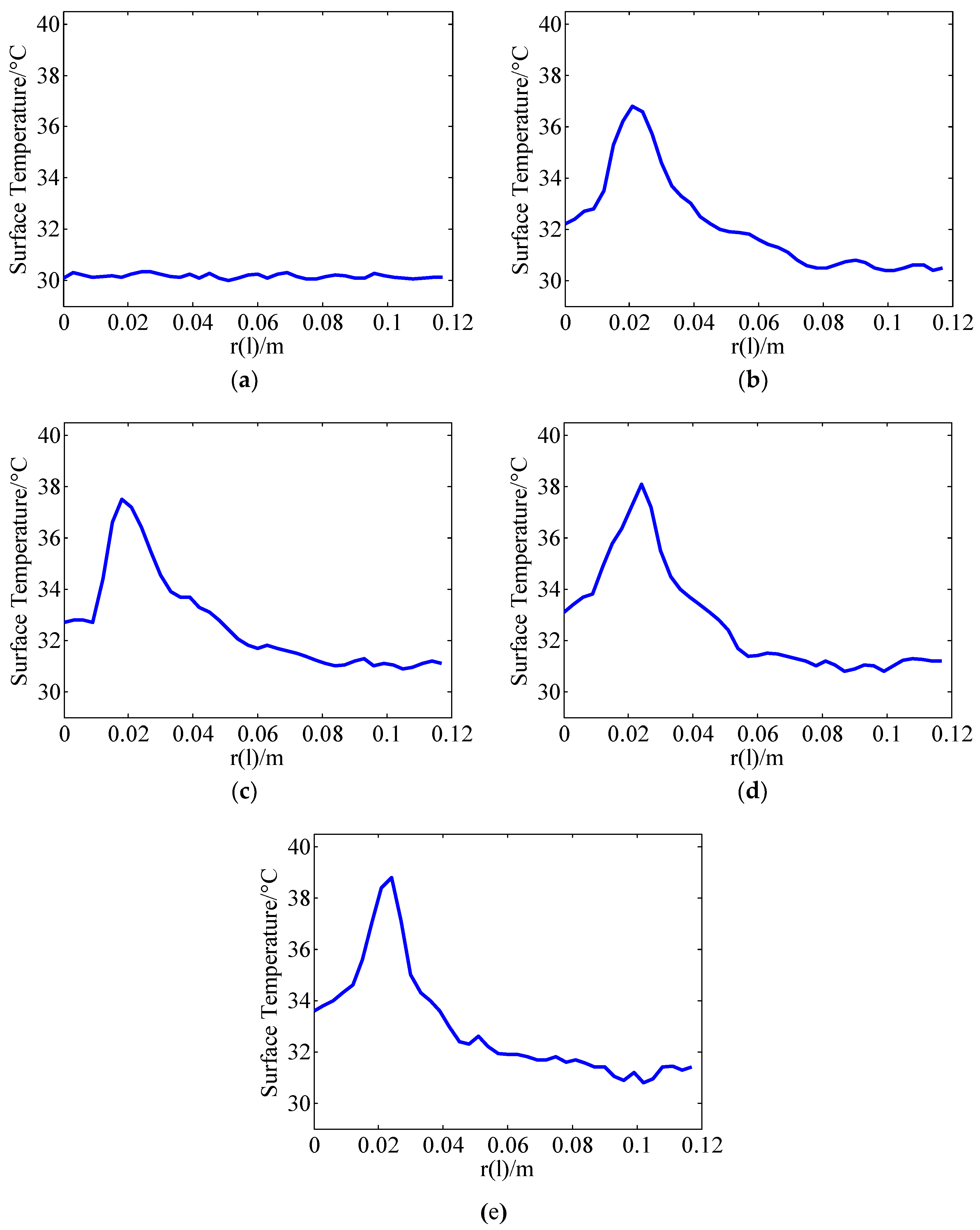
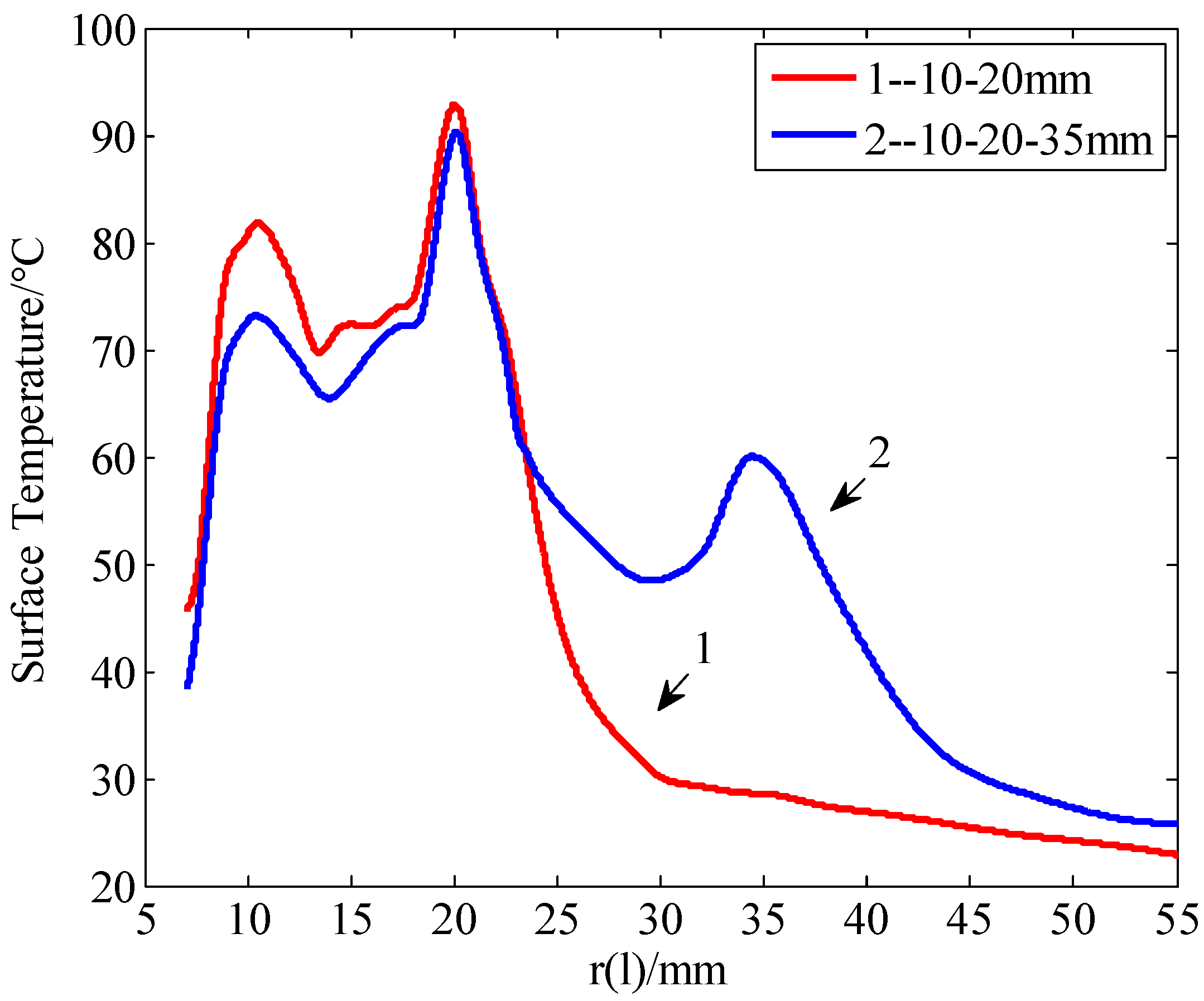
2.1. Measurement of Temperature Distribution on Insulator Surface

The grade of pollution on an insulator and the ambient humidity mainly affects the surface temperature distribution by affecting the surface resistivity of the wetted and polluted layer. In this paper, XP-70 disc suspension porcelain insulators are studied with a maximum diameter of 250 mm, a form factor of $f=0.825$, and a distributed voltage $U_f$ of $10\mathrm{kV}$ on the insulator. Figure 1 shows the temperature distribution on the bottom surface of a manually contaminated insulator measured by a Ti-32 infrared camera (Fluke Corporation, Everett, WA, USA). The experiment was prepared and implemented based on the IEC 60507 standard. Kaolin was utilized to substitute non-soluble substances in natural pollutants. NaCl was utilized to substitute soluble salts in natural pollutants. Values of the salt deposit density (SDD) of each grade were selected as 0.05 mg/cm² (grade I), 0.08 mg/cm² (grade II), 0.15 mg/cm² (grade III), and 3 mg/cm² (grade IV). The value of non-soluble deposit density (NSDD) was set at 1 mg/cm². The test voltage was set at 10 kV, which was the rated voltage of the XP-70 insulator. The experiment was carried out at 90% relative humidity (RH) and 30 °C ambient temperature. In Figure 1, the horizontal axis represents the distance from the center of the disc. In the central area, the steel ball pin had excellent thermal conductivity and protruded into the air. Therefore, the temperatures of the steel ball pin and its surroundings were not too high. The temperature was the highest at a certain distance from the center of rotation. The maximum value of the disk surface temperature appeared at about one-fifth from the center, where the temperature was higher than the ambient temperature by about 7 to 9 °C. On the outer side of the temperature peak, the temperature decreased with the increase of distance from the center. The temperature at the outermost edge was only about 1 °C higher than the ambient temperature. Figure 2 shows the infrared images of wet contaminated insulators. As shown in Figure 2, the brighter the area, the higher the temperature. The bright annular area near the steel ball pin had the maximum temperature. The clean insulator has no obvious temperature rise, and the overall temperature is basically the same as the ambient temperature.

The ultraviolet discharge images of manually polluted insulators captured with a CoroCAM-504 ultraviolet imager (Council for Scientific and Industrial Research, Pretoria, South Africa) are shown in Figure 3, where the relative humidity is 90%. The shooting of the ultraviolet image was synchronous with the shooting of the infrared image. It can be seen that the discharge spots were mainly distributed near the steel ball pin on the bottom disc surface. This area had the maximum temperature among the entire disc, and it was the area where the dry bands formed. Discharge intensity can be characterized by the number of white pixels. For each contamination grade, the average number of white pixels of 25 images was calculated. For grades from Ⅰto Ⅳ, the average number of white pixels were 137, 233, 321, and 408, respectively. There was no discharge on the clean insulator. At the same relative humidity, insulators with higher contamination grades have stronger discharge intensity.

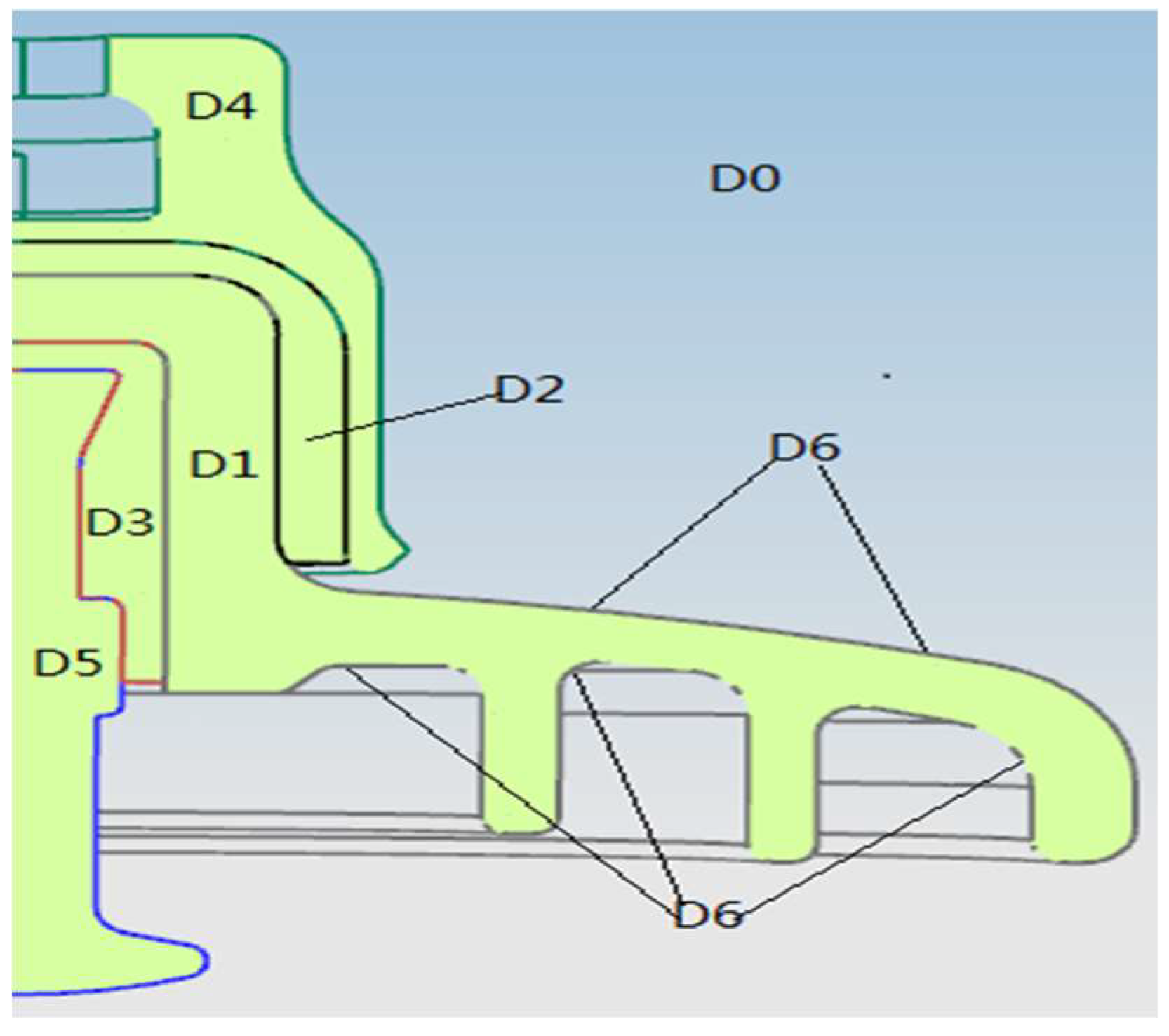
2.2. Analysis of Electrothermal Coupling Temperature Field of Wet Contaminated Insulator

The temperature distribution on an insulator is determined by the shape, surface resistivity of the pollution layer, and thermal effect of the leakage currents. The model for the numerical simulation of the electrothermal coupled temperature field of a wetted and polluted insulator is shown in Figure 4. The insulator, pollution layer, and surrounding space were divided into seven regions: air (D₀), the porcelain shell (D₁), the adhesive between the steel socket cap and porcelain shell (D₂), the adhesive between the porcelain shell and the steel ball pin (D₃), the steel socket cap (D₄), the steel ball pin (D₅), and the pollution layer (D₆). This division facilitates the calculation of the temperature field distribution of the simulated insulator in different regions. Physical parameters such as densities and heat transfer coefficients of various mediums were selected according to materials handbook.

In the numerical simulation, the distributed voltage $U_f$ was $10 \mathrm{kV}$, ambient temperature $T_0$ was 20 °C, and the convective heat transfer coefficient between the insulator surface and the air ($h$) was $20 \mathrm{W}/\left({\mathrm{m}}^2·\mathrm{K}\right)$ [14]. The heat flux density at each point of the insulator depends on the resistance heating power of the pollution layer ($P_s$). According to [15], $P_s$ is determined by Equation (1). If the pollution is evenly distributed on the insulator along the creepage path L, the resistance heating power of the pollution layer per unit area ($p_s$) is

$$p_s=\frac{U_f^2}{4{\rho }_{ws}{\pi }^2{f}^2{r}^2\left(l\right)}$$

(1)

where $U_f$ is the distributed voltage on the insulator in V; ${\rho }_{ws}$ is the surface resistivity of the wetted and polluted insulator in Ω; $r\left(l\right)$ is the distance between a creepage distance element and the axis of rotation of the insulator in m; and $f$ is the form factor defined as

$$f={{\displaystyle \int }}_0^L\frac{dl}{2\pi r\left(l\right)}$$

(2)

where L is the creepage distance in m.

Figure 5 shows the numerically simulated temperature distribution on the surface of the insulator. It can be seen that the temperature near the steel ball pin was the highest, which is consistent with the experimental result. The steel ball pin had a large thermal conductivity, and its heat dissipation capability was stronger than that of the porcelain. Therefore, the temperature of the steel ball pin itself was not very high. As the grade of pollution increased, the surface resistivity decreased, and the surface temperature of the insulator increased.

3. Formation of Dry Bands on the Surface of Wet Contaminated Insulators

3.1. Hygroscopicity of Contaminated Layer of Insulator

The wetting of the contamination layer on the insulator surface occurs through two main mechanisms: moisture absorption and wet deposition. The composition of the contamination layer of outdoor insulators is very complex, and the contamination components are different in different areas, but they generally contain water-soluble substances and water-insoluble powder substances, both of which have the ability to hold water. The size of insulator contamination is generally 10 to tens of microns, which belongs to the category of powder. The natural contaminant typically includes inorganic soluble cations (such as NH₄⁺, Ca²⁺, K⁺, Na⁺, Mg²⁺, Zn²⁺, Al³⁺, Mn²⁺, Cu²⁺, Li⁺, and Fe³⁺), inorganic soluble anion (such as SO₄²⁻, Cl⁻, F⁻, NO₂⁻, NO₃⁻, HCO₃⁻, CO₃²⁻, and PO₄²⁻), inorganic insoluble metal oxides (such as Fe₂O₃, CaO, MgO, K₂O, Na₂O, CuO, Al₂O₃, and ZnO), other inorganic insoluble components (such as SiO₂, SO₃, P₂O₅, CaSO₄, MgSO₄, and C), and organics (CH₄N₂O, C₆H₁₄N₂O·HCl, C₇H₄N₂O₂, CHBrN₄, C₄H₇KO₂S₂, and C₂H₂COOK) [16]. Hygroscopicity is the expression of affinity between substance molecules and water molecules, which is caused by the diffusion of water molecules into the inner layer of substance. Hygroscopicity is related to the properties of matter itself such as crystal appearance, particle size, and specific surface area. Under natural conditions, the moisture content of substances is mainly related to their hygroscopicity and environmental relative humidity (RH).

When the ambient relative humidity is greater than the critical relative humidity (CRH) of a water-soluble substance, the water absorption rate of this substance increases rapidly. As a result of the water absorption, the resistivity of the water-soluble substance decreases significantly. The pollution layer on an insulator is a mixture of multiple substances. The CRH of the water-soluble mixture is approximately equal to the product of CRHs of all the water-soluble components. It is independent of the amount of each component. This is expressed as

$$CR{H}_{AB}\approx CR{H}_A\times CR{H}_B$$

(3)

where CRH_A, CRH_B, and CRH_AB denote the CRHs of substances A, B, and the mixture of A and B, respectively. As the CRHs of soluble components are all decimal, the CRH of a water-soluble mixture is lower than the CRH of any substance in the mixture. Hence, at the same RH (above the CRH of the mixture), the resistivity of the mixture is also lower than that of any single substance. As the water-soluble component in a naturally contaminated insulator is a mixture of a variety of soluble substances, its CRH is quite low. Therefore, at the same RH, even if the artificially contaminated insulators and the naturally contaminated insulators have the same equivalent salt deposit density (ESDD) and the same non-soluble deposit density (NSDD), the hygroscopicity and resistivity of the soluble substances of artificially contaminated insulators and naturally contaminated insulators are quite different. Artificially contaminated insulators and naturally contaminated insulators with the same ESDD and NSDD can have different experimental performances (such as leakage current and flashover voltage), even in the same experiment condition. The reduction of CRH caused by the complexity of soluble substances in the contaminant of naturally contaminated insulators can be considered as one of the reasons for the inconsistency between artificial contamination tests and natural contamination tests. Water-insoluble substances have no critical relative humidity (CRH), and the hygroscopicity of its mixture is additive. As a mixture of various types of substances, a pollution layer has a very low CRH and a high hygroscopicity.

Wet deposition includes water vapor condensate and precipitation in the atmosphere. When water vapor reaches a supersaturated state and takes dust particles in the atmosphere as condensation nodules, dew and frost are formed on objects. The conditions of dew and frost can be formed by temperature changes and the alternation of day and night. When the cloud layer composed of liquid water droplets reaches the conditions at which the cloud droplets increase to rain droplets, rainfall will occur. Drizzle is a common way of wetting insulator contamination due to wet deposition.

3.2. Evaporation of Water in Contaminated Layer of Insulator

On the surface of wetted and polluted insulators, water is evaporated due to heat generation or weather change. When the water evaporation rate is larger than water precipitation and absorption rate, dry bands are formed on the areas with higher temperatures. Thus, the condition for generating dry bands on the surface of wetted and polluted insulators can be written as

$$E_p> E_j$$

(4)

where $E_p$ is the water evaporation rate where the temperature is the highest; and $E_j$ is the water precipitation and absorption rate. The unit of both $E_p$ and $E_j$ is m/s. According to the empirical formula for water evaporation, $E_p$ can be calculated as [17]

$$E_p=\frac{1}{998}\left(4.6\times {10}^{-5}+3.63\times {10}^{-5}{S}_f\right)\left(p_w-p_a\right)\frac{101.325}{B}$$

(5)

where $p_w$ is the saturation vapor pressure where the temperature is the highest; $p_a$ is the ambient water vapor pressure; and B is the atmospheric pressure. The unit of these three is kPa. $S_f$ is the wind speed, with m/s as the unit. The ambient water vapor pressure can be calculated from relative humidity (RH) as

$$p_a=p_w^0\times RH$$

(6)

where $p_w^0$ is the saturation water vapor pressure at the ambient temperature in kPa; and RH is the ambient relative humidity. When the ambient temperature is 20 °C and the relative humidity is 90%, $p_w^0=2.338 \mathrm{kPa}$ and $p_a=2.104 \mathrm{kPa}$.

The moisture of the pollution layer of an insulator is generally a dilute salt solution. According to the behavior of the colligative properties of the dilute electrolyte solution, the saturation vapor pressure of the solution ($p_w$) is related to the saturation pressure of solvent ($p_j$) by

$$p_w=p_j-\Delta p=p_j-i{K}_0{b}_B=p_j-i{p}_j\frac{M_A}{M_B}\frac{m_B}{m_A}$$

(7)

where $i$ is a correction factor, which is approximately equal to the number of ions that can be ionized in one molecule. For $AB$-type electrolytes, $i$ tends to be 2, and for $A_{2}B$ or $A{B}_2$-type electrolytes, $i$ tends to be 3. The symbols $M_A$ and $M_B$ denote the molar masses of the solvent and the solute in $\mathrm{g}/\mathrm{mol}$, respectively. $m_A$ and $m_B$ denote the masses of the solvent and the solute in $\mathrm{g}$, respectively. When the electrolyte content in the pollution layer of an insulator is low, the saturation vapor pressure of the solvent (water) can be used to approximate the saturation vapor pressure of the electrolyte solution. Such an approximation always results in a calculated water evaporation rate that is higher than the exact value. The saturation water vapor pressure changes with temperature, and the saturation water vapor pressure at different temperatures can be found in handbooks for chemical engineering.

Substituting Equation (5) into Equation (4), the condition for forming dry bands on a wetted and polluted insulator is obtained as

$$E_p=\frac{1}{998}\left(4.6\times {10}^{-5}+3.63\times {10}^{-5}{S}_f\right)\left(p_w-p_a\right)\frac{101.325}{B}>E_j.$$

(8)

The maximum temperature on the insulator can be measured by an infrared camera. Through relevant handbooks, the corresponding saturation vapor pressure can be found. The water precipitation and absorption rate can be determined by referring the rainfall intensity of the drizzle, which has a range of $0–1.1 \mathsf{\mu }\mathrm{m}/\mathrm{s}$ [18].

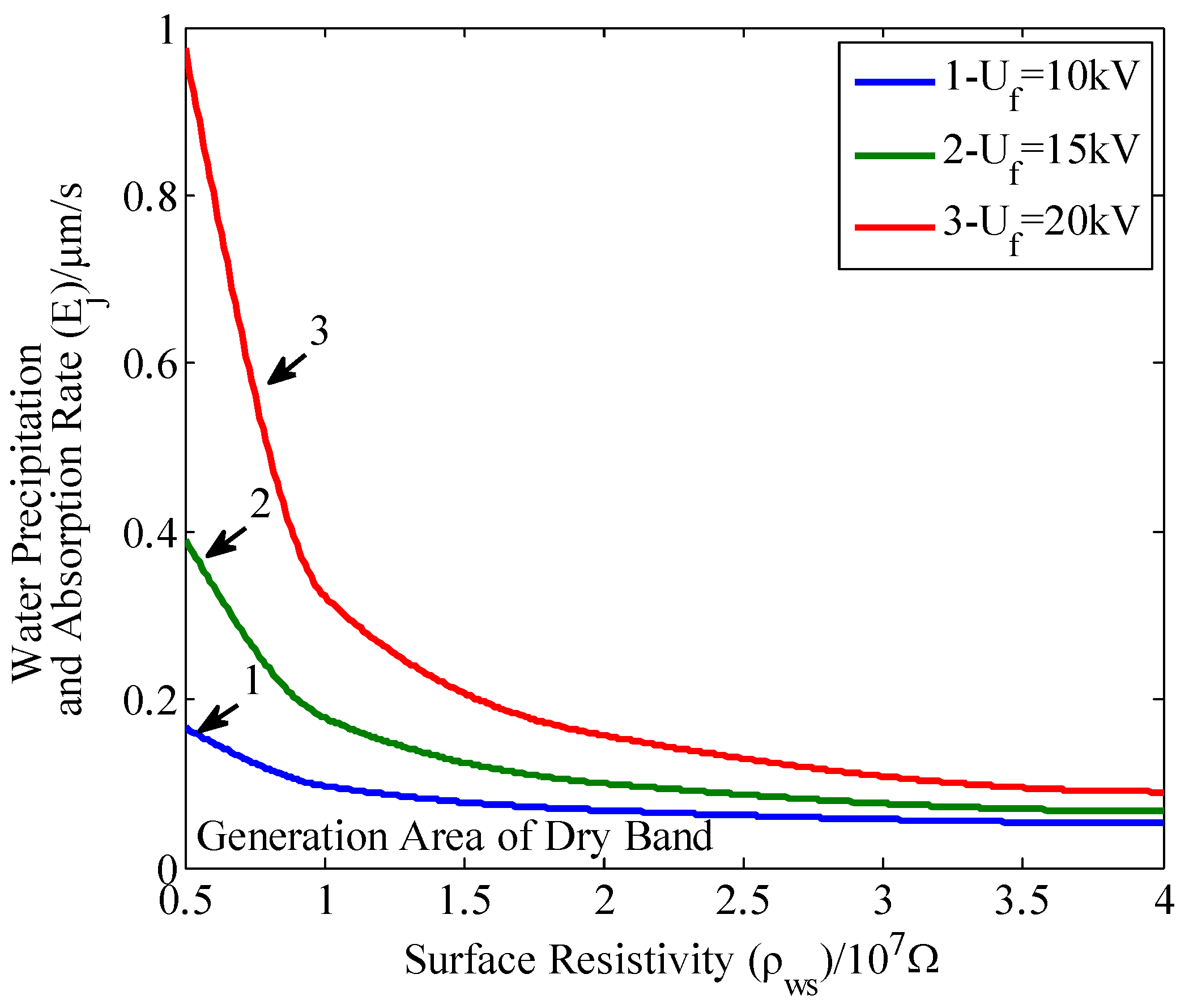
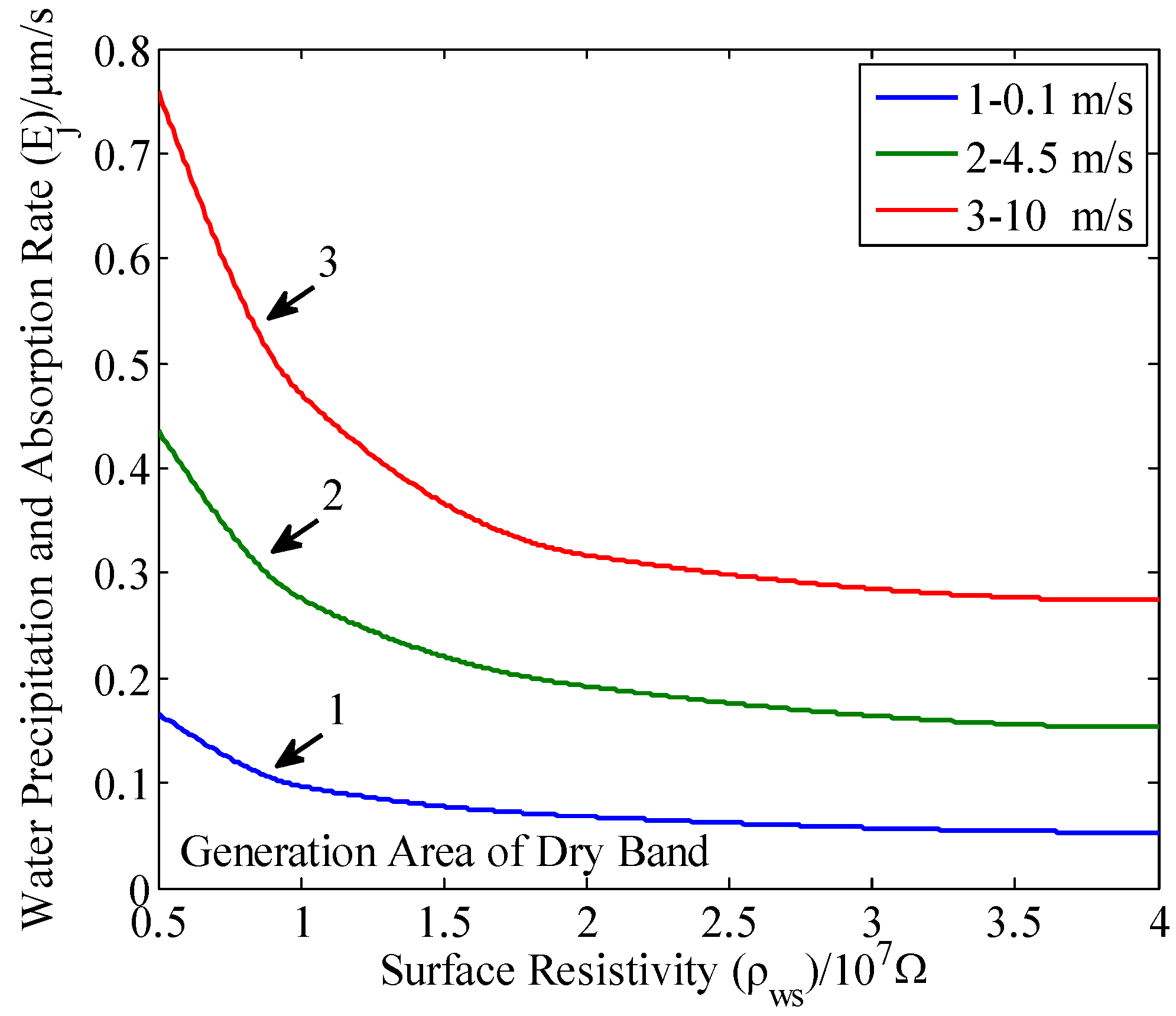
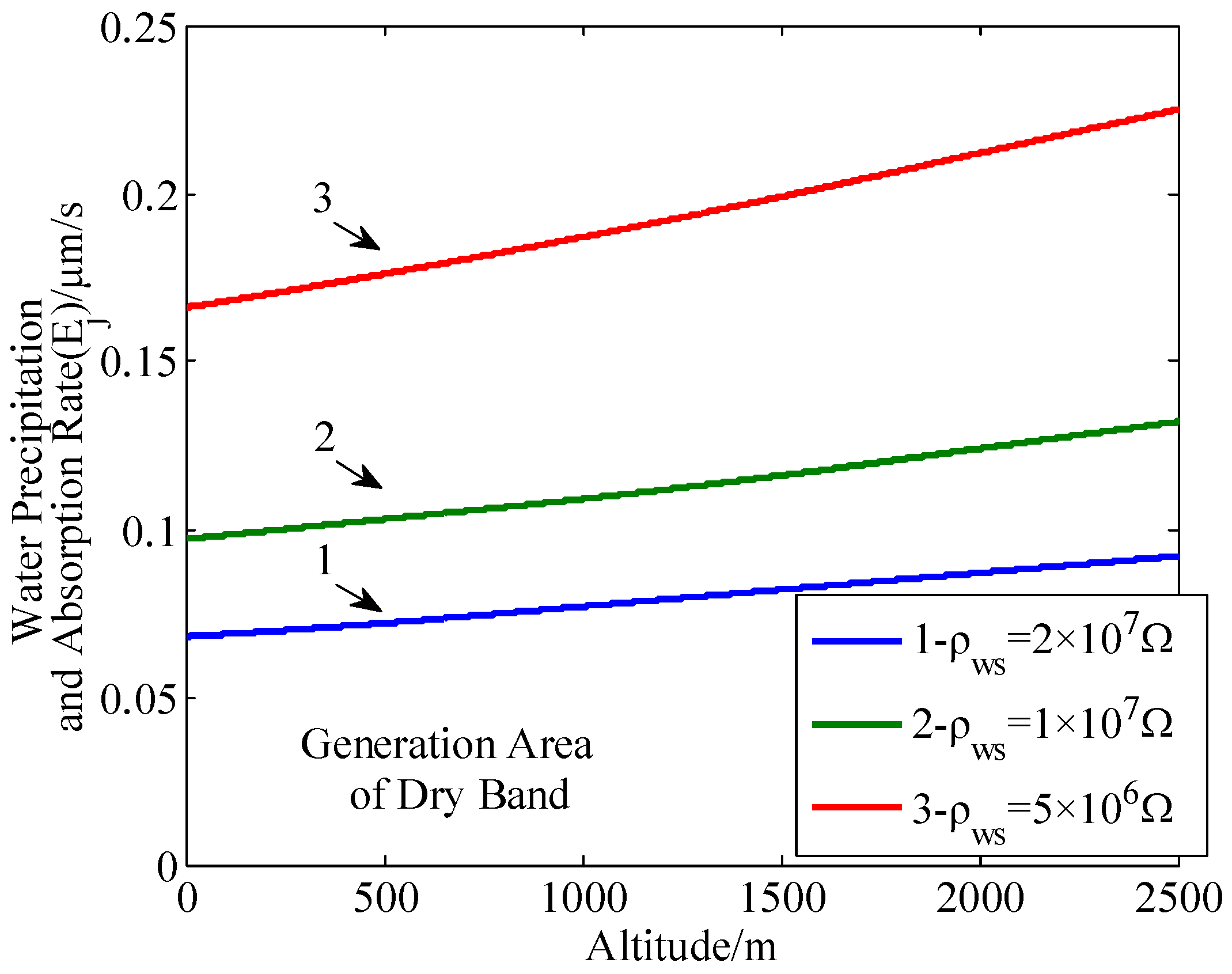
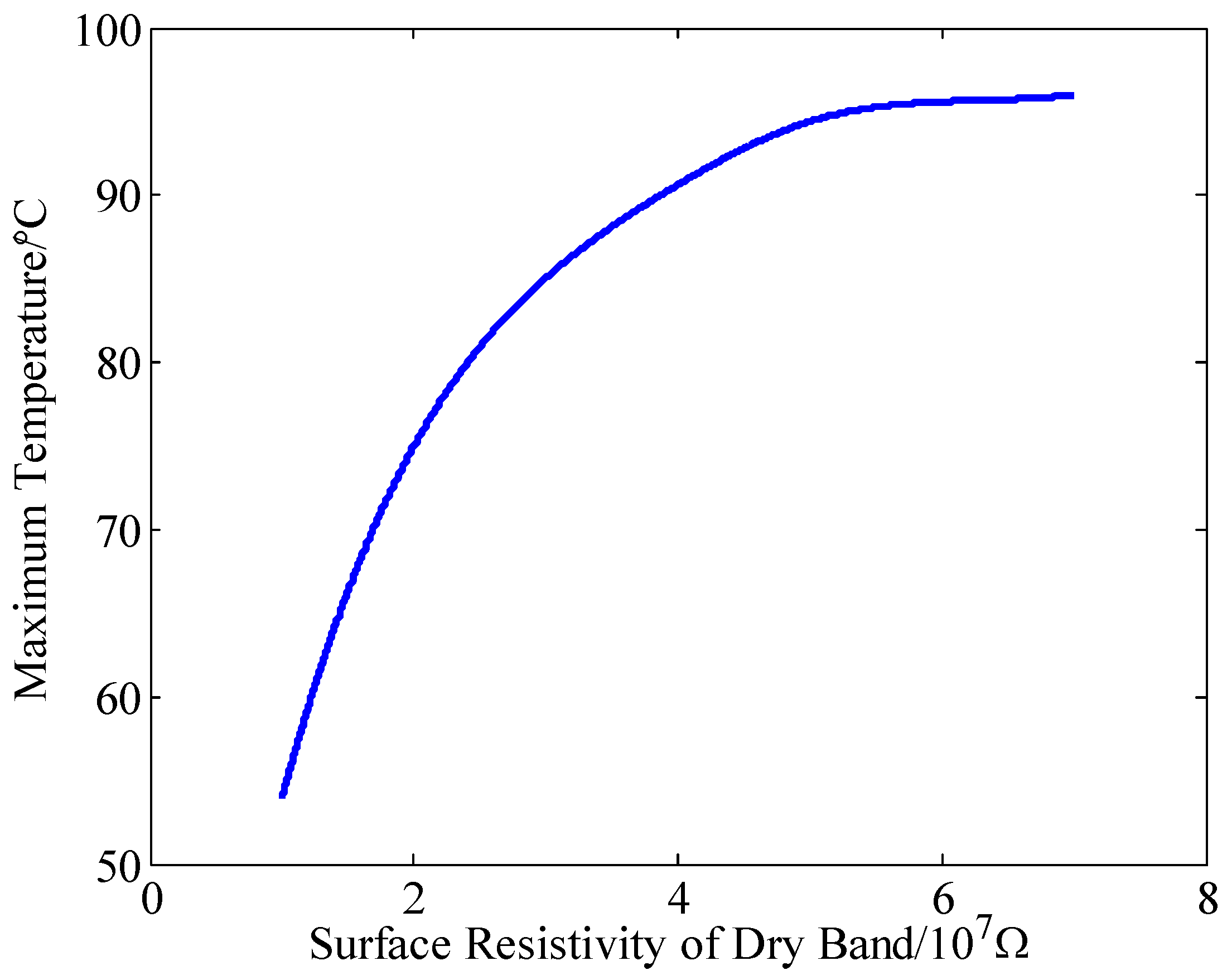
3.3. The Formation of Dry Bands

On the surface of insulators, the water evaporation rate is relatively large where the surface temperature is high. At $r=0.02 \mathrm{m}$ (as shown in Figure 1), where the temperature is the highest, the water evaporation rate is the largest, and a dry band is most easily formed. When the surface resistivity of the pollution layer of an insulator is relatively small, the variety of the surface water evaporation rates increases, increasing the probability of local dry band formation. When the surface resistivity of the pollution layer of an insulator is relatively large, the variety of the surface water evaporation rates decreases, and the probability of local dry band formation is relatively small.

By calculating and comparing the water evaporation rate, water precipitation, and the absorption rate at $r=0.02 \mathrm{m}$, the conditions for dry band formation on disc insulators were obtained (Figure 6). In this figure, the area under the curve represents the area where dry bands were formed, when the ambient relative humidity was 90%, the ambient temperature was 20 °C, and the wind speed was $S_f=0.55 \mathrm{m}/\mathrm{s}$. When the distributed voltage is increased, the water evaporation rate rapidly increases where the surface temperature of the insulator was the highest, and the areas where dry bands formed increased (Figure 6). This acceleration of water evaporation was apparent when the insulator was heavily polluted and the surface resistivity was small.

Wind lowers the surface temperature of an insulator and reduces the saturation vapor pressure on the insulator where the temperature is the highest, resulting in a decreased water evaporation rate in the pollution layer. Meanwhile, the wind moves the water vapor near the surface of the insulator, increasing the water evaporation rate of the pollution layer. The wind almost causes uniform water evaporation on the insulator, and different areas on the insulator almost dried simultaneously, as shown in Figure 7. In this figure, disc suspension porcelain insulators were studied with a surface resistivity of ${\rho }_{ws}=5\times {10}^6\mathsf{\Omega }$ and an ambient relative humidity of 90%. The distributed voltage was 10 kV. The ambient temperature was set as 20 °C. Wind speeds were set as 0.1 m/s, 4.5 m/s, and 10 m/s separately. In Figure 7, the area under the curve represents the area where dry bands were formed.

It can be seen from Figure 6 and Figure 7 that when the insulator is heavily polluted, the ambient humidity is high, there is no wind, and the distributed voltage is high, the probability of locally generating dry bands on the surface of the wetted and polluted insulator is significantly increased. Reference [19] discussed the effect of the altitude at which the power line is located on the wet flashover voltage. As the altitude increases, the atmospheric pressure, temperature, and absolute humidity decrease, and the electrical strength of the insulator also changes. The results show that the wet flashover voltage of insulator strings decreases as the altitude $H$ increases. Equation (8) can be analyzed focused on the conditions of the dry band formation. Since the atmospheric pressure decreases when the altitude of the power line insulator increases, the evaporation rate of the pollution layer increases if other variables are fixed. Figure 8 shows the effect of altitude on the dry band formation trend of disc porcelain insulators, where the area under the curve represents the area where dry bands were formed. In this figure, the wind speed was 0.55 m/s, the distributed voltage was 10 kV, the ambient temperature was 20 °C, and the relative humidity was 90%.

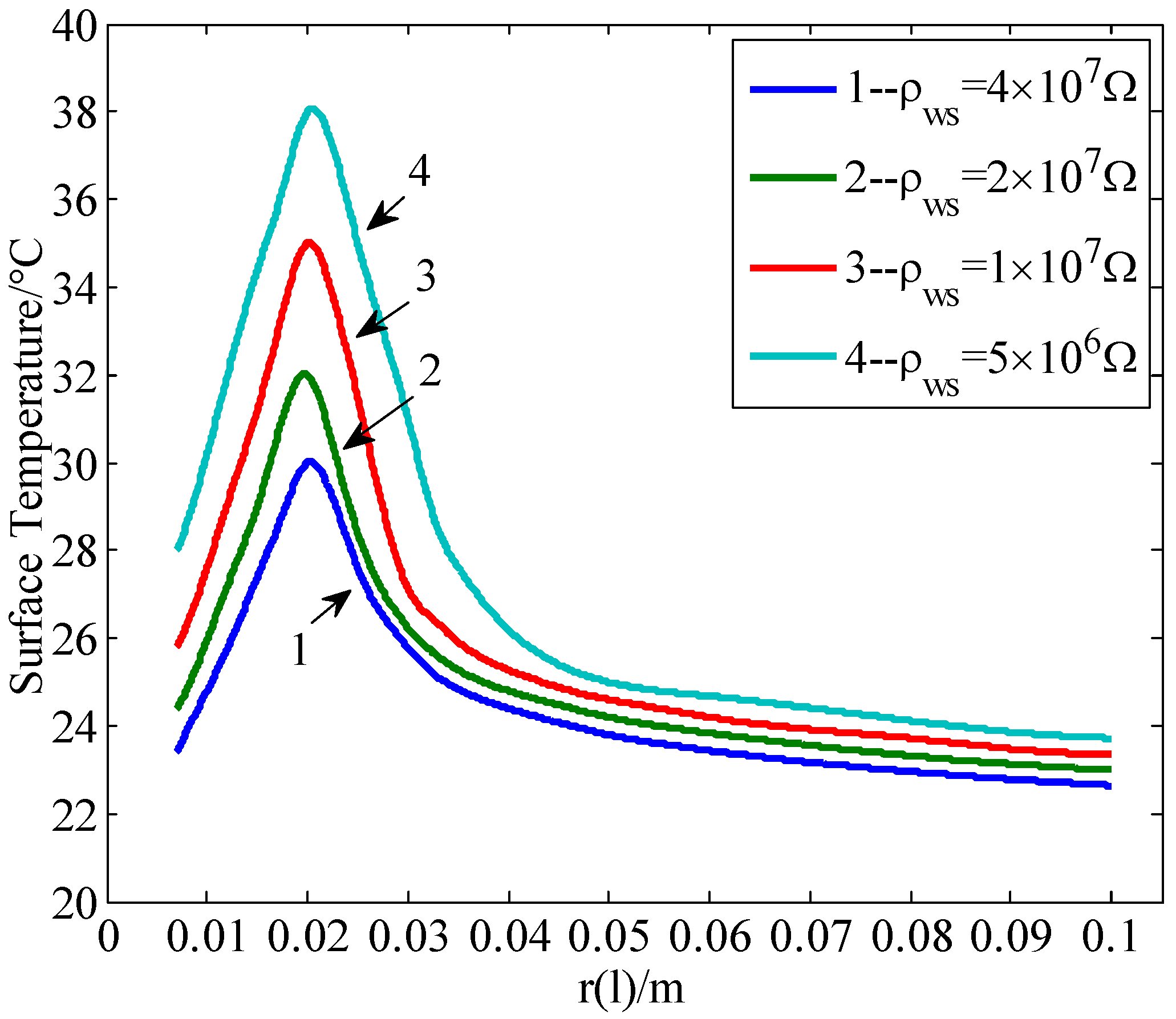
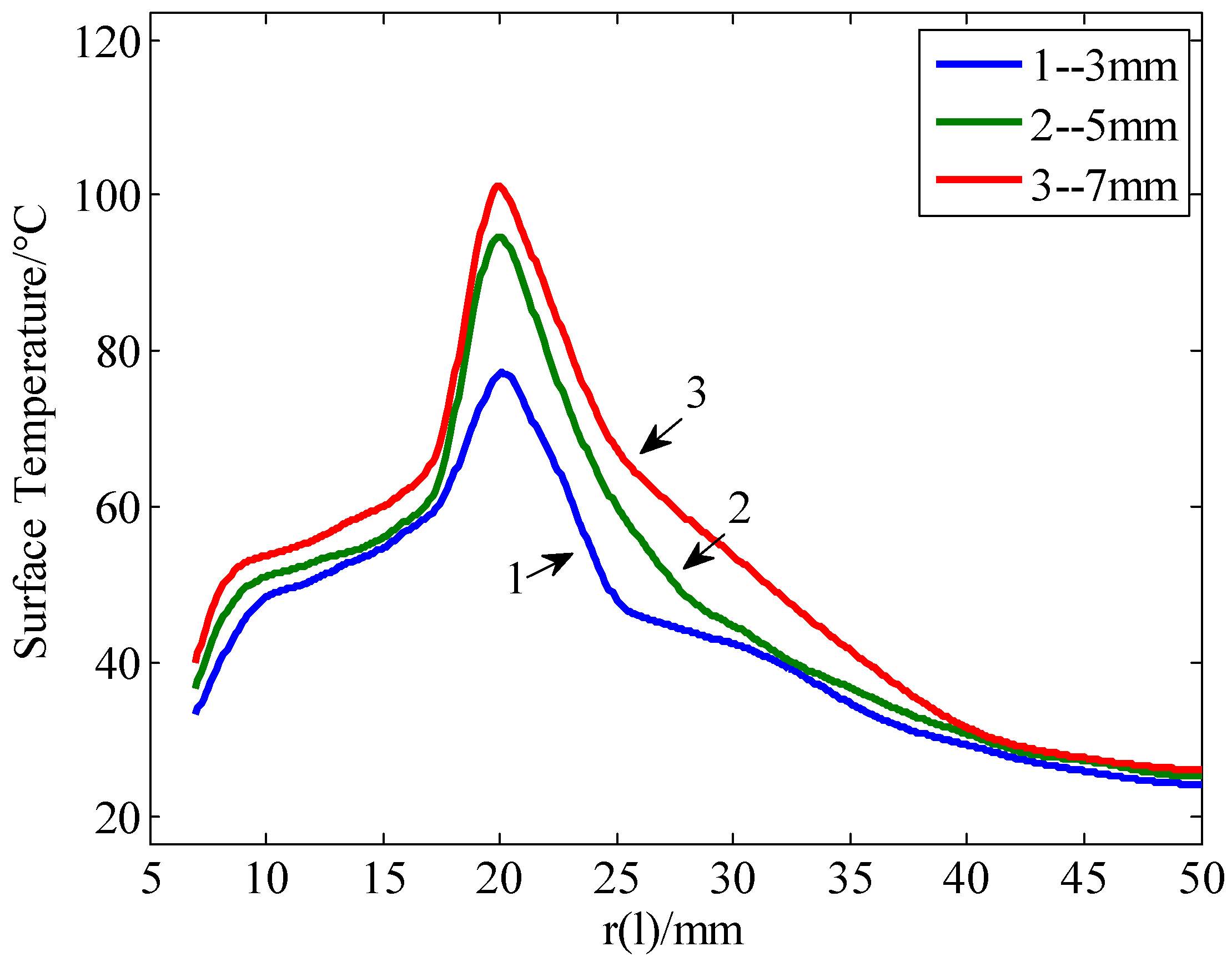
4. Influence of Dry Bands on Temperature Distribution of Insulator Surfaces

When the water evaporation rate on an insulator is higher than the water precipitation and absorption rate, the areas on the insulator with higher temperatures gradually becomes dry as the water evaporates. As the pollution layer in the annular high-temperature area gradually dries, the surface resistivity of the dry band increases. In addition, the surface resistivity of other areas on the insulator changes a little, resulting in a significant increase in the heating power and the heat flux density of the dry bands. The temperature of the dry band will further increase, which accelerates the formation of dry bands. Figure 9 shows a numerically simulated curve, in which the maximum temperature on an insulator gradually increases as the surface resistivity of the dry band increases. The resistivity of the pollution layer out of the dry bands was set to ${\rho }_{ws}=5\times {10}^6\mathsf{\Omega }$, and the width of the dry bands was 5 mm. The ambient temperature was set as 20 °C.

The width of the dry bands also has a significant influence on the temperature distribution on an insulator. The dry band on the bottom surface of the insulator, where the radial distance from the axis of rotation was 20 mm, was selected for temperature field simulation. The surface resistivity of the dry band (${\rho }_{ds}$) was set to $7\times {10}^7\mathsf{\Omega }$, and the resistivity of the pollution layer outside the dry band was set to ${\rho }_{ws}=5\times {10}^6\mathsf{\Omega }$. The ambient temperature was set as 20 °C. Dry bands that had widths of 3, 5, and 7 mm were simulated, and the results are shown in Figure 10. As the width of the dry bands increased, the surface temperature of the dry bands gradually increased, and the surface temperature of the entire insulator also increased substantially.

Generally speaking, the dry band forms in the annular region with the highest temperature, but due to the influence of many factors, the location of the dry band can also be changed to a certain degree. Figure 11 is the numerical simulation result of the insulator surface temperature field when the distance between the dry band and disc center is 15 mm, 20 mm, 25 mm, and 35 mm respectively. The width of the dry band was 5 mm. The ambient temperature was set at 20 °C. The surface resistivity of the dry band (${\rho }_{ds}$) was set to $7\times {10}^7\mathsf{\Omega }$, and the resistivity of the pollution layer outside the dry band was set to ${\rho }_{ws}=5\times {10}^6\mathsf{\Omega }$. Comparing Figure 11 with Figure 5 and Figure 10, when a dry band occurred in the annular region with the maximum temperature on a uniformly wetted insulator, the temperature rise in this region was substantial. If the dry band occurred outside the annular region with the maximum temperature, the temperature rise in the corresponding region was not as dramatic as the previous case. Due to the heat generation caused by the high current density near the disc center, when the dry band appears far from the disc center (35 mm, for instance), the temperature rise in the region between the dry band and the disc center is obvious.

Due to the randomness of the generation of dry bands, sometimes there are several dry bands on the insulator surface at the same time, which leads to great changes in the temperature distribution on the insulator surface. Figure 12 is the numerical simulation of the influence of the number of dry bands on the temperature distribution on the insulator surface. Curve 1 is the temperature distribution curve when there are two dry bands 10 mm and 20 mm away from the disc center. Curve 2 is the temperature distribution curve when there are dry bands 10 mm, 20 mm, and 35 mm away from the disc center. The width of the dry band was 5 mm. The ambient temperature was set to 20 °C. The surface resistivity of the dry band (${\rho }_{ds}$) was set to $7\times {10}^{7 }\mathsf{\Omega }$, and the resistivity of the pollution layer outside the dry band was set to ${\rho }_{ws}=5\times {10}^{6 }\mathsf{\Omega }$. It can be seen that with the increase of the number of dry bands on the insulator surface, the maximum temperature decreased gradually. Meanwhile, the region where the dry bands were located was the region where the peak temperature was located. The number of dry bands on the insulator surface was the same as the number of peak temperatures on the insulator surface. The overall temperature rise of insulators with more dry bands was more obvious than that of insulators with less dry bands.

5. Conclusions

When the ambient humidity is high, the pollution layer absorbs water and generates leakage currents. Affected by the shape and structure of an insulator, the surface temperatures of specific areas on the insulator are higher than those of other areas, resulting in accelerated water evaporation and increased surface resistivity in these specific areas. These effects further increase the surface temperatures of these specific areas, and dry bands are formed. The critical relative humidity (CRH) of the soluble mixture in the contamination layer decreases with the increase of the variety of soluble substances. The reduction of CRH caused by the complexity of soluble substances in the contaminant of naturally contaminated insulators can be considered as a previously neglected reason for the inconsistency between the result of an artificial contamination test and that of a natural contamination test. The hygroscopic characteristics of soluble substances in a contamination mixture should be considered as a factor in subsequent artificial contamination experiments. The formula for the formation conditions of dry bands is obtained by theoretical analysis. Based on this formula, the distribution rule regarding the insulator surface temperature and the influence of parameters such as distribution voltage, wind speed, and altitude on the formation of dry bands are quantitatively studied through theoretical calculation and numerical simulation. Meanwhile, the influence of the width, position, and quantity of dry bands on the surface temperature distribution of insulators is also quantitatively studied. For insulators with contamination grades of Ⅰ to Ⅳ, the brightest ring region in infrared images and the main discharge region in ultraviolet images are consistent with the highest temperature region and the distribution region of dry bands obtained by theoretical calculation and numerical simulation.