Grid-Synchronization Stability Analysis for Multi DFIGs Connected in Parallel to Weak AC Grids
Abstract
:1. Introduction
2. Modeling
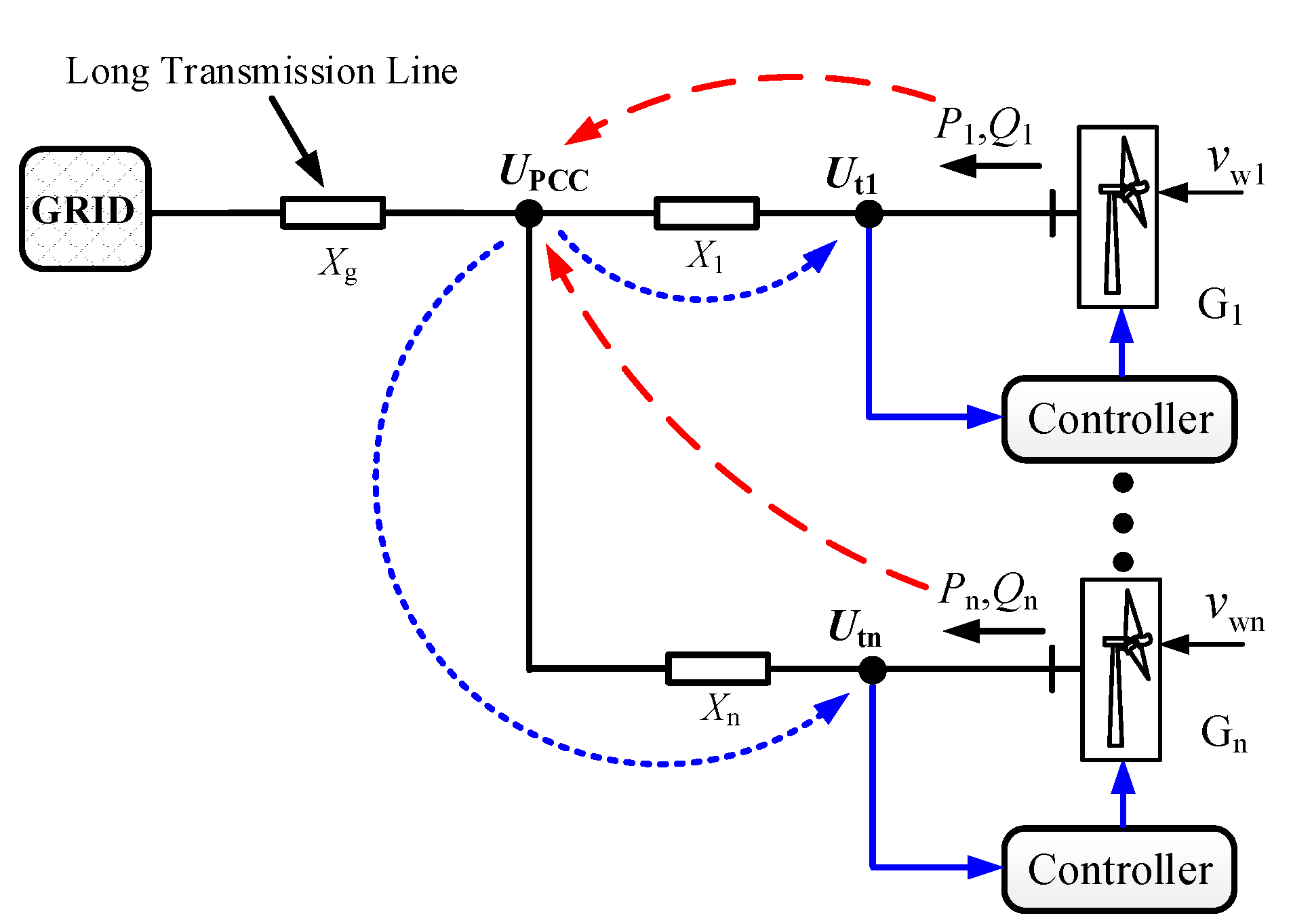
2.1. System Configuration and Multi-WT Interactions
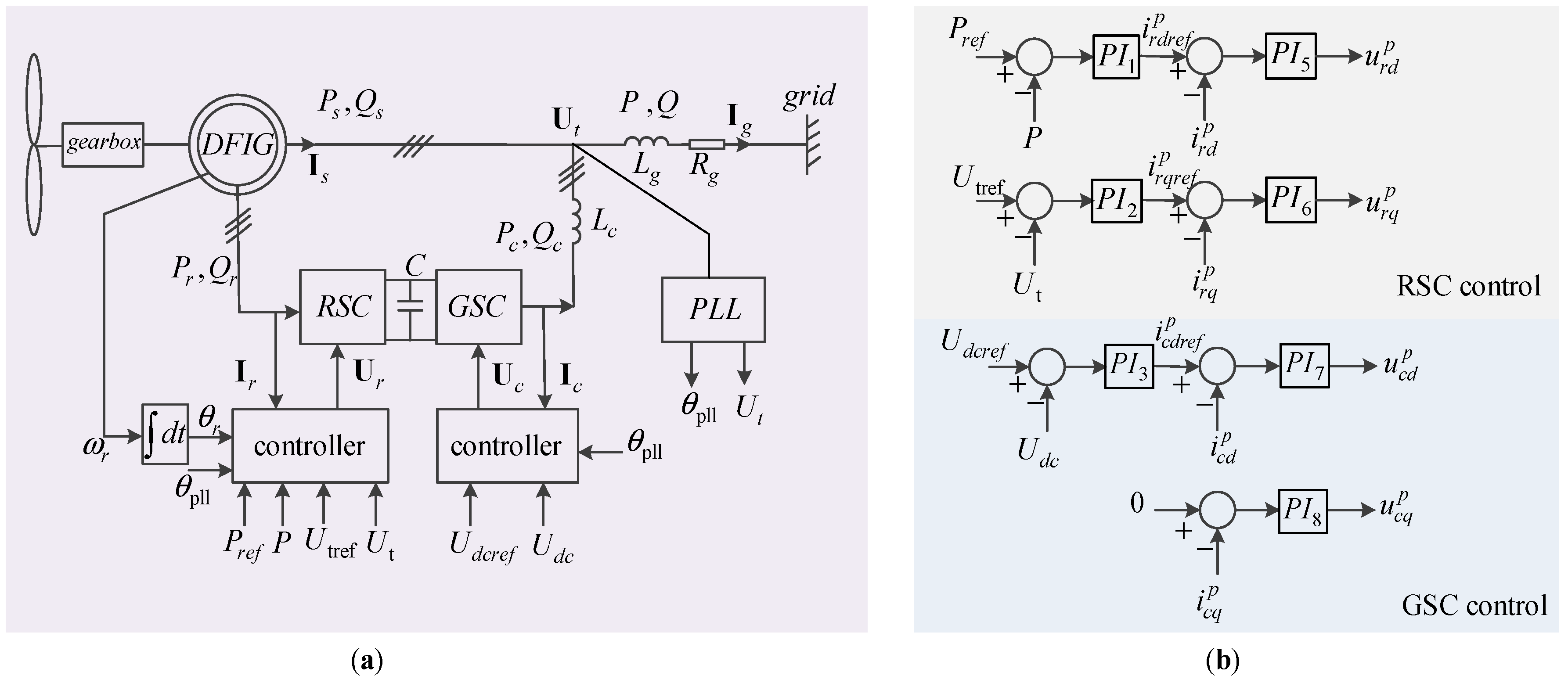
2.2. System Modeling
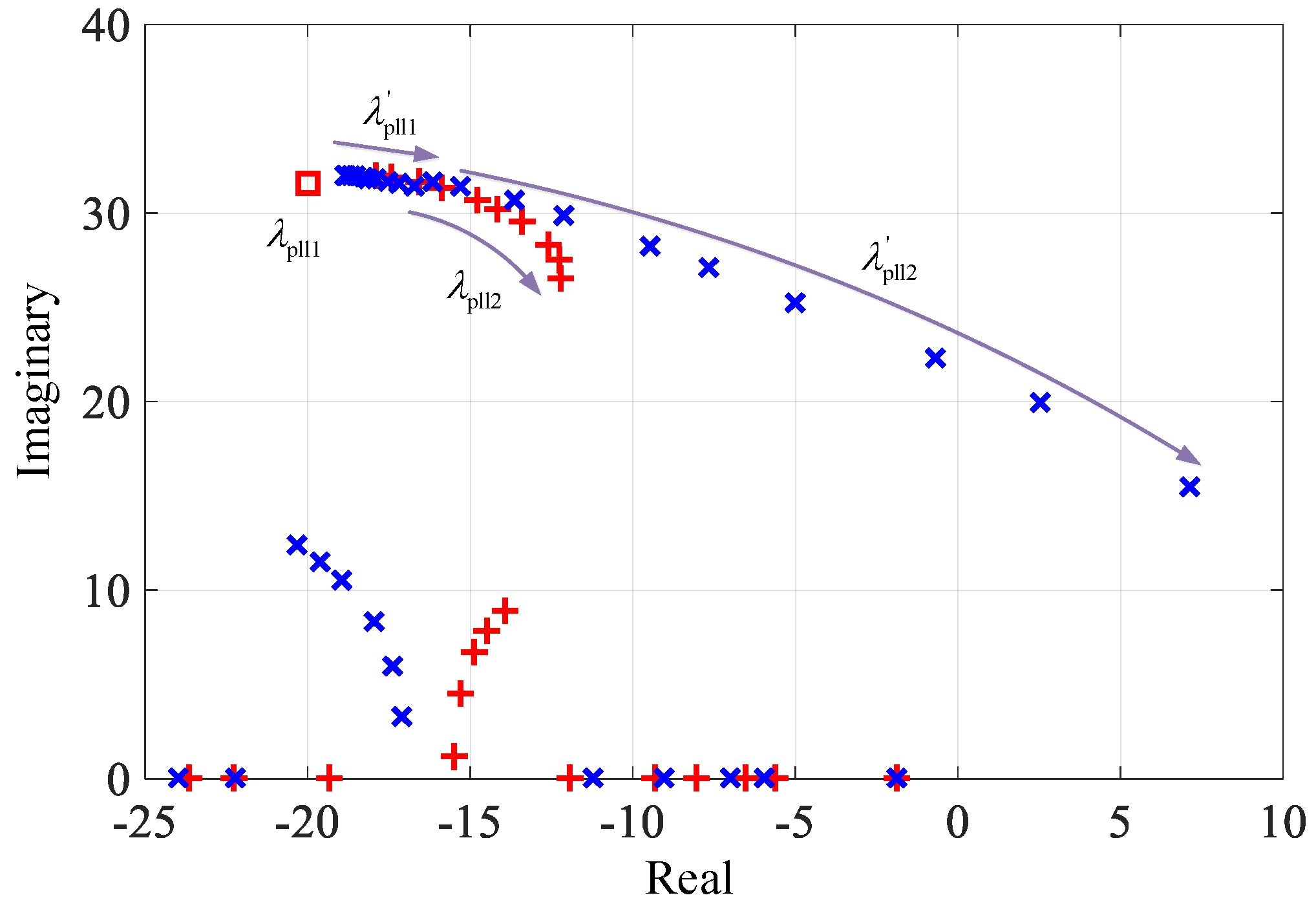
3. Eigenvalue Sensitivity Analysis
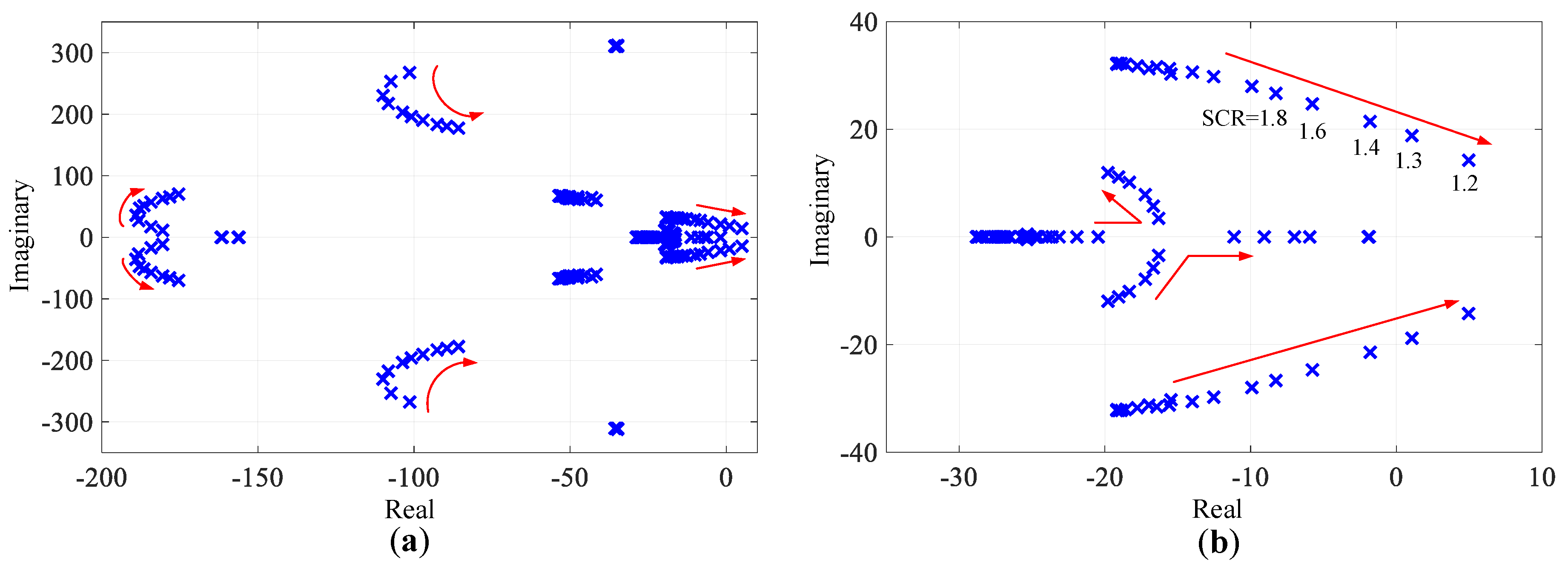
3.1. The Impact of Grid Strengths
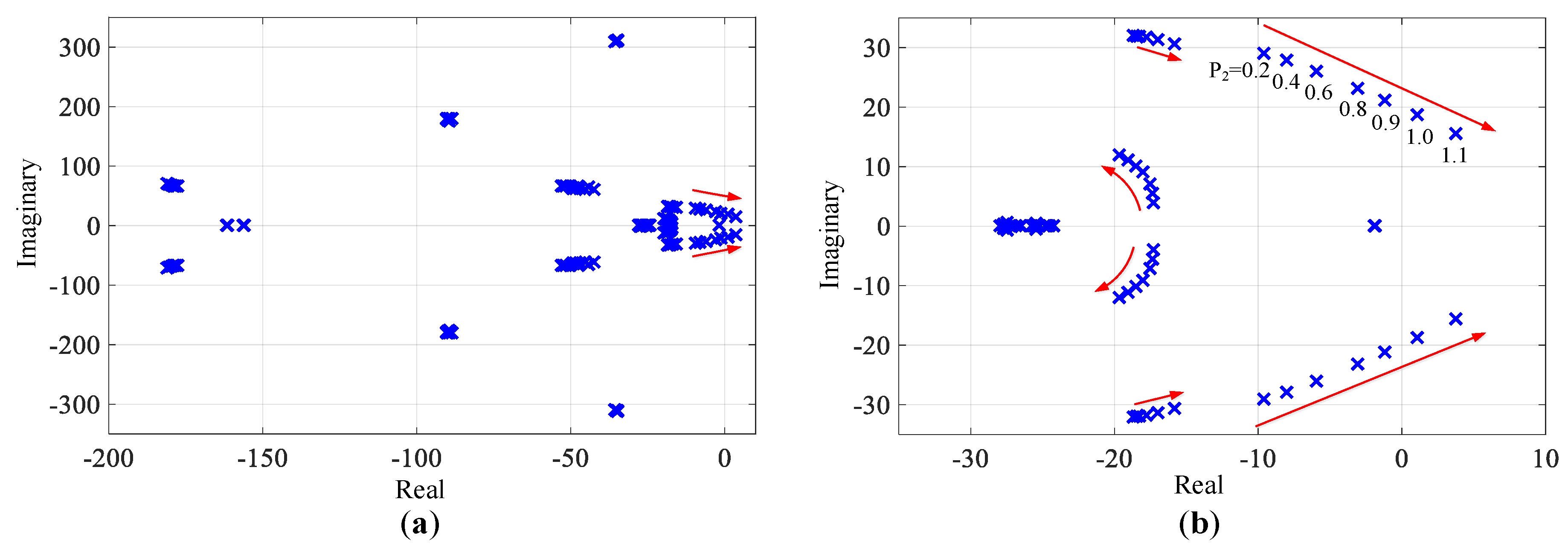
3.2. The Impact of Operating Points
3.3. Participation Factor Analysis
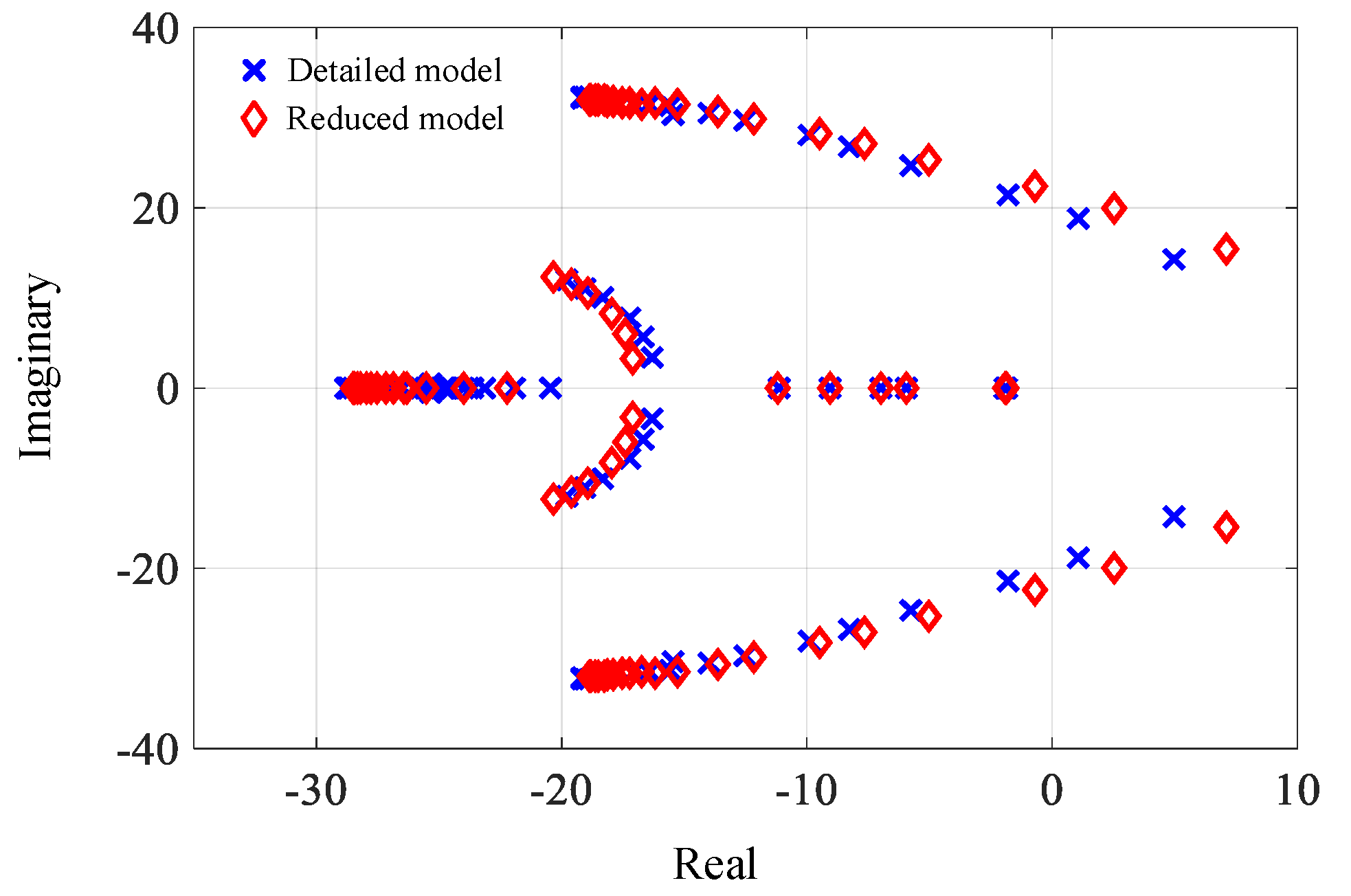
4. Proposed Reduced-Order Model
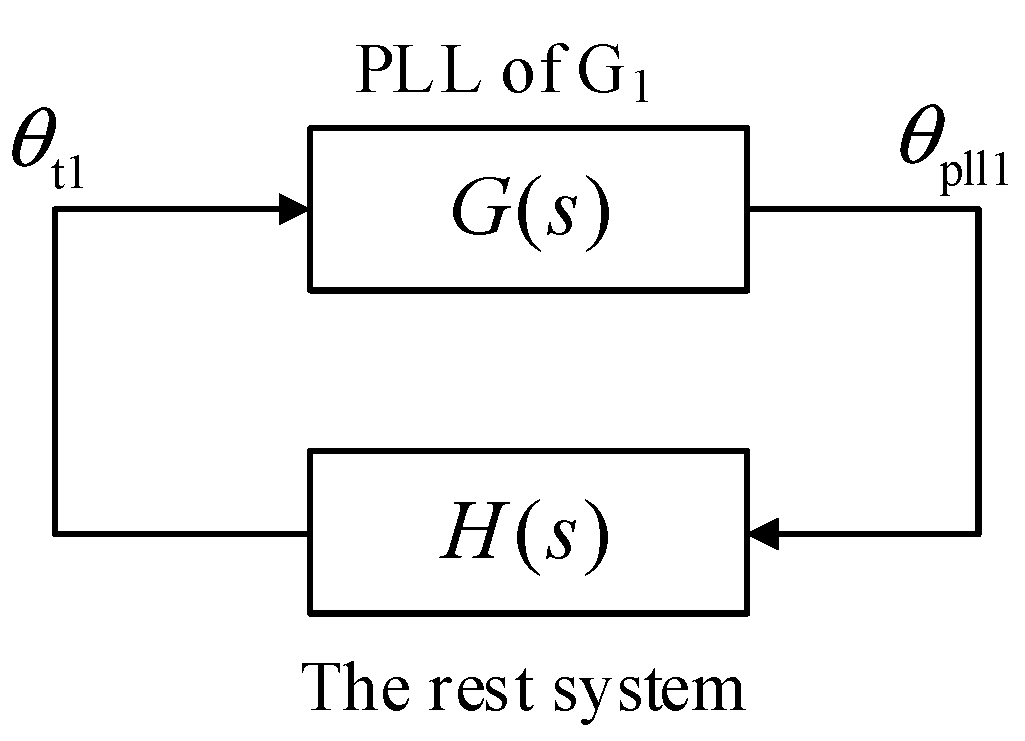
5. Residue-Based Explanation on Weak-Grid Instability
5.1. Transfer Function Residue
5.2. Explanation on Weak-Grid Instability
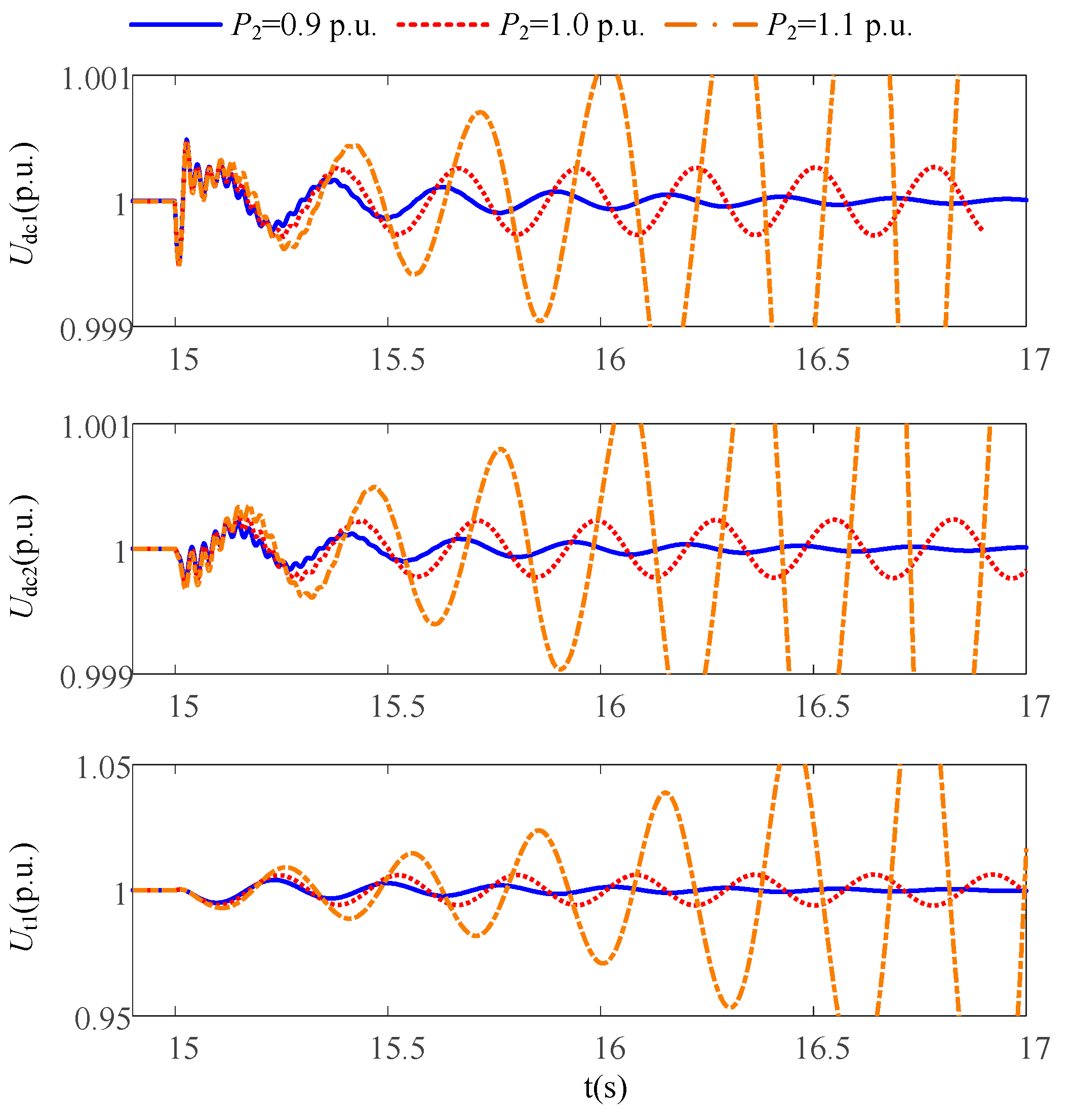
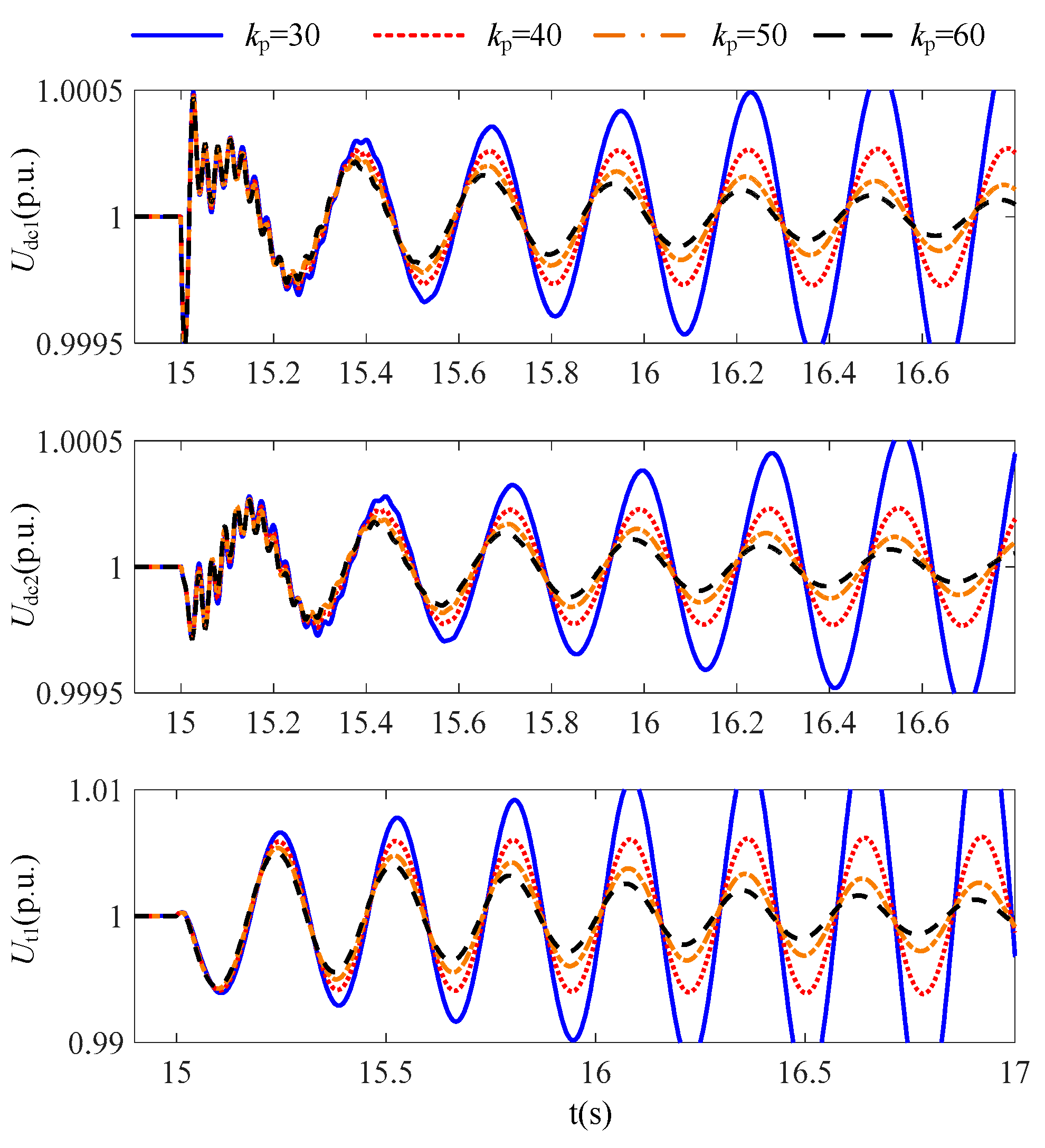
6. Simulation Studies
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ls, Lr, Lm | Stator, rotor and mutual inductances |
| Lls, Llr | Stator and rotor leakage inductances |
| Rs, Rr | Stator and rotor resistances |
| ω1, ωr | Synchronous and rotor angular frequency |
| Ut, θt | Terminal voltage magnitude and phase |
| Ps, Qs | Stator active and reactive powers |
| Pr, Qr | Rotor active and reactive powers |
| Pc, Qc | Grid-side converter active and reactive powers |
| Pi, Qi | Active and reactive powers sent to grid by generator i |
| Uc, Ur | Output voltage of grid-side converter and rotor-side converter |
| Is, Ir, Ic | Stator, rotor and grid-side converter current |
| Ψs, Ψr | Stator and rotor flux |
| Lc | Filter inductance of grid-side converter |
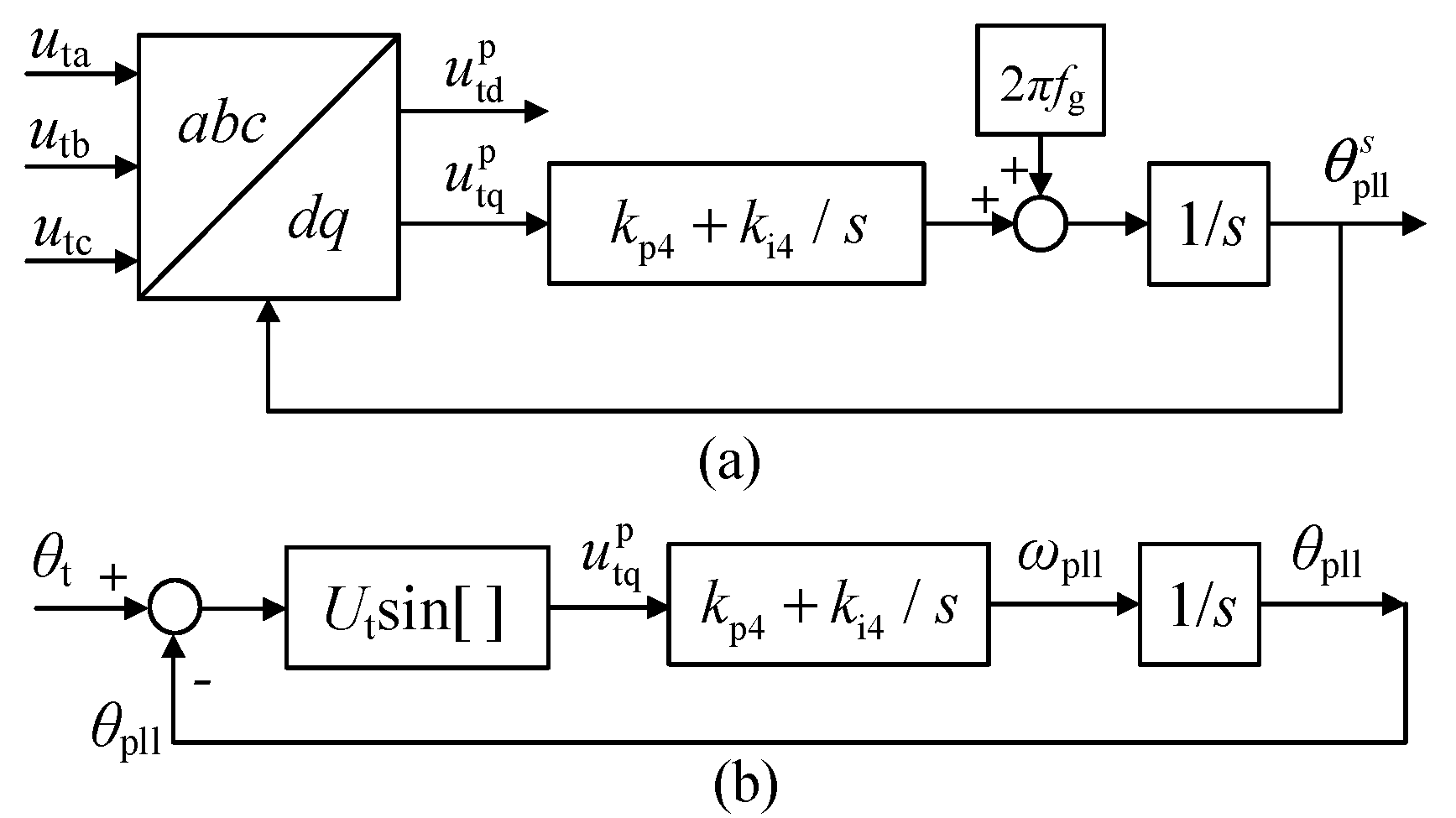
| θpll, ωpll | PLL output angle and frequency |
| Udc, C | DC-link voltage and capacitance |
| PCC | Point of common connection |
| kp, ki | Proportion and integral control gain |
| Lg | Transmission line inductance between the PCC and the infinite bus |
| Li | Equivalent line inductance between generator terminal bus and the PCC |
| Subscripts: | |
| 0 | Steady-state value |
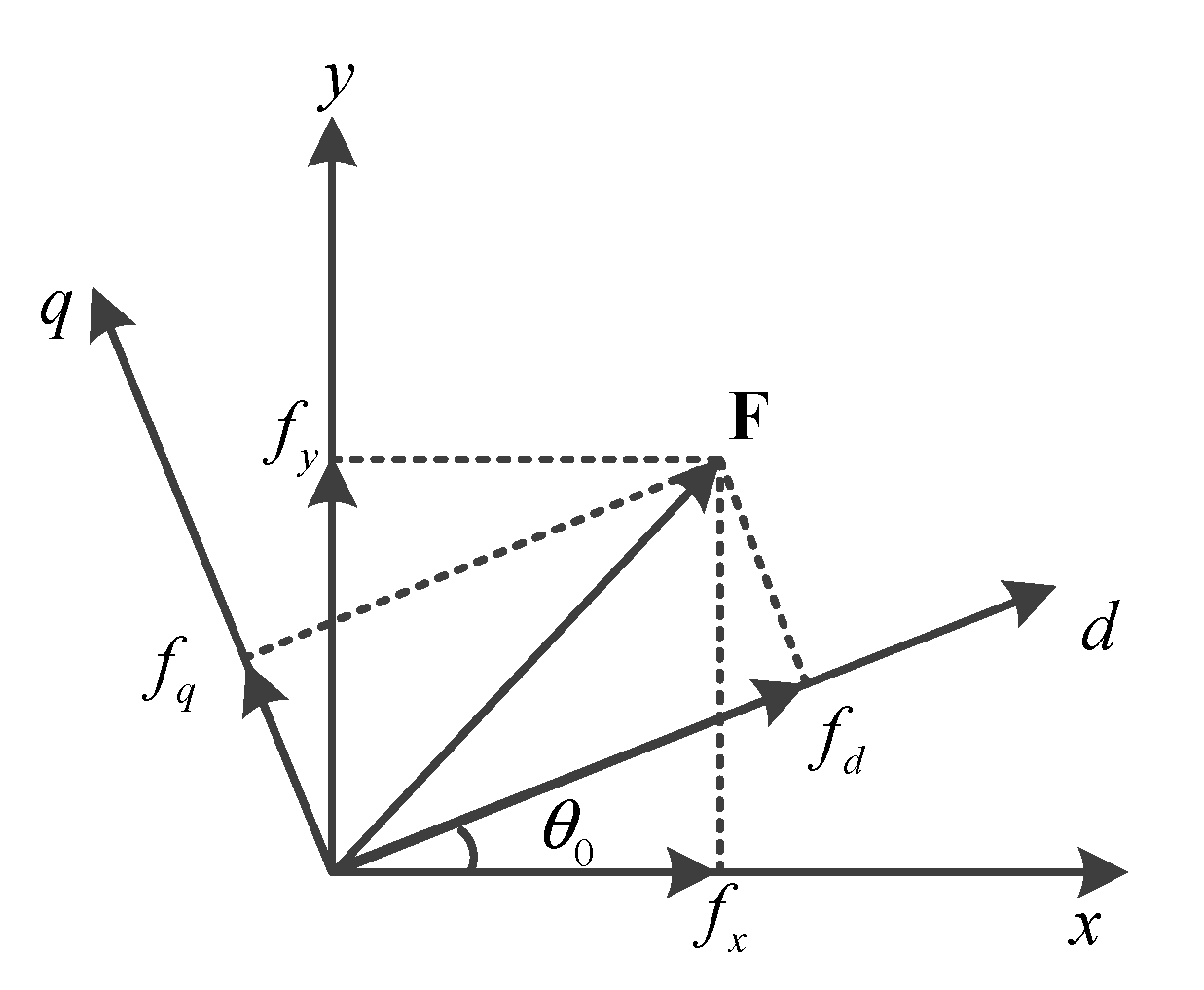
| d, q | Synchronous rotating reference frame signal d-axis and q-axis components |
| x, y | Global reference frame signal x-axis and y-axis components |
| s, r | Stator and rotor components |
| ref | Reference signal |
| Superscript: | |
| p | Components in PLL rotating frame |
Appendix A
| Sbase = 2 MW | Ubase = 690 V(phase to phase RMS value) | ||
| ωbase = 2 πfbase | fbase = 50 Hz | Rs = 0.022 p.u. | Rr = 0.009 p.u. |
| Lls = 0.171 p.u. | Llr = 0.156 p.u. | Lm = 3.9 p.u. | Lc = 0.3 p.u. |
| Udcref = 1200 V | C = 0.02 F | Ug = 1 p.u. | Rg = 0.1 ω1Lg |
| RSC active power control | kp1 = 0.4 | ki1 = 40 |
| RSC terminal voltage control | kp2 = 0.25 | ki2 = 25 |
| DC-link voltage control | kp3 = 1.5 | ki3 = 100 |
| Phase-locked loop | kp4 = 40 | ki4 = 1400 |
| RSC current control | kp5 = kp6 = 0.6 | ki5 = ki6 = 80 |
| GSC current control | kp7 = kp8=8 | ki7 = ki8 = 200 |
References
- Zhou, J.Z.; Gole, A.M. VSC transmission limitations imposed by AC system strength and AC impedance characteristics. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC), Birmingham, UK, 4–5 December 2012; pp. 1–6. [Google Scholar]
- Yang, D.; Wang, X.; Liu, F.; Xin, K.; Liu, Y.; Blaabjerg, F. Adaptive reactive power control of PV power plants for improved power transfer capability under ultra-weak grid conditions. IEEE Trans. Smart Grid 2019, 10, 1269–1279. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.; Jiang, Q.; Liu, H.; Li, Y.; Liu, H. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system. IEEE Trans. Power Syst. 2015, 30, 2772–2779. [Google Scholar] [CrossRef]
- Huang, S.H.; Schmall, J.; Conto, J.; Adams, J.; Zhang, Y.; Carter, C. Voltage control challenges on weak grids with high penetration of wind generation: Ercot experience. In Proceedings of the IEEE Power Energy Social General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Messo, T.; Jokipii, J.; Mäkinen, A.; Suntio, T. Modeling the grid synchronization induced negative-resistor-like behavior in the output impedance of a three-phase photovoltaic inverter. In Proceedings of the IEEE Fourth International Symposium on Power Electron, For Distributed Generations System, Rogers, AR, USA, 8–11 July 2013; pp. 1–8. [Google Scholar]
- Wang, D.; Liang, L.; Shi, L.; Hu, J.; Hou, Y. Analysis of modal resonance between PLL and DC-link voltage control in weak-grid tied VSCs. IEEE Trans. Power Syst. 2019, 34, 1127–1138. [Google Scholar] [CrossRef]
- Hu, J.; Huang, Y.; Wang, D.; Yuan, H.; Yuan, X. Modeling of grid connected DFIG-based wind turbines for DC-link voltage stability analysis. IEEE Trans. Sustain. Energy 2015, 6, 1325–1336. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Wang, S.; Hu, J.; Yuan, X. Virtual synchronous control for grid-connected DFIG-based wind turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 932–944. [Google Scholar] [CrossRef]
- Wen, B.; Dong, D.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Impedance-based analysis of grid-synchronization stability for three-phase paralleled converters. IEEE Trans. Power Electron. 2016, 31, 26–38. [Google Scholar] [CrossRef]
- Rosso, R.; Andresen, M.; Engelken, S.; Liserre, M. Analysis of the interaction among power converters through their synchronization mechanism. IEEE Trans. Power Electron. 2019, 34, 12321–12332. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, D.; Shang, L.; Zhu, G.; Tang, H.; Li, Y. Modeling and stability analysis of DC-link voltage control in multi VSCs with integrated to weak grid. IEEE Trans. Energy Convers. 2017, 32, 1127–1138. [Google Scholar] [CrossRef]
- Akagi, H.; Sato, H. Control and performance of a doubly-fed induction machine intended for a flywheel energy storage system. IEEE Trans. Power Electron. 2002, 17, 109–116. [Google Scholar] [CrossRef]
- Gole, A.; Sood, V.K.; Mootoosamy, L. Validation and analysis of a grid control system using D-Q-Z transformation for static compensator system. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Montreal, PQ, Canada, 17–20 September 1989; pp. 745–748. [Google Scholar]
- He, W.; Yuan, X.; Hu, J. Inertia provision and estimation of PLL-based DFIG wind turbines. IEEE Trans. Power Syst. 2017, 32, 510–521. [Google Scholar] [CrossRef]
- Wind Farm-DFIG Detailed Model, MATLAB Simulink. Available online: https://uk.mathworks.com/help/physmod/sps/examples/wind-farm-dfig-detailed-model.html (accessed on 8 October 2019).
- Zhou, J.; Ding, H.; Fan, S. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; The EPRI Power System Engineering Series; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Rogers, G. Power System Oscillations; Kluwer Academic Publishers: New York, NY, USA, 2000. [Google Scholar]
- Heniche, A.; Kamwa, I. Assessment of two methods to select wide-area signals for power system damping control. IEEE Trans. Power Syst. 2008, 23, 572–581. [Google Scholar] [CrossRef]
- Pagola, F.L.; Perez-Arriaga, I.J.; Verghese, G.C. On sensitivities residues and participations: Applications to oscillatory stability and control. IEEE Trans. Power Syst. 1989, 14, 278–285. [Google Scholar] [CrossRef]
- Morato, J.; Knüppel, T.; Østergaard, J. Residue-based evaluation of the use of wind power plants with full converter wind turbines for power oscillation damping control. IEEE Trans. Sustain. Energy 2014, 5, 82–89. [Google Scholar] [CrossRef]


| Eigenvalue | Participating Factors | Related Controls | |
|---|---|---|---|
| λ1,2 | −15.409 ± j31.153 | = 0.261 | G1 PLL |
| = 0.245 | G2 PLL | ||
| λ3,4 | −19.183 ± j32.153 | = 0.243 | G1 PLL |
| = 0.259 | G2 PLL |
| Eigenvalue | Participating Factors | Related Controls | |
|---|---|---|---|
| λ1,2 | −1.812 ± j21.389 | = 0.105 | G1 RSC P and Q |
| = 0.180 | G1 PLL | ||
| = 0.107 | G2 RSC P and Q | ||
| = 0.179 | G2 PLL | ||
| λ3,4 | −17.79 ± j31.727 | = 0.015 | G1 RSC P |
| = 0.248 | G1 PLL | ||
| = 0.018 | G2 RSC P | ||
| = 0.253 | G2 PLL |
| Detailed Model Eigenvalues | Reduced-Order Model Eigenvalues | |
|---|---|---|
| λ1,2 | −9.935 ± j28.022 | −9.47 ± j28.27 |
| λ3,4 | −16.324 ± j3.396 | −17.093 ± j3.266 |
| λ5,6 | −19.038 ± j32.256 | −18.286 ± j31.906 |
| λ7 | −1.888 | −1.888 |
| λ8 | −27.237 | −27.938 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Huang, Y.; Liao, M.; Zhu, G.; Deng, X. Grid-Synchronization Stability Analysis for Multi DFIGs Connected in Parallel to Weak AC Grids. Energies 2019, 12, 4361. https://doi.org/10.3390/en12224361
Wang D, Huang Y, Liao M, Zhu G, Deng X. Grid-Synchronization Stability Analysis for Multi DFIGs Connected in Parallel to Weak AC Grids. Energies. 2019; 12(22):4361. https://doi.org/10.3390/en12224361
Chicago/Turabian StyleWang, Dong, Yunhui Huang, Min Liao, Guorong Zhu, and Xiangtian Deng. 2019. "Grid-Synchronization Stability Analysis for Multi DFIGs Connected in Parallel to Weak AC Grids" Energies 12, no. 22: 4361. https://doi.org/10.3390/en12224361
APA StyleWang, D., Huang, Y., Liao, M., Zhu, G., & Deng, X. (2019). Grid-Synchronization Stability Analysis for Multi DFIGs Connected in Parallel to Weak AC Grids. Energies, 12(22), 4361. https://doi.org/10.3390/en12224361





