Design of Disturbance Extended State Observer (D-ESO)-Based Constrained Full-State Model Predictive Controller for the Integrated Turbo-Shaft Engine/Rotor System
Abstract
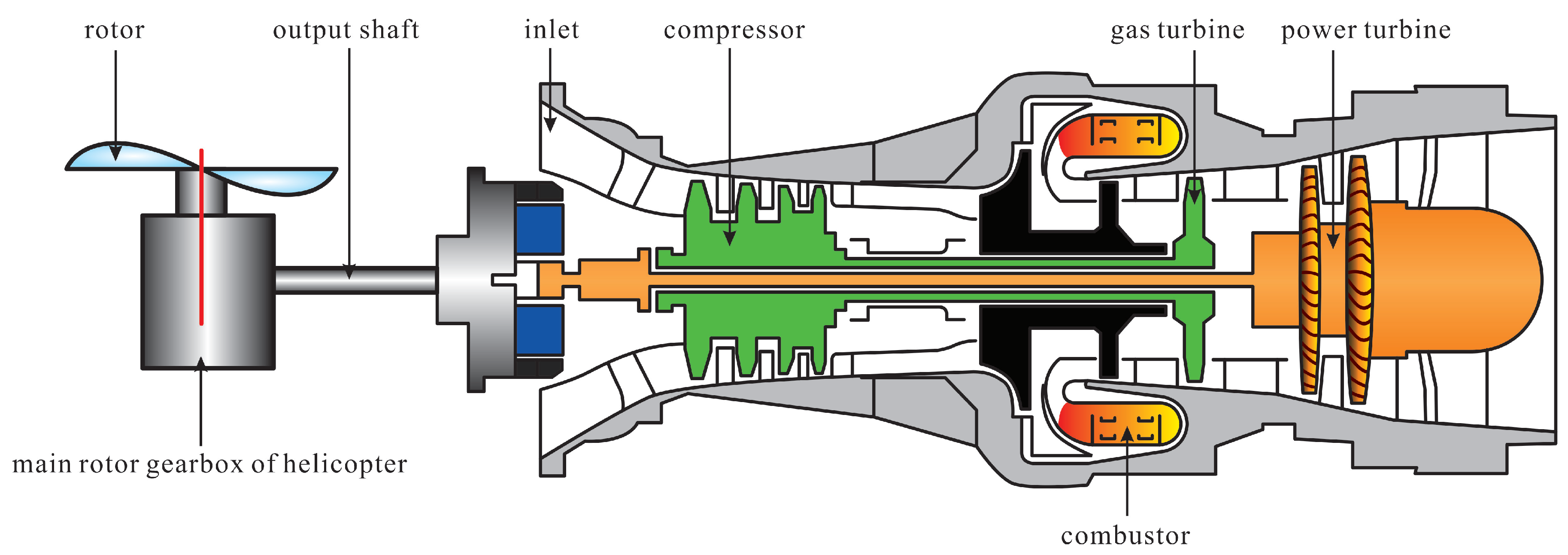
:1. Introduction
- The D-ESO method can overcome the mismatch problem of the predictive model.
- For the LPV system, we give a sufficient condition for the convergence of the D-ESO in Theory 1.
- In comparison with the nonlinear MPC case, MPC based on the LPV model and the D-ESO method in this paper has the advantage of minor calculation.
- A new D-ESO-based MPC controller is designed in this paper to achieve the constrained full-state control of the turbo-shaft engine/rotor system. Compared with M-M-STC strategy, it can not only conquer the high cost and conservation problem of traditional methods, but also leave out the complex structure of Min-Max selection logic strategy.
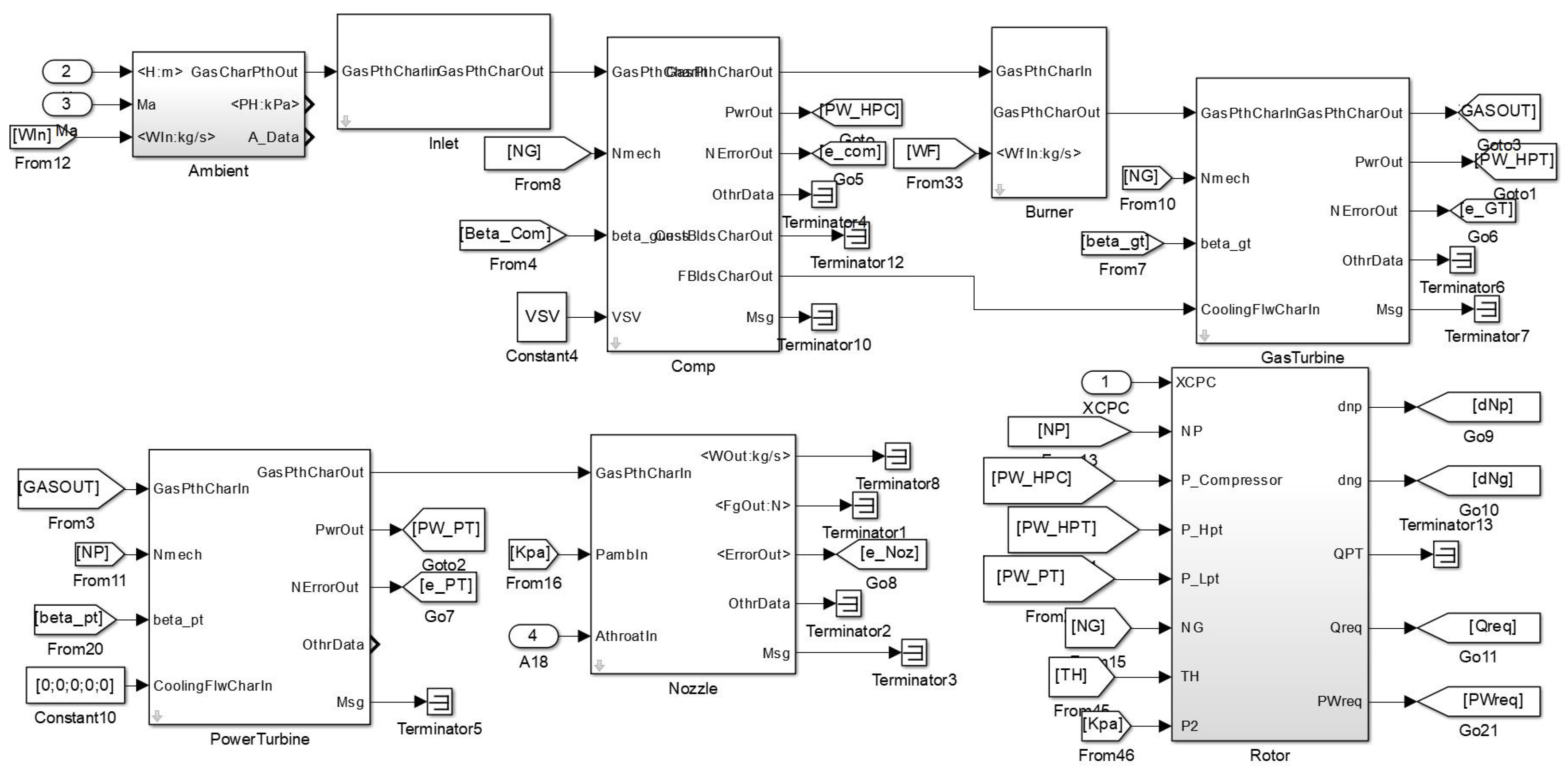
2. Predictive Model-LPV System
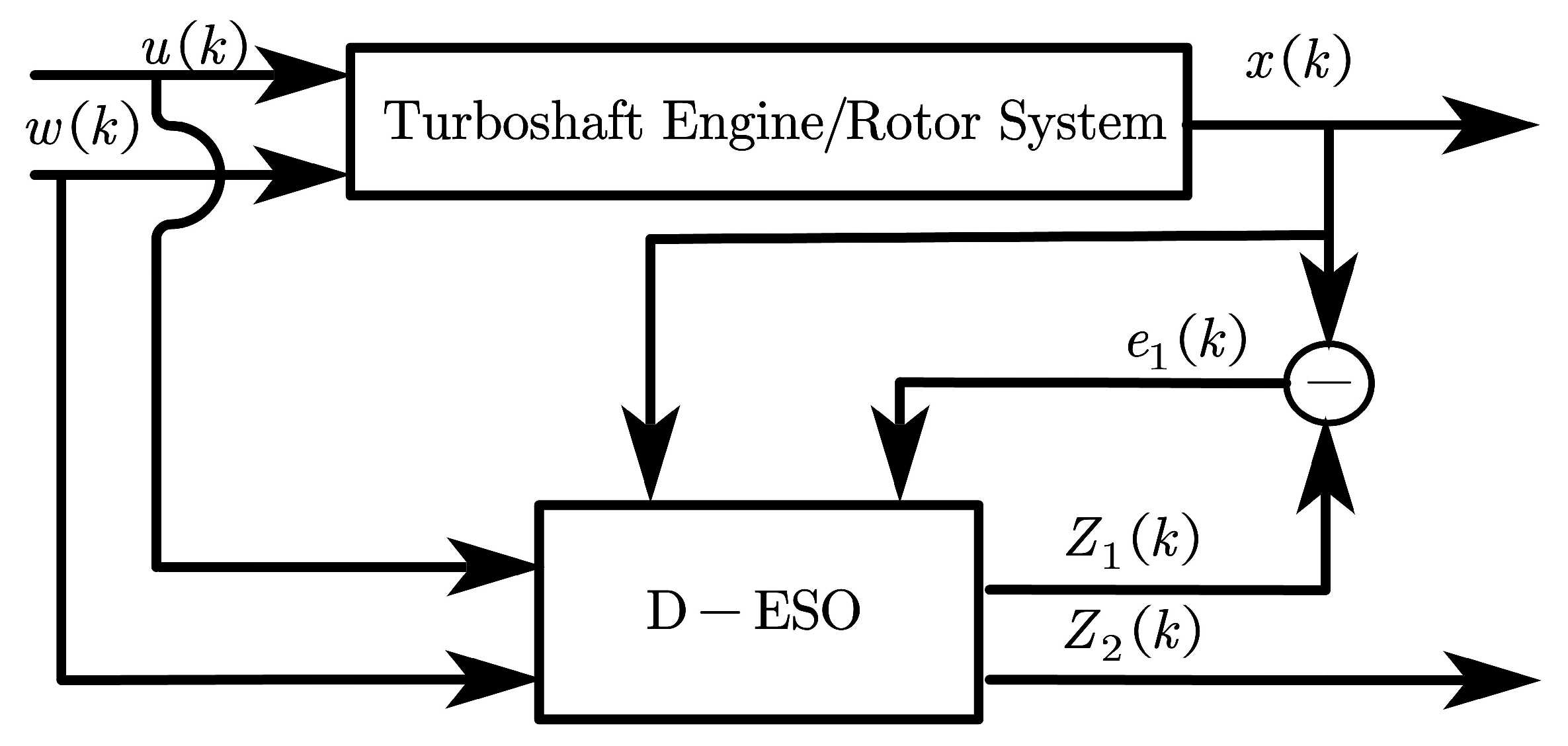
3. Disturbance Based Extended State Observer (D-ESO)
3.1. D-ESO Design
3.2. D-ESO Convergence Condition
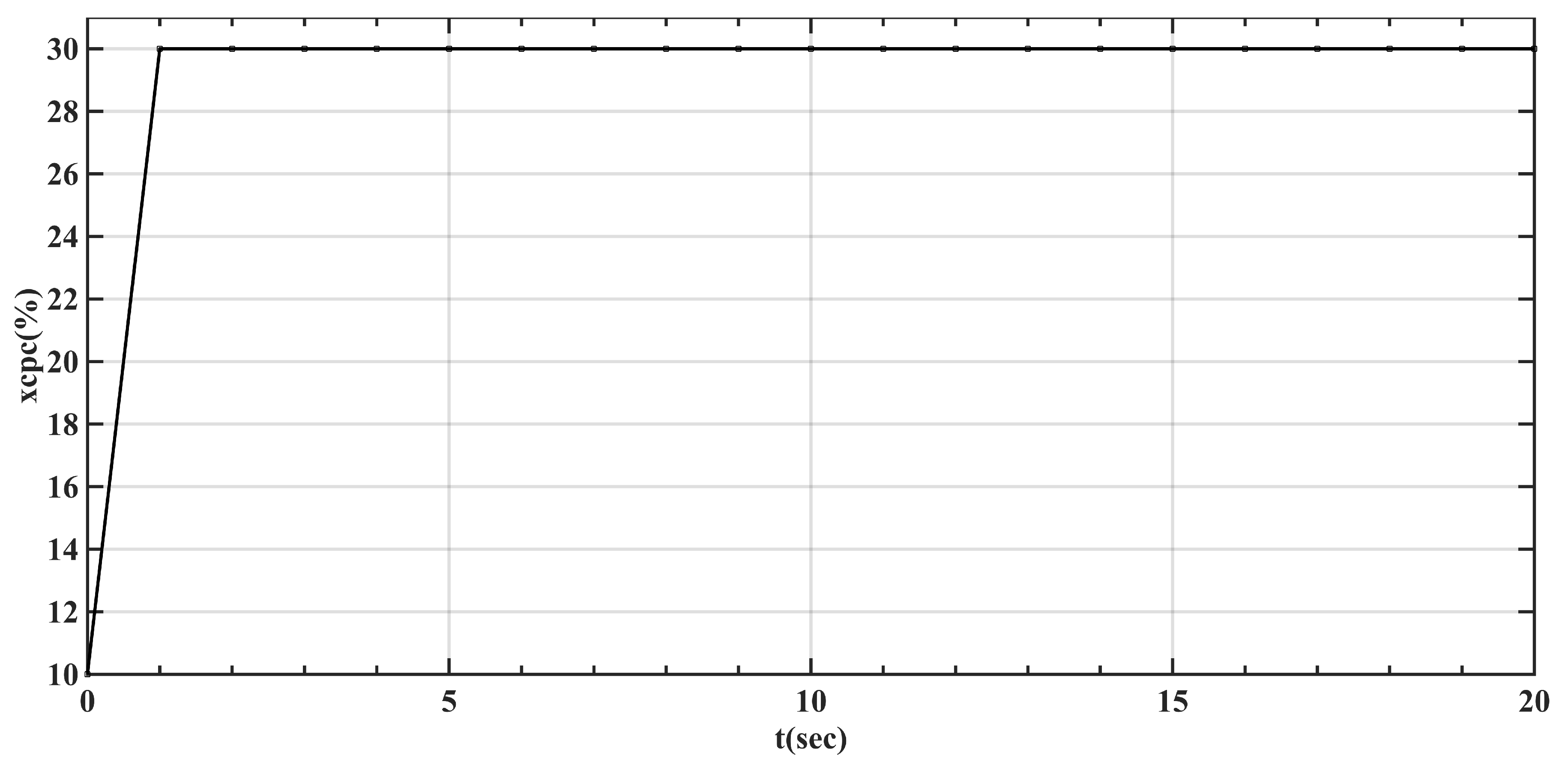
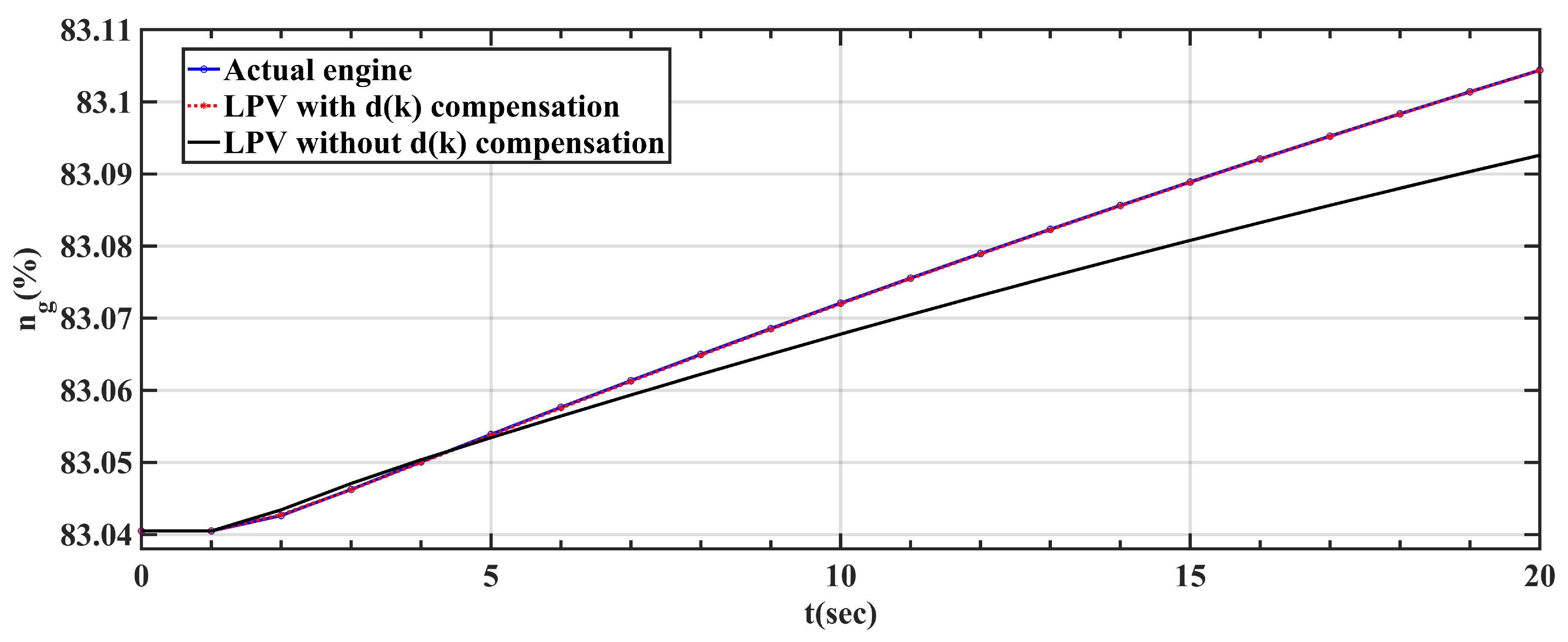
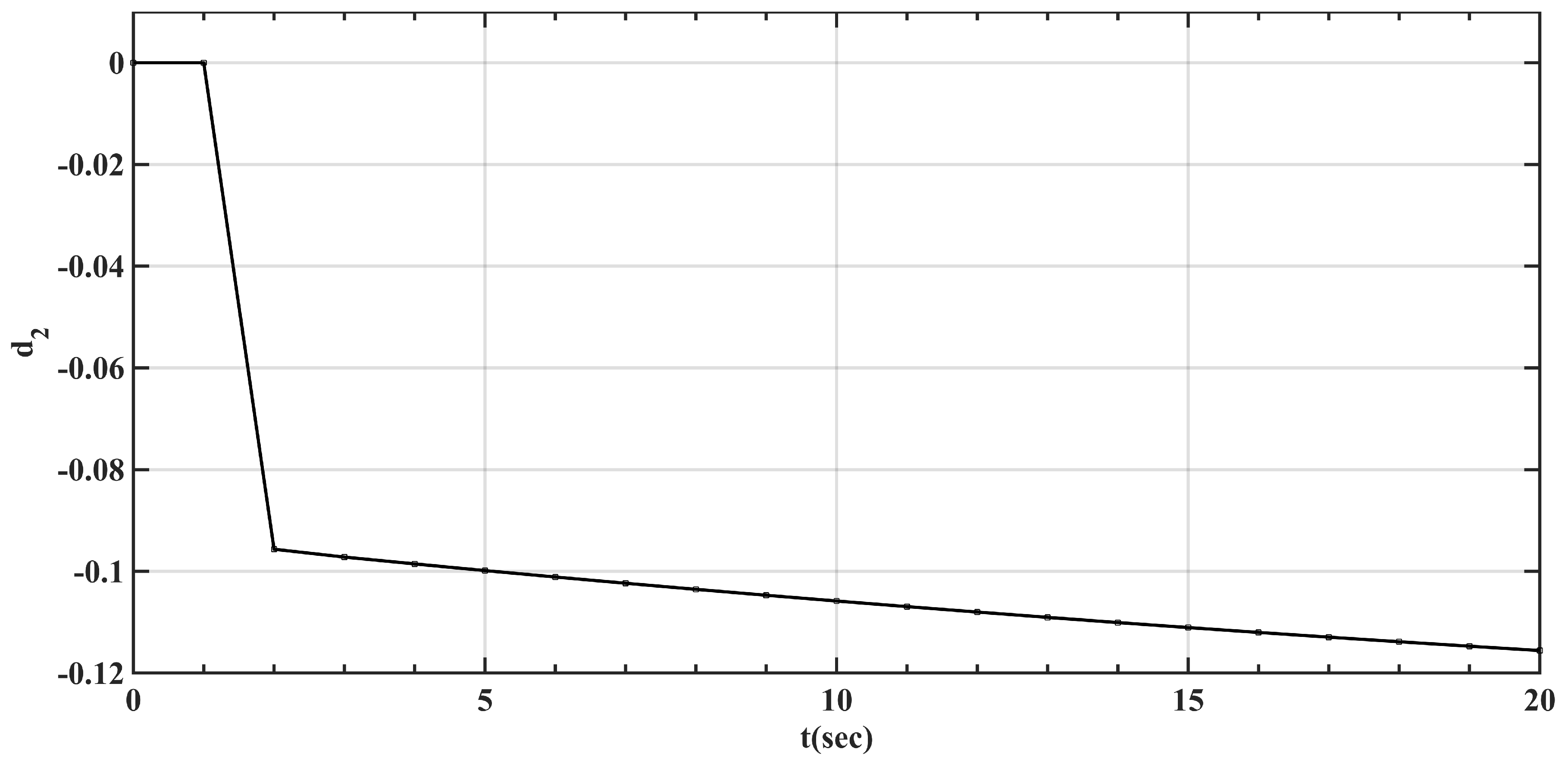
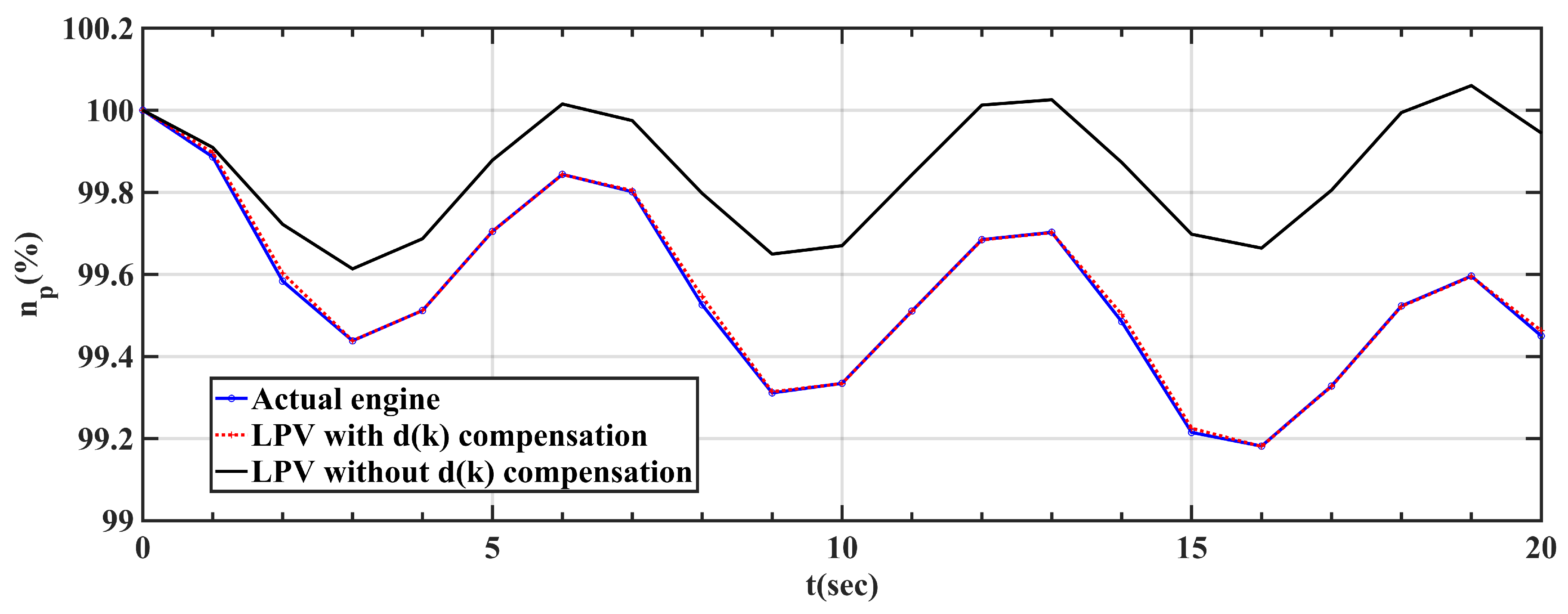
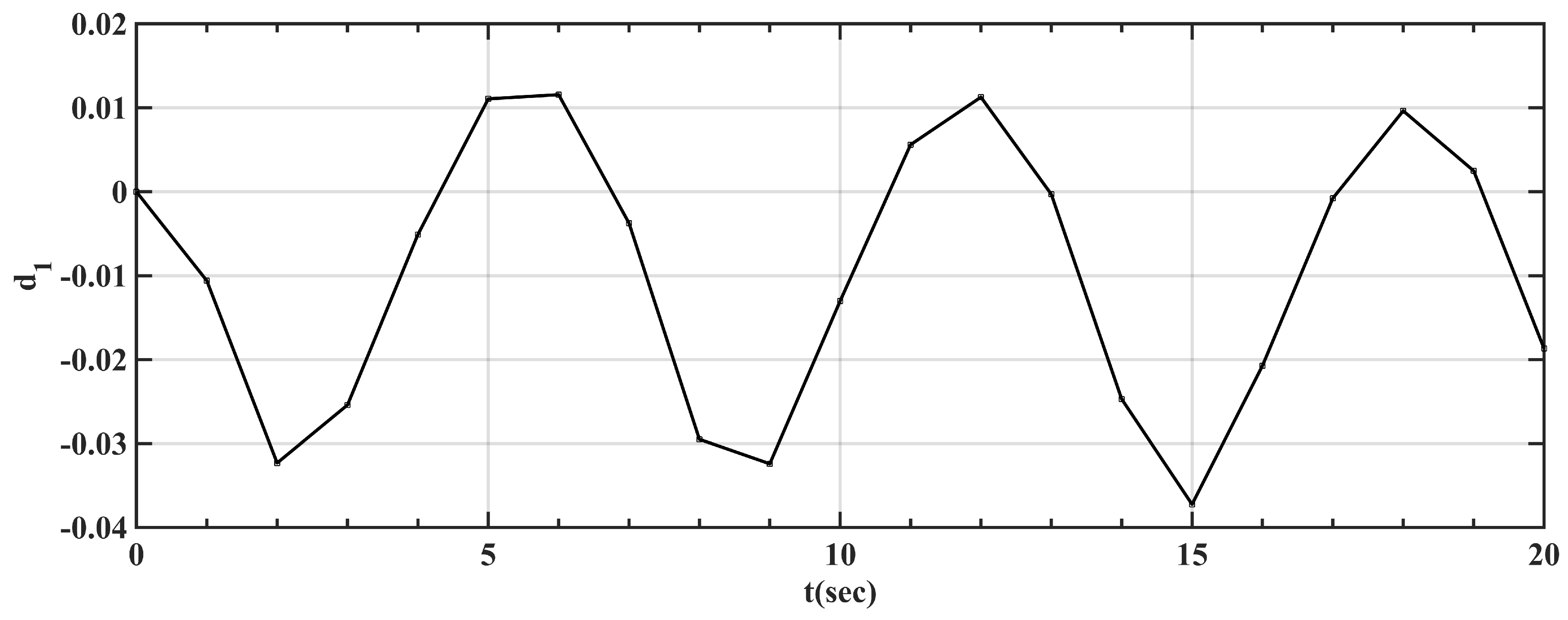
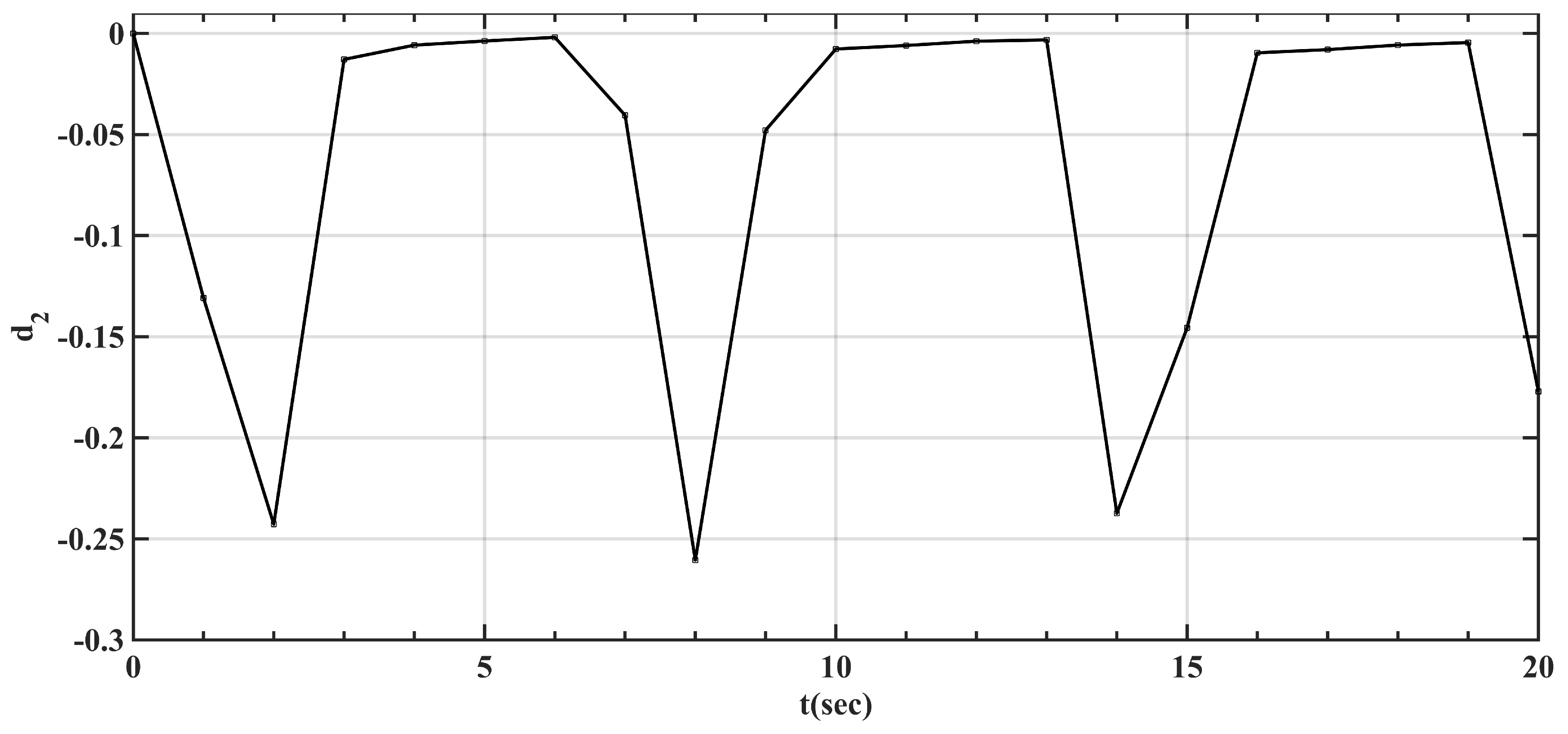
3.3. Validation of D-ESO
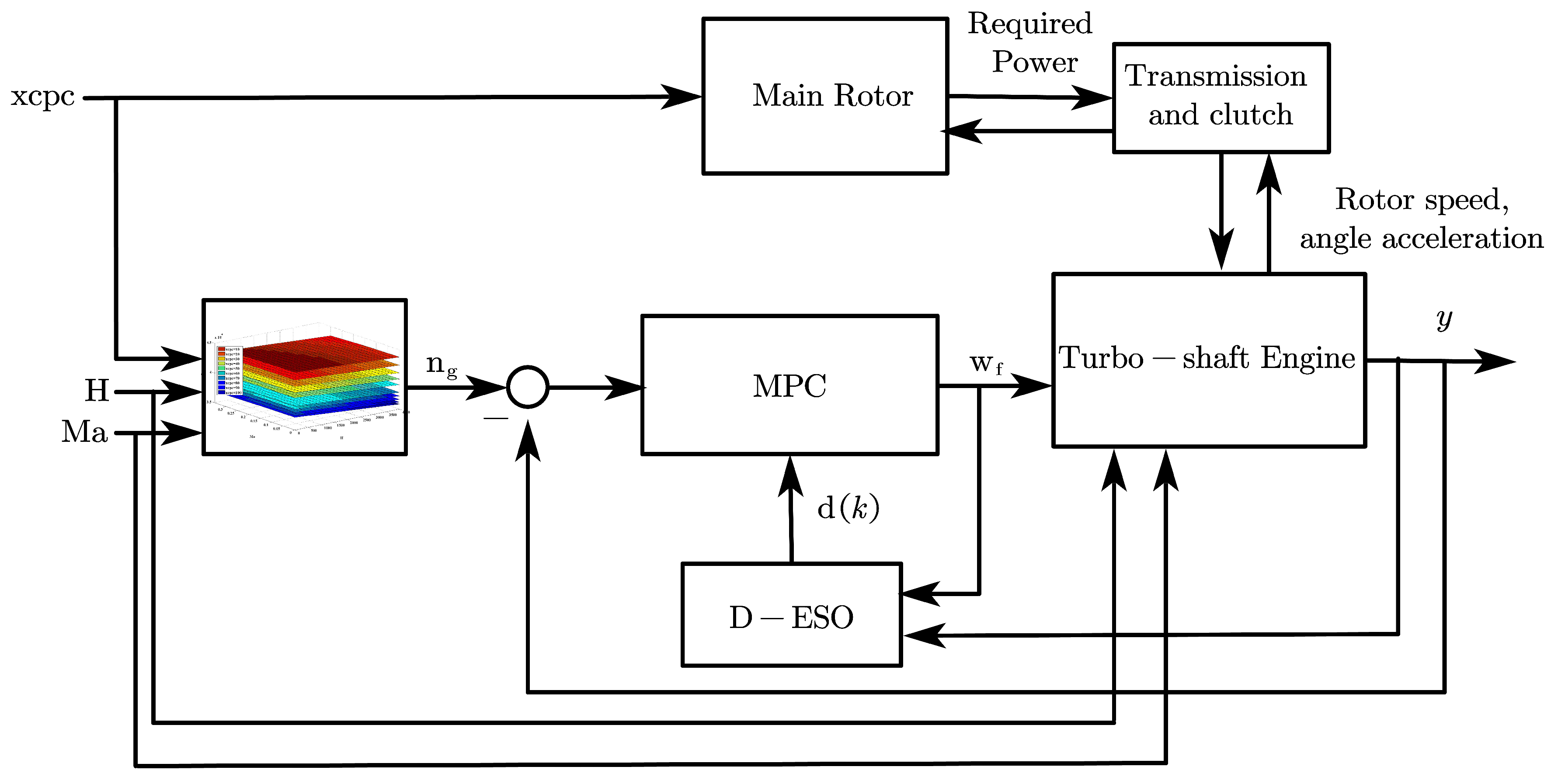
4. D-ESO-Based Constrained Full-State MPC Controller
4.1. Control Objective
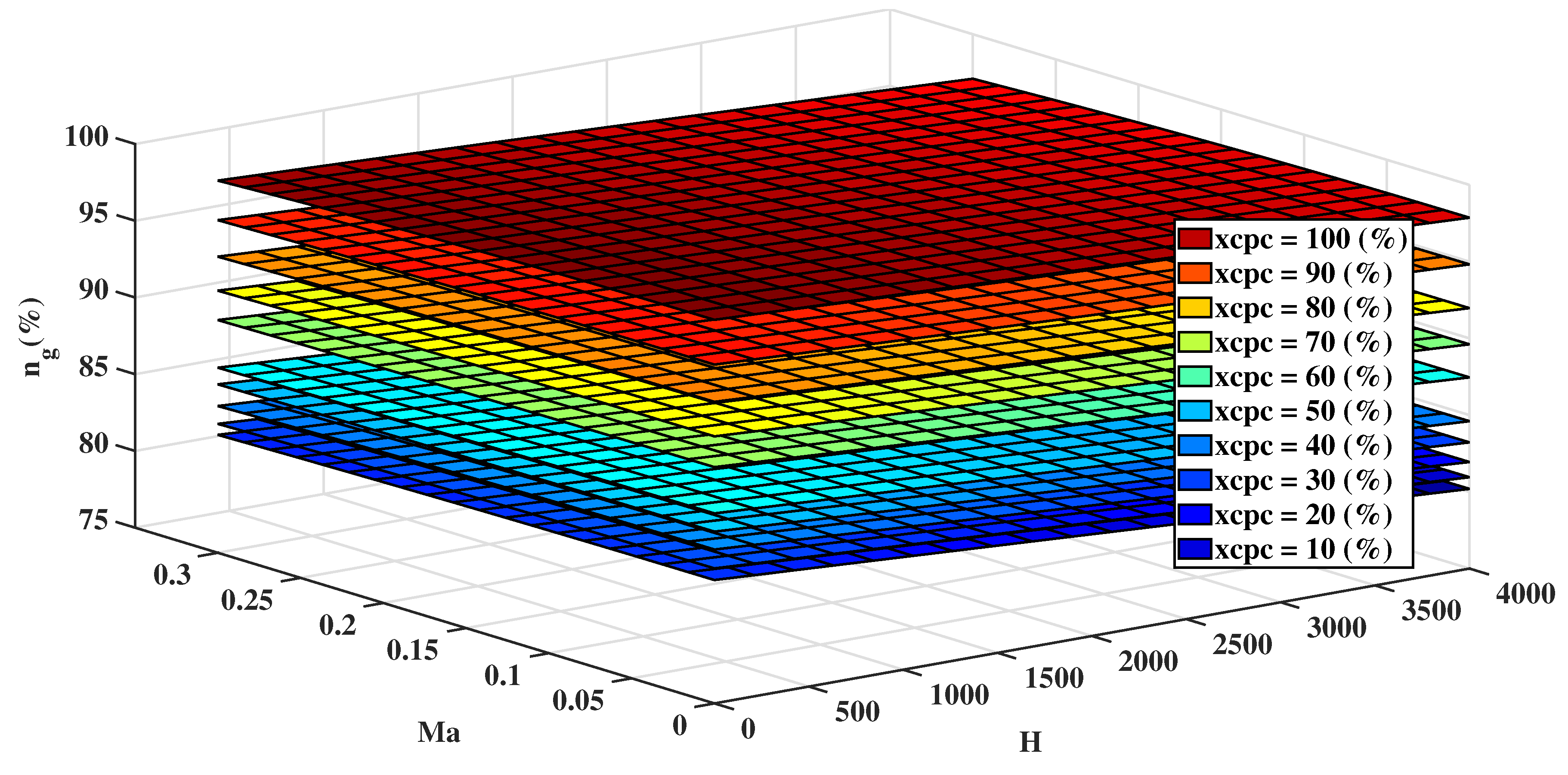
- Rationality. When the collective pitch input and flight conditions (operation altitude , Mach number ) are all specified, there exists a one-to-one mapping relationship between and .
- Feasibility. The relationship mentioned above can be realized by establishing the three-dimension model, see Figure 16.
- Superiority. The benefit is that the fast response of is fully utilized so that the control window of MPC is relatively smaller. In this way, the computational cost will be reduced.
4.2. MPC Controller Design
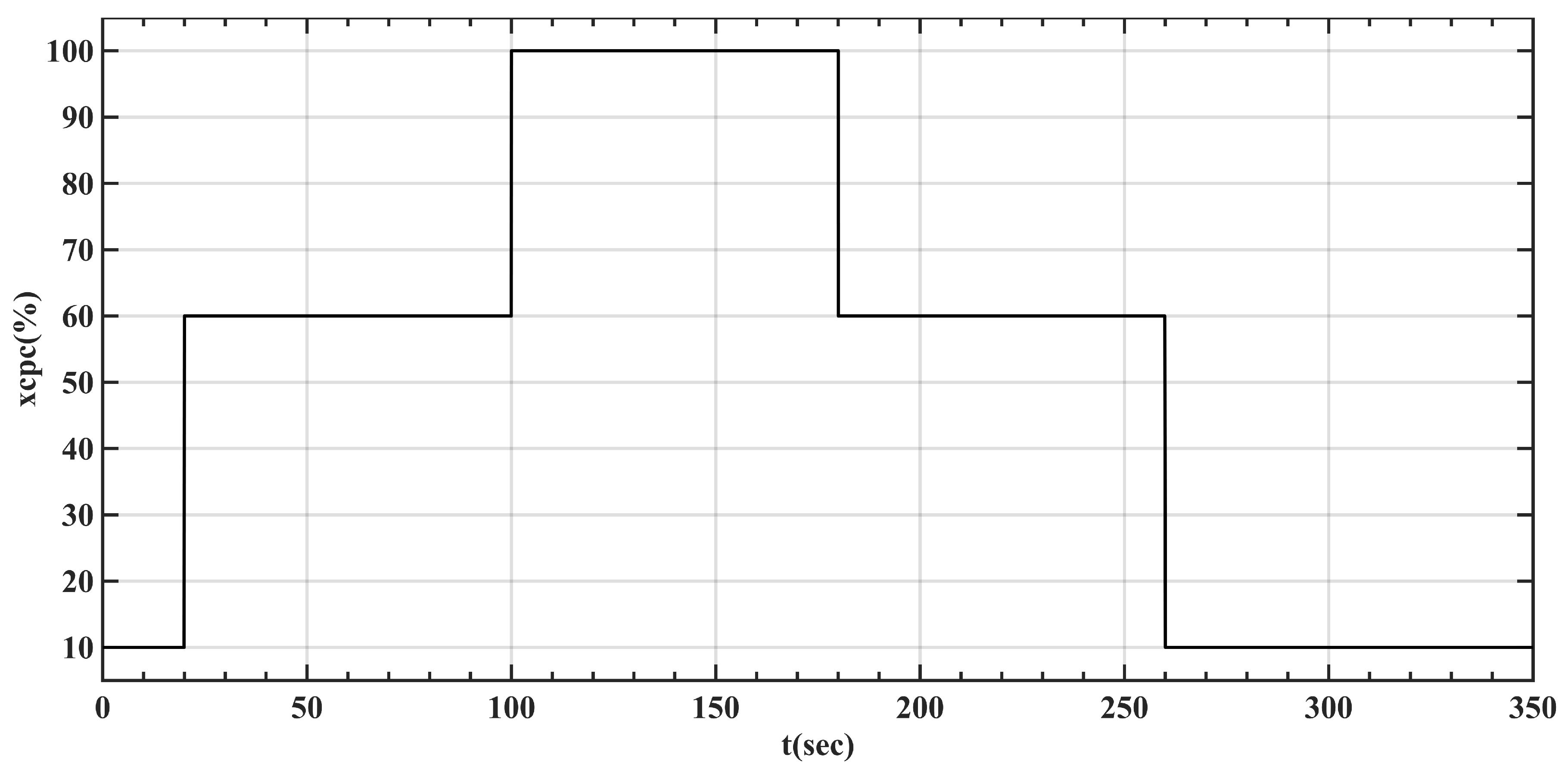
5. Simulation and Discussion
MPC Controller Validation
6. Conclusions
- Through the above simulation, the effectiveness of D-ESO has been proven as follows: D-ESO can compensate the linearization error between LPV and real turbo-shaft engine/rotor systems.
- Convergence conditions of D-ESO are deduced in Theory 1.
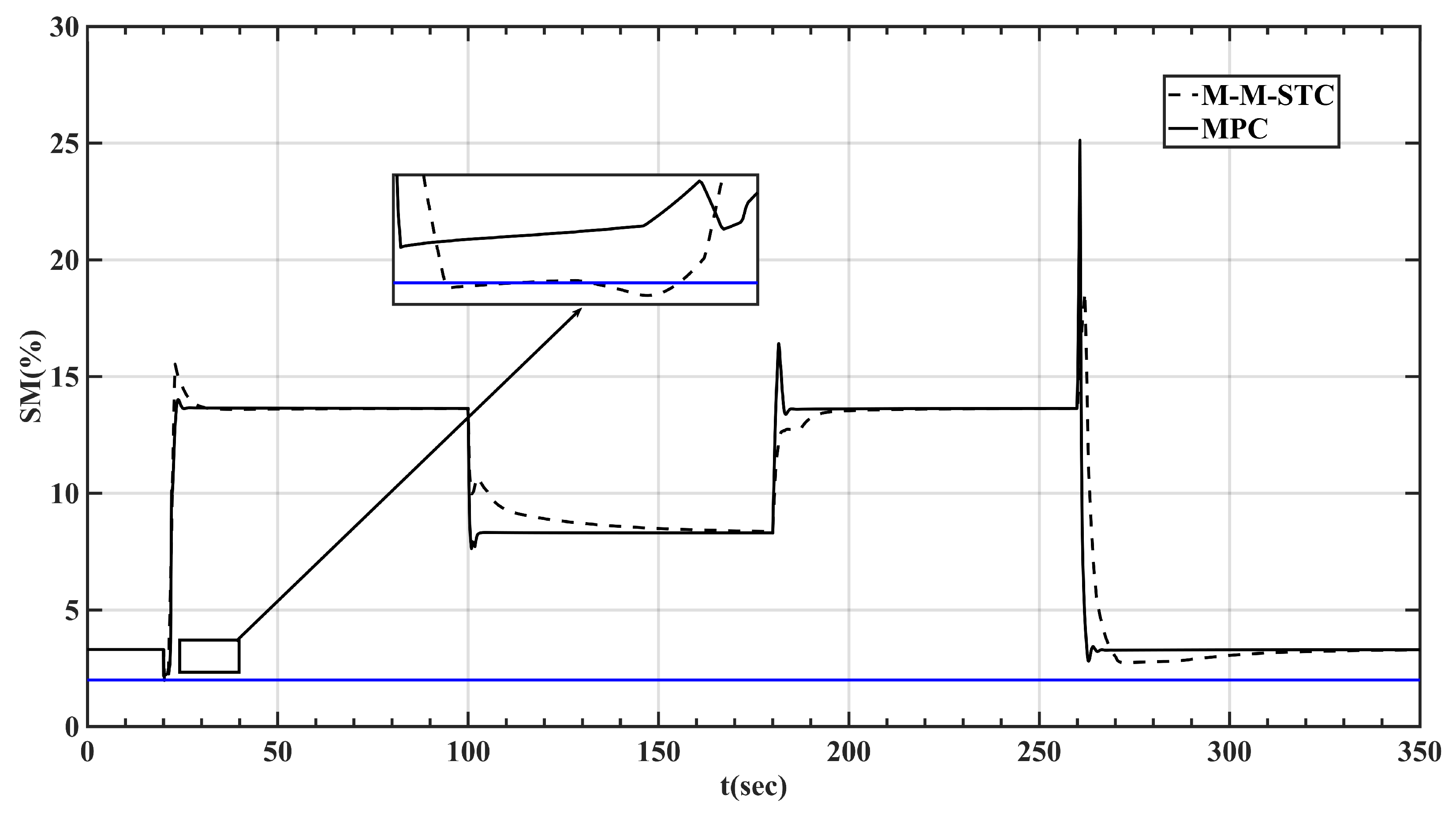
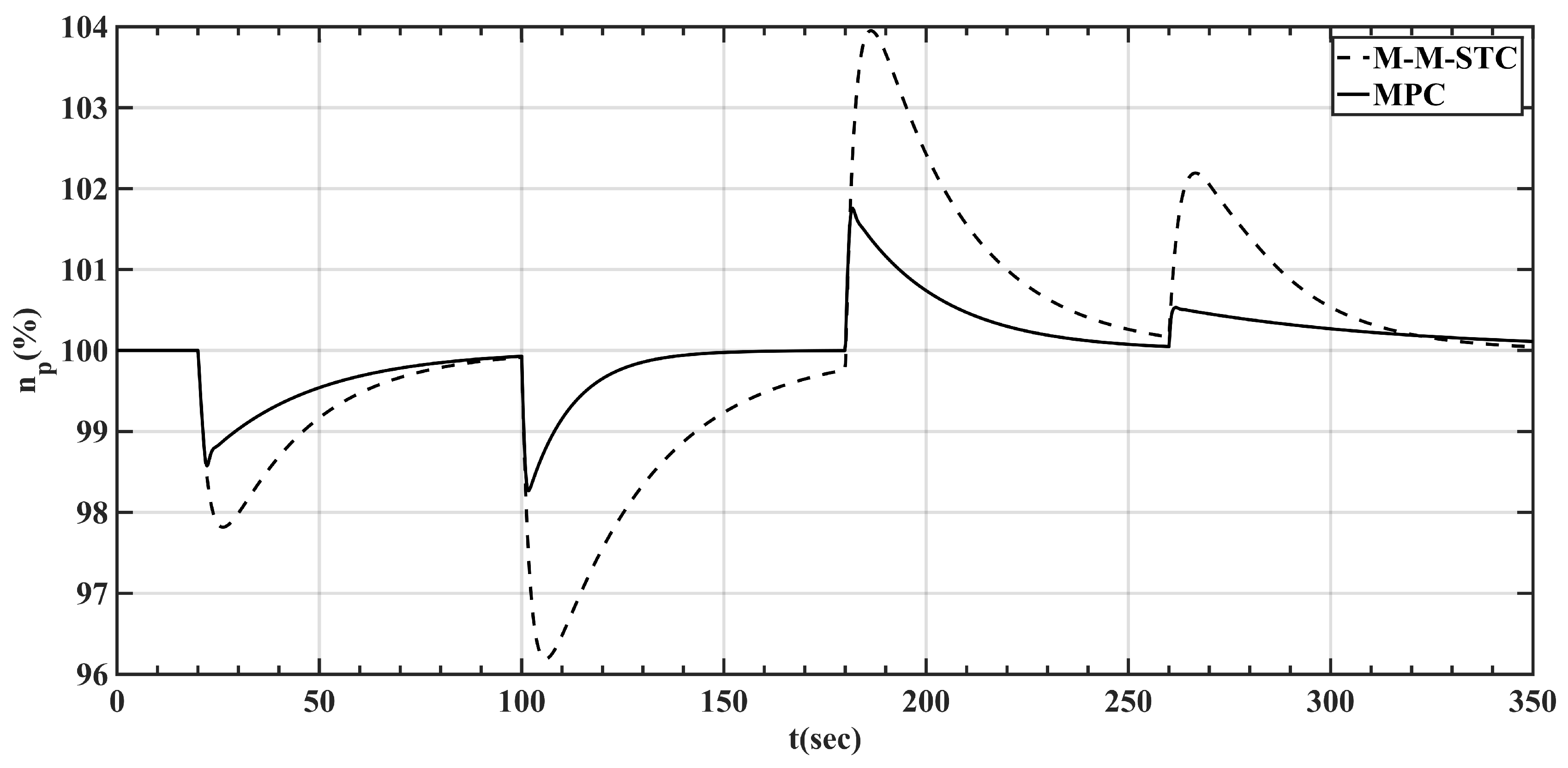
- During the transient state process, MPC can keep the limit parameters within the limited range. Meanwhile, it leaves out the Min-Max selection logic, which makes the controller structure more concise and simpler.
- Fast response and high-quality control of a turbo-shaft engine can be available. The drop of the power turbine speed is less than 2%. In addition, the steady-state error is below 0.2% through adopting the MPC controller based on the LPV model and D-ESO.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Gas turbine speed | |
| Power turbine speed | |
| Output predictive horizon | |
| Control horizon | |
| D-ESO | Disturbance extended state observer |
| M-M-STC | Min-Max structure and schedule based transient controller |
| MPC | Model predictive controller |
| LPV | Linear parameter varying |
| ACC | Acceleration control plan |
| DEC | Deceleration control plan |
Appendix A
Appendix B
References
- Liu, X.F.; Luo, C.S. Stability analysis for GE T700 turboshaft distributed engine control systems. IEEE Access 2017, 5, 22485–22491. [Google Scholar] [CrossRef]
- Pakmehr, M.; Fitzgerald, N.; Eric, F. Physics based dynamic modeling of a turboshaft engine driving a variable pitch propeller. J. Propuls. Power 2016, 32, 646–658. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Gummer, V. The potential of helicopter turboshaft engines incorporating highly effective recuperators under various flight conditions. Aerosp. Sci. Technol. 2019, 88, 84–94. [Google Scholar] [CrossRef]
- Andrea, G.; Ernesto, B. Preliminary study on a wide-speed-range helicopter rotor/turboshaft system. J. Aircr. 2012, 49, 1032–1038. [Google Scholar]
- Smith, B.J.; Zagranski, R.D. Next generation control system for helicopter engines. In Proceedings of the International Annual Forum of AHS, Washington, DC, USA, 9–11 May 2001. [Google Scholar]
- Smith, B.J.; Zagranski, R.D. Closed loop bench testing of the next generation control system for helicopter engines. In Proceedings of the International Annual Forum of AHS, Montreal, QC, Canada, 11–13 June 2002. [Google Scholar]
- Jaw, L.C.; Garg, S. Propulsion Control Technology Development in the United States: A Historical Perspective; Technical Report; The NASA STI Program Office: Washington, DC, USA, 2005. [Google Scholar]
- Merrill, W.; Lehtinen, B.; Zeller, J. The role of modern control theory in the design of controls for aircraft turbine engines. J. Guid. Control Dyn. 1984, 7, 652–661. [Google Scholar] [CrossRef]
- Dang, W.; Wang, X.; Wang, H.W. Design of transient state control mode based on rotor acceleration. In Proceedings of the International Bhurban Conference on Applied Sciences and Technology, Islamabad, Pakistan, 13–17 January 2015. [Google Scholar]
- Richter, H. Advanced Control of Turbofan Engines; Springer: Berlin, Germany, 2011. [Google Scholar]
- Richter, H. A multi-regulator sliding mode control strategy for output-constrained systems. Automatica 2011, 47, 2251–2259. [Google Scholar] [CrossRef]
- Krstic, M.; Banaszuk, A. Multivariable adaptive control of instabilities arising in jet engines. Control Eng. Pract. 2006, 14, 833–842. [Google Scholar] [CrossRef]
- Brunell, B.J.; Viassolo, D.E.; Prasanth, R. Model adaptation and nonlinear model predictive control of an aircraft engine. In Proceedings of the ASME Turbo Expo, Vienna, Austria, 14–17 June 2004. [Google Scholar]
- Richter, H.; Singaraju, A.; Lit, J.S. Multiplexed predictive control of a large commercial turbofan engine. J. Guid. Control Dyn. 2008, 31, 273–281. [Google Scholar] [CrossRef]
- Cutler, C.R.; Ramaker, B.L. Dynamic matrix control—A computer control algorithm. In Proceedings of the Joint Automatic Control Conference, San Francisco, CA, USA, 13–15 August 1980. [Google Scholar]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized predictive control-part I: the basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Morteza, M.G.; Ali, R. Comparison of model predictive controller and Min-Max approach for aircraft engine fuel control. In Proceedings of the International Conference on Control, Instrumentation, and Automation, Shiraz, Iran, 21–23 November 2017. [Google Scholar]
- Garriga, J.L.; Soroush, M. Model predictive control tuning methods: A review. Ind. Eng. Chem. Res. 2010, 49, 3505–3515. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballance, D.J.; Reilly, O.J. Model predictive control of nonlinear systems: Computational burden and stability. Syst. Control Lett. 2000, 147, 387–394. [Google Scholar] [CrossRef]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Wan, Z.Y.; Kothare, M.V. Robust output feedback model predictive control using off-line linear matrix inequalities. J. Process. Control 2002, 12, 763–774. [Google Scholar] [CrossRef]
- DeCastro, J.A. Rate-based model predictive control of turbofan engine clearance. J. Propuls. Power 2007, 23, 804–813. [Google Scholar] [CrossRef]
- Su, Y.X.; Duan, B.Y. Disturbance-rejection high-precision motion control of a Stewart platform. IEEE Trans. Control Syst. Technol. 2004, 12, 364–374. [Google Scholar] [CrossRef]
- Zheng, Q.; Dong, L.l.; Lee, D.H.; Gao, Z.Q. Active disturbance rejection control and implementation for MEMS gyroscopes. IEEE Trans. Control Syst. Technol. 2009, 17, 1432–1438. [Google Scholar] [CrossRef]
- Zheng, Q.; Chen, Z.z.; Gao, Z.Q. A dynamic decoupling control approach and its applications to chemical processes. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 5176–5181. [Google Scholar]
- Li, Z.l.; Xu, F.; Liang, D.N.; Chen, H. Design of model predictive controller based on extended state observer. In Proceedings of the Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017; pp. 7421–7426. [Google Scholar]
- Zhao, Z.L.; Guo, B.Z. On convergence of nonlinear active disturbance rejection control for SISO nonlinear systems. J. Dyn. Control Syst. 2016, 22, 385–413. [Google Scholar] [CrossRef]
- Praly, L.; Jiang, Z.P. Linear output feedback with dynamic high gain for nonlinear systems. Syst. Control Lett. 2004, 53, 107–116. [Google Scholar] [CrossRef]











| Equilibrium Points | A | B | |
|---|---|---|---|
| Equilibrium Points | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
| 0 | 0 | 0 | ||||
| 0 | 0 | 0 | ||||
| 0 | 0 | 0 | ||||
| 0 | 0 | 0 |
| Parameters | |||
|---|---|---|---|
| 7 | 3 |
| Parameters | |||||
|---|---|---|---|---|---|
| 0.1043 (kg/s) | 0.031 (kg/s) | 0.003 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, N.; Wang, X.; Lin, F. Design of Disturbance Extended State Observer (D-ESO)-Based Constrained Full-State Model Predictive Controller for the Integrated Turbo-Shaft Engine/Rotor System. Energies 2019, 12, 4496. https://doi.org/10.3390/en12234496
Gu N, Wang X, Lin F. Design of Disturbance Extended State Observer (D-ESO)-Based Constrained Full-State Model Predictive Controller for the Integrated Turbo-Shaft Engine/Rotor System. Energies. 2019; 12(23):4496. https://doi.org/10.3390/en12234496
Chicago/Turabian StyleGu, Nannan, Xi Wang, and Feiqiang Lin. 2019. "Design of Disturbance Extended State Observer (D-ESO)-Based Constrained Full-State Model Predictive Controller for the Integrated Turbo-Shaft Engine/Rotor System" Energies 12, no. 23: 4496. https://doi.org/10.3390/en12234496
APA StyleGu, N., Wang, X., & Lin, F. (2019). Design of Disturbance Extended State Observer (D-ESO)-Based Constrained Full-State Model Predictive Controller for the Integrated Turbo-Shaft Engine/Rotor System. Energies, 12(23), 4496. https://doi.org/10.3390/en12234496




