An Averaged-Value Model of an Asymmetrical Hybrid Multi-Level Rectifier
Abstract
:1. Introduction
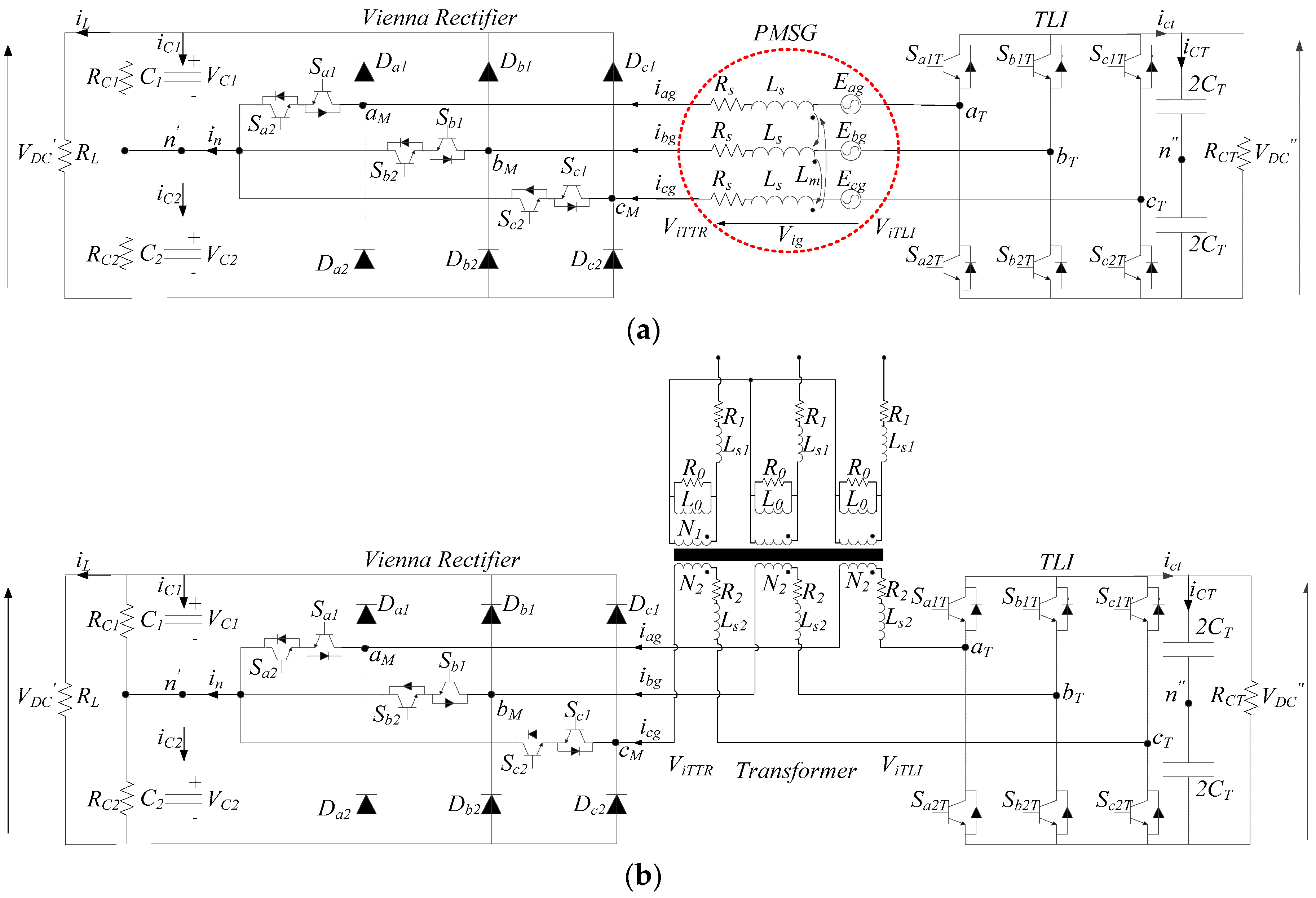
2. Asymmetrical Hybrid Unidirectional T-Type Rectifier
3. Averaged-value Model of the System
3.1. Open-Winding PMSG Model
3.2. Vienna Rectifier Model
3.3. TLI Model
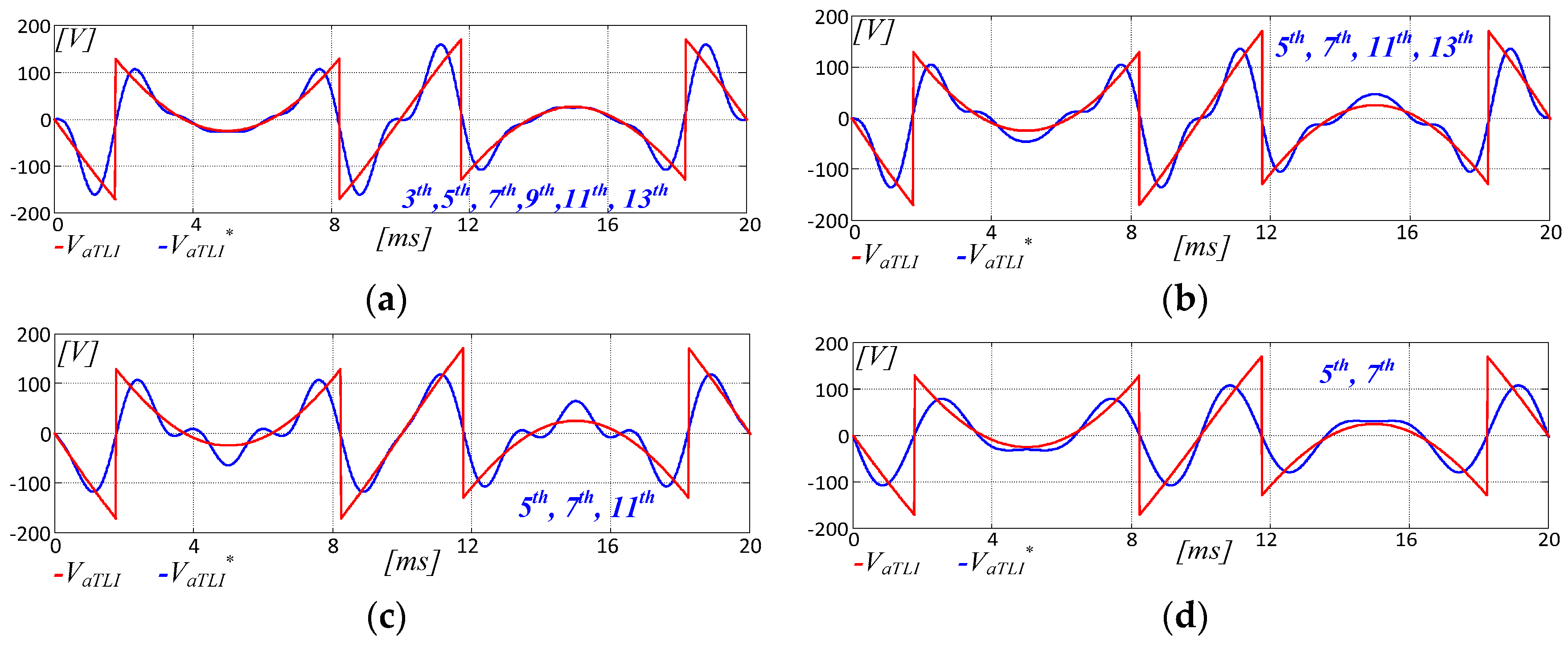
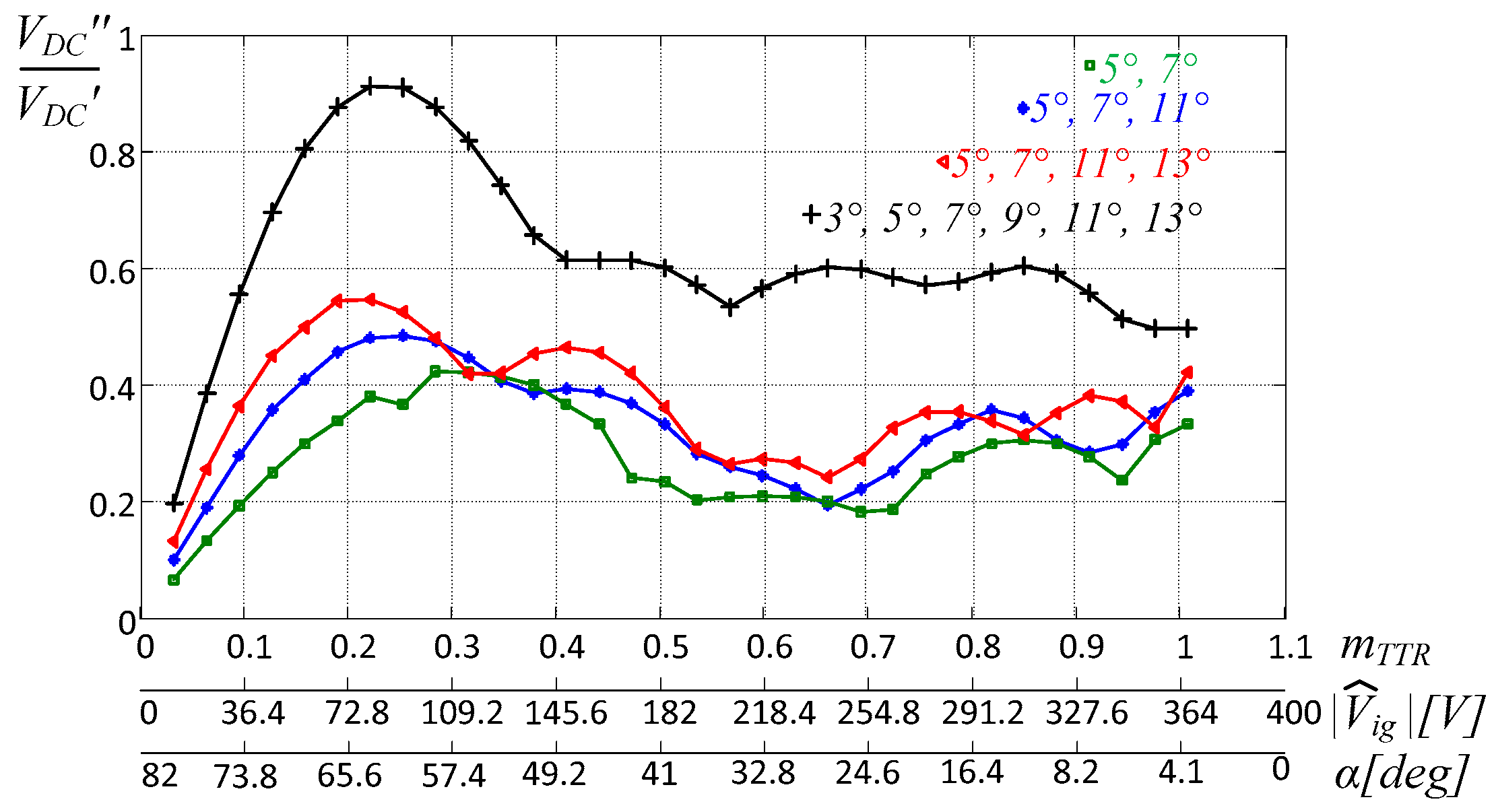
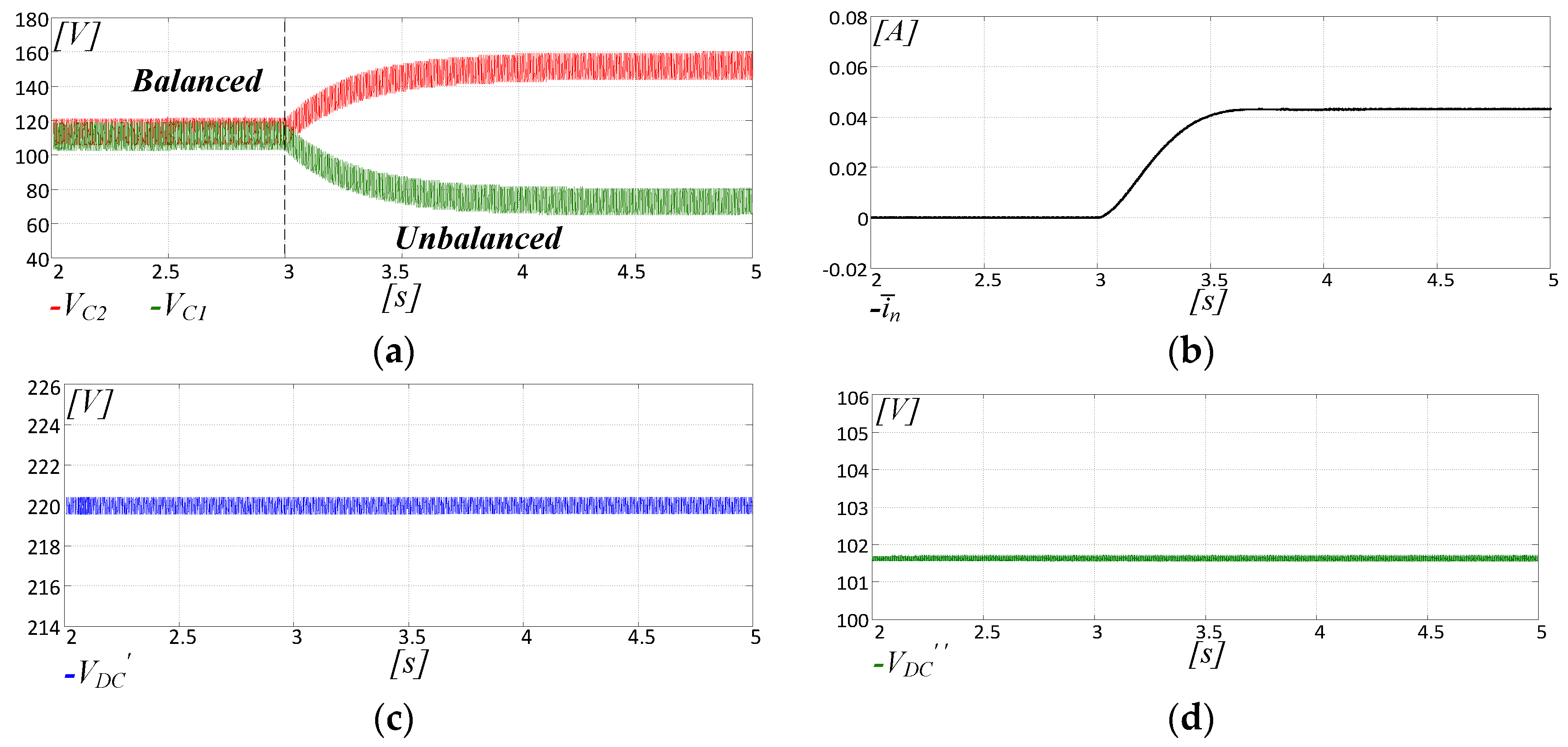
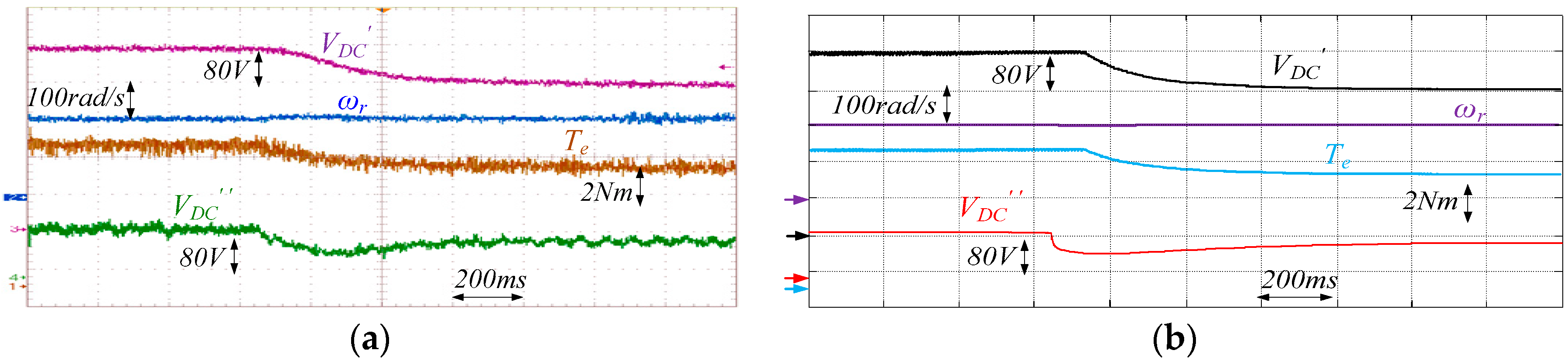
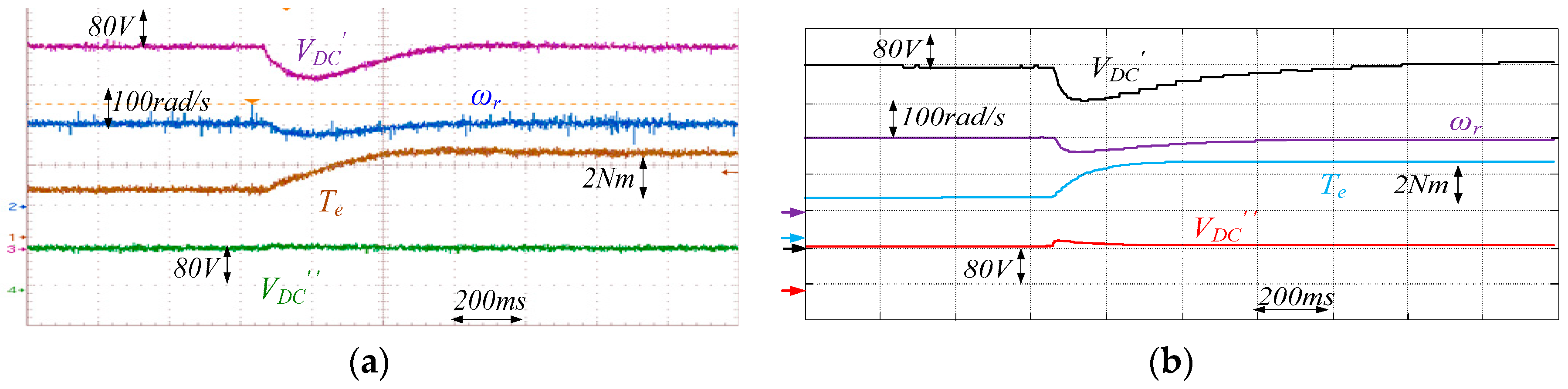
4. Model Validation
5. Experimental Assessment
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Kaarthik, R.S.; Gopakumar, K.; Mathey, J.; Underland, T. Medium Voltage Drive for Induction Machine with Multilevel Dodecagon Voltage Space Vectors with Symmetric Triangles. IEEE Trans. Ind. Electron. 2015, 62, 79–87. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- De Caro, S.; Foti, S.; Scimone, T.; Testa, A.; Cacciato, M.; Scarcella, G.; Scelba, G. THD and efficiency improvement in multi-level inverters through an open end winding configuration. In Proceedings of the IEEE 2016 Energy Conversion Congress and Expo, Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Edpuganti, A.; Rathore, A. A Survey of Low Switching Frequency Modulation Techniques for Medium-Voltage Multilevel Converters. IEEE Trans. Ind. Appl. 2015, 51, 4212–4228. [Google Scholar] [CrossRef]
- Mondal, G.; Sivakumar, K.; Ramchand, R.; Gopakumar, K.; Levi, E. A Dual Seven-Level Inverter Supply for an Open-End Winding Induction Motor Drive. IEEE Trans. Ind. Electron. 2009, 56, 1665–1673. [Google Scholar] [CrossRef]
- Wang, Y.; Panda, D.; Lipo, T.A.; Pan, D. Open-Winding Power Conversion Systems Fed by Half-Controlled Converters. IEEE Trans. on Power Electron. 2013, 28, 2427–2436. [Google Scholar] [CrossRef]
- Mohapatra, K.K.; Gopakumar, K.; Somasekhar, V.T.; Umanand, L. A Harmonic Elimination and Suppression Scheme for an Open-End Winding Induction Motor Drive. IEEE Trans. Ind. Electron. 2003, 50, 1187–1198. [Google Scholar] [CrossRef]
- Kawabata, Y.; Nasu, M.; Nomoto, T.; Ejiogu, E.C.; Kawabata, T. High-efficiency and low acoustic noise drive system using open-winding AC motor and two space-vector-modulated inverters. IEEE Trans. Ind. Electron. 2002, 49, 783–789. [Google Scholar] [CrossRef]
- Sivakumar, K.; Das, A.; Ramchand, R.; Patel, C.; Gopakumar, K. A hybrid multilevel inverter topology for an open-end winding induction-motor drive using two-level inverters in series with a capacitor-fed H- bridge cell. IEEE Trans. Ind. Electron. 2010, 57, 3707–3714. [Google Scholar] [CrossRef]
- Somasekhar, V.T.; Gopakumar, K.; Bajiu, M.R.; Mohapatra, K.K.; Umanand, L. A multilevel inverter system for an inductor motor with open-end windings. IEEE Trans. Ind. Electron. 2015, 52, 824–836. [Google Scholar] [CrossRef]
- Edpuganti, A.; Rathore, A.K. Optimal Pulsewidth Modulation for Common-Mode Voltage Elimination Scheme of Medium-Voltage Modular Multilevel Converter-Fed Open-End Stator Winding Induction Motor Drives. IEEE Trans. Ind. Electron. 2017, 64, 848–856. [Google Scholar] [CrossRef]
- Foti, S.; Testa, A.; Scelba, G.; De Caro, S.; Cacciato, M.; Scarcella, G.; Scimone, T. An Open-End Winding Motor Approach to Mitigate the Phase Voltage Distortion on Multilevel Inverters. IEEE Trans. Power Electron. 2018, 33, 2404–2416. [Google Scholar] [CrossRef]
- Foti, S.; Testa, A.; Scelba, G.; Sabatini, V.; Lidozzi, A.; Solero, L. A symmetrical hybrid unidirectional T-type rectifier for high-speed gen-set applications. In Proceedings of the IEEE Energy Conversion Congress and Expo, Cincinnati, OH, USA, 1–5 October 2017; pp. 4887–4893. [Google Scholar]
- Foti, S.; De Caro, S.; Scelba, G.; Scimone, T.; Testa, A.; Cacciato, M.; Scarcella, G. An Optimal Current Control Strategy for Asymmetrical Hybrid Multilevel Inverters. IEEE Trans. Ind. Appl. 2018, 54, 4425–4436. [Google Scholar] [CrossRef]
- Mengoni, M.; Amerise, A.; Zarri, L.; Tani, A.; Serra, G.; Casadei, D. Control Scheme for Open-Ended Induction Motor Drives with a Floating Capacitor Bridge Over a Wide Speed Range. Trans. Ind. Applications 2017, 53, 4504–4514. [Google Scholar] [CrossRef]
- Pan, Z.; Peng, F.Z.; Corzine, K.A.; Stefanovic, V.R.; Leuthen, J.M.; Gataric, S. Voltage balancing control of diode-clamped multilevel rectifier/inverter systems. IEEE Trans. Ind. Applications 2005, 41, 1698–1706. [Google Scholar] [CrossRef]
- Yan, G.; Duan, S.; Zhao, S.; Li, G.; Wu, W.; Li, H. Research on the mechanism of neutral-point voltage fluctuation and capacitor voltage balancing control strategy of three-phase three-level T-type inverter. J. Electr. Eng. Technol. 2017, 12, 2227–2236. [Google Scholar]
- Zhang, Y.; Li, J.; Li, X.; Cao, Y.; Sumner, M.; Xia, C. A Method for the Suppression of Fluctuations in the Neutral-Point Potential of a Three-Level NPC Inverter with a Capacitor-Voltage Loop. IEEE Trans. Power Electron. 2017, 32, 825–836. [Google Scholar] [CrossRef]


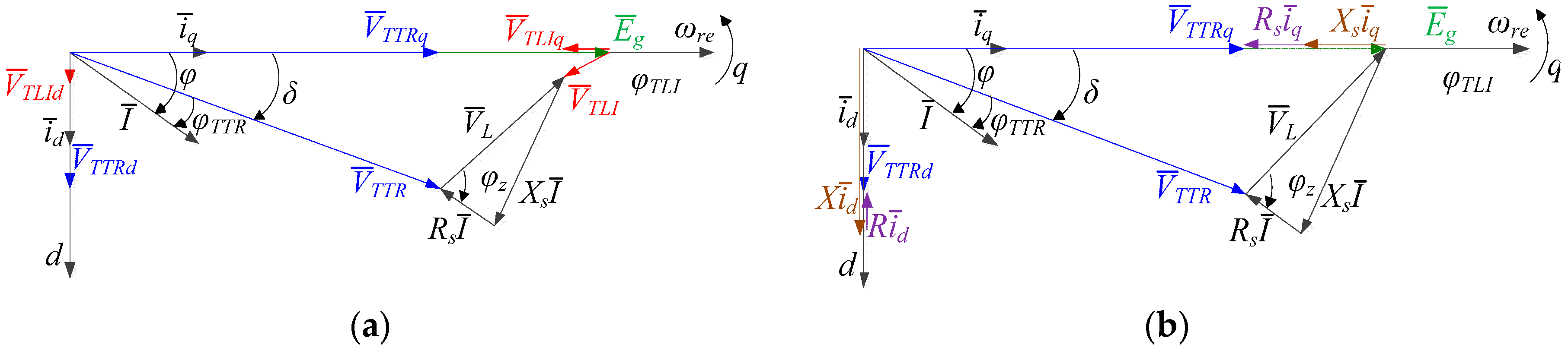
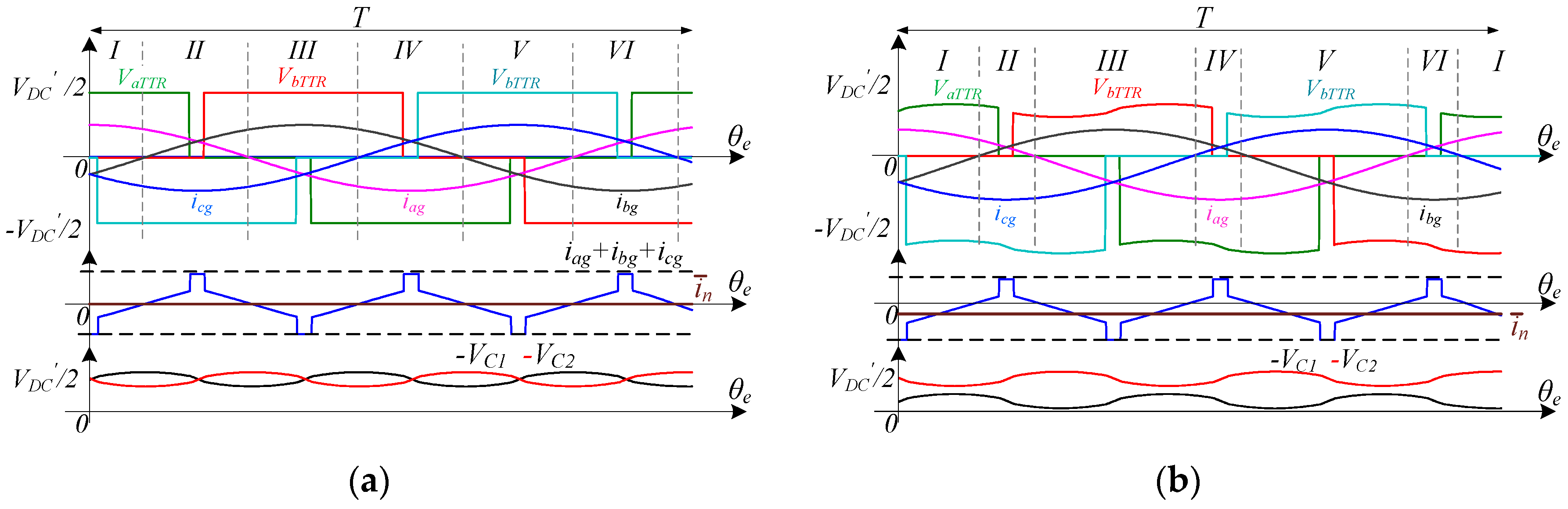









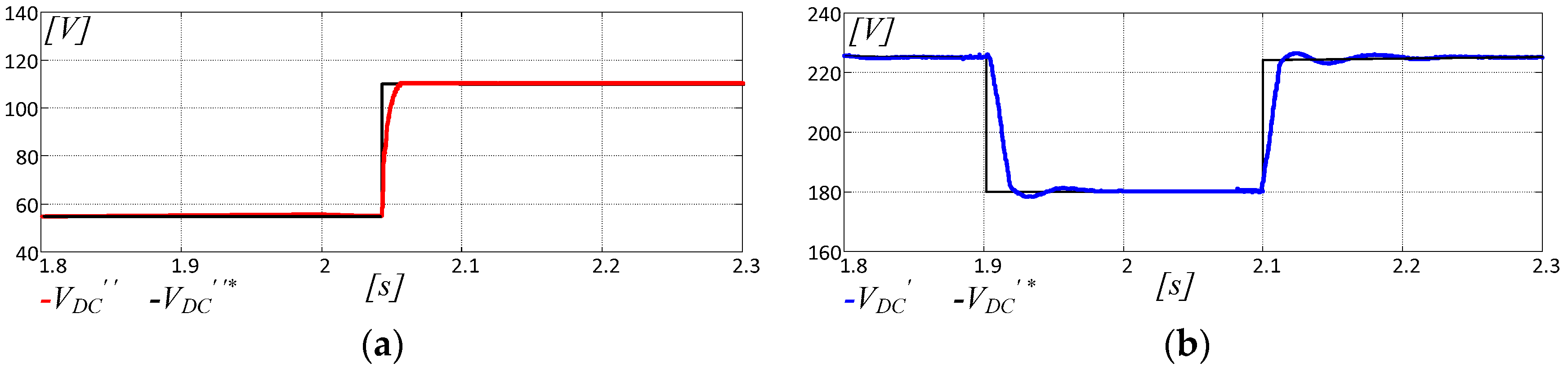
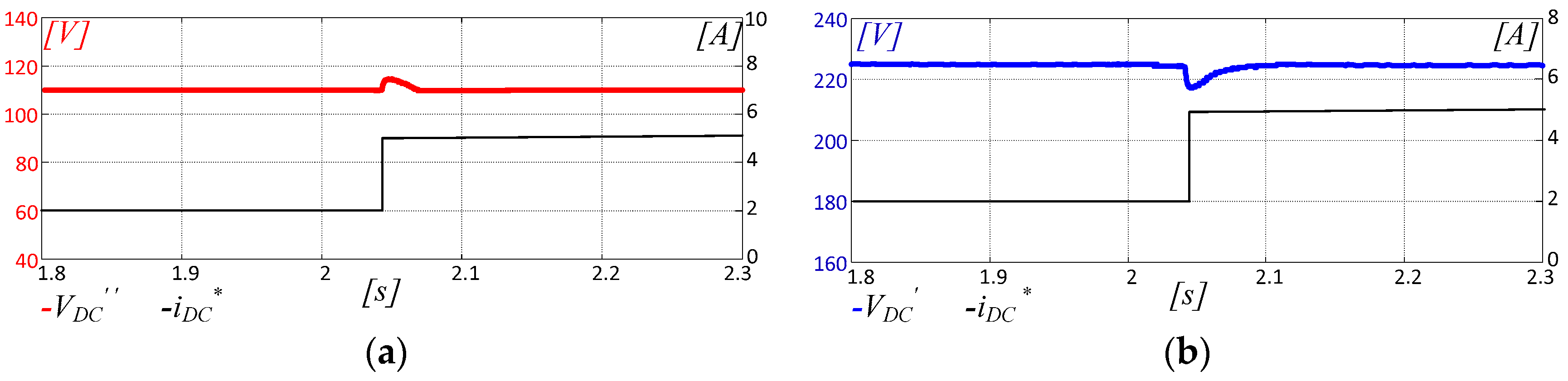





| Phase a | 0 < θe < α π − α < θe < π + α 2π − α < θe < 2π | if iag > 0 => Sa1 ON Sa2 OFF if iag < 0 => Sa1 OFF Sa2 ON |
| Phase b | 2/3π < θe < α + 2/3π 5/3π − α < θe < 5/3π + α 2/3π − α < θe < 2/3π | if ibg > 0 => Sb1 ON Sb2 OFF if ibg < 0 => Sb1 OFF Sb2 ON |
| Phase c | 4/3π < θe < α + 4/3π 1/3π − α < θe < 1/3π + α 4/3π − α < θe < 4/3π | if icg > 0 => Sc1 ON Sc2 OFF if icg < 0 => Sc1 OFF Sc2 ON |
| Sector I Va1TTR > 0 Vb1TTR < 0 Vc1TTR < 0 | Sector II Va1TTR > 0 Vb1TTR > 0 Vc1TTR < 0 | Sector III Va1TTR < 0 Vb1TTR > 0 Vc1TTR < 0 | Sector VI Va1TTR < 0 Vb1TTR > 0 Vc1TTR > 0 | Sector V Va1TTR < 0 Vb1TTR < 0 Vc1TTR > 0 | Sector IV Va1TTR > 0 Vb1TTR < 0 Vc1TTR > 0 |
|---|---|---|---|---|---|
| PMSG | Vienna | TLI | Control Gains | ||
|---|---|---|---|---|---|
| Power Rating | 3 kW | IGBT Ratings | 600 V, 20 A | 200 V, 10 A | KPα = 0.1, KIα = 10 |
| Rated Voltage | 575 VDC | DC-Link Voltage | 200 V | 100 V | KPiqg = 80, KIiqg = 1000 |
| Rated Current | 6.5 A | DC Bus Capacitors | 470 μF (C1, C2) | 470 μF (CT) | KPidg = 80, KIidg = 1000 |
| Phase Inductance | 20 mH | Load | 50 Ω | // | KPin = 0.2, KIin = 2 |
| Stator Resistance | 4.3 Ω | Capacitors Resistance | 1000 Ω (RC1, RC2) | 600 Ω (RCT) | KPTLI = 2, KITLI = 30 |
| PM Flux | 0.57 Wb | Switching Frequency | 50 Hz | 40 kHz | |
| Pn (kW) | Ls (mH) | Vs (V) | Rs (Ω) | Is (A) | λPM (Wb) | ωr (krpm) | Pole Pairs |
|---|---|---|---|---|---|---|---|
| 1 | 20 | 565 | 4.8 | 6.5 | 1.53 | 2 | 3 |
| Vce (V) | Vce(on) (V) | iRMS (A) | trise (ns) | tfall (ns) |
|---|---|---|---|---|
| 600 | 2.1 | 30 | 27 | 160 |
| VDS (V) | RDS (m) | ID (A) | trise (ns) | tfall (ns) |
|---|---|---|---|---|
| 150 | 32 | 35 | 8.9 | 17.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foti, S.; Scelba, G.; Testa, A.; Sciacca, A. An Averaged-Value Model of an Asymmetrical Hybrid Multi-Level Rectifier. Energies 2019, 12, 589. https://doi.org/10.3390/en12040589
Foti S, Scelba G, Testa A, Sciacca A. An Averaged-Value Model of an Asymmetrical Hybrid Multi-Level Rectifier. Energies. 2019; 12(4):589. https://doi.org/10.3390/en12040589
Chicago/Turabian StyleFoti, Salvatore, Giacomo Scelba, Antonio Testa, and Angelo Sciacca. 2019. "An Averaged-Value Model of an Asymmetrical Hybrid Multi-Level Rectifier" Energies 12, no. 4: 589. https://doi.org/10.3390/en12040589
APA StyleFoti, S., Scelba, G., Testa, A., & Sciacca, A. (2019). An Averaged-Value Model of an Asymmetrical Hybrid Multi-Level Rectifier. Energies, 12(4), 589. https://doi.org/10.3390/en12040589





