Numerical Investigation of Passive Vortex Generators on a Wind Turbine Airfoil Undergoing Pitch Oscillations
Abstract
:1. Introduction
2. Numerical Modelling
2.1. Geometry and Mesh Generation
2.2. Discretization and Turbulence Modelling
2.3. Mesh Dependency Study
3. Results and Discussion
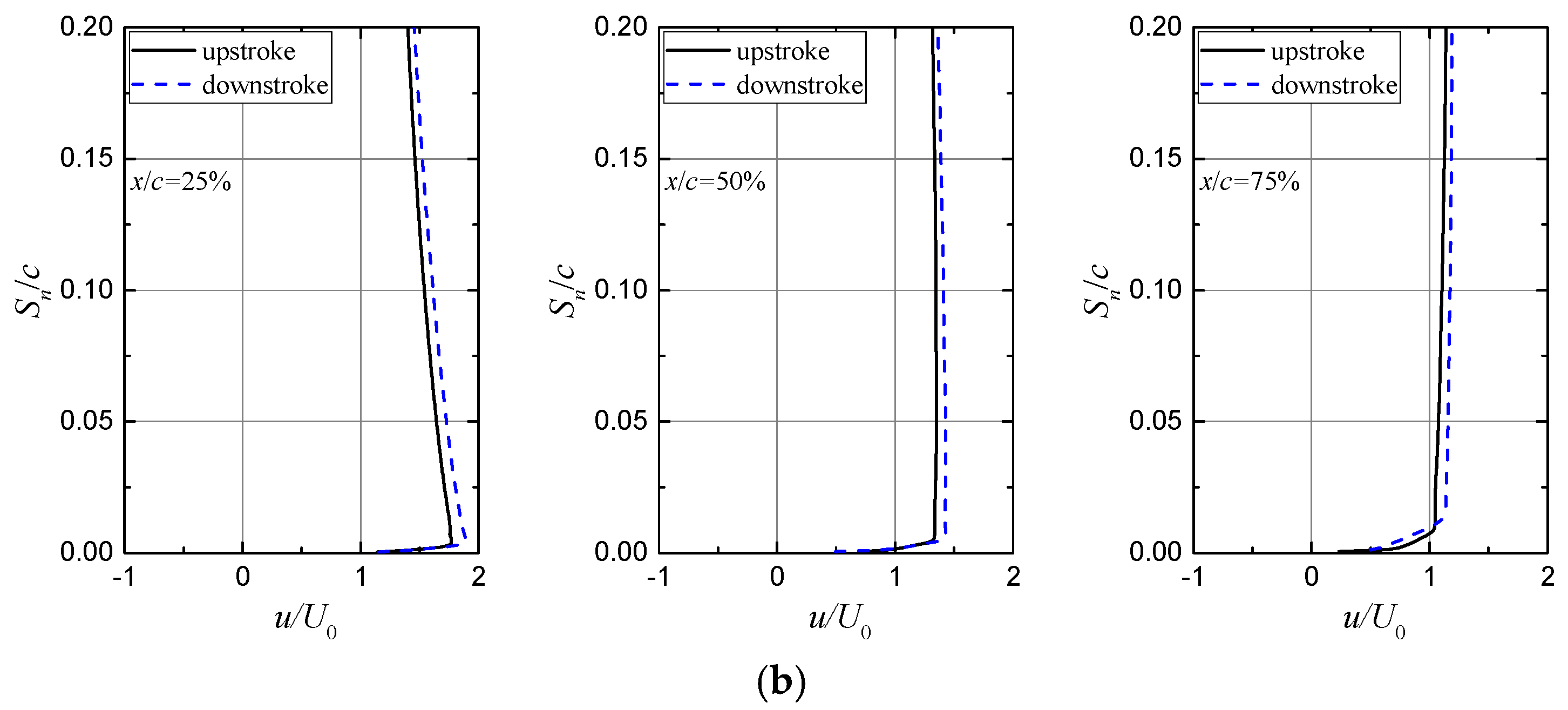
3.1. Assessment of Unsteady Numerical Modelling
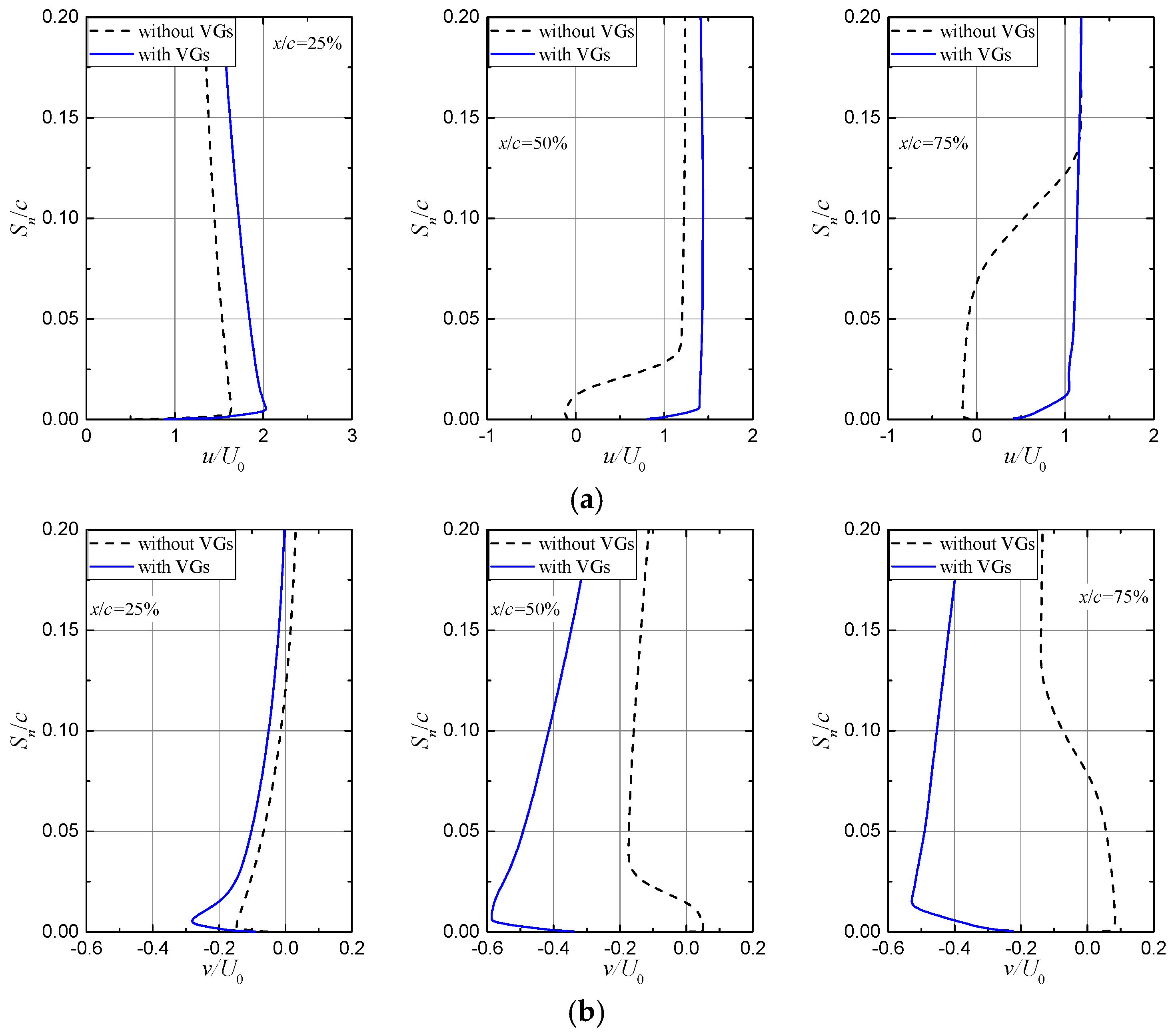
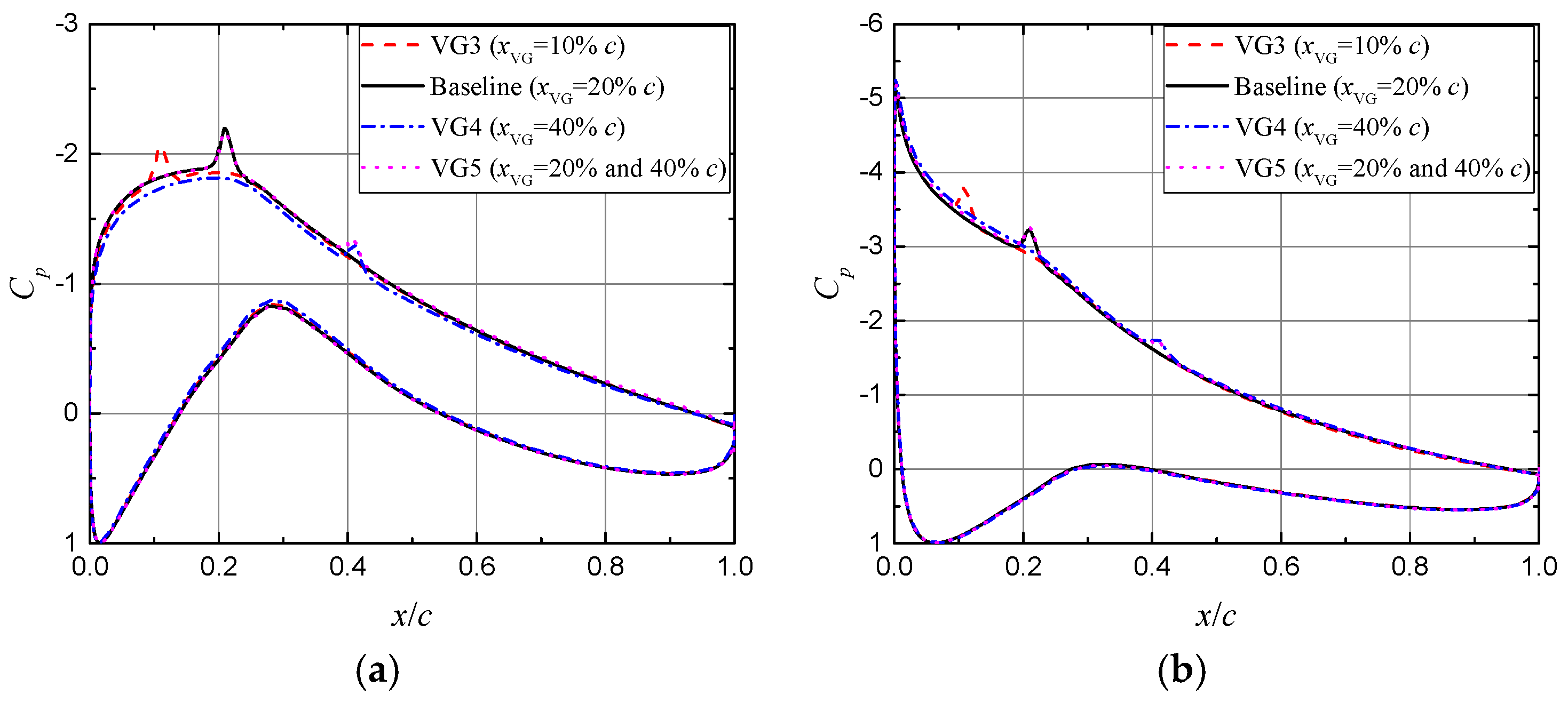
3.2. Validation and Effect of Vortex Generators on the Steady Airfoil Flow
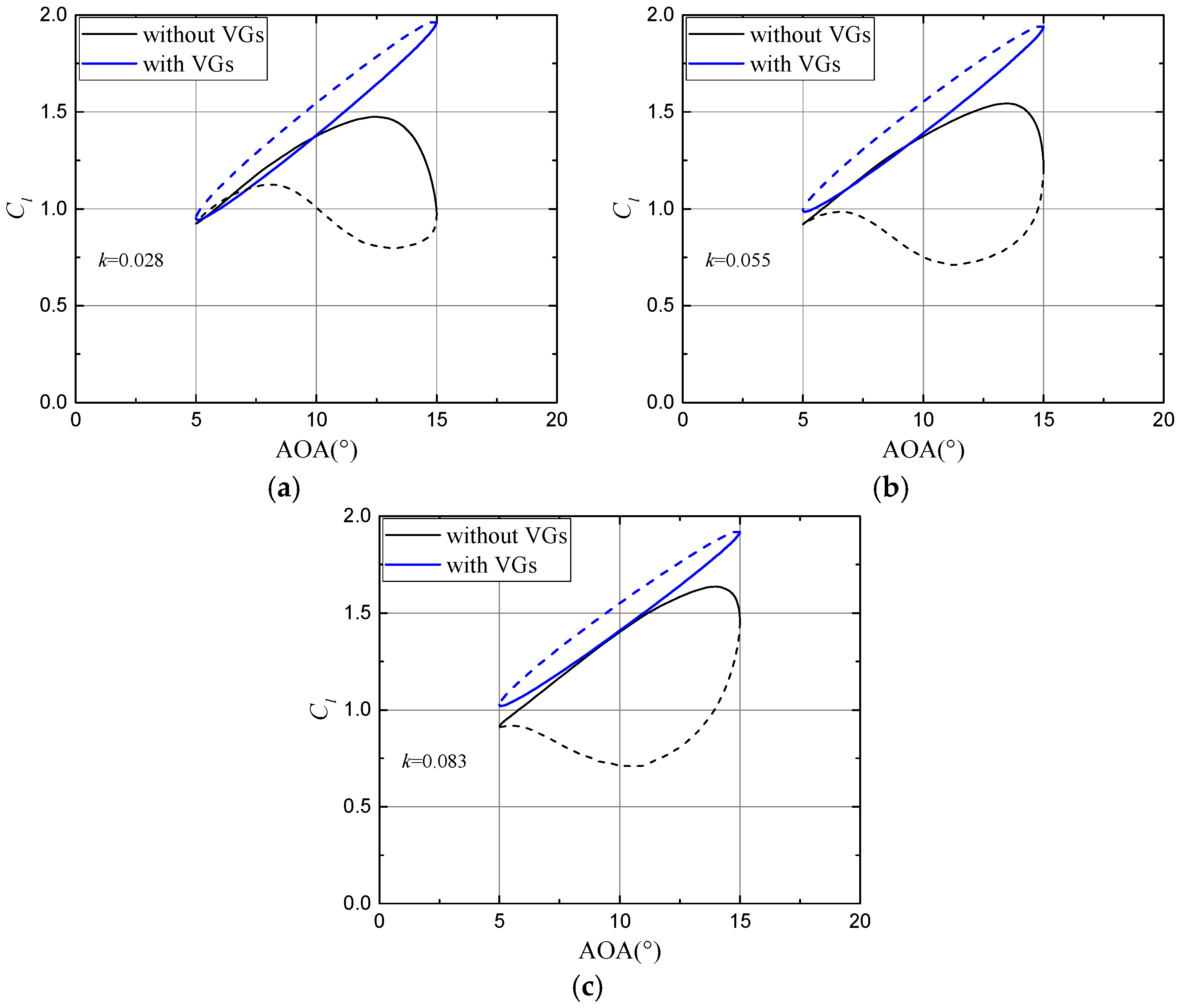
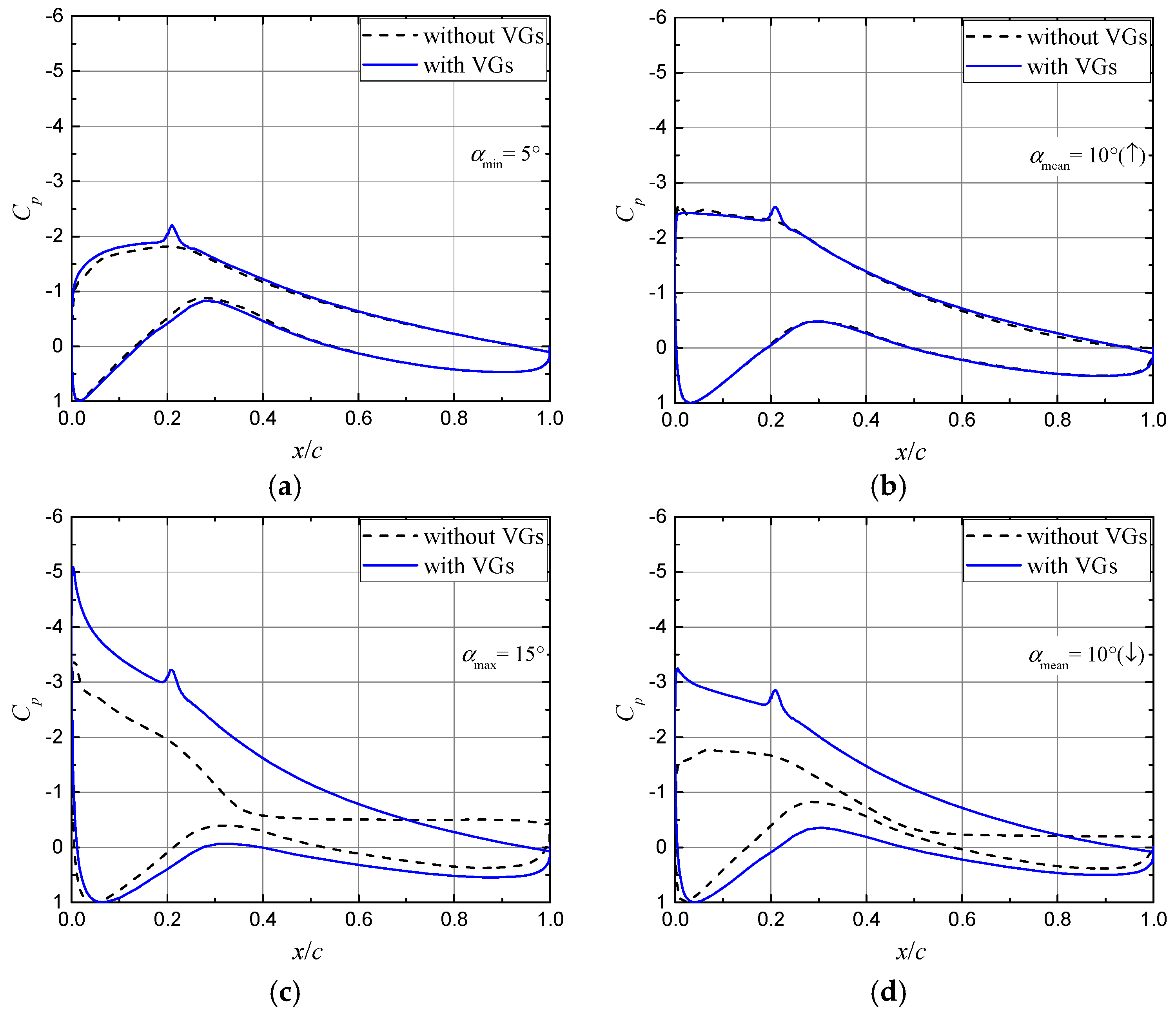
3.3. Effect of Vortex Generators on the Unsteady Airfoil Flow under Pitch Oscillations
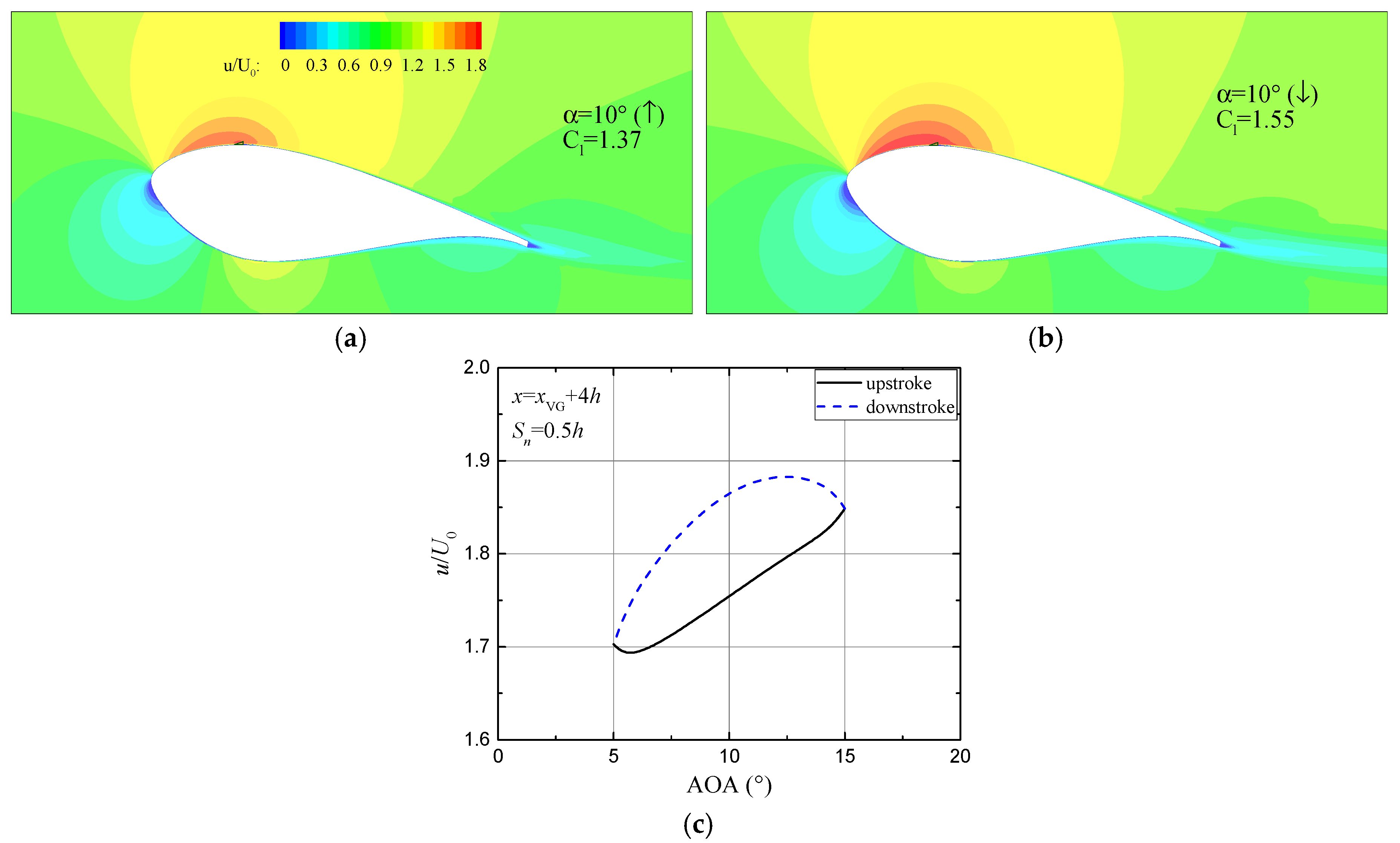
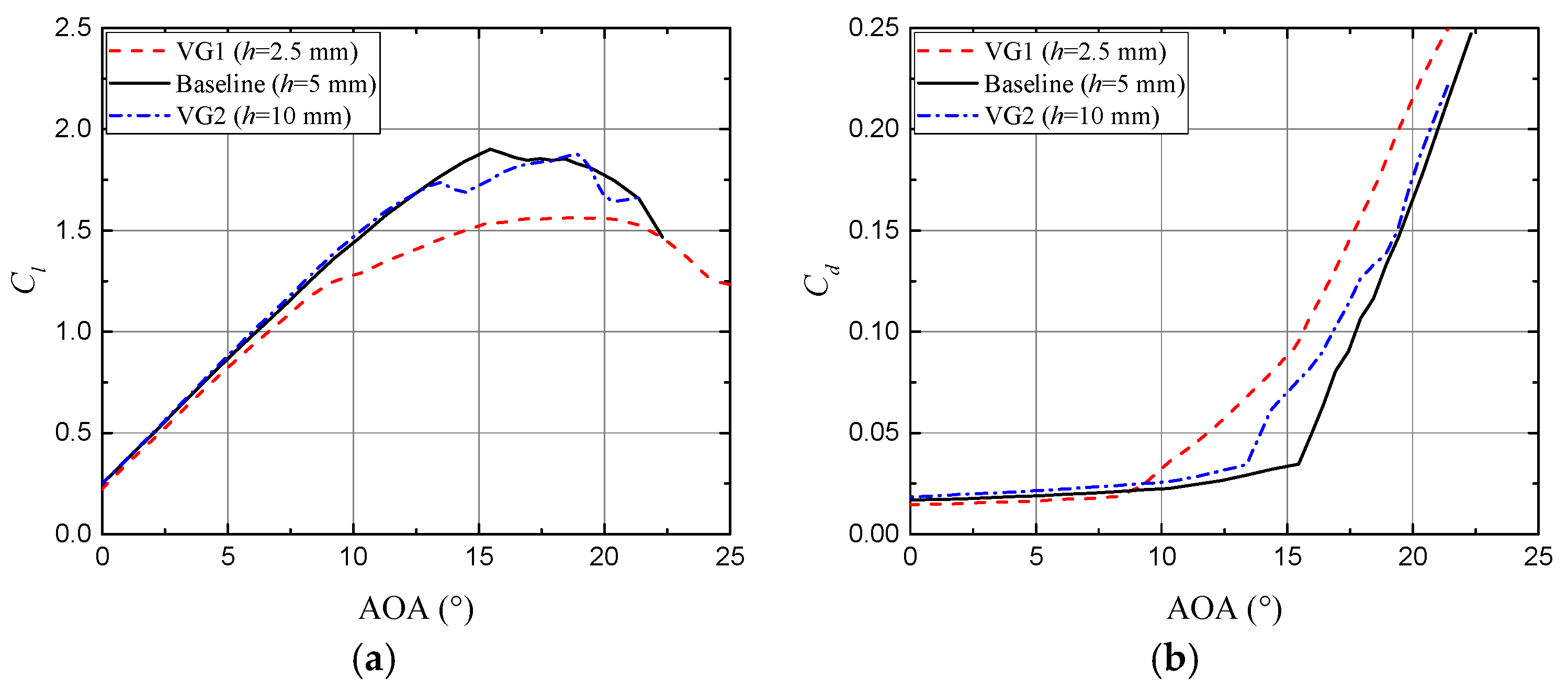
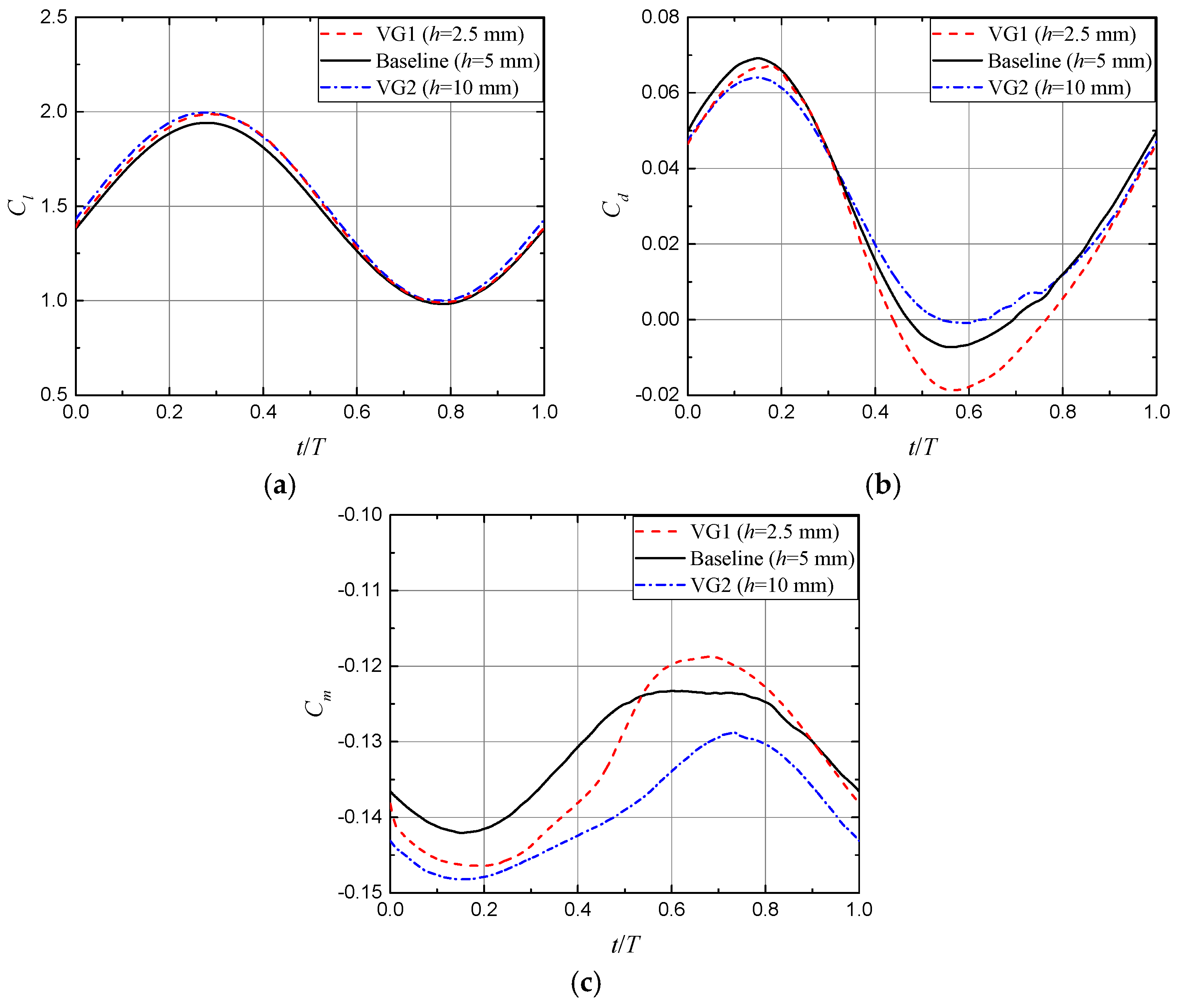
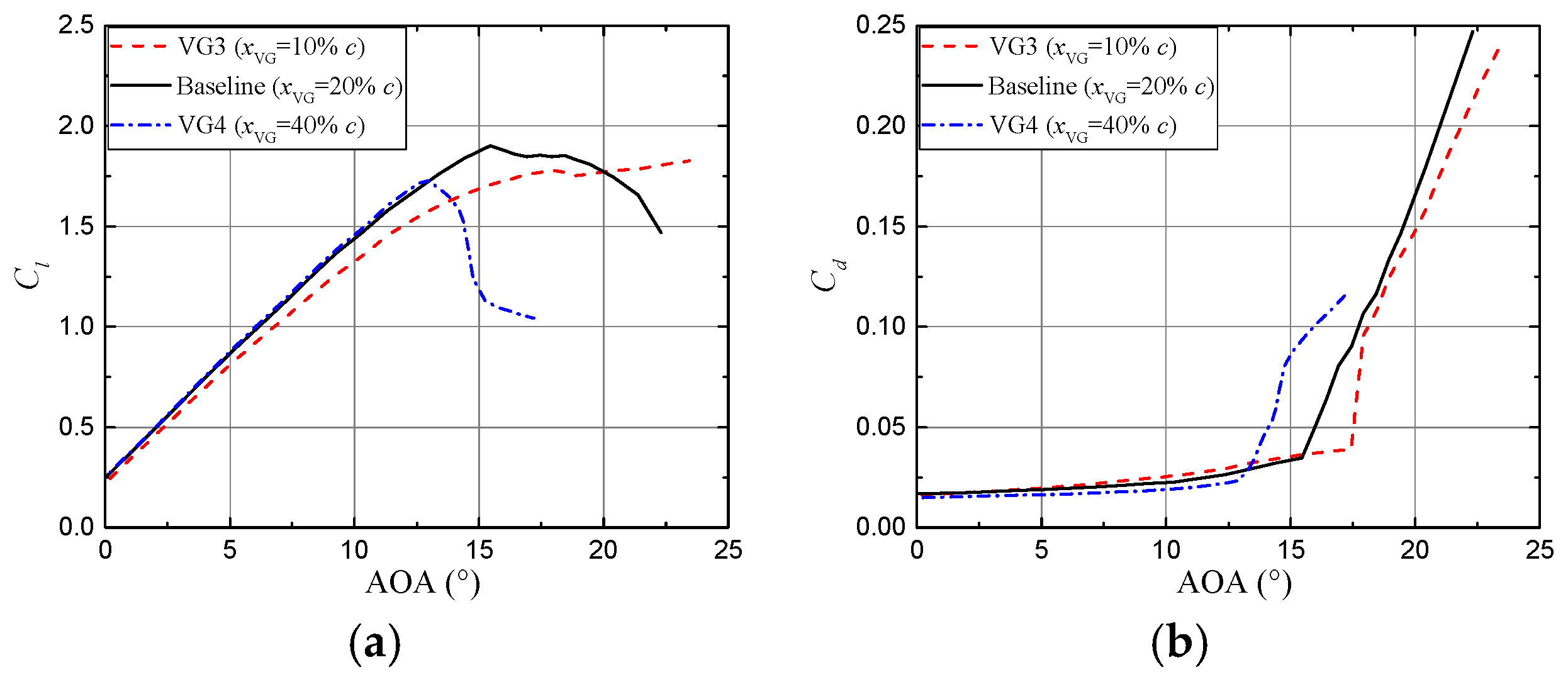
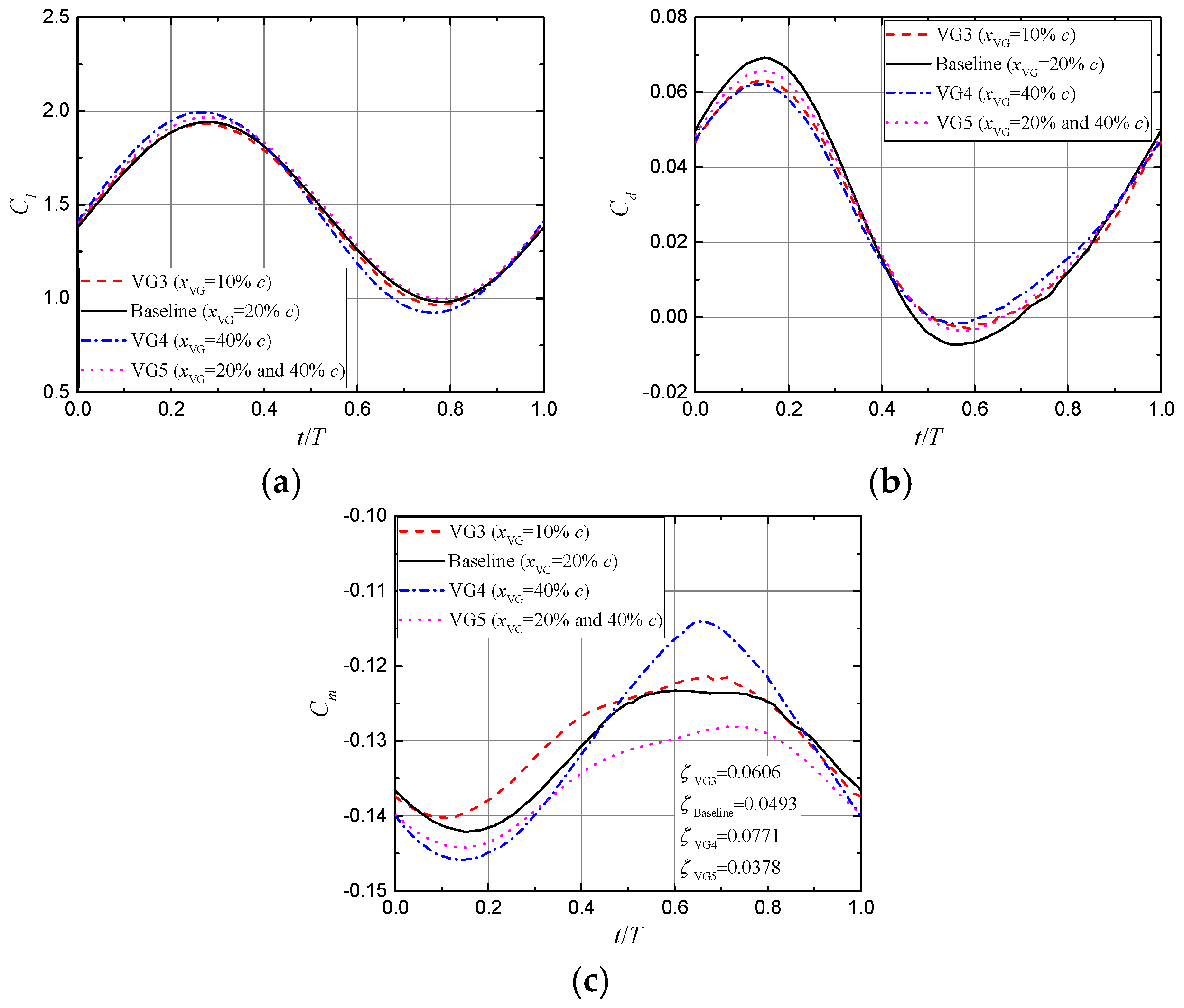
3.4. Effect of Vortex Generator Parameters on the Unsteady Aerodynamic Responses
3.4.1. Vane Height
3.4.2. Chordwise Position
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| ζ | aerodynamic pitch damping |
| α | angle of attack (AOA) |
| η | exponential decay exponent of streamwise peak vorticity |
| β | geometric vane inflow angle |
| ε | hysteresis intensity of the lift coefficient |
| αmean | mean AOA |
| ωx,max | streamwise peak vorticity |
| A | AOA amplitude |
| c | chord length |
| Cd | drag coefficient |
| Cl | lift coefficient |
| Cl,max | maximum lift coefficient |
| Cm | pitching moment coefficient about the quarter-chord axis |
| Cp | pressure coefficient |
| D | inter-vane spacing |
| d | intra-vane spacing |
| f | frequency of oscillation |
| h | vane height |
| k | reduced frequency |
| L | vane length |
| Sn | normal distance away from the wall surface |
| T | period of airfoil motion |
| u | streamwise velocity |
| U0 | freestream velocity |
| v | normal velocity |
| x | chordwise location |
| xVG | chordwise installation of VGs, measured between the airfoil and VG leading edges |
| xVG,TE | chordwise location of VG trailing edge |
References
- Godard, G.; Stanislas, M. Control of a decelerating boundary layer. Part 1: Optimization of passive vortex generators. Aerosp. Sci. Technol. 2006, 10, 181–191. [Google Scholar] [CrossRef]
- Barlas, T.K.; van Kuik, G.A.M. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Griffin, D.A. Investigation of Vortex Generators for Augmentation of Wind Turbine Power Performance; National Renewable Energy Lab.: Golden, CO, USA, 1996.
- Øye, S. The ELKRAFT 1 MW Wind Turbine: Results from the Test Program. In Proceedings of the 1996 European Union Wind Energy Conference, Göteborg, Sweden, 20–24 May 1996; pp. 251–255. [Google Scholar]
- Mueller-Vahl, H.; Pechlivanoglou, G.; Nayeri, C.N.; Paschereit, C.O. Vortex generators for wind turbine blades: A combined wind tunnel and wind turbine parametric study. In Proceedings of the Asme Turbo Expo 2012; American Society Mechanical Engineers: New York, NY, USA, 2012; Volume 6, pp. 899–914. [Google Scholar]
- Tian, Q.; Corson, D.; Baker, J. Application of Vortex Generators to Wind Turbine Blades. In Proceedings of the 34th Wind Energy Symposium, AIAA SciTech Forum, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Lin, J.C. Review of research on low-profile vortex generators to control boundary-layer separation. Prog. Aerosp. Sci. 2002, 38, 389–420. [Google Scholar] [CrossRef]
- Martinez-Filgueira, P.; Fernandez-Gamiz, U.; Zulueta, E.; Errasti, I.; Fernandez-Gauna, B. Parametric study of low-profile vortex generators. Int. J. Hydrog. Energy 2017, 42, 17700–17712. [Google Scholar] [CrossRef]
- Velte, C.M. Vortex Generator Flow Model Based on Self-Similarity. Aiaa J. 2013, 51, 526–529. [Google Scholar] [CrossRef]
- Logdberg, O.; Fransson, J.H.M.; Alfredsson, P.H. Streamwise evolution of longitudinal vortices in a turbulent boundary layer. J. Fluid Mech. 2009, 623, 27–58. [Google Scholar] [CrossRef]
- Baldacchino, D.; Ferreira, C.; De Tavernier, D.; Timmer, W.A.; van Bussel, G.J.W. Experimental parameter study for passive vortex generators on a 30% thick airfoil. Wind Energy 2018, 21, 745–765. [Google Scholar] [CrossRef]
- Wang, H.P.; Zhang, B.; Qiu, Q.G.; Xu, X. Flow control on the NREL S809 wind turbine airfoil using vortex generators. Energy 2017, 118, 1210–1221. [Google Scholar] [CrossRef]
- Spalart, P.R.; Shur, M.L.; Strelets, M.K.; Travin, A.K. Direct Simulation and RANS Modelling of a Vortex Generator Flow. Flow Turbul. Combust. 2015, 95, 335–350. [Google Scholar] [CrossRef]
- Velte, C.M.; Hansen, M.O.L.; Cavar, D. Flow analysis of vortex generators on wing sections by stereoscopic particle image velocimetry measurements. Environ. Res. Lett. 2008, 3, 11. [Google Scholar] [CrossRef]
- Jirasek, A. Vortex-generator model and its application to flow control. J. Aircr. 2005, 42, 1486–1491. [Google Scholar] [CrossRef]
- Baldacchino, D.; Manolesos, M.; Ferreira, C.; Salcedo, A.G.; Aparicio, M.; Chaviaropoulos, T.; Diakakis, K.; Florentie, L.; Garcia, N.R.; Papadakis, G.; et al. Iop, Experimental benchmark and code validation for airfoils equipped with passive vortex generators. In Science of Making Torque from Wind; Iop Publishing Ltd.: Bristol, UK, 2016; Volume 753. [Google Scholar]
- Troldborg, N.; Zahle, F.; Sorensen, N.N. Simulation of a MW rotor equipped with vortex generators using CFD and an actuator shape model. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- McCroskey, W.J. The Phenomenon of Dynamic Stall; National Aeronautics and Space Administration: Washington, DC, USA, 1981.
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Aircr. 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Schepers, J.G. Engineering Models in Wind Energy Aerodynamics: Development, Implementation and Analysis using Dedicated Aerodynamic Measurements; Delft University of Technology: Delft, The Netherlands, 2012. [Google Scholar]
- Ekaterinaris, J.A.; Platzer, M.F. Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 1997, 33, 759–846. [Google Scholar] [CrossRef]
- Gharali, K.; Johnson, D.A. Numerical modeling of an S809 airfoil under dynamic stall, erosion and high reduced frequencies. Appl. Energy 2012, 93, 45–52. [Google Scholar] [CrossRef]
- Gao, L.Y.; Zhang, H.; Liu, Y.Q.; Han, S. Effects of vortex generators on a blunt trailing-edge airfoil for wind turbines. Renew. Energy 2015, 76, 303–311. [Google Scholar] [CrossRef]
- Timmer, W.A.; van Rooij, R. Summary of the Delft University wind turbine dedicated airfoils. J. Sol. Energy Eng. Trans. ASME 2003, 125, 488–496. [Google Scholar] [CrossRef]
- ANSYS Inc. FLUENT Theory Guide, Release 16.0; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Zhu, C.; Wang, T. Comparative Study of Dynamic Stall under Pitch Oscillation and Oscillating Freestream on Wind Turbine Airfoil and Blade. Appl. Sci. 2018, 8, 1242. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Transport Turbulence Model for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Volker, S. A correlation-based transition model using local variables—Part I: Model formulation. J. Turbomach. Trans. ASME 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Somers, D.M. Design and Experimental Results for the S809 Airfoil; National Renewable Energy Laboratory: Golden, CO, USA, 1997.
- Ramsay, R.F.; Hoffman, M.J.; Gregorek, G.M. Effects of Grit Roughness and Pitch Oscillation on the S809 Airfoil; National Renewable Energy Laboratory: Golden, CO, USA, 1995.
- Karbasian, H.R.; Esfahani, J.A.; Barati, E. Effect of acceleration on dynamic stall of airfoil in unsteady operating conditions. Wind Energy 2016, 19, 17–33. [Google Scholar] [CrossRef]
- Gupta, S.; Leishman, J.G. Dynamic stall modelling of the S809 aerofoil and comparison with experiments. Wind Energy 2006, 9, 521–547. [Google Scholar] [CrossRef]
- Johansen, J. Unsteady Airfoil Flows with Application to Aeroelastic Stability; Risø National Laboratory: Roskilde, Denmark, 1999. [Google Scholar]
- Leishman, J.G. Principles of Helicopter Aerodynamics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Leishman, J.G.; Beddoes, T.S. A Semi-Empirical Model for Dynamic Stall. J. Am. Helicopter Soc. 1989, 34, 3–17. [Google Scholar] [CrossRef]

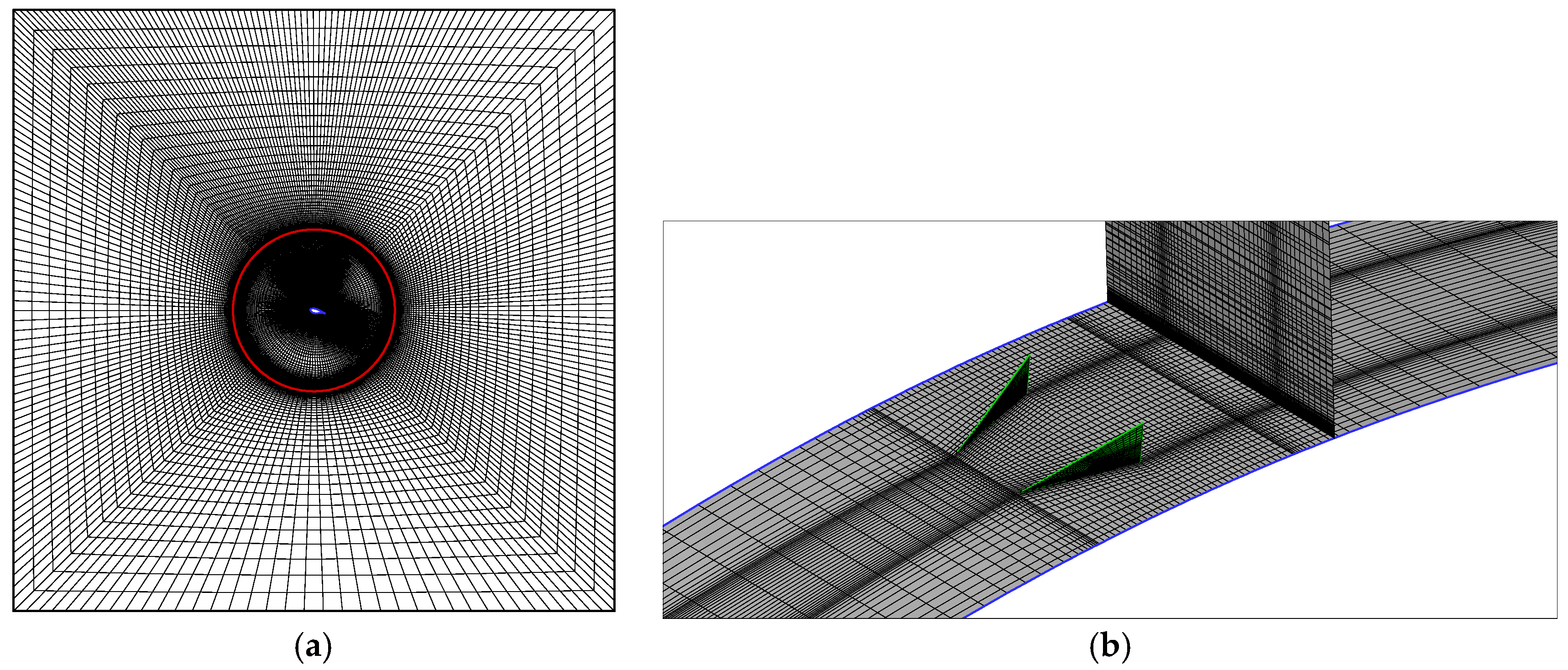
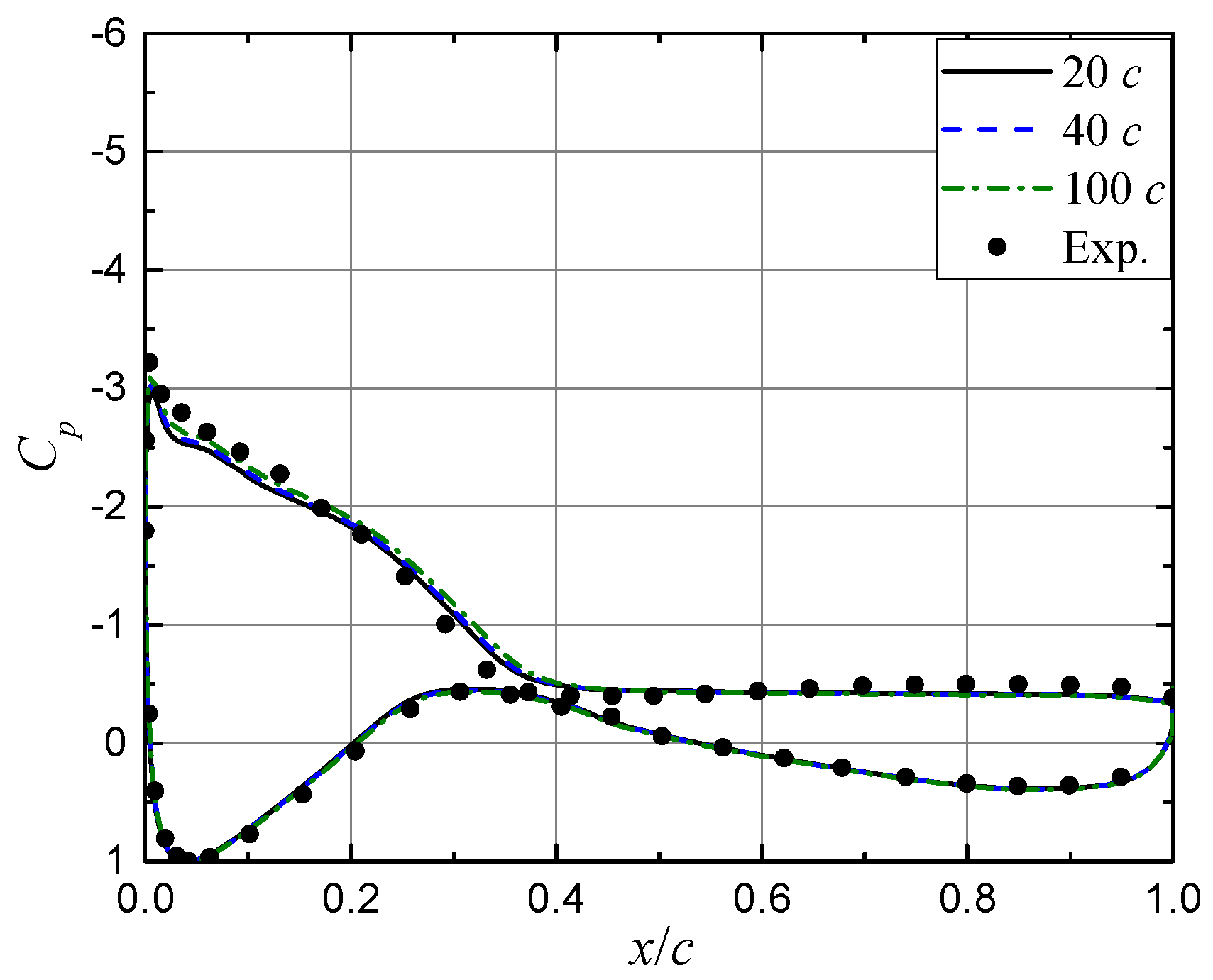
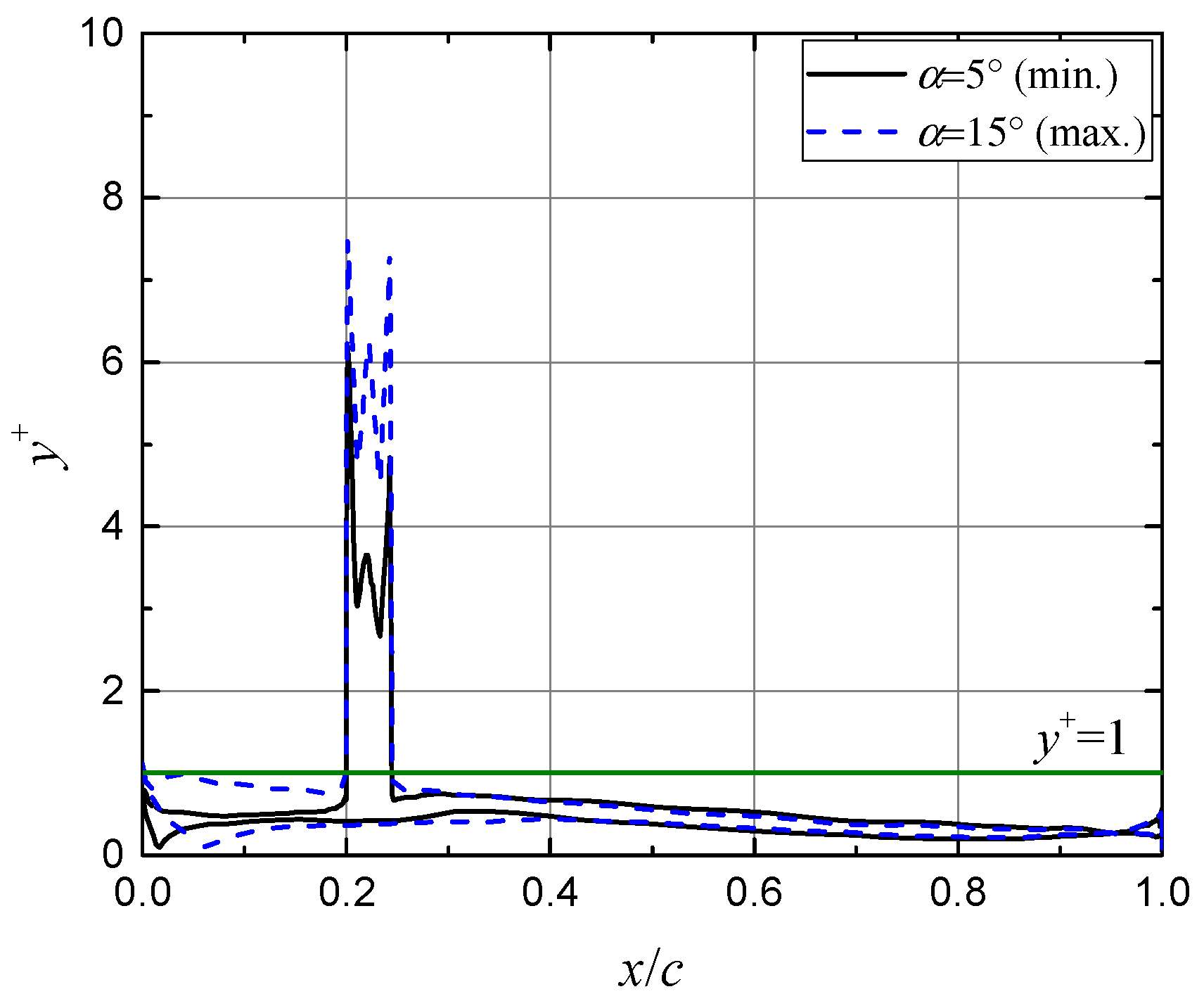
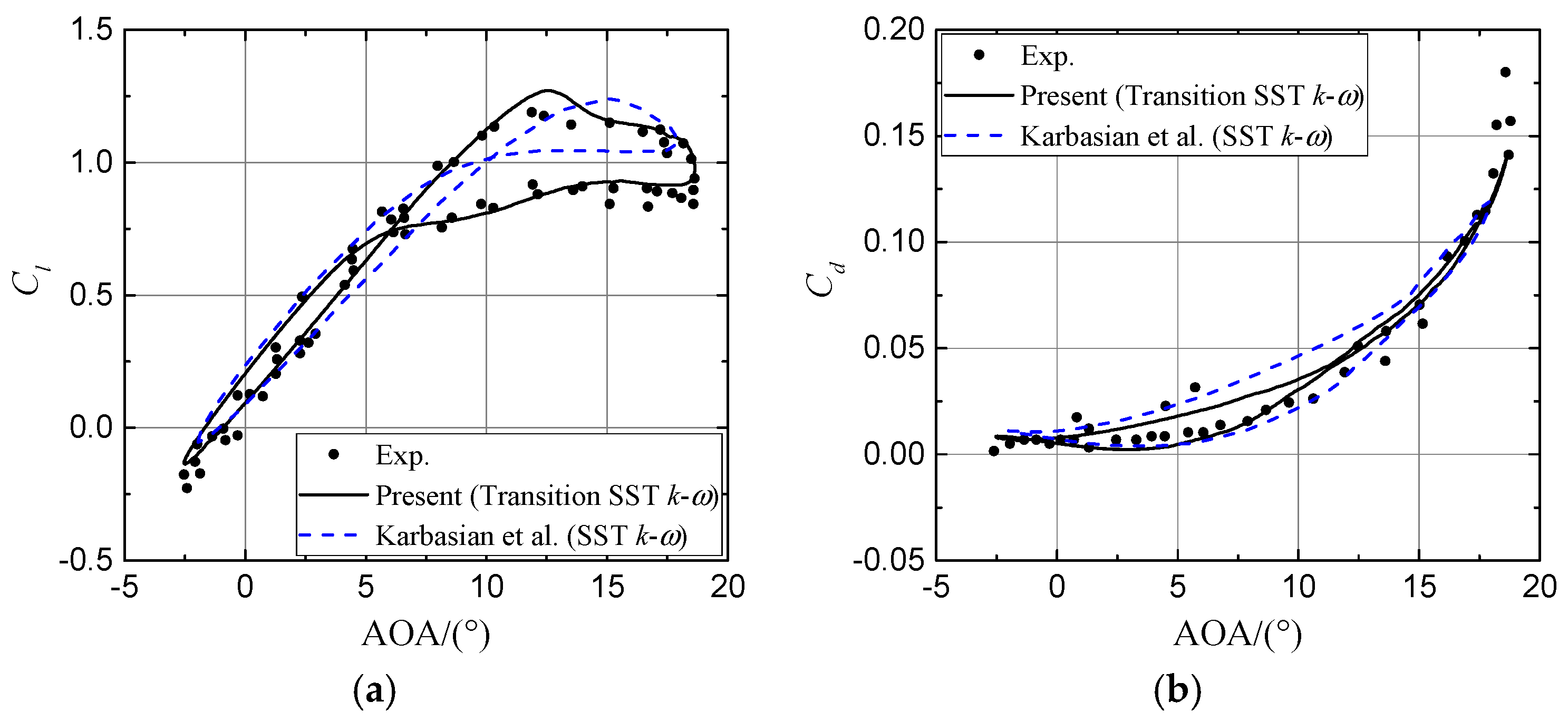






| Case Name | xVG/c (%) | h (mm) | d/h | D/h | L/h |
|---|---|---|---|---|---|
| Baseline | 20 | 5 | 3.5 | 7 | 3 |
| VG1 | 20 | 2.5 | 3.5 | 7 | 3 |
| VG2 | 20 | 10 | 3.5 | 7 | 3 |
| VG3 | 10 | 5 | 3.5 | 7 | 3 |
| VG4 | 40 | 5 | 3.5 | 7 | 3 |
| VG5 | 20 and 40 | 5 | 3.5 | 7 | 3 |
| Variable | Mesh Resolution | Richardson Extrapolation | ||||
|---|---|---|---|---|---|---|
| Coarse (N) | Medium (N) | Fine (N) | RE (N) | p | R | |
| Lift force | 44.970 | 45.119 | 45.226 | 47.364 | 0.237 | 0.716 |
| Drag force | 0.744 | 0.704 | 0.689 | 0.660 | 2.403 | 0.370 |
| Unsteadiness | k | εclean | εVGs | (εclean−εVGs)/εclean |
|---|---|---|---|---|
| Low | 0.028 | 0.640 | 0.268 | 58.2% |
| Moderate | 0.055 | 0.944 | 0.258 | 72.7% |
| High | 0.083 | 1.027 | 0.225 | 78.1% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Wang, T.; Wu, J. Numerical Investigation of Passive Vortex Generators on a Wind Turbine Airfoil Undergoing Pitch Oscillations. Energies 2019, 12, 654. https://doi.org/10.3390/en12040654
Zhu C, Wang T, Wu J. Numerical Investigation of Passive Vortex Generators on a Wind Turbine Airfoil Undergoing Pitch Oscillations. Energies. 2019; 12(4):654. https://doi.org/10.3390/en12040654
Chicago/Turabian StyleZhu, Chengyong, Tongguang Wang, and Jianghai Wu. 2019. "Numerical Investigation of Passive Vortex Generators on a Wind Turbine Airfoil Undergoing Pitch Oscillations" Energies 12, no. 4: 654. https://doi.org/10.3390/en12040654
APA StyleZhu, C., Wang, T., & Wu, J. (2019). Numerical Investigation of Passive Vortex Generators on a Wind Turbine Airfoil Undergoing Pitch Oscillations. Energies, 12(4), 654. https://doi.org/10.3390/en12040654





