1. Introduction
Exploration of renewable energy sources (RES) is an important way to address the energy and environmental crisis, which has become one of the main tasks and strategic subjects for the development of the national economy and for establishing a prosperous society in the 21st century [
1]. China spans a large geographical area with rural areas associated with prolonged sunshine durations and abundant renewable energy sources, such as solar and biomass resources, which have unique advantages. It is estimated that the total amount of biomass resources is approximately equivalent to 460 billion kg of standard coal in China each year. However, at present, most of the biomass is directly used for combustion, and the conversion efficiency is only 10%–20%, thus resulting in serious energy waste, environmental pollution and ecological damage. Simultaneously, the rural residents in China have a prominent feature of small dispersion, and the centralized supply model is unable to alleviate the difficulties of heating supply and local pollution in the vast rural and remote areas. Therefore, the traditional electricity-based energy supply is no longer advisable.
The combined cooling, heating and power (CCHP) system, based on the principle of energy cascade utilization, can simultaneously meet the electricity, cooling, and heating loads, which improves the energy efficiency and reduces air pollutant emissions dramatically [
2,
3,
4,
5,
6]. Simultaneously the CCHP system provides an effective way for solar and biomass energy utilization [
7,
8,
9,
10,
11], which especially has received widespread attention in Europe [
12,
13,
14]. The choices of primary energy sources and system capacity have a significant impact on the overall performance of the CCHP system, which has been extensively studied by researchers [
15,
16,
17,
18,
19].
Most of the current researches choose a number of algorithms for the traditional CCHP system driven by natural gas to determine the optimal system capacity. Zeng et al. [
20] selected the genetic algorithm (GA) to optimize the capacity of a combined cooling, heating and power system with ground source heat pump (CCHP–GSHP), and the integrated performances of the coupling system were improved. Liu et al. [
21] presented a matrix modeling approach to optimize the CCHP system with hybrid chillers, and the optimal power generation unit (PGU) capacity was determined based on the use of the enumeration algorithm, then an illustrative case study was conducted to show that the proposed method performed much better compared to traditional strategies. Wei et al. [
22] adopted the non-dominated sorting genetic algorithm-II (NSGA-II) to find a set of Pareto optimal configurations of the CCHP system. Wang et al. [
23] applied a particle swarm optimization algorithm (PSOA) to obtain the optimal design of the building cooling heating and power (BCHP) system.
Several documents have focused on the CCHP system with renewable energy sources. Yousefi et al. [
24] proposed a CCHP system with photovoltaic/thermal (PV/T) panels, which was optimized based on the economy, energy, and emission objective functions. The GA optimization and an analytical hierarchical process were used to find the best size of the system components. Fani et al. [
25] studied a solar-assisted combined cooling, heating, and power (SCCHP) system in office buildings in Iran. Noussan et al. [
26] found out the optimal configuration of a biomass-fired CHP system with thermal energy storage from the economic and energetic points of view. Gazda [
27] proposed a distributed energy system driven by solar energy and biogas, then analyzed the energy and environmental performance of the system. Ameri et al. [
28] developed a mixed integer linear programming (MILP) model for determining the optimal capacity of CCHP systems with photovoltaic systems so that the initial and operating costs of the energy supply system were minimized. Ebrahimi et al. [
29] designed a hybrid-CCHP system that consisted of a basic CCHP system and a solar collector for a residential building in five different climates. The maximum rectangle method was applied to identify the optimal size of the prime mover. Ju et al. [
30] compared the performance of a CCHP and renewable energy-based hybrid energy system driven by distributed energy resources (DERs CCHP) and a CCHP system driven by natural gas (NG CCHP), which indicated that the former had better operational performance. Li et al. [
31] applied the preference-inspired coevolutionary algorithm (PICEA-g) to the configuration of the CCHP system with renewable energies.
Owing to the volatility and intermittency of renewable energy sources and the time-varying load, a source–load mismatch problem emerges, whereby the addition of RES makes the CCHP system structure and energy flow more complicated. Most of the optimization design methods only optimize the capacity of the PGU while primary energy sources have not been optimized, which is applicative for the natural gas-driven CCHP system to achieve the optimal targets since natural gas is sufficient and stable. However, biomass energy is completely different from natural gas since the utilization of biomass energy is affected by daily production, which is a constraint for optimal design. Therefore, the current optimization design of CCHP system is rendered not applicable.
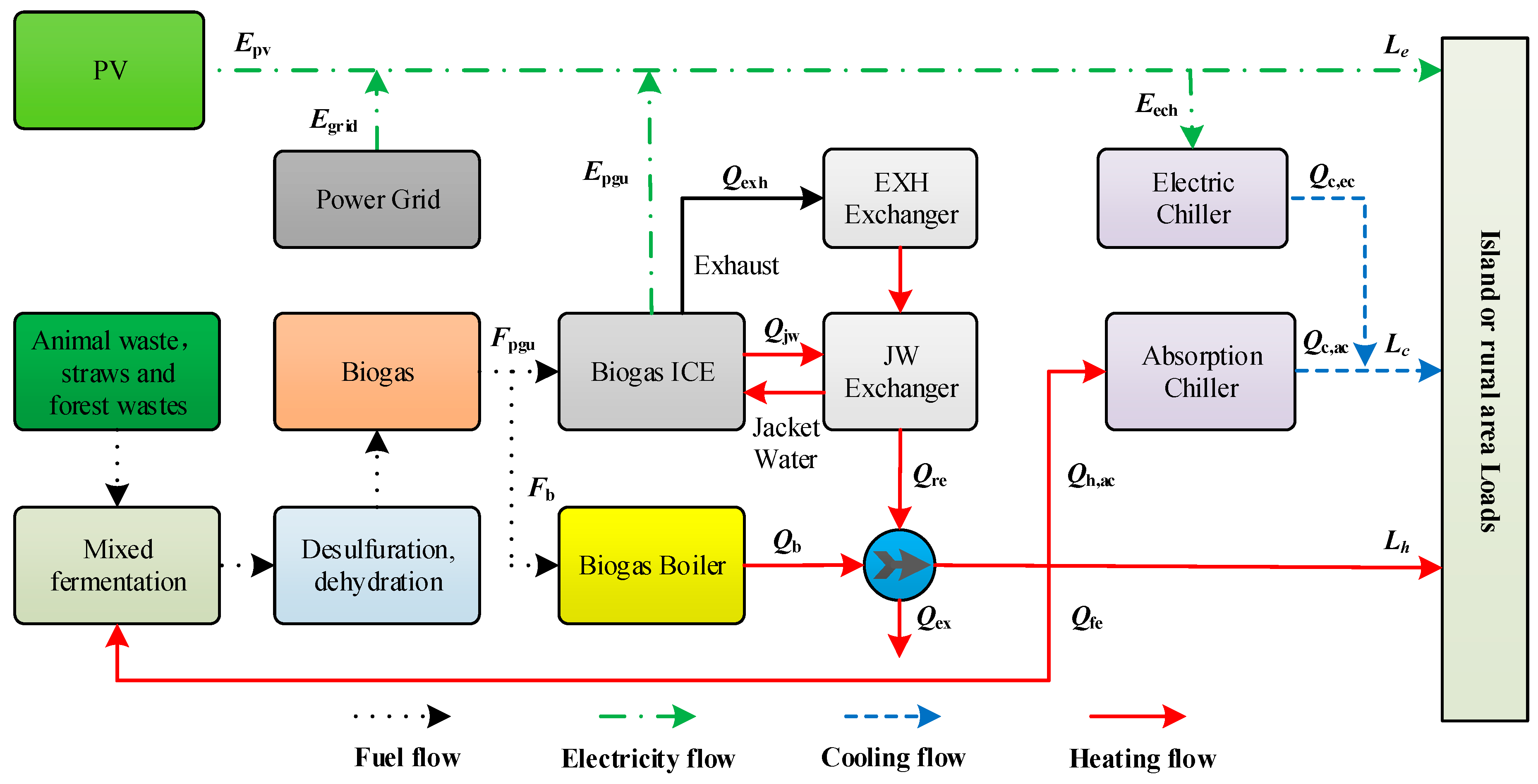
This study presents a RES–CCHP system driven by a biogas-fueled internal combustion engine (ICE) and photovoltaic (PV) panels. Separate optimization of PV and PGU, would not elicit the best results. Thus, comprehensive consideration of renewable energy and load characteristics, four-decision variables (the capacity of the PGU, the number of PV panels, the on–off coefficient of PGU, and the ratio of electric cooling to cooling load) were selected to be optimized in order to achieve collaborative optimization. A multi-objective integrated optimization model that maximizes the annual total cost saving rate (ATCSR), primary energy saving ratio (PESR), and carbon emission reduction ratio (CERR), and considers the off-design performance of the PGU, is proposed. The GA is adopted to determine the capacity and key operation parameters of the RES–CCHP system. In addition, a case study of a small farm in Jinan, China is conducted to ascertain the feasibility of the proposed RES–CCHP system structure and the corresponding optimization design method.
The remainder of this study is organized as follows:
Section 2 describes the structure and energy flows of the RES–CCHP system.
Section 3 presents the optimization model. Results of the simulation and optimization are given and analyzed in
Section 4. The conclusions are summarized in the last section.
Compared with existing approaches, the main contributions of this paper are summarized as follows:
- (1)
Considering the fluctuation of solar energy and the limitation of biomass energy, the PGU will frequently operate in a variable operating condition. This paper analyzed off-design performance of the PGU, and the daily biogas production was added into the optimization model as a constraint condition, so that the obtained equipment capacity can be more guaranteed to operate in an efficient operation area and the renewable energy has higher utilization.
- (2)
The capacity of the PGU, the number of PV panels, the on–off coefficient of PGU, and the ratio of electric cooling to cooling load were collectively optimized to improve the energetic, economic and environmental performances of the system.
- (3)
The influence of the volatility of renewable energy sources on the design results and system performance is analyzed to prove the proposed RES–CCHP system and the design method are robust.
5. Conclusions
This study presented a RES–CCHP system driven by a biogas-fueled ICE and PV panels, which capitalized on the respective advantages of the RES and CCHP systems. Comprehensive consideration of renewable energy and load characteristics, four-decision variables (the capacity of power generation unit (PGU), the number of PV panels, the on–off coefficient of PGU, and the ratio of electric cooling to cooling load) were selected to be optimized in order to achieve collaborative optimization. A multi-objective optimization model was proposed that aimed to maximize the PESR, ATCSR, and CERR of the RES–CCHP system. Given the proposed optimization model, a GA was adopted to determine the capacity and operation of the RES–CCHP system.
A case study of a small farm in Jinan, China, was conducted to ascertain the feasibility of the proposed RES–CCHP system structure and the corresponding optimal operation strategy. The results illustrated that the implementation of the optimization design was beneficial to energy conservation, cost saving and emission reduction. The values of PESR, ATCSR, and CERR are 20.94%, 11.73% and 40.79%, respectively, which demonstrates the advantages of the RES–CCHP system are clear compared with the SP system. The annual energy distribution results show that equipment capacity and operating parameters obtained by using the optimization design method can match efficiently with the energy demands and reduce the operating cost. Finally, the influences of the volatility of solar energy and the changes of biogas production on the optimization design method are analyzed, which show that the RES–CCHP system and the method proposed are robust.
The RES–CCHP system can effectively stabilize the randomness and volatility of the solar energy and biomass energy through the optimization design proposed in this study. It can significantly improve the energy efficiency and the solar and biomass energy utilization rate, and is suitable for supplying energy to a decentralized rural area.
To capitalize on the advantages of the RES–CCHP system in energy saving and emission reduction, and to improve the economic index, future research will combine the system design optimization and the output plan of key equipment in accordance to load changing, so as to further enhance the system performance.