Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models

Abstract

This paper presents measurement uncertainty propagation through four basic photovoltaic cell models: One-diode model without resistances, with one resistance and with two resistances and two-diode model with two resistances. The expressions for the output current of all photovoltaic cell models is presented as a function of global irradiance G and temperature T. Next, the expressions for all fill factor parameters: short-circuit current, open-circuit voltage, current and voltage at the maximum power point, depending on the global irradiance G and temperature T are derived as well. For each parameter, Monte Carlo simulations to calculate the measurement uncertainty of the parameter are performed and the results were used as input values for the calculation of measurement uncertainty of fill factor. Practical calculations are performed in laboratory for renewable energy sources located on 45°32′ N and 18°44′ E. Final fill factor calculations are compared for three different module technologies.

1. Introduction

In metrological practice, indirect measurements, where the measured value is calculated from several directly measured input quantities are commonly performed [1,2]. Thereby, measurements of multiparametric (multidimensional) quantities, including measurements carried out using multiple sensors, have become one of the most important problems of metrology [3]. The most difficult task in this procedure is the propagation of the information, in particular the measurement uncertainty, from input quantities $\mathit{X}={\left(X_1,X_2,\dots ,X_N\right)}^T$ which information is written in the form of a probability density function (PDF), via a mathematical model of the measurement $\mathit{Y}=f\left(\mathit{X}\right)$ which describes the relationship between $\mathit{X}$ and $\mathit{Y}$, in the PDF of one or more output quantities $\mathit{Y}={\left(Y_1,Y_2,\dots ,Y_N\right)}^T$ [4]. In this case, $\mathit{\xi }={\left({\xi }_1,{\xi }_2,\dots ,{\xi }_N\right)}^T$ represent the possible values of $\mathit{X}$ and $\mathit{\eta }={\left({\eta }_1,{\eta }_2,\dots ,{\eta }_N\right)}^T$ represent the possible values of $\mathit{Y}$ [5]. The traditional practice of solving such problems is within the internationally accepted document, Guide to the Expression of Uncertainty in Measurement (GUM) [6,7]. The main task of this method is the propagation of standard uncertainties of input quantities, via a mathematical model of the measurement to the standard uncertainties of the output quantities. Depending on the desired coverage level, an expanded uncertainty usually with 95% confidence level, is used. This procedure is widely accepted due to its simplicity and in most cases, it satisfies. However, its implementation requires a number of assumptions such as: Input quantities are mutually independent, the mathematical model of the measurement is linear, the input values have a normal distribution that after propagation results in a normal distribution of the output quantities and a number of other assumptions that are widely described in the literature [1,4,8]. Therefore, it follows that the GUM procedure has some disadvantages and is not satisfactory in all cases. Such examples are described in [4,8,9] as well as in Supplement 1 [10] on the main GUM document [6]. In particular, Supplement 1 recommends the use of the Monte Carlo method (MCM) for the calculation of measurement uncertainty which has a number of advantages over the traditional GUM method [11]. The main difference from the GUM is in fact that MCM perform numerical random sampling from the PDF of input quantities and propagate them through a mathematical model of the measurement that results in a numerical approximation of the PDF of output quantities [12,13,14]. In contrast to the GUM procedure, which propagates only information about the standard uncertainties (Law of Propagation of Uncertainties), MCM carries much richer information from the PDF of input quantities $g_{X_i}\left({\xi }_i\right)$ in the form of a PDF’s output quantities $g_Y\left(\eta \right)$ (Law of Propagation of Distributions). After that, it is easy to calculate the desired parameters of output quantities, e.g., the mean, the standard deviation, uncertainty limits with the desired confidence level. MCM is performed with a predetermined number of iterations M [15]. It is generally assumed that M = 10⁶ iterations satisfy for the 95% confidence level [8,10]. More details about the implementation of the MCM method could be found in the authors’ previous work [16,17,18].

2. The Fill Factor of the Photovoltaic Cell—State of the Art

Current-voltage (I-V) characteristic (see Figure 1), is a measurement of the photovoltaic (PV) cell quality. The I-V characteristic is determined by three parameters. The first parameter is the short-circuit current $I_{SC}$. Its value is, depending on the irradiance G, the maximum value of the PV cell output current $I=I_{SC}$.

Open-circuit voltage $V_{0C}$, as the second parameter, indicates the maximum voltage of the PV cell. Generally, $V_{0C}$ is determined by diode reverse saturation current $I_{D0}$, which depends on the material and cell structure design, and a temperature of the PV cell [19].

The product of $V_{0C}$ and $I_{SC}$ describes the theoretically maximum PV cell power output [20,21,22]. Due to the recombination and resistive losses, maximum power output $P_{MPP}$ of the PV cell is lower, i.e., it is represented as a point on I-V curve, which is defined as the product of the current $I_{MPP}$ and voltage $V_{MPP}$ at the maximum power point. As shown in Figure 1, maximum power point $P_{MPP}$ determines the rectangle with the largest surface area for any point on the I-V curve [23,24]. The ratio of surface areas of rectangle specified by $P_{MPP}$ point and ideal rectangle, specified by the product of $V_{0C}$ and $I_{SC}$, defines the Fill Factor (FF) and it is the third important parameter of each PV cell [25]. The PV cell model is generally composed of the diodes, which represent recombination losses, and parasitic resistances $(R_{SH}$ and $R_S)$ which represent the power losses [26]. Series resistance $R_S$ represents the resistance of the metal bar and metal contacts [25] while the shunt resistance $R_{SH}$ represents non-ideality and the impurities of the p-n junction. By increasing the amount of the shunt resistance $R_{SH}$ and reducing the series resistance $R_S$, the FF increases (see Figure 2), and typically ranges between 0.7–0.85 [25].

The change in the amount of serial resistance $R_S$ is one of the main reasons for changing the output power of the PV cell. Increasing resistance $R_S$, according to [27,28] is due to solder bond degradation. Exposure of the PV module to the climatic conditions creates thermomechanical fatigue or cracks in the development of the solder bonds leading. Changing the solder joint geometry of the lump reduces the number of redundant solder joints, and with that, the module efficiency decreases. These changes in the solder joint geometry and fatigue can be directly attributed to the increase the $R_S$, resulting in a decrease in the charge fill factor and loss of power.

The FF is significantly influenced by recombination currents flowing through the diodes. The first diode current is defined by recombination density of the saturation current of quasi-neutral regions while the second diode current is defined by recombination density of the saturation current in an impoverished area [29].

As a matter of fact, the FF cannot be calculated directly from global irradiance G and temperature T, i.e., an analytical expression for FF cannot be developed due to exponential terms in diode equations. Hence, a calculation of FF components directly from global irradiance G and temperature T should be avoided while retaining the basic idea of FF calculation without calculation of its components ($I_{SC}$, $V_{0C}$, $I_{MPP}$ and $V_{MPP}$) separately. Hence, the main goal is developing the two stage MC procedure for calculation of the associated measurement uncertainty of the FF and its components for four basic models of PV cell: One-diode model without resistance [30,31], one-diode model with one resistance [31,32,33], one-diode model with two resistances [31,34,35] and two-diode model with two resistances [31,36,37]. Namely, in the process of planning, operation and/or evaluation of the PV power plant, and of course technical systems in general, one often relies on mathematical models due to their many advantages (calculation speed, low costs, easy parameter variation, etc.). Modeling and value calculation of particular model elements of the PV power plant is very important [38,39,40], but it is out of the scope of this paper, because the paper introduces another important issue—in which way the measurement uncertainty has an impact to Fill Factor. The Fill Factor describes the internal electrical activity degree, i.e., defines the quality of photovoltaic cells, and any uncertainty in this context is relevant in the process of planning, operation and/or evaluation of the PV power plant.

3. Fill Factor Components Calculation Procedure

FF is defined as follows

$$FF=\frac{I_{MPP}{V}_{MPP}}{I_{SC}{V}_{OC}}.$$

(1)

Each of its four components can be expressed as a function of global irradiance G and temperature T. It follows that the FF measurement uncertainty is calculated as combined measurement uncertainty that essentially arises from the measurement uncertainties of irradiance $u\left(G\right)$ and temperature $u\left(T\right)$.

The equations for the output current $I_{MPP}$ of the PV cell model (

Table 1. Basic model of PV cell.

Name	Model	Expression
One-diode model without resistance		$I_{MPP}=I_{S{C}_{REF}}\frac{G}{G_{REF}}+2\alpha \left(T-T_{REF}\right)-I_{D0}\left(e^{\frac{q{V}_{MPP}}{nkT}}-1\right).$
One-diode model with one resistance		$I_L-I_{D0}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{nkT}\right\}-\frac{q{V}_{MPP}{I}_{D0}}{nkT}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{nkT}\right\}+I_{D0}=0.$
One-diode model with two resistances		$I_L-I_{D0}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{nkT}\right\}-\frac{q{V}_{MPP}{I}_{D0}}{nkT}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{nkT}\right\}+I_{D0}-\frac{2V_{MPP}+I_{MPP}{R}_S}{R_{SH}}=0.$
One-diode model with two resistances		$I_L-I_{D01}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{n_{1}kT}\right\}-\frac{q{V}_{MPP}{I}_{D0}}{n_{1}kT}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{n_{1}kT}\right\}+I_{D01}-I_{D02}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{n_{2}kT}\right\}-\frac{q{V}_{MPP}{I}_{D0}}{n_{2}kT}\ast exp\left\{\frac{q\left(V_{MPP}+I_{MPP}{R}_S\right)}{n_{2}kT}\right\}+I_{D02}-\frac{2V_{MPP}+I_{MPP}{R}_S}{R_{SH}}=0.$

) must be satisfied at the maximum power point $P_{MPP}$. Solving the system of the equations results with the current $I_{MPP}$ and the voltage $V_{MPP}$ at the maximum power point. Because the equations are nonlinear, the system of the equations is solved using the numerical method [41].

4. Practical Results of the Uncertainty Calculation Procedure

Practical measurement uncertainty calculation procedure is performed using the Monte Carlo method (MCM) with $M={10}^6$ iterations as recommended in Supplement 1 [10].

As presented in the previous section, the components of the FF are nonlinear functions of global irradiance G and temperature T and in most cases, they cannot be expressed in the explicit form. For that reason, each component is calculated individually using MCM and the results are used as uncertainty budget for calculation of the FF measurement uncertainty. Hence, MCM is performed in two stages: At the first stage MCM is used for calculation of FF components and at the second stage MCM is used for calculation of FF (see Figure 3).

4.1. Site Information

The calculations are performed under real operation conditions, i.e., the input values are measured in laboratory for renewable energy sources located on 45°32′ N and 18°44′ E. The laboratory for renewable energy sources is located at the Faculty of Electrical Engineering, Computer Science and Information Technology Osijek and was established in 2014 within the IPA cross-border program Hungary-Croatia project called Regional Impacts of Different Photovoltaic Systems funded by the European Union [42]. The laboratory has its own PV power plant with total installed power 10 kWp built up from five different module technologies: The monocrystalline module of 250 Wp (BISOL 250 Wp), thin-film CIS module of 150 Wp, thin-film amorphous silicon module of 100 Wp, high-efficiency monocrystalline module of 240 Wp (PANASONIC VBHN240SE10) and polycrystalline module of 250 Wp (BISOL BMU250). The specified power of the power plant and individual PV modules show the maximum output power at the standard test conditions (STC) conditions. The laboratory investigates how the different technologies behave under the same weather conditions (Figure 4). In this paper, measurements lasted for thirty days (started from 01 June 2017 and ended 30 June 2017). All results provide averaged 1-minute values (voltage, current, etc.) only on silicon technology of photovoltaic modules, respectively Bisol BMO250, Bisol BMU 250 and Panasonic VBHN240SE10 are studied (Figure 4). Obtained measurement on the PV modules are used for the calculations related to one PV cell. Simulation results presented in the tables are also related to one PV cell.

4.2. Measurement System Definition and Measurement Results

Measurement system is configured as presented in Figure 5. Measured values are temperature T, output current I, output voltage V and global irradiance G and are recorded in one-second periods. It is worth noting that irradiance G is measured with one probe for all modules together and temperature T is measured for each module separately.

The laboratory owns the meteorological station and records weather conditions in five-minute periods. All measurement results are available online at [43]. Measurement uncertainty budget follows from the measurement uncertainty scheme and values follow from the manufacturer’s technical specifications (

Table 2. Uncertainty budget.

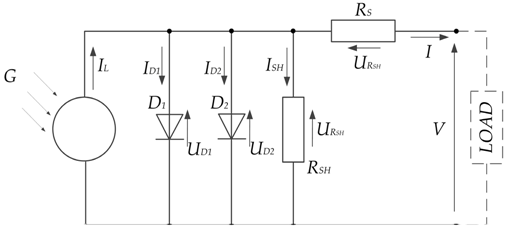Parameter	Nature of the Contribution	Probability Distribution	Value
T	Systematic	Rectangular	±0.5 °C
G	Systematic	Rectangular	±2.62%
I	Systematic	Rectangular	±1.5%
U	Systematic	Rectangular	±1%
$I_{d0},I_{d01},I_{d02}$	Systematic	Rectangular	±1.5%
$R_S,R_{SH}$	Systematic	Rectangular	±1.5%

).

Output current I and output voltage U define the output energy delivered to the 230V AC grid and are out of scope for this paper which deals with FF of the PV cell. Hence, measurement uncertainties of temperature T, irradiance G are considered for next practical calculations. Measurement uncertainties of T, G, diode reverse saturation currents $I_{d0}$ (for one diode model), $I_{d01}$ and $I_{d02}$ (for the two-diode model), series resistance $R_S$ and shunt resistance $R_{SH}$ are formulated as deviation from the measured value, which is equally likely through its whole interval. It imposes their rectangular probability distribution. Other input quantities used in calculations are treated as constant: Diode ideality factor $n_1=1;n_2=2$ [44,45]. At this stage, MCM is performed by generating $M={10}^6$ samples for each parameter from rectangular distribution (Table 2) and calculating particular FF. All results are expressed as a mean value and the expanded measurement uncertainty $U_p$ with p = 95% confidence level.

The manufacturers of the photovoltaic panels usually provide the specific electrical quantities for photovoltaic panels obtained under STC conditions and these are usually $V_{0C}$, $I_{SC}$, $I_{MPPT}$, $V_{MPPT}$ and $P_{MPPT}$. In order to use the characteristic equations we need to know the following main parameters: $R_S$, $R_{SH}$, $I_L$, $I_{d0},I_{d01}$ and $I_{d02}$. In this paper, we have used the A. Wagner method [40,46] and the results of calculations are presented in

Table 3. Calculation results for additional resistances and diode saturation currents.

Module Technologies	RS [Ω]	RSH [Ω]	Id0 [A]	Id01 [A]	Id02 [A]
Monocrystalline	0.01784	379.863	3.0318 × 10−7	6.607 × 10−8	5.3917 × 10−4
High-efficiency monocrystalline	0.006887	1412.587	7.7591 × 10−10	1.5653 × 10−10	2.6169 × 10−5
Polycrystalline	0.01113	343.891	6.06137 × 10−7	2.15999 × 10−7	7.9486 × 10−4

. This method for $R_S$ measurement needs two I-V characteristics of the same temperature (permissible tolerance ±2 °C) but different irradiances. Procedure for the determination of the two working points are following the international standard IEC 60 891.

Measurement results for temperature T and global irradiance G are exported for June 2017. Figure 4 presents measurement results in one-minute periods in graphical form for all modules, i.e., for all used technologies on this site. Standard test conditions (STC) are defined as the solar irradiance of 1 kW/m², module temperature of 25 °C and a solar irradiance angle of 45° [25]. STC conditions are presented as circle on Figure 6.

An average irradiance G and temperature T measured at June 2017 are presented in

Table 4. Measurement results of global irradiance G and temperature T for all three module technologies.

All Modules	Monocrystalline	High-Efficiency Monocrystalline	Polycrystalline
Global irradiance G [W/m2]	389.96	389.96	389.96
Temperature T [°C]	37.23	35.30	37.61

. and will be used for all calculations in this section.

4.3. Calculation Results for One-Diode Model without Resistance

Table 5. Uncertainty budget for one-diode model without resistance.

One-Diode Model without Resistance
	Monocrystalline				High-Efficiency Monocrystalline				Polycrystalline
Parameter	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit
$I_{SC}[\mathrm{A}]$	4.8640	0.0729	4.7447	4.9826	3.2452	0.0483	3.1648	3.3231	4.8649	0.0727	4.7485	4.9868
$V_{OC}[\mathrm{V}]$	0.4552	0.0006	0.454	0.4564	0.4212	0.0006	0.4201	0.4224	0.6201	0.0007	0.6187	0.6214
$V_{MPP}[\mathrm{V}]$	0.3709	0.0008	0.3693	0.3724	0.3388	0.0008	0.3373	0.3404	0.5268	0.0009	0.5251	0.5286
$I_{MPP}[\mathrm{A}]$	4.7027	0.0725	4.5827	4.8220	3.1444	0.0484	3.0652	3.2251	4.7569	0.0730	4.6375	4.8767

shows the uncertainty calculation results of all FF components for the one-diode model without resistance as well as the final FF value for all three module technologies. Figure 7 graphically presents the solution of equation from Table 1, which shows the values of MPP points for the three analyzed PV module technologies for the one-diode model without resistance.

4.4. Calculation Results for One-Diode Model with One Resistance

Table 6. Uncertainty budget for one-diode model with one resistance.

One-Diode Model with One Resistance
	Monocrystalline				High-Efficiency Monocrystalline				Polycrystalline
PARAMETER	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit
$I_{SC}[\mathrm{A}]$	4.8630	0.0731	4.7434	4.9792	3.2441	0.0476	3.1697	3.3270	4.8616	0.0716	4.7403	4.9742
$V_{OC}[\mathrm{V}]$	0.4552	0.0006	0.4540	0.4564	0.4212	0.0006	0.4200	0.4224	0.6201	0.0007	0.6186	0.6215
$V_{MPP}[\mathrm{V}]$	0.3069	0.0010	0.3052	0.3091	0.3305	0.0004	0.3297	0.3313	0.4882	0.0008	0.4867	0.4896
$I_{MPP}[\mathrm{A}]$	4.4647	0.0662	4.3598	4.5748	3.0015	0.0452	2.9241	3.0705	4.6081	0.0697	4.4925	4.7177

shows the uncertainty calculation results of all FF components for the one-diode model with one resistance as well as final FF value for all three module technologies.

Figure 8 graphically presents the solution of equation from Table 1, which shows the values of MPP points for the three analyzed PV module technologies for the one-diode model with one resistance.

4.5. Calculation Results for One-Diode Model with Two Resistances

Table 7. Uncertainty budget for one-diode model with two resistances.

One-Diode Model with Two Resistances
	Monocrystalline				High-Efficiency Monocrystalline				Polycrystalline
Parameter	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit
$I_{SC}[\mathrm{A}]$	4.8641	0.0723	4.7477	4.9811	3.2450	0.0483	3.1704	3.3265	4.8626	0.0736	4.7490	4.9886
$V_{OC}[\mathrm{V}]$	0.4551	0.0006	0.4540	0.4564	0.4212	0.0006	0.4201	0.4224	0.6201	0.0007	0.6188	0.6215
$V_{MPP}[\mathrm{V}]$	0.3069	0.0010	0.3052	0.3089	0.3305	0.0004	0.3296	0.3313	0.4882	0.0008	0.4869	0.4898
$I_{MPP}[\mathrm{A}]$	4.4635	0.0652	4.3614	4.5765	3.0002	0.0453	2.9288	3.0744	4.6038	0.0673	4.4905	4.7131

shows the uncertainty calculation results of all FF components for the one-diode model with two resistances as well as final FF value for all three module technologies. Figure 9 graphically presents the solution of equation from Table 1, which shows the values of MPP points for the three analyzed PV module technologies for the one-diode model with two resistances.

4.6. Calculation Results for Two-Diode Model with Two Resistances

Table 8. Uncertainty budget for the two-diode model with two resistances.

Two-Diode Model with Two Resistances
	Monocrystalline				High-Efficiency Monocrystalline				Polycrystalline
Parameter	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit	Mean	Measurement Uncertainty	Low Limit	High Limit
$I_{SC}[\mathrm{A}]$	4.8615	0.0717	4.7488	4.9864	3.2460	0.0481	3.1637	3.3220	4.8641	0.0737	4.7444	4.9809
$V_{OC}[\mathrm{V}]$	0.4709	0.0008	0.4694	0.4724	0.4243	0.0007	0.4229	0.4257	0.6670	0.0011	0.6648	0.6689
$V_{MPP}[\mathrm{V}]$	0.3078	0.0008	0.3063	0.3094	0.3165	0.0006	0.3155	0.3177	0.4920	0.0008	0.4905	0.4934
$I_{MPP}[\mathrm{A}]$	4.1920	0.0617	4.0944	4.2999	2.8143	0.0424	2.7447	2.8826	4.3753	0.0649	4.2682	4.4823

shows the uncertainty calculation results of all FF components for the two-diode model with two resistances as well as final FF value for all three module technologies Figure 10 graphically presents the solution of equations from Table 1, which shows the values of MPP points for the three analyzed PV module technologies for the two-diode model with two resistances.

Table 9. Results overview for the mean and expanded measurement uncertainty of fill factor for all presented models.

	Fill Factor
	Monocrystalline		High-Efficiency Monocrystalline		Polycrystalline
	Mean	Measurement Uncertainty	Mean	Measurement Uncertainty	Mean	Measurement Uncertainty
One diode model without resistance	0.7880	0.0171	0.7795	0.0168	0.8309	0.0179
One diode model with one resistance	0.6191	0.0133	0.7262	0.0153	0.7464	0.0158
One diode model with two resistances	0.6190	0.0131	0.7256	0.0155	0.7456	0.0158
Two diode model with two resistances	0.5638	0.0125	0.6469	0.0138	0.6637	0.0142

shows results overview of the FF values for all presented models of the PV cell and all module technologies. The mean value for monocrystalline technology for the one-diode model without resistance (ideal PV cell) is higher (0.7880) in comparison to the other three models, i.e., it decreases with adding the parasitic resistances (0.6191 for the one-diode model with one resistance, 0.6190 for the one-diode model with two resistances and 0.5638 for the two-diode model with two resistances). The cause of the latter fact lies in the Kirchhoff currents law represented by expressions (2), (16) and (22), where is evident that, with the gradual addition of parasitic resistances $R_S$ and $R_{SH}$ and additional diode, current that flows through the added elements increases and output current of the PV cell decreases in total photo-generated current $I_L$. Measurement uncertainty for monocrystalline technology has the widest range (0.0171) for the one-diode model with one resistance and decreases for the other three models (0.0133 for the one-diode model without resistances, 0.0131 for the one-diode model with two resistances and 0.0125 for the two-diode model with two resistances.

Figure 11 and Figure 12 graphically present a comparison for the FF mean value and measurement uncertainty for all four PV cell models and all three technologies of the PV module.

The same decreasing trend of the FF with adding the parasitic resistances to the PV cell model is obtained for the polycrystalline module (0.8309 for the one-diode model without resistances, 0.7464 for the one-diode model with one resistance, 0.7456 for the one-diode model with two resistances and 0.6637 for the two-diode model with two resistances) and for high-efficiency monocrystalline module technology (0.7795 for the one-diode model without resistances, 0.7262 for the one-diode model with one resistance, 0.7256 for the one-diode model with two resistances and 0.6469 for the two-diode model with two resistances). Measurement uncertainty has the same trend as mean values. Polycrystalline technology has the greatest value for the one-diode model without resistances (0.0179) and 0.0158 for the one-diode model with one resistance, 0.0158 for the one-diode model with two resistances and 0.0142 for the two-diode model with two resistances. High-efficiency monocrystalline module technology has the greatest value for the one-diode model without resistances (0.0168) and 0.0153 for the one-diode model with one resistance, 0.0155 for the one-diode model with two resistances and 0.0138 for the two-diode model with two resistances. A conclusion which model better fits FF depends on the chosen PV cell technology and should be based on the measurement uncertainty values. According to the presented numerical results, it can be concluded that all presented module technologies have the smallest uncertainty values for the two-diode model with two resistances.

5. Conclusions

The article presents the FF measurement uncertainty propagation through four basic PV cell models. First, we have presented the expressions for the output currents of all PV cell models in dependence on the global irradiance G and the temperature T. From the short-circuit, open-circuit and load tests, expressions for all FF components are developed, depending on the irradiance G and the temperature T as well. Next, Monte Carlo simulations for calculating the measurement uncertainty of all FF components are performed and the results are used as input quantities for the calculation of FF measurement uncertainty. The results show that the mean value and measurement uncertainty decreases with adding the parasitic resistances to the PV cell model for all presented PV cells. The cause of these results is in the fact that, according to the Kirchhoff’s current law, by adding the parasitic resistances $R_S$ and $R_{SH}$ and additional diode, the current that flows through the added elements increases and output current of the PV cell decreases in total photo-generated current $I_L$.

Calculation of measurement uncertainty provides complete expression of the FF measurement result. This supports the proper validation of FF including measurement uncertainty assessment as an important parameter in decision making on the acceptability of the observed PV system, choosing the model that has an acceptable level of accuracy and uncertainty, but which is at the same time as simple as possible, in order to avoid unnecessary complexity of the model. Presented comparisons between the models shows how particular PV cell model affects the calculation of FF and associated measurement uncertainty. Significant deviations between FF results confirm that the impact of the chosen model is significant when FF is calculated from the model. Which model is to be chosen is a trade-off between model accuracy, uncertainty, and simplicity, and it is up to the metrologist to decide depending on the purpose of the research and corresponding results.