Risk Assessment for the Power Grid Dispatching Process Considering the Impact of Cyber Systems
Abstract
:1. Introduction
2. Transition of the Grid State in the Dispatching Process
2.1. Risk Source
- sRnd: Before the SC is operated, a random grounding fault may occur at lines (such as transmission lines and main transformer branches). Then, the protection of fault lines responds and certain breakers are tripped.
- sOpr: After the SC is operated, the grid transitions as a result of the transition of the SC state.
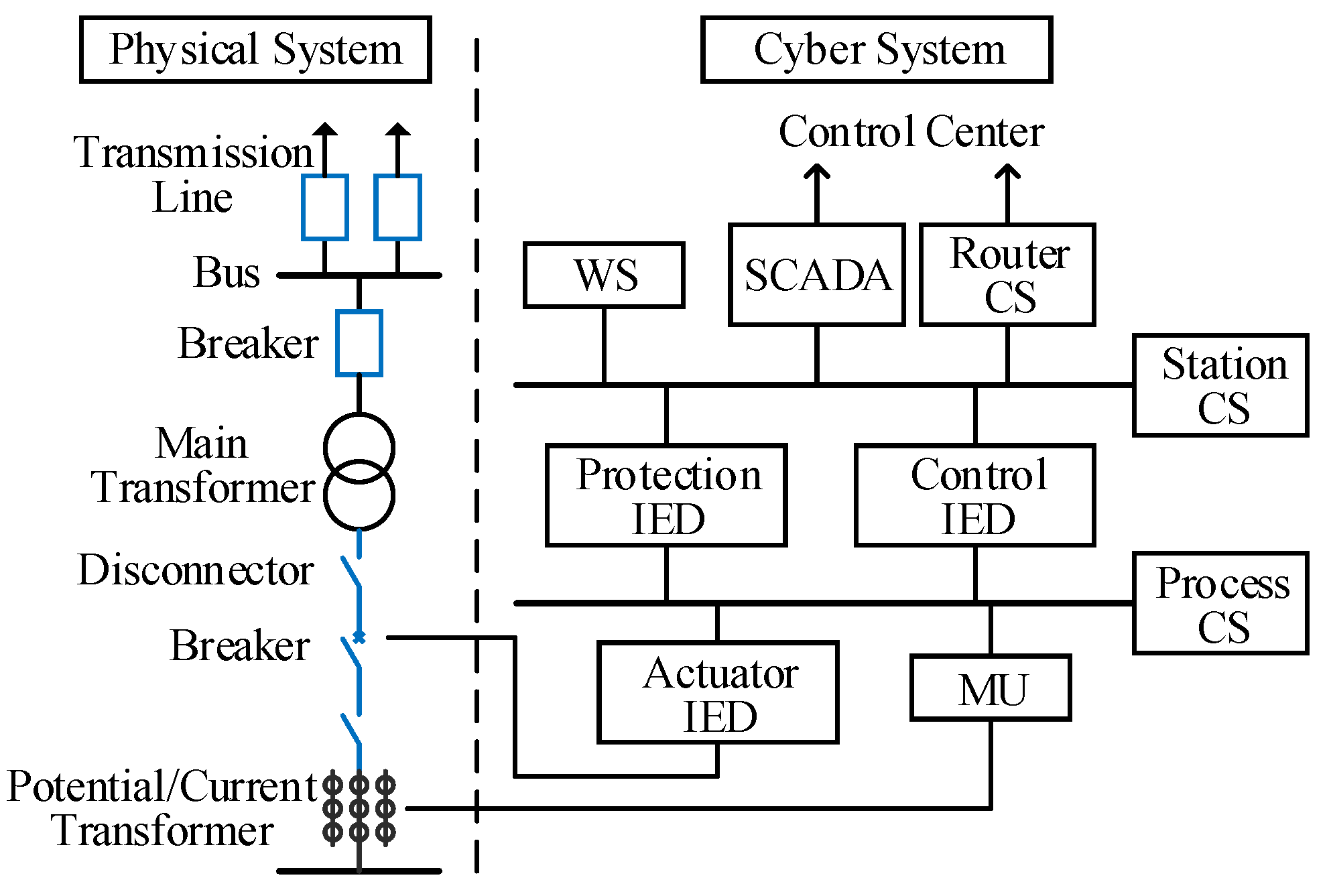
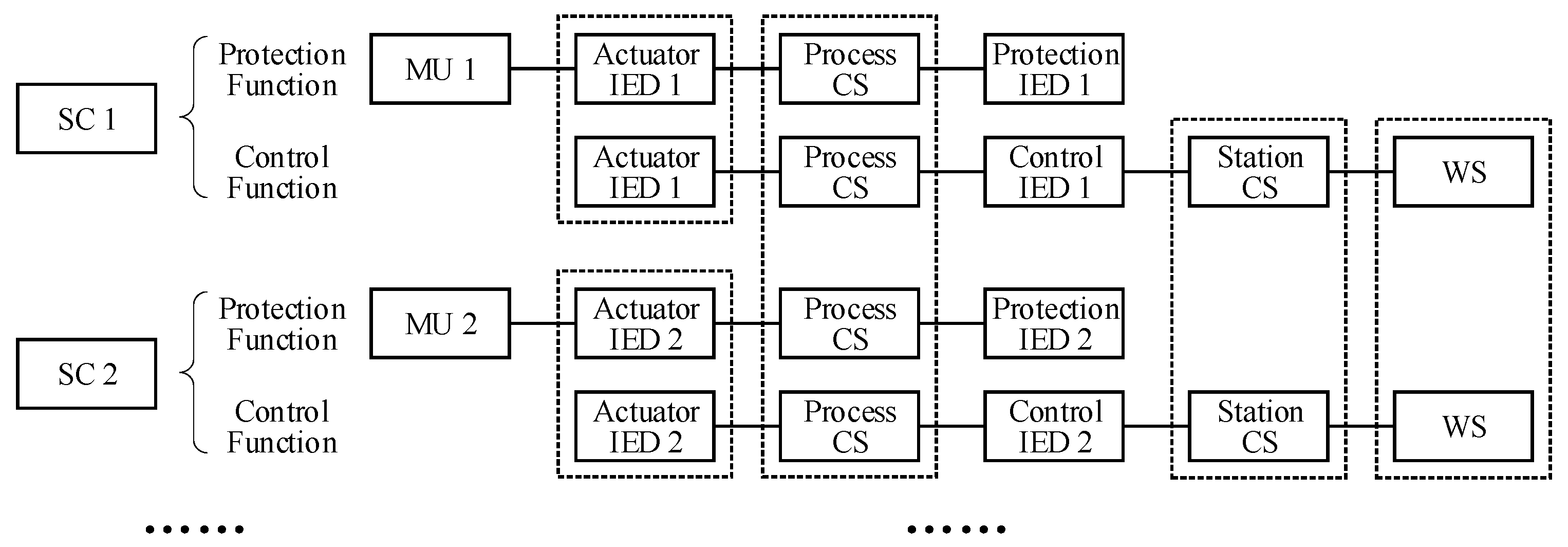
2.2. Dispatching Process in a Cyber-Physical System (CPS)
- Control function: A control signal issued by the dispatcher is transmitted by WSs, CLs, CSs, and IEDs to operate the SC.
- Protection function: A control signal issued by relay protection devices is transmitted by MUs, CLs, CSs and IEDs, to the SC. First, the electrical measurements collected by MUs are calculated and analyzed in a protection IED. Then, the protection IED issues a signal to operate the SC.
2.3. The Transition of sOpr
- Normal: The state of the SC transits as expected.
- Malfunction: The state of the SC is not transited.
- Fault: The state of the SC transits unexpectedly, which causes a grounding fault at the bus connected to this SC.
- Line I-II and bus II will be disconnected from the grid if both the protection functions of line I-II and bus II are normal, which results in the tripping of breakers B, E, and F.
- Line I-II and bus I and II will be disconnected if the protection function of line I-II fails, which results in the tripping of breakers A, C, E, and F.
- Line I-II, II-III, and bus II will be disconnected if the protection function of bus II fails, which results in the tripping of breakers B and G.
2.4. The Transition of sRnd
- A line will be disconnected if its protection function is normal, which results in the tripping of the breakers connected to this line.
- A line and adjacent buses will be disconnected if the protection function of this line fails, which results in the tripping of the breakers connected to these buses.
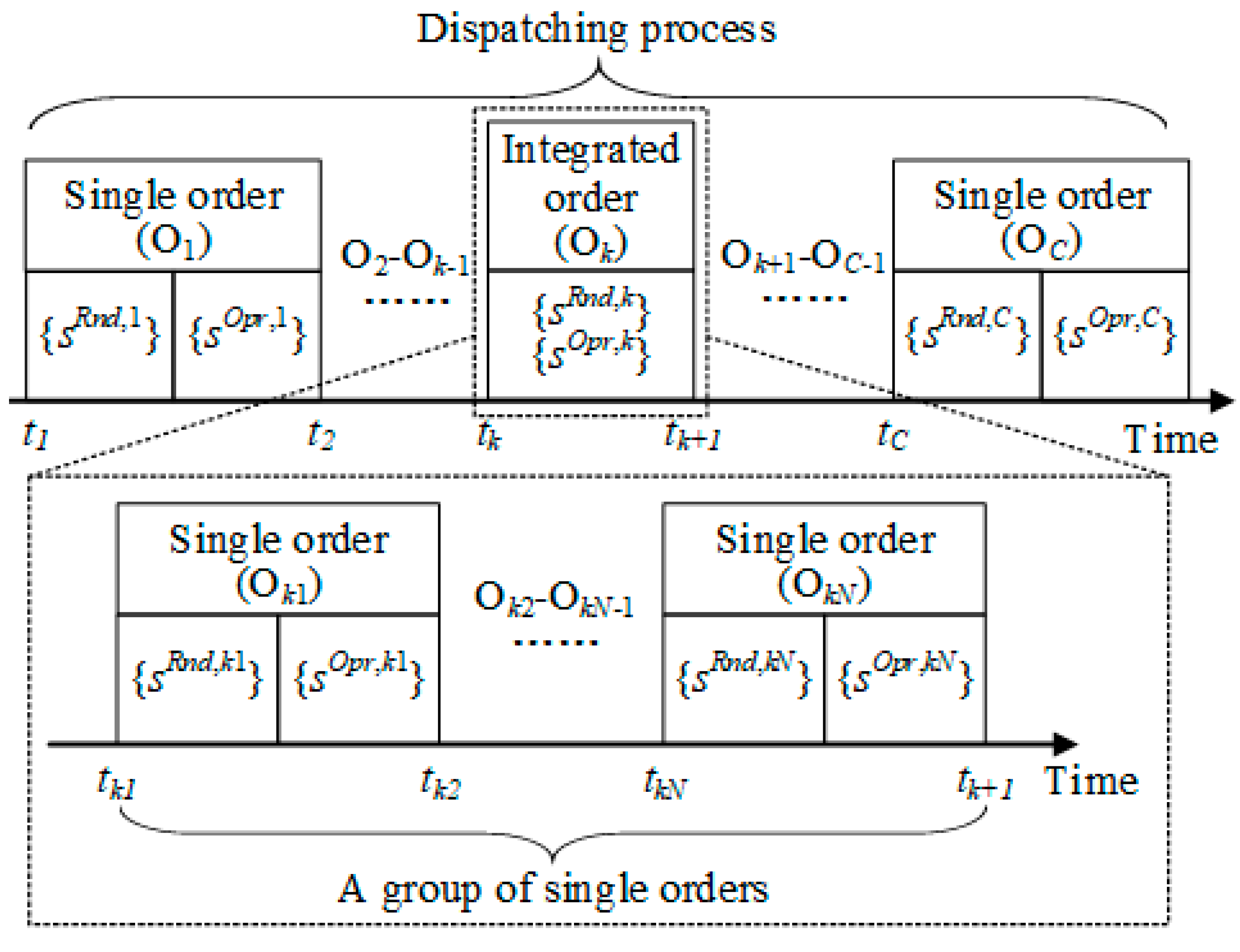
2.5. The Transitions of Grid states in the Dispatching Process
3. Risk Assessment Model
3.1. Risk Probability
3.1.1. The Probability of sOpr
3.1.2. The Probability of sRnd
3.2. Risk Consequence
- Load loss at buses, which are disconnected to the grid after the breakers trip, resulting from the protection of fault buses or lines. It is represented by IGrd and calculated by (16).
- Load shedding at buses, resulting from the operation constraints of the power system. It is represented by IShd and calculated by (17)–(29), which are given as the optimal power flow models.
3.3. Risk Calculation
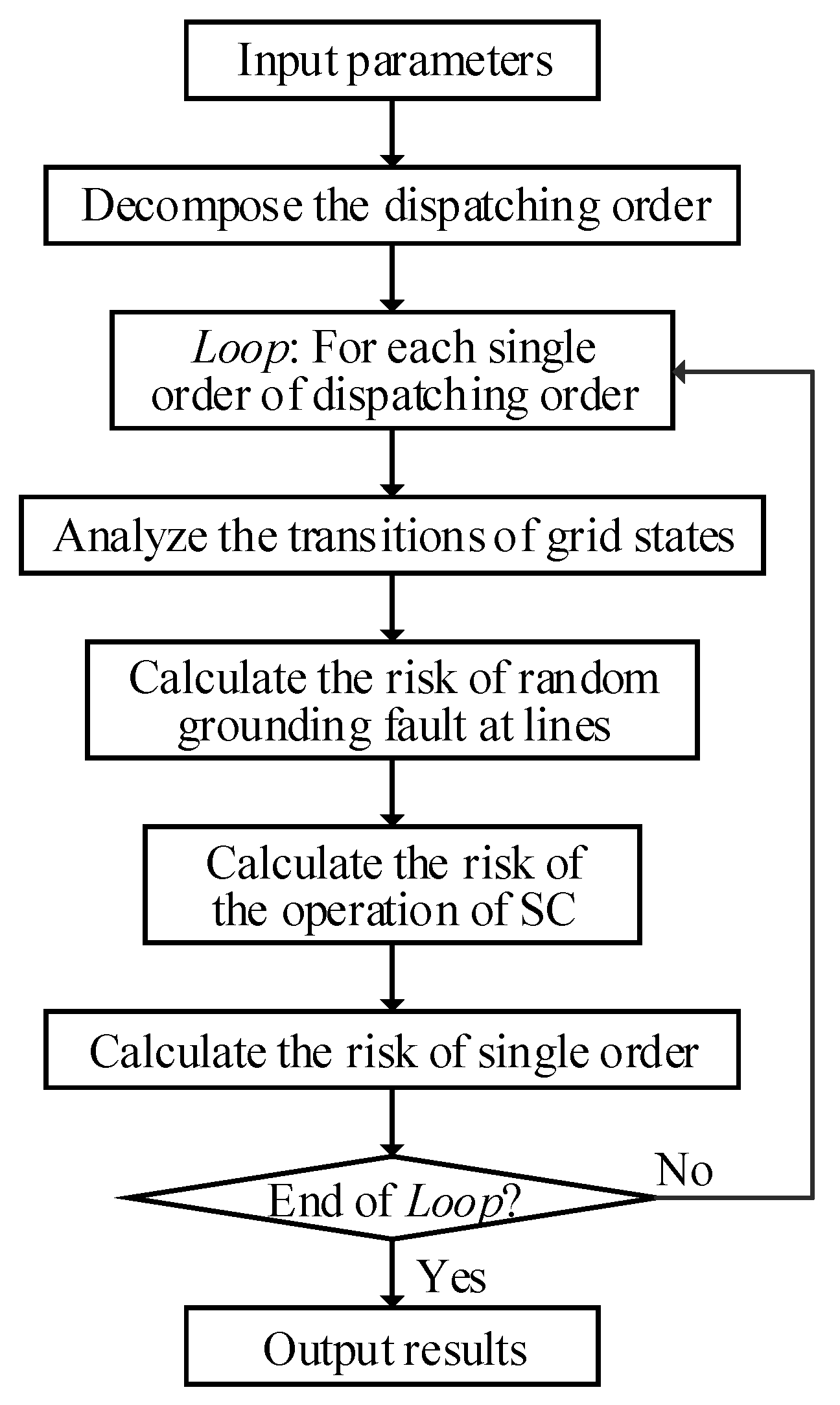
3.4. Risk Assessment Process
- Input parameters including dispatching order, the reliability of components, and grid parameters, etc.
- Decompose the dispatching order into a group of single orders.
- Analyze the transitions of sOpr and sRnd for each single order.
- Calculate RRnd. First, generate grid states by setting grounding fault at lines and using N-1 criterion. Then, calculate risk probabilities of and by (9)–(14) according to the reliability of components and grid parameters. Finally, calculate risk consequences of such grid states by (15)–(29).
- Calculate ROpr. Calculate the risk probabilities and consequences of , , , and by (3)–(8) and (15)–(29) respectively.
- Calculate the risk R of single orders by (30)–(32).
- If all single orders of the dispatching order are analyzed, the algorithm ends; otherwise, go to Step 3.
4. Numerical Results
4.1. Parameters and Computational Platforms
4.2. Simulation Results
4.3. Cyber System Impacts on Risk Results
- In CPS, both physical system and cyber system are considered.
- In PS, only physical system is considered.
4.3.1. Risk Value
4.3.2. Risk Consequence
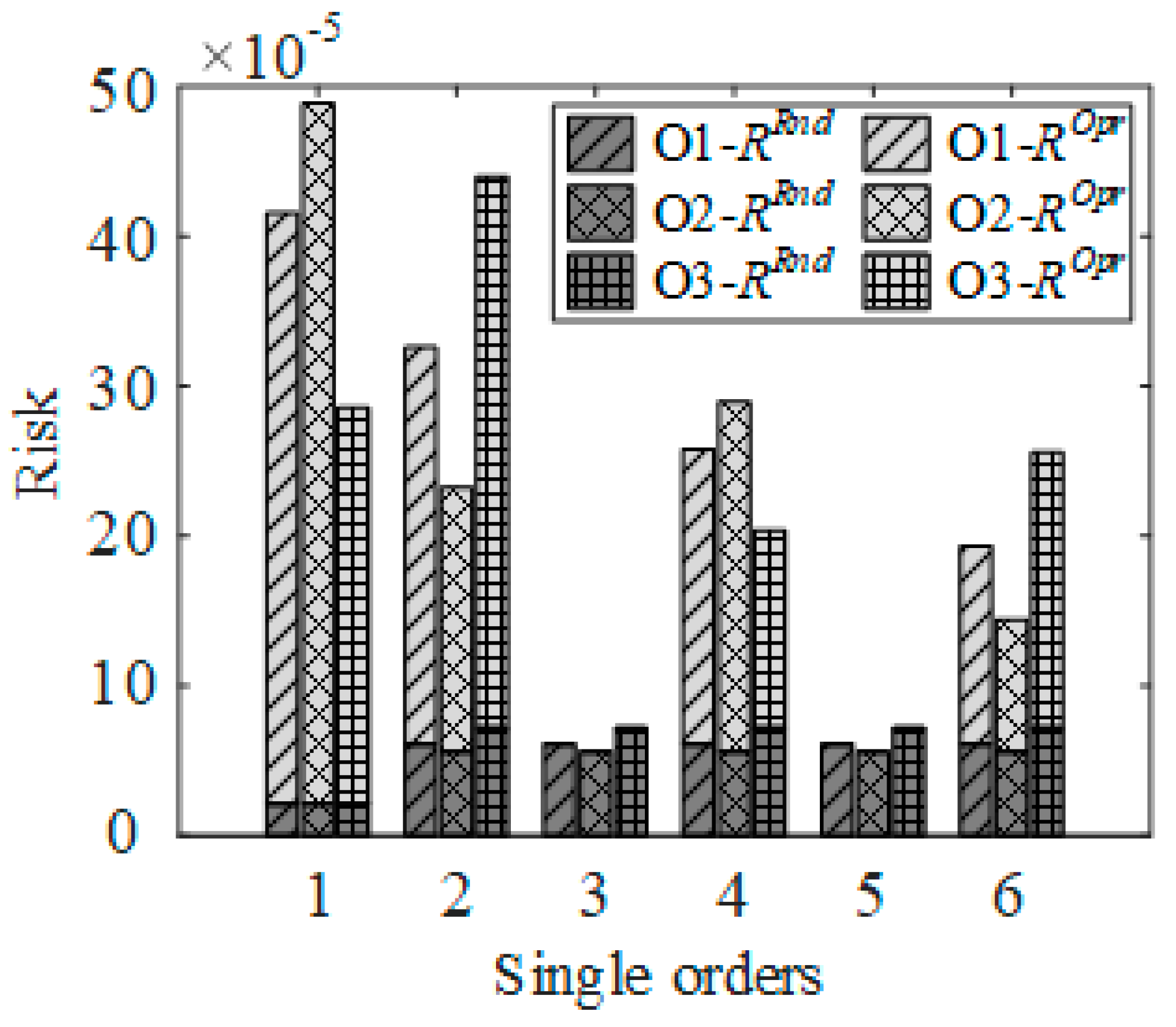
4.4. Risk Results of Different Dispatching Orders
4.4.1. Dispatching Orders for Different Components
- ‘Transit the state of line 14–16 from operation to overhaul’.
- ‘Transit the state of transformer 10–12 from operation to overhaul’.
- ‘Transit the state of line 16–19 from operation to overhaul’.
4.4.2. Different Types of Dispatching Orders
4.5. Assessment Results of Dispatching Process Risk and Power Grid Operation Risk
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| The breaker at the other end of the same line in which breaker n is at. | |
| The event under the condition that some other events have occurred. | |
| CPS | Cyber-Physical System |
| CL | Communication Line |
| CS | Communication Switch |
| IED | Intelligent Electronic Device |
| MU | Merging Unit |
| PS | Physical System |
| SC | Switchgear Component. |
| WS | Workstation Server. |
| Sets and Indices | |
| Set of buses, index i | |
| Set of buses that disconnect from the grid after the breakers trip, index h | |
| Set of lines, indices (i, j). | |
| Set of breakers, index n | |
| Set of breakers that need to trip when the operating SC is in fault, index a. | |
| Set of breakers that need to trip when line (i, j) is in fault, index b. | |
| Set of grid states when the operating SC is in fault and the protection is in failure, index u | |
| Set of grid states when line (i, j) is in fault and the protection is in failure, index v | |
| Parameters and Constants | |
| Normal probability of WS, CL, CS, IED, and MU, respectively | |
| Normal, malfunction, and fault probability of the operating SC, respectively | |
| Fault probability of line (i, j) | |
| , | Conductance and susceptance for line (i, j), respectively |
| , | Minimum and maximum active power (MW) limit of generation at bus i, respectively |
| , | Minimum and maximum reactive power (MVar) limit of generation at bus i, respectively |
| , | Minimum and maximum voltage magnitude (p.u.) at bus i, respectively. |
| Maximum capacity (MVA) limit for line (i, j) | |
| , | Active and reactive power of load at bus i, respectively. |
| Variables | |
| , | Voltage magnitude and angle at bus i, respectively |
| , | Active and reactive power of generation at bus i, respectively |
| , | Active and reactive power of load shedding at bus i, respectively |
| , | Active and reactive power flow for line (i, j), respectively |
| Risk value of a single order in the dispatching process | |
| Risk value of the operation of the SC | |
| Risk value of random grounding fault occurrence at lines | |
| Probability of grid states or events. | |
| Risk consequence of grid states | |
| Risk consequence of load loss from disconnecting the bus | |
| Risk consequence of load shedding from operation constraints of the power system. | |
| Events and Grid states | |
| Event that control function at the operating SC is available | |
| Event that the protection function at the nth breaker is available | |
| Grid state | |
| Grid state after SC is operated in the dispatching process | |
| Grid state before SC is operated in the dispatching process | |
| Grid state if SC is operated normally | |
| Grid state if SC does not respond | |
| Grid state if SC is in fault and the protection function is normal | |
| Grid state if SC is in fault and the protection function fails | |
| Grid state after a random grounding fault occurs at line, before the SC is operated | |
| Grid state when the protection of line (i, j) is in normal after line (i, j) is in fault | |
| Grid state when the protection of line (i, j) is in failure after line (i, j) is in fault | |
References
- Amin, S.M.; Wollenberg, B.F. Toward a smart grid: Power delivery for the 21st century. IEEE Power Energy Mag. 2005, 3, 34–41. [Google Scholar] [CrossRef]
- Zhang, P.; Li, F.; Bhatt, N. Next-Generation Monitoring, Analysis, and Control for the Future Smart Control Center. IEEE Trans. Smart Grid 2010, 1, 186–192. [Google Scholar] [CrossRef]
- Xin, S.; Guo, Q.; Sun, H.; Zhang, B.; Wang, J.; Chen, C. Cyber-Physical Modeling and Cyber-Contingency Assessment of Hierarchical Control Systems. IEEE Trans. Smart Grid 2015, 6, 2375–2385. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Y.; Li, Y.; Cao, Y.; Zeng, X. Reliability Analysis of Cyber–Physical Systems: Case of the Substation Based on the IEC 61850 Standard in China. Energies 2018, 11, 2589. [Google Scholar] [CrossRef]
- Li, J.S.; Zhou, H.W.; Meng, J.; Yang, Q.; Chen, B.; Zhang, Y.Y. Carbon emissions and their drivers for a typical urban economy from multiple perspectives: A case analysis for Beijing city. Appl. Energy 2018, 226, 1076–1086. [Google Scholar] [CrossRef]
- Andersson, G.; Donalek, P.; Farmer, R.; Hatziargyriou, N.; Kamwa, I.; Kundur, P.; Martins, N.; Paserba, J.; Pourbeik, P.; Sanchez-Gasca, J.; et al. Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 2005, 20, 1922–1928. [Google Scholar] [CrossRef]
- Lin, W.; Tang, Y.; Sun, H.; Guo, Q.; Zhao, H.; Zeng, B. Blackout in Brazil Power Grid on February 4, 2011 and Inspirations for Stable Operation of Power Grid. Autom. Electr. Power Syst. 2011, 35, 1–5. [Google Scholar]
- Lai, L.-L.; Zhang, H.-T.; Mishra, S.; Ramasubramanian, D.; Lai, C.-S.; Xu, F.-Y. Lessons learned from July 2012 Indian blackout. In Proceedings of the 9th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2012), Hong Kong, China, 18–21 November 2012; pp. 1–6. [Google Scholar]
- Liang, G.; Weller, S.-R.; Zhao, J.; Luo, F.; Dong, Z.-Y. The 2015 Ukraine blackout: Implications for false data injection attacks. IEEE Trans. Power Syst. 2017, 32, 3317–3318. [Google Scholar] [CrossRef]
- Lin, W.-M.; Yang, C.-Y.; Tu, C.-S.; Tsai, M.-T. An Optimal Scheduling Dispatch of a Microgrid under Risk Assessment. Energies 2018, 11, 1423. [Google Scholar] [CrossRef]
- Lyu, Z.; Wei, Q.; Zhang, Y.; Zhao, J.; Manla, E. Adaptive Virtual Impedance Droop Control Based on Consensus Control of Reactive Current. Energies 2018, 11, 1801. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Yin, X.; Han, J.; Wang, Y.; Chen, G. A Load-Shedding Model Based on Sensitivity Analysis in on-Line Power System Operation Risk Assessment. Energies 2018, 11, 727. [Google Scholar] [CrossRef]
- Negnevitsky, M.; Nguyen, D.H.; Piekutowski, M. Risk Assessment for Power System Operation Planning With High Wind Power Penetration. IEEE Trans. Power Syst. 2015, 30, 1359–1368. [Google Scholar] [CrossRef]
- Wang, Q.; McCalley, J.-D. Risk and “N-1” Criteria Coordination for Real-Time Operations. IEEE Trans. Power Syst. 2013, 28, 3505–3506. [Google Scholar] [CrossRef]
- Chen, S.; Onwuachumba, A.; Musavi, M.; Lerley, P. A Quantification Index for Power Systems Transient Stability. Energies 2017, 10, 984. [Google Scholar] [CrossRef]
- Huang, D.; Chen, Q.; Ma, S.; Zhang, Y.; Chen, S. Wide-Area Measurement—Based Model-Free Approach for Online Power System Transient Stability Assessment. Energies 2018, 11, 958. [Google Scholar] [CrossRef]
- Ren, C.; Xu, Y.; Zhang, Y. Post-disturbance transient stability assessment of power systems towards optimal accuracy-speed tradeoff. Prot. Control Mod. Power Syst. 2018, 3, 194–203. [Google Scholar] [CrossRef]
- Žarković, M.; Stojković, Z. Artificial intelligence based thermographic approach for high voltage substations risk assessment. IET Gener. Transm. Distrib. 2015, 9, 1935–1945. [Google Scholar] [CrossRef]
- Hamoud, G.; Toneguzzo, J.; Yung, C.; Wong, A. Methodology for Assessing Safety Risk From Failure of Transmission Station Equipment. IEEE Trans. Power Deliv. 2007, 22, 1972–1978. [Google Scholar] [CrossRef]
- Li, W.; Lu, J. Risk Evaluation of Combinative Transmission Network and Substation Configurations and its Application in Substation Planning. IEEE Trans. Power Syst. 2005, 20, 1144–1150. [Google Scholar] [CrossRef]
- Liu, J.; Chao, Z.; Zhong, H.; Hu, S.; Jia, H. The Risk Assessment Method for the Dispatching Operation Based on Generalized Sections. Trans. China Electrotech. Soc. 2016, 3, 155–163. [Google Scholar]
- Luo, W.; Xie, M.; Liu, M.; Liu, J.; Hu, S. Modeling and application of power grid dispatching operation risk consequences. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–6. [Google Scholar]
- Lu, D.; Hou, K.; Zeng, Y.; Wei, W.; Guo, L. A risk assessment approach for dispatching operations based on critical equipment search. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Liu, J.; Hu, S.; Chen, D.; Li, B. A dispatching operation risk assessment method based on real-time probabilistic model. In Proceedings of the 2013 IEEE International Conference of IEEE Region 10 (TENCON 2013), Xi’an, China, 22–25 October 2013; pp. 1–4. [Google Scholar]
- Xie, M.; Yin, Y.; Lu, E.; Hu, S. Study on Human Factor Risk Quantification and Evaluation Model in Power Grid Dispatching Risk Assessment. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–5. [Google Scholar]
- Ashok, A.; Govindarasu, M.; Wang, J. Cyber-Physical Attack-Resilient Wide-Area Monitoring, Protection, and Control for the Power Grid. Proc. IEEE 2017, 105, 1389–1407. [Google Scholar] [CrossRef]
- Liu, X.; Shahidehpour, M.; Li, Z.; Liu, X.; Cao, Y.; Li, Z. Power System Risk Assessment in Cyber Attacks Considering the Role of Protection Systems. IEEE Trans. Smart Grid 2017, 8, 572–580. [Google Scholar] [CrossRef]
- Vellaithurai, C.; Srivastava, A.; Zonouz, S.; BerthierM, R. CPINDEX: Cyber-Physical Vulnerability Assessment for Power-Grid Infrastructures. IEEE Trans. Smart Grid 2015, 6, 566–575. [Google Scholar] [CrossRef]
- Gao, H.; Dai, Z.; Peng, Y.; Lu, H. Cyber Security Risk Assessment of Communication Network of Substation Based on Improved Grey Clustering. In Proceedings of the 2014 Tenth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kitakyushu, Japan, 27–29 August 2014; pp. 524–527. [Google Scholar]
- Taylor, C.; Oman, P.; Krings, A. Assessing Power Substation Network Security and Survivability: A Work in Progress Report. In Proceedings of the International Conference on Security and Management, SAM’03, Las Vegas, NV, USA, 23–26 June 2003; pp. 1–7. [Google Scholar]
- Falahati, B.; Fu, Y. A study on interdependencies of cyber-power networks in smart grid applications. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–8. [Google Scholar]
- Falahati, B.; Fu, Y.; Wu, L. Reliability assessment of smart grid considering direct cyber-power interdependencies. IEEE Trans. Smart Grid 2012, 3, 1515–1524. [Google Scholar] [CrossRef]
- Falahati, B.; Fu, Y. Reliability assessment of smart grids considering indirect cyber-power interdependencies. IEEE Trans. Smart Grid 2014, 5, 1677–1685. [Google Scholar] [CrossRef]
- Lei, H.; Singh, C.; Sprintson, A. Reliability Modeling and Analysis of IEC 61850 Based Substation Protection Systems. IEEE Trans. Smart Grid 2014, 5, 2194–2202. [Google Scholar] [CrossRef]
- Lei, H.; Singh, C. Non-Sequential Monte Carlo Simulation for Cyber-Induced Dependent Failures in Composite Power System Reliability Evaluation. IEEE Trans. Power Syst. 2017, 32, 1064–1072. [Google Scholar]
- Liu, Y.; Lu, D.; Deng, L.; Bai, T.; Hou, K.; Zeng, Y. Risk assessment for the cascading failure of electric cyber-physical system considering multiple information factors. IET Cyber-Phys. Syst. Theory Appl. 2017, 2, 155–160. [Google Scholar] [CrossRef]
- Li, M. Risk Analysis of Differential Protection Caused by the Communication Delay and Error; Nanjing University of Posts and Telecommunications: Nanjing, China, 2015. [Google Scholar]
- Zhao, D.; Sun, Y. A preliminarily analysis of characteristics of code error and time delay of protective relaying signals transmitted by SDH optical fiber communication system. Power Syst. Technol. 2002, 26, 66–70. [Google Scholar]
- Huang, J.; Ge, S.; Han, J.; Li, H.; Zhou, X.; Liu, H.; Wang, B.; Chen, Z. A diagnostic method for distribution networks based on power supply safety standards. Prot. Control Mod. Power Syst. 2016, 1, 63–70. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, H.; Zhang, Y.; Li, X.; Fang, J.; Liu, Y.; Liao, C.; Li, Y.; Zhao, J. Dissolved Gases Forecasting Based on Wavelet Least Squares Support Vector Regression and Imperialist Competition Algorithm for Assessing Incipient Faults of Transformer Polymer Insulation. Polymers 2019, 11, 85. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, H.; Liu, J. An Anomaly Identification Model for Wind Turbine State Parameters. J. Clean. Prod. 2018, 195, 1214–1227. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Zheng, H.; Zhang, Y.; Zhang, C.; Lai, B.; Wang, J.; Ren, G.; Zhang, E. Aging condition assessment of transformer oil-immersed cellulosic insulation based upon the average activation energy method. Cellulose 2019. [Google Scholar] [CrossRef]
- Subcommittee, P.-M. IEEE Reliability Test System. IEEE Trans. Power Appar. Syst. 1979, 98, 2047–2054. [Google Scholar] [CrossRef]


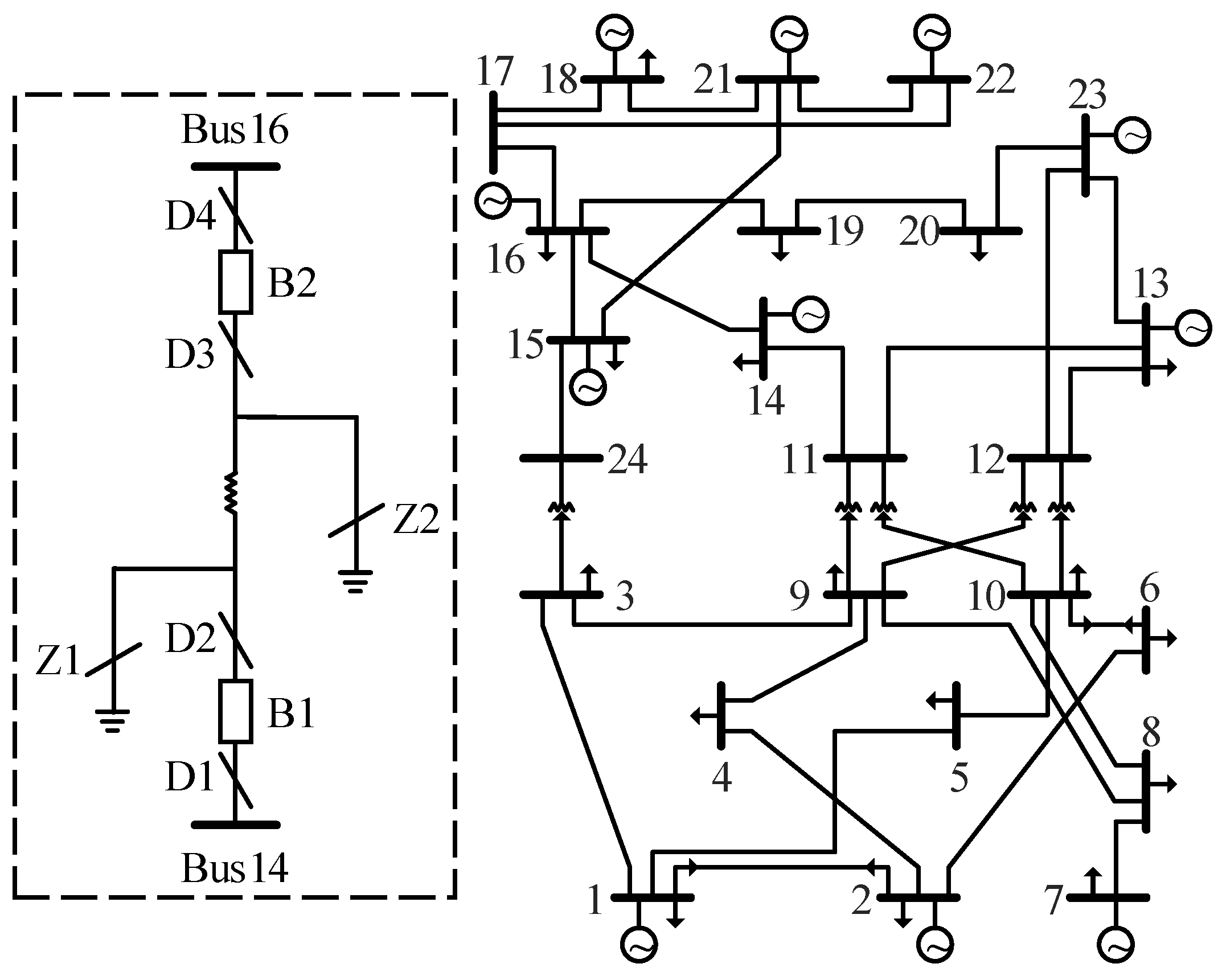


| Single Order | Operation | Switchgear Component | Operating Time |
|---|---|---|---|
| 1 | tripping | B1 | 6 min |
| 2 | tripping | B2 | 6 min |
| 3 | tripping | D2 | 6 min |
| 4 | tripping | D1 | 6 min |
| 5 | tripping | D3 | 6 min |
| 6 | tripping | D4 | 6 min |
| Cyber Component | MTTF/Year | /Year | Failure Probability |
|---|---|---|---|
| WS | 14.27 | 0.07 | 0.011612 |
| CS | 50 | 0.02 | 0.003328 |
| IED | 19.18 | 0.052 | 0.008653 |
| MU | 19.18 | 0.052 | 0.008653 |
| CL | 1341.32 | 0.000746 | 0.000124 |
| Switchgear Component | Normal | Malfunction | Fault |
| Breaker | 0.99 | 0.0098 | 0.0002 |
| Disconnector | 0.99 | 0.0099 | 0.0001 |
| Single Order | ||||||
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 37.62 | 1.789 | 1.003 | 1.113 |
| 2 | 0 | 0 | 24.71 | 1.789 | 4.53 | 1.555 |
| 3 | 0 | 0 | 0 | 0 | 4.53 | 1.555 |
| 4 | 0 | 0 | 18.81 | 0.894 | 4.53 | 1.555 |
| 5 | 0 | 0 | 0 | 0 | 4.53 | 1.555 |
| 6 | 0 | 0 | 12.355 | 0.894 | 4.53 | 1.555 |
| Single Order | ||||||
|---|---|---|---|---|---|---|
| CPS | PS | CPS | PS | CPS | PS | |
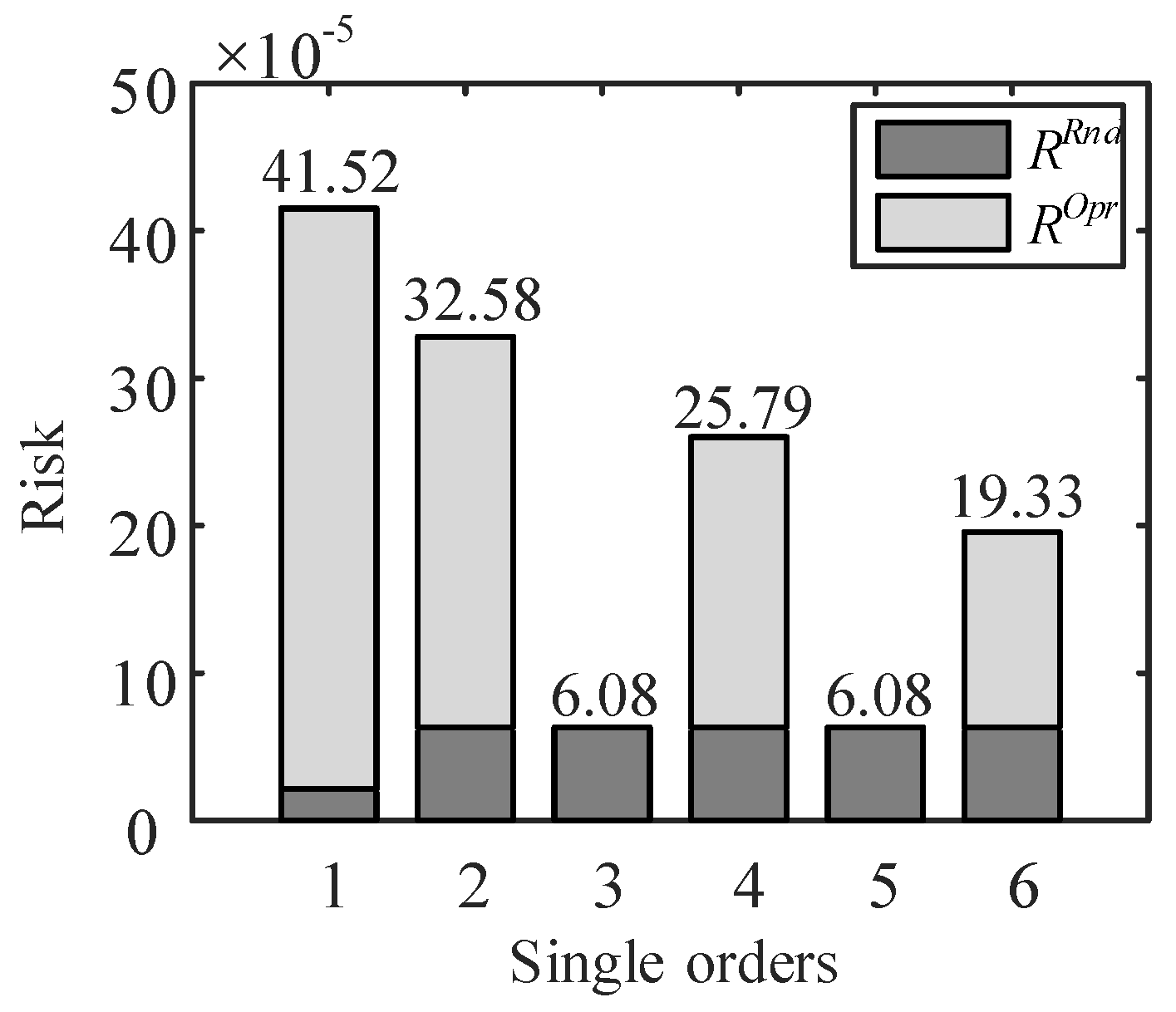
| 1 | 39.408 | 38.8 | 2.116 | 1.411 | 41.524 | 40.211 |
| 2 | 26.498 | 25.484 | 6.084 | 5.234 | 32.582 | 30.718 |
| 3 | 0 | 0 | 6.084 | 5.234 | 6.084 | 5.234 |
| 4 | 19.704 | 19.4 | 6.084 | 5.234 | 25.788 | 24.634 |
| 5 | 0 | 0 | 6.084 | 5.234 | 6.084 | 5.234 |
| 6 | 13.249 | 12.742 | 6.084 | 5.234 | 19.333 | 17.976 |
| Single Order | ||||||
|---|---|---|---|---|---|---|
| CPS | PS | CPS | PS | CPS | PS | |
| 1 | 2.94 | 1.94 | 0.274 | 0 | 3.214 | 1.94 |
| 2 | 2.94 | 1 | 0.274 | 0.274 | 3.214 | 1.274 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 2.94 | 1.94 | 0.274 | 0 | 3.214 | 1.94 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 2.94 | 1 | 0.274 | 0.274 | 3.214 | 1.274 |
| Single Order | Operation | Switchgear Component | Operating Time |
|---|---|---|---|
| 1 | tripping | B4 | 6 min |
| 2 | tripping | D10 | 6 min |
| 3 | tripping | D11 | 6 min |
| 4 | closing | D12 | 6 min |
| 5 | closing | D10 | 6 min |
| 6 | closing | B4 | 6 min |
| Single Order | |||
|---|---|---|---|
| 1 | 70.301 | 2.116 | 72.47 |
| 2 | 0.254 | 3.230 | 3.484 |
| 3 | 35.998 | 3.230 | 39.228 |
| 4 | 11.390 | 3.230 | 14.620 |
| 5 | 0.254 | 3.230 | 3.484 |
| 6 | 22.580 | 3.230 | 25.810 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, H.; Zhang, Y.; Zhao, J.; Manla, E. Risk Assessment for the Power Grid Dispatching Process Considering the Impact of Cyber Systems. Energies 2019, 12, 1084. https://doi.org/10.3390/en12061084
Chen B, Chen H, Zhang Y, Zhao J, Manla E. Risk Assessment for the Power Grid Dispatching Process Considering the Impact of Cyber Systems. Energies. 2019; 12(6):1084. https://doi.org/10.3390/en12061084
Chicago/Turabian StyleChen, Biyun, Haoying Chen, Yiyi Zhang, Junhui Zhao, and Emad Manla. 2019. "Risk Assessment for the Power Grid Dispatching Process Considering the Impact of Cyber Systems" Energies 12, no. 6: 1084. https://doi.org/10.3390/en12061084
APA StyleChen, B., Chen, H., Zhang, Y., Zhao, J., & Manla, E. (2019). Risk Assessment for the Power Grid Dispatching Process Considering the Impact of Cyber Systems. Energies, 12(6), 1084. https://doi.org/10.3390/en12061084








