Thermal Stress and Cyclic Stress Analysis of a Vertical Water-Cooled Wall at a Utility Boiler under Flexible Operation
Abstract
1. Introduction
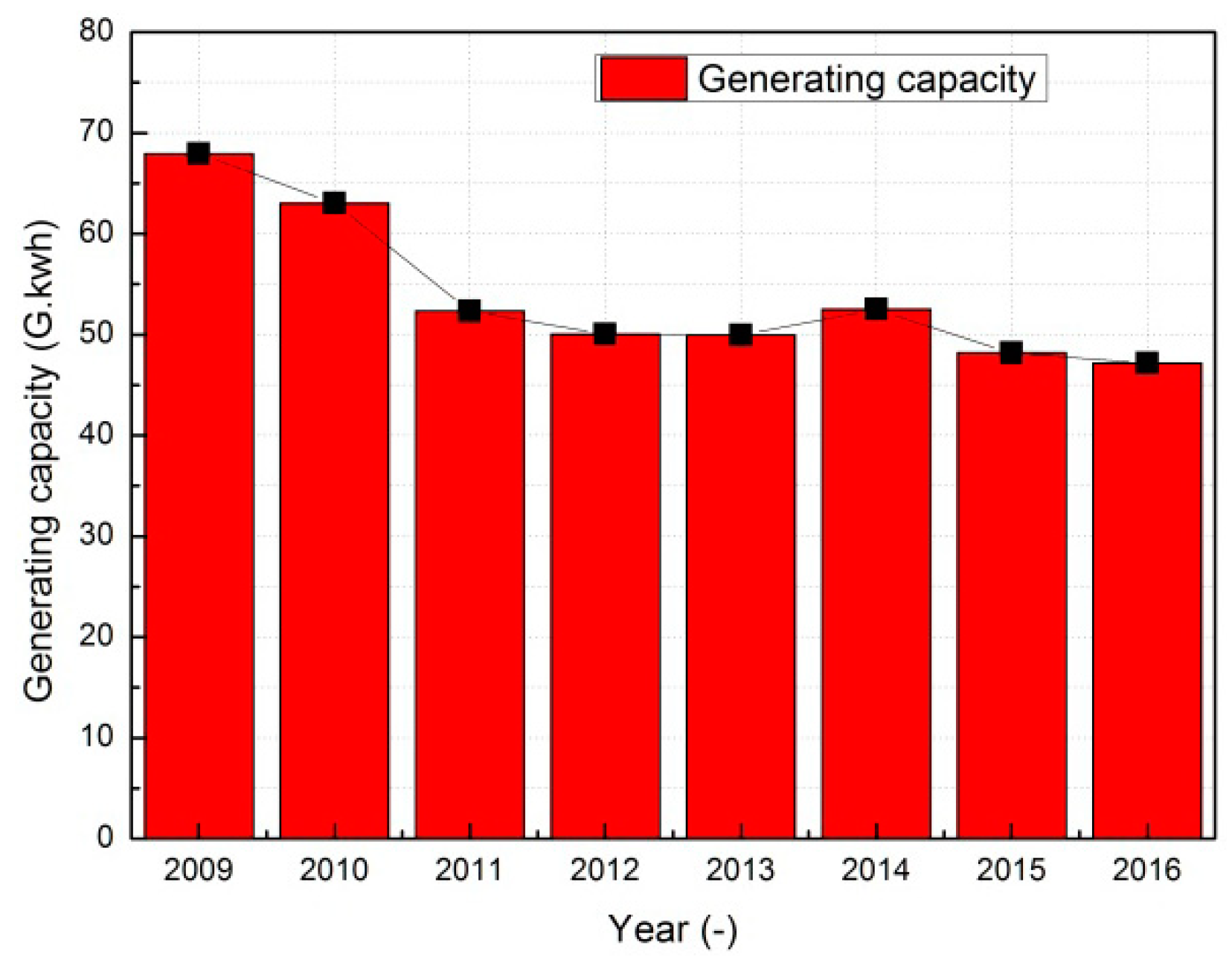
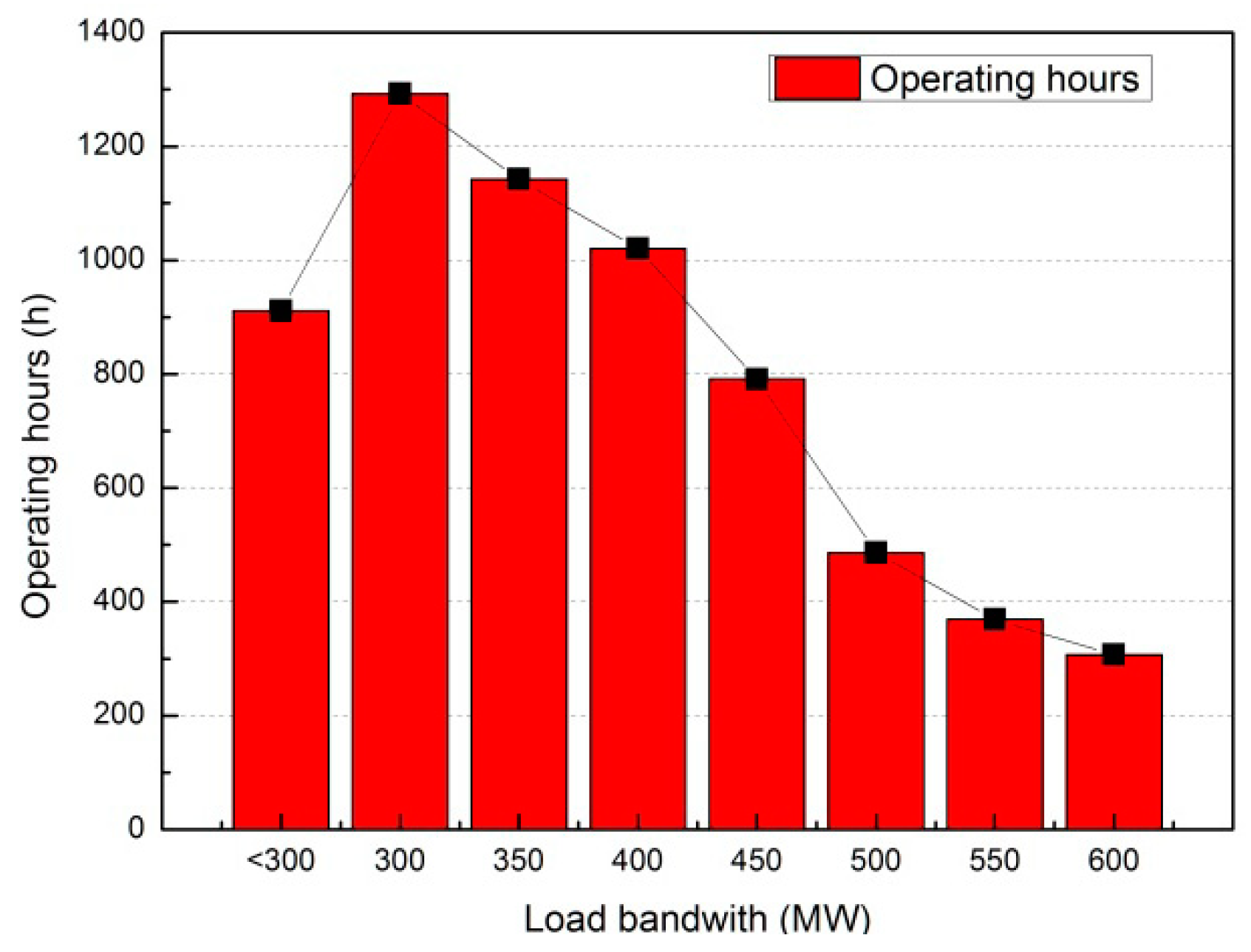
2. Case Study of a Utility Boiler
2.1. Parameters of the Utility Boiler
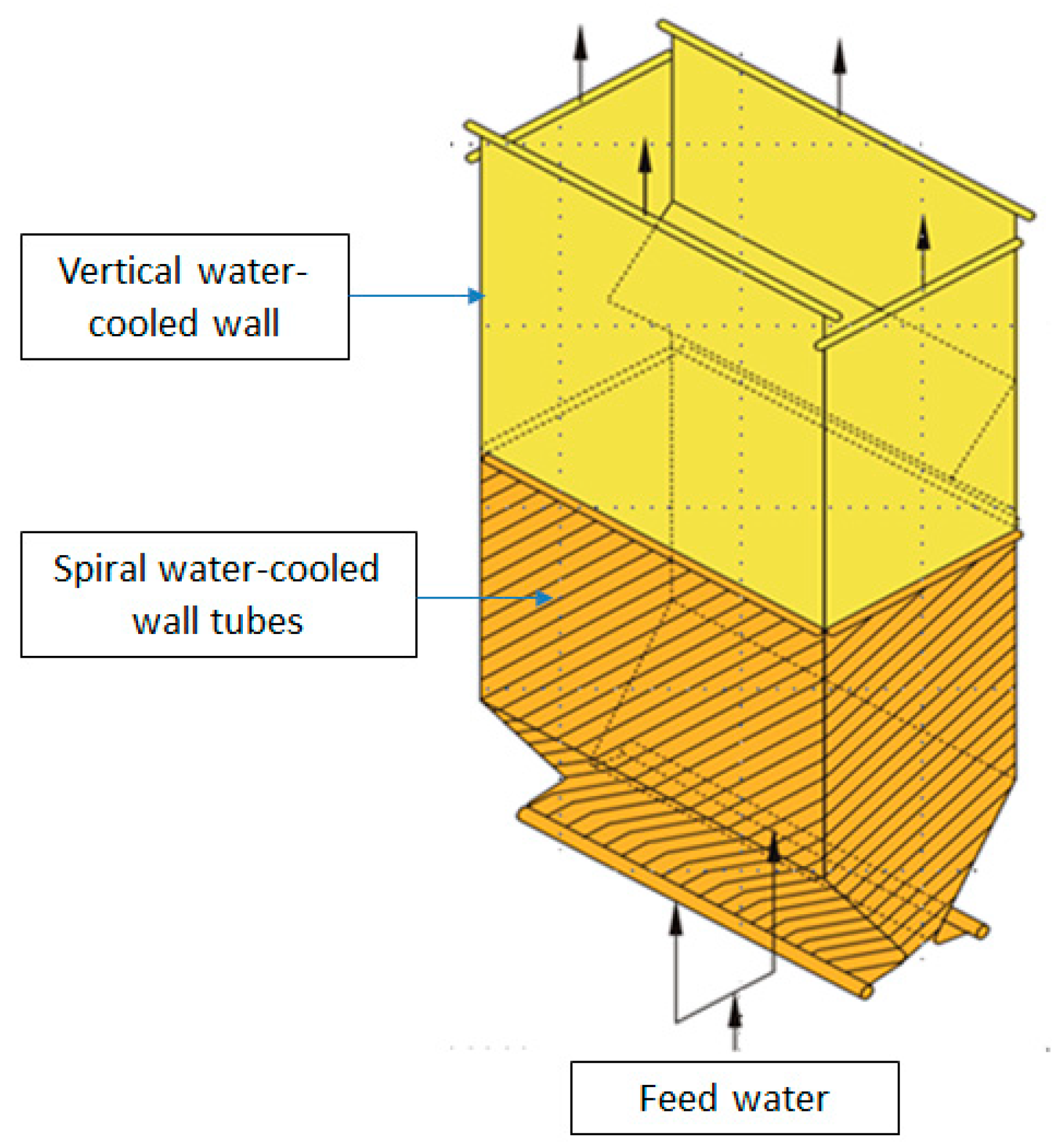
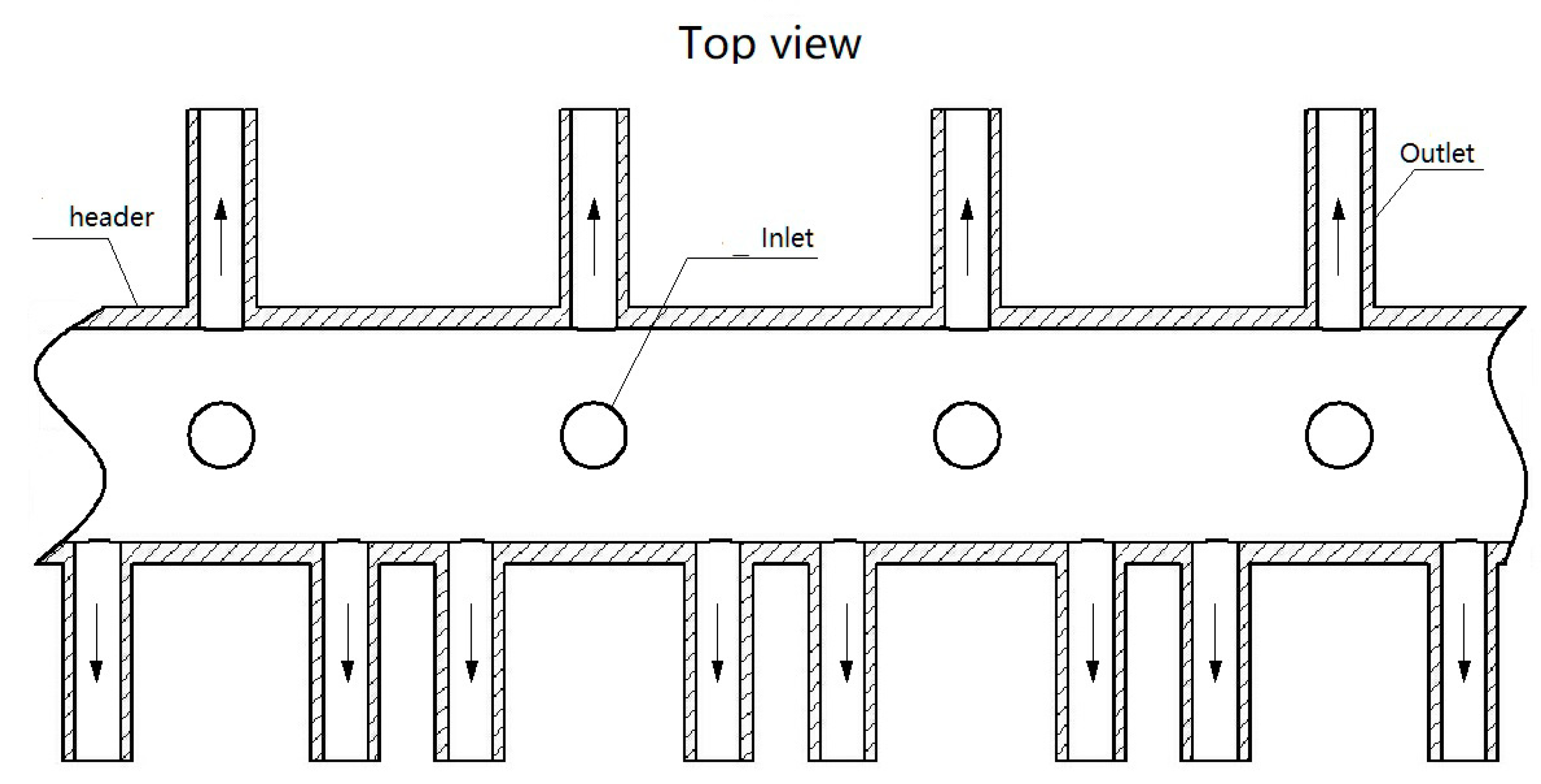
2.2. Water-Cooled Wall Structure of the Utility Boiler
3. Data Reduction
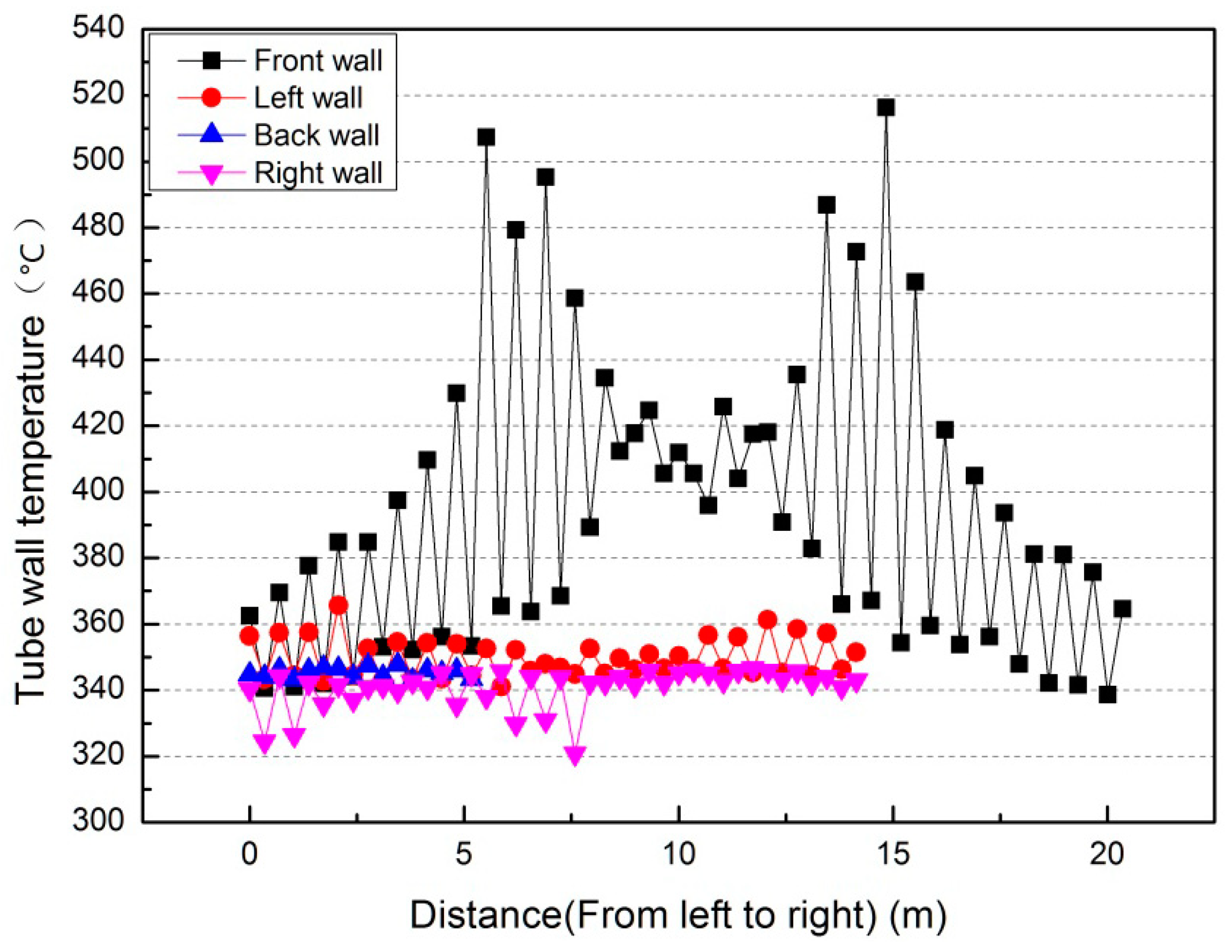
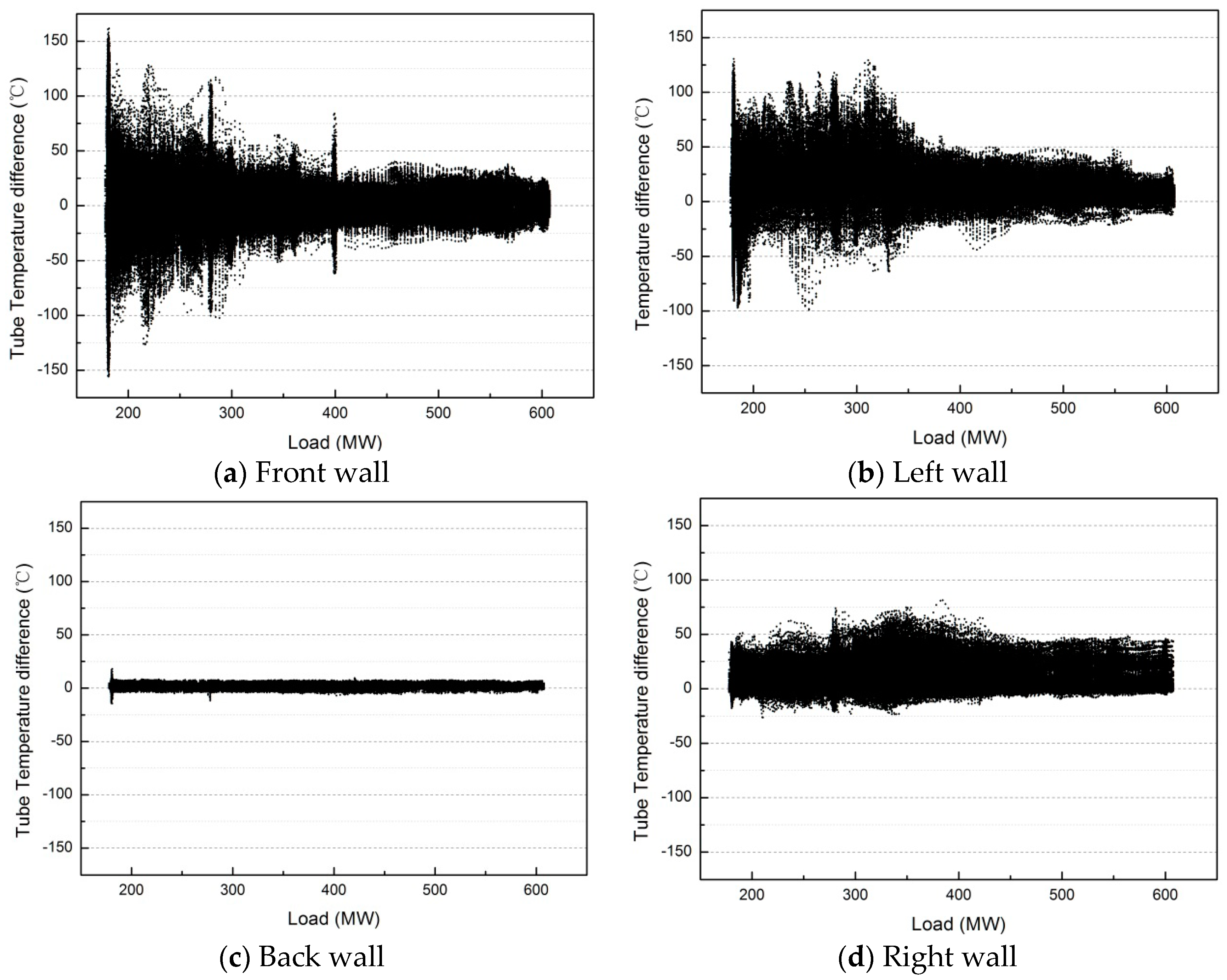
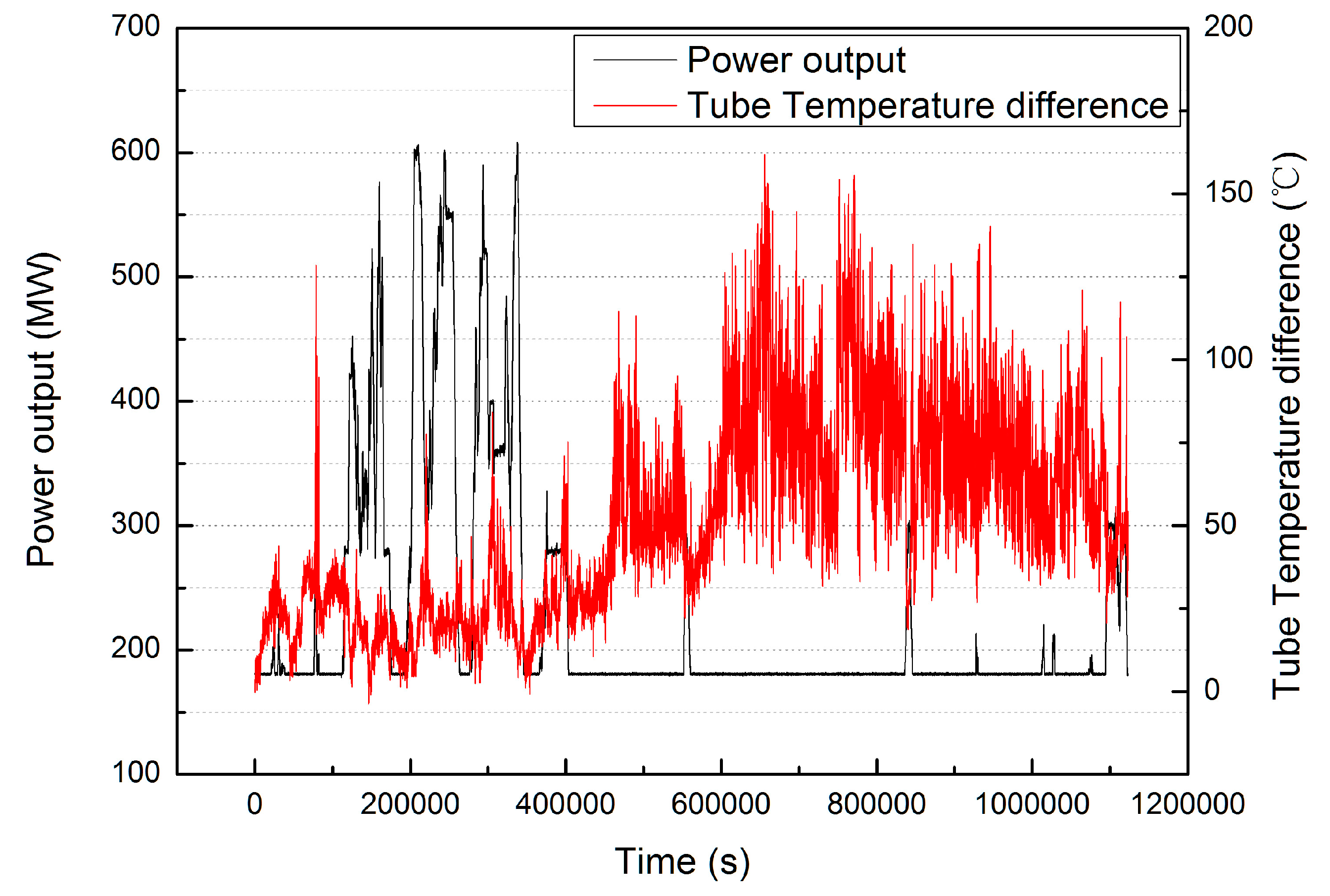
3.1. Water-Cooled Wall Tube Temperature Variation and Temperature-Difference Distribution Analysis
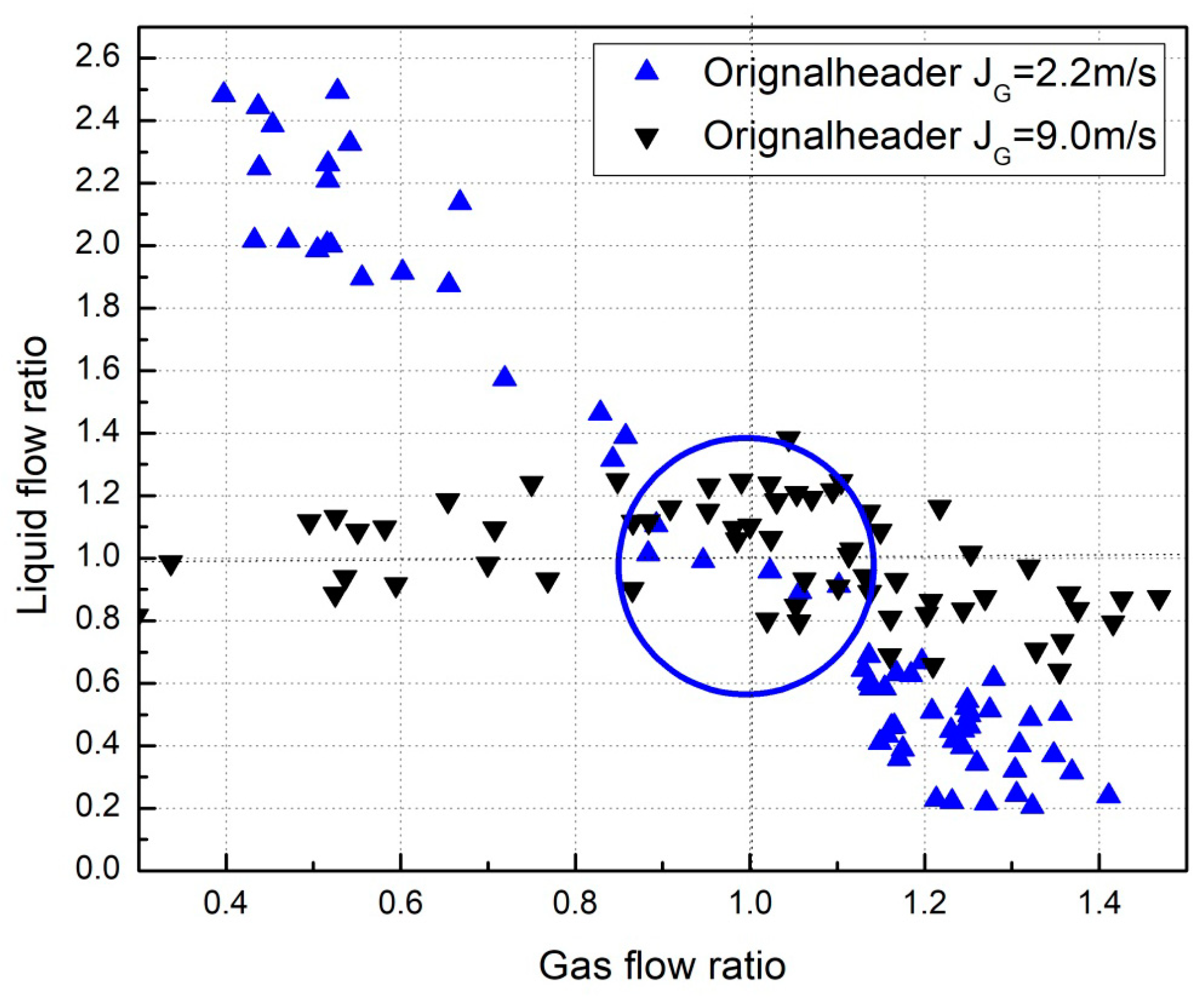
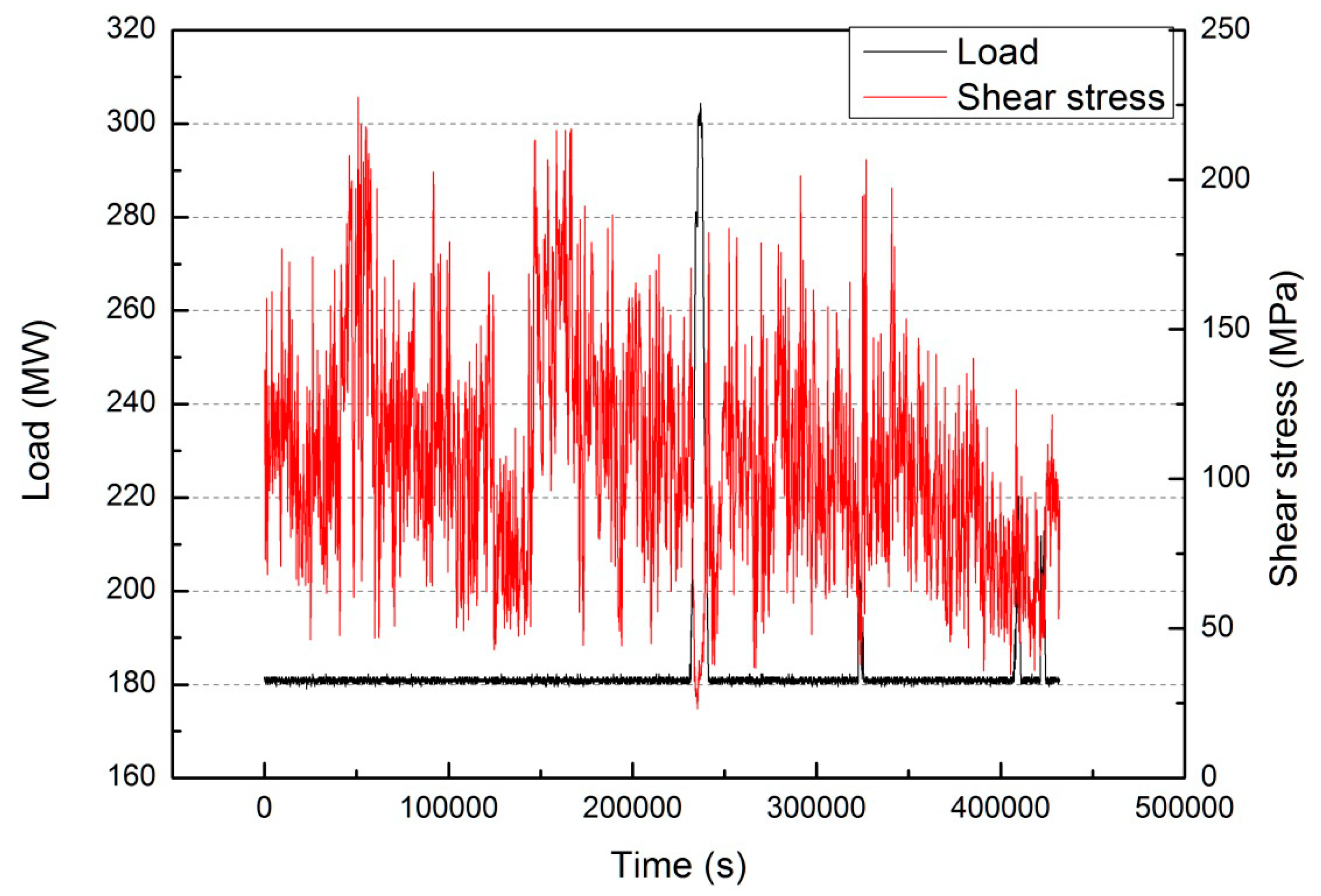
3.2. The Reason for the Temperature Fluctuations at Front and Left Walls under Flexible Operation
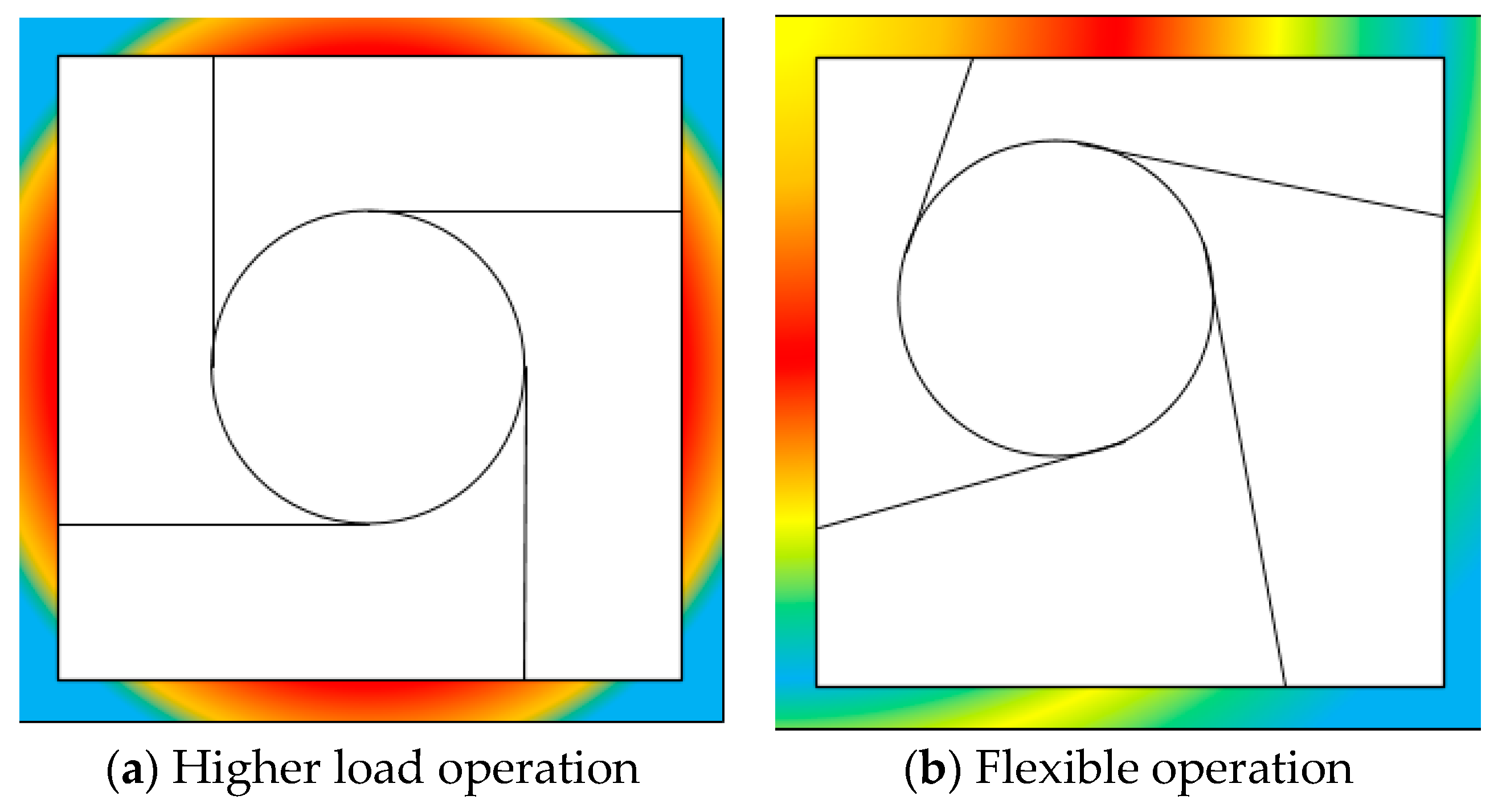
4. Thermal Stress and Cyclic Stress Analyses
4.1. Geometrical Model
4.2. Planar Stress Equation
4.3. Material Properties
4.4. Boundary Condition
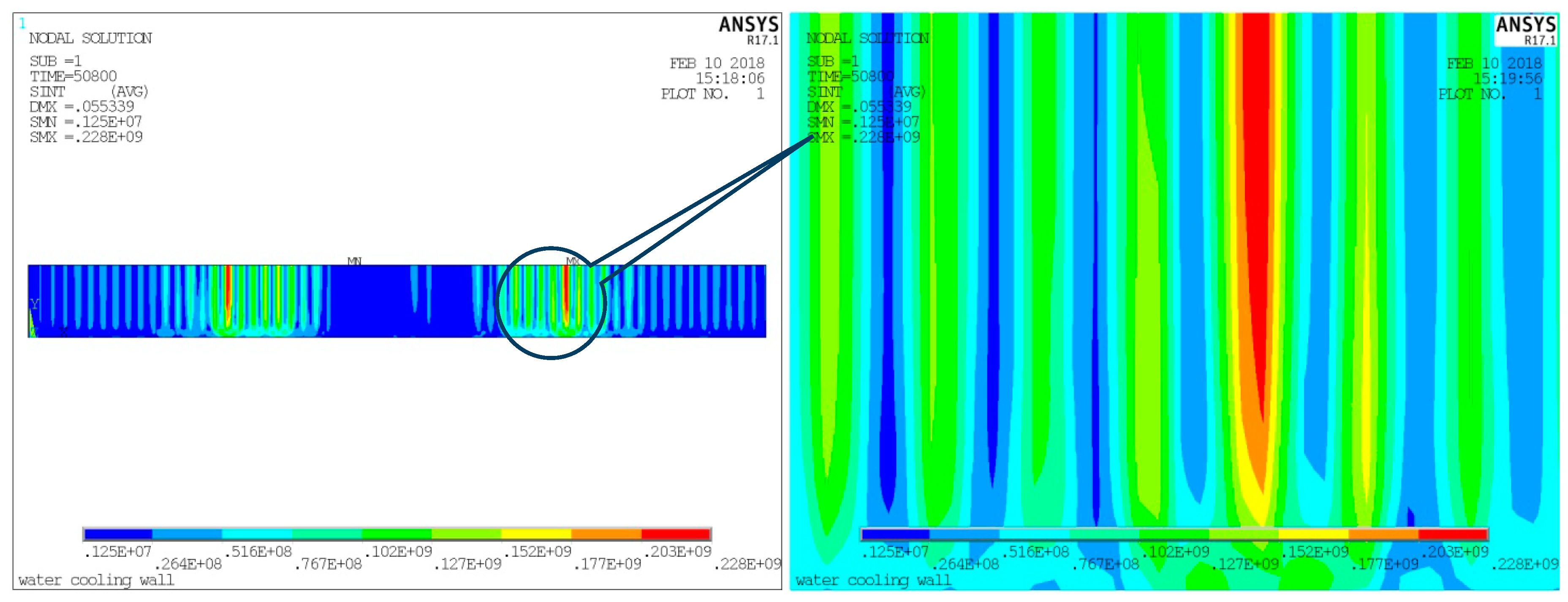
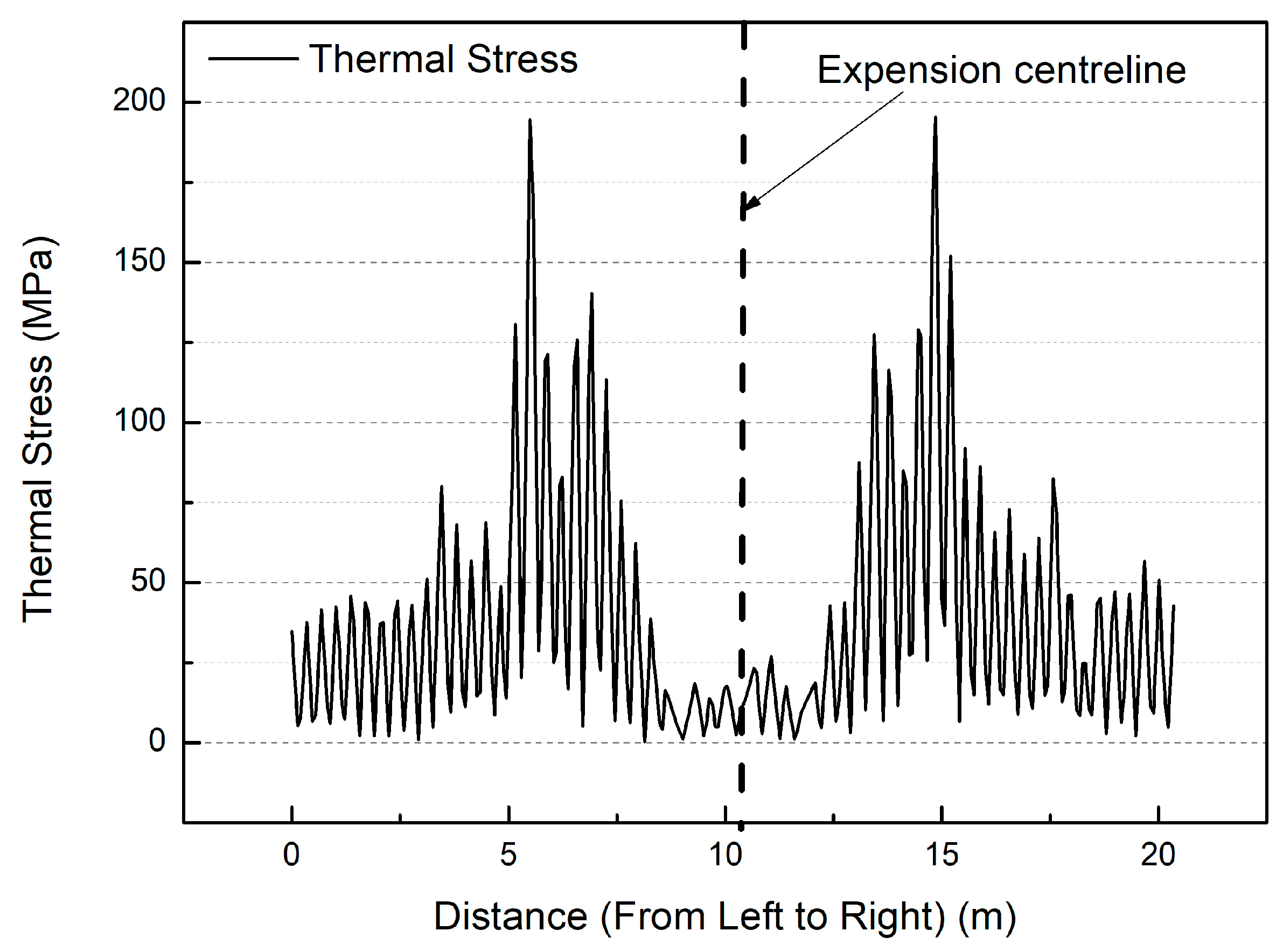
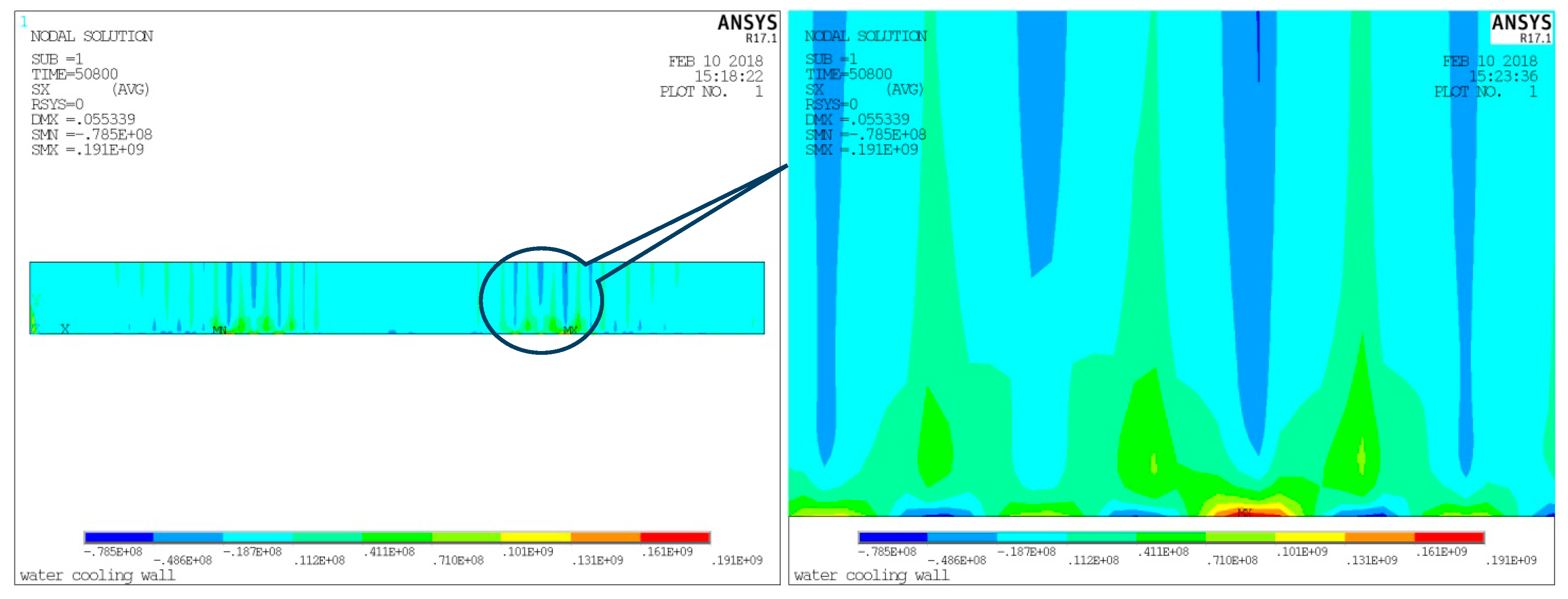
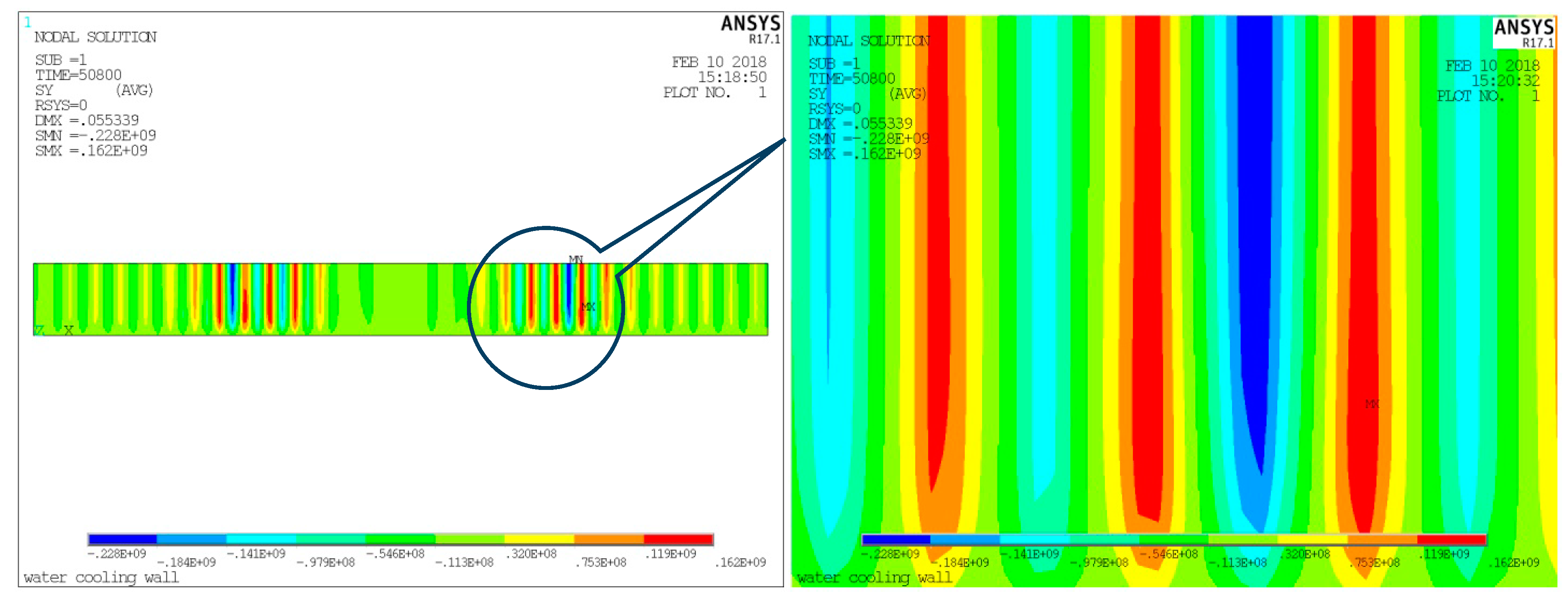
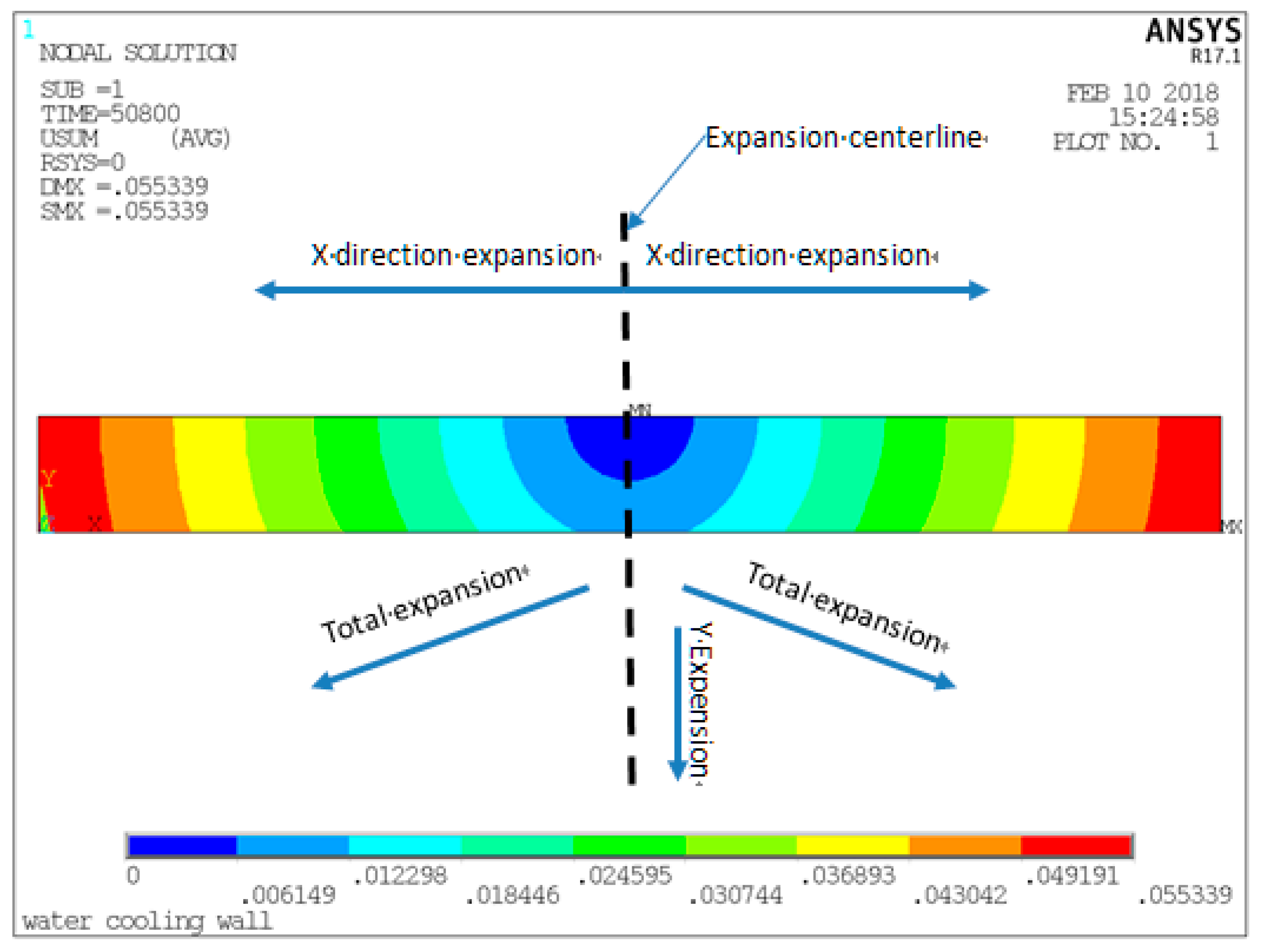
4.5. Thermal Stress and Cyclic Stress Results and Analysis
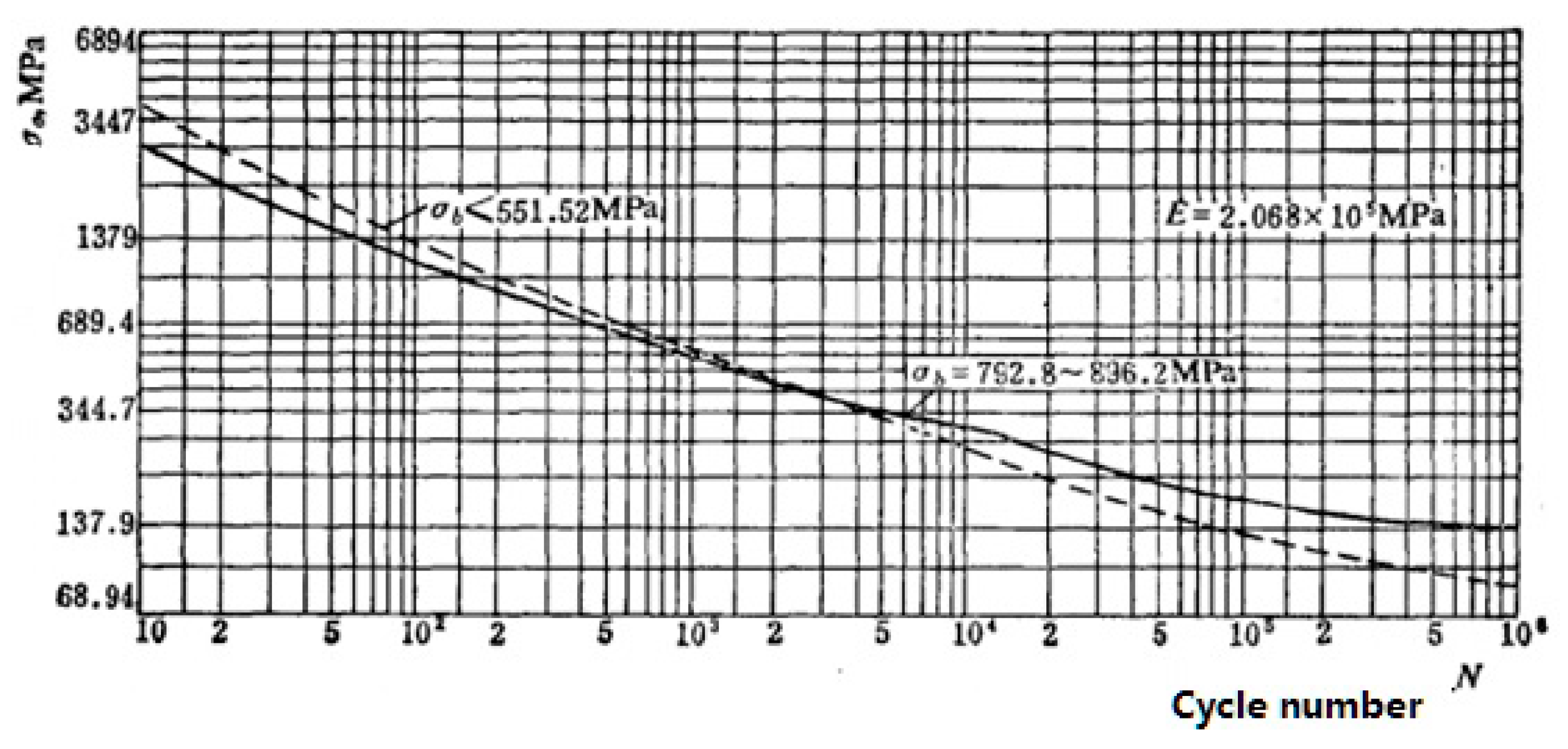
4.6. Cyclic Stress Analyses
5. Conclusions
Author Contributions
Funding
Acknowledgment
Conflicts of Interest
Nomenclature
| Abbreviation | |
| DCS | Distributed Control System |
| ZGM | Z medium speed; G- Great; M-Mill |
| EPRI | Electric Power Research Institute |
| BMCR | Boiler Maximum Continuous Rate |
| ASME | American Society of Mechanical Engineers |
| HRSG | Heat Recovery Steam Generator |
| NOx | Nitric Oxide metabolite |
| Symbols | |
| σ | stress |
| τ | strain |
| x | X direction in the rectangular coordinate system |
| y | Y direction in the rectangular coordinate system |
| ε | gas steam combined cycle |
| γ | shearing strain |
| α | thermal expansion coefficient |
| μ | Poisson ratio |
| E | elastic modulus |
| T | material temperature |
| G | body force |
| β | gas or liquid flow ratio |
| w | gas or liquid mass flow rate |
| N | the total amount of parallel tube numbers |
| k | Gas or liquid phase, g-means gas phase, l means liquid phase |
| Subscripts | |
| a | actual cyclic amplitude |
| aij | cyclic amplitude |
| d | design |
| i | tube temperature thermocouple number |
| j | parallel tube number |
| X | Cartesian coordinate X direction |
| Y | Cartesian coordinate Y direction |
References
- Stappel, M.; Gerlach, A.K.; Scholz, A.; Pape, C. The European Power System in 2030: Flexibility Challenges and Integration Benefit; Agora Energiewende: Berlin, Germany, 2017. [Google Scholar]
- EPRI. Electric Power System Flexibility Challenges and Opportunities; Electric Power Research Institute: Palo Alto, CA, USA, 2016. [Google Scholar]
- Jones, D.; Sakhel, A.; Buck, M.; Graichen, P. The European Power Sector in 2017: State of Affairs and Review of Current Developments; Agora Energiewende and Sandbag: Berlin, Germany, 2018. [Google Scholar]
- Henderson, C. Increasing the Flexibility of Coal-Fired Power Plants; IEA Clean Coal Centre: London, UK, 2014. [Google Scholar]
- Modliński, N.; Szczepanek, K.; Nabagło, D.; Madejski, P.; Modliński, Z. Mathematical procedure for predicting tube metal temperature in the second stage reheater of the operating flexibly steam boiler. App. Therm. Eng. 2019, 146, 854–865. [Google Scholar] [CrossRef]
- Viswanathan, R. An Overview of Failure Mechanisms in High Temperature Componentd in Power Plants. Available online: https://www.gruppofrattura.it/ocs/index.php/ICF/ICF10/paper/download/4443/6452 (accessed on 21 March 2019).
- Farragher, T.P.; Scully, S.; O’Dowd, N.P.; Leen, S.B. Development of life assessment procedures for power plant headers operated under flexible loading scenarios. Int. J. Fatigue 2013, 49, 50–61. [Google Scholar] [CrossRef]
- Taler, J.; Węglowski, B.; Taler, D.; Sobota, T.; Dzierwa, P.; Trojan, M.; Madejski, P.; Pilarczyk, M. Determination of start-up curves for a boiler with natural circulation based on the analysis of stress distribution in critical pressure components. Energy 2015, 92, 153–159. [Google Scholar] [CrossRef]
- Pearson, J.M.; Anderson, R.W. Root Causes of Transient Tube Temperature Anomalies Measured in Horizontal Gas Path HRSGS. Available online: http://competitivepower.us/pub/pdfs/ROOT-CAUSES-OF-TRANSIENT-TUBE-TEMPERATURE-EPRI-2001.pdf (accessed on 21 March 2019).
- Cochran, J.; Lew, D.; Kumar, N. Making Coal Flexible: Getting From Baseload to Peaking Plant. Available online: https://www.21stcenturypower.org/assets/pdfs/cornerstone-flexible-coal.pdf (accessed on 21 March 2019).
- Cochran, J.; Miller, M.; Zinaman, O.; Milligan, M.; Arent, D.; Palmintier, B.; O’Malley, M.; Mueller, S.; Lannoye, E.; Tuohy, A.; et al. Flexibility in 21st Century Power Systems. Available online: https://www.osti.gov/biblio/1130630 (accessed on 21 March 2019).
- Ma, J. A review of flexible operation and high efficency technology with wide load in thermal power units. Therm. Turbine 2017, 46, 108–116. [Google Scholar]
- Mu, C.; Ju, W.; Huang, J.; Zhang, J. Review and prospect of technologies of enhancing the flexibility of thermal power units. Therm. Power Gener. 2018, 47, 1–7. [Google Scholar]
- Pescia, D. Flexibility in Thermal Power Plants-With a Focus on Existing Coal-Fired Power Plants; Agora Energiewende: Berlin, Germany, 2017. [Google Scholar]
- Otegui, J.L. Failure Analysis—Fundamentals and Applications in Mechanical Components; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Coleman, K.; Hack, H. Potential impacts of flexible operations on subcritical conventional coal-fired boilers. Environ. Eng. 2009, 135, 449–458. [Google Scholar]
- Rosinski, S.T.; Coleman, K.; Berasi, M.; Carney, C.; Woerz, U.; Sanchez, A.; Sigali, S.; Rossi, N. Online creep-fatigue monitoring of cyclic operation in a coal-fired power plant. In Proceedings of the ASME 2017 Pressure Vessels and Piping Conference, Waikoloa, HI, USA, 16–20 July 2017. [Google Scholar]
- Taler, J.; Dzierwa, P.; Taler, D.; Jaremkiewicz, M.; Trojan, M. Monitoring of Thermal Stresses and Heating Optimization Including Industrial Applications; Nova Science Publishers: New York, NY, USA, 2016. [Google Scholar]
- Taler, J.; Węglowski, B.; Sobota, T.; Taler, D.; Trojan, M.; Dzierwa, P.; Jaremkiewicz, M.; Pilarczyk, M. Thermal performance and stress monitoring of power boiler. In Proceedings of the ASME 2016 Power Conference, Charlotte, NC, USA, 26–30 June 2016. [Google Scholar]
- Li, B.; Wang, H.; Liang, X.; Wang, C.; Shi, B. The Study on temperature distribution of water-cooled wall in Ultra-supercritical utility boiler based on finite element numercial simulation. Util. Boil. Tech. 2016, 47, 67–71. [Google Scholar]
- Noda, N.; Hetnarski, R.B.; Tanigawa, Y. Thermal Stress, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Parker, J.; Shingledecker, J. EPRI Initiatives related to Flexible Operation of High Temperature Power Plant. Available online: https://www.gruppofrattura.it/ocs/index.php/ICF/icf13/paper/download/11312/10691 (accessed on 21 March 2019).


| Parameter | Value | Unit |
|---|---|---|
| Power output | 600 | MW |
| Main steam flow rate | 1950 | t/h |
| Main steam temperature | 571 | °C |
| Main steam pressure | 25.4 | MPa |
| Reheated steam flow rate | 1653.4 | t/h |
| Reheated steam temperature | 569 | °C |
| Reheated steam pressure | 4.56 | MPa |
| Economizer inlet water temperature | 290 | °C |
| Parameters | Value and Unit |
|---|---|
| Water-cooled wall tube diameter, thickness, and pinches | 31.8 × 5.5, 57.5 mm |
| Tube material | 15CrMoG |
| Front and back wall tube numbers | 385 × 2 |
| Left and right wall tube numbers | 271 × 2 |
| Front, back, left, and right wall tube temperature thermocouples at the vertical water-cooled wall | 175 |
| Item/Unit | Values | ||||||
|---|---|---|---|---|---|---|---|
| Temperature/°C | 20 | 100 | 200 | 300 | 400 | 500 | 600 |
| Yield Strength /MPa | 295 | - | 269 | 242 | 216 | 198 | - |
| Allowable Stress /MPa | 147 | - | - | 143 | 128 | 96 | - |
| Elastic Modulus /GPa | 206 | 199 | 190 | 181 | 172 | 163 | - |
| Thermal expansion coefficient/10−6/°C | - | 11.9 | 12.6 | 13.2 | 13.7 | 14.00 | - |
| Thermal Conductivity/W/(m·C) | - | 40.6 | 40.1 | 38.7 | 36.8 | 34.8 | 32.8 |
| Density/kg/m3 | 7800 | - | - | - | - | - | - |
| Specific heat capacity/J/(kg·K) | - | - | 590 | 607 | 657 | 712 | 800 |
| Poisson’s ratio/- | 0.284 | 0.295 | 0.3 | 0.301 | 0.304 | 0.308 | - |
| Operating State | Rated Pressure (MPa) | Low Pressure (MPa) | Cyclic Amplitude (MPa) |
|---|---|---|---|
| Cold | 27.26 | 0 | 55.981 |
| Warm | 27.26 | 4.9033 | 45.912 |
| Hot | 27.26 | 7.0205 | 41.564 |
| Ultra-hot | 27.26 | 9.1079 | 37.277 |
| Load following | 27.26 | 10.18 | 35.076 |
| Flexible operation (180–350 MW) | 17.5037 | 15.0855 | 88.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, L.; Yi, S.; Duan, L.; Li, W.; Yang, Y. Thermal Stress and Cyclic Stress Analysis of a Vertical Water-Cooled Wall at a Utility Boiler under Flexible Operation. Energies 2019, 12, 1170. https://doi.org/10.3390/en12061170
Pang L, Yi S, Duan L, Li W, Yang Y. Thermal Stress and Cyclic Stress Analysis of a Vertical Water-Cooled Wall at a Utility Boiler under Flexible Operation. Energies. 2019; 12(6):1170. https://doi.org/10.3390/en12061170
Chicago/Turabian StylePang, Liping, Size Yi, Liqiang Duan, Wenxue Li, and Yongping Yang. 2019. "Thermal Stress and Cyclic Stress Analysis of a Vertical Water-Cooled Wall at a Utility Boiler under Flexible Operation" Energies 12, no. 6: 1170. https://doi.org/10.3390/en12061170
APA StylePang, L., Yi, S., Duan, L., Li, W., & Yang, Y. (2019). Thermal Stress and Cyclic Stress Analysis of a Vertical Water-Cooled Wall at a Utility Boiler under Flexible Operation. Energies, 12(6), 1170. https://doi.org/10.3390/en12061170





