Correlation of Ventilative Cooling Potentials and Building Energy Savings in Various Climatic Zones
Abstract
:1. Introduction
2. Methodology
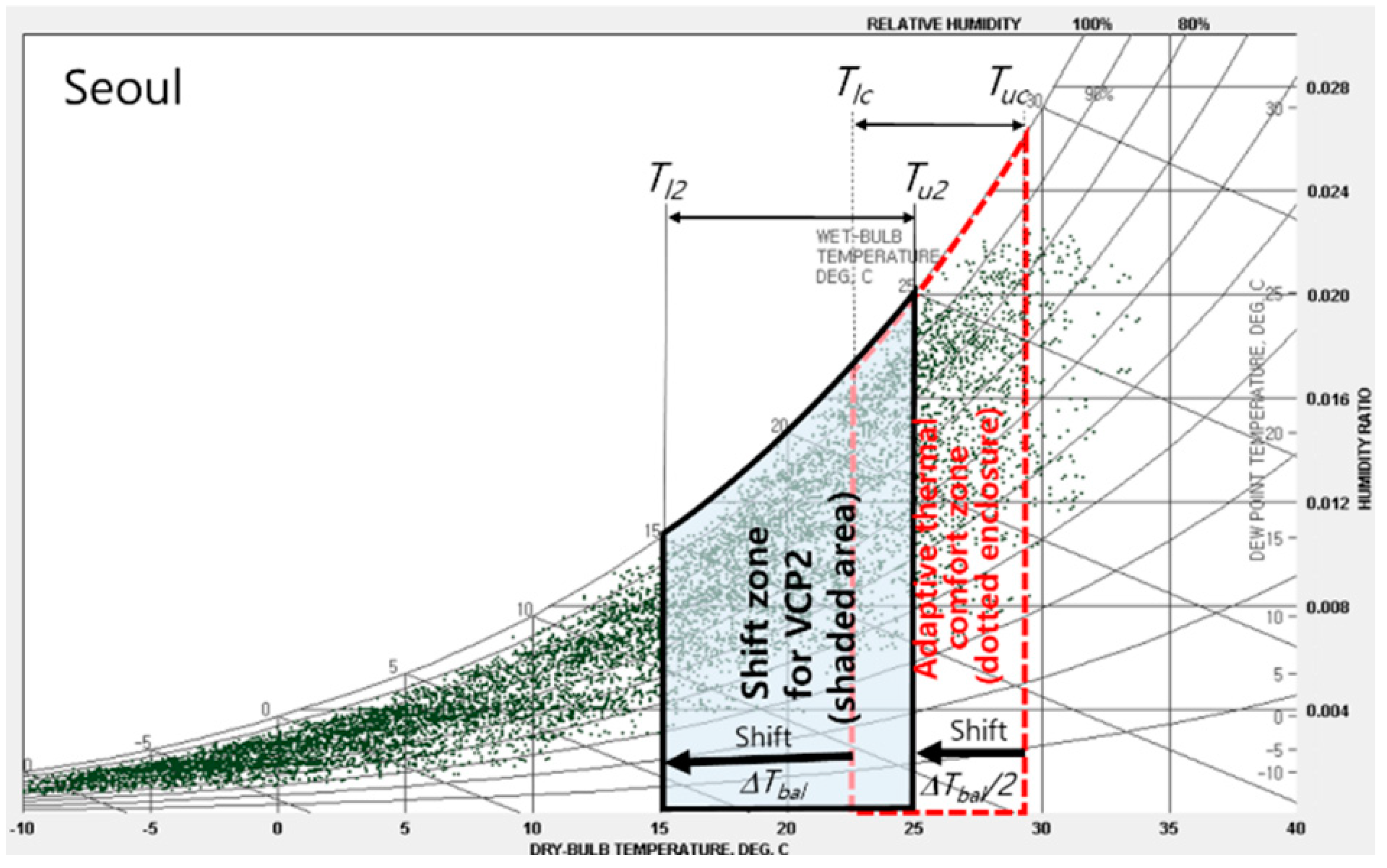
2.1. Balance Temperature Difference
2.2. Definition of VCPs
2.3. Climates
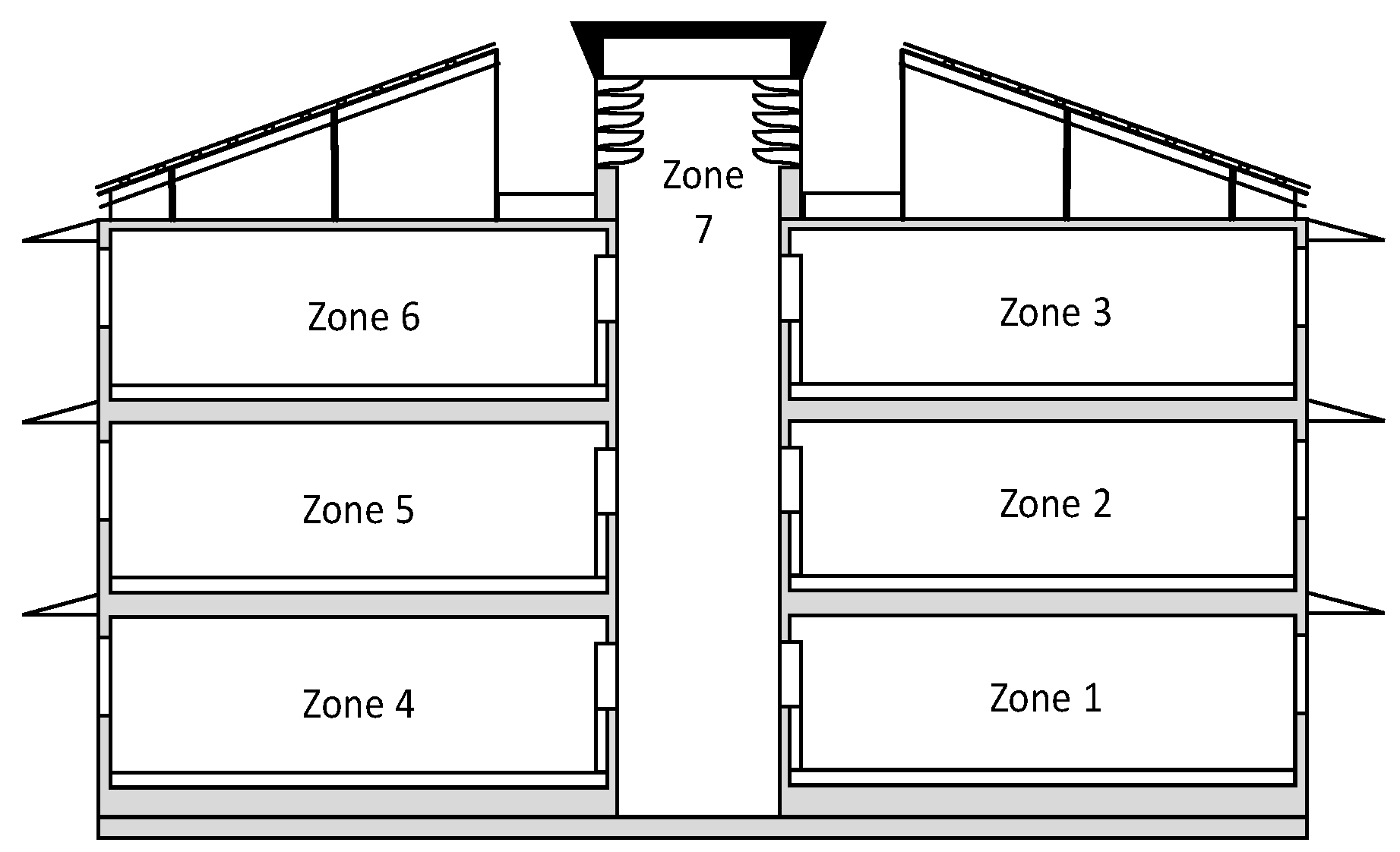
2.4. Building and Energy Simulation Model
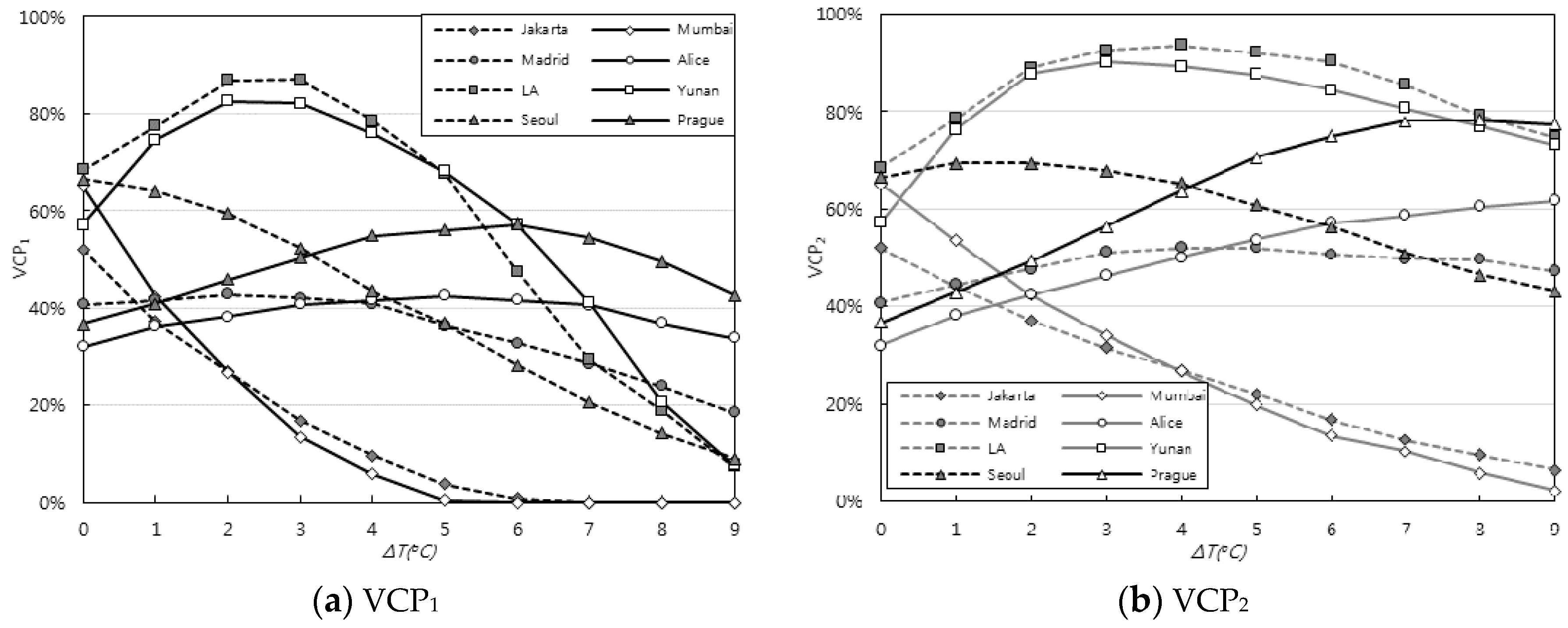
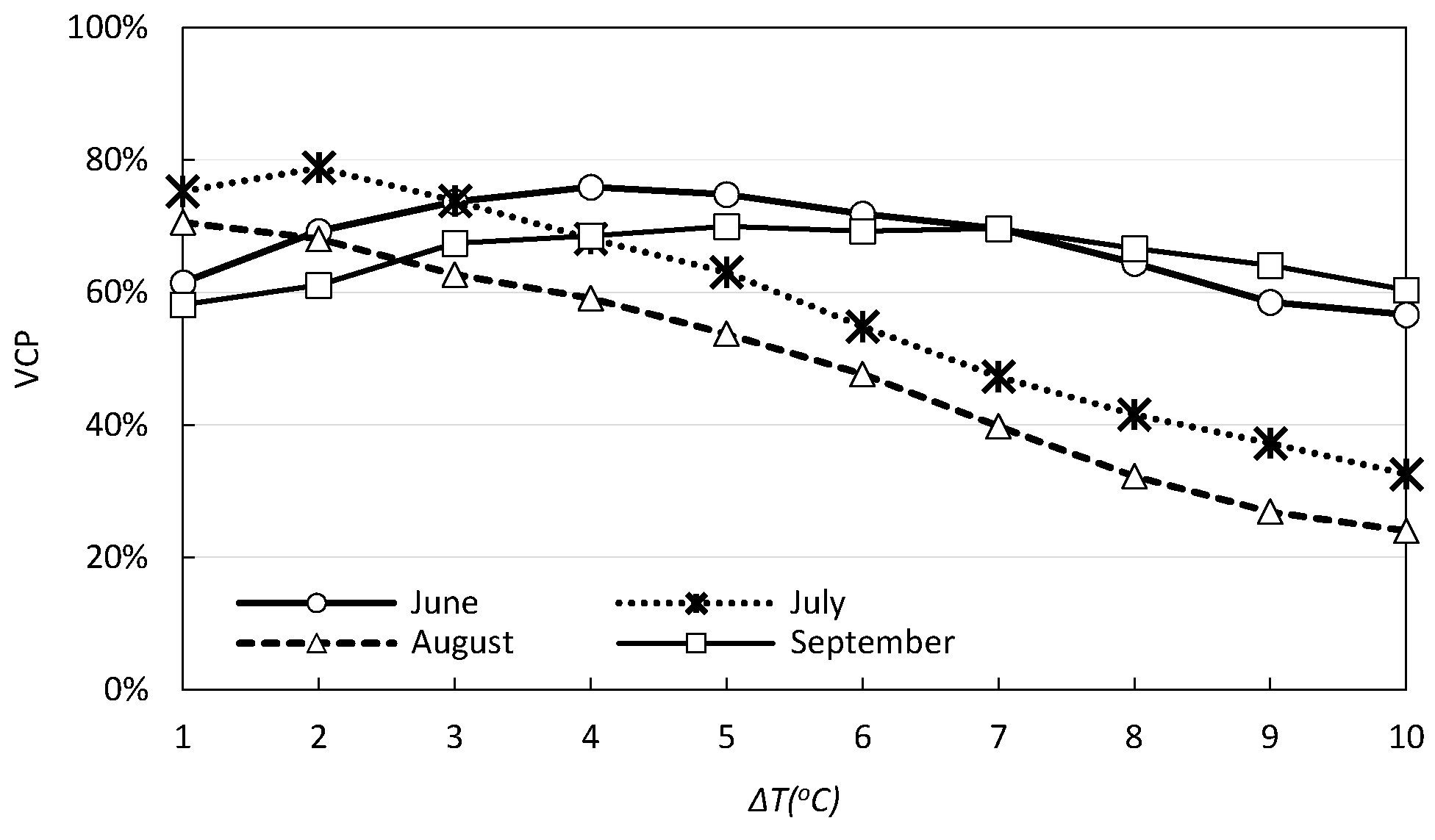
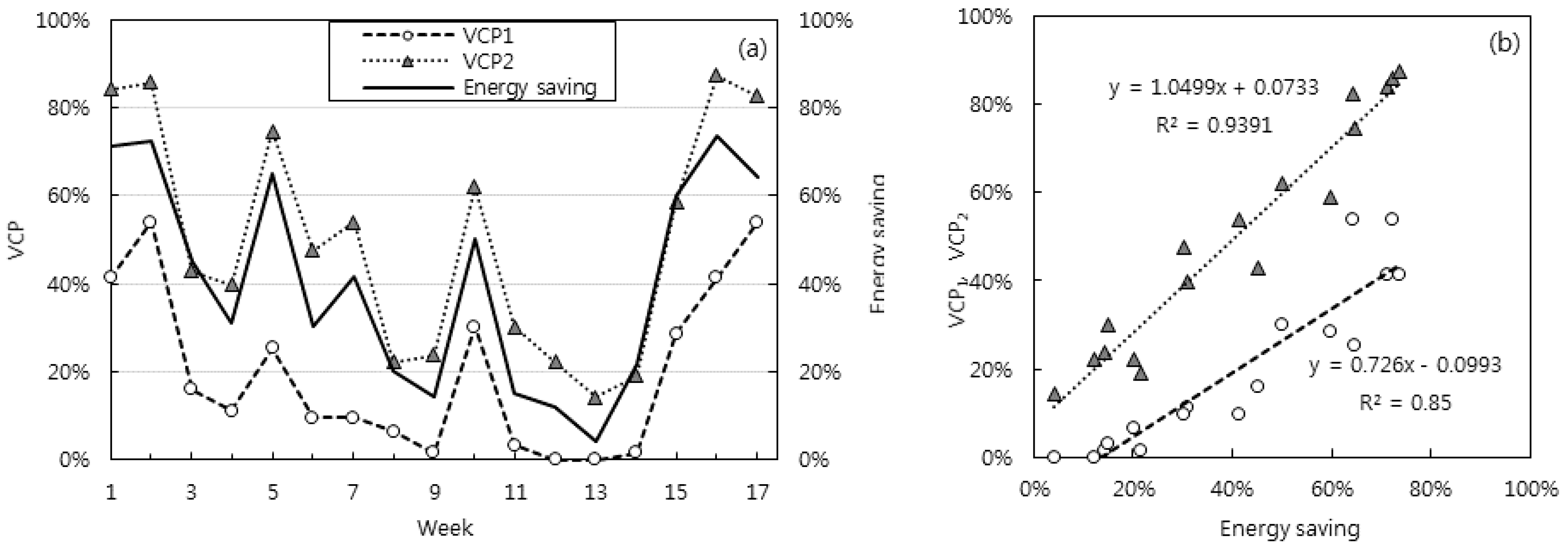
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kolokotroni, M.; Heiselberg, P. Ventilative Cooling State of the Art Review; Annex 62 Ventilative Cooling: Aalborg, Denmark, 2015. [Google Scholar]
- Artmann, N.; Manz, H.; Heiselberg, P. Climatic potential for passive cooling of buildings by night-time ventilation in Europe. Appl. Energy 2007, 84, 187–201. [Google Scholar] [CrossRef]
- Haase, M.; Amato, A. An investigation of the potential for natural ventilation and building orientation to achieve thermal comfort in warm and humid climates. Sol. Energy 2009, 83, 389–399. [Google Scholar] [CrossRef]
- Yao, R.; Li, B.; Steemers, K.; Short, A. Assessing the natural ventilation cooling potential of office buildings in different climate zones in China. Renew. Energy 2009, 34, 2697–2705. [Google Scholar] [CrossRef]
- Causone, F. Climatic potential for natural ventilation. Arch. Sci. Rev. 2016, 59, 212–228. [Google Scholar] [CrossRef]
- Campaniço, H.; Hollmuller, P.; Soares, P.M.M. Assessing energy savings in cooling demand of buildings using passive cooling systems based on ventilation. Appl. Energy 2014, 134, 426–438. [Google Scholar] [CrossRef] [Green Version]
- Campaniço, H.; Soares, P.M.M.M.; Hollmuller, P.; Cardoso, R.M. Climatic cooling potential and building cooling demand savings: High resolution spatiotemporal analysis of direct ventilation and evaporative cooling for the Iberian Peninsula. Renew. Energy 2016, 85, 766–776. [Google Scholar] [CrossRef] [Green Version]
- Belleri, A.; Avantaggiato, M.; Psomas, T.; Heiselberg, P. Evaluation tool of climate potential for ventilative cooling. Int. J. Vent. 2017, 2044–4044. [Google Scholar] [CrossRef]
- British Standards Institution. PrEN 16798-1. (2016-02-07 under Approval). In Energy Performance of Buildings—Part 1: Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics; British Standards Institution: London, UK, 2016. [Google Scholar]
- ASHRAE. Thermal Environmental Conditions for Human Occupancy. Available online: http://www.aicarr.org/Documents/Editoria_Libri/ASHRAE_PDF/STD55-2004.pdf (accessed on 12 February 2019).
- De Dear, R.J.; Brager, G.S.; Artmann, N. Thermal comfort in naturally ventilated buildings: Revisions to ASHRAE Standard 55. Energy Build. 2002, 34, 549–561. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; Mcmahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. Discuss. 2007, 4, 439–473. [Google Scholar] [CrossRef]
- Energyplus, Weather Data. 2016. Available online: https://energyplus.net/weather (accessed on 12 February 2019).
- Deru, M.; Field, K.; Studer, D.; Benne, K.; Griffith, B.; Torcellini, P.; Liu, B.; Halverson, M.; Winiarski, D.; Rosenberg, M.; et al. U.S. Department of Energy Commercial Reference Building Models of the National Building Stock; NREL/TP-5500-46861; NREL: Lakewood, CO, USA, 2011; p. 19. [Google Scholar]
- Maria-Alenjandra, B.M.; Glicksman, L. Coolvent: A multizone airflow and thermal analysis simulator for natural ventilation in building. In Proceedings of the 3rd National Conference of IBPSA-USA, Berkeley, CA, USA, 30 July–1 August 2008. [Google Scholar]
- Rahman, H.; Han, H. Ventilative cooling potential based on climatic condition and building thermal characteristics. In Proceedings of the AIVC Conference, Nottingham, UK, 13–14 September 2017. [Google Scholar]




| Climate Zone | City | Location | Average Outdoor Temperature (°C) | Average Wind Speed (m/s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jun | Jul | Aug | Sep | Jun | Jul | Aug | Sep | |||
| Tropical (Megathermal) | Jakarta (Indonesia) | 6.13 S, 106.75 E | 29.0 | 29.0 | 29.4 | 29.6 | 4.51 | 4.76 | 5.11 | 4.89 |
| Mumbai (India) | 18.9 N 72.82 E | 29.0 | 27.8 | 27.2 | 27.6 | 2.74 | 3.26 | 3.23 | 2.08 | |
| Dry (Arid) | Madrid (Spain) | 40.45 N, 3.55 W | 23.2 | 27.0 | 20.6 | 25.5 | 2.73 | 3.26 | 3.61 | 3.46 |
| Alice (Australia) | 23.8 S 133.88 E | 11.5 | 12.0 | 13.1 | 20.4 | 2.62 | 1.39 | 1.66 | 3.52 | |
| Temperate (Mesothermal) | Los Angles (USA) | 33.93 N, 118.4 W | 24.7 | 20.1 | 21.9 | 21.6 | 4.54 | 5.00 | 5.10 | 4.49 |
| Yunnan (China) | 22.78 N 100.97 E | 22.5 | 22.0 | 21.8 | 21.2 | 1.04 | 0.76 | 0.76 | 0.66 | |
| Continental (Microthermal) | Seoul, (Korea) | 37.57 N, 126.97 E | 23.2 | 26.2 | 27.0 | 22.3 | 2.46 | 2.60 | 2.25 | 2.17 |
| Prague (Czech) | 50.1 N 14.28 E | 15.6 | 17.3 | 17.6 | 13.3 | 4.03 | 3.07 | 3.40 | 3.80 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, H.; Han, H. Correlation of Ventilative Cooling Potentials and Building Energy Savings in Various Climatic Zones. Energies 2019, 12, 968. https://doi.org/10.3390/en12060968
Rahman H, Han H. Correlation of Ventilative Cooling Potentials and Building Energy Savings in Various Climatic Zones. Energies. 2019; 12(6):968. https://doi.org/10.3390/en12060968
Chicago/Turabian StyleRahman, Haolia, and Hwataik Han. 2019. "Correlation of Ventilative Cooling Potentials and Building Energy Savings in Various Climatic Zones" Energies 12, no. 6: 968. https://doi.org/10.3390/en12060968
APA StyleRahman, H., & Han, H. (2019). Correlation of Ventilative Cooling Potentials and Building Energy Savings in Various Climatic Zones. Energies, 12(6), 968. https://doi.org/10.3390/en12060968





