Next Article in Journal
An Influencing Parameters Analysis of District Heating Network Time Delays Based on the CFD Method
Next Article in Special Issue
How Big Is an Error in the Analytical Calculation of Annular Fin Efficiency?
Previous Article in Journal
Data Analytics-Based Multi-Objective Particle Swarm Optimization for Determination of Congestion Thresholds in LV Networks
Previous Article in Special Issue
A Stability Analysis for Magnetohydrodynamics Stagnation Point Flow with Zero Nanoparticles Flux Condition and Anisotropic Slip
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 12
Issue 7
10.3390/en12071296
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Simulation of Vortex Heat Transfer Enhancement in the Turbulent Water Flow in the Narrow Plane-Parallel Channel with an Inclined Oval-trench Dimple of Fixed Depth and Spot Area

by
Sergey Isaev
1,*,
Alexandr Leontiev
2,
Yaroslav Chudnovsky
3,
Dmitry Nikushchenko
4,
Igor Popov
5 and
Alexandr Sudakov
1
1
Saint-Petersburg State University of Civil Aviation, Pilots Str. 38, Saint-Petersburg 196210, Russia
2
Bauman Moscow State Technical University, 2nd Bauman Str. 5/1, Moscow 105005, Russia
3
Gas Technology Institute, 1700 S Mount Prospect Road, Des Plaines, IL 60018, USA
4
Saint-Petersburg State Marine Technical University, Lotsmanskaya, 3, Saint-Petersburg 190121, Russia
5
A. N. Tupolev Kazan National Research Technical University (Kazan Aviation Institute), Kazan 420111, Russia
*
Author to whom correspondence should be addressed.
Energies 2019, 12(7), 1296; https://doi.org/10.3390/en12071296
Submission received: 1 February 2019 / Revised: 18 March 2019 / Accepted: 29 March 2019 / Published: 4 April 2019
(This article belongs to the Special Issue Numerical Simulation of Convective-Radiative Heat Transfer)
Browse Figures
Versions Notes

Abstract

:
This article is devoted to the development of the multiblock technique for numerical simulation of vortex heat transfer enhancement (VHTE) by inclined oval-trench dimples. Special attention is paid both to the analysis of numerical predictions of different-type boundary conditions at the wall: T = const and q = const and to the comparison of the standard and modified shear stress transport models. The article discusses the mechanism of change in the flow structure and secondary flow augmentation due to an increase in a relative length of an oval-trench dimple (at its fixed spot area, depth and orientation) where a long spiral vortex is formed.

1. Introduction

The use of a structured surface with discrete artificial roughness is a popular method of vortex heat transfer enhancement (VHTE) in energy equipment [1]. Tubes with periodic protrusions many times enhance heat transfer in comparison to smooth tubes. However, hydraulic losses in this case grow faster, thus, an increased total pressure drop is required. Replacing protrusions by grooves allows hydraulic losses to be decreased cardinally.
Prior to the three-dimensional (3D) printing era, the type of discrete roughness was mainly determined by technology. Cylindrical cavities made by mechanical extrusion [2,3,4] were the simplest and well-studied technological forms. However, hydraulic losses in ducts with such cavities appeared to be rather high.
Another simple form of a surface cavity is a semi-spherical dimple formed by a sphere that was pressed into the wall. In the late 20th century, such cavities attracted the attention of researchers and engineers [5,6,7,8], although at a later date segment-spherical dimples of a relative depth of less than 0.5 (in terms of spot diameter) [9,10] were quite often considered. It is interesting to note that the self-oscillatory flow regime was for the first time revealed in a semi-circular dimple, on the sides of which vortex jets were alternatively formed [5].
One of the first researchers who drew attention to the vortex mechanism of heat transfer intensification using spherical dimples were Kiknadze et al. [11] and Ligrani et al. [12].
In the 1990s, Afanasiev et al. [13] and Chyu et al. [14] have carried out a series of pioneering experimental investigations of turbulent convective heat transfer at a dimpled plane wall in rectangular channels. The most complete complex study of hydrodynamics and heat transfer on surfaces with spherical recesses was conducted By Terekhov [10]. Results of this work were used as a basis for studying flow characteristics in dimpled channels at the University of Rostock [15].
A large number of experimental works on hydrodynamics and heat transfer in dimpled channels were performed at the beginning of the new millennium [16,17,18,19,20,21]. Later, these publications were supplemented [22,23,24] using new experimental methods with the implication of gradient heat flux sensors and pressure pulsation detectors. The studies on the visualization of vortex flows in the vicinity of dimples such as [25,26] should also be mentioned here.
Recent interest in laminar heat transfer enhancement was initiated by the research of heat transfer in microchannels [27]. The research in [28] analyzed the detailed maps of flow around single spherical dimples. There has also been research that [29,30] contained the important results that were used for verification and validation of numerous numerical predictions. Lastly, there has been research [31] that analyzed the technique of making longer non-spherical dimples at the wall.
The analysis of the experimental works as presented here shows that most of them are devoted to spherical dimples. As noted in [11,12], the jet-vortex nature of heat transfer enhancement by such dimples is beyond doubt; however, the intensity to form swirled flows appears to be low and the problem to select rational shapes of vortex generators with the highest thermal and hydraulic performance still remains open. In [29], it was experimentally established that heat fluxes decay on the leeward side of the spherical dimple in the zone of low-velocity separated flow in comparison to the plane wall. Heat transfer coefficients are low inside the dimple.
The objective of the present study was to apply the specialized multiblock computational technique (MCT) based on simple-topology different-scale structured grids with their partial overlapping as being realized in the VP2/3 code in order to calculate convective heat transfer in dimpled channels. The authors analyzed different interpretations of turbulent transfer, including the consideration of the flow curvature influence on turbulent characteristics. We validated the numerical predictions and verified the turbulence models when comparing predicted and experimental results.
This study analyzes the physical mechanisms of VHTE based on the control of large-scale spiral vortices in single oval-trench dimples with fixed spot area and depth at an angle of inclination to the main flow at a Reynolds number of 104. It is shown that increasing the dimple length changes the flow structure in the dimple. The separation zone substantially decreases, backflow enhances, which leads to an almost two-fold growth of heat transfer occurring in the separation zone and also results in an increase in the secondary flow velocity comparable to the bulk velocity in the channel.

2. Problem Statement

In this work, we considered the convective heat transfer in the channel with a cross-sectional aspect ratio of 2.5 × 0.33 (the dimensions are related to the dimple diameter). At the entrance to the channel, we set the velocity profile of a fully developed turbulent flow. We are looking at an incompressible fluid. On the walls, the conditions of non-slip are observed. The profiles of the longitudinal, vertical and transverse components of the velocity u, v, w, as well as the turbulence characteristics (energy k, specific scattering velocity ω, vortex viscosity µt) are found from the solution of a special problem in the development of the flow in the computational domain of the selected section of the channel under periodic boundary conditions under the selected Reynolds number 104. As parameters are assigned to the normalization of the volumetric velocity U, a spot diameter d of basic spherical and 10°-truncated conical dimples, the density ρ and viscosity μ of the coolant-water (Pr = 7). The depressions of the average depth of 0.13 (according to the classification [32]) are located at some distance (about 3) from the selected channel input. The center of the Cartesian coordinates x, y, z are in the longitudinal middle plane of the channel at the point of projection of the center of the dimple on the section coinciding with the wall of the lower plane (Figure 1). The rounding radius of dimple edges is taken as equal to 0.025. While maintaining the area of the oval dimple spot equal to the area of the spherical dimple, its width b varies from 0.731 to 0.346 in width from 1.68 to 6.78 (Figure 1 and Table 1).
The channel ends at a distance L = 7 after the dimple (normalized by the diameter of the dimple spot).
We solved the problems of heat transfer and hydrodynamics separately. The flow at the channel inlet is isothermal at Tref = 293 K. The streamed bottom wall of the dimpled channel was heated and a supplied constant heat flux q was re-calculated in dimensionless form by the equation (of order 3.4 × 10−5).
q ¯ = q λ Pr Re T r e f / D
Here, λ is the thermal conductivity of water. The side walls of the channel are adiabatic, while the top wall is isothermal at Tref (taken as the normalization scale). The outflow conditions are predetermined for T at the channel outlet.
Since the previous studies [32,33] considered heated isothermal walls, the testing part of this work compares the boundary conditions T = const and q = const; the heated wall temperature was assigned as equal to 1.036 in terms of Tref. We need to note that in [32,33], air was considered as a heat carrier and the wall temperature was set to 373 °C.

3. Models, Methods, Computational Grids

In the section below, suggestions on turbulence model and computation methodology selection are presented, multi-block mesh structure is described; also in addition, we pay attention to iteration process convergence of the problem solution.

3.1. Turbulence Models

To solve the problem of convective heat transfer in a turbulent flow of incompressible fluid in a channel with single dimple on the heated walls, a mathematical model based on a system of Reynolds-averaged stable Navier-Stokes equations (RANS) and an energy equation similar to [32,33] was used.
To close them, the standard Menter SST (Shear Stress Transport) model and the modified Menter SST model were successfully used for typical wall flows, including those with separation [34,35]. The k-ω model proposed by Menter is a generalization of two turbulence models: the Launder–Spalding k-ε model for shear flow zones far from the wall and the Saffman–Wilcox k-ω model for the near-wall region. In addition, designing the zonal shear stress transport model the ideas were taken from the Johnson–King turbulence model. As earlier mentioned, in determining eddy viscosity, the Menter 1993 model [34] uses the vorticity modulus Ω, and the Menter 2003 model [34], as the majority of semi-empirical models of differential type, includes the strain tensor modulus S into the expression for eddy viscosity. It is important to emphasize that the semi-empirical models are calibrated mainly in near-wall flows. As a result, there is a need to correct them to high-intensity separated flows. As noted in [36], the Rodi–Leschziner approach to correcting eddy viscosity within the framework of the high-Reynolds version of the Launder–Spalding dissipative two-parameter turbulence model [37] widely used in the 1980–1990s [37] is that it is affected by the correction function fc = 1/(1 + Cc × Rit). The constant Cc equal to 0.57 was determined analytically when calculating turbulent annular and twin parallel jets [38] and a limitation was imposed on the product fc × Cµ: 0.02 < fc × Cµ < 0.15 (in the standard k-ε model [37], the semi-empirical constant Cµ = 0.09 in the expression for eddy viscosity). Isaev generalized the Rodi–Leschziner approach (RLI approach) to the Menter 2003 model. Kharchenko, Usachov and Isaev selected the constant Cc = 0.02 [36] from the condition of the best agreement of numerical predictions and experimental data for numerous separated flows. Recently Smirnov and Menter [39] have proposed one more correction of the Menter 2003 model (SM correction) when they extended the Shur–Spalart correction in the Spalart–Allmares eddy viscosity model [40] to the Menter two-parameter model.
Near-wall conditions for SST models are formulated so that the normal derivative to the wall for turbulence energy is equal to zero and the specific dissipation rate of turbulence energy in the near-wall cell is determined as in [41].

3.2. Computational Methodology

It is beyond doubt that software based on solving the Reynolds-averaged Navier–Stokes equations with the use of semi-empirical models became a powerful tool to predict flow parameters and turbulence characteristics. The present study used the multiblock computational technique [42] realized in the original research VP2/3 code (velocity-pressure, two-dimensional (2D)/3D). Computational algorithms realized in this code are based both on the concept of splitting with respect to physical processes and on the application of grid methods for solution of the governing equations [42,43].
The use of the concept of splitting allows a system of partial differential equations to be divided into blocks containing momentum equations in natural variables (including Cartesian velocity components for incompressible viscous liquid flows), which replace the continuity equation, as well as the pressure correction equation (SIMPLEC (Semi-Implicit Method for Pressure Linked Equations Consistent) [44,45]) and the equations for their closure (from the chosen turbulence model).
Thus, the system of steady equations in discrete form is solved block by block at each time step during the global iteration process (about 10–20 iterations), when at each time step for one iteration in the course of solution of the momentum equation, several (about 10–15 iterations) iterations are performed in the pressure correction block and about four–six iterations in the turbulence and energy blocks. The governing equations are preliminarily linearized [46].
In the calculation algorithm we used: (1) the pressure correction procedure SIMPLEC [44,47,48]; (2) the approximation of the convective terms in the explicit hand-side of the momentum equation using Leonard’s one-dimensional quadratic upwind scheme [49] to reduce the influence of numerical difference specific for a considered type of separated flows and using van Leer's scheme [50]; (3) the representation of the convective terms in the implement hand-side of transport equations using the upwind scheme with one-sided differences; (4) methods with preconditioners for solution of difference equations [51].
In this paper, we used a Rhie–Chow’s generalized approach [48] to avoid difficulties in the calculation of unsteady flows. The method for solution of algebraic equations is the BiCGSHAB (biconjugate gradient stabilized method) preconditioner [51] with an AMG (Algebraic Multigrid) preconditioner from Demidov’s library (amgl) [52] for pressure correction and the ILU0 preconditioner for another variables.
MCTs realized in the VP2/3 code are outlined elsewhere [42,53]. Their essence is to introduce a set of difference-scale, tier and structured overlapping grids to resolve the flow structure in the physical problem of corresponding scale. The parameters for two rows of near-boundary cells of each of the overlapping or overset grids are determined using linear interpolation [42,54] in the manner, as done in [55]. Computation from grid to grid with the use of MCTs involving linear interpolation is a source of errors; however, the test calculations [54] showed that the errors were acceptable.

3.3. Computational Grids

In this paper, we used multiblock overlapping structured grids of different scale (Figure 2). We considered grid structures similar in topology to those used in [32,33,56]; however, these are more condensed and have a greater number of cells. A rectangular channel is covered with a Cartesian grid condensing to the walls and to the area around a dimple. The total number of cells in the channel is 700,000–1,500,000.
In the case of spherical and conical dimples, a detailed grid is Cartesian and in the case of oval dimples, it is curvilinear, fitted to the streamlined bottom wall of the channel.
The area around spherical and conical grids is divided by a cylindrical grid adjusted to the dimple surface (Figure 2a,b); an additional grid close to a rectangular one (‘patch’) is introduced to prevent nodes from condensing in the near-axis zone. The minimum grid step near the edge is 0.002. In the case of oval dimples, a special edge grid is introduced to describe high-gradient zones. The total number of multiblock grid cells is about 1.5–3 mln cells.
Figure 3a illustrates the multiblock computational grid in the axonometric projection for an oval-trench dimple.

3.4. Data Processing

The integral characteristics of flow and heat transfer in the narrow channel with single dimples were calculated in terms of the selected channel sections surrounding the dimple. As in [32,33], hydraulic losses in the channel were determined between the assigned cross sections A-B shown in Figure 3. Since we analyzed very long oval dimples, the size of the channel section (in comparison to [32,33,57]) was somewhat increased to assess relative heat transfer and to take it equal to 3 × 2 in the dimple center at a distance of 1 from the front boundary of the section (Figure 3b). In the present work, the thermal and hydraulic performance of the oval dimple was for the first time determined in the rectangular section surrounding the oval dimple at the 45° angle of orientation to the flow (Figure 3c).
We analyzed local dimensionless and relative characteristics of flow and heat transfer, including static pressure, friction, temperature and Nusselt number, as a function of longitudinal and transverse coordinates in the middle sections of the channel and the dimple at the bottom, heated and isothermal top walls. We compared Cartesian velocity components, turbulence energy and eddy viscosity normalized by the Reynolds number as profiles in the vertical coordinate in the dimple centers.
Temperature and Nusselt number fields are combined with the flow maps. We also considered vortex structures that are formed in dimples and obtained by computer visualization of labeled liquid particles.

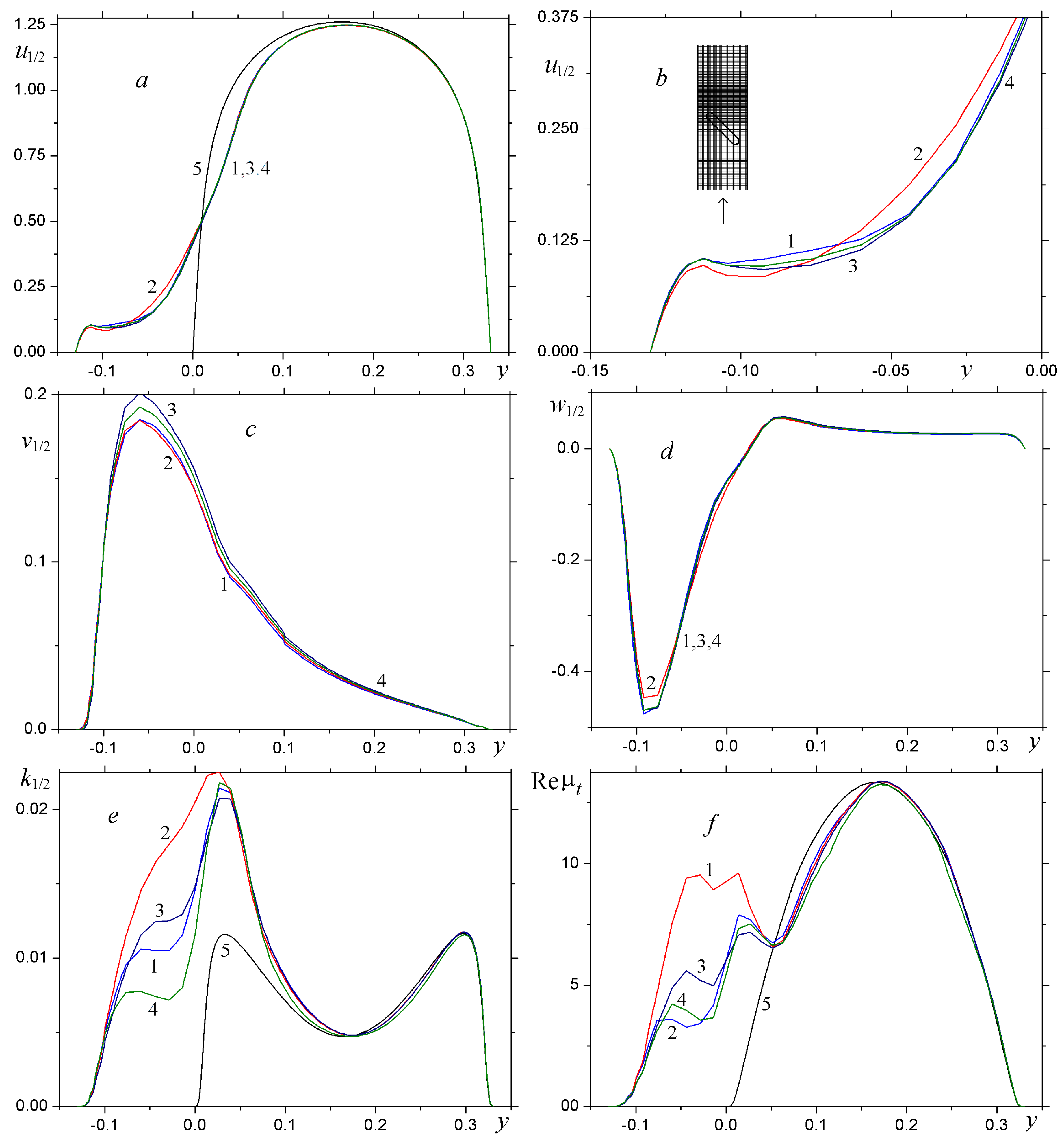
3.5. Analysis of Convergence

Similarly [32,33] the SST model [36] with curvature correction within the RLI approach is chosen as the basic model.
Figure 4 shows the plots of maximum errors versus iteration step: convergence trajectories, transverse load and total Nusselt number determined within the dimple when the size of an additional grid is assigned (Figure 3a). Figure 4 illustrates the convergence trajectories chosen for maximum errors of the following variables u, p, T, k at each iteration step Nit: Erru, Errp, ErrT, Errk at linear and logarithmic scales.
Calculation is over when the maximum error does not exceed 10−5. However, the experience with calculating separated flows [58] shows that it is not enough to control how a solution is set only in terms of errors and that it is necessary to observe the convergence in terms of integral characteristics. In the current study, transverse load Rz and heat transfer Nus in the dimple region are chosen as integral parameters.
The analysis of the convergence trajectories for conical and oval-trench dimples says that despite a greater number of iterations sometimes because of the use of a more detailed grid in the case of an oval dimple, the decrease in errors due to an increase in Nit is generally regressive in character and close to a linear one (Figure 4a,b,e,f). In the case of the conical dimple, Rz needs much time to be set and practically this takes place during the entire convergence process (about 3000 iterations).
This is mainly associated with the fact that a symmetrical vortex is formed in the dimple. At the same time, in the case of the oval dimple, Rz was set during 1500–3000 iterations, whereas the entire process occurred during more than 10,000 iterations. Approximately, the same situation was observed when total heat is transported from the dimpled region, although in the case of the conical dimple Nus was set slightly faster than Rz. In the case of the oval dimple, Nus was set to the 1000th iteration; wherein Rz still significantly changes. As a whole, the convergence for integral characteristics in the case of the oval dimple was set faster than in the case of the conical dimple.

4. Testing, Verification, Validation

The test block contained several series of results. First, there is the verification of methodology and turbulence model by comparison of numerical predictions with Terekhov’s experiments in area of heat exchange in a spherical dimple on a thin channel wall. Second is a comparison of boundary conditions by T = const and q = const on example of flow over a spherical dimple. Third is the validation of computations in evaluation of influence of multi-block meshes on accuracy of solution of problem of convective heat exchange close to a tiled oval-trench dimple on wall of a thin channel.

4.1. Comparison of the Numerical Predictions with V.I. Terekhov’s Experimental Data

Figure 5 presents some numerical and assessed calculations of flow and heat transfer in the narrow channel with a spherical dimple of depth 0.13 at the thermally insulated channel wall with a heated dimple as done in [10].
In Figure 5a, the methods for assessment of hydraulic losses ζ in the narrow plane-parallel channel [32] are verified by comparing the obtained numerical predictions with the estimates according to the data [59]. A satisfactory agreement is obtained between the results that attest to the acceptable accuracy of the methods used.
The comparison of the calculated and measured distributions of the longitudinal distribution of the pressure coefficient Cp in the middle section of the dimple (Figure 5b), the Reynolds number dependences of heat transfer on the dimple spot and hydraulic losses (Figure 5c), as well as the longitudinal and transverse relative Nusselt number distributions in the middle section of the dimple (Figure 5d,e) shows as a whole their satisfactory agreement.

4.2. Predictions of Convective Heat Transfer in the Narrow Channel with a Spherical Dimple at T = const and q = const

Figure 6 and Figure 7 and Table 2 demonstrate some of the comparative analysis results for the influence of boundary conditions at the heated bottom wall with a spherical dimple. As in [32,33], three sections near a dimple are chosen for analysis and are numbered as in Table 3: 10—2.5 × 1.5 section with a spherical dimple center at a distance of 1 from the front boundary of the section; 20—square section surrounding the spherical dimple; 30—2 × 1.5 section in the dimple wake.
As follows from Table 2, the integral characteristics of the thermal and hydraulic performance of the channel with a spherical dimple are practically independent of the type of boundary conditions for heat transfer within the turbulent flow regime. However, the local distributions (Figure 6 and Figure 7) are significantly different in the near-edge zone and in the dimple center. Difference in maximum relative local heat transfer values is of the order of 1.5; at T = const, the loads against the near-edge zone are significantly higher than those at q = const.

4.3. Comparison of the Predictions Obtained by the Modified SST Models

In addition to the testing of the standard SST model [34] and the modified SST model [35] with curvature correction within the RLI and SM approaches for steady and unsteady two-dimensional separated flows [36,60,61,62]: circulation flow in square and circular cavities at the walls of plane-parallel and return channels and flow around a semi-circular body at a zero angle of attack, we compared the numerical predictions obtained using the modified SST models for three-dimensional steady separated flows in the narrow channel with an oval-trench dimple of width b = 0.383. Figure 8 and Table 3 show some of the obtained results.
We compared the local and integral characteristics of flow and heat transfer in the narrow channel with an oval dimple. We predicted about 1.6 mln cells at the wall. Table 4 is also supplemented by the refined calculations obtained by the modified SST model [35] with curvature correction within the RLI approach on the grid with 3 mln cells.
As shown by the two-dimensional tests, especially in the calculation of unsteady vortex flows, the modified SST model [35] predicts artificial turbulent viscosity in the cores of large-scale vortices. The reason for this is the strain rate tensor modulus introduced into the definition of eddy viscosity. As a result, there is a need to modify the SST model [35] in order to eliminate this non-physical viscosity. Here, two approaches were under consideration: direct viscosity correction in terms of the inverse linear dependence on turbulent Richardson number, when the semi-empirical constant Cc = 0.02 is added (RLI approach), and correction functions introduced into the system of equations for the modified SST model [35] (SM approach). We assumed that the correction within the RLI approach is preferable according to the test results [36,60,61,62].
The comparison of the integral characteristics of Table 3, as well as of the distributions of the local parameters at the streamlined surface and of the strip-integrated Nusselt numbers around and inside the dimple showed rather a good proximity of the numerical predictions obtained by all modified SST models. Some distinctions of the modified SST models [35] are not big but noticeable, especially in the case of local high heat fluxes.
The qualitative differences in the numerical predictions of local flow parameters and turbulence characteristics determined by different SST models manifested themselves in the vertical distributions in the dimple center (Figure 9). The differences in the velocity component distributions obtained by the modified SST model [35] are very noticeable, and the scatters of turbulence energy and Re-normalized eddy viscosity are particularly large. The overestimation of k and Reνt is especially noticeable in the spiral vortex core. This indicates that an error is present in the modified SST model [35] in the calculation of high-intensity 3D separated flows.

4.4. Validation

We compared the calculation results for convective heat transfer in the narrow channel wall with an oval dimple of width 0.383 on grids having 1.6 mln cells (Grid A) and about 3 mln cells (Grid B). These data are cited in Table 3 and Table 4 and shown in Figure 9 and Figure 10. The modified SST model corrected within the RLI approach [35] was used in the present study.
The comparisons of the numerical predictions of local and integral characteristics of flow and heat transfer in the channel with an oval-trench dimple on grids with about 1.6 mln cells and about 3 mln cells demonstrate their proximity. This means that the accuracy of the data for a moderate-depth grid is quite acceptable.

5. Results and Discussion

In the present study, main attention was paid both to the assessment of the influence of increase in the oval dimple length on fluid dynamics and heat transfer in the narrow channel with a dimple of fixed spot area and to the comparison of an oval dimple with spherical and conical dimples. The objective of the study was to select an oval dimple that is the best in the thermal and hydraulic performance. The work done was the embodiment of the concept of heat transfer enhancement by spiral vortices formed in oval-trench dimples in order to enhance secondary flow in the channel. The study as presented here clarifies and develops the research began in [63].
Figure 11 illustrates the temperature field variations at the heated wall of the narrow channel and the streamlines. First of all, it is of interest to note that in solving the thermal problem, where a fully developed isothermal flow at the channel inlet was assigned, heat transfer had time to stabilize in the vicinity of the dimple. As the dimple width decreased, the regions with a temperature close to characteristic and equal to 293 К increased. It can be seen that the flow structure near the dimple changes and the temperature field transformed. Very long decreased temperature regions appeared behind the dimple in comparison to the temperature regions at the plane wall of the narrow plane-parallel channel.
Figure 12, Figure 13 and Figure 14 compare the temperature fields and dimple width variations for the sake of a careful analysis of the changes in the flow structure and their influence on heat transfer. It is noteworthy that when considering conical, spherical and oval dimples with cylindrical insert lengths of 0.5 and 0.625 (Figure 12), the increased wall temperature regions were related to the stagnated flow regions (leeward region of a conical dimple) and to the places, where vortices wer generated, on the sides of the spherical dimple and in the leeward edge vicinity of oval dimples.
All flow patterns demonstrated a separated flow within the entire space of dimples, although for the spherical dimple the flow was attached on the windward side rather far from the trailing edge. Varying the cylindrical insert length and the dimple width transformed the internal flow on the leeward side of the oval dimple. A line appeared that separated the separated backflow zone behind the leading edge from the flow issuing from the dimple.
The oval dimple with the insert of length L = 0.675 (Figure 13a) is characteristic of two separating streamlines formed on the leeward side. In the dimple with the insert of length L = 0.75 (Figure 13b), a local vortex structure formed in the vicinity of the trailing edge and is accompanied by an increased temperature region. In the dimple with the cylindrical insert of length L = 0.9, a spiral vortex finally formed (Figure 13c). First, the separation zone was localized in the vicinity of the leading edge. Second, the backflow zone started forming behind the trailing edge. The dimple with the cylindrical insert of length L = 1 is one of the basic dimples analyzed; in fact, the flow around this dimple repeats flow around the dimple with L = 0.9 (Figure 13d). The dimple with the insert of length L = 1.25 (Figure 14a) revealed some flow instability. The flow in the vicinity of the trailing edge became separated in character. The spiral vortex formed in the dimple was ready to leave it. The flow structure changed in the dimple with the cylindrical insert of length L = 1.5 (Figure 14b).
It can be seen how the spiral vortex leaves the oval-trench dimple, not having reached the vicinity of the trailing edge. It is interesting to note that in this zone, a sink with an increased temperature region formed. Increasing the insert length L to 1.75 (Figure 14c) is accompanied by a further development of a secondary vortex zone in the vicinity of the trailing edge. The increased temperature region has rather large sizes. The largest oval dimple had a cylindrical insert of length L = 2 and a relative length of 6.78 (in terms of dimple width). As a whole, it is interesting to note that temperature fields in the vicinity of long dimples (L = 1.5, 1.75, 2) were similar, if their geometric sizes are considered in terms of dimple width. This is fairly indicative of the fact that a self-similar vortex is formed in the oval-trench dimple. The relative friction distributions f/fpl(s) in the central section of the oval-trench dimple at different cylindrical insert lengths L are shown in Figure 15a,b. The coordinate s is taken from the leading edge of the dimple. In Figure 12, the group of oval dimples of moderate length (L = 0.5–0.625) is characteristic of the formation of a large-scale separated flow zone covering almost the entire inner surface of dimples. A minimum relative friction value is −0.5, and a sharp friction increase (of order 2) is seen at the trailing edge of dimples.
Decreasing the width of the oval dimple, when its depth is increased and is kept constant, caused the flow structure to change in the separation zone. Backflow on the spherical portion of the dimple enhances while on the trench portion was slowed down. At L = 0.9 (dashed line), relative friction on the trench portion becomes positive, i.e., the separation zone was localized on the entrance portion of the oval-trench dimple, while (f/fpl)min decreased to −0.8.
As seen from Figure 15a,b, with a further increase in the dimple length, the separated flow intensity considerably enhances. At L = 2, (f/fpl)min decreases to −1.5. Behind the separation zone, the trench portion is characteristic of the flow acceleration zone with a local maximum relative friction value equal to 0.3–0.4.
As the width of the oval dimple is decreased, the relative Nusselt number distribution changes (Figure 16c,d). Similar to decreasing the minimum relative friction value in Figure 15a,b, the maximum value of Nu/Nupl increased in the vicinity of the spherical portion of the oval dimple from 1.2 to 1.6 when L is varied from 0.5 to 0.9. With a further increase in the dimple length, the maximum value of the Nusselt number (Nu/Nupl) in the separation zone reached 2.1 at L = 1.5–2.
In many ways, the behavior of the Nusselt number is defined by the wall temperature (Figure 15e,f). Thus, the mentioned minimum value of heat loads at L = 1.75 corresponds to a maximum value of Tw/Twpl equal to 1.055. The fact is that high wall temperatures in the oval dimple with a moderate length of the cylindrical insert correlate with low heat transfer in separation zones. At the same time, the subcooling of the surface of the dimple, i.e., when the surface temperature decreases below the temperature of the plane-parallel channel wall and is accompanied by the growth of heat transfer.
As the length of the cylindrical insert of the oval dimple L is increased above 1.25, Tw/Twpl becomes less than 1 in the separation zone. The region of dimple subcooling coincides with the zone of enhanced heat transfer and, vice versa, the increased temperature regions correspond to the low heat transfer zones.
To determine the influence of the oval dimple width b on the integral characteristics of flow and heat transfer is an important subject of the present study (Figure 16). With a decrease in b, when the dimple spot area is kept constant, the length of the cylindrical insert of the dimple is increased from 1 to 6.78, and therefore, the degree of influence of the dimple on flow in the near-wake. The total Nusselt number Nun is calculated on the control area of the rectangular section 3 in length and 2 in width (with a shift by 0.5 relative to the center downstream) around the dimple without and with regard to the increase in the curvilinear surface of the dimple. Figure 16 serves to illustrate the ratio of the total Nusselt number Nun in the section (in Table 3 the section is designated by 1) of the dimpled wall to the equivalent characteristic for the plane channel Nunpl. Hydraulic losses are determined, as described in [32], in terms of the boundaries of the control section of the dimpled (ζ) and plane (ζpl) channels (Figure 3). Thermal and hydraulic performance (THP) are calculated as the ratio of the thermal performance Nun/Nunpl in the selected section to relative hydraulic losses ζ/ζpl at the boundaries of the section.
With increasing the length of the cylindrical insert of the oval dimple to 6.78 (in terms of width), the thermal and hydraulic performance of the rectangular section of the dimpled channel were dramatically improved in comparison to the spherical dimple: THP = 1.17 versus 1.002; for the last THP with the consideration of increase in the area of the streamlined wall of the channel, it was less than 1.
For the rectangular section with longer oval dimples, the rate of increasing the thermal performance was considerably ahead of increase in hydraulic losses. The thermal performance of the dimple with L = 2 was six times higher than that of the spherical dimple with no regard to the area of the inner surface of dimples and was four times more preferred with regard to the area of the streamlined wall (Nun/Nunpl = 1.245 versus 1.063 and 1.19 versus 1.054, respectively).
Hydraulic losses in the section with the oval dimple were maximum at the dimple width b = 0.549 (the cylindrical insert length was equal to 1) that exceed by a factor of 1.5 hydraulic losses in the case of the spherical dimple. Hydraulic losses in the section with a narrow dimple with L = 2 appeared to be the smallest and practically equal to hydraulic losses in the section with a basic spherical dimple.

6. Conclusions

  • The analysis of longer oval dimples located at a 45° angle of orientation to the flow in the channel showed that methodologically, it was important to fix a spot area of a dimple and its depth for the same channel.
  • Tasks of hydrodynamics and heat transfer were solved with the use of original MCTs on different-scale structured overlapping grids of simple topology. These technologies meant for solution of RANS—steady Reynolds-averaged Navier–Stokes equations—were implemented in the VP2/3 code and were tested in the present study using the turbulence models and boundary conditions for heat transfer.
  • Testing calculations:
    • Testing was performed on the experimental setup [9] for determining characteristics of convective heat transfer near a heated spherical dimple of depth 0.13 over the Re number range 104–105 (MCTs) with the use of the VP2/3 code and the shear stress transport (SST) model [34] with curvature correction within the Rodi–Leschziner–Isaev (RLI) approach [36]. A fair agreement between numerical predictions and measurement data was obtained.
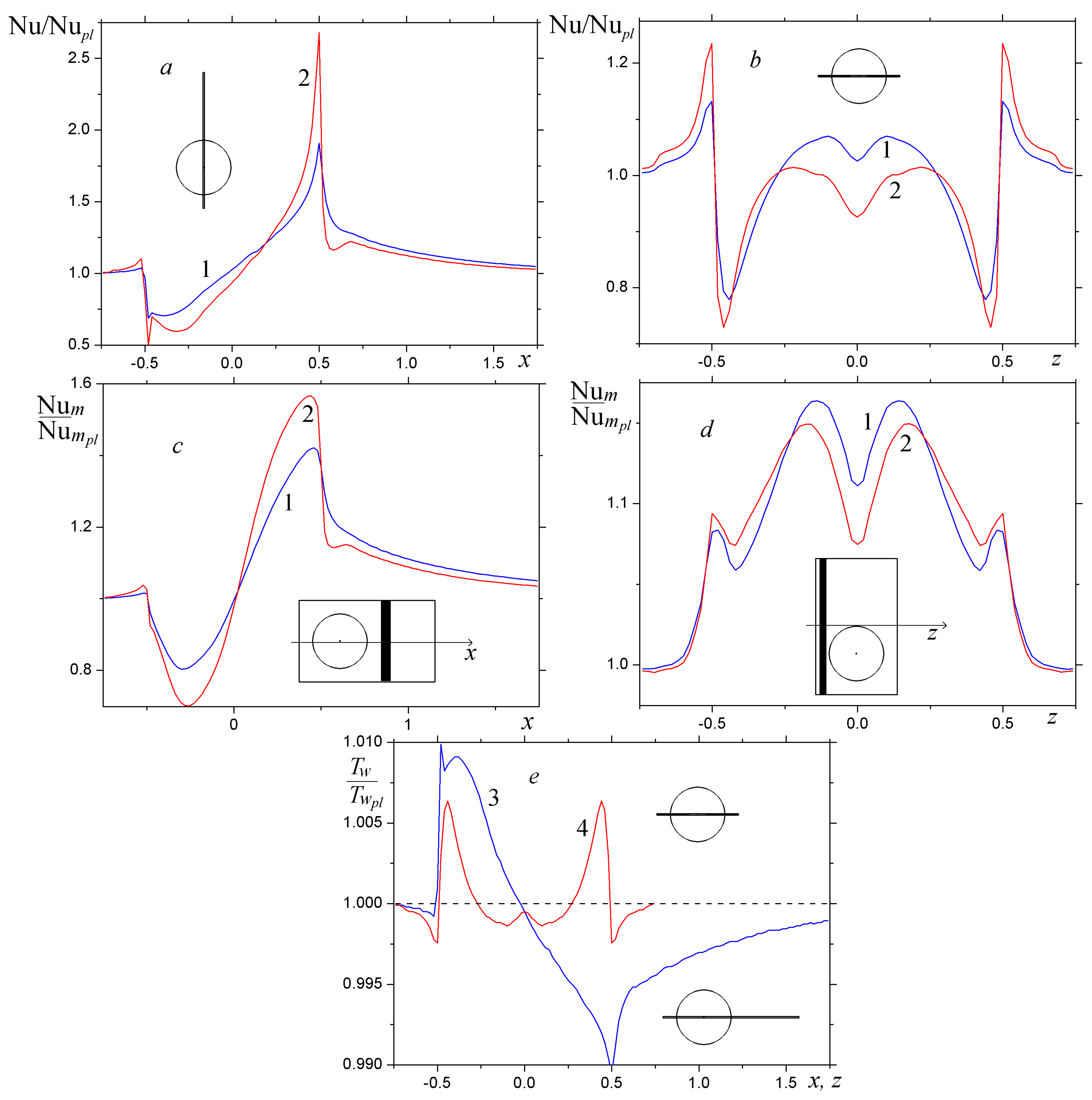
    • The comparison of the boundary conditions T = const and q = const in the problem on heat transfer in the vicinity of a shallow spherical dimple in the narrow channel showed that integral characteristics of the thermal and hydraulic performance of the channel with a spherical dimple practically are independent of the type of boundary conditions for heat transfer within the turbulent flow regime. However, local distributions are substantially different in the near-edge zone and in the dimple center. Difference in maximum relative local heat transfer values is 1.5; at the same time, loads against the near-edge zone are much higher at T = const than at q = const.
    • The comparison of the SST models [34,35] and the SST model [36,39] with curvature correction within the Rodi–Leschziner–Isaev (RLI) approach and the Smirnov–Menter (SM) approach showed that the numerical predictions of integral characteristics are pretty close according to the standard and modified SST models. Some differences in the SST model [35] are small, but noticeable, especially in zones of extreme local heat fluxes. However, it was seen that the values of k and Reνt in the spiral vortex core were too high. This is indicative of the fact that error is available in the standard SST model [34] in the calculation of high-intensity 3D separated flows.
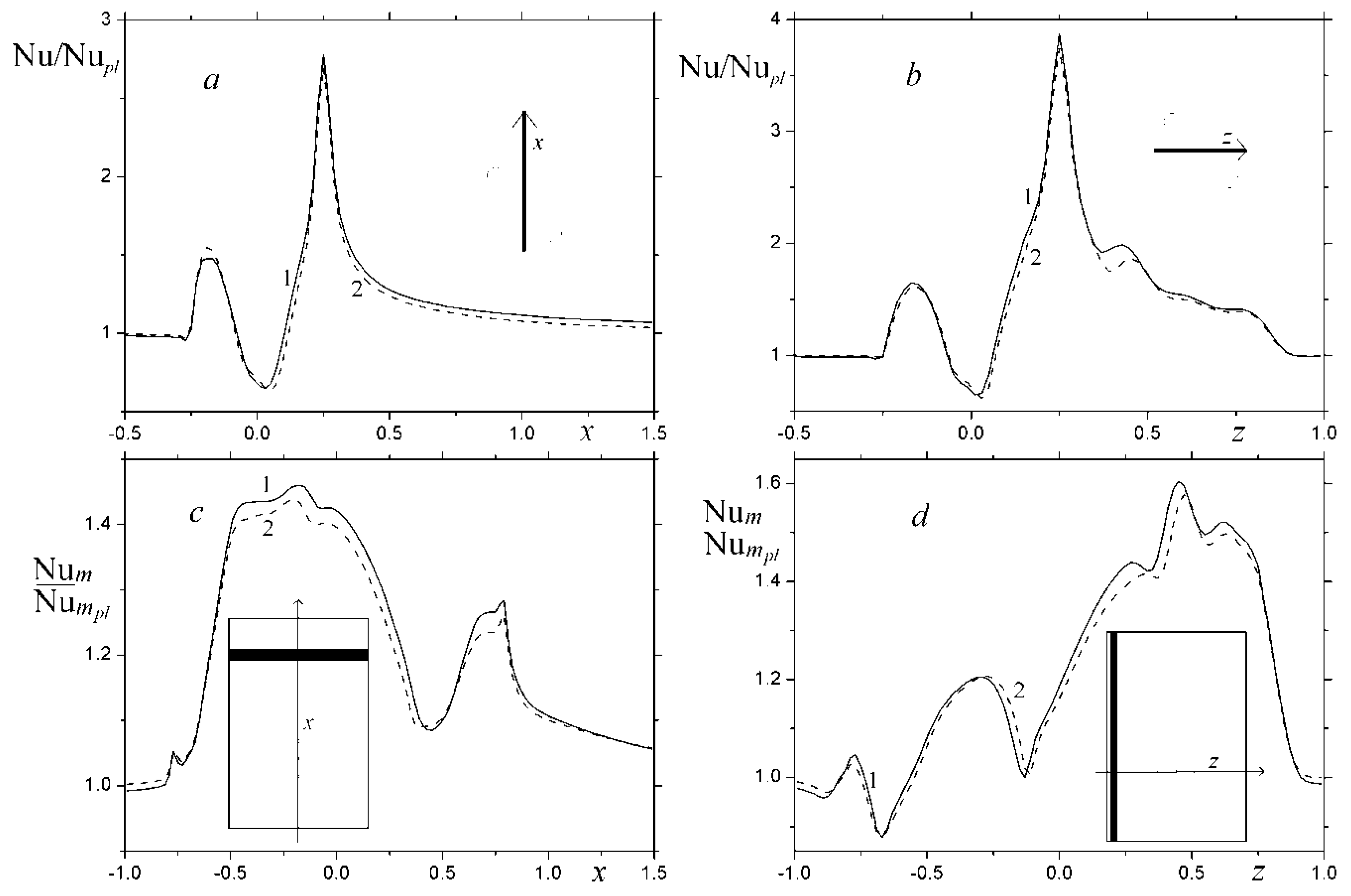
    • The computational algorithm was validated by comparing numerical predictions for local and integral characteristics of flow and heat transfer in the channel with an oval-trench dimple that were obtained on the grids with 1.6 mln cells and about 3 mln cells. Their fair agreement shows that the data for the dimple with a moderate cylindrical insert length are quite acceptable in accuracy.
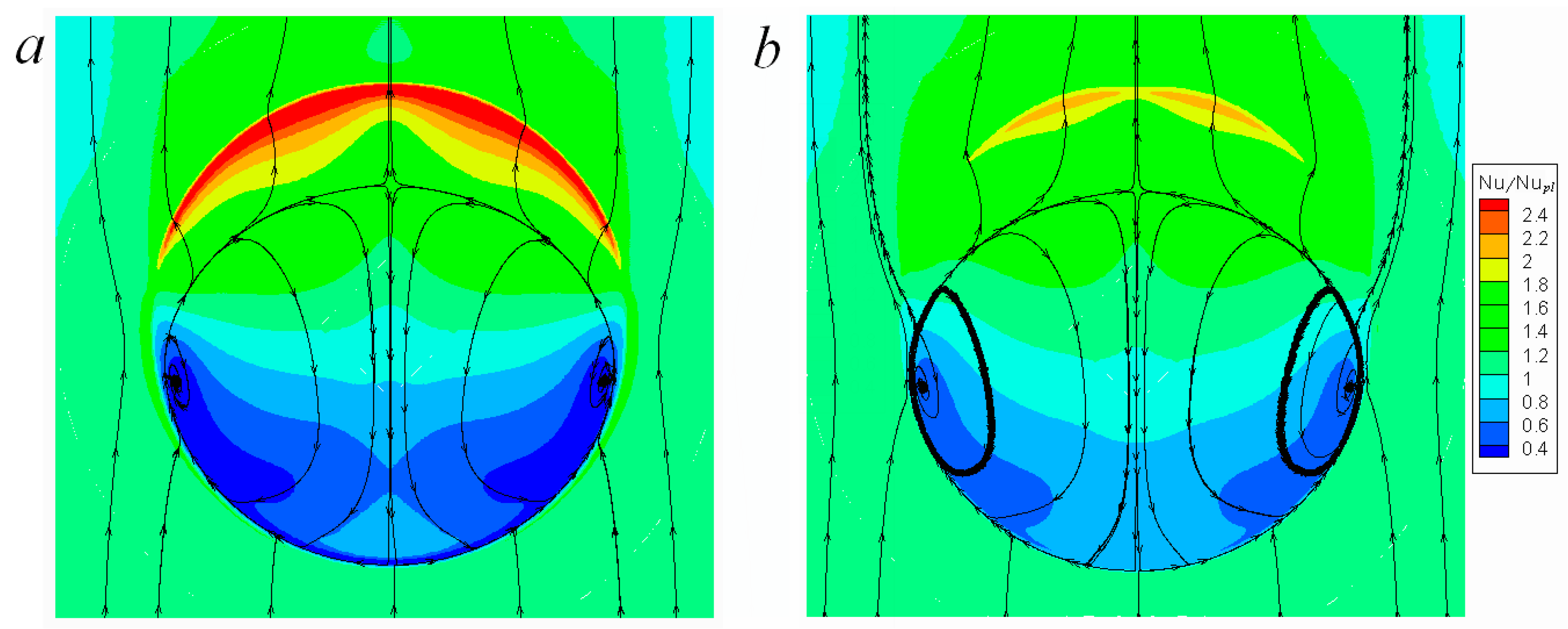
  • We revealed a series of oval-trench dimples with the cylindrical insert length 0.625–0.9, in which the separated flow structure gradually changed, the separation zone was localized behind the leading edge and backflow enhanced in it. The oval-trench dimple becomes flowing and non-separated throughout behind the separation zone.

Author Contributions

Conceptualization, S.I. and A.L.; Methodology, S.I. and A.S.; Software, S.I.; Validation, S.I., Y.C. and I P.; Formal Analysis, S.I.; Investigation, S.I. and D.N.; Resources, A.S.; Data Curation, S.I. and D.N.; Writing-Original Draft Preparation, S.I. and D.N.; Writing-Review & Editing, Y.C. and I.P.; Visualization, I.P.; Supervision, S.I. and A.L.; Project Administration, S.I.; Funding Acquisition, S.I.

Funding

This research was funded by the Russian Scientific Foundation grant number 19-19-00259.

Acknowledgments

The authors thank Professor Victor Terekhov for the discussion of the project results.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Dreitser, G.A. Problems in developing highly efficient tubular heat exchangers. Therm. Eng. 2006, 53, 279–287. [Google Scholar] [CrossRef]
  2. Hagen, R.L.; Danak, A.M. Heat transfer in the field of the turbulent boundary layer separation over a dimple. Heat Transf. 1967, 4, 62–69. [Google Scholar]
  3. Presser, K.H. Empirische gleichungen zur berechnung der stoff–und warmeubertragung fur den spezialfal der abgerissenen stromung. Int. J. Heat Mass Transf. 1972, 15, 2447–2471. [Google Scholar] [CrossRef]
  4. Hiwada, M.; Kawamura, T.; Mabuchi, J.; Kumada, M. Some characteristics of flow pattern and heat transfer past a circular cylinder cavity. Bull. JSME 1983, 26, 1744–1758. [Google Scholar] [CrossRef]
  5. Snedeker, S.; Donaldson, D.P. Observation of bistable flow in hemispherical cavity. AIAA J. 1966, 4, 735–736. [Google Scholar]
  6. Gromov, P.R.; Zobnin, A.B.; Rabinovich, M.I.; Sushchik, M.M. Creation of solitary vortices in a flow around shallow spherical depressions. Sov. Tech. Phys. Lett. 1986, 12, 1323–1328. [Google Scholar]
  7. Kesarev, V.S.; Kozlov, A.P. Convective heat transfer in turbulized flow past a hemispherical cavity. Heat Transf. Sov. Res. 1993, 25, 156–160. [Google Scholar]
  8. Syred, N.; Khalatov, A.; Kozlov, A.; Shchukin, A.; Agachev, R. Effect of surface curvature on heat transfer and hydrodynamics within a single hemispherical dimple. ASME J. Turbomach. 2001, 123, 609–613. [Google Scholar] [CrossRef]
  9. Terekhov, V.I.; Kalinina, S.V.; Mshvidobadze, Y.M. Pressure field and resistance of a single cavity with sharp and rounded edges. J. Appl. Mech. Tech. Phys. 1993, 34, 331–338. [Google Scholar] [CrossRef]
  10. Terekhov, V.I.; Kalinina, S.V.; Mshvidobadze, Y.M. Heat transfer coefficient and aerodynamic resistance on a surface with a single dimple. Enhanc. Heat Transf. 1997, 4, 131–145. [Google Scholar] [CrossRef]
  11. Kiknadze, G.I.; Gachechiladze, I.A.; Gorodkov, A.Y. Self-organization of tornado-like jets in flows of gases and liquids and the technologies utilizing this phenomenon. In Proceedings of the 2009 ASME Summer Heat Transfer Conference, San Francisco, CA, USA, 19–23 July 2009. Paper No. HT 2009–88644. [Google Scholar]
  12. Ligrani, P.M.; Oliveira, M.M.; Blaskovich, T. Comparison of heat transfer augmentation techniques. AIAA J. 2003, 41, 337–362. [Google Scholar] [CrossRef]
  13. Afanasyev, V.N.; Chudnovsky, Y.P.; Leontiev, A.I.; Roganov, P.S. Turbulent ow friction and heat transfer characteristics of spherical cavities on a plate. Exp. Therm. Fluid Sci. 1993, 7, 1–8. [Google Scholar] [CrossRef]
  14. Chyu, M.K.; Yu, Y.; Ding, H. Heat transfer enhancement in rectangular channels with concavities. Enhanc. Heat Transf. 1999, 6, 429–439. [Google Scholar] [CrossRef]
  15. Turnow, J. Flow Structure and Heat Transfer on Dimpled Surfaces. Ph.D. Thesis, University of Rostock, Rostock, Germany, 2011. [Google Scholar]
  16. Ligrani, P.M.; Harrison, J.L.; Mahmmod, G.I.; Hill, M.L. Flow structure due to dimple depressions on a channel surface. Phys. Fluids 2001, 13, 3442–3451. [Google Scholar] [CrossRef]
  17. Mahmood, G.I.; Sabbagh, M.Z.; Ligrani, P.M. Heat transfer in a channel with dimples and protrusions on opposite walls. J. Thermophys. Heat Transf. 2001, 15, 275–283. [Google Scholar] [CrossRef]
  18. Ligrani, P.M.; Mahmood, G.I.; Harrison, J.L.; Clayton, C.M.; Nelson, D.I. Flow structure and local Nusselt number variations in a channel with dimples and protrusions on opposite walls. Int. J. Heat Mass Transf. 2001, 45, 2011–2020. [Google Scholar] [CrossRef]
  19. Ekkad, S.V.; Nasir, H. Dimple enhanced heat transfer in high aspect ratio channels. J. Enhanc. Heat Transf. 2003, 10, 395–405. [Google Scholar] [CrossRef]
  20. Mahmood, G.I.; Ligrani, P.M. Heat transfer in a dimpled channel combined influences of aspect ratio, temperature, Reynolds number and flow structure. Int. J. Heat Mass Transf. 2004, 45, 2011–2020. [Google Scholar] [CrossRef]
  21. Hwang, S.D.; Kwon, H.G.; Cho, H.H. Heat transfer with dimple/protrusion arrays in a rectangular duct with a low Reynolds number range. Int. J. Heat Fluid Flow 2008, 29, 916–926. [Google Scholar] [CrossRef]
  22. Mityakov, V.Y.; Mityakov, A.V.; Sapozhnikov, S.Z.; Isaev, S.A. Local heat fluxes on the surfaces of dimples. Ditches and cavities. Therm. Eng. 2007, 54, 200–203. [Google Scholar] [CrossRef]
  23. Voskoboinik, A.V.; Voskoboinik, V.A.; Isaev, S.A.; Zhdanov, V.L.; Kornev, N.V.; Turnow, J. Bifurcation of vortex flow inside a spherical dimple in the narrow channel. Appl. Hydromech. 2011, 13, 3–21. (In Russian) [Google Scholar]
  24. Voskoboinick, V.; Kornev, N.; Turnow, J. Study of Near Wall Coherent Flow Structures on Dimpled Surfaces Using Unsteady Pressure Measurements. Flow Turbul. Combust. 2013, 90, 709–722. [Google Scholar] [CrossRef]
  25. Mitsudharmadi, H.; Tay, C.M.J.; Tsai, H.M. Effect of rounded edged dimple arrays on the boundary layer development. Vis. Soc. Jpn. J. Vis. 2009, 12, 17–25. [Google Scholar] [CrossRef]
  26. Tay, C.M.; Chew, Y.T.; Khoo, B.C.; Zhao, J.B. Development of flow structures over dimples. Exp. Therm. Fluid Sci. 2014, 52, 278–287. [Google Scholar] [CrossRef]
  27. Xiao, N.; Zhang, Q.; Ligrani, P.M.; Mongia, R. Thermal performance of dimpled surfaces in laminar flows. Int. J. Heat Mass Transf. 2009, 52, 2009–2017. [Google Scholar] [CrossRef]
  28. Kovalenko, G.V.; Terekhov, V.I.; Khalatov, A.A. Flow regimes in a single dimple on the channel surface. J. Appl. Mech. Tech. Phys. 2010, 51, 839–848. [Google Scholar] [CrossRef]
  29. Kwon, H.G.; Hwang, S.D.; Cho, H.H. Measurement of local heat/mass transfer coefficients on a dimple using naphthalene sublimation. Int. J. Heat Mass Transf. 2011, 54, 1071–1080. [Google Scholar] [CrossRef]
  30. Lan, J.; Xie, Y.; Zhang, D. Effect of leading edge boundary layer thickness on dimple flow structure and separation control. J. Mech. Sci. Technol. 2011, 25, 3243–3251. [Google Scholar] [CrossRef]
  31. Heo, S.-C.; Seo, Y.-H.; Ku, T.-W.; Kang, B.-S. Formability evaluation of dimple forming process based on numerical and experimental approach. J. Mech. Sci. Technol. 2011, 25, 429–439. [Google Scholar] [CrossRef]
  32. Isaev, S.A.; Kornev, N.V.; Leontiev, A.I.; Hassel, E. Influence of the Reynolds number and the spherical dimple depth on the turbulent heat transfer and hydraulic loss in a narrow channel. Int. J. Heat Mass Transf. 2010, 53, 178–197. [Google Scholar] [CrossRef]
  33. Isaev, S.A.; Schelchkov, A.V.; Leontiev, A.I.; Baranov, P.A.; Gulcova, M.E. Numerical simulation of the turbulent air flow in the narrow channel with a heated wall and a spherical dimple placed it for vortex heat transfer enhancement depending on the dimple depth. Int. J. Heat Mass Transf. 2016, 94, 426–448. [Google Scholar] [CrossRef]
  34. Menter, F.R. Zonal two equation k–ω turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. AIAA Paper No. 93-2906. [Google Scholar]
  35. Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Turbulence, Heat and Mass Transfer 4; Hajalic, K., Nogano, Y., Tummers, M., Eds.; Begell House Inc.: Danbury, CT, USA, 2003; 8p. [Google Scholar]
  36. Isaev, S.A.; Baranov, P.A.; Zhukova, Y.V.; Usachov, A.E.; Kharchenko, V.B. Correction of the shear-stress-transfer model with account for the curvature of streamlines in calculating separated flows of an incompressible viscous fluid. J. Eng. Phys. 2014, 87, 1002–1015. [Google Scholar] [CrossRef]
  37. Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flow. Comp. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
  38. Leschziner, M.; Rodi, W. Calculation of annular and twin parallel jets using various discretization schemes and turbulence-model variations. Trans. ASME. J. Fluids Eng. 1981, 103, 352–365. [Google Scholar] [CrossRef]
  39. Smirnov, P.E.; Menter, F. Sensitization of the SST turbulence model to rotation and curvature by applying the Spalart-Shur correction term. J. Turbomach. 2009, 131, 041010. [Google Scholar] [CrossRef]
  40. Spalart, P.R.; Shur, M.L. On the sensitization of turbulence models to rotation and curvature. Aerosp. Sci. Technol. 1997, 1, 297–302. [Google Scholar] [CrossRef]
  41. Menter, F.; Ferreira, J.C.; Esch, T.; Konno, B. Turbulence model with improved wall treatment for heat transfer predictions in gas turbines. In Proceedings of the Internatinal Gas Turbine Congress, Tokyo, Japan, 2–7 November 2003. [Google Scholar]
  42. Isaev, S.A.; Baranov, P.A.; Usachov, A.E. Multiblock Computational Technologies in the VP2/3 Package on Aerothermodynamics; LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2013; 316p. [Google Scholar]
  43. Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999; 389p. [Google Scholar]
  44. Van Doormaal, J.P.; Raithby, G.D. Enhancement of the SIMPLE method for predicting incompressible fluid flow. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
  45. Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, University of London and Diploma of Imperial College of Science, Technology and Medicine, London, UK, 1996. [Google Scholar]
  46. Isaev, S.A.; Kudryavtsev, N.A.; Sudakov, A.G. Numerical modeling of a turbulent incompressible viscous flow along bodies of a curvilinear shape in the presence of a mobile shield. J. Eng. Phys. Thermophys. 1998, 71, 613–626. [Google Scholar]
  47. Rhie, C.M.; Chow, W.L. A numerical study of the turbulent flow past an isolated airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
  48. Pascau, A.; Garcia, N. Consistency of SIMPLEC scheme in collocated grids. In Proceedings of the V European Conference on Computational Fluid Dynamics ECCOMAS CFD 2010, Lisbon, Portugal, 14–17 June 2010. [Google Scholar]
  49. Leonard, B.P. A stable and accurate convective modeling procedure based on quadratic upstream interpolation. Comp. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
  50. Van Leer, B. Towards the ultimate conservative difference scheme V. A second order sequel to Godunov’s method. J. Comp. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
  51. Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003; 567p. [Google Scholar]
  52. Demidov, D. AMGCL: C++ Library for Solving Large Sparse Linear Systems with Algebraic Multigrid Method. Available online: http://amgcl.readthedocs.org (accessed on 3 April 2019).
  53. Isaev, S.A.; Zhdanov, V.L.; Niemann, H.-J. Numerical study of the bleeding effect on the aerodynamic characteristics of a circular cylinder. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1217–1226. [Google Scholar] [CrossRef]
  54. Isaev, S.A.; Sudakov, A.G.; Baranov, P.A.; Zhukova, Y.V.; Usachov, A.E. Analysis of errors of multiblock computational technologies by the example of calculating a circulation flow in a square cavity with a moving cover at Re = 1000. J. Eng. Phys. 2013, 86, 1134–1150. [Google Scholar]
  55. Zheng, Y.; Liou, M.-S. A novel approach of three-dimensional hybrid grid methodology: Part 1. Grid generation. Comput. Methods Appl. Mech. Eng. 2003, 192, 4147–4171. [Google Scholar] [CrossRef] [Green Version]
  56. Isaev, S.A.; Leontiev, A.I.; Gul’tsova, M.E.; Popov, I.A. Transformation and intensification of tornado-like flow in a narrow channel during elongation of an oval dimple with constant area. Tech. Phys. Lett. 2015, 41, 606–609. [Google Scholar] [CrossRef]
  57. Isaev, S.A.; Leontiev, A.I. Numerical simulation of vortex enhancement of heat transfer under conditions of turbulent floe past a spherical dimple on the wall of a narrow channel. High Temp. 2003, 41, 665–679. [Google Scholar] [CrossRef]
  58. Isaev, S.A.; Baranov, P.A.; Kudryavtsev, N.A.; Lisenko, D.A.; Usachov, A.E. Complex analysis of turbulence models, algorithms, and grid structures at the computation of recirculating flow in a cavity by means of VP2/3 and FLUENT packages. Part. 1. Scheme factors influence. Thermophys. Aeromech. 2005, 12, 549–569. [Google Scholar]
  59. Idelchik, I.E. Handbook on Hydraulic Resistance; Mashinostroyeniye: Moscow, Russia, 1992; 672p. [Google Scholar]
  60. Isaev, S.A.; Baranov, P.A.; Usachov, A.E.; Zhukova, Y.V.; Vysotskaya, A.A.; Malyshkin, D.A. Simulation of the turbulent air flow over a circular cavity with a variable opening angle in an U-shaped channel. J. Eng. Phys. Thermophys. 2015, 88, 902–917. [Google Scholar] [CrossRef]
  61. Isaev, S.A.; Baranov, P.A.; Zhukova, Y.V.; Kalinin, E.I.; Miau, J.J. Verification of the shear-stress transfer model and its modifications in the calculation of a turbulent flow around a semicircular airfoil with a zero angle of attack. J. Eng. Phys. Thermophys. 2016, 89, 73–89. [Google Scholar] [CrossRef]
  62. Isaev, S.; Baranov, P.; Popov, I.; Sudakov, A.; Usachov, A.; Guvernyuk, S.; Sinyavin, A.; Chulyunin, A.; Mazo, A.; Demidov, D. Ensuring safe descend of reusable rocket stages–numerical simulation and experiments on subsonic turbulent air flow around a semi-circular cylinder at zero angle of attack and moderate Reynolds number. Acta Astronaut. 2018, 150, 117–136. [Google Scholar] [CrossRef]
  63. Isaev, S.A.; Schelchkov, A.V.; Leontiev, A.I.; Gortyshov, Y.F.; Baranov, P.A.; Popov, I.A. Tornado-like heat transfer enhancement in the narrow plane-parallel channel with the oval-trench dimple of fixed depth and spot area. Int. J. Heat Mass Transf. 2017, 109, 40–62. [Google Scholar] [CrossRef]
Energies 12 01296 g001 550
Figure 1. Channels with spherical (a), 10°-truncated conical (b) and oval dimples of width b = 0.731 (c), 0.549 (d), 0.429 (e) and 0.346 (f).
Figure 1. Channels with spherical (a), 10°-truncated conical (b) and oval dimples of width b = 0.731 (c), 0.549 (d), 0.429 (e) and 0.346 (f).
Energies 12 01296 g001
Energies 12 01296 g002 550
Figure 2. Spherical (a) and 10°-truncated conical (b) inserts in the multiblock structured grids in the narrow channel with single spherical (c,e), conical (d), oval (f,g) grids of different topology and width: (c,d,f,g)—view from the heated wall; e—middle section of the channel; (f–b) = 0.731; (g)—0.346.
Figure 2. Spherical (a) and 10°-truncated conical (b) inserts in the multiblock structured grids in the narrow channel with single spherical (c,e), conical (d), oval (f,g) grids of different topology and width: (c,d,f,g)—view from the heated wall; e—middle section of the channel; (f–b) = 0.731; (g)—0.346.
Energies 12 01296 g002
Energies 12 01296 g003 550
Figure 3. Multiblock grid for a narrow channel with an oval-trench dimple covered with a detailed grid in the dimple area and with edge selection (a), 3 × 2 dimpled section (b) and rectangular area of oval dimple (c). Channel cross sections A-B serve for determination of hydraulic losses.
Figure 3. Multiblock grid for a narrow channel with an oval-trench dimple covered with a detailed grid in the dimple area and with edge selection (a), 3 × 2 dimpled section (b) and rectangular area of oval dimple (c). Channel cross sections A-B serve for determination of hydraulic losses.
Energies 12 01296 g003
Energies 12 01296 g004 550
Figure 4. Convergence trajectories at linear (a,e) and logarithmic (b,f) scales, the dependences of the transverse load Rz (c,g) and the Nusselt number Nus (d,h) in the dimple region. Numbered curves: 1—Erru; 2—Errp; 3—ErrT; 4—Errk.
Figure 4. Convergence trajectories at linear (a,e) and logarithmic (b,f) scales, the dependences of the transverse load Rz (c,g) and the Nusselt number Nus (d,h) in the dimple region. Numbered curves: 1—Erru; 2—Errp; 3—ErrT; 4—Errk.
Energies 12 01296 g004
Energies 12 01296 g005 550
Figure 5. Verification: the comparison of the experimental data [10] with the numerical predictions of flow and heat transfer characteristics in the narrow channel with a spherical dimple (dimple spot heating at q = const): 1, 3—experiment [10]; 2, 4—calculation; 3, 4—hydraulic losses; 5—data [59]. (a) ζpl(Re); (b) Cp(x); (c) Nun(Re), 104ζ(Re); (d) Nu/Nupl(x); (e) Nu/Nupl(z)
Figure 5. Verification: the comparison of the experimental data [10] with the numerical predictions of flow and heat transfer characteristics in the narrow channel with a spherical dimple (dimple spot heating at q = const): 1, 3—experiment [10]; 2, 4—calculation; 3, 4—hydraulic losses; 5—data [59]. (a) ζpl(Re); (b) Cp(x); (c) Nun(Re), 104ζ(Re); (d) Nu/Nupl(x); (e) Nu/Nupl(z)
Energies 12 01296 g005
Energies 12 01296 g006 550
Figure 6. Calculated distributions of relative Nusselt numbers: local (a,b) and integrated over transverse (c) and longitudinal (d) strips of the selected section, as well as of relative wall temperature (e) in longitudinal (a,c,3) and transverse (b,d,4) middle sections of the dimple at different boundary conditions q = const (curves 1,3,4) and T = const (curves 2) at the heated wall of the narrow channel as in V.I. Terekhov’s setup.
Figure 6. Calculated distributions of relative Nusselt numbers: local (a,b) and integrated over transverse (c) and longitudinal (d) strips of the selected section, as well as of relative wall temperature (e) in longitudinal (a,c,3) and transverse (b,d,4) middle sections of the dimple at different boundary conditions q = const (curves 1,3,4) and T = const (curves 2) at the heated wall of the narrow channel as in V.I. Terekhov’s setup.
Energies 12 01296 g006
Energies 12 01296 g007 550
Figure 7. Calculated relative Nusselt number fields near the spherical dimple at the heated wall of the narrow channel at different boundary conditions and the streamlines: (a)—T = const; (b)—q = const.
Figure 7. Calculated relative Nusselt number fields near the spherical dimple at the heated wall of the narrow channel at different boundary conditions and the streamlines: (a)—T = const; (b)—q = const.
Energies 12 01296 g007
Energies 12 01296 g008 550
Figure 8. Distributions of longitudinal (a,b), vertical (c), transverse, (d) components of local flow velocity, turbulence energy (e) and normalized vortex viscosity (f) in the center of the oval dimple of width 0.383 obtained by the modified SST model: 1—SST model [34]; 2—SST model [35]; 3—SST model [35] with RLI correction; 4—SST model [35] with SM correction; 5—plane-parallel channel. b—longitudinal velocity component distribution (enlarged fragment).
Figure 8. Distributions of longitudinal (a,b), vertical (c), transverse, (d) components of local flow velocity, turbulence energy (e) and normalized vortex viscosity (f) in the center of the oval dimple of width 0.383 obtained by the modified SST model: 1—SST model [34]; 2—SST model [35]; 3—SST model [35] with RLI correction; 4—SST model [35] with SM correction; 5—plane-parallel channel. b—longitudinal velocity component distribution (enlarged fragment).
Energies 12 01296 g008
Energies 12 01296 g009 550
Figure 9. Relative Nusselt number distributions in the section of the narrow channel with the oval dimple of width 0.383 calculated on different grids: (a)—initial variant (about 1.6 mln cells); (b)—refinement (about 3 mln cells).
Figure 9. Relative Nusselt number distributions in the section of the narrow channel with the oval dimple of width 0.383 calculated on different grids: (a)—initial variant (about 1.6 mln cells); (b)—refinement (about 3 mln cells).
Energies 12 01296 g009
Energies 12 01296 g010 550
Figure 10. Distributions of relative local Nusselt numbers (a,b) and Nusselt numbers averaged over transverse (c) and longitudinal (d) strips of the rectangular section with the oval dimple (c,d) in longitudinal (a,c) and lateral (b,d) directions calculated on different grids: 1—initial variant (about 1.6 mln cells); 2—refinement (about 3 mln cells).
Figure 10. Distributions of relative local Nusselt numbers (a,b) and Nusselt numbers averaged over transverse (c) and longitudinal (d) strips of the rectangular section with the oval dimple (c,d) in longitudinal (a,c) and lateral (b,d) directions calculated on different grids: 1—initial variant (about 1.6 mln cells); 2—refinement (about 3 mln cells).
Energies 12 01296 g010
Energies 12 01296 g011 550
Figure 11. Temperature fields at the heated wall with oval dimples of width 1 (a), 0.731 (b), 0.549 (c), 0.429 (d) and the streamlines.
Figure 11. Temperature fields at the heated wall with oval dimples of width 1 (a), 0.731 (b), 0.549 (c), 0.429 (d) and the streamlines.
Energies 12 01296 g011
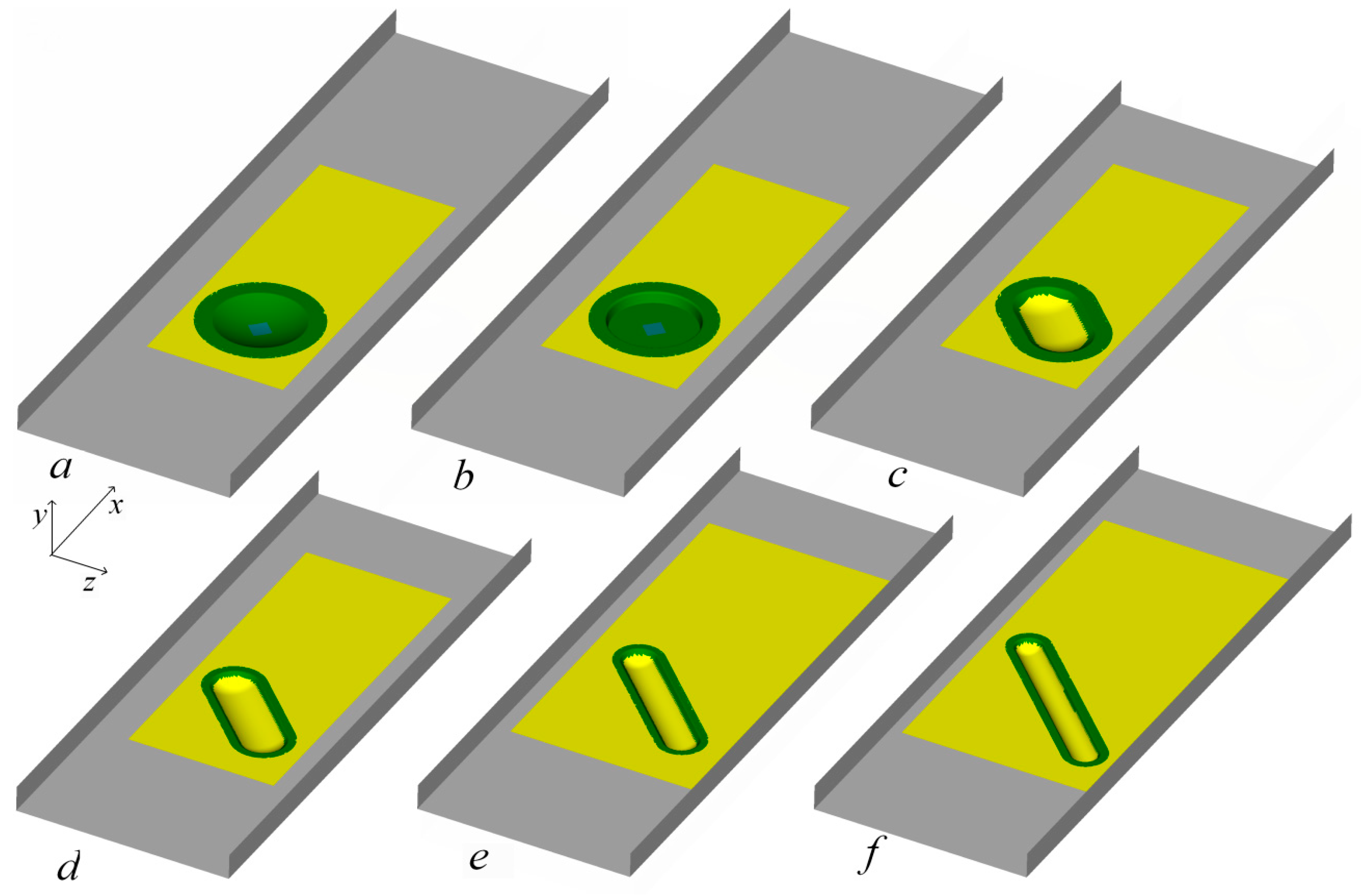
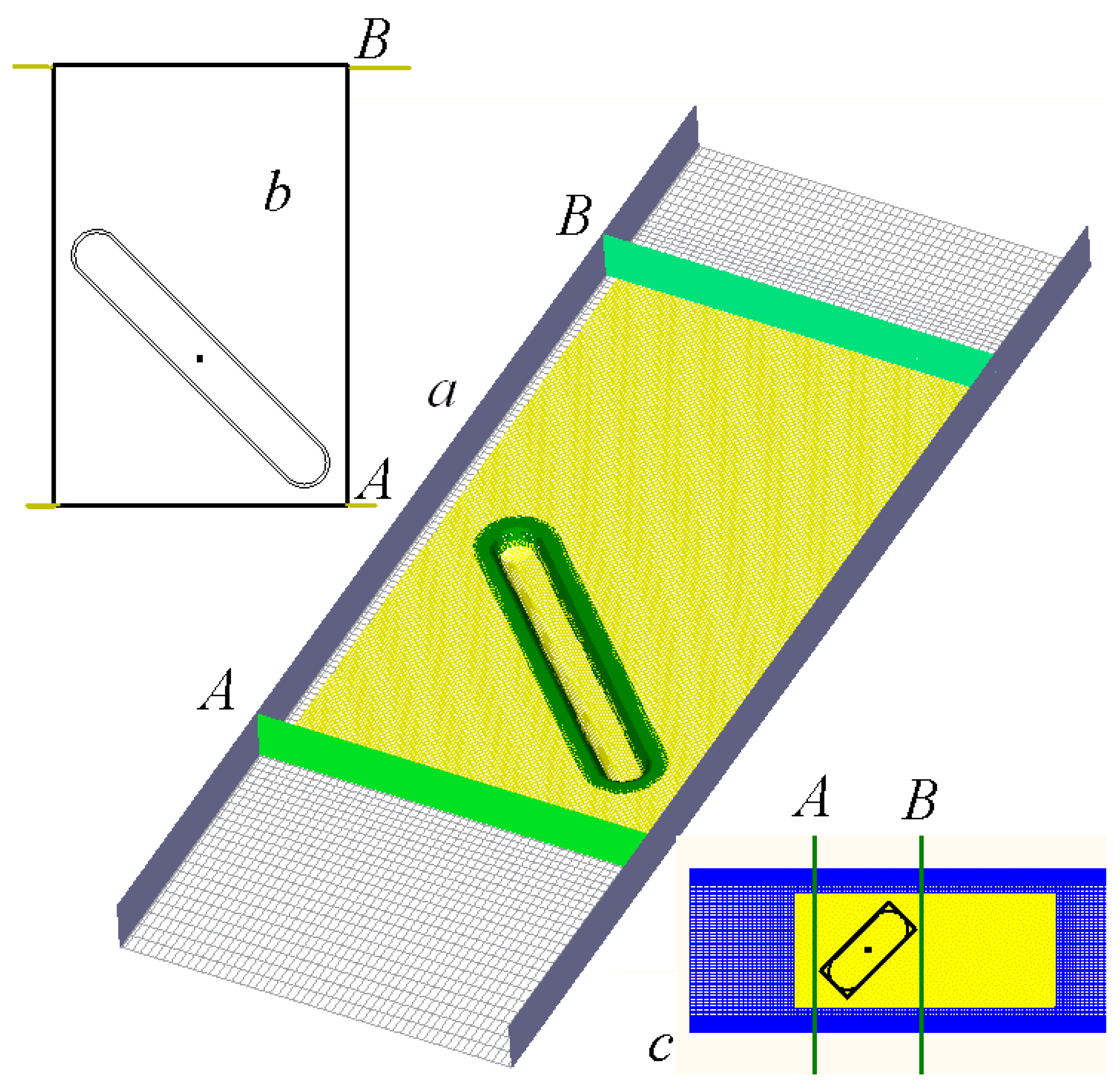
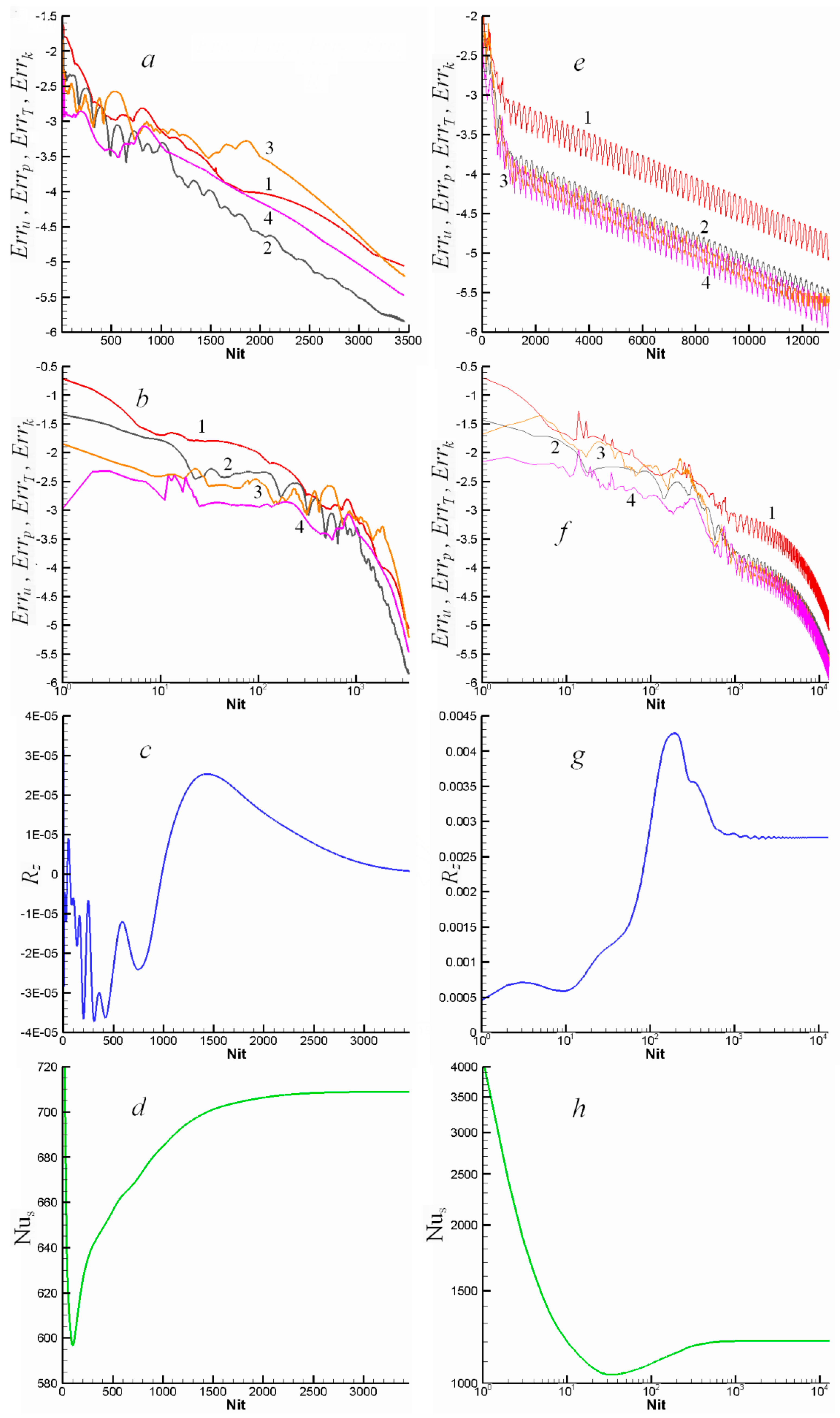
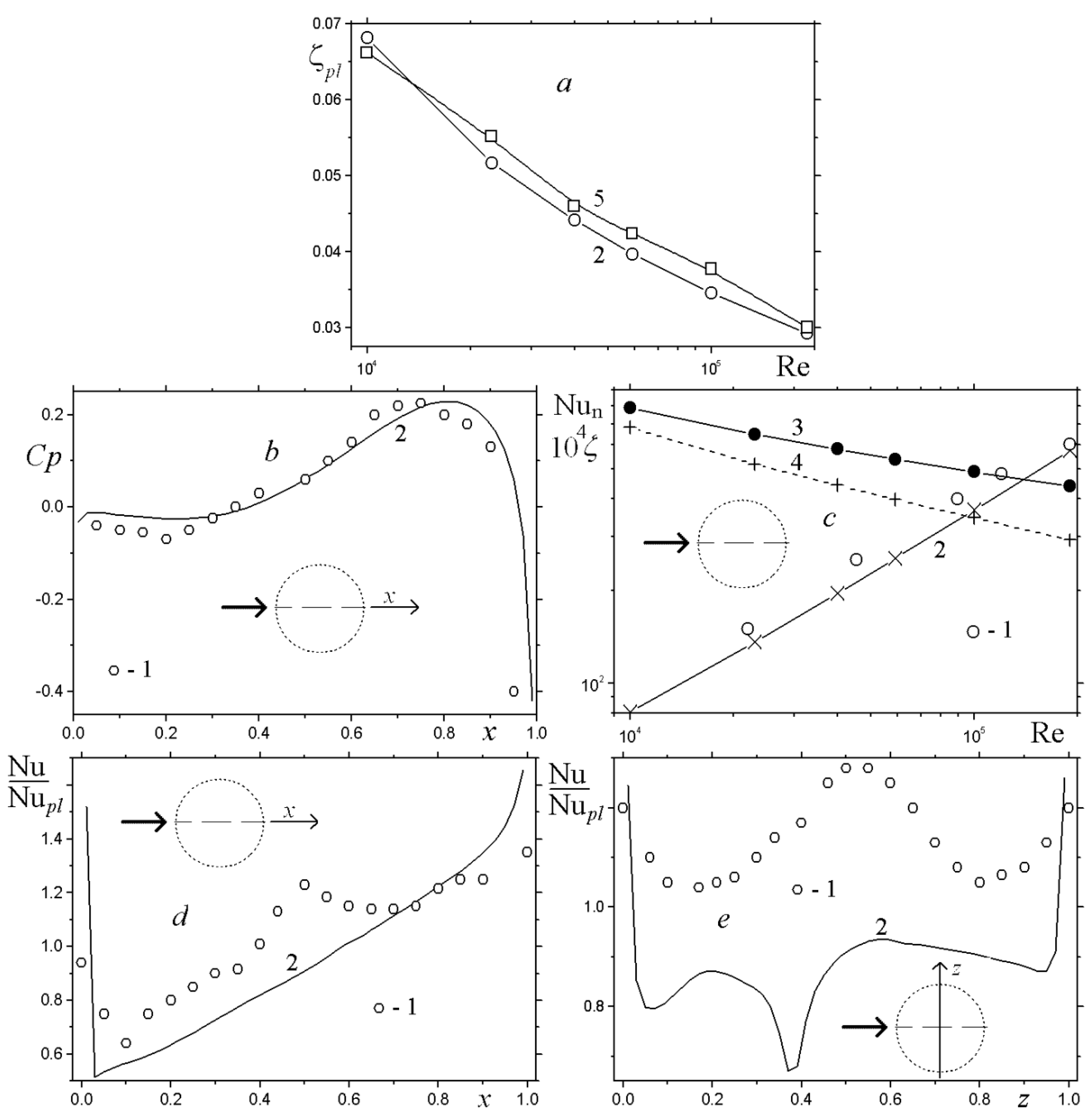
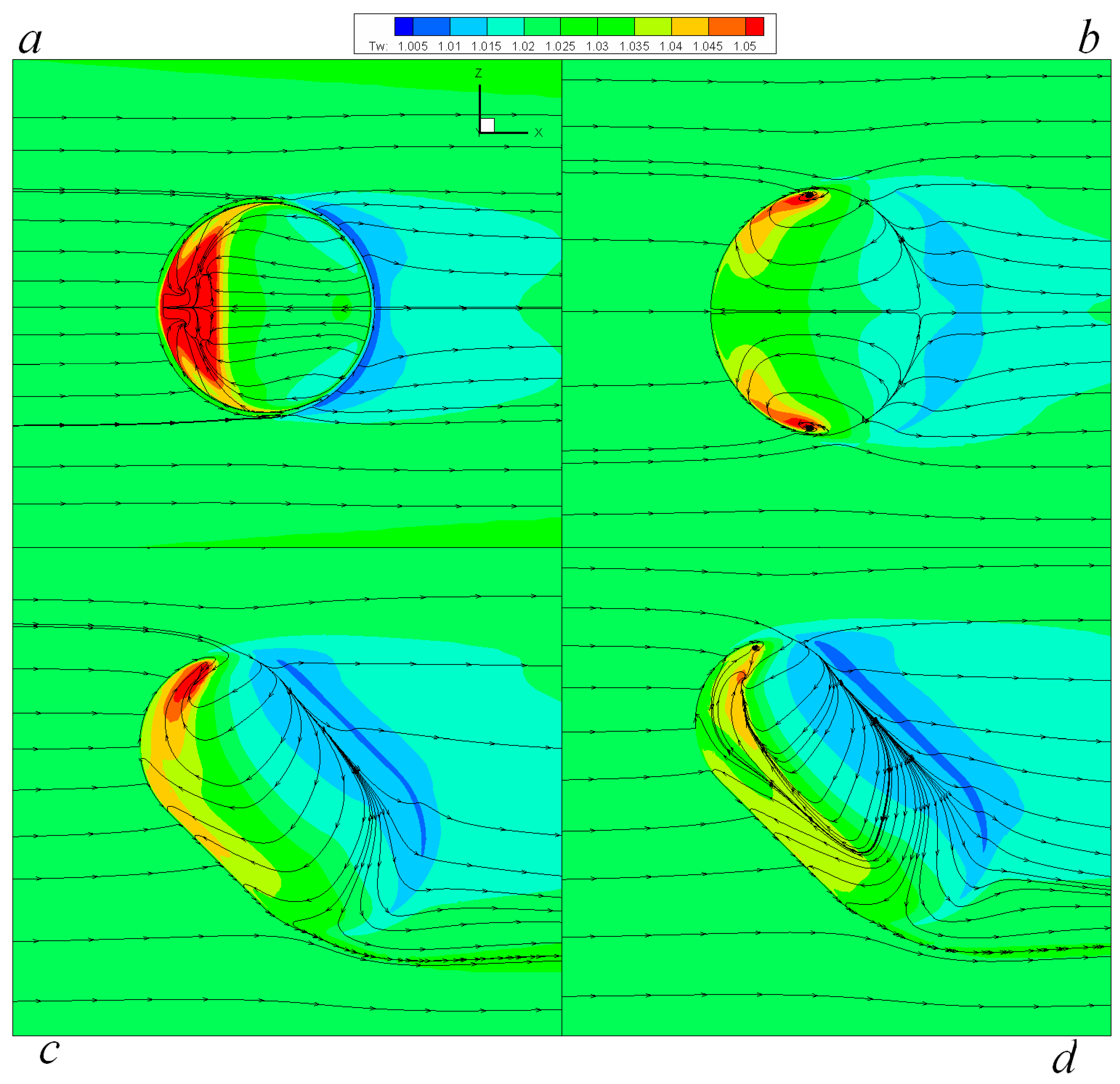
Energies 12 01296 g012 550
Figure 12. Temperature fields at the heated wall with conical (a) and oval dimples of width 1 (b), 0.731 (c), 0.678 (d) and the streamlines.
Figure 12. Temperature fields at the heated wall with conical (a) and oval dimples of width 1 (b), 0.731 (c), 0.678 (d) and the streamlines.
Energies 12 01296 g012
Energies 12 01296 g013 550
Figure 13. Temperature fields at the heated wall with oval dimples of width 0.659 (a), 0.631 (b), 0.58 (c) and 0.549 (d) and the streamlines.
Figure 13. Temperature fields at the heated wall with oval dimples of width 0.659 (a), 0.631 (b), 0.58 (c) and 0.549 (d) and the streamlines.
Energies 12 01296 g013
Energies 12 01296 g014 550
Figure 14. Temperature fields at the heated wall with oval dimples of width 0.482 (a), 0.429 (b), 0.383 (c) and 0.346 (d) and the streamlines.
Figure 14. Temperature fields at the heated wall with oval dimples of width 0.482 (a), 0.429 (b), 0.383 (c) and 0.346 (d) and the streamlines.
Energies 12 01296 g014
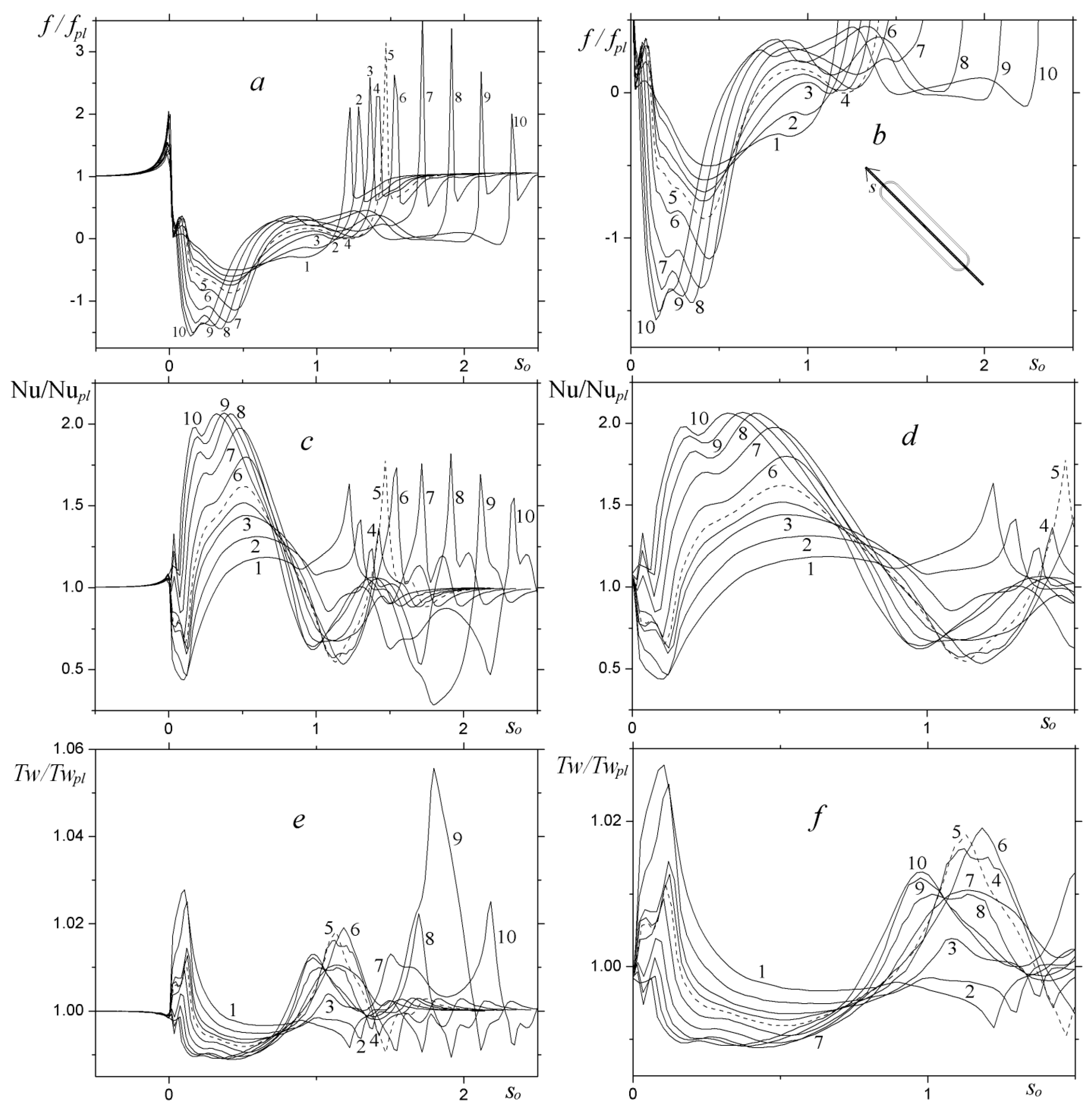
Energies 12 01296 g015 550
Figure 15. Comparison of the dependences of relative friction (a,b), Nusselt number (c,d), wall temperature (e,f) in the middle longitudinal cross sections for single oval dimples of different insert length: 1—L = 0.5; 2—0.625; 3—0.75; 4—0.825; 5—0.9; 6—1; 7—1.25; 8—1.5; 9—1.75; 10—2. b, d, f—enlarged fragments of the dependences.
Figure 15. Comparison of the dependences of relative friction (a,b), Nusselt number (c,d), wall temperature (e,f) in the middle longitudinal cross sections for single oval dimples of different insert length: 1—L = 0.5; 2—0.625; 3—0.75; 4—0.825; 5—0.9; 6—1; 7—1.25; 8—1.5; 9—1.75; 10—2. b, d, f—enlarged fragments of the dependences.
Energies 12 01296 g015
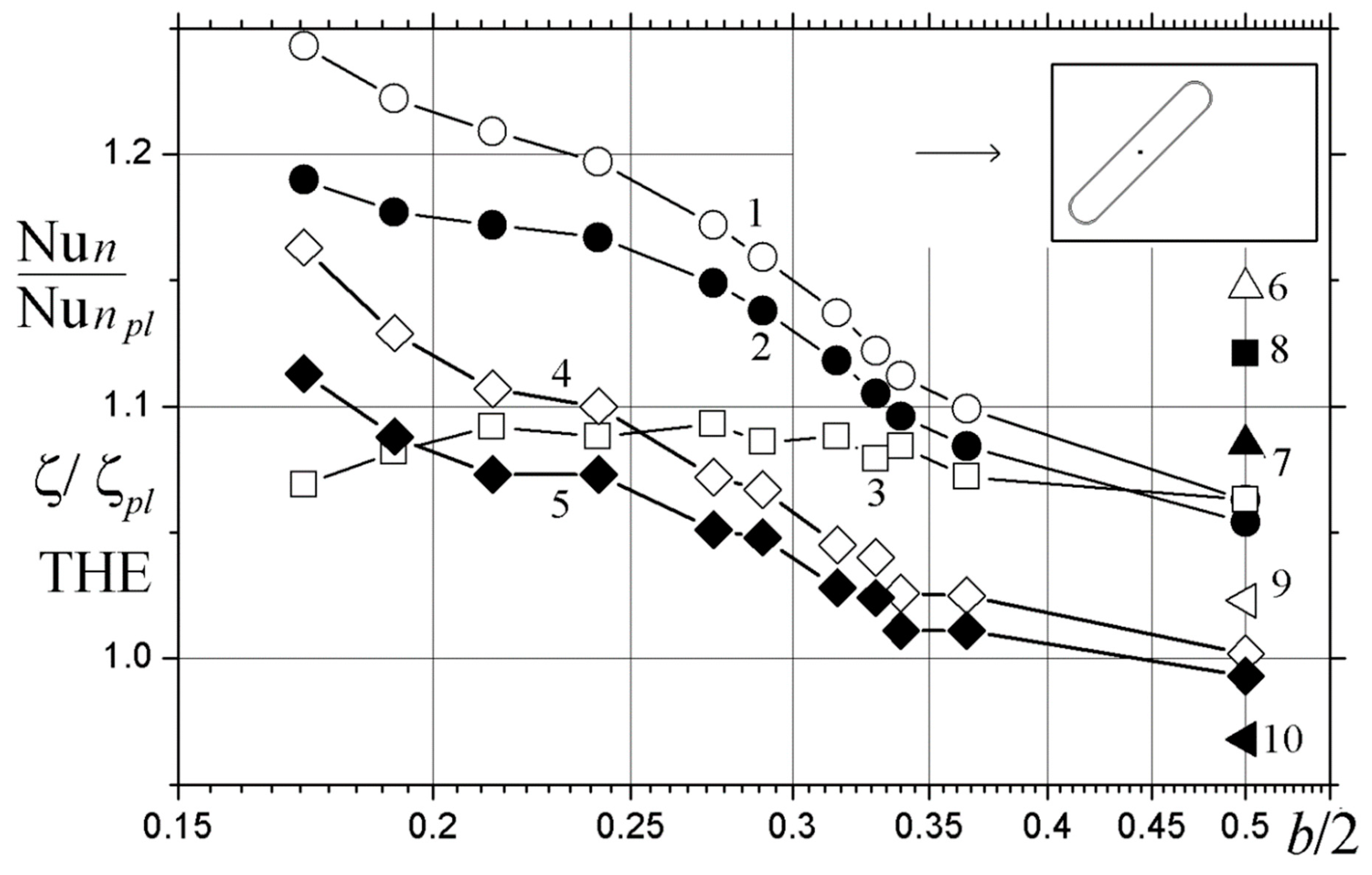
Energies 12 01296 g016 550
Figure 16. Influence of the oval dimple width b on thermal (1,2,6,7) and thermal-hydraulic (4,5,9,10) performances, as well as relative hydraulic losses (3,8); 6,7,8,9,10—conical dimple; 2,5,7,10—with regard to the area of the dimple inner surface in the 3 × 2 section and the shift of the dimple center by 1 from the front boundary.
Figure 16. Influence of the oval dimple width b on thermal (1,2,6,7) and thermal-hydraulic (4,5,9,10) performances, as well as relative hydraulic losses (3,8); 6,7,8,9,10—conical dimple; 2,5,7,10—with regard to the area of the dimple inner surface in the 3 × 2 section and the shift of the dimple center by 1 from the front boundary.
Energies 12 01296 g016
Table
Table 1. The cylindrical insert length, the width of the oval dimple and its length in terms of width.
Table 1. The cylindrical insert length, the width of the oval dimple and its length in terms of width.
Lbχ
0.50.7311.68
0.6250.6781.92
0.6750.6592.02
0.750.6312.19
0.90.582.55
10.5492.82
1.250.4823.59
1.50.4294.50
1.750.3835.57
20.3466.78
Table
Table 2. Thermal and hydraulic performance of three sections of the narrow channel with a spherical dimple at different boundary conditions q = const and T = const.
Table 2. Thermal and hydraulic performance of three sections of the narrow channel with a spherical dimple at different boundary conditions q = const and T = const.
Boundary Condition TypeNun10/Nunp110ζ/ζpl10Nun20/Nunpl20ζ/ζpl20Nun30/Nunpl30ζ/ζpl30
q = const1.098
(1.083)		1.0721.138
(1.083)		1.161.0851.010
T = const1.094
(1.08)		1.0711.17
(1.11)		1.161.0641.008
Table
Table 3. Predictions of thermal and hydraulic performance of two sections of the narrow channel with the oval dimple of width b = 0.383 obtained by the modified SST models and different grids.
Table 3. Predictions of thermal and hydraulic performance of two sections of the narrow channel with the oval dimple of width b = 0.383 obtained by the modified SST models and different grids.
ModelNun1/Nunpl1ζ1/ζpl1(Nun1/Nunpl1)/(ζ1/ζpl1)Nun2/Nunpl2ζ2/ζpl2(Nun2/Nunpl2)/(ζ2/ζpl2)
SST-model Standard [34] 1.242
(1.196)		1.0791.151
(1.108)		1.953
(1.518)		1.1501.698
(1.320)
SST-modelModified [35]1.231
(1.185)		1.0691.152
(1.109)		1.933
(1.502)		1.1341.705
(1.325)
SST-model [35] modified within RLI approach1.233
(1.187)		1.0681.155
(1.111)		1.949
(1.515)		1.1321.726
(1.338)
SST-model [35] modified within SM approach1.228
(1.183)		1.0641.154
(1.112)		1.950
(1.516)		1.1271.730
(1.345)
SST-model [35] modified within RLI approach *1.222
(1.177)		1.0821.129
(1.088)		1.836
(1.427)		1.1441.605
(1.247)
(* the grid contains 3 mln cells).
Table
Table 4. VP2/3 code validation of the predictions of extreme flow, heat transfer and turbulence parameters for the narrow channel with the oval dimple of width b = 0.383.
Table 4. VP2/3 code validation of the predictions of extreme flow, heat transfer and turbulence parameters for the narrow channel with the oval dimple of width b = 0.383.
TypeuminvminvmaxwminwmaxkmaxνtmaxTwmax
Grid A −0.473−0.3490.526−0.8470.3310.04120.001411.083
Grid B−0.472−0.3370.508−0.8180.3770.04050.001421.085

Share and Cite

MDPI and ACS Style

Isaev, S.; Leontiev, A.; Chudnovsky, Y.; Nikushchenko, D.; Popov, I.; Sudakov, A. Simulation of Vortex Heat Transfer Enhancement in the Turbulent Water Flow in the Narrow Plane-Parallel Channel with an Inclined Oval-trench Dimple of Fixed Depth and Spot Area. Energies 2019, 12, 1296. https://doi.org/10.3390/en12071296

AMA Style

Isaev S, Leontiev A, Chudnovsky Y, Nikushchenko D, Popov I, Sudakov A. Simulation of Vortex Heat Transfer Enhancement in the Turbulent Water Flow in the Narrow Plane-Parallel Channel with an Inclined Oval-trench Dimple of Fixed Depth and Spot Area. Energies. 2019; 12(7):1296. https://doi.org/10.3390/en12071296

Chicago/Turabian Style

Isaev, Sergey, Alexandr Leontiev, Yaroslav Chudnovsky, Dmitry Nikushchenko, Igor Popov, and Alexandr Sudakov. 2019. "Simulation of Vortex Heat Transfer Enhancement in the Turbulent Water Flow in the Narrow Plane-Parallel Channel with an Inclined Oval-trench Dimple of Fixed Depth and Spot Area" Energies 12, no. 7: 1296. https://doi.org/10.3390/en12071296

APA Style

Isaev, S., Leontiev, A., Chudnovsky, Y., Nikushchenko, D., Popov, I., & Sudakov, A. (2019). Simulation of Vortex Heat Transfer Enhancement in the Turbulent Water Flow in the Narrow Plane-Parallel Channel with an Inclined Oval-trench Dimple of Fixed Depth and Spot Area. Energies, 12(7), 1296. https://doi.org/10.3390/en12071296

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop