Implementation of User Cuts and Linear Sensitivity Factors to Improve the Computational Performance of the Security-Constrained Unit Commitment Problem

Abstract

Power system operators must schedule the available generation resources required to achieve an economical, reliable, and secure energy production in power systems. This is usually achieved by solving a security-constrained unit commitment (SCUC) problem. Through a SCUC the System Operator determines which generation units must be on and off-line over a time horizon of typically 24 h. The SCUC is a challenging problem that features high computational cost due to the amount and nature of the variables involved. This paper presents an alternative formulation to the SCUC problem aimed at reducing its computational cost using sensitivity factors and user cuts. Power Transfer Distribution Factors (PTDF) and Line Outage Distribution Factors (LODF) sensitivity factors allow a fast computation of power flows (in normal operative conditions and under contingencies), while the implementation of user cuts reduces computational burden by considering only biding N-1 security constraints. Several tests were performed with the IEEE RTS-96 power system showing the applicability and effectiveness of the proposed modelling approach. It was found that the use of Linear Sensitivity Factors (LSF) together with user cuts as proposed in this paper, reduces the computation time of the SCUC problem up to 97% when compared with its classical formulation. Furthermore, the proposed modelling allows a straightforward identification of the most critical lines in terms of the overloads they produce in other elements after an outage, and the number of times they are overloaded by a fault. Such information is valuable to system planners when deciding future network expansion projects.

1. Introduction

The electric power sector is currently facing rapid changes, mostly related to the integration of renewable energy resources and the new trend of smart grids. In this context, power system operators are continuously seeking novel sources of operational flexibility and improved methods to manage and integrate generation resources, guaranteeing a secure operation. Within the daily operation planning of a power system the unit commitment (UC) is one of the most important decision-making activities. The UC brings up the task of finding an optimal schedule and production level of a set of generation units over a given period of time. It also serves for clearing daily prices in power markets and as a tool used by generation companies for optimizing bidding strategies [1]. In its traditional approach, the UC is run within a typical time horizon of 24 h aiming at minimizing the total operation costs while meeting network demand.

UC is a widely studied problem. Recent works emphasize the inclusion of renewable energy [2,3,4], energy storage [5,6], uncertainty [7,8] and security constraints [9,10]. This paper focuses on the last issue. Within the daily operation planning of power systems, an important aspect to take into account is monitoring the limits of the electric network not only for normal operating conditions but also under credible contingencies; especially, at periods of peak demand when transmission capacity margins are reduced. Therefore, solving the UC problem considering security constraints becomes a fundamental condition for obtaining an economic, safe and reliable system operation [11]. When transmission limits and security constraints (N-1 criterion) are included in the UC, system operators find themselves dealing with a much more complex problem, namely the security-constraint unit commitment (SCUC) problem.

The SCUC is a non-linear, large-scale, mixed-integer combinatorial optimization problem that considers numerous operating constraints, such as ramp rates, minimum up/down time, start-up time as well as transmission and generation limits. The SCUC also incorporates contingency analyses that take into account forced outages of network elements. This problem can be represented as a mixed-integer programming (MIP) problem, and from the point of view of its computational complexity is NP-complex [9]. Several optimization methods have been used to approach the SCUC problem. These methods can be broadly classified in three groups: mathematical programming approaches, metaheuristic techniques, and hybrid methods. Classical mathematical programming approaches include Lagrangian Relaxation (LR) [12,13], Benders Decomposition (BD) [14,15,16,17] and Branch and Cut (BC) methods [18,19]. Several metaheuristic techniques have also been applied to solve the UC and SCUC problem such as genetic algorithms [20,21,22,23,24], cuckoo search algorithm [25] and swarm intelligence [26]. Finally, hybrid methodologies are presented in [27,28]. The literature regarding the SCUC problem is very extensive. A comparison of transmission constrained unit commitment formulations is presented in [29]. A survey of research work made in the domain of UC and SCUC using various techniques is presented in [30]. Also, literature reviews approaching specific issues such as stochasticity and uncertainty within the SCUC problem are addressed in [31,32], respectively.

The inclusion of security constraints is one of the main complicating factors of the UC problem. That is because its number is directly proportional to the product of the number of transmission lines and the discrete steps of the commitment horizon. Therefore, the SCUC can be greatly simplified if inactive security constraints are identified and eliminated. In [10], the authors show that inactive constraints can be identified by solving a series of small-scale mixed-integer linear programming (MILP) problems and propose an analytical condition to identify such constraints. They also found that computational requirements and numerical error of the SCUC are greatly reduced if inactive constraints are eliminated. Furthermore, the authors show that the crucial transmission lines affecting the total operating costs are among those associated with the remaining security constraints. In [33], the authors provide a systematic method to construct feasible solutions for the SCUC problem within a LR framework, based on a group of analytical feasibility conditions. In line with the work presented in [10] the authors, in [34] present the concept of umbrella constraints for the security-constraint optimal power flow (SCOPF) problem. This is because few of the constraints actually serve to enclose the feasible region of a typical SCOPF. Hence, the constraints that are not contributing directly to the feasible space can be discarded. The authors establish the necessary and sufficient conditions of the set of feasible solutions by ruling out unnecessary constraints of the SCOPF. Although these conditions allow the identification of inactive and binding constraints, they also involve solving MILP problems, which despite being less complex than the original formulation are not trivial in their solution, especially when dealing with large-scale problems, and therefore BD may be needed [10,34]. In [35] the authors propose an iterative algorithm to speed up the solution of an AC Preventive Security-Constrained Optimal Power Flow (AC-PSCOPF) through contingency filtering techniques; non-dominated N-1 contingencies are the security constraints bounded to the AC-PSCOPF model. Nevertheless, for performing the N-1 contingency analysis, AC-power flows, into this algorithm, must be computed.

A fundamental aspect in the modelling of the SCUC problem is the representation of the electrical network. A linear representation of the network (DC model) as in [13,15,16], instead of an AC modelling as in [36,37,38] allows the use of linear sensitivity factors (LSF) such as power transfer distribution factors (PTDF) and line outage distribution factors (LODF), commonly used in the analysis of electrical systems [39,40]. These factors represent the approximate change in power flows in transmission assets due to a change in power injection (PTDF) or due to a new topology configuration of the network when a transmission element fails (LODF). The use of these factors allows reducing the number of variables and constraints of the SCUC model, increasing computational efficiency. In [41], the authors use PTDF and LODF to calculate generation shifts so that power flows on transmission lines are kept within security limits after single and multiple-line outage events. In [9], the authors present an N-1 security-constraint formulation of the SCUC problem based on LODF combined with an iterative methodology for filtering N-1 congestion constraints. The authors show that such filtering through lazy constraints greatly reduces the computational time of the SCUC problem. A method for estimating these sensitivity factors based on near-real-time measurements and their applications can be found in [42]. Despite advantages of these linear factors, ref [43] proposes a new formulation to reduce the number of variables and constraints to speed up the SCUC solution in large-scale power systems, using BD and the BC in an iterative framework. Nonetheless, post-contingency power flows are modelled using the bus voltage angles.

This paper presents a novel formulation of the SCUC problem that considerably reduces its computing time. This is done through the implementation of user cuts and the use of LSF. On the one hand, the user cuts approach proposed in this paper serves as umbrella constraints which results in a considerable computational burden reduction when considering N-1 security constraints. This is because most of the N-1 contingency constraints are superfluous and do not set up the feasibility space of the SCUC problem [9]. On the other hand, PTDF and LODF sensitivity factors allow a fast computation of power flows both in normal operation and under contingencies. Furthermore, some indexes are proposed to identify the most severe faults as well as the most critical lines. The later information is of paramount importance to system planners since this can be included in expansion plan studies.

This paper is organized as follows: Section 2 describes the mathematical formulation of the SCUC problem. Section 3 presents the proposed approach to solve the SCUC problem. Section 4 shows tests and results. Finally, Section 5 reports conclusions.

2. Problem Statement

2.1. Linear Sensitivity Factors

Distribution factors are linear approximations of the sensitivities of power flows with respect to changes in nodal injections [39]. PTDF represent changes in power flows in lines as regards the transfer of one MW from an injection node to a consumption node. On the other hand, LODF represent the distribution of power flows in the remaining lines after an outage has taken place. The DC model of the transmission network is one of the most used in power system studies. With this model it is possible to compute the power flows using the vector of power injections in each bus $\overline{\mathit{P}}$ and the susceptance matrix $\overline{\mathit{B}}$. Power flows are given in terms of angular differences that can be obtained from Equation (1). Since matrix $\overline{\mathit{B}}$ is non-invertible, the row and column corresponding to the slack bus are eliminated resulting in matrix ${\overline{\mathit{B}}}^{{}^{\prime }}$ as indicated in Equation (2). The computation of the power flow in a transmission line is obtained as the product of the susceptance of the line by the angular difference between the two buses that connect it. This operation can be expressed in matrix form as shown in Equation (3), where $\overline{\mathit{D}}$ is the diagonal matrix of susceptances, $\overline{\mathit{A}}$ is the incidence matrix of the system and $\overline{\mathit{\theta }}$ is the vector of bus voltages angles. Power flows in lines can be expressed as a function of $\overline{\mathit{P}}$, by replacing Equation (2) in Equation (3), as shown in Equation (4). Finally, Equation (5) shows how to compute the matrix of PTDF. It is worth mentioning that when calculating matrix $\overline{\mathit{A}}$, the row corresponding to the slack bus must be removed to perform matrix operations without dimensional problems. This leads to the PTDF matrix not considering the slack bus until this instance of the calculation. Subsequently, to account for the slack bus, a column of zeros in the position of this node is added to the PTDF matrix. This is because there is no power flow change in the transmission lines when the power injection is made in the slack bus and withdrawn from it.

$$\overline{\mathit{P}}=\overline{\mathit{B}}·\overline{\mathit{\theta }}$$

(1)

$$\overline{\mathit{\theta }}={\overline{\mathit{B}}}^{{}^{\prime }-1}·\overline{\mathit{P}}$$

(2)

$$\overline{\mathit{F}}=\overline{\mathit{D}}\overline{\mathit{A}}\overline{\mathit{\theta }}$$

(3)

$$\overline{\mathit{F}}=\overline{\mathit{D}}\overline{\mathit{A}}{\overline{\mathit{B}}}^{{}^{\prime }-1}·\overline{\mathit{P}}$$

(4)

$$\overline{\mathit{PTDF}}=\overline{\mathit{D}}\overline{\mathit{A}}{\overline{\mathit{B}}}^{{}^{\prime }-1}$$

(5)

The computation of LODF indices is done by means of an auxiliary matrix $\overline{\mathit{H}}$ as shown in Equation (6). One of the drawbacks of this methodology lies on the fact that there are no defined values of LODF for radial lines. To address this problem, it is suggested in [44] to assign values of 0 (see Equation (7); that is to say, contingencies associated with radial lines are not taken into account. Furthermore, in the main diagonal of the LODF matrix, −1 is assigned, since there is no post-fault power flow for the line that is out of operation. With these established rules, the post-contingency power flow in line l when line k fails $\left({\mathit{F}}_{l,k}\right)$ is given as shown in Equation (8).

$$\overline{\mathit{H}}=\overline{\mathit{PTDF}}·{\overline{\mathit{A}}}^T$$

(6)

$$\overline{\mathit{LODF}}=\left\{\begin{array}{cc}\frac{{\mathit{H}}_{i,j}}{1-{\mathit{H}}_{j,j}}& \mathrm{if}{\mathit{H}}_{i,j}\ne 0\\ 0& \mathrm{if}{\mathit{H}}_{j,j}=1\\ -1& \mathrm{if}i=j\end{array}\right.$$

(7)

$${\mathit{F}}_{l,k}={\mathit{F}}_l+{\overline{\mathit{LODF}}}_{\mathit{l},\mathit{k}}·{\mathit{F}}_k$$

(8)

where ${\mathit{F}}_l$ and ${\mathit{F}}_k$ are the power flows in normal operation state, that is, prior to the contingency k.

2.2. Modelling Approach: Classic UC Formulation

The SCUC model proposed in this paper uses as starting point the classic UC formulation described and modelled in [29,45], respectively. From this initial model, a new one was developed adopting LSF to account for power flow constraints both in normal operative conditions and under contingencies. In this way, the UC model described in [29] is turned into a SCUC problem. The base UC formulation is given by Equations (9)–(29). The objective function, given by Equation (9) consists of minimizing the total generation cost of a set power plants over a given time horizon. In this case, $C_i\left(t\right)$ is the cost of power plant i at time t, $c^{sh}$ is the cost of non-attended demand, and $L_s^{sh}$ is the unserved load at bus s at time t. This objective function is subject to a set of constraints as explained below.

$$\mathrm{Minimize}\sum _{t=1}^T\sum _{i=1}^I{C}_i\left(t\right)+\sum _{t=1}^T\sum _{s=1}^S{c}^{sh}·L_s^{sh}\left(t\right)$$

(9)

Constraints given by Equations (10) and (11) are used to preserve the logic of running, start-up, and shut-down status of generators. Where $y_i\left(t\right)$ and $z_i\left(t\right)$ are binary variables that are equal to 1 if generator i is started or shut down at the beginning of time interval t, respectively, and 0 otherwise. On the other hand, $x_i\left(t\right)$ is a binary variable that is equal to 1 if generator i is committed in time interval t, and 0 otherwise. Equation (10) is used to preserve the logic of running units, while Equation (11) indicates that a given generator cannot be simultaneously on and off.

$$y_i\left(t\right)-z_i\left(t\right)=x_i\left(t\right)-x_i(t-1)\forall t\le T,i\le I$$

(10)

$$y_i\left(t\right)+z_i\left(t\right)\le 1\forall t\le T,i\le I$$

(11)

Although there are several technologies of eclectic power plants, for the sake of simplicity only thermal generators were considered. The cost curve of thermal generator units was modelled using B linear segments and is described by Equation (12). In this case, $a_i$ is a fixed production cost that is taken into account only if generator i is committed as indicated by the binary variable $x_i\left(t\right)$; $k_{i,b}$ is the slope of the cost curve for segment b of generator i, $g_{i,b}\left(t\right)$ is the output of generator i in segment b at time t and ${SUC}_i\left(t\right)$ is the start-up cost of generator i at time t. Equation (13) indicates that the total generation output given by $g_i\left(t\right)$ must be equal to the sum of the generation in each segment of the cost curve. Equations (14) and (15) indicate the minimum and maximum output limits for each generation level, respectively.

$$C_i\left(t\right)=a_i·x_i\left(t\right)+\sum _{b=1}^B{k}_{i,b}·g_{i,b}\left(t\right)+{SUC}_i\left(t\right)\forall t\le T,i\le I$$

(12)

$$g_i\left(t\right)=\sum _{b=1}^B{g}_{i,b}\left(t\right)\forall t\le T,i\le I$$

(13)

$$g_i\left(t\right)\ge g_i^{min}·x_i\left(t\right)\forall t\le T,i\le I$$

(14)

$$g_{i,b}\left(t\right)\le g_i^{max}·x_i\left(t\right)\forall t\le T,i\le I,b\le B$$

(15)

Minimum up/down time constraints are expressed by Equations (16)–(18). Where $g_i^{on-off}$ represents the on-off status of generator i at $t=0$, $L_i^{up,min}$ is the minimum length of time generator i must be on once it is committed, and $L_i^{down,min}$ is the minimum length of time generator i must be off before being committed again.

$$x_i\left(t\right)=g_i^{on-off}\forall i\le I,t\le L_i^{up,min}+L_i^{down,min}$$

(16)

$$\sum _{tt=t-g_i^{up}+1}^t{y}_i\left(tt\right)\le x_i\left(t\right)\forall t\ge L_i^{up,min}$$

(17)

$$\sum _{tt=t-g_i^{down}+1}^t{z}_i\left(tt\right)\le 1-x_i\left(t\right)\forall t\ge L_i^{down,min}$$

(18)

Ramping constraints are given by Equations (19)–(21). These are added to take into consideration how fast a generator can increase or decrease its output. In this case, ${ramp}_i^{up}$ and ${ramp}_i^{down}$ are the up and down ramp limits of generator i, $g_i\left(t\right)$ is the generator output at time t, and $g_i^0$ is the output of generator i at t = 0.

$$-{ramp}_i^{down}\le g_i\left(t\right)-g_i(t-1)\forall i\le I,2\le t\le T$$

(19)

$${ramp}_i^{up}\le g_i\left(t\right)-g_i(t-1)\forall i\le I,2\le t\le T$$

(20)

$$-{ramp}_i^{down}\le g_i\left(t_1\right)-g_i^0\forall i\le I$$

(21)

$${ramp}_i^{up}\le g_i\left(t_1\right)-g_i^0\forall i\le I$$

(22)

Generator off counter set-up constraints are given by Equations (23)–(25). These equations are used to take into account the initial conditions of generators. The symbols | and $\wedge$ indicate the logical conditions IF and AND, respectively.

$$\begin{array}{cc}\hfill w_{i,j}\left(t\right)\le & \sum _{tt=SU{C}_{i,j}^{lim}}^{min\{t-1,SU{C}_{i,j+1}^{lim}-1\}}{z}_i(t-j)\hfill \\ & +1\left|\right\{j=J-1\wedge SU{C}_{i,j}^{lim}\le g_i^{down,init}+t-1<SU{C}_{i,j+1}^{lim}\}\hfill \\ & +1\left|\right\{j=J\wedge SU{C}_{i,j}^{lim}\le g_i^{down,init}+t-1\}\forall t\le T,i\le I,j\le J\hfill \end{array}$$

(23)

$$\sum _{j=1}^J{w}_{i,j}\left(t\right)=y_i\left(t\right)\forall t\le T,i\le I$$

(24)

$${SUC}_i\left(t\right)=\sum _{j=1}^J{w}_{i,j}\left(t\right)\forall t\le T,i\le I$$

(25)

Equations (26)–(29) take into account transmission constraints within a DC modelling of the network. Equation (26) indicates the active power balance constraint. This means that the supply and demand must be equal over all time intervals on each node. In this case, ${\theta }_s\left(t\right)$ is the voltage angle at bus s at time t, and $B_{s,m}$ is the admittance connecting nodes $s-m$. Equation (27) accounts for power flow limits, where $l_{s,m}^{max}$ is the maximum power flow allowed in line connecting nodes $s-m$. Finally, Equations (28) and (29) indicate limits on bus angles and the angular value of the reference bus, respectively.

$$\begin{array}{cc}\hfill \sum _{i=1}^I{g}_i\left(t\right)-& \sum _{\{s,m\}\in L|m>s}{B}_{s,m}({\theta }_s\left(t\right)-{\theta }_m\left(t\right))+\hfill \\ & \sum _{\{s,m\}\in L|m<s}{B}_{m,s}({\theta }_m\left(t\right)-{\theta }_s\left(t\right))=d_s\left(t\right)\forall t\le T,s\le S\hfill \end{array}$$

(26)

$$-F_{s,m}^{max}\le B_{s,m}({\theta }_s\left(t\right)-{\theta }_m\left(t\right))\le F_{s,m}^{max}\forall t\le T,\{s,m\}\in L$$

(27)

$$-\pi \le {\theta }_s\left(t\right)\le \pi \forall t\le T,s\le S\backslash s:referencebus$$

(28)

$${\theta }_s\left(t\right)=0\forall t\le T,s:referencebus$$

(29)

2.3. Improvements and Adaptations to the Classic UC Model

Several modifications were introduced to the aforementioned UC model aiming at considering contingency constraints and improving computational time. The improvements and adaptations performed on the UC model are described below.

• Net power injection and power balance
  The first modification introduced in the UC model given by Equations (9)–(29) is the reformulation of the power balance constraint given by Equation (26). We introduce the variable $P_{\mathit{s},\mathit{t}}^{Net}$ in Equation (30) that indicates the net power injection in bus s at time t. In this case, $A_{s,i}^g$ is a matrix that identifies which generator is in each bus. If generator i is located at bus s the corresponding position of $A_{s,i}^g$ is equal to one. Otherwise, it is zero; $g_i\left(t\right)$ is the output of generator i at time t, $D_{s,t}$ is the forecasted demand at bus s at time t. To guarantee the power balance, the sum of the total generation must be equal to the sum of the total demand for each period of time, as indicated by Equation (31). The formulation of the net power injection provided in Equations (30) and (31) replaces Equation (26). Please note that such formulation does not take into account bus angles, reducing the number of variables and rendering constraints (28) and (29) unnecessary.

  $$P_s^{Net}\left(t\right)=\sum _i{A}_{s,i}^g{g}_i\left(t\right)-D_s\left(t\right)+L_s^{sh}\left(t\right)\forall s\le S,t\le T$$

  (30)

  $$\sum _s{P}_s^{Net}\left(t\right)=0\forall t\le T$$

  (31)
• Power flows and post-contingency power flows
  Power flows in lines can be obtained as the product of the PTDF matrix and the vector of net power injections. Power flows must be within minimum and maximum limits as indicated in Equation (32). On the other hand, post-contingency power flows can be obtained using the LODF matrix as indicated in Equation (33). In this case, $TCF$ stands for Transmission Capacity Factor, which is a parameter used to adjust transmission capacity limits. When post-contingency constraints are included in the UC formulation, this one is turned into a SCUC problem. Nevertheless, as it will be explained later, not all security constraints given by Equation (33) need to be incorporated in the model to guarantee network security. This is because most of these constraints may not be binding in the optimal solution. Therefore, only the security constraints that need to be enforced to avoid post-contingency overloads are added as user cuts as explained in the next section.

  $$-F_l^{\max }·TCF\le \sum _s{\overline{PTDF}}_{l,s}·P_s^{Net}\left(t\right)\le F_l^{\max }·TCF\forall l\le L,t\le T$$

  (32)

  $$-F_l^{max}·TCF\le F_l\left(t\right)+{\overline{LODF}}_{l,k}·F_k\left(t\right)\le F_l^{max}·TCF\forall l\le L,k\le K,t\le T$$

  (33)

3. Methodology

The proposed modelling approach to the SCUC problem was inspired by [9], and it has two main features: the use of LSF (described in Section 2.1) for a straightforward computation of power flows and post-contingency power flows (see Equations (32)–(33); and the implementation of user cuts that reduce computational burden by considering only biding N-1 security constraints. In this section, a detailed description of the so-called user cuts is provided along with its implementation within the SCUC problem.

3.1. User Cuts

For large power systems, most single-element contingencies (N-1) do not result in power flow violations of other lines; that is to say, the majority of the N-1 security constraints may be superfluous and do not set up the feasibility space of the SCUC problem. Therefore, user cuts are implemented in this paper to consider only biding security constraints. In a MILP problem, a user cut is basically an additional linear constraint defined by the user, which is not part of the original model and does not rule out any feasible integer solutions [46]. Suppose the hypothetical two variable pure integer linear programming problem presented in Figure 1. In this case, the black dots indicate the feasible region of the problem and the black polygon indicates the integer hull or IP hull, which is the smallest convex set containing all integer-feasible solutions. The polygon bounded in blue represents the feasible region of the linear relaxation, also known as the linear hull or LP hull. This one is obtained when relaxing integrality constraints while enforcing variable bounds and functional constraints. Please note that the IP hull is always a subset of the LP hull. A user cut is illustrated by a red line, the shaded area shows the portion of the original LP hull that is removed by the user cut. Please note that none of the integer solutions of the original problem are removed by the cut.

In the approach proposed in this paper, the original problem is represented by the classic UC formulation presented in Section 2.2 considering the LSF through Equations (33) to (35). Please note that this first modification of the modelling does not include Equation (33). In consequence, it only deals with normal operative conditions. However with an alternative expression for power flow limits and power flow balance as a function of the PTDF and net power injections.

To turn a classic UC into a SCUC problem it must be guaranteed that N-1 security constraints are properly dealt with. However, in the operation of a power system not every contingency results in overloads. Therefore, it is not necessary or practical to consider the whole set of all security constraints given by Equation (33). Only those single contingencies that result in overloads must be considered. This is done by adding new security constraints as user cuts.

3.2. Adding N-1 Security Constraints to the UC Problem

The addition of N-1 security constraints to the UC problem is done by means of user cuts as described below (see Figure 2).

• Step 0: read system data.
• Step 1: set the Security-Constraint Recorder $SC{R}_{l,k}\left(t\right)$ to zero as indicated in Equation (34). This with the aim of only accounting for the normal operation state and excluding the security constraints (given by Equation (33) in the first iteration of the algorithm.

  $$SC{R}_{l,k}\left(t\right)=0\forall l\le L,k\le K,t\le T$$

  (34)
• Step 2: solve the model given by Equations (9) to (25) and (30) to (32). Additionally, set the parameter $O{P}_{\mathit{l},\mathit{k}}\left(t\right)$ to zero, which will store the overloads of every transmission line l, under every contingency k in every period of time t.
• Step 3: Estimate post-contingency power flows ${\widehat{F}}_{\mathit{l},\mathit{k}}\left(t\right)$ as indicated in Equation (35), using the optimal power flows $F_l^{*}\left(t\right)$ and $F_k^{*}\left(t\right)$ prior to the contingencies.

  $${\widehat{F}}_{l,k}\left(t\right)=F_l^{*}\left(t\right)+{\overline{LODF}}_{l,k}·F_k^{*}\left(t\right)\forall t\le T,l\le L,k\le K$$

  (35)
• Step 4: verify post-contingency power flow limits in every line l for every period of time t, under every contingency k. If there is an overload in line l, for a contingency k, in the period of time t, assign a value of 1 in the corresponding position of $SC{R}_{\mathit{l},\mathit{k}}\left(t\right)$, as indicated in Equation (36).

  $$\mathrm{If}\left|{\widehat{F}}_{l,k}\left(t\right)\right|\ge F_l^{\max }·TCF\to SC{R}_{l,k}\left(t\right)=1\forall t\le T,l\le L,k\le K$$

  (36)
  For those lines presenting overloads, the excess value is stored in the Overload Parameter $O{P}_{\mathit{l},\mathit{k}}\left(t\right)$. If there is not an overload in line l, under contingency k in the period of time t the corresponding position of $O{P}_{\mathit{l},k}\left(t\right)$ is set to zero as indicated in Equation (37). The sum over the sets of periods, lines and contingencies yields the total overload ($TO$) of the system as indicated by Equation (38).

  $$O{P}_{l,k}\left(t\right)=\left\{\begin{array}{cc}\left|{\widehat{F}}_{l,k}\left(t\right)\right|-F_l^{\max }·TCF& \mathrm{If}\left|{\widehat{F}}_{l,k}\left(t\right)\right|\ge F_l^{max}·TCF\\ 0& \mathrm{If}\left|{\widehat{F}}_{l,k}\left(t\right)\right|<F_l^{\max }·TCF\end{array}\right.\forall t\le T,l\le L,k\le K$$

  (37)
• Step 5: compute the total overload ($TO$) as indicated in Equation (38).

  $$TO=\sum _{l,k,t}O{P}_{l,k}\left(t\right)$$

  (38)
• Step 6: check convergence verifying if $TO$ is lower than a given tolerance ($tol$). If it is true, stop the algorithm and report the solution. Otherwise, return to Step 2 introducing user cuts by adding new security constraints through Equation (33). This is done with the values of l, k, and t for which $\left|{\widehat{F}}_{l,k}\left(t\right)\right|\ge F_l^{\max }$; which in turn correspond to the positions where $SC{R}_{l,k}\left(t\right)=1$.

3.3. Identification of Vulnerable Lines and Critical Contingencies

Using the information stored in $SC{R}_{l,k}\left(t\right)$ it is possible to identify the most vulnerable lines and critical contingencies. For example, adding $SC{R}_{l,k}\left(t\right)$ over t and k as indicated in Equation (39) yields $L_l^v$; this is a vector that contains the number of times each line is overloaded due to every contingency in each period of time t. Thus, $L_l^v$ provides information regarding the most vulnerable lines of the system.

$$\sum _{t,k}SC{R}_{l,k}\left(t\right)=L_l^v\forall l\le L$$

(39)

The identification of the most critical contingencies (in terms of the number of overloads they cause) is obtained by adding $SC{R}_{l,k}\left(t\right)$ over t and l as indicated in Equation (40). In this case, $L_k^s$ is a vector that contains the number of lines that are overloaded due to a given contingency k over the set t. In consequence, $L_k^s$ identifies the most critical contingencies of the system.

$$\sum _{t,l}SC{R}_{l,k}\left(t\right)=L_k^s\forall k\le K$$

(40)

Finally, it is possible to obtain a mapping of contingencies and overloads adding $SC{R}_{l,k}\left(t\right)$ over t. In this case, $L_{l,k}^c$ is a matrix that maps every contingency with every line overloaded, permitting identification of which contingencies impact which lines. This information is valuable to system planners when deciding over reinforcements on the network or eventual expansion plans.

$$\sum _{t}SC{R}_{l,k}\left(t\right)=L_{l,k}^c\forall k\le K\forall l\le L$$

(41)

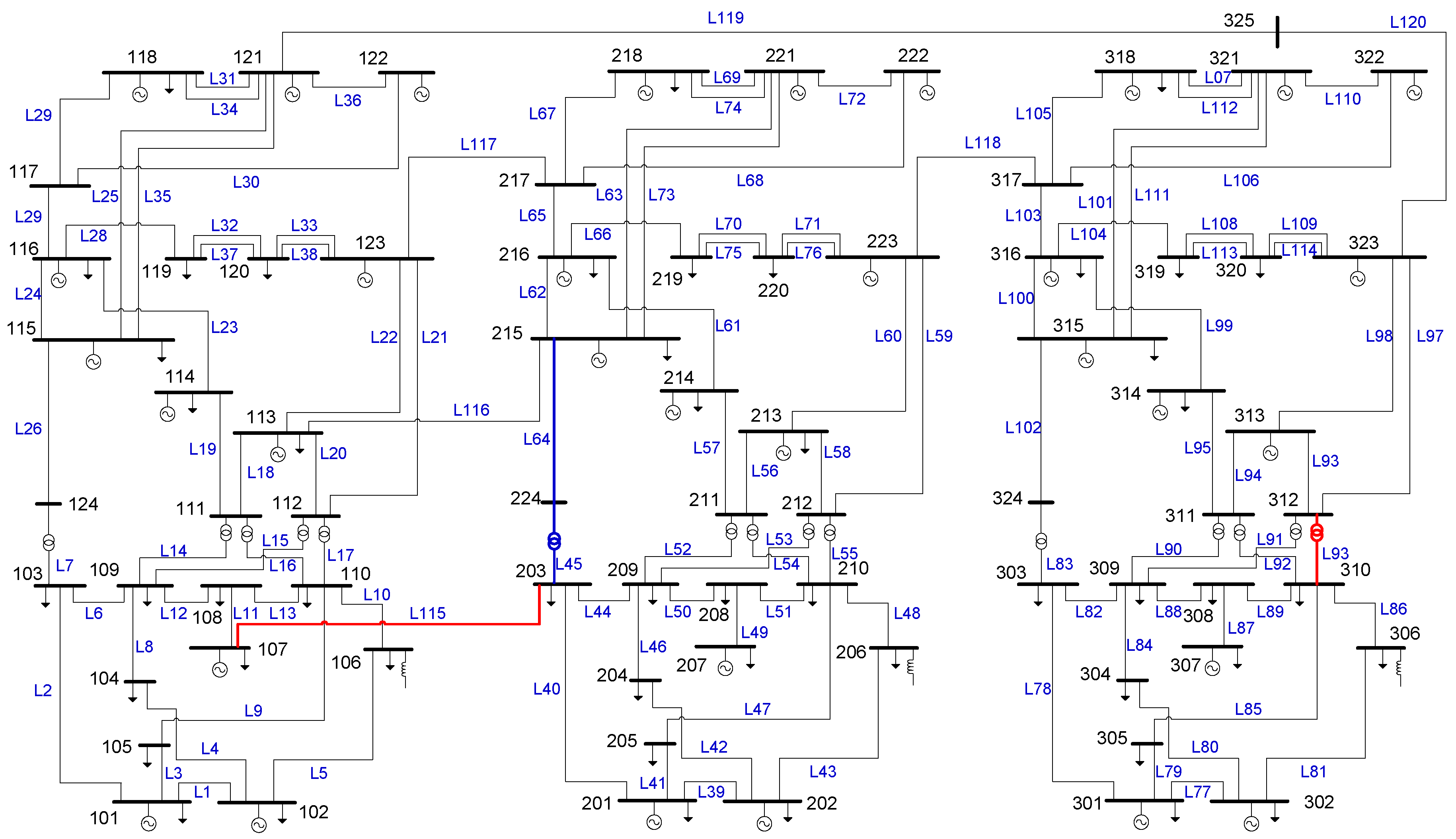
4. Tests and Results

To show the applicability of the proposed modelling approach several tests were performed using the IEEE RTS-96 for a time horizon of 24 h. This power system is made of 73 buses, 120 transmission lines, 96 thermal generators, and 51 loads that add up a maximum demand of 7539 MW. Figure 3 depicts the power system under study. Information regarding initial conditions of generators is necessary to enforce ramping constraints as well as minimum up/down time constraints denoted by Equations (19)–(21) and (16)–(18), respectively. Cost data of generators and their initial conditions are presented in

Table A1. Generator cost data.

Unit	Range	kib	Range	kib	Range	kib
Type	(MW)	($/MW)	(MW)	($/MW)	(MW)	($/MW)
1	5.4–7.6	29.453	7.6–9.8	30.120	9.8–12	30.856
2	8–12	28.967	12–16	29.243	16–20	29.703
3	26–34	28.313	34–42	29.256	43–50	30.498
4	40–52	18.423	52–64	19.228	64–76	20.102
5	40–60	17.590	60–80	18.280	80–100	18.966
6	54.24–87.83	23.810	87.83–121.41	24.525	121.41–155	25.240
7	104–135	17.193	135–166	17.708	166–197	18.225
8	140–210	26.213	210–280	26.708	280–350	27.200
9	100–200	6.961	200–300	7.230	300–400	7.499

and

Table A2. Initial conditions of generators.

G	On/off	Init	G	On/off	Init	G	On/off	Init
1	1	20	33	8	20	65	900	20
2	400	20	34	89	20	66	90	20
3	220	70	35	66	70	67	789	70
4	2	0	36	66	0	68	456	0
5	17	0	37	66	0	69	375	0
6	4	0	38	66	0	70	375	0
7	66	0	39	66	0	71	170	0
8	33	0	40	1	0	72	170	0
9	11	100	41	1	100	73	170	100
10	2	90	42	56	90	74	800	90
11	2	80	43	56	80	75	2500	80
12	2	177	44	56	177	76	2500	177
13	2	155	45	56	155	77	2500	155
14	2	0	46	56	0	78	2500	0
15	6	12	47	56	12	79	1000	12
16	7	12	48	56	12	80	203	12
17	8	12	49	98	12	81	600	12
18	9	0	50	124	0	82	46	0
19	5	0	51	1000	0	83	236	0
20	8	134	52	1000	134	84	236	134
21	8	123	53	1000	123	85	64	123
22	8	0	54	50	0	86	6	0
23	8	377	55	50	377	87	8	377
24	8	47	56	90	47	88	90	47
25	8	48	57	900	48	89	5	48
26	8	0	58	900	0	90	6	0
27	8	0	59	900	0	91	7	0
28	8	50	60	900	50	92	8	50
29	8	50	61	900	50	93	9	50
30	8	150	62	900	150	94	7	150
31	8	0	63	900	0	95	66	0
32	8	0	64	900	0	96	55	0

, respectively. The system data and classic UC model used in this paper as starting point can be found in [45]. Furthermore, data and models are available at GitHub [47].

Three different formulations as described in

Table 1. Formulations of the SCUC problem.

Formulation	Description
A	Conventional network formulation given by Equations (9)–(29) Contingency constraints computed using LODF (Equation (33))
B	Network formulation using PTDF (Equations (26) to (29) are replaced by Equations (30) to (32) Contingency constraints computed using LODF (Equation (33)
C	Network formulation using PTDF (Equations (26) to (29) are replaced by Equations (30) to (32) Contingency constraints computed using LODF (Equation (33) Implementation of user cuts as described in Section 3.1

were implemented for comparative purposes. Two instances of the problem were considered for all formulations varying line ratings and the gap of relative optimality (inGAP). The inGAP is a user-defined parameter that indicates the grade of optimality (quality of solution) required for the software. The first instance of the problem is solved with an inGAP of 0.001 and a TCF of 1.0 (nominal line ratings); the second one considers an inGAP of 0.005 and a TCF of 0.8 (line rating reduction of 20%). The proposed model was solved using the commercial software of algebraic modelling GAMS version 24.8.5, under CPLEX solver in an 8-core 3.4 GHz Intel Core i7 desktop computer with an 8 GB RAM memory. The results of the simulations are presented in

Table 2. Results obtained for different formulations of the SCUC problem.

Formulation	Objective Function [M$]		Time [s]		inGAP		outGAP
	TCF = 1	TCF = $0.8$	TCF = 1	TCF = $0.8$	TCF = 1	TCF = $0.8$	TCF = 1	TCF = $0.8$
A	$2.6968$	$2.7024$	1220	519	$0.0010$	$0.0050$	$0.00250$	$0.00480$
B	$2.6943$	$2.7041$	1209	345	$0.0010$	$0.0050$	$0.00109$	$0.00490$
C	$2.6940$	$2.7016$	169	321	$0.0010$	$0.0050$	$0.0010$	$0.00430$
B*	$2.6970$	$2.7024$	495	687	$0.00254$	$0.0045$	$0.00254$	$0.00437$

.

4.1. Impact of Linear Sensitivity Factors in the Performance of the SCUC Problem

A comparison of results with formulations A and B is initially presented to illustrate the impact of including LSF within the SCUC formulation. As described in Table 1 formulation A considers a classic network modelling and although it considers LODF to account for contingencies, it does not take into account PTDF to model network constraints. It can be seen in Table 2 that formulations A and B require similar computing time to solve the SCUC problem when using a TCF equal to 1 (formulation A takes 1220 seconds and formulation B 1209). Although the same inGAP was used for both formulations, the outGAP (which is indicative of the quality of the solution reached by the solver) obtained when using formulation B is almost half the one obtained when using formulation A. This means that including LSF to represent network constraints leads to better solutions as can be verified in the first column of Table 2. To illustrate, even more, the superior computational efficiency of formulation B compared to formulation A, an additional simulation with an inGAP of 0.00254, labeled as $B*$ was carried out. Such inGAP is used to basically force the solver to reach a solution with a similar quality as the one already obtained with formulation A. In this case, formulation B* finds such solution in significantly less time (495 seconds). Please note that for obtaining results of similar quality, formulation A takes 1220 seconds while formulation B* takes 495 seconds. This corresponds to a time reduction of nearly 60%. On the other hand, when using a TCF of 0.8 the outGAPs of both formulations are similar (0.00480 for formulation A and 0.00490 for formulation B). However, formulations A takes 519 seconds while formulation B only takes 345 seconds. This indicates a reduction of computational time of 33.5%.

4.2. Impact of User Cuts in the Performance of the SCUC Problem

As described in Table 1 formulation C considers user cuts (described in Section 3.1 and Section 3.2) to account for security constraints. As can be observed in Table 2 for a TCF equal to 1, this formulation takes 169 seconds to solve the SCUC problem. This represents an important time reduction (approximately 86%) when compared with formulations A and B that take 1220 and 1209 seconds to solve the same problem, respectively. Furthermore, the outGAP obtained with formulation C is lower than the ones obtained with formulations A and B. This indicates that the proposed formulation not only improves computational time but also quality of solutions. This last aspect can be verified by comparing the data presented in the second column of Table 2. When a TCF of 0.8 is considered, formulation C also outperforms formulations A, B and $B^{*}$ both in terms of computational time and quality of solutions. As regards computational time, formulation C takes 321 seconds to solve the SCUC problem while formulation A takes 519 seconds. On the other hand, to achieve a solution with a similar quality (see outGAP in the last column of Table 2) formulation B* takes 687 seconds. Consequently, formulation C provides in this case a time reduction of 53.2%.

Table 3. Performance of the SCUC formulation (TCF = 0.8 and inGAP = 0.005).

Iteration	Added Constraints N-1	Elapsed Time of Simulation [s]	Objective Function [M$]
1	-	25	$2.6947$
2	68	66	$2.6986$
3	21	87	$2.6980$
4	7	53	$2.7021$
5	27	57	$2.7025$
6	21	33	$2.7016$
total	144	321	-

presents details of each iteration when using formulation C with an inGAP of 0.005 and TCF = 0.8. The solution to the SCUC problem is found after 6 iterations in 321 seconds. Please note that in the first iteration, normal operation state of the system is solved, that is, security constraints are not considered. However, in the second iteration 68 security constraints are added as user cuts. These correspond to the positions where $SC{R}_{l,k}\left(t\right)=1$. Subsequently, more user cuts are added in every iteration until all post-contingency power flows under every single contingency over all periods of time are within limits. This is achieved with 144 additional constraints. In contrast, classic modelling approaches (formulations A and B) require 13816 additional constraints to account for security in the UC problem. This corresponds to a reduction of 99% in the number of security constraints required to solve the SCUC problem.

4.3. Most Vulnerable Lines and Critical Contingencies

As mentioned in Section 3.3, the proposed approach also allows identification of the most vulnerable lines and critical contingencies over the time horizon under consideration and for every N-1 contingency. Figure 4a presents the most vulnerable lines when the SCUC is solved with TFC = 0.8. It can be observed that the lines labeled as L115 and L93 are overloaded 54 and 11 times, respectively due to every N-1 contingency over the 24h time horizon. These lines are indicated in red in Figure 3. The most critical contingencies are presented in Figure 4b. Please note that the outage of lines labeled as L45 or L64 impacts 22 other lines. These are indicated in blue in Figure 3. Figure 5 presents a mapping of critical contingencies and vulnerable lines. Please note that it is possible to identify which contingencies cause overloads in which lines. For example, the most critical line already identified in Figure 4a presents 54 overloads. This is line L115 indicated in the first position of the x-axis. In this case, 20 of the overloads of line L115 are due to the outage of line L45, another 20 are due to the outage of line L64, and the remaining 12 are caused by outages of lines L119 and L120, each of them contributing with 6 overloads. This information is valuable to the system planner who may decide over future reinforcements of the corridor where line L115 is located to reduce its criticality. Furthermore, the mapping of critical contingencies vs. Vulnerable lines can be used for the assessment of generation and transmission expansion plans on the security of the system operation.

4.4. Scalability Evaluation

To show the robustness and flexibility of the proposed approach, several tests were performed with a larger power system. The new test system was built duplicating the original IEEE RTS-96 depicted in Figure 3. The new buses were labeled following the same pattern as the original IEEE RTS-96 (prefixing numbers 4, 5, and 6 for each subsystem). The two power systems were connected through two double circuits at 220 kV between buses 221 and 612 and 114 and 613; each with a transmission capacity of 500 MW and a reactance of 0.084 pu. The TCF was modified by a factor of 1.6 to avoid infeasibilities when evaluating contingencies of the circuits connecting the two power systems. The equivalent test system is composed of 146 buses, 244 lines, 192 generators, and 102 demand sides.

Table 4. Results obtained for scaled test system.

Formulation	Objective Function [M$]	Time [s]	inGAP	outGAP
B	4.8748	7494.001	0.01	0.00178
C	4.8701	209.687	0.01	0.00100

presents the results with formulations B and C for the new test system. Simulations were performed in an Intel ® Xeon E5 @ 2.40 GHz, 44 cores, and 256 GB memory RAM processor.

According to the results presented in Table 4 formulation C outperforms formulation B in both computation time and quality of the solution found. Formulation C takes approximately 209.7 seconds to find a solution, while formulation B takes 7494 seconds. Please note that in this case a time reduction of 97.2% is achieved when using formulation C. For comparative purposes, the same inGAP was used in both formulations. However, the outGAP of formulation C turned out to be lower than the one reached with formulation B. This might be attributable to the fact that formulation C is more compact than formulation B. The quality of solutions can be verified in the second column of Table 4. It is worth mentioning that for this particular power system, formulation B must deal with a set of 1,446,480 constraints associated with the N-1 criterion, while implementing user cuts only requires 16,511 additional N-1 constraints. This represents a reduction of 98.85% of the number of N-1 constraints when using formulation C. Additional simulations were run using a desktop computer which characteristics are previously described in Section 4. In this case, the solution found with formulation C, takes approximately 15 minutes reaching an objective function of 4.8731 MUSD and an outGAP of 0.00158; however, the same simulation could not be performed with formulation B due to lack of RAM memory. Therefore, an additional decomposition algorithm might be necessary to run formulation B in a desktop computer, which is not required when using formulation C. This further emphasizes the advantage of the proposed approach.

5. Conclusions

This paper presented a new modelling approach of the SCUC problem based on PTDF and LODF LSF and user cuts. On the one hand PTDF are used to model power injection balance constraints, avoiding the use of voltage angles and reducing the number of variables and constraints of the UC formulation. On the other hand, LODF are used to evaluate post-contingency power flows and check overloads quickly and reliably. Finally, user cuts are iteratively added to the base problem to account for security constraints. This is because most security constraints of the SCUC problem are not binding in the optimal solution.

The proposed model uses as starting point a classic UC formulation. Subsequently, security constraints are taken into account through an array that registers whether a given contingency in a given time produces overloads on other lines. If this happens, new security constraints are added as user cut to the current problem. This is done iteratively until no overloads are produced by any contingency.

Several tests performed on a benchmark IEEE power system evidenced the robustness and applicability of the proposed model. The main advantage of considering LSF and user cuts to model the SCUC problem lies on the reduction of computing time. Furthermore, better solutions are found with the proposed model. Results show that time reduction ranges from 53% to 97% when compared with a classic formulation set to reach a solution of similar quality (same inGAP parameters). A scalability test showed that such reduction of computing time increases with the size of the test system. Moreover, decomposition techniques as BD or LR are not needed to efficiently address the SCUC problem.

An additional advantage of the proposed methodology lies on its flexibility and ease of implementation. The proposed approach to deal with the SCUC problem was devised to be solver-independent. Therefore, unlike other research works reported in the specialized literature, it does not depend on built-in functions or callbacks.

A value-added element of the methodology is the identification of the most critical lines and most severe contingencies. The mapping of critical contingencies vs. vulnerable lines can be used for the assessment of generation and transmission expansion plans on the security of the system operation. Finally, the tight and compact modelling proposed in this paper can be used in a future work as a basis for other studies such as the integration of renewable energy resources within a SCUC problem.